Para el topólogo, un nudo es una curva continua, cerrada y sin puntos dobles. Esta curva está situada en un espacio de tres dimensiones y se admite que pueda ser deformada, estirada, comprimida, aunque está “prohibido” hacerle cortes. Cuando se puede, a través de diversas manipulaciones, se pasa de un nudo a otro y se dice que son equivalentes. Claro que, algunos se abstraen en cuestiones con otras, al parecer, no relacionadas.

Un viejo amigo bromeaba diciendo que el Andante en do menor de la Sinfonía Concertante de Mozart conseguía devolverle a su intimidad anímica de partida, y que por eso, en su opinión, plasmaba de forma inefable el tiempo cíclico, o mejor aún, una CTC (“curva de género de tiempo cerrada”). Y transcurridos los doce minutos que dura ese movimiento, volvíamos a escucharlo una vez más. Mientras, discutíamossin cesar sobre el tiempo.

                                                       No es bueno perder la perspectiva

Hay un tiempo para cada cosa. Un tiempo para soñar, inconmensurable, un tiempo para vivir, siempre corto, un tiempo para filosofar, misterioso,…, y un tiempo para la ciencia, sujeto a número.

Me gustaría empezar definiendo el tiempo, pero no sé. Sesudos pensadores, como Platón y Aristóteles, lo ensayaron con brillantez. El tiempo es una imagen móvil de la eternidad. Esta imagen es eterna, pero se mueve según número, dirá Platón en el TIMEO. El tiempo es el número de movimiento según el antes y el después…El tiempo no es movimiento, sino movimiento en tanto en cuanto admite enumeración. El tiempo es una especie de número. El tiempo es obviamente aquello que se cuenta, no aquello con lo cual contamos, escribirá Aristóteles en su FÍSICA.

           Alguna vez, en simbiosis con la Naturaleza, podemos sentir como se ha parado el tiempo

Son definiciones muy sugestivas, aunque teñidas de circularidad: movimiento en el tiempo, tiempo a través del movimiento. Agustín de Hipona vio esto claramente. Célebre es asimismo su declaración: Si nemo a me quaerat, scio; si quaerenti explicari velim, nescio (CONFESIONES). En uno de los análisis más penetrantes del tema, sugirió Agustín la mente como fuente de tiempo: En ti es, mente mía, donde mido los tiempos.

Time is what happens when nothing else happens, afirma Feynman; para a continuación advertir que toda definición del tiempo es necesariamente circular, y que lo importante no es decir qué es el tiempo, sino decir cómo se mide lo que llamamos tiempo. En su enciclopédico tratado sobre la gravitación, Misner, Thorne y Wheeler nos recuerdan de forma sencilla y profunda lo que toda medida del tiempo físico debe cumplir: Time is defined so that motion looks simple.

El tiempo es un concepto inventado por el hombre para ordenar, primero, sus sensaciones y actos, y luego, los fenómenos. Decían los escolásticos: Tempus est ens rationis cum fundamento in re. La primera unidad natural debió ser el día, por la ciclidad conspicua de las salidas del Sol. Los grandes avances científicos y tecnológicos a lo largo de los siglos han estado vinculados a los adelantos en la precisión con que se ha ido midiendo el tiempo. Hoy disponemos de relojes que aseguran un segundo en 20 millones de años, y el paso de la femtoquímica a la attofísica empieza a ser una realidad.

No pocas veces nos podemos ver perdidos en la vorágina de lo que llamamos tiempo, algo tan enorme que, en realidad, no sabemos lo que es. No lo hemos llegado a comprender, y, por si fuero poco, tampoco sabemos, si en realidad existe.

El tiempo antes de Einstein.

La física nació en torno al tiempo. Las regularidades en los ciclos astrales permitieron al acierto en las predicciones apoyadas en esta periodicidad, y con ello despertó sin duda la confianza del hombre en la racionalidad, inclinándole a escoger el cosmos frente al caos.

Breve historia de la medida del tiempo

La longitud de las sombras fue uno de los primeros métodos usados para fijar las horas. En el Museo Egipcio de Berlín hay un fragmento de piedra que posiblemente sea de un reloj de sol de alrededor de 1500 a.C. Los babilonios desarrollaron los relojes de sol, y se dice que el astrónomo Anaximandro de Mileto los introdujo en Grecia en el siglo VI a.C.

En el siglo II a C, Eratóstenes, de la biblioteca de Alejandría, concibió y llevó a cabo la primera medida de las dimensiones de la Tierra de la que se tiene noticia. En el Año Internacional de la Astronomía, una de las actividades que se llevaron a cabo fue, precisamente averiguar el radio terrestre por el mismo método.

Aparte de relojes de sol, en la antigüedad se usaron también relojes de arena, de agua, cirios y lámparas de aceite graduadas.

En la segunda mitad del siglo XIII aparecen los primeros relojes mecánicos. Su precisión era muy baja (10-20%). En el XIV se mejoran, con el invento del escape de rueda catalina, y ya se alcanzan precisiones de 20 a 30 minutos por día (1-2%). Por allá al año 1345 se empieza a dividir las horas en minutos y segundos.

El tiempo físico asoma en el siglo XIV, en el Merton College Oxford y luego en la Universidad de París, con Oresme. Se representa en una línea horizontal, mientras en vertical se disponen las cualidades variables. Son los primeros gráficos de función (en este caso, función del tiempo). La cinemática celeste brinda un buen reloj a través de la segunda ley de Kepler, midiendo tiempos mediante áreas. La ley armónica de Kepler permitirá medirlos a través de longitudes. Galileo desarrolló la cinemática terrestre, y sugirió el reloj de péndulo. A Huygens debemos la técnica de medida del tiempo que ha llegado a nuestros días, y que suministró relojes más precisos y transportables mediante volantes oscilatorios acoplados a resortes de calidad.

Diseño del reloj de péndulo de Huygens, 1656 (imagen de dominio público).

La importancia, no sólo científica sino económica, de disponer de relojes precisos y estables, queda reflejada en el premio ofrecido por el gobierno inglés de la reina Ana en 1714, que dispuso that a reward be settled by Parliament upon such person o persons as shall discover a more certain and practicable method of ascertainig longitude that any yet in practice. La recompensa era de 20, 000 libras para el que presentara un cronómetro capaz de determinar la longitud con error menor de 30´ de arco al término de un viaje a las Indias occidentales, equivalente a mantener el tiempo con error menor de 2 minutos tras seis semanas de viaje. Se la llevó casi medio siglo después el relojero británico John Harrison (1693-1776), con un reloj, conocido como H4, que incorporaba correcciones por variación en la temperatura, y que en un primer viaje de 81 días desde Porstmouth a Puerto Real (Jamaica) en 1761-62 se retrasó 5 s, esto es, de precisión 10⁻⁶ (10; 44).

Después se pasó a los de diapasón, de aquí a los de cuarzo, y hoy los atómicos ofrecen precisiones desde 10⁻¹² – 10⁻¹⁵ (Cs) hasta 10⁻¹⁶ (máser de H).

Una red de relojes atómicos de cesio, sincronizados mediante ondas de radio, velan actualmente por la exactitud de la hora sobre el planeta. Como señala Davies (10), ya no nos sirve como cronómetro el giro de la Tierra alrededor de su eje. Aunque durante siglos ha sido este viejo trompo un magnífico reloj de referencia, la falta de uniformidad de su giro (las mareas, por ejemplo, lo frenan incesantemente y alargan con ello el día en un par de milésimas de segundo por siglo, perceptible para los finos cronómetros actuales), y otras desviaciones estacionales, cuantitativamente similares a estos retrasos seculares, pero irregulares y de signo variable, son circunstancias que en conjunto obligan a añadir al tiempo civil un segundo intercalar cada uno o dos años (el último lo fue el 1 de enero de 1999, a las 0 horas) con el fin de remediar la asincronía entre los tiempos atómicos y los días astronómicos. El día no tiene 86 400 s justos (donde el segundo se define como la duración de 9 192 631 770 períodos de una determinada vibración de los átomos de Cs. Hoy la tecnología alcanza precisiones fabulosas: relojes que en treinta millones de años se desviarían a lo sumo en un diminuto segundo, como el NIST-F1 (Boulder, Colorado).

Por norma general y para mayor exactitud del sistema, dentro del campo visual de cualquier receptor GPS siempre hay por lo menos 8 satélites presentes. Cada uno de esos satélites mide 5 m de largo y pesa 860 kg . La energía eléctrica que requieren para su funcionamiento la adquieren a partir de dos paneles compuestos de celdas solares adosadas a sus costados. Están equipados con un transmisor de señales codificadas de alta frecuencia, un sistema de computación y un reloj atómico de cesio, tan exacto que solamente se atrasa un segundo cada 30 mil años.

La posición que ocupan los satélites en sus respectivas órbitas facilita que el receptor GPS reciba, de forma constante y simultánea, las señales de por lo menos 6 u 8 de ellos, independientemente del sitio donde nos encontremos situado. Mientras más señales capte el receptor GPS, más precisión tendrá para determinar las coordenadas donde se encuentra situado.

Incluso hay relojes de pulsera comerciales (receptores de señales de radio) con precisión de un segundo por millón de años garantizada por un reloj atómico en una lejana estación. La naturaleza de altísima precisión: la estabilidad del púlsar binario b1855+09 puede ser de unas partes en 10¹⁵ o incluso mejor.

El tiempo en Newton:

En los PRINCIPIA, Newton empieza con una renuncia a definir el tiempo: El tiempo, el espacio, el lugar y el movimiento son de todos bien conocidos. Y no los defino. Pero digo que el vulgo no concibe esas cantidades más que por su relación a cosas sensibles. Para evitar ciertos prejuicios que de aquí se originan, es conveniente distinguirlas en absolutas y relativas, verdaderas y aparentes, matemáticas y vulgares.

A continuación, sin embargo, Newton se arrepiente de su primer impulso y aclara: El tiempo absoluto, verdadero y matemático, de suyo y por su propia naturaleza fluye uniformemente sin relación a nada externo y se llama también duración: el tiempo relativo, aparente y vulgar es cualquier medida sensible y externa (exacta o no uniforme) de la duración por medio del movimiento y se usa vulgarmente en lugar del tiempo verdadero: tal como la hora, el día, el mes, el año.

¿Qué significa que el tiempo fluye? ¿Qué el tiempo “se mueve en el tiempo”? De nuevo la pescadilla mordiéndose la cola. El absolutismo del tiempo newtoniano recibió encendidas críticas. Leibniz opuso su idea de espacio y tiempos puramente relativos, el primero como un orden de coexistencia, el segundo como un orden de sucesiones de las cosas; ambos, espacio y tiempo, son phœnomena bene fundata. Los argumentos dinámicos con que Newton arropa su tesis de la naturaleza absoluta de la rotación y con ello la de un espacio absoluto, apoyo posterior para el tiempo absoluto, también hallan fuertes objeciones. Para Berkeley esas razones de Newton lo único que muestran es la importancia del giro respecto de las masas lejanas del Universo y no respecto de un espacio absoluto, que él no acepta. Ernst Mach, en la segunda mitad del XIX, insistirá decididamente en este punto de vista, y desde su positivismo acosará los absolutos newtonianos. De “medieval”, “no científico”, “metafísico”, tilda Mach a Newton: No tenemos derecho a hablar de un tiempo “absoluto”: de un tiempo independiente de todo cambio. Tal tiempo absoluto no puede medirse por comparación con ningún movimiento; por tanto no tiene valor práctico ni científico, y nadie tiene derecho a decir que sabe algo de él. Es una concepción metafísica vana.

El tiempo en Einstein:

El tiempo newtoniano, absoluto, el nos es familiar, tuvo que dejar paso al tiempo einsteniano, mutable y relativo, con tantos “ahora” por suceso cuantos estados de movimiento mutuo imaginemos.

El tercero de los trabajo enviados por Albert Einstein (AE) en su Annus Mirabilis de 1905 a Annalen der Physik lleva por título “Zur Elektrodynamik Bewegter Körper” (“Sobre la electrodinámica de los cuerpos en movimiento”). Junto con el quinto, titulado “Ist der Trägheit eines Körpers von seinem Energieinhalt abhängig?” (“¿Depende la inercia de un cuerpo de su contenido de energía?”), constituyen lo que hoy se llama TEORÍA ESPECIAL DE LA RELATIVIDAD.

Da A.E. un par de razones para justificar su tercer trabajo:

1. La insatisfacción que le produce la asimetría en la descripción maxwelliana de los fenómenos electromagnéticos: la acción entre un conductor y un imán depende solo del movimiento relativo entre ambos, pero la teoría de Maxwell distingue entre el caso de conductor en reposo y el caso de imán en reposo: a) En el primer caso el campo magnético móvil engendra un campo eléctrico, con una energía determinada, que a su vez produce corrientes en el conductor en reposo. b) En el segundo caso, no se produce ningún campo electrónico, sino una fuerza electromotriz en el conductor, sin energía asociada, que engendra una corriente como en el caso anterior.
2. La incapacidad de la óptica y del electromagnetismo (EM) para detectar el movimiento respecto del lichtmedium, es decir, de un inercial privilegiado. Esto le sugiere que la óptica y el EM tienen las mismas ecuaciones en todos los inerciales (sistemas en los que las leyes de la mecánica de Newton son las mismas). Y AE eleva esto a un principio, que llama “Prinzip der Relativität”, y le añade un compañero, aparentemente incompatible con él: “La velocidad de la luz en vacío es siempre la misma, con independencia del estado de movimiento del cuerpo emisor”.

¿Será ese de arriba el rayo de luz de Einstein, o, por el contrario, será un asteroide que se nos viene encima?

Siendo todavía muy joven, en 1895-1896, ya le preocupaba el EM y la luz, como recordaba en 1955: “Si persiguiéramos a la velocidad de la luz un rayo de luz, veríamos una onda independiente del tiempo. ¡Tal cosa, sin embargo, no existe! Este fue el primer experimento mental, infantil, en relación con la teoría especial de la relatividad”.

Este tercer trabajo de Einstein en 1905 no contiene ninguna referencia a otros trabajos, ni suyos ni de otros (como Lorentz o Poincaré).

Consciente de que su postulado de la constancia de la velocidad de la luz choca frontalmente con la ley galileana de adición de velocidades, Albert Einstein revisa los cimientos de la Física, empezando por definir físicamente y con sumo cuidado el concepto de Gleichzeitigkeit o simultaneidad entre sucesos. Considera un sistema inercial, para el que supone válida la geometría euclidiana para calcular distancias entre objetos estacionarios a través de sus coordenadas respecto de sus ejes cartesianos. Si A, B son dos observadores estacionarios, provistos de relojes iguales, y A (B) manda una señal luminosa a B (A), quien la devuelve sin tardanza a A (B), diremos que el reloj de A está sincronizado con el reloj de B si

t(B) – t(A) = t’(A) – t(B),

donde t(A) es el tiempo marcado por el reloj de A cuando envía la señal a B, t(B) lo que marca el reloj de B al llegarle la señal de A y reemitirla, y t’(A) la lectura del reloj de A al recibir la devolución de B.

No parece el mejor método para medir la velocidad de la luz, el empleado por Galileo. Claro que, en aquellos tiempos…¿Qué se podía hacer?

Supone Albert Einstein que esta definición no lleva a contradicciones, que es en principio posible entre cualquier par de observadores estacionarios en el inercial, y que la relación de sincronización anterior es de equivalencia: Si A está sincronizada con B, también B lo está con A, y si además B lo está con C, también A y C lo están. A esto le siguen ecuaciones que quiero obviar para no dar complejidad al trabajo.

No existe “el” presente

Pasa Albert Einstein a enunciar con precisión el principio de relatividad y el postulado de la constancia de la velocidad de la luz en el vacío:

1. Las leyes que rigen los cambios de los sistemas físicos son las mismas en todos los inerciales.
2. Todo rayo de luz se mueve en cualquier inercial con una misma velocidad, c, independientemente del movimiento de su fuente.

Como consecuencia, demuestra que el concepto de sincronía, y por ende de simultaneidad, es relativo, no absoluto. La noción de “presente”, “ahora” o cualquier instante determinado depende del referencial inercial.

           Algunos incluso hablaron de ernegía taquiónica

¿Más rápido que la luz?

¿Existen partículas que se muevan con velocidad superior a la de la luz? Sí; por ejemplo, cualquier partícula que lleve en agua, a temperatura entre 0 y 50 ºC, una velocidad ν > c / n, n = 1.3, irá más deprisa en ese medio que los fotones del espectro visible. Lo mismo ocurre con la mayoría de los rayos cósmicos que llegan a la atmósfera; son superlumínicos en relación con la velocidad de la luz en el aire. Precisamente en esta posibilidad de rebasar la velocidad de la luz en un medio reside el efecto Cerenkov.

Lo que no se conocen son taquiones, o partículas que se muevan más deprisa que la luz en el vacío. Si existieran, podrían utilizarse para mandar información al pasado. Violando el orden causa-efecto. Por ello se “decreta” su inexistencia.

En fin, que la velocidad de la luz en el vacío, al menos que sepamos, es infranqueable. Es un límite impuesto por la Naturaleza al que habrá que vencer, no superándolo (que no se puede), sino mediante una artimaña física inteligente que logre burlar dicho límite.

Aparte de algún que otro añadido, el artículo (parcialmente expuesto aquí -se obviaron partes complejas), es del Físico de la Universidad Complutense D. Alberto Galindo Tixaire. Fue publicado en el Volumen 19, número 1 de la Revista Española de Física en 2005 Año Mundial de la Física

En realidad, un Homenaje a Einstein por haber pasado más de un siglo desde aquel acontecimiento memorable de la Relatividad Especial en el año 1.905 y estar a punto de cumplirse otro siglo desde su relatividad general de 1905. Dos acontecimientos que marcaron el camino de la Física y la Cosmología. Precisamente ahora, se cumplen los 100 años desde que Einstein diera al mundo la segunda parte de su Teoría.

emilio silvera

 

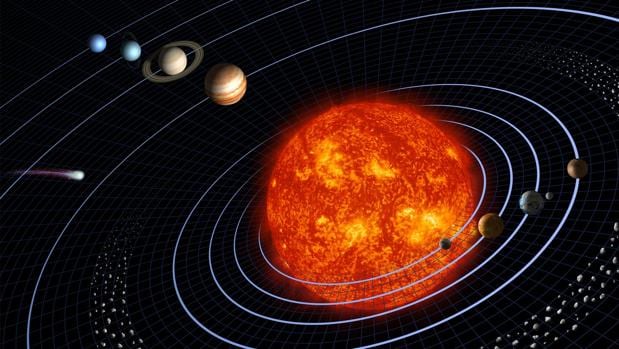
Esquema clásico del Sistema Solar. Si las distancias estuvieran a escala, no podría verse ni Mercurio, el primero de los planetas – NASA/JP

Los esquemas y dibujos son muy engañosos. En realidad las distancias son enormes en comparación con el tamaño del Sol y los planetas

 

 

 

El ser humano tiene una mente maravillosa que le permite imaginar y contar historias acerca de lo que ve y conoce. Pero esa fantástica capacidad, gracias a la cual crea la cultura, la ciencia o la literatura, a veces le hace perder contacto con la realidad que tiene delante de los ojos: pareciera que los esquemas, los conceptos y las palabras se interponen entre lo que realmente puede verse. Por eso, si alguien le pide que piense en un árbol, probablemente recordará un dibujo de su infancia, en el que un árbol de copa redonda y verde tiene un tronco claramente marrón, cosa que poco tiene que ver con cualquier árbol real (puede hacer la prueba).

De la misma forma, muchas personas tienen una imagen errónea del Sistema Solar. Cualquiera recuerda el esquema que aprende en el colegio y que muestra los ocho planetas apilados cerca del Sol, perfectamente colocados y nítidos. El problema es que este esquema no hace justicia a lo que realmente es el Sistema Solar.

El Sistema Solar está vacío

 

 

 

 

El principal problema es que nuestro vecindario está prácticamente vacío. Los planetas son extremadamente pequeños en comparación con las distancias que les separan. Así que si quisiéramos construir un esquema fidedigno y que cupiera en una pantalla tendríamos que dibujar el Sol y los planetas a una escala microscópica.

Si el Sol midiera 1,5 metros de diámetro, la Tierra sería tan grande como una canica y estaría a una distancia de la estrella de 176 metros

 

 

 

En la web Nineplanets.org se muestra un esquema con los tamaños reales de las órbitas, primero en el Sistema Solar interior (hasta Marte), y después en la zona exterior.

 

 

 

 

Comparación de tamaño de las órbitas en el Sistema Solar interior (ni el Sol ni los planetas están a escala) – Nineplanets.org/overview

 

 

Sin embargo, lo cierto es que incluso los píxeles que representan los planetas en la imagen de arriba son demasiado grandes para el tamaño que les correspondería. En todo caso llama la atención apreciar que el Sistema Solar interior está mucho más compactado que el exterior, donde las órbitas son cada vez más extensas.

 

 

 

 

 

Comparación de tamaño de las órbitas en el Sistema Solar exterior (los planetas no están a escala) – Nineplanets.org/overview

 

 

Otra opción que tenemos para apreciar el tamaño real del Sistema Solar es alargar el esquema: en esta web puede verse una representación «tediosamente precisa» de la escala real del nuestro sistema planetario. Necesitará bastante paciencia para llegar hasta Plutón si viaja a la velocidad de la luz (abajo a la derecha hay un botón para hacerlo). También puede saltarse las leyes de la física y simplemente hacer click en los símbolos de los planetas, arriba, en la pantalla. Eso sí, Einstein no lo vería con buenos ojos. (Aquí también pueden apreciarse las distancias, pero no los objetos, a escala).

Otra opción es cambiar la escala y buscar una llanura de varios kilómetros de extensión donde colocar modelos a medida del Sol y los planetas.

 

 

 

 

Si el Sol midiera 1,5 metros de diámetro, la Tierra estaría a 176 metros y sería tan grande como una canica – Captura de Youtube/To Scale

 

 

En 2015, un grupo de cineastas lo hizo. Rodó una película corta en la que colocaban un Sistema Solar en miniatura en el desierto de Black Rock, en Nevada (EE.UU.). Construyeron un Sol con un disco de 1,5 metros de diámetro, que iluminaron con un foco, y modelos a escala de cada planeta. En esas dimensiones, la Tierra es una canica y Júpiter, el mayor planeta de todo el Sistema Solar, un poco más pequeño que una pelota de fútbol.

 

 

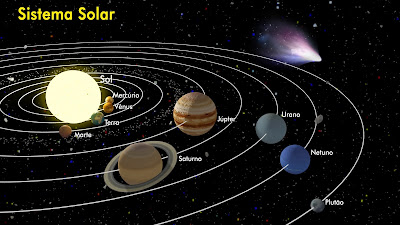
La falsa imagen que tenemos de nuestro Sistema solar

 

 

Acto seguido, mostraron cuáles serían las distancias medias de los planetas a esa escala. Los resultados son espectaculares. Si el Sol midiera 1,5 metros de diámetro (y no 1.393.684 kilómetros), Mercurio estaría a una distancia de 68 metros (más que una piscina olímpica). Venus quedaría a 120 y la Tierra (tan grande como una canica) a 176 metros. A Marte podríamos llegar caminando, después de recorrer 268 metros.

 

 

 

 

Si el Sol midiera 1,5 metros de diámetro, Júpiter sería más pequeño que una pelota de fútbol y estaría a 920 metros de la estrella (al fondo) – Captura de Youtube/To Scale

 

 

Para llegar a Júpiter ya se podría pensar en coger una bicicleta. El planeta más gigante del Sistema Solar (él solo acumula el 70 por ciento de la masa de todos los planetas juntos), está a 920 metros. Desde esa distancia, el disco iluminado que representa el Sol es un punto en la lejanía. Saturno, el elegante mundo de los anillos, queda a 1.700 metros. Las afueras del Sistema Solar ya se encuentran a la distancia de una caminata: Urano está a 3.400 metros y Neptuno a 5.600. Desde allí, ese Sol hecho de un disco de 1,5 metros es absolutamente imposible de ver.

Un sistema interior y otro exterior

 

 

 

 

Si llevamos las distancias a su dimensión real, pero queremos evitar hablar de millones de kilómetros, podemos contar el tiempo que necesita un rayo de luz, a la máxima velocidad posible en todo el Universo, para recorrer la distancia entre el Sol y los planetas.

Así, Mercurio está a 3,2 minutos luz del Sol, Venus a seis, la Tierra a 8,3 y Marte a 12,7. Pero más allá, los planetas gaseosos dan un gran salto: Júpiter se encuentra a 43,3 minutos luz, Saturno a 79,7, Urano a 159,9, Neptuno a 250,3 y Plutón, el planeta enano, a 328,3 minutos luz.

Esto ya nos indica que en ese esquema escolar del Sistema Solar no se refleja realmente la diversidad de sus planetas, porque vemos que los planetas rocosos forman una pequeña isla dentro de la zona más extensa del vecindario planetario.

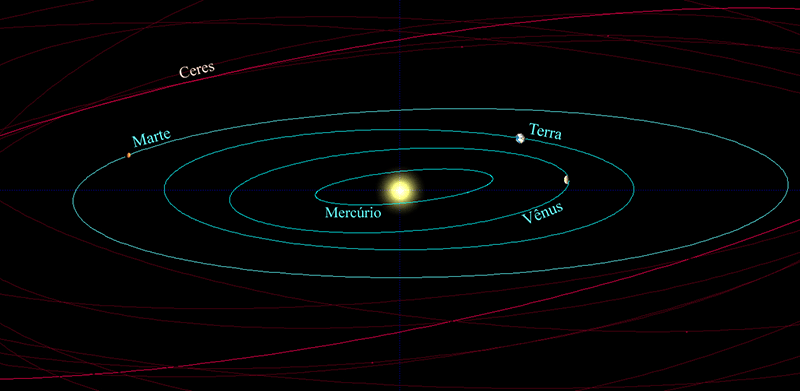
De hecho en realidad existe un sistema interior formado por planetas hechos de roca y metales. Está rodeado por un cinturón de asteroides que se formó con los objetos rocosos, de esa misma composición, que no «consiguieron» formar ningún planeta, durante el nacimiento del Sistema Solar.

Más allá comienza una zona dispersa en la que están los planetas lejanos que capturaron grandes cantidades de gas y se hicieron enormes. Están compuestos en gran medida por hidrógeno, helio, metano y agua.

A partir de Neptuno comienza una zona completamente distinta, en la que quedó un enorme anillo de objetos helados, parecidos a cometas y entre los que hay también planetas enanos, como Plutón o Eris. Todos ellos han perdurado desde los primeros tiempos del Sistema Solar. A esta región con forma de anillo se la denomina cinturón de Kuiper, y está formado por pequeños objetos ricos en compuestos volátiles congelados, como metano, amoniaco y agua. Esta región se extiende desde la órbita de Neptuno hasta los 415,8 minutos luz.

Más allá, hay evidencias de que existe una zona muy dispersa poblada por pequeños fragmentos, y ya en el límite entre el Sistema Solar y el espacio exterior. Se llama nube de Oort, y se cree que llega hasta los 1,87 años luz.

Sin embargo, lo cierto es que tanto la región situada entre el cinturón de Kuiper y la nube de Oort, como la que se encuentra entre Mercurio y el Sol, son territorios ignotos, en los que se podrían encontrar más objetos.

En todo caso, y al contrario de lo que se ve en los esquemas, no hay que olvidar que el Sistema Solar es mucho más que el Sol y sus ocho planetas clásicos. Por lo que sabemos hasta ahora, hay ocho planetas, cinco planetas enanos (aunque se cree que podría haber cientos en el cinturón de Kuiper). Se ha contado 19 lunas grandes y redondas, 185 más pequeñas, 4.000 cometas y casi 779.000 pequeños objetos, mayores que un asteroide o un cometa pero menores a un planeta enano.

 

Comparativa de tamaños – WP

 

 

 

¿Cómo se mantiene todo unido?

 

 

 

 

En todo caso, si las distancias que separan al Sol de todo lo demás son tan enormes, ¿cómo es posible que todo permanezca unido a la estrella por la fuerza invisible de la gravedad?

El secreto de esta atracción está en un impactante dato: el 99,86 por ciento de la masa del Sistema Solar está en el Sol. Solo el 0,1% está en los planetas.

De esta porción, el 70% está en Júpiter y el 20 en Saturno. Los planetas rocosos (Mercurio, Venus, Tierra y Marte), apenas engloban el 1% de esta cantidad, es decir, el 0,001 % de todo el Sistema Solar.

Gracias a esta enorme desproporción, el Sol es el rey indiscutible. Se calcula que su campo gravitatorio domina frente a la gravedad de otras estrellas hasta una distancia de dos años luz. Este es uno de los límites más claros que muestra el verdadero tamaño del Sistema Solar.