Sep
9
¡Las matemáticas! o, demostración de nuestro ingenio
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Origen de las matemáticas ~
Clasificado en Origen de las matemáticas ~
 Comments (2)
Comments (2)
Alguien nacido en la India y que más tarde, se trasladó a Inglaterra donde se dedicó a la docencia, en cierta ocasión dijo: “Como la cola de un pavo real, como la gema en la cabeza de una serpiente, así están las matemáticas a la cabeza de todo el conocimiento”. Pocos científicios del mundo moderno estarían en desacuerdo con estas palabras. Las matemáticas están presentes (de una u otra manera) en todas las disciplinas del saber y, sin duda, es uno de los mayores logros de la Humanidad.

Nuestra historia tradicional (de Occidente), nos dice que fueron los griegos quienes crearon las matemáticas hacia el año 600 a. C. y que fue la cultura grecorromana la que las elaboró hasta el año 400 d. C., época en la cual esta disciplina cayó en profundo letargo que duraría unos mil años y no despertaría hasta la llegada de la Europa posrenacentista. Sin embargo, hay pruebas abundantes de que las culturas no occidentales realizaron importantes contribuciones a las matemáticas europeas -o, al menos, desarrollaron técnicas matemáticas que precedieron a los descubrimientos europeos. Por ejemplo:

Lo principal de los trabajos de Ramanujan está en sus “Cuadernos Perdidos”, escritos por él en nomenclatura y notación particular, con ausencia de demostraciones, lo que ha provocado una hercúlea tarea de desciframiento y reconstrucción, aún no concluida. Fascinado por el número pi, desarrolló potentes algoritmos para calcularlo. Uno de ellos, reelaborado por los hermanos Jonathan y Peter Borwein (que fueron los matemáticos a los que encargaron traducir sus Cuadernos Perdidos, resultó así:

Los tres cuadernos que escribió y que son una de las hazañas más asombrosas de todo el pensamiento humano amarillean y se pudren víctimas del clima y los insectos en la universidad Tata de la India. Pero, de Ramanujan hemos hablado aquí en otras ocasiones, sigamos con el trabajo que nos ocupa sobre las matemáticas.
• Los Hindúes desarrollaron el uso del cero y los números negativos quizá unos mil años antes de que estos conceptos fueran aceptados en Europa. Los mayas inventaron su propio cero -de hecho, una gran cantidad de ellos- más o menos al mismo tiempo que los hindúes.
• Ciertas tablillas de barro escritas unos mil años antes de la civilización griega revelan indicios de la existencia de un álgebra bastante sofisticada entre los sumerios. Existen papiros del siglo XVIII a. C., y también anteriores a esa fecha, en los que se ve que los egipcios utilizaban ecuaciones simples para abordar problemas relativos a la distribución de alimentos y otros suministros.
Los egipcios sabían que, la trigonometría es una rama de las matemáticas que significa “medición de triángulos”.
Los antiguos egipcios y babilonios conocían los teoremas sobre los lados de los triángulos semejenates. Las sociedades pre-helénicas carecían de estos conocimientos, por lo que estudiaban los lados en su medida (trilaterometría). En el segundo milenio a.C, los egipcios utilizaban la trigonometría para la construcción de pirámides.

Esta imagen muestra el Papiro de Ahmes que contiene el siguiente problema de trigonometría: ” Si una pirámide es de 250 codos de alto y al lado de su base de 360 codos de largo, ¿cúal es su Seked?” Solución: la cantidad para la Seked es la cotangente del ángulo que forman la base de la pirámide y su cara.
• En el tercer milenio a. C. los babilonios desarrollaron un sistema de numeración que contemplaba el principio del valor según la posición. (En nuestro sistema de base 10, por ejemplo, 348 significa 8 unidades, 4 decenas y 3 centenas.) El Sistema de numeración Sexagesimal (base 60) de los babilonios puede parecer incómodo en un principio, pero Copérnico utilizó fracciones sexagesimales para construir su modelo del sistema solar y nosotros utilizamos este sistema para medir el tiempo y los ángulos (la hora tiene 60 minutos y cada minuto se divide en 60 segundos).

Sistema Sexagesimal Babilónico
• Los escribas que trabajaban en los templos de Egipto conocían la fórmula que se usa para calcular el volumen del cilindro mucho antes de que existieran griegos que supiesen leer y escribir, por lo que conocieron la existencia del misterioso factor π mucho antes que los griegos. Los egipcios inventaron también el conceopto de mínimo comín denominador, así como una tabla de fracciones cuya preparación, según estimaciones de expertos modernos, requirió la realización de veintiocho mil tediosos cálculos.

Sí, el conocimiento de los números y las matemáticas se pierde en la noche de los tiempos y, desde hace milenios están alojados en la Mente de la Humanidad que, los tiene en sus manos para hacer el uso requerido en cada caso y lugar para hacernos más comprensible y fácil la vida. ¿Qué sería de nosotros sin las matemáticas?

• En el año 2000 a. C., los sacerdotes en Mesopotamia (una región de la que hemos hablado hace muy poco tiempo, y, donde la Civilización sumeria desarrolló todo su talento e inventiva para el progreso), desarrollaron unas extensas tablas de cuadrados. Sabemos esto por las tablillas de barro con textos en escritura cuneiforme que han sido halladas en las bibliotecas de los templos. Hay que recordar que los europeos en el siglo XIV ni siquiera tenían Tablas de multiplicar.
• Gottfried Leibniz, el coinventor del cálculo, afrimaba haber descubierto el secreto del modo de descifrar los diagramas del sabio chino de la antigüedad Fu Hsi. Leibniz sostenía que los diagramas de Fu Hsi se correspondían con su propio sistema binario moderno de aritmética.
• Los hindúes inventaron una incipiente forma de cálculo siglos antes de que Leibniz inventara el cálculo en Europa.


Mohammed Ibn Musa abu Djafar Al-Khwarizmi. Murió: hacia el 850 en Bagdad (hoy Irak)
Matemático, astrónomo y geógrafo musulmán, Mohammed Ibn Musa abu Djafar Al-Khwarizmi, nació probablemente en la ciudad persa de Khwarizm (actual Khiva, en Uzbekistan), situada al sudeste del mar de Aral, en la vieja ruta de la seda, que había sido conquistada 70 años antes por los árabes. Su nombre significa “Mohamed, hijo de Moisés, padre de Jafar, el de Khwarizm”.
Hacia el 820, Al’Khwarizmi fue llamado a Bagdad por el califa abasida Al Mamun, segundo hijo de Harun ar Rashid, conocido por todos gracias a las “Mil y una noches”. Al Mamun continuó el enriquecimiento de la ciencia árabe y de la Academia de Ciencias creada por su padre, llamada la Casa de la Sabiduría. Se tradujeron al árabe obras científicas y filosóficas griegas e hindúes, y contaba con observatorios astronómicos. En este ambiente científico y multicultural se educó y trabajó Al-Khwarizmi, el cual dedicó sus tratados de álgebra y astronomía al propio califa. Todo este florecimiento traería importantes consecuencias en el desarrollo de la ciencia en Europa, principalmente a través de España.
• Así, los árabes acuñaron el término álgebra e inventaron las fracciones decimales: 0,25 para ¼, etc. Los europeos, antes de sacar pecho cuando de matemáticas se habla, debemos mirar hacia atrás en el tiempo y hacia otros pueblos que, antes que nosotros, hicieron bien su trabajo.

Aristóteles supo reconocer el mérito de los egipcios a los que atorgó la autoría de haber desarrollado las matemáticas antes de que sus paisanos lo hicieran, aunque los expresó de una forma un poco ambigua: “Las ciencias matemáticas nacieron en el entorno de Egipto porque allí la clase sacerdotal disfrutaba de tiermpo de ocio”.
De todas las maneras, es de justicia reconocer las cosas y, el historiador de matemáticas Morris Kline, el más prominente de América, nos dice: “Comparar las matemáticas de los egipcios y los babilonios con los logros de sus sucesores inmediatos, los griegos, es como comparar los grabados de los niños que aprenden a escribir con la gran literatura”. Esto, sin dejar de reconocer que sumerios, babilonios y egipcios fueron los pioneros, junto a los hundues y chinos, de las matemáticas que más tarde, fueron desarrolladas por griegos.
La historia es más extensa pero, el tiempo se me acaba y el trabajo me espera, otro día seguiremos desarrollando este tema fascinante de las matemáticas que, junto con la escritura y el lengujae, viene a ser uno de los mayores logros de la Humanidad.
emilio silvera
Sep
9
Las Galaxias y…¡La Vida!
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Astronomía y Astrofísica ~
Clasificado en Astronomía y Astrofísica ~
 Comments (0)
Comments (0)
“…en alguna pequeña charca caliente, tendrían la oportunidad de hacer el trabajo y organizarse en sistemas vivos…”

Esas palabras de arriba reflejaban los pensamientos de Darwin
Que, dicho sea de paso, en lo que a la vida se refiere, ésta se abre paso en los lugares más estremos e inesperados por muy malas condiciones que allí puedan estar presentes. Así ocurre con los llamaodos extremófilos que, pueden estar, casi en cualquier sitio.
Hasta que supimos que existían otros sistemas planetarios en nuestra Galaxia, ni siquiera se podía considerar esta posibilidad como una prueba de que la vida planetaria fuera algo común en la Vía Láctea. Pero ahora se sabe que más de cien estrellas de nuestra zona de la galaxia tienen planetas que describen órbitas alrededor de ellas. Casi todos los planetas descubiertos hasta ahora son gigantes de gas, como Júpiter y Saturno (como era de esperar, los planetas grandes se descubrieron primero, por ser más fáciles de detectar que los planetas pequeños), sin embargo es difícil no conjeturar que, allí, junto a estos planetas, posiblemente estarán también sus hermanos planetarios más pequeños que, como la Tierra, pudieran tener condiciones para generar la vida en cualquiera de sus millones de formas.


En otros comentarios, ya nos referimos a los elementos más abundantes del Universo: carbono, hidrógeno, oxígeno y nitrógeno (CHON). Lee Smolin, de la Universidad de Waterloo, Ontario, ha investigado la relación existente entre, por una parte, las estrellas que convierten unos elementos más sencillos en algo como el CHON y arroja esos materiales al espacio, y, por otra parte, las nubes de gas y polvo que hay en éste, que se contrae para formar nuevas estrellas.
Nuestro hogar dentro del espacio, la Vía Láctea, es una entre los cientos de miles de millones de estructuras similares dispersas por todo el Universo visible, y parece ser una más, con todas las características típicas – de tipo medio en cuanto a tamaño, composición química, etc.- La Vía Láctea tiene forma de disco plano, con alrededor de cien mil años luz de diámetro, y está formada por doscientos mil millones de estrellas que describen órbitas en torno al centro del disco.
El Sol, en realidad, sólo es importante para nosotros al ser el cuerpo central de nuestro Sistema Solar, y con mucho, la estrella más cercana al planeta Tierra y la única que se puede estudiar con todo lujo de detalles. Se clasifica como una estrella G2V: una estrella amarilla con una temperatura efectiva de 5.770 K (tipo espectral G2) y una enana de la secuencia principal (clase de luminosidad V). Los detalles de su composición son sobradamente sabidos por todos y cabe destacar su abundancia de hidrógeno – 71% en masa- y de helio el 27% y elementos más pesados hasta completarlo. Por lo tanto, nuestro Sol no destaca por nada entre esa multitud de de cientos de miles de millones de estrellas.
Recorre su órbita a una distancia del centro que viene a ser más o menos dos tercios del diámetro. En el centro de la Galaxia las estrellas forman una protuberancia, de tal modo que desde el exterior daría la sensación de estar viendo un enorme huevo frito, en el que la protuberancia sería la yema. Sin embargo, el modo en que este disco gira revela que todo el material brillante (materia bariónica) que compone la parte visible de la Vía Láctea queda sujeto por el tirón gravitatorio de una materia invisible que no brilla ni emite radiación y que viene a ser más o menos diez veces mayor que la materia visible de la Galaxia y que muchos suponen que está diseminada en un halo situado alrededor de ella, extendiéndose mucho más allá del borde del disco de estrellas brillantes.

Recreación artística del WHIM en la Pared del Escultor
Descubrir qué es realmente esta materia oscura (yo prefiero llamarla -hasta que sepamos que es…si es algo- no luminosa o materia escondida) constituye un tema de crucial interés para los astrónomos, pero no entraremos ahora en eso, ya que, para lo que estamos tratando, no tiene importancia. Muchas galaxias en forma de disco se caracterizan por una especie de serpentinas que se alejan en espiral desde su centro, lo que hace que se les aplique el nombre de galaxias espirales. Es fácil estudiar las pautas que siguen los llamados “brazos espirales”, porque las galaxias se encuentran relativamente cerca unas de otras, si comparamos estas distancias con sus tamaños.
Andrómeda, la galaxia espiral más cercana comparable a la Vía Láctea, se encuentra con respecto a nosotros a una distancia de poco más de dos millones de años luz; parece una gran distancia, pero la galaxia de Andrómeda es tan grande (un poco mayor que la Vía Láctea) que, incluso a esa distancia, vista desde la Tierra cubre un trozo de cielo del tamaño de la Luna, y puede observarse a simple vista en una noche despejada y sin luz lunar, si nos situamos lejos de las ciudades y de otras fuentes de emisión de luz.

NGC 5584 es una bonita galaxia que exhibe orgullosa sus inmensos criaderos de estrellas en los brazos espirales que azulean el contorno y que, con mas de 50 mil años-luz de diámetro. Se encuentra a 72 millones de años-luz de distancia, en dirección de la constelación de Virgo.
Los brazos espirales, que son una característica tan llamativa en galaxias como la nuestra, son visibles porque están bordeados por estrellas calientes de gran masa que relucen con mucho brillo. Esto significa que también son estrellas jóvenes, ya que no hay estrellas viejas que tengan gran cantidad de masa.
No hay misterio alguno en cuanto al modo en que mantienen esa forma espiral. Se debe exclusivamente a un fenómeno de retroalimentación. c Las nubes gigantescas a partir de las cuales se forman las estrellas pueden contener hasta un millón de veces la masa del Sol cuando empieza a contraerse gravitatoriamente para formar estrellas. Cada nube que se contrae produce, no una sola estrella de gran tamaño, sino todo un conglomerado de estrellas, así como muchas estrellas menores. Cuando las estrellas brillantes emiten luz, la energía de esta luz estelar (especialmente en la parte ultravioleta del espectro) forma una burbuja dentro de la nube, y tiende a frenar la formación de más estrellas. Sin embargo, una vez que las estrellas de gran masa han recorrido sus ciclos vitales y han explotado, sembrando además el material interestelar con elementos de distintos tipos, la onda expansiva ejerce presión sobre las nubes interestelares cercanas y hace que éstas comiencen a contraerse.

Las ondas procedentes de distintas supernovas, al entrecruzarse unas con otras, actúan mutuamente para barrer el material interestelar y formar nuevas nubes de gas y polvo que se contraen produciendo más estrellas y supernovas, en un ejemplo clásico de interacción que se mantiene por sí sola en la que intervienen una absorción de energía (procedentes de las supernovas) y una retroalimentación.
Si la nube es demasiado densa, su parte interna se contraerá gravitatoriamente de manera rápida, formando unas pocas estrellas grandes que recorren sus ciclos vitales rápidamente y revientan la nube en pedazos antes de que puedan formarse muchas estrellas. Esto significa que la generación siguiente de estrellas nace de una nube más delgada, porque ha habido pocas supernovas que barrieran material formando pedazos densos. Si la nube es tan delgada que su densidad queda por debajo de la densidad óptima, nacerán muchas estrellas, y habrá gran cantidad de explosiones supernovas, lo cual producirá gran número de ondas de choque que barrerán el material interestelar, acumulándolo en nubes más densas.
De esta manera, por ambas partes, las retroalimentaciones operan para mantener un equilibrio aproximadamente constante entre la densidad de las nubes y el número de supernovas (y estrellas de tipo Sol) que se producen en cada generación. La propia pauta espiral resulta del hecho de que la galaxia realiza movimiento de rotación y está sometida al tirón gravitatorio que crea la fuerza de marea proveniente de esa materia no luminosa.

Con la gentil autorización de NASA and The Hubble Heritage Team (STScI/AURA)
¿Existen los espíritus? Esta toma del telescopio Hubble casi lo sugiere. Muestra una nube de materia interestelar con el nombre de IC 349, que es inundado con radiación, por la joven estrella Merope, en las Pléyades, y es incitada a brillar. La enorme radiación de la estrella, prontamente dispersará a esta nube y la destruirá. Las Pléyades son conocidas como incubadoras de muchas nuevas estrellas masivas, que en su estado “juvenil” emiten enormes cantidades de irradiación.
Claro que, la materia interestelar es variada. Existen nubes de gas y polvo fríos, que son ricas en interesantes moléculas y se llaman nubes moleculares gigantes; a partir de estas nubes se forman nuevas estrellas (y planetas). Hay nubes de lo que consideraríamos gas “normal”, formadas por átomos y moléculas de sustancias tales como el hidrógeno, y quizá tan caliente como una habitación cerrada durante toda la noche y con la temperatura de dos cuerpos dormidos y emitiendo calor. Además, hay regiones que se han calentado hasta temperaturas extremas mediante la energía procedente de explosiones estelares, de tal modo que los electrones han sido arrancados de sus átomos para formar un plasma cargado de electricidad.
También existe una amplia variedad de densidades dentro del medio interestelar. En la modalidad más ligera, la materia que está entre las estrellas es tan escasa que sólo hay un átomo por cada mil centímetros cúbicos de espacio: en la modalidad más densa, las nubes que están a punto de producir nuevas estrellas y nuevos planetas contienen un millón de átomos por centímetro cúbico. Sin embargo, esto es algo muy diluido si se compara con el aire que respiramos, donde cada centímetro cúbico contiene más de diez trillones de moléculas, pero incluso una diferencia de mil millones de veces en densidad sigue siendo un contraste espectacular.
La cuestión es que, unos pocos investigadores destacaron allá por 1.990 en que todos estos aspectos –composición, temperatura y densidad- en el medio interestelar dista mucho de ser uniforme. Por decirlo de otra manera más firme, no está en equilibrio, y parece que lo que lo mantiene lejos del equilibrio son unos pocos de procesos asociados con la generación de las pautas espirales.
Esto significa que la Vía Láctea (como otras galaxias espirales) es una zona de reducción de la entropía. Es un sistema auto-organizador al que mantienen lejos del equilibrio, por una parte, un flujo de energía que atraviesa el sistema y, por otra, como ya se va viendo, la retroalimentación. En este sentido, nuestra Galaxia supera el test de Lovelock para la vida, y además prestigiosos astrofísicos han argumentado que las galaxias deben ser consideradas como sistemas vivos.
Creo que llevan toda la razón.
emilio silvera
Sep
9
Consecuencias biológicas si las constantes variaran con el paso del tiempo
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Constantes universales ~
Clasificado en Constantes universales ~
 Comments (0)
Comments (0)
No varían con el paso del Tiempo. Existen muchas constantes físicas; algunas de las más conocidas son la constante de Planc racionalizada 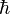 , la constante de gravitación
, la constante de gravitación  , la velocidad de la luz
, la velocidad de la luz  , la permitividad en el vacío
, la permitividad en el vacío 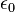 , La constante de estructura fina α, la permeabilidad magnética en el vacío
, La constante de estructura fina α, la permeabilidad magnética en el vacío  y la carga elemental
y la carga elemental  . Todas éstas, por ser tan fundamentales, son llamadas constantes universales.
. Todas éstas, por ser tan fundamentales, son llamadas constantes universales.

Nuestro Universo es como es porque, las constantes no varían con el paso del tiempo
Según todos los indicios de los que podemos disponer, si esas constantes hubieran tenido variables, en tan sólo unas simples fracciones infinitesimales de millonésimas, la vida, no habría podido surgir en nuestro planeta.
Muchos han sido los que se han sentido atraídos por las posibles consecuencias biológicas de las teorías cosmológicas en que las “constantes” tradicionales cambian con el paso del tiempo o donde los procesos gravitatorios se despliegan de acuerdo con un reloj cósmico diferente del de los procesos atómicos (¿será precisamente por eso que la relatividad general – el cosmos –, no se lleva bien con la mecánica cuántica – el átomo –?).
La radiactividad natural es el proceso de emisión espontánea de radiaciones por parte de núcleos atómicos inestables, que se fisionan y se transforman en otros núcleos. No hace mucho tiempo que sabemos de ella. Las radiaciones nos llegan de distintas fuentes, estamos constantemente expuestos a radiaciones naturales.
Universos de dos tiempos habían sido propuestos por Milne y fueron las primeras sugerencias de que Gpodría no ser constante. Unos procesos, como la desintegración radiactiva o los ritmos de interacción molecular, podrían ser constantes sobre una escala de tiempo pero significativamente variables con respecto a la otra. Esto daba lugar a un escenario en el que la bioquímica que sustentaba la vida sólo se hacía posible después de una particular época cósmica, y, algunos, como Haldane, han sugerido que:

“Hubo, de hecho, un momento en el que se hizo posible por primera vez la vida de cualquier tipo, y las formas superiores de vida sólo pueden haberse hecho posibles en una fecha posterior. Análogamente, un cambio en las propiedades de la materia puede explicar algunas de las peculiaridades de la geología precámbrica.”
Este imaginativo escenario no es diferente del que ahora se conoce como “equilibrio interrumpido”, en el que la evolución ocurre en una sucesión discontinua de brotes acelerados entre los que se intercalan largos periodos de cambio lento. Sin embargo, Haldane ofrece una explicación para los cambios.
Lo que tienen en común todas estas respuestas a las ideas de Eddington y Dirac es una apreciación creciente de que las constantes de la naturaleza desempeñan un papel cosmológico vital en el Universo para todo lo que contiene y, sobre todo, para la vida de las estrellas y, también, para la vida de seres como nosotros que, con unas constantes diferentes, simplemente no estaríamos aquí.

El mayor misterio que rodea a los valores de las constantes de la naturaleza es sin duda la ubicuidad de algunos números enormes que aparecen en una variedad de consideraciones aparentemente inconexas. El número de Eddington es un ejemplo notable. El número total de protones que hay dentro del alcance del universo observable esta próximo al número
1080
Si preguntamos ahora por la razón entre las intensidades de las fuerzas electromagnéticas y gravitatoria entre dos protones, la respuesta no depende de su separación, sino que es aproximadamente igual a
1040
Es un misterio. Es bastante habitual que los números puros que incluyen las constantes de la naturaleza difieran de 1 en un factor del orden de 102, ¡pero 1040, y su cuadrado 1080, es rarísimo! Y esto no es todo. Si seguimos a Max Planck y calculamos en valor estimado para la “acción” del universo observable en unidades fundamentales de Planck para la acción, obtenemos.
10120

Existe un lazo entre la estructura del universo en conjunto y las condiciones locales internas que se necesitan para que la vida se desarrolle y persista. Si las constantes tradicionales varían, entonces las teorías astronómicas tienen grandes consecuencias para la biología, la geología y la propia vida.
No podemos descartar la idea ni abandonar la posibilidad de que algunas “constantes” tradicionales de la naturaleza pudieran estar variando muy lentamente durante el transcurso de los miles de millones de años de la historia del universo. Es comprensible por tanto el interés por los grandes números que incluyen las constantes de la naturaleza. Recordemos que Newton nos trajo su teoría de la Gravedad Universal, que más tarde mejora Einstein y que, no sería extraño, en el futuro mejorará algún otro con una nueva teoría más completa y ambiciosa que explique lo grande (el cosmos) y lo pequeño (el átomo), las partículas (la materia) y la energía por interacción de las cuatro fuerzas fundamentales.


Gravitación universal de Isaac Newton.
Aquí, hablamos de lo que pasaría con la vida en caso de que esas constantes universales pudieran variar con el tiempo, y, según todos los indicios, la cosa no pinta nada bien.
La Carga del electrón, la Constante de Planck, la Constante Gravitacional, la masa en reposo del electrón, protón o neutron, o, la velocidad de la luz, se tienen todas por constantes de la naturaleza, es decir, no varían con el paso del tiempo, y, los cálculos que se han realizado en el sentido de una pequeña variación en alguna de ellas, son catastróficas, por ejemplo, si la carga del eletrón, variará, tan solo una diez millónesima, sería más que suficiente que no se conformaran los átomos y, la materia no podría existir tal como la conocemos y, siendo así (que lo es) ¿qué pasaría con la vida?

Bueno, el cambio de las constantes no es que pusiera el mundo del revés, sino que, simplemente, el mundo tal como lo conocemos, no sería. Igualmente, el Universo sería también distinto y, vaya usted a saber que clase de universos y mundos serían. ¿Un electrón diferente? ¿Qué pasaría con los átomos y la materia, y las estrellas y…nosotros?

Contrapuestas pero iguales traen la estabilidad
El Universo es como es gracias a equilibrios fuerzas contrapuestas de similares potencias y, por ejemplo, en un átomo la carga negativa de los electrones es similar a la carga positiva de los protones, y, tal equilibrio de fuerzas hace posible la estabilidad para que se formen y se junten para formar moléculas y materia. En las estrellas, una fuerza, la fusión tiende a expandir a la estrella, otra fuerza, la de Gravedad, tiende a comprimirla, y, de esta manera, aparece el equilibrio necesario para que las estrellas brillen durante miles de millones de años y lancen al espacio interestelar su luz y su calor, creen elementos complejos, y, en su final, hagan que sea posible sembrar de materiales diversos en inmensas nubes la materia primigenia para la vida, y, todo ello, en presencia de las fuerzas fundamentales y las constantes de la naturaleza.
Así que, sería preferible que las constantes de la Naturaleza se queden tal cual. ¿Qué ganaríamos nosotros si cambiaran? ¿Desaparecer? No gracias. Aunque no como quisieramos pero, estamos bien aquí, al menos hay una oportunidad para cambiar las cosas.




Sep
8
El “mundo” que nos rodea
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (0)
Comments (0)
No siempre sabemos ver el mundo que nos rodea. El que miremos no significa que estemos viendo lo que realmente hay delante de nuestros ojos y, muchas veces, no son los ojos los únicos que pueden “ver” lo que hay más allá de lo que la vista puede alcanzar. Anoche, hasta una hora avanzada, estuve releyendo el Libro “Así de Simple” de John Gribbin, y, pareciéndome interesante os saqué un pequeño resumen del comienzo. Aquí os lo dejo.
El mundo que nos rodea parece ser un lugar complicado. Aunque hay algunas verdades sencillas que parecen eternas (las manzanas caen siempre hacia el suelo y no hacia el cielo; el Sol se levanta por el este, nunca por el oeste), nuestras vidas, a pesar de las modernas tecnologías, están todavía, con demasiada frecuencia, a merced de los complicados procesos que producen cambios drásticos y repentinos. La predicción del tiempo atmosférico tiene todavía más de arte adivinatorio que de ciencia; los terremotos y las erupciones volcánicas se producen de manera impredecible y aparentemente aleatorias; las fluctuaciones de la economía siguen ocasionando la bancarrota de muchos y la fortuna de unos pocos.


Sobre la posición de la salida del sol
Desde la época de Galileo (más o menos, a comienzos del siglo XVII) la ciencia ha hecho progresos –enormes-, ignorando en gran medida estas complejidades y centrándose en cuestiones sencillas, intentando explicar por qué las manzanas caen al suelo y por qué el Sol se levanta por el este. Los avances fueron de hecho tan espectaculares que hacia mediados del siglo XX ya se había dado respuesta a todas las cuestiones sencillas. Conceptos tales como la teoría general de la relatividad y la mecánica cuántica explicaron el funcionamiento global del universo a escalas muy grandes y muy pequeñas respectivamente, mientras el descubrimiento de la estructura del ADN y el modo en que éste se copia de una generación a otra hizo que la propia vida, así como la evolución, parecieran sencillas a nivel molecular. Sin embargo, persistió la complejidad del mundo a nivel humano –al nivel de la vida-. La cuestión más interesante de todas, la que planteaba cómo la vida pudo haber surgido a partir de la materia inerte, siguió sin respuesta.
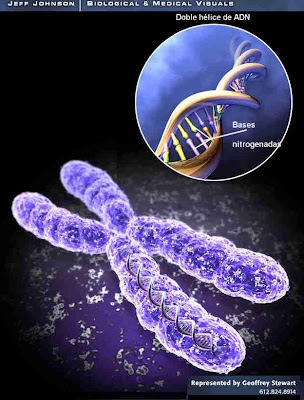
Un descubrimiento así no podía dejar al mundo indiferente. En unos años el mundo científico se puso al día y la revolución genética cambió los paradigmas establecidos. Mucha gente aún no está preparada para aceptar el comienzo de una era poderosa en la que el ser humano tiene un control de sí mismo mayor al habitual. Había nacido la Ingeniería genética.

Más neuronas que estrellas en la Vía Láctea
No debe extrañarnos que sea precisamente a escala humana donde se den las características más complejas del universo. Las que se resisten más a rendirse ante los métodos tradicionales de la investigación científica. Realmente, es posible que seamos lo más complejo que existe en el universo. La razón es que, a escalas más reducidas, entidades tales como los átomos se comportan individualmente de un modo relativamente sencillo en sus interacciones mutuas, y que las cosas complicadas e interesantes surgen, cuando se unen muchos átomos de maneras complicadas e interesantes, para formar organismos tales como los seres humanos.
Pero este proceso no puede continuar indefinidamente, ya que, si se unen cada vez más átomos, su masa total aumenta hasta tal punto que la Gravedad aplasta toda la estructura importante y la aniquila. Un átomo, o incluso una molécula tan simple como la del agua, es algo más sencillo que un ser humano, porque tiene poca estructura interna; una estrella, o el interior de un planeta, es también algo más sencillo que un ser humano porque la gravedad aplasta cualquier estructura hasta aniquilarla. Esta es la razón por la cual la ciencia puede decirnos más sobre el comportamiento de los átomos y el funcionamiento interno de las estrellas o los planetas que sobre el modo en que las personas nos comportamos.
Sí, hemos podido llegar a conocer lo que ocurre en el Sol, y sabemos de sus procesos interiores y exteriores, de las ráfagas de partículas que en sus épocas activas, nos envía continuamente hacía la superficie del planeta y, que no sólo provoca esas bonitas Auroras, sino que, su intensa radiación y magnetismo incide en todos los atilugios que tenemos para leer los datos de… ¡tántas cosas!
Cuando los problemas sencillos se rindieron ante el empuje de la investigación, fue algo natural que los científicos abordaran rompecabezas más complicados que iban asociados con sistemas complejos, para que por fin fuera posible comenzar a comprender el funcionamiento del mundo a una escala más humana compleja y, para ello, hubo que esperar hasta la década de 1960, que fue cuando aparecieron los poderosos y rápidos (para lo que se estilaba en aquella época) ordenadores electrónicos. Estos nuevos inventos empezaron a ser conocidos por un público más amplio entre mediados y finales de la década de 1980, primero con la publicación del libro, ahora convertido en un clásico, Order out of Chaos, de Ilya Prigogine e Isabelle Stergers, y luego, con Chaos, de James Gleick.

Las personas sencillas que, aunque tengan una educación aceptable, no están inmersas en el ámbito de la ciencia, cuando oyen hablar de Complejidad y Caos en esas áreas, sienten, de primeras, una especie de rechazo por aquello que (ellos creen) no van a comprender. Sin embargo, la cuestión no es tan difícil como a primera vista pudiera parecer, todo consiste en tener la posibilidad de que alguien, de manera “sencilla” (dentro de lo posible), nos explique las cosas dejando a un lado las matemáticas que, aunque describen de manera más amplia y pura aquellos conceptos que tratamos, también es verdad que, no siempre, están al alcance de todos. Un conocimiento básico de las cosas más complicadas, es posible. También la relatividad general y la mecánica cuántica, se consideraron, cuando eran nuevas, como unas ideas demasiado difíciles para que cualquiera las entendiera, salvo los expertos –pero ambas se basan en conceptos sencillos que son inteligibles para cualquier persona lega en la materia, siempre que esté dispuesta a aceptar su parte matemática con los ojos cerrados-. E la misma manera, el Caos y la Complejidad, también pueden ser entendidos y, si tenemos la suerte de tener un buen interlocutor que nos sepa explicar, aquellos conceptos básicos sobre los que se asientan tanto el Caos como la Complejidad, veremos maravillados como, de manera natural, la luz se hace en nosotros y podemos entender lo que antes nos parecía inalcanzable.

Se cree que las galaxias se han formado por la acumulación gravitacional de gas, algún tiempo después de la época de la recombinación. Las nubes de gas podrían haber comenzado a formar estrellas, quizás como resultado de las colisiones mutuas. El tipo de galaxia generado podría depender del ritmo al que el gas era transformado en estrellas, formándose las elípticas cuando el gas se convertía rápidamente en estrellas, y las espirales si la transformación de estrellas era lo suficientemente lenta como para permitir crecer de forma significativa un disco de gas.

Nubes moleculares en Orión que son los materiales primigenios para complejidades futuras
Las galaxias evolucionan al convertir progresivamente su gas remanente en estrellas, si bien no existe probablemente una evolución entre las diferentes tipos de la clasificación del conocido sistema de Hubble. No obstante, algunas galaxias elípticas pudieron haberse creado por la colisión y posterior fusión de dos galaxias espirales.

NGC 5426 y NGC 5427 son dos galaxias espirales de tamaños similares involucradas en una danza espectacular. No es seguro que esta interacción culmine en una colisión y a la larga en la fusión de las dos galaxias, aunque éstas ya han sido ya afectadas. Conocidas ambas con el nombre de Arp 271, su danza perdurará por decenas de millones de años, creando nuevas estrellas como resultado de la mutua atracción gravitacional entre las galaxias, un tirón observable en el borde de las estrellas que ya conectan a ambas. Ubicada a 90 millones de años-luz de distancia hacia la constelación de Virgo (la Virgen), el par Arp 271 tiene unos 130.000 años-luz de extensión. Fue descubierta originalmente en 1785 por William Herschel. Muy posiblemente nuestra Vía Láctea sufrirá una colisión similar en unos cinco mil millones de años más con la galaxia vecina Andrómeda, que ahora está ubicada a cerca de 2,6 millones de años-luz de la Vía Láctea.
Sí, mirando las imagenes nos da la sensación de cierto Caos y Complejidad
Tenemos que entender que, algunos sistemas (“sistema” no es más que una palabra de la jerga científica para asignar cualquier cosa, como un péndulo que oscila, o el sistema solar, o el agua que gotea de un grifo) son muy sensibles a sus condiciones de partida, de tal modo que una diferencia mínima en el “impulso” inicial que les damos ocasiona una gran diferencia en cómo van a acabar, y existe una retroalimentación, de manera que lo que un sistema hace afecta a su propio comportamiento. Así, a primera vista, parece que la guía es sencilla y, nos puede parecer mentira que así sea. Sin embargo, esa es la premisa que debemos tener en cuenta. Nos podríamos preguntar: ¿Es realmente verdad, que todo este asunto del Caos y de la Complejidad se basaba en dos ideas sencillas –la sensibilidad de un sistema a sus condiciones de partida, y la retroalimentación-¿ La respuesta es que sí.
 La mayor parte de los objetos que pueden verse en el cielo nocturno son estrellas, unos pocos centenares son visibles a simple vista. Una estrella es una bola caliente principalmente compuesta por hidrógeno gaseoso. El Sol es un ejemplo de una estrella típica y común. La gravedad impide que el gas se evapore en el espacio y la presión, debida a la alta temperatura de la estrella, y la densidad impiden que la bola encoja. En el corazón de la estrella, la temperatura y la densidad son lo suficientemente altas para sustentar a las reacciones de fusión nuclear, y la energía, producida por estas reacciones, hace su camino a la superficie y la irradia al espacio en forma de calor y luz. Cuando se agota el combustible de las reacciones de fusión, la estructura de la estrella cambia. El proceso de producir elementos, cada vez más pesados, a partir de los más livianos y de ajustar la estructura interna para balancear gravedad y presión, es llamado evolución estelar.
La mayor parte de los objetos que pueden verse en el cielo nocturno son estrellas, unos pocos centenares son visibles a simple vista. Una estrella es una bola caliente principalmente compuesta por hidrógeno gaseoso. El Sol es un ejemplo de una estrella típica y común. La gravedad impide que el gas se evapore en el espacio y la presión, debida a la alta temperatura de la estrella, y la densidad impiden que la bola encoja. En el corazón de la estrella, la temperatura y la densidad son lo suficientemente altas para sustentar a las reacciones de fusión nuclear, y la energía, producida por estas reacciones, hace su camino a la superficie y la irradia al espacio en forma de calor y luz. Cuando se agota el combustible de las reacciones de fusión, la estructura de la estrella cambia. El proceso de producir elementos, cada vez más pesados, a partir de los más livianos y de ajustar la estructura interna para balancear gravedad y presión, es llamado evolución estelar.
Observar una estrella a través del telescopio permite conocer muchas de sus importantes propiedades. El color de una estrella es un indicador de su temperatura y ésta, a su vez, depende de una combinación entre la masa de la estrella y su fase evolutiva. Usualmente, las observaciones también permiten encontrar la luminosidad de la estrella o la tasa con la cual ella irradia energía, en forma de calor y luz.
Todas las estrellas visibles a simple vista forman parte de nuestra galaxia, la Vía Láctea. La Vía Láctea es un sistema compuesto por unos cien mil millones de estrellas, junto con una considerable cantidad de material interestelar. La galaxia tiene forma de un disco chato sumergido en un halo débil y esférico. La gravedad impide que las estrellas se escapen y, sus movimientos, hacen que el sistema no colapse. La Vía Láctea no posee un límite definido, la distribución de las estrellas decrece gradualmente con distancias crecientes del centro. El SDSS detecta estrellas más de un millón de veces más débiles que las que podemos ver a simple vista, lo suficientemente lejos para ver la estructura de la Vía Láctea.

De algún modo, esto es como decir que “todo lo que hay” sobre la teoría especial de la relatividad es que la velocidad de la luz es la misma para todos los observadores. Sin embargo, la complejidad de la estructura que se levanta sobre este hecho sencillo resulta asombrosa y requiere algunos conocimientos matemáticos para poder apreciarla plenamente. Claro que, eso no quita para que, un buen comunicador le pueda transmitir a otras personas mediante explicaciones sencillas lo esencial de la relatividad especial y general y también, sobre la esencia de la mecánica cuántica, y, de la misma manera, podríamos hablar del Caos y de la Complejidad. Debemos ser conscientes de que, el Caos, puede surgir a partir del Orden y que, la Complejidad, siempre llega a través de la sencillez de un comienzo. Podemos estar al borde del Caos y, de manera milagrosa ver que, también a partir de él surge la normalidad y lo nuevo que, no en pocas ocasiones pueden ser nuevas formas de vida. De la misma manera, las transformaciones de los elementos sencillos, bajo ciertas condiciones, llegan a adquirir una complejidad inusitada que, de alguna manera, es necesaria para que, en este mundo que nos rodea, existan seres que, como nosotros, sean el ejemplo más real y de más alto nivel que está presente en el Universo. Y, de la misma manera que nosotros estamos aquí, en un minúsculo sistema solar habitando un pequeño planeta que reúne todas las condiciones necesarias para la vida, de la misma forma digo, estarán poblados otros muchos planetas de otros muchos sistemas solares repartidos por nuestra Galaxia y por las otras que, a cientos de miles pululan por el Universo, y, todos esos seres “racionales”, se preguntaran las mismas cosas que nosotros y estarán interesados en descubrir los mismos misterios, los mismos secretos de la Naturaleza que, presintiendo que existen, tienen la intuición de que serán las respuestas esperadas para solucionar muchos de los problemas e inseguridades que ahora, en nuestro tiempo, nos aquejan.
Claro que, la mente nunca descansa. Acordaos de Aristarco de Samos que, en el siglo III a. C., ya anunció que la Tierra orbitaba alrededor del Sol y, Copérnico, que se llevó el premio, no lo dijo hasta el año 1543. Esto nos viene a demostrar que, a pesar de la complejidad del mundo, lo realmente complejo está en nosotros, en nuestras mentes que, presienten lo que pueda ser, intuyen el por qué de las cosas, fabrican pensamientos que, mucho más rápidos que la luz, llegan a las galaxias lejanas y, con los ojos de la mente pueden, atisbar aquellas cosas de las que, en silencio, ha oído hablar a su intuición dentro de su mente siempre atenta a todo aquello que puede ser una novedad, una explicación, un descubrimiento.

Vista de la Tierra y el Sol de la órbita
Ahora estamos centrados en el futuro aquí en la Tierra pero, sin dejar de la mano ese futuro que nos espera en el espacio exterior. Es pronto aún para que el hombre vaya a las estrellas pero, algún día, ese será su destino y, desde ya, debe ir preparándose para esa aventura que sólo está a la espera de tener los medios tecnológicos necesarios para hacerla posible. Mientras tanto, jugamos con las sondas espaciales que enviamos a planetas vecinos para que, nos vayan informando de lo que están hechos aquellos mundos –grandes y pequeños- que, en relativamente poco tiempo, serán visitados por nuestra especie para preparar el salto mayor.
emilio silvera
Sep
8
¿La sustancia cósmica? La semilla de la materia
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en El Universo misterioso ~
Clasificado en El Universo misterioso ~
 Comments (0)
Comments (0)
Debajo de ésta imagen se puede leer:
“Hallan indicios de materia oscura unida al Cosmos. La evidencia muestra nuevos fenómenos físicos que podrían ser la extraña y desconocida materia oscura o la energía que se origina de los pulsares. Un detector de rayos cósmicos de dos mil millones de dólares en la Estación Espacial Internacional halló la huella de algo que pudiera ser la materia oscura, la misteriosa sustancia que se cree mantiene unido al cosmos.”
Pero los primeros resultados del Espectrómetro Magnético Alfa (AMS, por sus siglas en inglés) son casi tan enigmáticos como la materia oscura en sí, la cual nunca ha sido observada directamente. Muestran evidencia de nuevos fenómenos físicos que podrían ser la extraña y desconocida materia oscura o la energía que se origina de los pulsares, anunciaron el miércoles científicos en el laboratorio europeo de física de partículas cerca de Ginebra.”
Como no me canso de repetir, cualquiera de estas noticias nos vienen a decir que, de la “materia oscura”, nada sabemos. Sería conveniente, para que las cuentas cuadren, que exista esa dichosa clase de materia o lo que pueda ser, toda vez que, sin ella, no resulta fácil llegar a una conclusión lógica de cómo se pudieron formar las galaxias, o, de por qué se mueven las estrellas de la manera que lo hacen.
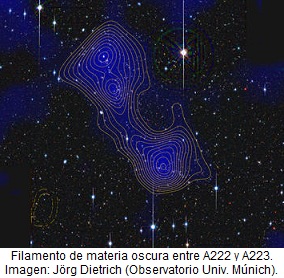
hace treinta años, los astrofísicos se enfrentan a este dilema: o bien las galaxias tienen mucha materia que no vemos, pero que causa una fuerte atracción gravitatoria sobre las estrellas externas (que por ello orbitarían tan rápido) o bien ni la ley de la gravedad de Newton ni la de Einstein serían válidas esas regiones externas de las galaxias. Las dos opciones son revolucionarias para la física: la primera implica la existencia de materia oscura en el universo (materia que no vemos pero que sí afecta al movimiento de las estrellas y galaxias), y la segunda implica que una ley básica (la de Newton/Einsteinde la gravitación) es incorrecta.

En el momento actual, no sabemos cual de esas dos opciones es la buena (podrían incluso ser buenas las dos, es decir, que existiera materia oscura y además que la teoría de Newton/Einstein estuviera mal. No creom que sea ese el problema, debe haber una tercera opción desconocida que debemos encontrar). La gran mayoría de los astrofísicos prefieren explicarlo con la materia oscura(un camino cómodo y fácil) antes que dudar de las leyes de la gravitación de Newton/Einstein. Esto no es sólo cuestión de gustos, es que las leyes de la gravitación funcionan con una increíble exactitud en todos los demás casos donde las hemos puesto a prueba (en los laboratorios, en las naves espaciales y los interplanetarios, en la dinámica del Sistema Solar, etc.).
problema de la materia oscura (si es que realmente existe y no es que las leyes de Newton sean incompletas) es uno de los más importantes con los que se enfrenta la astrofísica hoy en día.
Cuando pienso en la existencia ineludible de esa “materia cósmica” primigenia, la primera y más sencilla clase de materia que se formó en las primeras fracciones del primer segundo del big bang, en la mente se me aparece una imagen llena de belleza creadora a partir de la cual, todo lo que ahora podemos contemplar es posible. La belleza de la idea es que toma dos problemas -la ventana del tiempo inadecuada para la fromación de las galaxias y la existencia de la “materia oscura”- y los une para conformar una solución al problema central de la estructura del universo.

La “materia oscura”, por hipótesis, tiene una ventana de tiempo mucho más larga que la materia ordinaria, porque se despareja más pronto en el Big Bang. Tiene mucho tiempo para acumularse antes de que la materia ordinaria sea libre para hacerlo. La “materia oscura o sustancia cósmica primera, es de porte más sencillo y no tiene ni requiere la complejidad de la materia bariónica para formarse, es totalmente translúcida y se sitúa por todas partes, es decir, permea todo el universo invadiendo todas sus regiones a medida que este se expande más y más.
El hecho de que la materia ordinaria caiga entonces en el agujero gravitatorio creado de este modo sirve para explicar por qué encontramos galaxias rodeadas por un halo de algo que hemos dado en llamar “materia oscura”. Tal hipótesis mata dos pájaros de un sólo tiro.
Pero debemos recordar que en este punto sólo tenemos una idea que puede funcionar, no una teoría bien construida. Para pasar de la idea a la teoría, tenemos que responder dos preguntas importantes y difíciles:
1. ¿Cómo explicamos la estructura de la “materia oscura”?
2. ¿Que es la “materia oscura”?
Se habla de materia oscura caliente y fría.

Podríamos comenzar a examinar estas cuestiones pensando en el modo en que la “materia oscura” pudo separarse de la nube caliente en expansión, de materiales que constituía el universo en sus comienzos. Por analogía de la discusión del desaparejamiento de la materia ordinaria después de la formación de los átomos, llamaremos también desaparejamiento a la separación de la “materia oscura” de aquella fuente “infinita” de energía primera. Una transformarción como la que consujo a la formación de los átomos es necesaria para que ocurra el desaparejamiento. Todo lo que tiene que suceder es que la fuerza de la interacción de las partículas que forman la “materia oscura” caigan por debajo del punto en que el resto del universo puede ejercer una presión razonable sobre él. Después de esto, la “materia oscura” continuará a su aire, indiferente a todo lo que la rodee.

Resulta que desde el punto de vista de la creación de la estructura observada del universo, la característica más importante del proceso de desaparejamiento para la “materia oscura” es la velocidad de las partículas cuando son libres. Si el desaparejamiento tiene lugar muy pronto en el Big Bang, la “materia oscura” puede salir con sus partículas moviéndose muy rápidamente, casi a la velocidad de la luz. Si es así, decimos que la “materia oscura” está caliente. Si el desaparejamiento tiene lugar cuando las partículas están moviendose poco a poco -velocidad significativamente menor que la de la luz- decimos que la materia está fría.
De los tipos de “materia oscura” que los cosmólogos toman en consideración, los neutrinos serán el mejor ejemplo de “materia oscura” caliente. Los neutrinos han llamado la atención de los científicos en relación a la “materia oscura” durante mucho tiempo. Para tener una idea aproximada del número de neutrinos del universo, podríamos decir que existe actualmente un neutrino por cada reacción nuclear que tuvo lugar desde siempre. Los cálculos indican que hubo aproximadamente mil millones de neutrinos producidos durante el Big Bang por cada protón, neutrón o electrón. Cada volumen del espacio del tamaño de nuestro cuerpo contiene unos diez millones de estos neutrinos-reliquias y en ellos no se encuentran los que se produjeron más tarde en las estrellas. Está claro que toda partícula tan corriente como ésta podría tener en principio un efecto muy grande sobre la estructura del Cosmos, si tuviera una masa.

Pero resulta que la “materia oscura” caliente, actuando sola, casi con toda seguridad no podría explicar lo que observamos en el universo y que el escenario de “materia oscura-fria” debe modificarse por completo si queremos mantenerla como candidata a esa teoría última de la materia que “debe” existir en el universo pero, que no sabemos lo que es y la llamamos, precisamente por eso “materia oscura”.
El tema de la materia desconocida, invisible, oculta y misteriosa que hace que nuestro universo se comporte como la hace… ¿sigue siendo una gran incognita! Nadie sabe el por qué las galaxias se alejan las unas de las otras, el motivo de que las estrellas en la periferia de las galaxias se muevan a mayor velocidad de lo que deberían y otros extraños sucesos que, al desconocer los motivos, son achacados a la “materia oscura”, una forma de evadirse y cerrar los ojos ante la inmensa ignorancia que tenemos que soportar en relación a muchos secretos del Universo a los que no podemos dar explicación.

Claro que otros, han imaginado cuestiones y motivos diferente spara explicar las cosas. Ellos ven “materia oscura por todas partes.

Aunque no todas si son muchas las GUT y teorías de supersimetría las que predicen la de cuerdas en la congelación del segundo 10-35 despues del comienzo del tiempo, cuando la fuerza fuerte se congeló y el universo se infló. Las cuerdas se deben considerar un subproducto del proceso mismo de congelación. Es cierto que aunque las diversas teorías no predicen cuerdas idénticas, sí predicen cuerdas con las mismas propiedades generales. En primer lugar las cuerdas son extremadamente masivas y también extremadamente delgadas; la anchura de una cuerda es mucho menor que la anchura de un protón1. Las cuerdas no llevan carga eléctrica, así que no interaccionan con la radiación como las partículas ordinarias. Aparecen en todas las formas; largas lineas ondulantes, lazos vibrantes, espirales tridimensionales, etc. Sí, con esas propiedades podrían un candidato perfecto la “materia oscura”. Ejercen una atracción gravitatoria, no pueden ser rotas por la presión de la radiación en los inicios del Universo.

El espesor estimado de una cuerda es de 10-30 centímetros, comparados con los 10-13 de un protón. Además de ser la más larga, y posiblemente la más vieja estructura del universo conocido, una cuerda cósmica sería la más delgada: su diámetro sería 100.000.000.000.000.000 veces más pequeño que el de un protón.. Y cuerda sería terriblemente inquieta, algo así como un látigo agitándose por el espacio casi a la velocidad de la luz. Las curvas vibrarían como enloquecidas bandas de goma, emitiendo una corriente continua de ondas gravitacionales: rizos en la misma tela del espacio-tiempo. ¿Qué pasaría si una cuerda cósmica tropezara con un planeta? Al ser tan delgada, podría traspasarlo sin tropezar con un solo núcleo atómico. Pero de todos modos, su intenso gravitatorio causaría el cáos.
Lo cierto es que todavía no se ha encontrado ninguna cuerda de este tipo. Si bien en los últimos años han surgido muchas candidatas a estar formadas por un efecto de lente de este tipo, la mayoría han resultado ser dos cuerpos distintos pero muy similares entre sí. Pese a ello, los astrofísicos y los teóricos de cuerdas no puerden la esperanza de encontrar en los próximos años, y gracias a telescopios cada vez más potentes, como el GTC; evidencias directas de la existencia de este tipo de cuerdas; evidencias que no sólo nos indicarían que las teorías de cuerdas van por buen camino, si no que el modelo del Big Bang es un modelo acertado.

Simulación del efecto de lente generado por una cuerda cósmica. Crédito: PhysicsWorld.com
Por tanto, cuando observásemos un objeto con una cuerda cósmica en la trayectoria de nuestra mirada, deberíamos ver este objeto dos veces, con una separación entre ambas del orden del defecto de ángulo del cono generado por la curvatura del espacio-tiempo. Esta doble imagen sería característica de la presencia de una cuerda cósmica, pues otros cuerpos, como estrellas o agujeros negros, curvan el espacio-tiempo de manera distinta, generando al menos cuatro deformadas. Por tanto, una observación de este fenómeno no podría dar lugar a un falso positivo.
En este sentido, el nombre de cuerda cósmica está justificado debido a que son impresionantemente pesadas, pasando a ser objetos macroscópicos aun cuando su efecto es pequeño. Una cuerda de seis kilómetros de longitud cuya separación entre ambas geodésicas es de apenas 4 segundos de arco tendría ¡la masa de la Tierra!. Evidentemente, cuerdas de este calibre no se espera que existan en la naturaleza, por lo que los defectos de ángulo esperados son aún menores y, por tanto, muy difíciles de medir.
Una de las virtudes de teoría es que puede detectarse por la observación. Aunque las cuerdas en sí son invisibles, sus efectos no tienen por qué serlo. La idea de las súpercuerdas nació de la física de partículas, más que en el de la cosmología (a pesar del , la cuerdas cósmicas no tienen nada que ver con la teoría de las “súpercuerdas”, que mantiene que las partículas elementales tienen forma de cuerda). Surgió en la década de los sesenta cuando los físicos comenzaron a entrelazar las tres fuerzas no gravitacionales – electromagnetismo y fuerzas nucleares fuertes y débiles – en una teoría unificada.
En 1976, el concepto de las cuerdas se había hecho un poco más tangible, gracias a Tom Kibble. Kibble estudiaba las consecuencias cosmológicas de las grande teorías unificadas. Estaba particularmente interesado en las del 10^-35 segundo después del Big Bang, cuando las temperaturas en el cosmos embrionario bajaron más de billones de billones de grados. Ese fue el en que las fuerzas y las partículas se diferenciaron unas de otras.

Podrían estar por todas partes y formar de todo
Aunque no todas si son muchas las Grandes Teorías Unificadas y teorías de supersimetría las que predicen la formación de cuerdas en la congelación del segundo 10-35 después del comienzo del tiempo, cuando la fuerza fuerte se congeló y el universo se infló. Las cuerdas se deben considerar un subproducto del proceso mismo de congelación. Es cierto que aunque las diversas teorías no predicen cuerdas idénticas, sí predicen cuerdas con las mismas propiedades generales. En primer lugar las cuerdas son extremadamente masivas y también extremadamente delgadas; la anchura de una cuerda es mucho menor que la anchura de un protón1. Las cuerdas no llevan carga eléctrica, así que no interaccionan con la radiación como las partículas ordinarias. Aparecen en todas las formas; largas lineas ondulantes, lazos vibrantes, espirales tridimensionales, etc. Sí, con esas propiedades podrían un candidato perfecto la “materia oscura”. Ejercen una atracción gravitatoria, no pueden ser rotas por la presión de la radiación en los inicios del Universo.
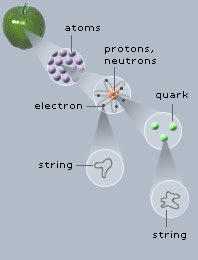
El espesor estimado de una cuerda es de 10-30 centímetros, comparados con los 10-13 de un protón. Además de ser la más larga, y posiblemente la más vieja estructura del universo conocido, una cuerda cósmica sería la más delgada: su diámetro sería 100.000.000.000.000.000 veces más pequeño que el de un protón.. Y cuerda sería terriblemente inquieta, algo así como un látigo agitándose por el espacio casi a la velocidad de la luz. Las curvas vibrarían como enloquecidas bandas de goma, emitiendo una corriente continua de ondas gravitacionales: rizos en la misma tela del espacio-tiempo. ¿Qué pasaría si una cuerda cósmica tropezara con un planeta? Al ser tan delgada, podría traspasarlo sin tropezar con un solo núcleo atómico. Pero de todos modos, su intenso campo gravitatorio causaría el caos.
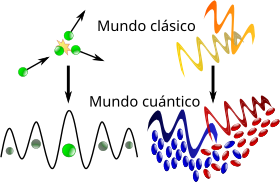

El misterioso “universo” de los campos cuánticos que nadie sabe lo que esconder
A los cosmólogos les gusta visualizar esta revolucionaria transición como una especie de “cristalización”: el espacio, en un principio saturado de energía, cambió a la más vacía y más fría que rodea actualmente nuestro planeta. Pero la cristalización fue, probablemente, imperfecta. En el cosmos recién nacido podría haberse estropeado con defectos y grietas, a medida que se enfriaba rápidamente y se hinchaba. En fin, muchas elucubraciones y conjeturas que surgen siempre que no sabemos explicar esa verdad que la Naturaleza esconde y, mientras tanto nosotros, simples mortales de la especie Homo, seguimos dejando volar nuestra imaginación que trata, cargada siempre de curiosidad, de desvelar esos misterios insondables del Universo.
emilio silvera
















 Totales: 74.291.487
Totales: 74.291.487 Conectados: 68
Conectados: 68