¿Cómo se desarrolló la Teoría de la Relatividad?

A ella se pudo llegar gracias al desarrollo de una serie de pensamientos que comienza por Faraday y Maxwell y asentados en el principio de que todo suceso físico debe atribuirse a acciones cercanas, o, dicho en términos más matemáticos, en ecuaciones a derivadas parciales. Maxwell consiguió expresarlo así para el caso de los fenómenos electromagnéticos en cuerpos inmóviles, desarrollando la idea del efecto magnético de la corriente de desplazamiento en el vacío y proponiendo la identidad entre los campos “electromotores” producidos por inducción y los campos electrostáticos.

Con esta reconocida imagen nos podemos hacer una idea del campo magnético

La ampliación de la electrodinámica al caso de los cuerpos en movimiento fue una tarea que quedó para los sucesores de Maxwell. H. Hertz intentó resolver el problema asignado al espacio vacío (éter) unas propiedades físicas totalmente similares a las de la materia ponderable; en particular, el éter, al igual que la materia debería poseer determinada velocidad en cada punto. La inducción electromagnética o magneto-eléctrica debía estar determinada por la velocidad de variación del flujo eléctrico, o magnético, como en los cuerpos en reposo, siempre que estas variaciones de velocidad se produjeran con respecto a elementos de la superficie que se movieran con el cuerpo. Sin embargo, la teoría de Hertz contradecía el experimento fundamental de Fizeau sobre la propagación de la luz a través de fluidos en movimiento. La ampliación más inmediata de la teoría de Maxwell a los cuerpos en movimiento era incompatible con el experimento.

                La física oculta del éter

En ese punto la salvación llegó de la mano de H. A. Lorentz. Siendo partidario incondicional de la teoría atomista de la materia, Lorentz no podía concebir esta última como un emplazamiento de campos electromagnéticos continuos. En consecuencia, concibió estos campos como condiciones o estados del éter, que se consideraba continuo. Lorentz se imaginaba el éter como algo que en esencia era independiente de la materia, tanto mecánica como físicamente. El éter no debía participar del movimiento de la materia y sólo debía mantener una interacción con ella en tanto que la materia se concebía como conductora de cargas eléctricas ligadas a ella.

Bien sabido es de todos que el átomo es un conglomerado de cargas eléctricas que, siendo positivas (protones) y negativas (electrones), al ser equivalentes se anulan las unas a las otras y se logra la armonía y estabilidad requerida para que, el universo pueda formar las moléculas y, éstas, se agrupan para conformar la materia.

El gran avance metodológico de la teoría de Lorentz residía en el hecho de que, gracias a ella, toda la electrodinámica de los cuerpos en reposo y en movimiento se podía reducir a las ecuaciones del espacio vacío de Maxwell. Esta teoría no sólo era superior a la de Hertz desde un punto de vista metodológico, sino que, además, gracias a ella, H. A. Lorentz consiguió dar una explicación asombrosamente acertada de los hechos experimentales.

Sólo hay un punto de importancia fundamental en el que la teoría no resulta satisfactoria. Parece ser que daba preferencia a un sistema de coordenadas que se encontrara en un determinado estado de movimiento (un sistema de coordenadas que estaba en reposo con respecto al éter luminífero) frente a todos los demás sistemas de coordenadas que se encontraran en movimiento con relación a éste. En este punto parecía que la teoría estaba en contradicción frontal con la mecánica clásica, en la cual todos los sistemas inerciales (que tienen un movimiento uniforme unos con respecto a otros) son equivalentes como sistemas de coordenadas (principio especial de la relatividad). En este sentido, todos los experimentos realizados en el ámbito de la electrodinámica (en particular el experimento de Michelson) ponía de manifiesto la equivalencia de todos los sistemas inerciales, es decir, apoyaban el principio especial de la relatividad.

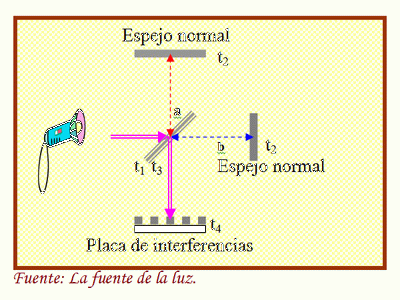
Experimento Michelson-Morley Reposo con el éter luminífero Interferómetro de Michelson y Morley en reposo respecto al éter luminífero

El movimiento del éter siempre fue un misterio que muchos quisieron resolver y, para ello, se hicieron experimentos de todo tipo. El de Michelson-Morley vino a dejar claro el tema y sirvió a Einstein para descartar el éter de su teoría. Sin embargo, pasado el tiempo, ahora mismo, se está hablando de nuevo de la existencia de una especie de “éter” que impregna todo el espacio.

Así las cosas, la teoría especial de la relatividad surgió precisamente gracias a esta dificultad inicial, que en sí misma resultaba insoportable. La teoría nació como respuesta a la pregunta: ¿Realmente existe una contradicción entre el principio especial de la relatividad y las ecuaciones de campo de Maxwell para el espacio vacío? Aparentemente la respuesta tenía que ser afirmativa. Las mencionadas ecuaciones son va´lidas para un sistema de coordenadas K y se introduce un nuevo sistema de coordenadas K¹ mediante las ecuaciones de transformación, aparentemente fáciles de justificar (aquí las obviaré) y que nos llevan a la transformación de Galileo y, entonces, las ecuaciones de campo de Maxwell ya no se cumplen para esas nuevas coordenadas.

Las coordenadas han sido muy útiles y de fructífero rendimiento

Pero siguiendo con en tema tenemos que decir que, muchas veces, las apariencias engañan. Mediante un análisis más profundo del significado físico del espacio y del tiempo se puede ver que la transformación de Galileo se basa en suposiciones arbitrarias, especialmente en la hipótesis de que la afirmación de la simultaneidad tiene un sentido independiente del estado de movimiento que tenga el sistema de coordenadas utilizado. Queda claro que las ecuaciones de campo en el vacío satisfacían el principio especial de la relatividad cuando se utilizaban las ecuaciones de la Transformación de Lorentz.

Es estas ecuaciones, x, y, z son las coordenadas medidas con una vara de medir que se encuentra en reposo con respecto al sistema de coordenadas (y aunque no las he querido reflejar aquí para no enredar), y en ellas, t representa el tiempo medido con un reloj que se encuentra en reposo y está debidamente ajustado.

Lo grande y lo pequeño: Eso es la Teoría

Ahora bien, para que pueda cumplirse el principio especial de la relatividad, es necesario que todas las ecuaciones de la física conserven invariable su forma al pasar de un sistema inercial a otro, cuando utilizamos para este cambio la Transformación de Lorentz. En lenguaje matemático, diremos que todos los sistemas de ecuaciones que expresan leyes físicas deben ser covariantes con respecto a la Transformación de Lorentz. Por consiguiente, bajo un punto de vista metodológico, el principio especial de la relatividad es comparable al principio de Carnot, que afirma la imposibilidad del perpetuum mobile (movimiento perpetuo o continuo) de segunda especie, ya que, al igual que este último, establece una condición general que deben cumplir todas las leyes naturales.

De manera que la transformación de Einstein, que es la transformación de Lorentz queda como

Podría dejarlo aquí, pero vamos a complicarlo un poco. Introducimos una nueva coordenada espacial a partir de ct, el producto de una velocidad por el tiempo es el espacio y utilizamos la siguiente notación:

Con lo que la transformación de Lorentz queda de la forma más simétrica.

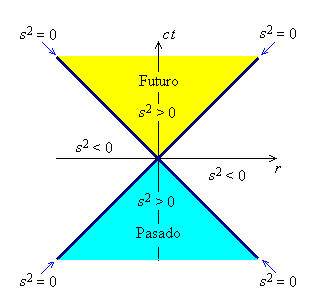
“El origen en el diagrama espacio-tiempo (ct, r) = (0, 0) representa el “ahora”. En la región de color amarillo que representa el “futuro” que le espera al observador predomina el componente temporal sobre el componente espacial, con lo cual s² siempre es mayor que cero (positivo) y por lo tanto es una región de intervalos tipo temporal. En la región de color ciano que representa el “pasado” que recorrió el observador también predomina el componente temporal sobre el componente espacial, con lo cual s² siempre es mayor que cero (positivo) y por lo tanto también es una región de intervalos tipo temporal (timelike). En las líneas que delimitan al cono de luz la componente temporal es igual a la componente espacial con lo cual s² = 0, y es aquí en donde tenemos a los intervalos tipo luminoso que involucran rayos de luz. Y fuera de todo esto tenemos a los intervalos en donde el componente espacial es mayor que el componente temporal con lo cual s² es menor que cero (negativo) siendo por lo tanto la región de intervalos tipo espacial.”

Para esta condición de covariancia encontró H. Minkowski una espresión especialmente bella y sugerente que revela un parentesco formal entre la geometría euclidea tridimensional y el continuo espacio-tiempo de la física.

Seguidamente tendría que exponer aquí un esquema con ecuaciones de la geometría euclidea tridimensional y otro (para comparar) de la teoría especial de la relatividad. Sin embargo, no queriendo complejidades que desvíen al lector de la historia esencial, diré que de ellas se deduce que el tiempo es equivalente a las coordenadas espaciales (dejando a un lado sus relaciones con la realidad), no por lo que respecta a su significado físico, sino por el papel que desempeña en las ecuaciones de la física. desde este punto de vista, la física es en cierto modo una geometría euclidea de cuatro dimensiones o, mejor dicho, un determinado tipo de estática en un continuo euclideo cuatridimensional.

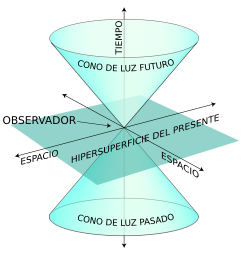
Cono de luz en un espacio-tiempo de Minkowski

El desarrollo de la teoría especial de la relatividad se desarrolló en dos pasos principales: la adaptación de la métrica espacio-temporal a la electrodinámica de Maxwell y una adaptación del resto de la físca a esa métrica espacio-temporal modificada. El primero de estos procesos de adaptación profujo la relativización de la simultaneidad, la influencia del mocimiento en varas de medir y relojes, una modificación de la cinemática y, en particular, un nuevo teorema de adiciín de las velocidades.

El segundo proceso de adaptación dio lugar a una modificación de las leyes newtonianas del movimiento para grandes velocidades, así como una aclaración sobre la naturaleza de la masa inercial cuya importancia es fundamental. Se descubrió que la inercia no es una propiedad fundamental de la materia, ni una magnitud irreducible, sino una propiedad de la energía. Si a un cuerpo se le suministra una energía E, su masa inercial aumenta en una cantidad E/c², donde c es la velocidad de la luz en el vacío; a la inversa, un cuerpo de masa m debe ser considerado como una reserva de energía de magnitud mc².

Cuando se intentó establecer el vínculo entre las teorías de la gravitación y la teoría especial de la relatividad, no tardó en verse que esto no era posible de una manera natural. A propósito de ello a Einstein de le ocurrió que la fuerza de la gravedad posee una propiedad fundamental que la distingue de la fuerza electromagnética: todos los cuerpos caen en un campo gravitatorio con la misma aceleración, o -formulando lo mismo de otra manera- la masa inercial y gravitatoria de un cuerpo son numéricamente iguales.

                                  La vinculación gravitatoria de los cuerpos es bien patente y, en la Tierra y la Luna, tenemos la mejor prueba de ello.

Esta igualdad numérica de la masa inercial y gravitatoria nos hace sospechar que ambas sean esencialmente idénticas; pero ¿pueden las masas inerciales y gravitatorias ser realmente iguales? Esta pregunta nos lleva directamente a la teoría general de la relatividad. ¿No sería posible considerar que la Tierra no realiza un movimiento de rotación, si concibo la fuerza centrífuga, que actúa sobre los cuerpos que están en reposo con respecto a la Tierra, como un campo gravitatorio “real” (o como una parte del campo gravitatorio)? Si esta idea es viable, entonces está realmente demostrado que las masas inercial y gravitatoria son idénticas, ya que el mismo efecto que se considera como inercia desde el punto de vista de un sistema que “no toma parte en la rotación”, puede interpretarse como gravedad si se observa desde un sistema que comparte la rotación. Según Newton, esta interpretación es imposible, porque no se puede considerar según la ley de Newton que el campo centrífugo esté generado por masas, y porque un campo “real” del tipo de “campo de Coriolis” no está contemplado en la teoría newtoniana.

Pero, ¿sería posible sustituir la ley de campos de Newton por alguna otra compatible con el campo que puede existir con respecto a un sistema de coordenadas “en rotación”? El convencimiento de que las masas inercial y gravitatoria son idénticas inspiró a Einstein una confianza incondicional en la validez de esta interpretación y, una idea le llenó de esperanza: conocemos los campos “aparentes” que son válidos con respecto a cualquier sistema de coordenadas que se mueve arbitrariamente con relación a un sistema inercial; utilizando los campos (especiales) se podrá estudiar la ley que cunplen en general los campos gravitatorios. para ello habrá que tener en cuanta que, como generadoras de estos campos, serán determinantes las masas ponderables, o bien lo será la densidad de energía (una magnitud que posee el carácter transformador de un tensor), según el resultado fundamental de la teoría especial de la relatividad.

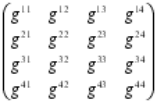
Tensor métrico de Riemann

A partir de aquí, tendríamos que entrar en el Tensor métrico de Riemann pero, ¡el tiempo! como pasa siempre, me lo impide así que, dejaremos para mejor ocasión el continuar con el tema que, como todo lo que concierne a Einstein, termina siendo fascinante porque, dentro de su complejidad, subyace una sencillez de ideas que, finalmente, terminan por conquistarnos.

emilio silvera

[?]