Las leyes que gobiernan el mundo físico tienen dos características importantes: muchas leyes de la naturaleza permanecen inalterables, no se alteran cuando cambia la escala, pero hay otros fenómenos, tales como una vela encendida o las gotas de agua, que no cambian del mismo modo. La implicación final es que el mundo de los objetos muy pequeños será completamente diferente del mundo ordinario.

Ahora tendríamos que hablar algo de la mecánica cuántica y, en ese ámbito, las reglas de la mecánica cuántica funcionan tan bien que resultaría realmente difícil refutarlas. Acordaos de los trucos ingeniosos descubiertos por Werner Hesinberg, Paul Dirac, o, Schrödinger que vinieron a mejorar y completar  las reglas generales. Sin embargo, algunos de aquellos pioneros (Einstein y el mismo Schrödinger), sin embargo, presentaron serias objeciones a dicha interpretación de la naturaleza de lo muy pequeño.

Esta cosita tan pequeñita, el electrón,  es inversamente proporcional en importancia para que el mundo, la Naturaleza, y,  nuestro Universo sea como es. Se ha conseguido fotografíar a un electrón. Poder filmar y fotografiar un electrón no es fácil por dos razones: primero, gira alrededor del núcleo atómico cada 0,000000000000000140 segundos , y, porque para fotografiar un electrón es necesario bombardearlo con partículas de luz (y cualquier que haya intentado sacarle una foto a un electrón sabe que hay que hacerlo sin flash). La imagen de la izquierda es el resultado.

El electrón fue descubierto en 1.897 por el físico británico Joseph John Thomson (1.856 – 1940). El problema de la estructura (si la hay) del electrón no está resuelto. Si el electrón se considera como una carga puntual, su autoenergía es infinita y surgen dificultades en la ecuación conocida como de Lorentz–Dirac.

Muchas veces hemos hablado del electrón que rodea el núcleo, de su carga eléctrica negativa que complementa la positiva de los protones y hace estable al átomo; tiene una masa de solamente 1/1.836 de la del núcleo más ligero, el del hidrógeno que está formado por un solo protón. La importancia del electrón es vital en el universo.

Pero busquemos los “cuantos”. La física del siglo XX empezó exactamente en el año 1900, cuando el físico alemán Max Planck propuso una posible solución a un problema que había estado intrigando a los físicos durante años. Es el problema de la luz que emiten los cuerpos calentados a una cierta temperatura, y también la radiación infrarroja emitida, con menor intensidad, por los objetos más fríos (radiación de cuerpo negro).

Estaba bien aceptado entonces que esta radiación tenía un origen electromagnético y que se conocían las leyes de la naturaleza que regían estas ondas electromagnéticas. También se conocían las leyes para el frío y el calor, la así llamada “termodinámica”, o al menos eso parecía. Pero si utilizamos las leyes de la termodinámica para calcular la intensidad de una radiación, el resultado no tiene ningún sentido. Los cálculos nos dicen que se emitiría una cantidad infinita de radiación en el ultravioleta más lejano y, desde luego, esto no es lo que sucede. Lo que se observa es que la intensidad de la radiación muestra un pico a una cierta longitud de onda característica, y que la intensidad disminuye tanto para longitudes mayores como para menores. Esta longitud de onda característica es inversamente proporcional a la temperatura absoluta de objeto radiante (la temperatura absoluta se define por una escala de temperatura que empieza a 273º bajo cero). Cuando a 1.000 ºC un objeto se pone al “rojo vivo”, el objeto está radiando en la zona de luz visible.

Lo que Planck propuso fue simplemente que la radiación sólo podía ser emitida en paquetes de un tamaño dado. La cantidad de energía de uno de esos paquetes, o cuantos, es inversamente proporcional a la longitud de onda, y por tanto, proporcional a la frecuencia de radiación emitida. La fórmula es E = hν, donde E es la energía del paquete, ν es la frecuencia y h es una nueva constante fundamental de la naturaleza, la constante de Planck. Cuando Planck calculó la intensidad de la radiación térmica imponiendo esta nueva condición, el resultado coincidió perfectamente con las observaciones.

Poco tiempo después, en 1905, Einstein formuló esta teoría de una manera mucho más tajante: él sugirió que los objetos calientes no son los únicos que emiten radiación en paquetes de energía, sino que toda la radiación consiste en múltiplos del paquete de energía de Planck. El príncipe francés Louis-Victor de Broglie, dándole otra vuelta a la teoría, propuso que no sólo cualquier cosa que oscila tiene energía, sino que cualquier cosa con energía se debe comportar como una “onda” que se extiende en una cierta región del espacio, y que la frecuencia ν de la oscilación verifica la ecuación de Planck. Por lo tanto, los cuantos asociados con los rayos de luz deberían verse como una clase de partículas elementales: el fotón. Todas las demás clases de partículas llevan asociadas  diferentes ondas oscilantes de campos de fuerza, pero esto lo veremos más adelante.

                                                          Onda y partícula

El curioso comportamiento de los electrones en el interior del átomo, descubierto y explicado por el famoso físico danés Niels Bohr, se pudo atribuir a las ondas de de Broglie. Poco después, en 1926, Edwin Schrödinger descubrió cómo escribir la teoría ondulatoria de de Broglie con ecuaciones matemáticas exactas. La precisión con la cual se podían realizar cálculos era asombrosa, y pronto quedó claro que el comportamiento de todos los objetos pequeños quedaba exactamente determinado por las recién descubiertas “ecuaciones de ondas cuánticas”.

Está bien comprobado que la mecánica cuántica funciona de maravilla…, pero, sin embargo, surge una pregunta muy formal: ¿qué significan realmente estas ecuaciones?, ¿qué es lo que están describiendo? Cuando Isaac Newton, allá en 1867 formuló cómo debían moverse los planetas alrededor del Sol, estaba claro para todo el mundo qué significaban sus ecuaciones: que los planetas estaban siempre en una posición bien definida des espacio y que sus posiciones y sus velocidades en un momento concreto determinan inequívocamente cómo evolucionarán las posiciones y las velocidades en el tiempo.

Pero para los electrones todo es diferente. Su comportamiento parece estar envuelto en misterio. Es como si pudieran “existir” en diferentes lugares simultáneamente, como si fueran una nube o una onda, y esto no es un efecto pequeño. Si se realizan experimentos con suficiente precisión, se puede determinar que el electrón parece capaz de moverse simultáneamente a lo largo de trayectorias muy separadas unas de otras. ¿Qué puede significar todo esto?

La notable capacidad de un electrón de existir en dos lugares al mismo tiempo ha sido controlada en el material electrónico más comun el – silicio – por primera vez, siendo este un gran avance para la electrónica moderna y tiene un potencial enorme para el futuro y para la creación de la computadora cuantica.

Imagen: El movimiento de los electrones en el silicio. El electrón gira alrededor de una átomo de fósforo embebido en la estructura cristalina del silicio, que se muestra en plata. La distribución de densidad electrónica no perturbado, a partir de la ecuaciones de la mecánica cuántica del movimiento se muestra en amarillo. Un pulso de láser de electrones puede modificar el estado de manera que tiene la distribución de la densidad se muestra en verde. Nuestro pulso láser en primer lugar, que llegan desde la izquierda, pone el electrón en una superposición de ambos estados, que podemos controlar con un segundo impulso, también desde la izquierda, para dar un pulso que se detecte que, saliendo a la derecha. Las características de este “eco” del pulso nos hablan de la superposición que hemos hecho.

Cuando podamos dominar el “universo” de lo muy pequeño… ¡Nuestro Universo será otro para nosotros!

Las leyes de la mecánica cuántica han sido establecidas con mucha precisión; permite cómo calcular cualquier cosa que queramos saber. Pero si queremos “interpretar” el resultado, nos encontramos con una curiosa incertidumbre fundamental: que varias propiedades de las partículas pequeñas no pueden estar bien definidas de manera simultánea. Por ejemplo, podemos determinar la velocidad de una partícula con mucha precisión, pero entonces no sabremos exactamente dónde se encuentra; o a la inversa, podemos determinar la posición con precisión, pero entonces su velocidad queda mal definida. Si una partícula tiene espín (rotación alrededor de su eje), la dirección alrededor de la cual está rotando (la orientación del eje) no puede ser definida con gran precisión.

No es fácil explicar de forma sencilla de dónde viene esta incertidumbre, pero existen ejemplos en la vida cotidiana que tienen algo parecido. La altura de un tono y la duración en el tiempo durante el cual oímos el tono tienen una incertidumbre mutua similar. Para afinar un instrumento musical se debe escuchar una nota durante un cierto intervalo de tiempo y compararla, por ejemplo, con un diapasón que debe vibrar también durante un tiempo. Notas muy breves no tienen bien definido el tono.

              Sí, la música influye en el cerebro

Para que las reglas de la mecánica cuántica funcionen, es necesario que todos los fenómenos naturales en el mundo de las cosas pequeñas estén regidos por las mismas reglas. Esto incluye a los virus, bacterias e incluso a las personas. Sin embargo, cuando más grande y más pesado es un objeto, más difícil es observar las desviaciones de las leyes del movimiento “clásicas” debidas a la mecánica cuántica. Me gustaría referirme a esta exigencia tan importante y tan peculiar de la teoría con la palabra “holismo”. Esto no es exactamente lo mismo que entienden algunos filósofos por holismo, y que podría definir como “el todo es más que la suma de sus partes”. Si la física nos ha enseñado algo es justo lo contrario. Un objeto compuesto de un gran número de partículas puede ser entendido exactamente si se conocen las propiedades de sus partes (partículas); basta que sepamos sumar correctamente (¡y esto no es nada fácil en mecánica cuántica!). Lo que entiendo por holismo es que, efectivamente, el todo es la suma de las partes, pero sólo se puede hacer la suma si todas las partes obedecen a las mismas leyes. Por ejemplo,  la constante de Planck, h, que es igual a 6’626075… × 10^-34 Julios segundo, debe ser exactamente la misma para cualquier objeto en cualquier sitio, es decir, debe ser una constante universal.

Aunque la semilla la puso Planck en 1900, fue a partir de 1930 cuando la mecánica cuántica se aplicó con mucho éxito a problemas relacionados con núcleos atómicos, moléculas y materia en estado sólido. La mecánica cuántica hizo posible comprender un extenso conjunto de datos, de otra manera enigmáticos. Sus predicciones han sido de una exactitud notable. Ejemplo de ésto último es la increíble precisión de diecisiete cifras significativas del momento magnético del electrón calculadas por la EDC (Electrodinámica Cuántica) comparadas con el experimento.

Si viajamos hacia lo muy pequeño tendremos que ir más allá de los átomos, que son objetos voluminosos y frágiles comparados con lo que nos ocupará a continuación: el núcleo atómico y lo que allí se encuentra. Los electrones,  que ahora vemos “a gran distancia” dando vueltas alrededor del núcleo, son muy pequeños y extremadamente robustos. El núcleo está constituido por dos especies de bloques: protones y neutrones. El protón  (del griego πρώτος, primero) debe su nombre al hecho de que el núcleo atómico más sencillo, que es el hidrógeno, está formado por un solo protón. Tiene una unidad de carga positiva. El neutrón recuerda al protón como si fuera su hermano gemelo: su masa es prácticamente la misma, su espín es el mismo, pero en el neutrón, como su propio nombre da a entender, no hay carga eléctrica; es neutro.

La masa de estas partículas se expresa en una unidad llamada mega-electrón-voltio o MeV, para abreviar. Un MeV, que equivale a 10⁶ electrón-voltios, es la cantidad de energía de movimiento que adquiere una partícula con una unidad de carga (tal como un electrón o un protón) cuando atraviesa una diferencia de potencial de 10⁶ (1.000.000) voltios. Como esta energía se transforma en masa, el MeV es una unidad útil de masa para las partículas elementales.

                                            Sí, las reglas de la mecánica cuántica son extrañas y misteriosas, pero…

Las reglas de la mecánica cuántica funcionan tan bien que refutarlas resulta realmente difícil. Los trucos ingeniosos descubiertos por Werner Heisemberg, Paul Dirac y muchos otros mejoraron y completaron las reglas generales. Pero Einstein y otros pioneros como Erwin Schrödinger siempre presentaron serias objeciones a esta interpretación. Quizá funcione bien, pero ¿dónde está exactamente el electrón?, ¿en el punto x o en el punto y? En pocas palabras, ¿dónde está en realidad?, y ¿cuál es la realidad que hay detrás de nuestras fórmulas? Si tenemos que creer a Bohr, no tiene sentido buscar tal realidad. Las reglas de la mecánica cuántica, por sí mismas, y las observaciones realizadas con detectores son las únicas realidades de las que podemos hablar.

La mecánica cuántica puede ser definida o resumida así: en principio, con las leyes de la naturaleza que conocemos ahora se puede predecir el resultado de cualquier experimento, en el sentido que la predicción consiste en dos factores: el primer factor es un cálculo definido con exactitud del efecto de las fuerzas y estructuras, tan riguroso como las leyes de Isaac Newton para el movimiento de los planetas en el Sistema Solar; el segundo factor es una arbitrariedad estadística e incontrolable definida matemáticamente de forma estricta. Las partículas seguirán una distribución de probabilidades dadas, primero de una forma y luego de otra. Las probabilidades se pueden calcular utilizando la ecuación de Schrödinger de función de onda (Ψ) que, con muchas probabilidades nos indicará el lugar probable donde se encuentra una partícula en un momento dado.

              ¿Ganaré algún día esa lotería que me quite de trabajar por necesidad?

Muchos estiman que esta teoría de las probabilidades desaparecerá cuando se consiga la teoría que explique, de forma completa, todas las fuerzas; la buscada teoría del todo, lo que implica que nuestra descripción actual incluye variables y fuerzas que (aún) no conocemos o no entendemos. Esta interpretación se conoce como hipótesis de las variables ocultas.

Albert Einstein, Nathan Rosen y Boris Podolski idearon un “Gedankenexperiment”, un experimento hipotético, realizado sobre el papel, para el cual la mecánica cuántica predecía como resultado algo que es imposible de reproducir en ninguna teoría razonable de variables ocultas. Más tarde, el físico irlandés John Stewar Bell consiguió convertir este resultado en un teorema matemático; el teorema de imposibilidad.

emilio silvera

[?]

Desde que puedo recordar, he sido un amante de la física. Me asombran cuestiones como la luz, su naturaleza de un conglomerado de colores, ondas y partículas, su velocidad que nos marca el límite del máximo que podemos correr en nuestro universo, y en fin, muchos otros misterios que encierra esa cosa tan cotidiana que nos rodea y lo inunda todo haciendo posible que podamos ver por donde vamos, que las plantas vivan y emitan oxígeno o que nos calentemos. Realmente, sin luz, nuestra vida no sería posible. Entonces, ¿qué es realmente la luz?

                                          Ondas de luz de luces de colores, enjambres de fotones

Muchos (casi todos) opinan que es algo inmaterial. Los objetos materiales grandes o muy pequeños como las galaxias o los electrones, son materia. La luz, sin embargo, se cree que es inmaterial; dos rayos de luz se cruzan sin afectarse el uno al otro. Sin embargo, yo, que desde luego no soy un experto, opino en cambio que la luz es simplemente una forma de energía lumínica, otra forma en la que se puede presentar la materia. Nosotros mismos, en última instancia, somos luz.

  Ahora sabemos que la luz es una de las formas de radiación, la que el ojo humano puede captar

Está claro que los estudiosos de la época antigua y medieval estaban por completo a oscuras acerca de la naturaleza de la luz. Especulaban sobre que consistía en partículas emitidas por objetos relucientes o tal vez por el mismo ojo. Establecieron el hecho de que la luz viajaba en línea recta, que se reflejaba en un espejo con un ángulo igual a aquel con el que el rayo choca con el espejo, y que un rayo de luz se inclina (se refracta) cuando pasa del aire al cristal, al agua o a cualquier otra sustancia transparente.

Cuando la luz entra en un cristal o en alguna sustancia transparente, de una forma oblicua (es decir, en un ángulo respecto de la vertical), siempre se refracta en una dirección que forma un ángulo menor respecto de la vertical. La exacta relación entre el ángulo original y el ángulo reflejado fue elaborada por primera vez en 1.621 por el físico neerlandés Willerbrord Snell. No publicó sus hallazgos y el filósofo francés René Descartes descubrió la ley, independientemente, en 1.637.

Los primeros experimentos importantes acerca de la naturaleza de la luz fueron llevados a cabo por Isaac Newton en 1.666, al permitir que un rayo de luz entrase en una habitación oscura a través de una grieta de las persianas, cayendo oblicuamente sobre una cara de un prisma de cristal triangular. El rayo se refracta cuando entra en el cristal y se refracta aún más en la misma dirección cuando sale por una segunda cara del prisma (las dos refracciones en la misma dirección se originan porque los lados del prisma se encuentran en ángulo en vez de en forma paralela, como sería el caso de una lámina ordinaria de cristal).

Newton atrapó el rayo emergente sobre una pantalla blanca para ver el efecto de la refracción reforzada. Descubrió que, en vez de formar una mancha de luz blanca, el rayo se extendía en una gama de colores: rojo, anaranjado, amarillo verde, azul y violeta, en este orden. Newton dedujo de ello que la luz blanca corriente era una mezcla de varias luces que excitaban por separado nuestros ojos para producir las diversas sensaciones de colores. La amplia banda de sus componentes se denominó spectrum (palabra latina que significa espectro o fantasma). Newton llegó a la conclusión de que la luz se componía de diminutas partículas (“corpúsculos”), que viajaban a enormes velocidades. Le surgieron y se planteó algunas inquietantes cuestiones: ¿por qué se refractaban las partículas de luz verde más que las de luz amarilla? ¿Cómo se explicaba que dos rayos de luz se cruzaran sin perturbarse mutuamente, es decir, sin que se produjeran colisiones entre partículas?

En 1.678, el físico neerlandés Christian Huyghens (un científico polifacético que había construido el primer reloj de péndulo y realizado importantes trabajos astronómicos) propuso una teoría opuesta: la de que la luz se componía de minúsculas ondas. Y si sus componentes fueran ondas, no sería difícil explicar las diversas difracciones de los diferentes tipos de luz a través de un medio refractante, siempre y cuando se aceptara que la luz se movía más despacio en ese medio refractante que en el aire. La cantidad de refracción variaría con la longitud de las ondas: cuanto más corta fuese tal longitud, tanto mayor sería la refracción. Ello significaba que la luz violeta (la más sensible a este fenómeno) debía de tener una longitud de onda más corta que la luz azul; ésta, más corta que la verde, y así sucesivamente.

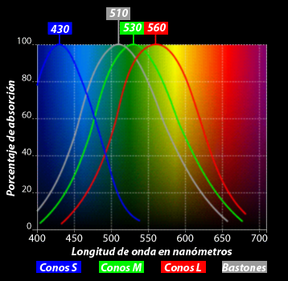
“La teoría del color se refiere a cómo el ojo humano percibe los colores, y a la descripción y gestión de dichos colores en el monitor y en la impresión. La Teoría del Color tiene relación con todas las áreas del proceso de producción gráfica: fotografía, escaneado, presentación en pantalla, pruebas finales e impresión. También es importante en el “mundo” astronómico.”

Lo que permitía al ojo distinguir los colores eran esas diferencias entre longitudes de onda. Y como es natural, si la luz estaba integrada por ondas, dos rayos podrían cruzarse sin dificultad alguna (las ondas sonoras y las del agua se cruzan continuamente sin perder sus respectivas identidades).

Pero la teoría de Huyghens sobre las ondas tampoco fue muy satisfactoria. No explicaba por qué se movían en línea recta los rayos luminosos, ni por qué proyectaban sombras recortadas, ni aclaraba por qué las ondas luminosas no podían rodear los obstáculos, del mismo modo que pueden hacerlo las ondas sonoras y de agua. Por añadidura, se objetaba que si la luz consistía en ondas, ¿cómo podía viajar por el vacío, ya que cruzaba el espacio desde el Sol y las estrellas? ¿Cuál era esa mecánica ondulatoria?

Aproximadamente durante un siglo, contendieron entre sí estas teorías. La teoría corpuscular de Newton fue, con mucho, la más popular, en parte porque la respaldó el famoso nombre de su autor. Pero hacia 1.801, un físico y médico inglés, de nombre Thomas Young, llevó a cabo un experimento que arrastró la opinión pública al campo opuesto. Proyectó un fino rayo luminoso sobre una pantalla, haciéndolo pasar antes por dos orificios casi juntos; si la luz estuviera compuesta por partículas, cuando los dos rayos emergieran de ambos orificios, formarían presuntamente en la pantalla una región más luminosa donde se superpusieran, y regiones menos brillantes, donde no se diera tal superposición. La pantalla mostró una serie de bandas luminosas, separadas entre sí por bandas oscuras; pareció incluso que en esos intervalos de sombra, la luz de ambos rayos contribuía a intensificar la oscuridad.

Propugnada por Christian Huygens en el año 1678, describe y explica lo que hoy se considera como leyes de reflexión y refracción. Define a la luz como un movimiento ondulatorio semejante al que se produce con el sonido.

Sería fácil explicarlo mediante la teoría ondulatoria; la banda luminosa representaba el refuerzo prestado por las ondas de un rayo a las ondas del otro, dicho de otra manera, entraban “en fase” dos trenes de ondas, es decir, ambos nodos, al unirse, se fortalecían el uno al otro. Por otra parte, las bandas oscuras representaban puntos en los que las ondas estaban “desfasadas” porque el vientre de una neutralizaba el nodo de la otra. En vez de aunar sus fuerzas, las ondas se interferían mutuamente, reduciendo la energía luminosa neta a las proximidades del punto cero.

Considerando la anchura de las bandas y la distancia entre los dos orificios por lo que surgen ambos rayos, se pudo calcular la longitud de las ondas luminosas, por ejemplo, de la luz roja a la violeta o de los colores intermedios. Las longitudes de onda resultaron ser muy pequeñas. Así, la de la luz roja era de unos 0’000075 cm. Hoy se  expresan las longitudes de las ondas luminosas mediante una unidad muy práctica ideada por Ángstrom; esta unidad, denominada igualmente Ángstrom (Å) en honor a su autor, es la cienmillonésima parte de un centímetro. Así pues, la longitud de onda de la luz roja equivale más o menos a 7.500 Å, y la de la luz violeta a 3.900 Å, mientras que las de colores visibles en el espectro oscilan entre ambas cifras.

La cortedad de estas ondas es muy importante. La razón de que las ondas luminosas se desplacen en línea recta y proyecten sombras recortadas se debe a que todas son incomparablemente más pequeñas que cualquier objeto; pueden contornear un obstáculo sólo si este no es mucho mayor que la longitud de onda. Hasta las bacterias, por ejemplo, tienen un volumen muy superior al de una onda luminosa, y por tanto, la luz puede definir claramente sus contornos bajo el microscopio. Sólo los objetos cuyas dimensiones se asemejan a la longitud de onda luminosa (por ejemplo, los virus y otras partículas subatómicas) son lo suficientemente pequeños como para que puedan ser contorneados por las ondas luminosas.

Un físico francés, Agustín-Jean Fresnel, fue quien demostró por vez primera en 1.818 que si un objeto es lo suficientemente pequeño, la onda luminosa lo contorneará sin dificultad. En tal caso, la luz determina el llamado fenómeno de “difracción”. Por ejemplo, las finísimas líneas paralelas de una “reja de difracción” actúan como una serie de minúsculos obstáculos, que se refuerzan entre sí. Puesto que la magnitud de la difracción va asociada a la longitud de onda, se produce el espectro. A la inversa, se puede calcular la longitud de onda midiendo la difracción de cualquier color o porción del espectro, así como la separación de las marcas sobre el cristal.

Fraunhofer exploró dicha reja de difracción con objeto de averiguar sus finalidades prácticas, progreso que suele olvidarse, pues queda eclipsado por su descubrimiento más famoso, los rayos espectrales. El físico americano Henry Augustus Roland ideó la reja cóncava y desarrolló técnicas para regularlas de acuerdo con 20.000 líneas por pulgada. Ello hizo posible la sustitución del prisma por el espectroscopio.

Ante tales hallazgos experimentales, más el desarrollo metódico y matemático del movimiento ondulatorio, debido a Fresnel, pareció que la teoría ondulatoria de la luz había arraigado definitivamente, desplazando y relegando para siempre a la teoría corpuscular.

No sólo se aceptó la existencia de ondas luminosas, sino que también se midió su longitud con una precisión cada vez mayor. Hacia 1.827, el físico francés Jacques Babinet sugirió que se empleara la longitud de onda luminosa (una cantidad física inalcanzable) como unidad para medir tales longitudes, en vez de las muy diversas unidades ideadas y empleadas por el hombre. Sin embargo, tal sugerencia no se llevó a la práctica hasta 1.880 cuando el físico germano-americano Albert Abraham Michelson inventó un instrumento denominado “interferómetro”, que podía medir las longitudes de ondas luminosas con una exactitud sin precedentes. En 1.893, Michelson midió la onda de la raya roja en el espectro del cadmio y determinó que su longitud era de 1/1.553.164 m.

Pero la incertidumbre reapareció al descubrirse que los elementos estaban compuestos por isótopos diferentes, cada uno de los cuales aportaba una raya cuya longitud de onda difería ligeramente de las restantes. En la década de 1.930 se midieron las rayas del criptón 86. Como quiera que este isótopo fuera gaseoso, se podía abordar con bajas temperaturas, para frenar el movimiento atómico y reducir el consecutivo engrosamiento de la raya.

En 1.960, el Comité Internacional de Pesos y Medidas adoptó la raya del criptón 86 como unidad fundamental de la longitud. Entonces se re-estableció la longitud del metro como 1.650.763’73 veces la longitud de onda de dicha raya espectral. Ello aumentó mil veces la precisión de las medidas de longitud. Hasta entonces se había medido el antiguo metro patrón con un margen de error equivalente a una millonésima, mientras que en lo sucesivo se pudo medir la longitud de onda con un margen de error equivalente a una milmillonésima.

emilio silvera

[?]

                           El núcleo atómico

El propio Rutherford empezó a vislumbrar la respuesta. Entre 1.906 y 1.908 (hace ahora un siglo) realizó constantes experimentos disparando partículas alfa contra una lámina sutil de metal (como oro o platino), para analizar sus átomos. La mayor parte de los proyectiles atravesaron la barrera sin desviarse (como balas a través de las hojas de un árbol), pero no todos. En la placa fotográfica que le sirvió de blanco tras el metal, Rutherford descubrió varios impactos dispersos e insospechados alrededor del punto central. Comprobó que algunas partículas habían rebotado. Era como si en vez de atravesar las hojas, algunos proyectiles hubiesen chocado contra algo más sólido. Rutherford supuso que aquella “balas” habían chocado contra una especie de núcleo denso, que ocupaba sólo una parte mínima del volumen atómico y ese núcleo de intensa densidad desviaban los proyectiles que acertaban a chocar contra él. Ello ocurría en muy raras ocasiones, lo cual demostraba que los núcleos atómicos debían ser realmente ínfimos, porque un proyectil había de encontrar por fuerza muchos millones de átomos al atravesar la lámina metálica.

                 El experimento de Rutherford

Era lógico suponer, pues, que los protones constituían ese núcleo duro. Rutherford representó los protones atómicos como elementos apiñados alrededor de un minúsculo “núcleo atómico” que servía de centro (después de todo eso, hemos podido saber que el diámetro de ese núcleo equivale a algo más de una cienmilésima del volumen total del átomo).

En 1.908 se concedió a Rutherford el premio Nobel de Química por su extraordinaria labor de investigación sobre la naturaleza de la materia. Él fue el responsable de importantes descubrimientos que permitieron conocer la estructura de los átomos en esa primera avanzadilla.

Desde entonces se pueden describir con términos más concretos los átomos específicos y sus diversos comportamientos. Por ejemplo, el átomo de hidrógeno posee un solo electrón. Si se elimina, el protón restante se asocia inmediatamente a alguna molécula vecina; y cuando el núcleo desnudo de hidrógeno no encuentra por este medio un electrón que participe, actúa como un protón (es decir, una partícula subatómica), lo cual le permite penetrar en la materia y reaccionar con otros núcleos si conserva la suficiente energía.

El helio, que posee dos electrones, no cede uno con tanta facilidad. Sus dos electrones forman un caparazón hermético, por lo cual el átomo es inerte. No obstante, si se despoja al helio de ambos electrones, se convierte en una partícula alfa, es decir, una partícula subatómica portadora de dos unidades de carga positiva.

Hay un tercer elemento, el litio, cuyo átomo tiene tres electrones. Si se despoja de uno o dos, se transforma en ión, y si pierde los tres, queda reducida a un núcleo desnudo, con una carga positiva de tres unidades.

Las unidades de carga positiva en el núcleo atómico deben ser numéricamente idénticas a los electrones que contiene por norma, pues el átomo suele ser un cuerpo neutro, y esta igualdad de lo positivo con lo negativo es el equilibrio. De hecho, los números atómicos de sus elementos se basan en sus unidades de carga positiva, no en las de carga negativa, porque resulta fácil hacer variar el número de electrones atómicos dentro de la formación iónica, pero en cambio se encuentran grandes dificultades si se desea alterar el número de sus protones.

Apenas esbozado este esquema de la construcción atómica, surgieron nuevos enigmas. El número de unidades con carga positiva en un núcleo no equilibró, en ningún caso, el peso nuclear ni la masa, exceptuando el caso del átomo de hidrógeno. Para citar un ejemplo, se averiguó que el núcleo de helio tenía una carga positiva dos veces mayor que la del núcleo de hidrógeno; pero como ya se sabía, su masa era cuatro veces mayor que la de este último. Y la situación empeoró progresivamente a medida que se descendía por la tabla de elementos, e incluso cuando se alcanzó el uranio, se encontró un núcleo con una masa igual a 238 protones, pero una carga que equivalía sólo a 92.

¿Cómo era posible que un núcleo que contenía cuatro protones (según se suponía el núcleo de helio) tuviera sólo dos unidades de carga positiva? Según la más simple y primera conjetura emitida, la presencia en el núcleo de partículas cargadas negativamente y con peso despreciable neutralizaba dos unidades de carga. Como es natural, se pensó también en el electrón. Se podría componer el rompecabezas si se suponía que en núcleo de helio estaba integrado por cuatro protones y dos electrones neutralizadores, lo cual deja libre una carga positiva neta de dos, y así sucesivamente, hasta llegar al uranio, cuyo núcleo tendría, pues, 238 protones y 146 electrones, con 92 unidades libres de carga positiva. El hecho de que los núcleos radiactivos emitieran electrones (según se había comprobado ya, por ejemplo, en el caso de las partículas beta), reforzó esta idea general. Dicha teoría prevaleció durante más de una década, hasta que por caminos indirectos, llegó una respuesta mejor como resultado de otras investigaciones.

Pero entre tanto se habían presentado algunas objeciones rigurosas contra dicha hipótesis. Por lo pronto, si el núcleo estaba constituido esencialmente de protones, mientras que los ligeros electrones no aportaban prácticamente ninguna contribución a la masa, ¿cómo se explicaba que las masas relativas de varios núcleos no estuvieran representadas por número enteros? Según los pesos atómicos conocidos, el núcleo del átomo cloro, por ejemplo, tenía una masa 35’5 veces mayor que la del núcleo de hidrógeno. ¿Acaso significaba esto que contenía 35’5 protones? Ningún científico (ni entonces ni ahora) podía aceptar la existencia de medio protón.

Este singular interrogante encontró una respuesta incluso antes de solventar el problema principal, y ello dio lugar a una interesante historia.

Isótopos; construcción de bloques uniformes

Allá por 1.816, el físico inglés William Prout había insinuado ya que el átomo de hidrógeno debía entrar en la constitución de todos los átomos. Con el tiempo se fueron desvelando los pesos atómicos, y la teoría de Prout quedó arrinconada, pues se comprobó que muchos elementos tenían pesos fraccionarios (para lo cual se tomó el oxígeno, tipificado al 16). El cloro, según dije antes, tiene un peso atómico aproximado de 35’5, o para ser exactos, 35’457. otros ejemplos son el antimonio, con un peso atómico de 121’75, el galio con 137’34, el boro con 10’811 y el cadmio con 112’40.

Hacia principios de siglo se hizo una serie de observaciones desconcertantes, que condujeron al esclarecimiento. El inglés William Crookes (el del tubo Crookes) logró disociar del uranio una sustancia cuya ínfima cantidad resultó ser mucho más radiactiva que el propio uranio. Apoyándose en su experimento, afirmó que el uranio no tenía radiactividad, y que ésta procedía exclusivamente de dicha impureza, que él denominó uranio X. Por otra parte, Henri Becquerel descubrió que el uranio purificado y ligeramente radiactivo adquiría mayor radiactividad con el tiempo, por causas desconocidas. Si se deja reposar durante algún tiempo, se podía extraer de él repetidas veces uranio activo X. Para decirlo de otra manera, por su propia radiactividad, el uranio se convertía en el uranio X, más radiactivo aún.

Por entonces, Rutherford, a su vez, separó del torio un torio X muy radiactivo, y comprobó también que el torio seguía produciendo más torio X. Hacia aquellas fechas se sabía ya que el más famoso de los elementos radiactivos, el radio, emitía un gas radiactivo, denominado radón. Por tanto, Rutherford y su ayudante, el químico Frederick Soddy, dedujeron que durante la emisión de sus partículas los átomos radiactivos se transformaron en otras variedades de átomos radiactivos.

Varios químicos que investigaron tales transformaciones lograron obtener un surtido muy variado de nuevas sustancias, a las que dieron nombres tales como radio A, radio B, mesotorio I, mesotorio II y actinio C. Luego los agruparon todos en tres series, de acuerdo con sus historiales atómicos. Una serie se originó del uranio disociado; otra del torio, y la tercera del actinio (si bien más tarde se encontró un predecesor del actinio, llamado protactinio).

En total se identificaron unos cuarenta miembros de esas series, y cada uno se distinguió por su peculiar esquema de radiación. Pero los productos finales de las tres series fueron idénticos: en último término, todas las cadenas de sustancias conducían al mismo elemento, el plomo.

Ahora bien, esas cuarenta sustancias no podían ser, sin excepción, elementos disociados. Entre el uranio (92) y el plomo (82) había sólo diez lugares en la tabla periódica, y todos ellos, salvo dos, pertenecían a elementos conocidos.

Hay que huir de los desechos radiactivos que produce la actividad del hombre para cubrir su necesidad energética. Sabemos de otras fuentes de energías más limpias pero… No sabemos como obtenerlas con menos coste del que supone el producirlas

En realidad, los químicos descubrieron que aunque las sustancias diferían entre sí por su radiactividad, algunas tenían propiedades químicas idénticas. Por ejemplo, ya en 1.907 los químicos americanos Herbert Newby McCoy y W. H. Ross descubrieron que el radiotorio (uno entre los varios productos de la desintegración del torio) mostraba el mismo comportamiento químico que el torio, y el radio D, el mismo que el plomo, tanto que a veces era llamado radioplomo. De todo lo cual se infirió que tales sustancias eran en realidad variedades de mismo elemento: el radiotorio, una forma de torio; el radioplomo, un miembro de una familia de plomos; y así sucesivamente.

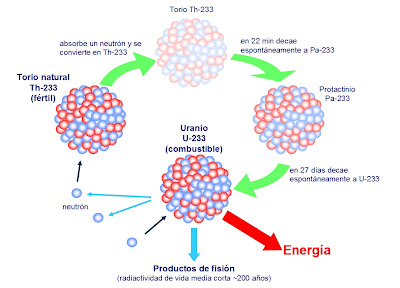
En 1.913, Soddy esclareció esta idea y le dio más amplitud. Demostró que cuando un átomo emitía una partícula alfa, se transformaba en un elemento que ocupaba dos lugares más abajo en la lista de elementos, y que cuando emitía una partícula beta, ocupaba, después de su transformación, el lugar inmediatamente superior. Con arreglo a tal norma, el radiotorio descendía en la tabla hasta el lugar del torio, y lo mismo ocurría con las sustancias denominadas uranio X y uranio Y, es decir, que los tres serían variedades del elemento 90. Así mismo, el radio D, el radio B, el torio B y el actinio B compartirían el lugar del plomo como variedades del elemento 82.

Soddy dio el nombre de isótopos (del griego iso y topos, “el mismo lugar”) a todos los miembros de una familia de sustancias que ocupaban el mismo lugar en la tabla periódica. En 1.921 se le concedió el premio Nobel de Química.

El modelo protón-electrón del núcleo concordó perfectamente con la teoría de Soddy sobre los isótopos. Al retirar una partícula alfa de un núcleo, se reducía en dos unidades la carga positiva de dicho núcleo, exactamente lo que necesitaba para bajar dos lugares en la tabla periódica. Por otra parte, cuando el núcleo expulsaba un electrón (partícula beta), quedaba sin neutralizar un protón adicional, y ello incrementaba en una unidad la carga positiva del núcleo, lo cual era como agregar una unidad al número atómico, y por tanto, el elemento pasaba a ocupar la posición inmediatamente superior en la tabla periódica de los elementos.

¡Maravilloso!

emilio silvera

[?]

El psicólogo Eric Ericsson llegó a proponer una teoría de estadios psicológicos del desarrollo. Un conflicto fundamental caracteriza cada fase. Si este conflicto no queda resuelto, puede enconarse e incluso provocar una regresión a un periodo anterior. Análogamente, el psicólogo Jean Piaget demostró que el desarrollo mental de la primera infancia tampoco es un desarrollo continuo de aprendizaje, sino que está realmente caracterizado por estadios discontinuos en la capacidad de conceptualización de un niño. Un mes, un niño puede dejar de buscar una pelota una vez que ha rodado fuera de su campo de visión, sin comprender que la pelota existe aunque no la vea. Al mes siguiente, esto resultará obvio para el niño.

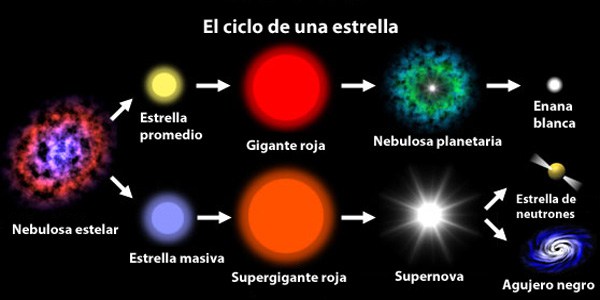
           Las estrellas pasan por diferentes ciclos que las convierten en algo distinto a lo que eran

Esta es la esencia de la dialéctica. Según esta filosofía, todos los objetos (personas, gases, estrellas, el propio universo) pasan por una serie de estadios. Cada estadio está caracterizado por un conflicto entre dos fuerzas opuestas. La naturaleza de dicho conflicto determina, de hecho, la naturaleza del estadio. Cuando el conflicto se resuelve, el objeto pasa a un objetivo o estadio superior, llamado síntesis, donde empieza una nueva contradicción, y el proceso pasa de nuevo a un nivel superior.

 Pequeños cambios cuantitativos se acumulan hasta que, eventualmente, se produce una ruptura cualitativa con el pasado. Esta teoría se aplica también a las sociedades o culturas. Las tensiones en una sociedad pueden crecer espectacularmente, como la hicieron en Francia a finales del siglo XVIII. Los campesinos se enfrenaban al hambre, se produjeron motines espontáneos y la aristocracia se retiró a sus fortalezas. Cuando las tensiones alcanzaron su punto de ruptura, ocurrió una transición de fase de lo cuantitativo a los cualitativo: los campesinos tomaron las armas, tomaron París y asaltaron la Bastilla.

                           El desorden es clave en las transiciones de fase de los materiales

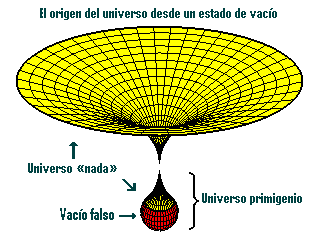
Las transiciones de fases pueden ser también asuntos bastante explosivos. Por ejemplo, pensemos en un río que ha sido represado. Tras la presa se forma rápidamente un embalse con agua a enorme presión. Puesto que es inestable, el embalse está en el falso vacío. El agua preferiría estar en su verdadero vacío, significando esto que preferiría reventar la presa y correr aguas abajo, hacia un estado de menor energía. Así pues, una transición de fase implicaría un estallido de la presa, que tendría consecuencias desastrosas.

También podría poner aquí el ejemplo más explosivo de una bomba atómica, donde el falso vacío corresponde al núcleo inestable de uranio donde residen atrapadas enormes energías explosivas que son un millón de veces más poderosas, para masas iguales, que para un explosivo químico.  De vez en cuando, el núcleo pasa por efecto túnel a un estado más bajo, lo que significa que el núcleo se rompe espontáneamente. Esto se denomina desintegración radiactiva. Sin embargo, disparando neutrones contra los núcleos de uranio, es posible liberar de golpe esta energía encerrada según la formula de Einstein E = mc². Por supuesto, dicha liberación es una explosión atómica; ¡menuda transición de fase!

Las nuevas características descubiertas por los científicos en las transiciones de fases es que normalmente van acompañadas de una ruptura de simetría. Al premio Nobel Abdus Salam le gusta la ilustración siguiente: consideremos una mesa de banquete circular, donde todos los comensales están sentados con una copa de champán a cada lado. Aquí existe simetría. Mirando la mesa del banquete reflejada en un espejo, vemos lo mismo: cada comensal sentado en torno a la mesa, con copas de champán a cada lado.  Asimismo, podemos girar la mesa de banquete circular y la disposición sigue siendo la misma.

Rompamos ahora la simetría. Supongamos ahora que el primer comensal toma la copa que hay a su derecha. Siguiendo la pauta, todos los demás comensales tomaran la copa de champán de su derecha. Nótese que la imagen de la mesa del banquete vista en el espejo produce la situación opuesta.  Cada comensal ha tomado la copa izquierda. De este modo, la simetría izquierda-derecha se ha roto.

Así pues, el estado de máxima simetría es con frecuencia también un estado inestable, y por lo tanto corresponde a un falso vacío.

Con respecto a la teoría de supercuerdas, los físicos suponen (aunque todavía no lo puedan demostrar) que el universo decadimensional original era inestable y pasó por efecto túnel a un universo de cuatro y otro de seis dimensiones. Así pues, el universo original estaba en un estado de falso vacío, el estado de máxima simetría, mientras que hoy estamos en el estado roto del verdadero vacío.

Al principio, cuando el universo era simétrico, sólo existía una sola fuerza que unificaba a todas las que ahora conocemos, la gravedad, las fuerzas electromagnéticas y las nucleares débil y fuerte, todas emergían de aquel plasma opaco de alta energía que lo inundaba todo. Más tarde, cuando el universo comenzó a enfriarse, se hizo transparente y apareció la luz, las fuerzas se separaron en las cuatro conocidas, emergieron las primeras quarks para unirse y formar protones y neutrones, los primeros núcleos aparecieron para atraer a los electrones que formaron aquellos primeros átomos.  Doscientos millones de años más tarde, se formaron las primeras estrellas y galaxias. Con el paso del tiempo, las estrellas sintetizaron los elementos pesados de nuestros cuerpos, fabricados en supernovas que estallaron, incluso antes de que se formase el Sol. Podemos decir, sin temor a equivocarnos, que una supernova anónima explotó hace miles de millones de años y sembró la nube de gas que dio lugar a nuestro sistema solar, poniendo allí los materiales complejos y necesarios para que algunos miles de millones de años más tarde, tras la evolución, apareciéramos nosotros.

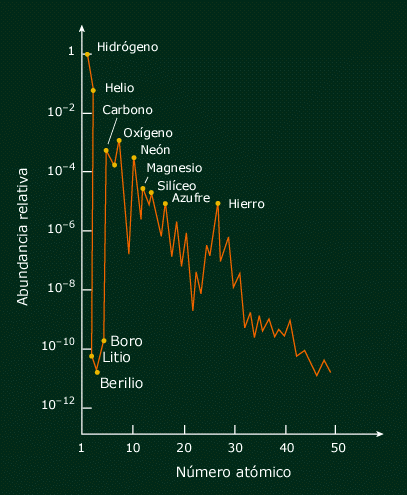
Las estrellas evolucionan desde que en su núcleo se comienza a fusionar hidrógeno en helio, de los elementos más ligeros a los más pesados.  Avanza creando en el horno termonuclear, cada vez, metales y elementos más pesados. Cuando llega al hierro y explosiona en la forma explosiva de  una supernova. Luego, cuando este material estelar es otra vez recogido en una nueva estrella rica en hidrógeno, al ser de segunda generación (como nuestro Sol), comienza de nuevo el proceso de fusión llevando consigo materiales complejos de aquella supernova.

Puesto que el peso promedio de los protones en los productos de fisión, como el cesio y el kriptón, es menor que el peso promedio de los protones de uranio, el exceso de masa se ha transformado en energía mediante E = mc². Esta es la fuente de energía que subyace en la bomba atómica.

La constelación de Orión. Betelgeuse, la estrella de la parte superior izquierda, es fría, por lo que parece enrojecida. Deneb, la estrella inferior derecha, es caliente, por lo que parece azulada. La temperatura de la estrella también puede determinarse a partir de su espectro -la distribución de colores o longitudes de onda en la luz de la estrella (figura 2). Esta figura ilustra la belleza de los colores de la luz de las estrellas. Esta luz ha pasado por la atmósfera exterior de la estrella, y los iones, átomos y moléculas en la atmósfera absorben longitudes de onda específicas del espectro. Esto produce líneas oscuras, o colores que faltan en el espectro (figura 2). Dependiendo de la temperatura de la atmósfera, los átomos pueden ser ionizados, excitados, o combinados en moléculas. El estado observado de los átomos, en el espectro, proporciona información sobre la temperatura.

Los espectros de muchas estrellas, desde la más caliente (O6.5: arriba) hasta la más fría (M5: abajo). Las diferentes apariencias de los espectros se deben a las diferentes temperaturas de las estrellas. Los tres espectros de abajo son de estrellas peculiares de alguna manera. (Fuente: Observatorio Nacional de Astronomía Óptica).

               Observadores del Universo +

Así pues, la curva de energía de enlace no sólo explica el nacimiento y muerte de las estrellas y la creación de elementos complejos que también hicieron posible que nosotros estemos ahora aquí y, muy posiblemente, será también el factor determinante para que, lejos de aquí, en otros sistemas solares a muchos años luz de distancia, puedan florecer otras especies inteligentes que, al igual que la especie humana, se pregunten por su origen y estudien los fenómenos de las fuerzas fundamentales del universo, los componentes de la materia y, como nosotros, se interesen por el destino que nos espera en el futuro.

Cuando alguien oye por vez primera la historia de la vida de las estrellas, generalmente (lo sé por experiencia), no dice nada, pero su rostro refleja escepticismo. ¿Cómo puede vivir una estrella 10.000 millones de años? Después de todo, nadie ha vivido tanto tiempo como para ser testigo de su evolución.

Sin embargo, tenemos los medios técnicos y científicos para saber la edad que tiene, por ejemplo, el Sol.

emilio silvera

[?]