El vacío superconductor – La máquina de Higgs-Kibble II

Lo único que no resulta ser lo mismo cuando se mira a través del microscopio (o, en la jerca de la física teórica, cuando se realiza una transformación de escala) es la masa de la partícula. Esto se debe a que el alcance de la fuerza parece mayor a través del microscopìo y, por lo tanto, la masa de la partícula parece ser menor. Nótese que esta situación es la opuesta a la que se presenta en vida corriente donde un grano de arena parece mayor -¿más pesado, por lo tanto?- cuando se observa con un microscopio.

                                          Granos de arena vistos al microscopio

Una consecuencia de todo esto es que en una teoría de Yang-Mills el termino de masa parece desaparecer cuando se realiza una transformación de escala, lo que implica que a través del microscopio se recupera la invariancia gauge. Esto es lo que causa la dificultad con la que se enfrentó Veltman. ¿Se puede observar directamente el potencial vector de Yang-Mills? Parece que puede observarse en el mundo de las cosas grandes, pero no en el mundo de lo pequeño. Esto es una contradicción y es una razón por la que ese esquema nunca ha podido funcionar adecuadamente.

En 2009, la empresa canadiense D-Wave Systems, conjuntamente con la NASA, desarrolló un ordenador cuántico de 128 cubits. Rainer contiene 128 dispositivos físicos (pequeños aros de metal niobidio) que a muy baja temperatura actúan como sistemas cuánticos con dos niveles (es decir, cubits) como consecuencia de la superconductividad.

¡Había una salida! Pero ésta procede de una rama muy diferente de la física teórica, la física de los metales a muy bajas temperaturas. A esas temperaturas, los “fenómenos cuánticos” dan lugar a efectos muy sorprendentes, que se describen con teorías cuánticas de campos, exactamente iguales a las que se utilizan en la física de partículas elementales. La física de partículas elementales no tienen nada que ver con la física de bajas temperaturas, pero las matemáticas son muy parecidas.

En algunos materiales, el “campo” que se hace importante a temperaturas muy bajas podría ser el que describe cómo los átomos oscilan alrededor de sus posiciones de equilibrio, o el que describe a los electrones en este tipo de material. A temperaturas muy baja nos encontramos con los “cuantos” de esos campos. Por ejemplo, el “fonón” es el cuanto del sonido. Su comportamiento recuerda al fotón, el cuanto de la luz, salvo que los números son muy diferentes: los fonones se propagan con la velocidad del sonido, a cientos o quizá miles de metros por segundo, y los fotones lo hacen a la velocidad de la luz que es de 300.000 km/s, ¡aproximadamente un millón de veces más deprisa! Las partículas elementales en las que estamos interesados generalmente tienen velocidades cercanas a las de la luz.

El fonon es la partícula elemental del sonido, como el foton lo es en la luz...

Uno de los “fenómenos cuánticos” más espectaculares que tienen lugar en los materiales muy fríos es la llamada superconductividad, fenómeno consistente en el hecho de que la resistencia que presenta ese material al paso de la corriente eléctrica se hace cero. Una de las consecuencias de ese estado es que el material no admite la más mínima diferencia de potencial eléctrico, porque ésta sería inmediatamente neutralizada por una corriente eléctrica “ideal”. El material tampoco admite la presencia de campos magnéticos porque, de acuerdo con las ecuaciones de Maxwell, la creación del campo magnético está asociada con una corriente eléctrica inducida, que al no encontrar resistencia neutralizaría completamente el campo magnético. Por lo tanto, en el interior de un superconductor no se puede crear ni un campo electrónico ni magnético. Esta situación sólo cambia si las corrientes inducidas son muy elevadas, como ocurre cuando se somete el superconductor a los campos de imanes muy potentes y que perturban el material. No siendo capaz de resistir una fuerza tan brutal, pierde la superconductividad y se rinde permitiendo la existencia de un campo magnético en su interior.

¿Pero, qué tiene que ver un superconductor con las partículas elementales? Bien, un material superconductor se puede entender como un sistema en el cual el campo electromagnético es un campo de muy corto alcance. Está siendo apantallado y, sin embargo, es un campo de Maxwell, un campo gauge. ¡Esto es lo que hace interesante un superconductor para alguien que quiera describir la interacción débil entre partículas como una teoría gauge! ¡Qué característica tan bella de la física teórica! Se pueden comparar dos mundos completamente diferentes simplemente porque obedecen a las mismas ecuaciones matemáticas.

¿Cómo funciona un superconductor? La verdadera causa de este fenómeno peculiar la descubrieron John Bardeen, Leon N. Cooper y John R. Schrieffer por lo que recibieron el premio Nobel en 1972). Los electrones de un trozo sólido de material tienen que reunir al mismo tiempo dos condiciones especiales para dar lugar a la superconductividad: la primera es apareamiento y la segunda condensación de Bose.

“Apareamiento” significa que los electrones forman pares y actúan en pares, y los que producen la fuerza que mantiene los pares unidos son los fonones. En cada par, los electrones rotan alrededor de su propio eje, pero en direcciones opuestas, de manera que el par (llamado “par de Cooper”), en su conjunto, se comporta como si no tuviera rotación (“momento angular”). Así, un par de Cooper se comporta como una “partícula” con espín 0 y carga eléctrica.

La “condensación de Bose” es un fenómeno típicamente mecánico-cuántico. Sólo se aplica a partículas con espín entero (bosones). Al igual que los lemmings, los bosones se agrupan juntos en el estado de menor energía posible, Recuérdese que a los bosones les gusta hacer a todos la misma cosa. En este estado todavía se puede mover, pero no pueden perder más energía y, en consecuencia, no sufren ninguna resistencia a su movimiento. Los pares de Cooper se mueven libremente, de manera que pueden crear corrientes eléctricas que no encuentran ninguna resistencia. Un fenómeno parecido tiene lugar en el helio líquido a muy bajas temperaturas. Aquí los átomos de helio forman una condensación de Bose y el líquido que forman puede fluir a través de los agujeros más pequeños sin la más mínima resistencia.

                      Condensado de Bose-Einstein

Como los electrones por separado tienen espín ⅟₂ no pueden sufrir una condensación de Bose. Las partículas cuyo espín es igual a un entero más un medio (fermiones) tienen que estar en estados cuánticos diferentes debido al principio de exclusión de Pauli. Esta es la razón por la que la superconductividad sólo se puede producir cuando se forman pares. Sí, comprendo que estas afirmaciones le sugerirán varias preguntas y me disculpo por adelantado, pero de nuevo he traducido fórmulas a palabras, lo que implica que el razonamiento pueda parecer poco satisfactorio. ¡Simplemente tome esto como una cierta “lógica cuántica” difícil de manejar! Fueron el belga François Englert, el americano Robert Brout y el inglés Peter Higgs los que descubrieron que la superconductividad podría ser importante para las partículas elementales. Propusieron un modelo de partículas elementales en el cual partículas eléctricamente cargadas, sin espín, sufrían una condensación de Bose. Esta vez, sin embargo, la condensación no tenía lugar en el interior de la materia sino el vacío. Las fuerzas entre las partículas tenían que ser elegidas de tal manera que se ahorrara más energía llenando el vacío de estas partículas que dejándolo vacío. Estas partículas no son directamente observables, pero podríamos sentir el estado, en cuyo espacio y tiempo están moviéndose las partículas de Higgs (como se las conoce ahora) con la mínima energía posible, como si el espacio tiempo estuviera completamente vacío.

Haber encontrado el bosón de Higgs puede resolver el misterio de la composición de masa de todos los objetos. Esta masa está presente en las partículas subatómicas y sin ellas la materia sólida no podría existir. El bosón de Higgs está relacionado a un campo energético, que se llama el campo de Higgs, el mismo que está presente en todo el universo de igual forma como el agua inunda una piscina. Es formando parte de ese campo, que las diversas partículas, como los protones, neutrones, electrones y otras, adquieren su masa. Las partículas más pequeñas encuentran menos dificultades para desplazarse, y las más grandes lo hacen con mayor dificultad. De todas las maneras, quedan muchas por explicar. Fandila nos prguntaba que, ¿de dónde adquiere su masa el mismo Bosón de Higgs?

Las partículas de Higgs son los cuantos del “campo de Higgs”. Una característica de este campo es que su energía es mínima cuando el campo tiene una cierta intensidad, y no cuando es nulo. Lo que observamos como espacio vacío no es más que la configuración de campo con la menor energía posible. Si pasamos de la jerga de campos a la de partículas, esto significa que el espacio vacío está realmente lleno de partículas de Higgs que han sufrido una condensación Bose”.

Este espacio vacío tiene muchas propiedades en común con el interior de un superconductor. El campo electromagnético aquí también es de corto alcance. Esto está directamente relacionado con el hecho de que, en tal mundo, el fotón tiene una cierta masa en reposo.

Y aún tenemos una simetría gauge completa, es decir, la invariancia gauge no se viola en ningún sitio. Y así, sabemos cómo transformar un fotón en una partícula “con masa” sin violar la invariancia gauge. Todo lo que tenemos que hacer es añadir estas partículas de Higgs a nuestras ecuaciones.

La razón por la que el efecto de invariancia gauge en las propiedades del fotón es tan diferente ahora es que las ecuaciones están completamente alteradas por la presencia del campo de Higgs en nuestro estado vacío. A veces se dice que “el estado vacío rompe la simetría espontáneamente”. Esto no es realmente correcto, pero el fenómeno está muy relacionado con otras situaciones en las que se produce espontáneamente una rotura de simetría.

Higgs sólo consideró campos electromagnéticos “ordinarios”, pero, desde luego, sabemos que el fotónordinario en un vacío auténtico no tiene masa en reposo. Fue Thomas Kibble el que propuso hacer una teoría de Yang-Mills superconductora de esta forma, simplemente añadiendo partículas sin espín, con carga de Yang-Mills en vez de carga ordinaria, y suponer que estas partículas podían experimentar una condensación de Bose. Entonces el alcance de las interacciones de Yang-Mills se reduce y los fotones de Yang-Mills se convierten en partículas con espín igual a 1 y masa distinta de cero.

La discontinuidad manifiesta junto con la invariancia de escala (autosemejanza), que presenta la energía de las fluctuaciones del vacío cuántico. Las consecuencias de la existencia del cuanto mínimo de acción fueron revolucionarios para la comprensión del vacío. Mientras la continuidad de la acción clásica suponía un vacío plano, estable y “realmente” vacío, la discontinuidad que supone el cuanto nos dibuja un vacío inestable, en continuo cambio y muy lejos de poder ser considerado plano en las distancias atómicas y menores. El vacío cuántico es de todo menos vacío, en él la energía nunca puede quedar estabilizada en valor cero, está fluctuando sobre ese valor, continuamente se están creando y aniquilando todo tipo de partículas, llamadas por eso virtuales, en las que el producto de su energía por el tiempo de su existencia efímera es menor que el cuanto de acción. Se llaman fluctuaciones cuánticas del vacío y son las responsables de que exista un campo que lo inunda todo llamado campo de punto cero.

Algunos físicos proponen una controvertida teoría en la que un extraño tipo de materia, el Singlet de Higgs, se movería hacia el pasado o el futuro en el LHC. ¡Qué imaginación! Claro que, puestos a imaginar…

Bien sabido es que mientras más profundizamos en el conocimiento de los secretos del mundo que nos rodea, más interrogantes y misterios sin resolver se nos muestran. Cada vez que abrimos una puerta, llegamos a una habitación que tiene otras muchas por abrir. Es la búsqueda incesante del hombre, su insoslayable afán por saber el por qué, el cómo y el cuándo de todas las cosas.

¿Estaremos entrando en una especie de locura?

Bueno…

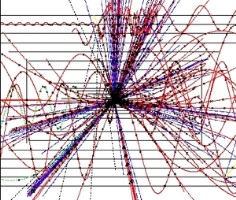
Por su parte, el científico británico Peter Higgs, de 80 años, que dio su nombre a la llamada “partícula divina” en 1964, afirmó que cree que su Bosón sería hallado gracias al Gran Colisionador. “Creo que es bastante probable” dijo pocas horas después de que entrara en funcionamiento el gigantesco acelerador. Y, según parece, se está saliendo con la suya.

De todas las maneras,  estaría bien saber, a ciencia cierta, cómo es el campo de Higgs del que toman la masa todas las partículas, y conocer, mediante que sistema se transfieren la masa, o, si cuando las partículas entran en el campo de Higgs e interrelacionan con él, es el efecto frenado el que les otorga la masa como nos dice nuestro amigo Ramón Marques en su teoría.

emilio silvera

[?]

“Inicialmente, se presenta, de modo simplificado, el Modelo Estándar como una teoría sofisticada que identifica las partículas elementales y sus interacciones. Después, en el ámbito de esa teoría, se enfocan aspectos –el vacuo no es vacío; partículas desnudas y vestidas; materia oscura y viento oscuro; materia y antimateria; el campo y el bosón de Higgs; neutrinos oscilantes– que pueden ser motivadores desde el punto de vista de la enseñanza y del aprendizaje de la Física. Finalmente, se discute la probable superación de esa teoría por otra más completa.”

“… el Modelo Estándar es, en la historia, la más sofisticada teoría matemática sobre la naturaleza. A pesar de la palabra “modelo” en su nombre, el Modelo Estándar es una teoría comprensiva que identifica las partículas básicas y especifica cómo interactúan. Todo lo que pasa en nuestro mundo (excepto los efectos de la gravedad) es resultado de las partículas del Modelo Estándar interactuando de acuerdo con sus reglas y ecuaciones.”

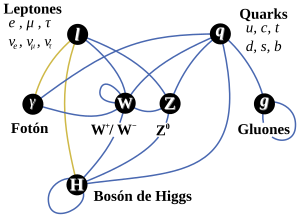
La Física actual busca una teoría más amplia que el modelo estándar . Una teoría que dé una descripción completa, unificada y consistente de la estructura fundamental del universo. ¿Será la compleja Teoría de cuerdas,que integra también la interacción gravitatoria?

El modelo estándar es una poderosa herramienta pero no cumple todas las expectativas; no es un modelo perfecto. En primer lugar, podríamos empezar por criticar que el modelo tiene casi veinte constantes que no se pueden calcular. Desde luego, se han sugerido numerosas ideas para explicar el origen de todos estos parámetros o números inexplicables y sus valores, pero el problema de todas estas teorías es que los argumentos que dan nunca han sido enteramente convincentes. ¿Por qué se iba a preocupar la naturaleza de una fórmula mágica si en ausencia de tal fórmula no hubiera contradicciones? Lo que realmente necesitamos es algún principio fundamental nuevo, tal como el principio de la relatividad, pero no queremos abandonar todos los demás principios que ya conocemos. Ésos, después de todo, han sido enormemente útiles en el descubrimiento del modelo estándar. El mejor lugar para buscar un nuevo principio es precisamente donde se encuentran los puntos débiles de la presente teoría y, construímos máquinas como el LHC para que nos diga lo que no sabemos.

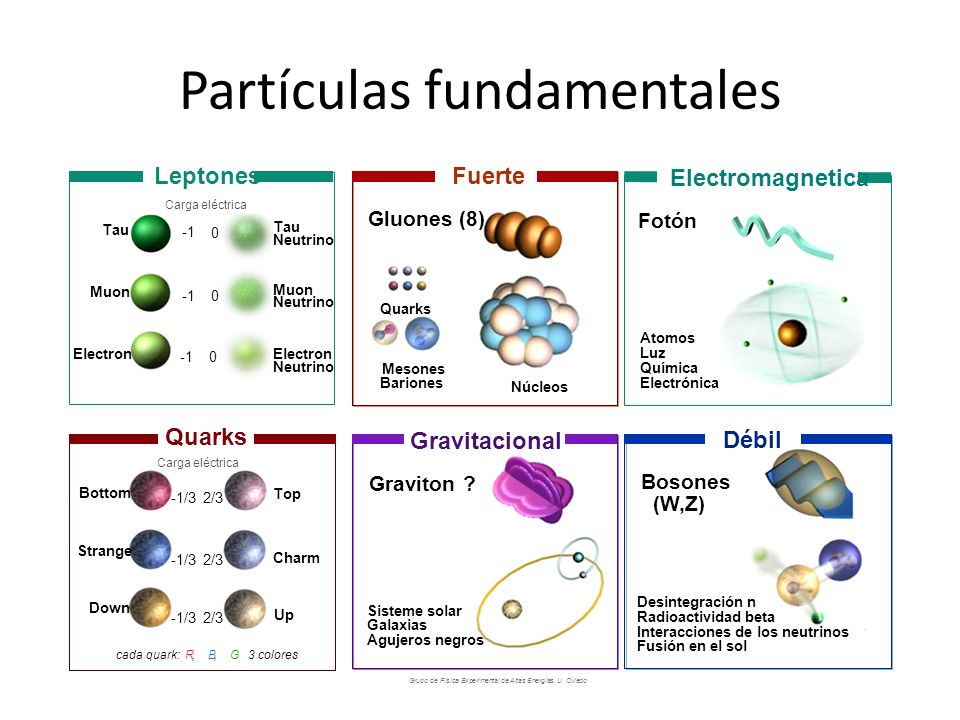
Una regla universal en la física de partículas es que para partículas con energías cada vez mayores, los efectos de las colisiones están determinados por estructuras cada vez más pequeñas en el espacio y en el tiempo. El modelo estándar es una construcción matemática que predice sin ambigüedad cómo debe ser el mundo de las estructuras aún más pequeñas. Pero existen varias razones para sospechar que sus predicciones pueden, finalmente (cuando podamos emplear más energía en un nivel más alto), resultar equivocadas.

Vistas a través del microscopio, las constantes de la naturaleza parecen estar cuidadosamente ajustadas sin ninguna otra razón aparente que hacer que las partículas parezcan lo que son. Hay algo muy erróneo aquí. Desde un punto de vista matemático no hay nada que objetar, pero la credibilidad del modelo estándar se desploma cuando se mira a escalas de tiempo y longitud extremadamente pequeñas, o lo que es lo mismo, si calculamos lo que pasaría cuando las partículas colisionan con energías extremadamente altas. ¿Y por qué debería ser el modelo válido hasta aquí? Podrían existir muchas clases de partículas súper pesadas que no han nacido porque se necesitan energías aún inalcanzables. ¿Dónde está la partícula de Higgs? ¿Cómo se esconde de nosotros el gravitón?

Allá donde se pueda encontrar el Gravitón, se estará riendo de nuestro  esfuerzo por encontrarlo

Parece que el Modelo estándar no admite la cuarta fuerza y tendremos que buscar más profundamente, en otras teorías que nos hablen y describan además de las partículas conocidas de otras nuevas que están por nacer y que no excluya la Gravedad. Ese es el Modelo que necesitamos para conocer mejor la Naturaleza.

Claro que las cosas no son tan sencilla y si deseamos evitar la necesidad de un delicado ajuste de las constantes de la naturaleza, creamos un nuevo problema: ¿cómo podemos modificar el modelo estándar de tal manera que el ajuste fino no sea necesario? Está claro que las modificaciones son necesarias, lo que implica que muy probablemente haya un límite más allá del cual el modelo tal como está deja de ser válido. El modelo estándar no será nada más que una aproximación matemática que hemos sido capaces de crear, de forma que todos los fenómenos que hemos observado hasta el presente están reflejados en él, pero cada vez que se pone en marcha un aparato más poderoso, tenemos que estar dispuestos a admitir que puedan ser necesarias algunas modificaciones del modelo para incluir nuevos datos que antes ignorábamos.

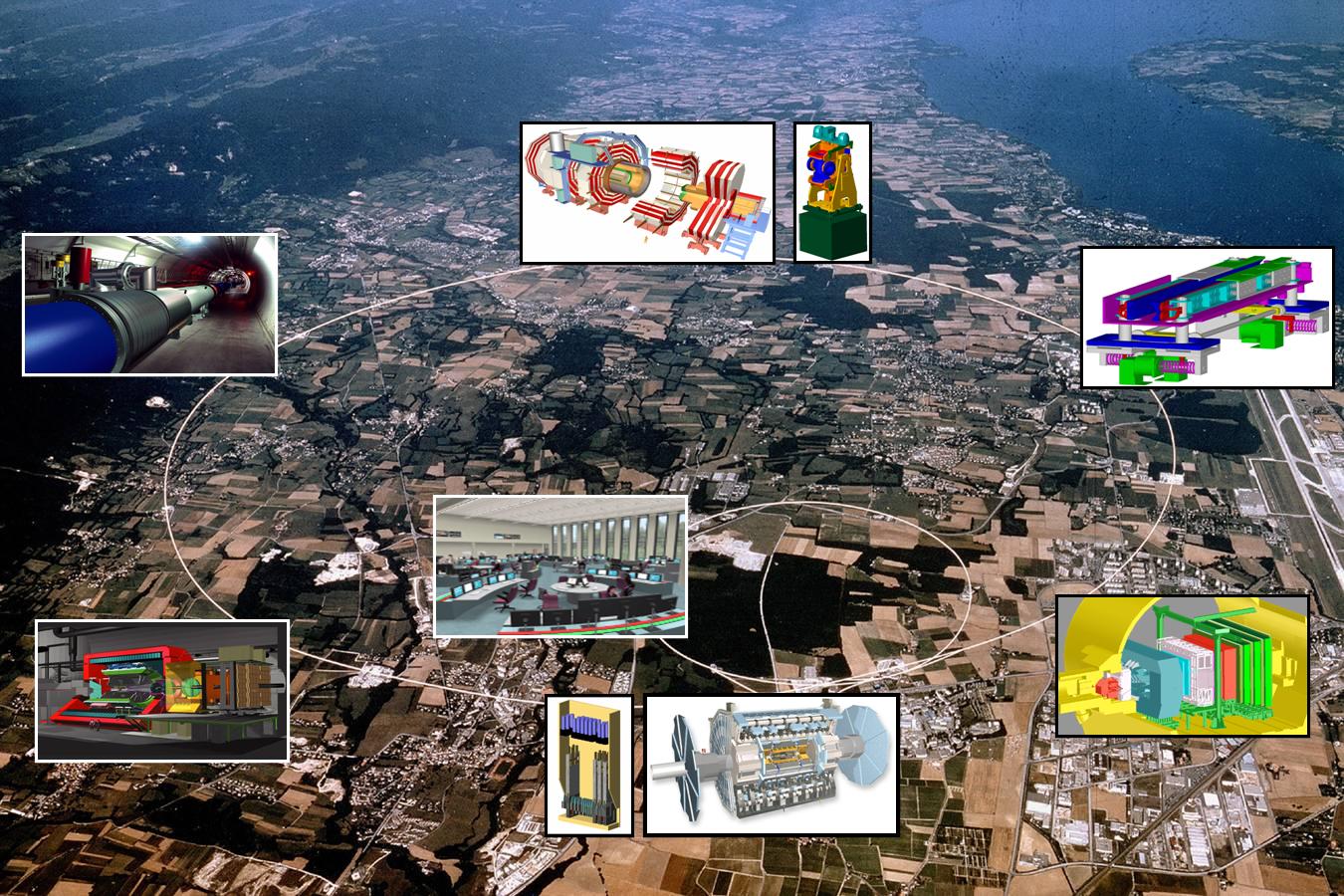
Más allá del modelo estándar habrá otras respuestas que nos lleven a poder hacer otras preguntas que en este momento, no sabemos ni plantear por falta de conocimientos.  Si no conociéramos que los protonesestán formados por Quarks, ¿cómo nos podríamos preguntar si habrá algo más allá de los Quarks?

El gobierno de Estados Unidos, después de llevar gastados miles de millones de dólares, suspendió la construcción del supercolisionador superconductor de partículas asestando un duro golpe a la física de altas energías, y se esfumó la oportunidad para obtener nuevos datos de vital importancia para el avance de este modelo, que de momento es lo mejor que tenemos.

Estas partículas compañeras supersimétricas de las usuales no se han visto. Esto quiere decir que sus masas no son iguales, las partículas supersimétricas …

Se han estado inventando nuevas ideas, como la supersimetría y el technicolor. Los astrofísicos estarán interesados en tales ideas porque predicen una gran cantidad de nuevas partículas superpesadas, y también varios tipos de partículas que interaccionan ultradébilmente, los technipiones. Éstas podrían ser las WIMP’s (Weakly Interacting Massive Particles, o Partículas Masivas Débilmente Interactivas) que pueblan los huecos entre las galaxias, y serían así las responsables de la masa perdida que los astrofísicos siguen buscando y llaman “materia oscura”.

Que aparezcan “cosas” nuevas y además, imaginarlas antes, no es fácil. Recordemos cómo Paul Dirac se sintió muy incómodo cuando en 1931 dedujo, a partir de su ecuación del electrón, que debería existir una partícula con carga eléctrica opuesta. Esa partícula no había sido descubierta y le daba reparo perturbar la paz reinante en la comunidad científica con una idea tan revolucionaria, así que disfrazó un poco la noticia: “Quizá esta partícula cargada positivamente, tan extraña, sea simplemente el protón”, sugirió. Cuando poco después se identificó la auténtica antipartícula del electrón (el positrón) se sorprendió tanto que exclamó: “¡Mi ecuación es más inteligente que su inventor!”. Este último comentario es para poner un ejemplo de cómo los físicos trabajan y buscan caminos matemáticos mediante ecuaciones de las que, en cualquier momento (si están bien planteadas), surgen nuevas ideas y descubrimientos que ni se podían pensar. Así pasó también con las ecuaciones de Einstein de la relatividad general, donde Schwarzschild dedujo la existencia de los agujeros negros.

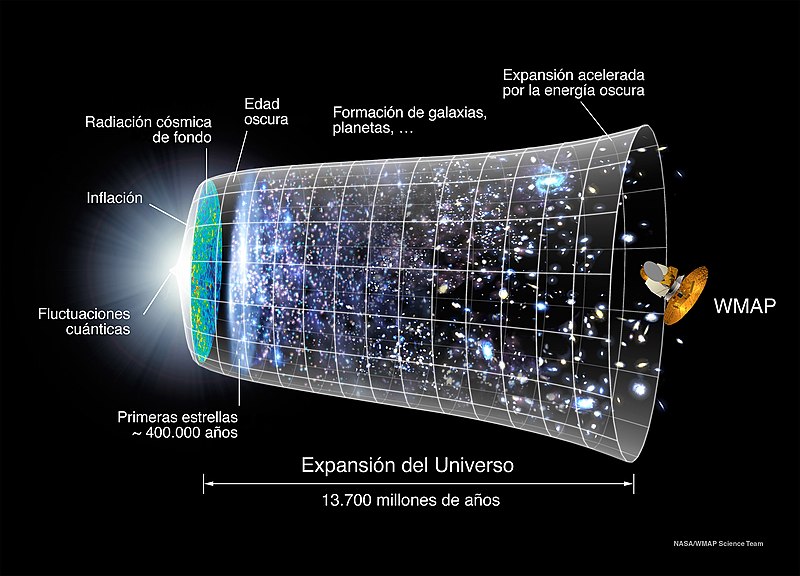
Se piensa que al principio del comienzo del tiempo, cuando surgió el Big Bang, las energías eran tan altas que allí reinaba la simetría total; sólo había una sola fuerza que todo lo englobaba. Más tarde, a medida que el universo se fue expandiendo y enfriando, surgieron las cuatro fuerzas que ahora conocemos y que todo lo rigen. Tenemos los medios, en los súpercolisionadores de partículas, para viajar comenzando por 1.000 MeV, hasta finalizar en cerca de 10¹⁹ MeV, que corresponde a una escala de longitudes de aproximadamente 10^–30 cm. Howard Georgi, Helen Quinn y Steven Weinberg descubrieron que ésta es la región donde las tres constantes de acoplamiento gauge se hacen iguales (U(1), SU(2) y SU(3)); resultan ser lo mismo. ¿Es una coincidencia que las tres se hagan iguales simultáneamente? ¿Es también una coincidencia que esto suceda precisamente en esa escala de longitud? Faltan sólo tres ceros más para alcanzar un punto de retorno. Howard Georgi y Sheldon Glashow descubrieron un modelo genuinamente unificado en el dominio de energías de 10¹⁹ MeV tal que, cuando se regresa de allí, espontáneamente surgen las tres fuerzas gauge tal como las conocemos. De hecho, ellos encontraron el modelo; la fórmula sería SU(5), que significa que el multiplete más pequeño debe tener cinco miembros.

Materia y Energía Oscura… Un Misterio…Sin resolver.

Y, a todo esto, ¿dónde está esa energía oculta? ¿Y donde la materia? Podemos suponer que la primera materia que se creo en el Universo fue la que llamamos (algún nombre había que ponerle) “Materia Oscura”, esa clase de Ylem o sustancia cósmica primera del Universo que mejor sería llamarla invisible, ya que, de no ser así, difícil sería explicar cómo se pudieron formar las primeras estrellas y galaxias de nuestro Universo, ¿dónde está el origen de la fuerza de Gravedad que lo hizo posible, sino en esa materia escondida?

¡Lo dicho! Necesitamos saber, y, deseo que de una vez por todas, se cumpla lo que dejó dicho Hilbert en su tumba de Gotinga (Alemania): “Tenemos que saber, ¡sabremos!. Pero…

¡Que sea pronto!

emilio silvera

[?]