¡Partículas subatómicas! Esos misteriosos objetos

                                       Están por todas partes y todo está conformado por ellas

Partículas, espín, familias, materia…

Conforme a lo que aceptamos hoy en día, toda la materia estaría constituida a partir de estados ligados de Quarks y Leptones, es decir de los quarks u “up” y d “down”, electrones e y neutrinos ѵ, y sus antipartículas. De todos estos objetos, pueden existir hasta un total de otras dos familias más en las que los quarks reciben otras denominaciones y los leptones, en vez de electrones podrían ser muones μ y partícula tau τ. Señalamos que estos objetos poseen distintas masas. Sin embargo, todas tienen en común que son partículas de espín ½. Si a estos objetos le añadimos los Bosones de espín 1, que son los responsables de las interacciones entre ellos, resulta que el poseer esa propiedad mecánica llamada espín es una de las características más importantes de los objetos elementales que constituyen la materia y de los vehículos que utilizan estas partículas elementales para su comunicación. Toda la materia que nos rodea se mueve y rota.

El espín del muón es ½. Cuando el espín de una partícula es semi-entero, se la clasifica como perteneciente al grupo denominado fermiones. La carga eléctrica de un muón es igual que la del electrón, pero su existencia es de sólo 2,2 microsegundos. En cambio el electrón es un elemento estable en la Naturaleza.

En el modelo físico de la mecánica cuántica, el muón es una partícula puntual y no tiene volumen. Pero no hay ningún problema para que se le asigne un momento angular (una rotación).

Podemos pensar en que el muón es como una bolita que gira sobre sí misma. Este momento angular se denomina espín y está cuantizado; es decir, que no puede tener cualquier valor, sino múltiplos de una cantidad mínima, que es 1/2. Este valor 1/2 se refiere a la constante reducida de Planck

El muón, al igual que todas las partículas elementales (cuatro en cada una de la tres familias), tiene espín de valor 1/2. A las partículas que tienen espín 1/2, se las denomina fermiones, en honor del físico italiano Enrico Fermi (1901-1954).

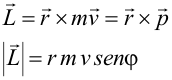
“Momento angular de una partícula. Consideremos una partícula de masa m que se mueve con respecto a O con una velocidad v. Definimos una nueva magnitud vectorial, llamada momento angular de la partícula con respecto a O (L): Sus unidades son: m²kg/s.”

Como decía al principio, toda la materia que nos rodea se mueve y rota. Las partículas constituyentes no podían ser menos, de ahí que no es de extrañar que las partículas elementales tengan momento angular, que es la expresión mecánica de la medida de su estado interno de rotación. La sorpresa es, quizá, que todas estas partículas tengan exclusivamente el valor no nulo, más bajo posible, que predice la mecánica cuántica.

Claro que, a todo esto, también tenemos que decir que todas estas partículas tienen su contraria, es decir, su antipartícula y, precisamente una nueva evidencia surgida de estudios realizados nos dicen que Materia y Antimateria pueden ser más distintas de lo que hasta ahora se había creído.

Los neutrinos, partículas elementales generadas por las reacciones nucleares en el Sol, padecen una “crisis de identidad” cuando cruzan el universo, metamorfoseándose entre tres “sabores” diferentes. Sus homólogos de antimateria (que son idénticos en masa pero opuestos en la carga y el espín) experimentan también una crisis de identidad. Sin embargo un equipo de físicos ha descubierto ahora diferencias sorprendentes entre neutrinos y antineutrinos en lo que se refiere a su conducta de cambio de “sabor”. Si se confirma, el hallazgo podría ayudar a explicar por qué es la materia y no la antimateria la que domina en nuestro universo.Cada partícula de materia tiene una antipartícula correspondiente de antimateria. Los electrones son partículas negativamente cargadas que rodean el núcleo de cada átomo. El positrón es una antipartícula con la misma masa y magnitud de carga del electrón pero exhibiendo una carga positiva. Cuando la materia ordinaria, como por ejemplo un electrón, se combina con una cantidad igual de antimateria, como por ejemplo un positrón, ambas se aniquilan mutuamente.

Si por el telescopio descubriéramos una galaxia lejana de antimateria…, no lo sabríamos, su comportamiento en todos los órdenes, sería el mismo que tendría una galaxia de materia como la Vía Láctea o Andrómeda. Seríamos conscientes de su naturaleza si alguna galaxia cercana se acercara y la gravedad tratara de unirlas, en el momento de la fusión… ¡Todo estallaría!

El aparentemente ineludible hecho de que las partículas de materia y antimateria se destruyen entre sí al contacto, ha desconcertado a los físicos desde hace tiempo, preguntándose cómo la vida, el Universo, o cualquier cosa puede existir. Pero unos nuevos resultados de un experimento de acelerador de partículas sugieren que la materia parece ganar finalmente.

Teniendo en cuenta esto último, así como que ambas fueron creadas en la formación del universo, y que el universo actual alberga materia pero virtualmente nada de antimateria, debe haber alguna razón por la cual la materia se acabó imponiendo a la antimateria. La única explicación es que, las partículas de materia excedían en número a las de antimateria y, una ves destruidas todas las antagonistas, quedarían sólo las de materia que eran más y, esas son las que podemos ver ahora formando estrellas y planetas entre otras cosas.

“La estrella masiva IRS 4 comienza a desplegar sus alas. Nacida hace sólo unos 100.000 años, el material expulsado de esta estrella recién nacida ha formado la nebulosa llamada Sharpless 2-106 (S106) que se ve en la imagen. El gran disco de polvo y de gas que orbita la fuente infrarroja IRS 4, visible en rojo oscuro cerca del centro de la imagen, da a la nebulosa la forma de un reloj de arena o de una mariposa.”

Todo está hecho de esas pequeñas partículas que conocemos por Quarks y Leptones y, si miramos la imagen de arriba, podemos contemplar esa maravillosa imagen en la que la estrella masiva IRS 4 comienza a desplegar sus alas. Nacida hace sólo unos 100.000 años, el material expulsado de esta estrella “recién” nacida ha formado la nebulosa llamada Sharpless 2-106 (S106). El gran disco de polvo y de gas que orbita la fuente infrarroja IRS 4, visible en rojo oscuro cerca del centro de la imagen, da a la nebulosa la forma de un reloj de arena o de una mariposa.

El gas de S106 cerca de 4 IRS actúa como una nebulosa de emisión ya que emite luz después de haber sido ionizado, mientras que el polvo lejano procedente de IRS4 refleja la luz de la estrella central y, por tanto, actúa como una nenulosa de reflexión. El examen detallado de imágenes como esta, ha revelado la existencia de cientos de estrellas marrones de masa baja que rondan por el gas de la nebulosa. S106 se extiende unos 2 años luz y se encuentra a unos 2.000 años-luz de distancia en la constelación del Cisne ( Cygnus ). Todo ese bello conjunto que podemos admirar, en realidad sólo son átomos formados por partículas subatómicas y la energía que está presente emitida por los objetos que forman en el Universo.

“Tomando el pensamiento de su maestro Leucipo, Demócrito supuso la existencia del átomo como parte indivisible de la materia, y además sentenció que existían distintos tipos de átomos que al combinarse de formas y con ordenaciones distintas formaban las distintas sustancias existentes.

La teoría atómica, pese a haber sido desarrollada más a fondo a comienzos del siglo XIX gracias a científicos como Dalton y Avogadro, fue propuesta por primera vez en la antigua Grecia. Cuando Dalton habló de átomos, fue porque físicamente tomaron sentido gracias a desarrollo de la ley de las proporciones múltiples, basada en la ley de conservación de la materia de Lavoisier y en la ley de las proporciones constantes de Proust. Por la contra, cuando Demócrito, Leucipo y Epicuro hablaron del átomo, fue simplemente como una necesidad filosófica fundando el atomismo como sistema filosófico.”

 

Aquella idea del átomo que nos dejó Demócrito, de que la materia se puede dividir en porciones cada vez más pequeñas hasta que este proceso tenga un final, puede ser o no cierta. No sabemos si lo que hoy consideramos como una partícula elemental, por ejemplo el electrón, se descubre en un futuro que está a su vez compuesto de otros objetos todavía por descubrir (aunque para mí, no parece que tal cosa sea posible en el electrón que, por sus características, no parece prestarse a ello). Pero, si finalmente existen esos objetos últimos, indivisibles, que hoy en vez de átomos les denominaríamos partículas elementales, es legítimo tratar de clarificar desde un punto de vista teórico qué es lo que distingue a un objeto elemental de otro que no lo es, es decir, encontrar una definición plausible de partícula elemental.

            Modelo Estándar de Partículas Elementales.

Una definición por exclusión podría ser que una partícula elemental es un sistema mecánico que no posee estados escitados, es decir, que no es posible modificar su estructura. Podremos aniquilarla, destruirla, pero nunca modificarla. En sentido positivo diríamos que se trata de un sistema mecánico cuyos únicos estados permitidos son solamente modificaciones cinemáticas de uno cualquiera de ellos. Conocido un estado cualquiera de la partícula, el resto de los estados posibles en los que la podamos encontrar son solamente las diferentes descripciones que de ese estado hacen el resto de los observadores inerciales, Esto también quiere decir que, un cierto observador inercial hace una descripción del estado en que se e4ncuentra una partícula elemental y debido a alguna influencia externa este estado cambia, siempre es posible encontrar otro observador inercial que, en el nuevo instante, describa la partícula exactamente en el mismo estado que en el instante anterior lo describía el otro observador.

Cualquier cambio en el valor de alguna de las variables que caracterizan el estado de una partícula elemental puede ser siempre compensado, mediante un cambio de sistema de referencia inercial, para lograr describir el sistema en el mismo estado, es decir, con exactamente los mismos valores de todas las variables que definen de forma única el estado del sistema.

En la segunda Imagen del microscopio electrónico de barrido de una partícula de aerosol compuesta principalmente por sodio y cloro. Cuando entramos en el “mundo” de lo muy pequeño, nos parece entrar en el ámbito extraño de la mecánica cuántica

 

Existen sofisticadas máquinas que nos permiten observar partículas y hacer exámenes granulométricos de las mismas, Cada día podemos acercarnos más y más a ese infinitesimal “universo de lo muy pequeño”, claro que, el mismo aparato que utilizamos que es un sistema electrónico, al emitir la luz que trata enfocar esas partículas, lanza miríadas de fotones sobre ellas y, en ese momento, se producen sucesos que impiden saber, de manera exacta donde está la partícula o, hacia donde se dirige. Es el Principio de Incertidumbre de Heisenberg.

“Principio de indeterminación de Heisenberg. W. Heisenberg ( Premio Nobel de Física 1932) enunció el llamado principio de incertidumbre o principio de indeterminación, según el cual es imposible medir simultáneamente, y con precisión absoluta, el valor de la posición y la cantidad de movimiento de una partícula.”

Esta forma de definir un objeto elemental puede parecer una trivialidad, pero supone sin embargo una enorme restricción con respecto al tipo de variables clásicas que podemos utilizar para describir sus estados. Para empezar, tenemos que conocer cómo estas variables cambian cuando cambiamos de sistema de referencia. Más aún, dados dos valores posibles de una cualquiera de estas variables, debe existir un cambio de sistema de referencia que nos relacione un valor con el otro, y así para todas las variables básicas que configuren el estado del sistema. Vemos por lo tanto la importancia que juega el Principio de Relatividad no solo a la hora de definir el conjunto de observadores inerciales equivalentes, sino también en la propia definición de partícula elemental, ya que condiciona el tipo de variables clásicas que podemos utilizar. Es ésta la definición de partícula elemental que vamos a adoptar y vamos a intentar hacer una descripción Lagrangiana de aquellos sistemas mecánicos sujetos a esta definición.

De todas las maneras, en esto de las partículas nos tenemos que andar con pies de plomo, nada se puede dar por hecho, y, es bien sabido que lo que nos dice la mecánica cuántica no siempre coincide con lo que nos dicta el sentido común. Y, sí, en la relatividad están inmersas transformaciones que no debemos dejar de lado cuando tratamos con partículas elementales, veamos por ejemplo:

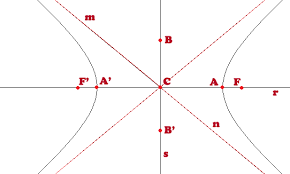
“Se llama hipérbola al lugar geométrico de los puntos del plano tales que la diferencia de sus distancias a dos puntos fijos, llamados focos, es una constante (se representa por 2a)

En las hipérbolas cabe destacar:

1. La recta que une los dos focos se llama eje real de la hipérbola y la mediatriz se llama eje imaginario de la hipérbola.
2. El punto donde se cortan ambos ejes (el punto medio de los focos) se llama centro de la hipérbola.
3. Los puntos donde la hipérbola corta a los ejes (en el eje real) se llaman vértices de la hipérbola.
4. Al igual que en la elipse, se llama distancia focal a la distancia entre dos focos y a las distancias desde un punto cualquiera de la hipérbola a ambos focos se les llama radio vectores del punto.
5. A diferencia de la elipse, aquí se tiene 2c > 2a (por tanto, c > a) y se puede considerar b = √(c² – a²). Este valor se llama semieje imaginario de la hipérbola.
6. El cociente e = c/a, que es un número mayor que 1, se llama excentricidad de la hipérbola.”

Que el grupo de Lorentz realiza una foliación del espacio en hipérbolas diferenciadas. Ahora bien… ¿qué ocurre si tenemos una partícula en la región para v>c? Al ser la hipérbola vertical, ¡¡una transformación desplaza punto en el tiempo!!. Por tanto, podría ocurrir que lo que para alguien es pasado, para otro sea futuro… Para entenderlo mejor supongamos la situación siguiente en la que una partícula, vista por un observador, va del punto A al punto B a una velocidad mayor que la de la luz. (¿Serán los neutrinos de aquellos italianos del Proyecto Opera?

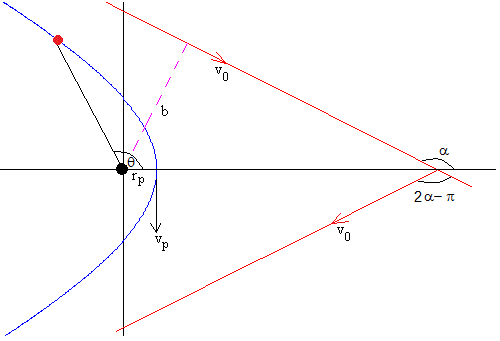
Consideremos el movimiento de una partícula superlumínica del punto A al punto B. Si aplicamos una transformación de Lorentz, al desplazar el punto B sobre la hipérbola, podría darse el caso de que este quedase por debajo de A, como en la figura siguiente:

Al aplicar la transformación, el punto B pasa del futuro al pasado. Por lo que, para este observador, ¡la partícula ha viajado en el tiempo! Claro que, nos topoamos de nuevo con el límite de la velocidad de la luz. Ni aquellos neutrinos de hace unos días, han podido quitarle el Record de velocidad a los fotones.

Una característica importante del principio de ralatividad es que lleva asociado un grupo de transformaciones espaciotemporales. Este grupo es el que nos indica la forma en que los diferentes observadores inerciales relacionan sus medidas respectivas de las tres coordenadas espaciales y una temporal de un mismo acontecimiento espacio-temporal. En la física Newtoniana o no relativista, este grupo es el grupo de Galileo, mientras que la física relativista toma como grupo cinemático de base el Grupo de Poincaré, que además de rotaciones y traslaciones, como en el caso del grupo de Galileo, contiene transformaciones de Lorentz puras entre observadores, con velocidad relativa constante. El arranque del formalismo comienza con aceptar uno de estos grupos G como el grupo que deja invariante las ecuaciones dinámicas.

Desde el punto de vista académico, el estudio general de la geometría de la cuarta dimensión en gran parte resultado de los trabajos de Bernhard Riemann.

Los trabajos matemáticos sobre geometrías multidimensionales y geometrías no euclídeas habían sido considerado por los físicos como simples abstracciones matemáticas hasta que Henri Poincaré probó que el grupo de transformaciones de Lorentz que dejaban invariantes las ecuaciones del electromagnetismo podían ser interpretadas como “rotaciones” en un espacio de cuatro dimensiones. Más tarde, los trabajos de Einstein y la interpretación geométrica de estos por parte de Hermann Minkowski llevaron a la aceptación de la cuarta dimensión como una descripción necesaria para explicar los hechos observados relacionados con el electromagnetismo. Sin embargo, aquí la “cuarta dimensión” no era un lugar separado del espacio tridimensional (como en varias de las obras de ficción de la época) ni tampoco una dimensión espacial análoga a las otras tres dimensiones espaciales, sino una dimensión temporal que sólo puede recorrerse hacia el futuro. En la teoría general de la relatividad el campo gravitatorio es explicado como un efecto geométrico de la curvatura de un espacio-tiempo de cuatro dimensiones.

Más tarde, la teoría de Kaluza-Klein propuso que no sólo el campo gravitatorio podía ser interpretado de forma más sencilla como curvatura de un “espacio” de más de tres dimensiones, sino que si se introducía una nueva dimensión espacial enrollada o «compactificada», también el campo electromagnético podía ser interpretado como un efecto geométrico de la curvatura de dimensiones superiores. Así, la Kaluza proponía una teoría de campo unificado del electromagnetismo y la gravedad en un espacio-tiempo de cinco dimensiones, con una dimensión temporal, tres dimensiones espaciales extendidas y una dimensión espacial «compactificada» adicional, que, debido a su condición de compactificada, no era directamente visible pero su efecto era perceptible en forma de campo electromagnético.

Bueno, como de costumbre (eo pasar una mosca y me distrae), me paso de las partículas a los grupos de Poincaré y Lorentz o, a la cuarta dimensión de Minkowski, son cosas de la mente que, no siempre actúa como nos propusimos al comenzar un trabajo que, la mayoría de las veces finaliza, de manera misteriosa, de manera diferente a la que nos propusimos al comenzar.

El Físico Martin del Riva del Departamento de Física Teórica del pais Vasco, tiene mucho que ver con todo lo que aquí contamos. Desde aquí le agradecemos sus conocimientos.

emilio silvera

[?]