Alguien dijo hace mucho tiempo: “Todo es número”

¿Conocieron los antiguos constructores los secretos del Universo?

¿Conocían los antiguos egipcios hace miles de años la que hoy día se conoce como la fórmula más bella del Universo? Si esto fuera cierto representaría que los antiguos constructores debieron entender el Universo de forma geométrica, como (de hecho) apuntan todas las evidencias. Y es que la fórmula de Euler es pura geometría, y, como tal, representa el lenguaje más perfecto en que puede expresarse el Universo: el lenguaje numérico.

Déjame explicarte la ecuación de Euler en términos coloquiales para que entiendas como convergen todos los conceptos, como podemos conciliar el antiguo conocimiento con nuestra forma, radicalmente opuesta, de pensar. Para ello utilizaré un razonamiento previo que considero irrefutable, ya que se basa en la más pura lógica. Y después haremos arqueología matemática.

Especular es conjeturar

Una conjetura no es más que una afirmación que aún no hemos podido refutar, que no sabemos si es o no cierta. En su versión opuesta una conjetura también es una afirmación, para la que tampoco nunca hemos podido demostrar que no sea cierta. De hecho todas las evidencias en las más importantes conjeturas matemáticas, después de millones o billones de intentos o experimentos, nos hacen pensar que éstas son ciertas, pero que aún no hemos encontrado la manera de demostrarlo inequívocamente.

Todas las conjeturas que tenemos hoy día, al menos en el campo que denominamos “Teoría de Números” indican que los números siguen en su composición algún tipo de patrón organizado, que…, de alguna manera, parecen comunicarse entre ellos. La más famosa de todas, la Conjetura de Riemann establece, por ejemplo, que los números primos siguen un criterio de densidad en su comportamiento. Si esto fuera cierto denotaría que los números tendrían de forma subyacente un criterio inteligente que dictaminaría su distribución. Si todas ellas fueran correctas implicaría que los números, de forma independiente, tienen un criterio subyacente que es totalmente independiente de la manera en que nos refiramos a él. En otras palabras, dicho patrón sería incluso independiente de las matemáticas, una especie de código fuente que es intemporal o, en otras palabras, que siempre ha sido y será.

 

 

“Los egipcios crearon un manual para geometría el cual daba demostraciones de suma y resta que posteriormente se transformaría en el primer papiro el cual tenía más de 84 problemas matemáticos y sus respectivas soluciones.”

Aunque suene antiguo decirlo, si todas esas conjeturas fueran ciertas, querría decir como pensaron los antiguos que los números son el Universo, pues siempre y en todo momento siguen un patrón organizado de comportamiento que es independiente incluso del espacio y del tiempo. Un patrón intemporal que siempre ha sido y será, y que siempre se cumplirá incluso en los extremos de nuestro Universo.

Por lo tanto si los números son intemporales e independientes de las matemáticas, podemos incluso prescindir de ellas y admirar la belleza conceptual (y visual) de la más pura identidad. Esta es la idea subyacente en este razonamiento.

“Desde que la vi no la he podido olvidar… Relaciona los números imaginarios ( i = raíz cuadrada de ( –1)), con las potencias ( número e y logaritmos neperianos ) y con las funciones trigonométricas. Me ha permitido recordar, sin esfuerzo, fórmulas trigonométricas como la del seno o coseno de una suma de ángulos, del ángulo doble o mitad, y calcular, con facilidad, derivadas de funciones trigonométricas.”

La ecuación de Euler se considera (con permiso de Pitágoras) como la ecuación más bella de las matemáticas, sin ninguna duda. Keith Devlin se refirió a ella en los siguientes términos: “ Como un soneto de Shakespeare que capta la esencia del amor o un cuadro que saca a relucir la belleza de la forma, que es mucho más profundo que solo la piel, la ecuación de Euler llega a lo más profundo de la existencia”.

La ecuación de Euler “vive” en muchos mundos, es “algo” que trasciende al lenguaje matemático. Vamos a tratar de entender la ecuación de Euler desde su perspectiva más trascendente, desde una perspectiva más humana, para llegar a comprobar finalmente que la ecuación de Euler es capaz de conectar incluso nuestras conciencias, dando sentido a la existencia de un patrón espacio-temporal que nos dirá claramente que nunca podremos determinar lo que es o no real. Y es que este patrón es incluso capaz de determinar nuestra forma de pensar. Realmente se trata de una especie de “código fuente” universal.

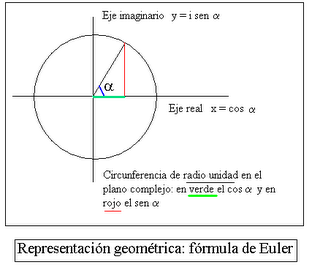
“Nos la podemos encontrar en cualquier sitio, en cualquier expresión matemática pura o relacionada con algo tan prosaico como las relaciones de impedancias en un circuito de corriente alterna. En la función de onda de la mecánica cuántica o en cualquier expresión de naturaleza ondulatoria o periódica. En la técnica, en la física o en las matemáticas más abstractas ( Roger Penrose reflexiona– en su último libro,en el capítulo sobre las diferenciales complejas – lo que habría disfrutado Euler con todas las maravillas de su fórmula y de los números imaginarios ).”

Lo primero que hay que decir al respecto es que la ecuación de Euler no es una ecuación normal. En contra de las creencias no se trata de una fórmula ni de un teorema matemático. Todas estas ideas hacen referencia a la existencia de un criterio humano y racional, es decir algo que es consecuencia de nuestra forma de pensar. La ecuación de Euler va más allá, porque es independiente de todos nuestros criterios. Dicha ecuación es una identidad numérica que podemos calificar de universal e intemporal. Tan sólo necesitamos números (aunque sean irracionales) para describirla, no utiliza ninguna variable, ninguna x arbitraría, tan sólo utiliza números universales.

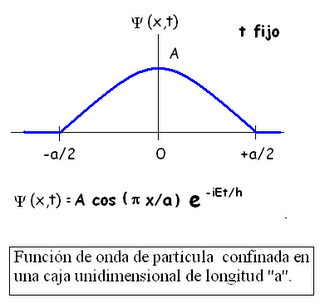
“La fórmula de Euler fué demostrada por primera vez por Roger Cotes en 1714, y luego redescubierta y popularizada por Euler en 1748. Es interesante notar que ninguno de los descubridores vió la interpretación geométrica ( circunferencia en el plano complejo): la visión de los números complejos como puntos en el plano surgió unos 50 años mas tarde con Caspar Wessel, y d’Argaud.”

En cualquier unidad siempre podremos inscribir, por ejemplo, la divina proporción, pues este valor es totalmente independiente de cualquier unidad de medida, el gran hándicap de la física. Toda distancia unitaria puede ser siempre dividida entre la media y la extrema razón. La divina proporción hace referencia a un tipo de equilibrio matemático, pero que también podemos observar en el mundo real, en la propia naturaleza. A esta relación hicieron referencia los antiguos egipcios con el símbolo de la balanza, o… inscribiendo sus medidas en las pirámides de Egipto. Bajo este punto de vista unificado también podemos comparar a esta ecuación, incluso, con nuestra propia evolución. Es decir… ¿Conoció otra civilización anterior este patrón? Esta es la idea subyacente, establecer que la identidad de Euler se puede entender de muchas formas diferentes, porque es independiente incluso del lenguaje.

Las matemáticas reflejan conceptos, ideas mentales, ideas abstractas que tienen lugar en un espacio mental e imaginario. En este contexto el simbolismo es necesario, para mecanizar de forma más eficiente el lenguaje que empleamos. La geometría también puede ser vista como un lenguaje conceptual e imaginario. La geometría es la parte más sensitiva, la más directa de todas las ramas matemáticas y, como tal, constituye un efectivo lenguaje visual.

Los símbolos matemáticos, como sabemos, son creaciones humanas, sin embargo en algunos casos incluso su simbolismo es independiente de las matemáticas, constituyen un lenguaje por sí mismo. Se trata del lenguaje áureo, un lenguaje propio que tienen estos valores sagrados e irracionales que aparecen en la identidad de Euler.

Keith Devlin nos decía que la ecuación de Euler es como un soneto de Shakespeare. Y debe de ser correcto, sobre todo si hacemos referencia al más famoso de todos ellos: “Ser o no ser, esa es la cuestión”. A lo que añadiríamos que, en efecto, esto es correcto, sólo que incompleto, porque ser o no ser también puede ser la solución. De esta forma podríamos compatibilizar la causa con el efecto o, en otros términos, comprobar cómo el “Todo” siempre está contenido en la parte. En términos totalmente opuestos, sería algo así como admitir que los últimos serán los primeros.

Ser o no ser expresa la existencia de dos formas diferentes de entender la realidad, en esencia expresa la dualidad, la necesaria presencia de dos conceptos opuestos entre ellos. Es como si nos dijera que la existencia del mundo físico y real que podemos observar necesitara de la existencia de un mundo opuesto, un mundo material que podemos simbolizar matemáticamente y, por lo tanto, que es meramente conceptual. En otras palabras, que las ideas matemáticas pueblan el mundo del alma, como decía Platón.

                               Una igualdad llena de belleza

La ecuación de Euler puede ser vista desde diferentes simbolismos, por lo que también es independiente incluso del simbolismo propiamente matemático. Así pues, libera tu mente, observa la Identidad de Euler de forma diferente. No la veas de forma lineal, como si de un simple teorema se tratará, vamos a ver cómo la ecuación de Euler es una ecuación multi-dimensional, la llave que abre la puerta a dimensiones diferentes, el patrón que impone un orden al ritmo de lo infinito y lo irracional. Una eterna verdad que nos dice claramente que todo está conectado como si fuera una unidad, nos dice cómo se conecta el mundo irracional y arbitrario con nuestra idea de un mundo determinado.

La esencia del problema de conectar dimensiones diferentes la Ecuación de Euler lo resuelve de una forma elegante e impecable y, a su vez, imposible de modificar, pues tan sólo se basa en la probabilidad. La ecuación de Euler nos dice que hay que apelar siempre a la regla universal: la dualidad que los opuestos representan. Piensa, por ejemplo, que un cuadro, como al que hacía referencia Devlin y la realidad sólo son dos concepciones diferentes de una misma existencia, que el cuadro no es más que el reflejo en el mundo inmaterial de las ideas, una especie de holograma, un reflejo de lo que vemos en el mundo “real”.

Los únicos valores en el infinito matemático que cumplen siempre la regla de la dualidad son los valores áureos o sagrados. Son los únicos que tienen la capacidad de moverse entre dos planos diferentes de la realidad: el plano real y el plano irracional o imaginario. Podemos decir nuevamente que sus formas siempre han sido y serán. Pongamos un ejemplo para cada uno de ellos para entenderlo mejor.

La divina proporción es el único valor matemático, cuyo valor (precisamente) coincide con el valor que representa su inversa. Realmente toda una incoherencia. Las matemáticas ocultan esta coincidencia, no le dan relevancia y relegan a una de las soluciones al plano de lo inexistente. Tan sólo la divina proporción, por tanto, es capaz de situarse a medio camino, realmente de forma equilibrada, entre el plano de lo que es real matemáticamente hablando y el plano opuesto, o el plano del (aparentemente) inexistente mundo imaginario. La divina proporción representa con exquisita perfección el concepto subyacente al número i, o número imaginario, la posibilidad de ser capaz de situarse en dos planos diferentes de la realidad.

Con pi pasa exactamente lo mismo. Pi es el único valor en el infinito matemático que puede dar lugar a la esfera tridimensional, una construcción matemática que situamos en una cuarta dimensión imaginaria.

Ricard Jiménez

[?]