May
7
La paradoja de Fermi
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en La Vida en otros mundos ~
Clasificado en La Vida en otros mundos ~
 Comments (0)
Comments (0)

¿Por qué si hay tantos planetas susceptibles de albergar vida inteligente, ninguna civilización extraterrestre se ha puesto en contacto con nosotros?

La conclusión a la que llegó el astrónomo Frank Drake a partir de su propia ecuación -una decena de civilizaciones capaces de comunicarse con nosotros en la Vía Láctea-, hoy, medio siglo después y a la vista de los últimos descubrimientos astronómicos, nos parece excesivamente prudente, y muchos creen que esas civilizaciones galácticas podrían contarse por cientos o miles.

A pesar de lo difícil que resulta detectar planetas extrasolares, ya se conocen más de tres mil, y algunos astrónomos consideran probable que la mayoría de las estrellas tengan planetas orbitando a su alrededor, lo que significaría que los “ecomundos” (planetas idóneos para albergar vida) se podrían contar por cientos de millones.

Y ahí es donde surge con renovada fuerza la conocida como “paradoja de Fermi”, pues el gran físico italiano, inspirador de la ecuación de Drake, se preguntó a mediados del siglo pasado por qué ninguno de esos supuestos vecinos galácticos se había puesto en contacto con nosotros ni había dejado ninguna huella perceptible de su presencia en el cosmos.

Una de las posibles explicaciones de esta paradoja es la denominada“hipótesis de la Tierra especial”, según la cual, aunque hubiera muchos planetas similares al nuestro, se requieren tal cantidad de condiciones para que se desarrolle la vida inteligente, que el proceso podría haberse dado en muy pocos planetas, tal vez solo en la Tierra. Pero esta hipótesis parte del supuesto de que la vida inteligente solo puede desarrollarse mediante un proceso análogo al que se ha dado en nuestro planeta, y no tiene por qué ser necesariamente así.
Invito a nuestras visitas a reflexionar sobre la paradoja de Fermi y sus implicaciones. Lo más lógico es pensar que, como nos pasa a nosotros mismos, esos posibles vecinos inteligentes estén en desarrollo de técnicas que le permitan vencer las distancias que nos separan. Esa es la verdadera razón del silencio de esas posibles civilizaciones y especies extraterrestres.
Visitando a nuestros vecinos

Supongamos que en nuestro entorno galáctico más próximo hay tres planetas habitados por seres inteligentes, a “solo” 10, 20 y 30 años luz de distancia de la Tierra respectivamente. ¿Cuál es la distancia mínima a la que pueden estar dos de esos exoplanetas entre sí? ¿Y la máxima?
Queremos visitar esos tres mundos, uno tras otro, en un solo viaje. ¿Cuál es la disposición espacial que haría que ese viaje fuera mínimo en cuanto a la distancia recorrida por nuestra astronave? ¿Y la disposición que daría lugar al recorrido más largo?
Carlo Frabetti es escritor y matemático, miembro de la Academia de Ciencias de Nueva York. Ha publicado más de 50 obras de divulgación científica para adultos, niños y jóvenes, entre ellos Maldita física, Malditas matemáticas o El gran juego. Fue guionista de La bola de cristal.
May
6
Alguien dijo hace mucho tiempo: “Todo es número”
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Las ecuaciones ~
Clasificado en Las ecuaciones ~
 Comments (1)
Comments (1)

¿Conocieron los antiguos constructores los secretos del Universo?
¿Conocían los antiguos egipcios hace miles de años la que hoy día se conoce como la fórmula más bella del Universo? Si esto fuera cierto representaría que los antiguos constructores debieron entender el Universo de forma geométrica, como (de hecho) apuntan todas las evidencias. Y es que la fórmula de Euler es pura geometría, y, como tal, representa el lenguaje más perfecto en que puede expresarse el Universo: el lenguaje numérico.
Déjame explicarte la ecuación de Euler en términos coloquiales para que entiendas como convergen todos los conceptos, como podemos conciliar el antiguo conocimiento con nuestra forma, radicalmente opuesta, de pensar. Para ello utilizaré un razonamiento previo que considero irrefutable, ya que se basa en la más pura lógica. Y después haremos arqueología matemática.

Especular es conjeturar
Una conjetura no es más que una afirmación que aún no hemos podido refutar, que no sabemos si es o no cierta. En su versión opuesta una conjetura también es una afirmación, para la que tampoco nunca hemos podido demostrar que no sea cierta. De hecho todas las evidencias en las más importantes conjeturas matemáticas, después de millones o billones de intentos o experimentos, nos hacen pensar que éstas son ciertas, pero que aún no hemos encontrado la manera de demostrarlo inequívocamente.
Todas las conjeturas que tenemos hoy día, al menos en el campo que denominamos “Teoría de Números” indican que los números siguen en su composición algún tipo de patrón organizado, que…, de alguna manera, parecen comunicarse entre ellos. La más famosa de todas, la Conjetura de Riemann establece, por ejemplo, que los números primos siguen un criterio de densidad en su comportamiento. Si esto fuera cierto denotaría que los números tendrían de forma subyacente un criterio inteligente que dictaminaría su distribución. Si todas ellas fueran correctas implicaría que los números, de forma independiente, tienen un criterio subyacente que es totalmente independiente de la manera en que nos refiramos a él. En otras palabras, dicho patrón sería incluso independiente de las matemáticas, una especie de código fuente que es intemporal o, en otras palabras, que siempre ha sido y será.

“Los egipcios crearon un manual para geometría el cual daba demostraciones de suma y resta que posteriormente se transformaría en el primer papiro el cual tenía más de 84 problemas matemáticos y sus respectivas soluciones.”
Aunque suene antiguo decirlo, si todas esas conjeturas fueran ciertas, querría decir como pensaron los antiguos que los números son el Universo, pues siempre y en todo momento siguen un patrón organizado de comportamiento que es independiente incluso del espacio y del tiempo. Un patrón intemporal que siempre ha sido y será, y que siempre se cumplirá incluso en los extremos de nuestro Universo.
Por lo tanto si los números son intemporales e independientes de las matemáticas, podemos incluso prescindir de ellas y admirar la belleza conceptual (y visual) de la más pura identidad. Esta es la idea subyacente en este razonamiento.

“Desde que la vi no la he podido olvidar… Relaciona los números imaginarios ( i = raíz cuadrada de ( –1)), con las potencias ( número e y logaritmos neperianos ) y con las funciones trigonométricas. Me ha permitido recordar, sin esfuerzo, fórmulas trigonométricas como la del seno o coseno de una suma de ángulos, del ángulo doble o mitad, y calcular, con facilidad, derivadas de funciones trigonométricas.”
La ecuación de Euler se considera (con permiso de Pitágoras) como la ecuación más bella de las matemáticas, sin ninguna duda. Keith Devlin se refirió a ella en los siguientes términos: “ Como un soneto de Shakespeare que capta la esencia del amor o un cuadro que saca a relucir la belleza de la forma, que es mucho más profundo que solo la piel, la ecuación de Euler llega a lo más profundo de la existencia”.
La ecuación de Euler “vive” en muchos mundos, es “algo” que trasciende al lenguaje matemático. Vamos a tratar de entender la ecuación de Euler desde su perspectiva más trascendente, desde una perspectiva más humana, para llegar a comprobar finalmente que la ecuación de Euler es capaz de conectar incluso nuestras conciencias, dando sentido a la existencia de un patrón espacio-temporal que nos dirá claramente que nunca podremos determinar lo que es o no real. Y es que este patrón es incluso capaz de determinar nuestra forma de pensar. Realmente se trata de una especie de “código fuente” universal.
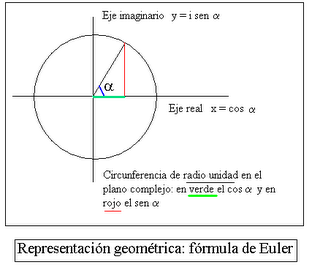
“Nos la podemos encontrar en cualquier sitio, en cualquier expresión matemática pura o relacionada con algo tan prosaico como las relaciones de impedancias en un circuito de corriente alterna. En la función de onda de la mecánica cuántica o en cualquier expresión de naturaleza ondulatoria o periódica. En la técnica, en la física o en las matemáticas más abstractas ( Roger Penrose reflexiona– en su último libro,en el capítulo sobre las diferenciales complejas – lo que habría disfrutado Euler con todas las maravillas de su fórmula y de los números imaginarios ).”
Lo primero que hay que decir al respecto es que la ecuación de Euler no es una ecuación normal. En contra de las creencias no se trata de una fórmula ni de un teorema matemático. Todas estas ideas hacen referencia a la existencia de un criterio humano y racional, es decir algo que es consecuencia de nuestra forma de pensar. La ecuación de Euler va más allá, porque es independiente de todos nuestros criterios. Dicha ecuación es una identidad numérica que podemos calificar de universal e intemporal. Tan sólo necesitamos números (aunque sean irracionales) para describirla, no utiliza ninguna variable, ninguna x arbitraría, tan sólo utiliza números universales.
“La fórmula de Euler fué demostrada por primera vez por Roger Cotes en 1714, y luego redescubierta y popularizada por Euler en 1748. Es interesante notar que ninguno de los descubridores vió la interpretación geométrica ( circunferencia en el plano complejo): la visión de los números complejos como puntos en el plano surgió unos 50 años mas tarde con Caspar Wessel, y d’Argaud.”
En cualquier unidad siempre podremos inscribir, por ejemplo, la divina proporción, pues este valor es totalmente independiente de cualquier unidad de medida, el gran hándicap de la física. Toda distancia unitaria puede ser siempre dividida entre la media y la extrema razón. La divina proporción hace referencia a un tipo de equilibrio matemático, pero que también podemos observar en el mundo real, en la propia naturaleza. A esta relación hicieron referencia los antiguos egipcios con el símbolo de la balanza, o… inscribiendo sus medidas en las pirámides de Egipto. Bajo este punto de vista unificado también podemos comparar a esta ecuación, incluso, con nuestra propia evolución. Es decir… ¿Conoció otra civilización anterior este patrón? Esta es la idea subyacente, establecer que la identidad de Euler se puede entender de muchas formas diferentes, porque es independiente incluso del lenguaje.
Las matemáticas reflejan conceptos, ideas mentales, ideas abstractas que tienen lugar en un espacio mental e imaginario. En este contexto el simbolismo es necesario, para mecanizar de forma más eficiente el lenguaje que empleamos. La geometría también puede ser vista como un lenguaje conceptual e imaginario. La geometría es la parte más sensitiva, la más directa de todas las ramas matemáticas y, como tal, constituye un efectivo lenguaje visual.

Los símbolos matemáticos, como sabemos, son creaciones humanas, sin embargo en algunos casos incluso su simbolismo es independiente de las matemáticas, constituyen un lenguaje por sí mismo. Se trata del lenguaje áureo, un lenguaje propio que tienen estos valores sagrados e irracionales que aparecen en la identidad de Euler.
Keith Devlin nos decía que la ecuación de Euler es como un soneto de Shakespeare. Y debe de ser correcto, sobre todo si hacemos referencia al más famoso de todos ellos: “Ser o no ser, esa es la cuestión”. A lo que añadiríamos que, en efecto, esto es correcto, sólo que incompleto, porque ser o no ser también puede ser la solución. De esta forma podríamos compatibilizar la causa con el efecto o, en otros términos, comprobar cómo el “Todo” siempre está contenido en la parte. En términos totalmente opuestos, sería algo así como admitir que los últimos serán los primeros.
Ser o no ser expresa la existencia de dos formas diferentes de entender la realidad, en esencia expresa la dualidad, la necesaria presencia de dos conceptos opuestos entre ellos. Es como si nos dijera que la existencia del mundo físico y real que podemos observar necesitara de la existencia de un mundo opuesto, un mundo material que podemos simbolizar matemáticamente y, por lo tanto, que es meramente conceptual. En otras palabras, que las ideas matemáticas pueblan el mundo del alma, como decía Platón.
Una igualdad llena de belleza
La ecuación de Euler puede ser vista desde diferentes simbolismos, por lo que también es independiente incluso del simbolismo propiamente matemático. Así pues, libera tu mente, observa la Identidad de Euler de forma diferente. No la veas de forma lineal, como si de un simple teorema se tratará, vamos a ver cómo la ecuación de Euler es una ecuación multi-dimensional, la llave que abre la puerta a dimensiones diferentes, el patrón que impone un orden al ritmo de lo infinito y lo irracional. Una eterna verdad que nos dice claramente que todo está conectado como si fuera una unidad, nos dice cómo se conecta el mundo irracional y arbitrario con nuestra idea de un mundo determinado.
La esencia del problema de conectar dimensiones diferentes la Ecuación de Euler lo resuelve de una forma elegante e impecable y, a su vez, imposible de modificar, pues tan sólo se basa en la probabilidad. La ecuación de Euler nos dice que hay que apelar siempre a la regla universal: la dualidad que los opuestos representan. Piensa, por ejemplo, que un cuadro, como al que hacía referencia Devlin y la realidad sólo son dos concepciones diferentes de una misma existencia, que el cuadro no es más que el reflejo en el mundo inmaterial de las ideas, una especie de holograma, un reflejo de lo que vemos en el mundo “real”.
Los únicos valores en el infinito matemático que cumplen siempre la regla de la dualidad son los valores áureos o sagrados. Son los únicos que tienen la capacidad de moverse entre dos planos diferentes de la realidad: el plano real y el plano irracional o imaginario. Podemos decir nuevamente que sus formas siempre han sido y serán. Pongamos un ejemplo para cada uno de ellos para entenderlo mejor.
La divina proporción es el único valor matemático, cuyo valor (precisamente) coincide con el valor que representa su inversa. Realmente toda una incoherencia. Las matemáticas ocultan esta coincidencia, no le dan relevancia y relegan a una de las soluciones al plano de lo inexistente. Tan sólo la divina proporción, por tanto, es capaz de situarse a medio camino, realmente de forma equilibrada, entre el plano de lo que es real matemáticamente hablando y el plano opuesto, o el plano del (aparentemente) inexistente mundo imaginario. La divina proporción representa con exquisita perfección el concepto subyacente al número i, o número imaginario, la posibilidad de ser capaz de situarse en dos planos diferentes de la realidad.
Con pi pasa exactamente lo mismo. Pi es el único valor en el infinito matemático que puede dar lugar a la esfera tridimensional, una construcción matemática que situamos en una cuarta dimensión imaginaria.
Ricard Jiménez
May
6
Estructuras fundamentales del Universo
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en El Universo dinámico ~
Clasificado en El Universo dinámico ~
 Comments (2)
Comments (2)
Estructuras Fundamentales de la Naturaleza
Hemos llegado a poder discernir la relación directa que vincula el tamaño, la energía de unión y la edad de las estructuras fundamentales de la Naturaleza. Una molécula es mayor y más fácil de desmembrar que un átomo; lo mismo podemos decir de un átomo respecto al núcleo atómico, y de un núcleo con respecto a los quarks que contiene.
La cosmología sugiere que esta relación resulta del curso de la historia cósmica, que los quarks se unieron primero, en la energía extrema del big bang original, y que a medida que el Universo se expandió, los protones y neutrones compuestos de quarks se unieron para formar núcleos de átomos, los cuales, cargados positivamente, atrajeron a los electrones cargados con electricidad negativa estableciéndose así como átomos completos, que al unirse formaron moléculas y estas, a su vez, juntas en una inmensa proporción, forman los cuerpos que podemos ver a lo largo y lo ancho de todo el universo. Grandes estructuras y cúmulos y supercúmulos de galaxias que están hechos de la materia conocida como bariónica, es decir, de Quarks y Leptones.

Si es así, cuanto más íntimamente examinemos la Naturaleza, tanto más lejos hacia atrás vamos en el tiempo. Alguna vez he puesto el ejemplo de mirar algo que nos es familiar, el dorso de la mano, por ejemplo, e imaginemos que podemos observarlo con cualquier aumento deseado.

Con un aumento relativamente pequeño, podemos ver las células de la piel, cada una con un aspecto tan grande y complejo como una ciudad, y con sus límites delineados por la pared celular. Si elevamos el aumento, veremos dentro de la célula una maraña de ribosomas serpenteando y mitocondrias ondulantes, lisosomas esféricos y centríolos, cuyos alrededores están llenos de complejos órganos dedicados a las funciones respiratorias, sanitarias y de producción de energía que mantienen a la célula.

Ya ahí tenemos pruebas de historia. Aunque esta célula particular solo tiene unos pocos años de antigüedad, su arquitectura se remonta a más de mil millones de años, a la época en que aparecieron en la Tierra las células eucariota o eucarióticas como la que hemos examinado.
Para determinar dónde obtuvo la célula el esquema que le indicó como formarse, pasemos al núcleo y contemplemos los delgados contornos de las macromoléculas de ADN segregadas dentro de sus genes. Cada una contiene una rica información genética acumulada en el curso de unos cuatro mil millones de años de evolución.
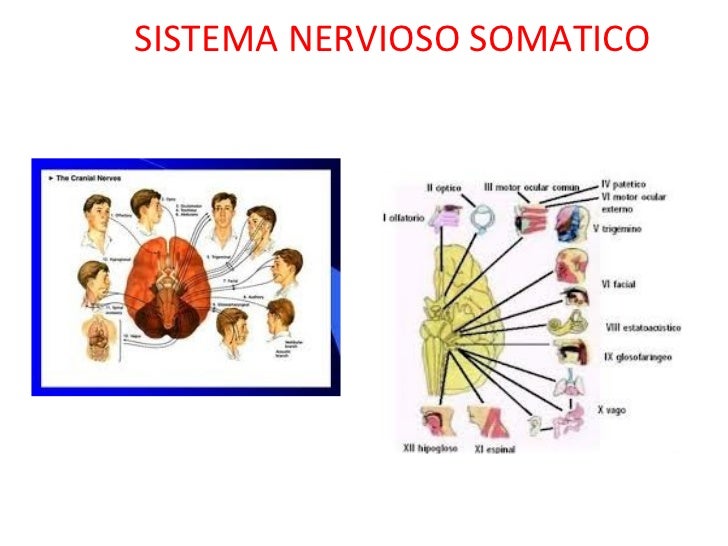
Sistema nervioso somático
Incluye grupos de neuronas que llevan información desde los órganos sensoriales (incluyendo toda la piel) hasta el sistema nervioso central (principalmente hasta el cordón espinal). A estos grupos de neuronas se les llama neuronas sensoriales o aferentes.
a. Las neuronas que recogen información directamente de los órganos sensoriales son neuronas especializadas con formas y sensibilidad particular. Por lo regular, estas neuronas tienen abundantes dendritas y axones cortos.

b. Por su parte, las neuronas que llevan información desde los órganos sensoriales hasta el sistema nervioso central suelen tener menos dendritas y axones largos. Grupos de estos axones forman lo que generalmente conocemos como nervios. Estos muestran un color blanco debido a la abundancia de capas de mielina, característico de los axones. A estos grupos de axones se les conoce como nervios sensoriales o aferentes.
Almacenado en un alfabeto de nucleótidos de cuatro “letras”- hecho de moléculas de azúcar y fosfatos, y llenos de signos de puntuación, reiteraciones para precaver contra el error, y cosas superfluas acumuladas en los callejones sin salida de la historia evolutiva-, su mensaje dice exactamente cómo hacer un ser humano, desde la piel y los huesos hasta las células cerebrales.
Si elevamos más el aumento veremos que la molécula de ADN está compuesta de muchos átomos, con sus capas electrónicas externas entrelazadas y festoneadas en una milagrosa variedad de formas, desde relojes de arena hasta espirales ascendentes como largos muelles y elipses grandes como escudos y fibras delgadas como puros. Algunos de esos electrones son recién llegados, recientemente arrancados átomos vecinos; otros se incorporaron junto a sus núcleos atómicos hace más de cinco mil millones de años, en la nebulosa de la cual se formó la Tierra.
El enlace: Adenina con Timina o Guanina con Citosina, constituyendo dicha secuencia el código genético en el que se organiza el funcionamiento celular.
Si elevamos el aumento cien mil veces, el núcleo de un átomo de carbono se hinchará hasta llenar el campo de visión. Tales núcleos átomos se formaron dentro de una estrella que estalló mucho antes de que naciera el Sol. Si podemos aumentar aún más, veremos los tríos de quarks que constituyen protonesy neutrones.

El microscopio electrónico nos enseña cosas alucinantes. Arriba un grano de Sal y un trozo de tiza. El tercero es la piel de la salamandra que le ayuda a pegarse a las paredes. Existe otro mundo pero está en este nuestro.

Los quarks han estado unidos desde que el Universo sólo tenía unos pocos segundos de edad.
Al llegar a escalas cada vez menores, también hemos entrado en ámbitos de energías de unión cada vez mayores. Un átomo puede ser desposeído de su electrón aplicando sólo unos miles de electrón-voltios de energía. Sin embargo, para dispersar los nucleones que forman el núcleo atómico se requieren varios millones de electrón-voltios, y para liberar los quarks que constituyen cada nucleón se necesitaría cientos de veces más energía aún.
Introduciendo el eje de la historia, esta relación da testimonio del pasado de las partículas: las estructuras más pequeñas, más fundamentales están ligadas por niveles de energía mayores porque las estructuras mismas fueron forjadas en el calor del big bang.

Hemos llegado hasta la consciencia de Ser, y, sabemos en qué lugar del Universo estamos
Nos cuesta asimilar que la evoluciòn de la materia se pudiera elevar (bajo un sin fin de parámetros y transmutaciones muy complejos), hasta alcanzar la consciencia y llegar a generar pensamientos. Parece como si el Universo hubiera sabido que nosotros (también otros seres similares e inteligentes en otros mundos del inmenso Cosmos), teníamos que venir y, para ello, creó sistemas idóneos para la vida como el planeta Tierra y muchos otros de su clase que ofrecen tal cobijo a criaturas vivas.

Los aceleradores de partículas, como los telescopios, funcionen como máquinas del tiempo. Un telescopio penetra en el pasado en virtud del tiempo que tarda la luz en desplazarse entre las estrellas; un acelerador recrea, aunque sea fugazmente, las condiciones que prevalecían en el Universo primitivo. En la imagen de arriba podemos ver como el Telescopio Espacial Hubble, poco a poco, ha podido ir avanzando hacia atrtás en el tiempo para enseñarnos las imágenes captadas cuando el Universo era muy joven. ¿Podremos algún día fabricar telescopios tan potentes que puedan captar imágenes del universo vecino?
Hemos llegado a dominar técnicas asombrosas que nos facilitan ver aquello que, prohibido para nuestro físico, sólo lo podemos alcanzar mediante sofisticados aparatos que bien nos introduce en el universo microscópico de los átomos, o, por el contrario nos llevan al Universo profundo y nos enseña galaxias situadas a cientos y miles de millones de años-luz de la Tierra.


Cuando vemos esos objetos cosmológicos lejanos, cuando estudiamos una galaxia situada a 100.000 mil años-luz de nosotros, sabemos que nuestros telescopios la pueden captar gracias a que, la luz de esa galaxia, viajando a 300.000 Km/s llegó a nosotros después de ese tiempo, y, muchas veces, no es extraño que el objeto que estamos viendo ya no exista o si existe, que su conformación sea diferente habiéndose transformado en diferentes transiciones de fase que la evolución en el tiempo ha producido.

Las entrañas de un protón
Siempre hemos querido saber lo que hay más allá de lo que el ojo ve
En el ámbito de lo muy pequeño, vemos lo que está ahí en ese momento pero, como se explica más arriba, en realidad, también nos lleva al pasado, a los inicios de cómo todo aquello se formó y con qué componentes que, en definitiva, son los mismos de los que están formadas las galaxias, las estrellas y los planetas, una montaña y un árbol y, cualquiera de nosotros que, algo más evolucionado que todo lo demás, podemos contarlo aquí.
Estas y otras muchas maravillas son las que nos permitirán, en un futuro relativamente cercano, que podamos hacer realidad muchos sueños largamente dormidos en nuestras mentes.
emilio silvera
May
6
¡El futuro! ¿Podremos diseñarlo nosotros?
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en El Futuro incierto ~
Clasificado en El Futuro incierto ~
 Comments (0)
Comments (0)
Rayos Cósmicos y otros temas del Universo

Inmensas máquinas del LHC que buscarán las partículas (hipotéticas) de la “materia oscura” (hipotética)
Lo cierto es que si creemos que nosotros podremos diseñar nuestro futuro, estaríamos dándonos más importancia de la que en realidad tenemos. Podemos hacer que algunas cosas sean de cierta manera durante un tiempo limitado pero, nada dura para siempre y, si interviene la Naturaleza, lo que nosotros queramos poca importancia puede tener. Es cierto que, también somos y formamos parte de esa Naturaleza que no podemos dominar y, siendo así (que lo es), podremos comprender lo incomprensible del comportamiento Humano.
¿Qué hay ahí realmente? ¿Sabremos alguna vez los procesos que fabrican los pensamientos?
He dado muchas vueltas a la IA y a la consciencia de los seres vivos. Las conclusiones a las que he podido son que el pensamiento consciente debe involucrar componentes que no pueden ser siquiera simulados adecuadamente por una mera computación; menos aún podría la computación por sí sola, provocar cualquier sentimiento o intención consciente. En consecuencia, la mente debe ser realmente algo que no puede describirse mediante ningún tipo de términos computacionales.
!La Nube!: el cielo en la computación

Uno de los términos de los que más se habla actualmente en materia de tecnología es “la nube”. Aunque para muchos puede resultar , no lo es. Este concepto de la computación moderna, nube, está tomando un auge que probablemente sea una variable en la economía basada en computadoras.

Computación por nube, o simplemente “la nube”, es una plataforma que te permite utilizar recursos, ya sea de una compañía o de tu mismo trabajo, por remoto, desde tu computadora a un servidor, casi siempre a través de la Internet. En otras palabras, puedes usar aplicaciones y/o hacer trabajos sin la necesidad de programas y tus trabajos no tienen que ser grabados en tu computadora.
Bien es verdad que no tenemos una comprensión científica de la mente humana. Sin embargo, esto no quiere decir que el fenómeno de la consciencia deba permanecer fuera de la explicación científica. Ya se están buscando caminos científicos para dar esa explicación del misterio más profundo (seguramente) del Universo.
La comprensión es, después de todo, de lo que trata la ciencia; y la ciencia es mucho más que la mera computación mecánica.

¿Cómo podríamos trasladar la conciencia a un ? Algunos ya lo están intentando y, no es algo que yo pueda asimilar, toda vez que, lo artificial siempre será “una copia” de lo natural pero… ¿Qué pasaría si llegan a conseguirlo? ¿Qué entes saldrán de ese… “paso adelante”? ¿Estamos llegando a niveles que van más allá de lo que nos podría convenir?
¿Cuál es el de acción de la ciencia? ¿Son solamente los atributos materiales de nuestro Universo los que son abordables con sus métodos, mientras nuestra existencia mental debe quedar para siempre fuera de su alcance? ¿O podríamos llegar algún día a una comprensión científica adecuada del profundo misterio de la mente? ¿Es el fenómeno de la consciencia humana algo que está más allá del dominio de la investigación científica, o podrá la potencia del método científico resolver algún día el problema de la propia existencia de nuestro yo consciente?

Nanorobots que introducidos en nuestros cuerpos, curarán dolencias hoy incurables

Creo que se avecina un cambio importante, y, nuestros cerebros que forman parte del mundo material del Universo, tiene un ingrediente que aún no hemos llegado a comprender. Incluso con nuestra limitada comprensión actual de la naturaleza de este ingrediente ausente en nuestro saber, sí podemos a señalar donde debe estar dejando su huella, y como debería estar aportando una contribución vital a lo que quiera que sea en que subyacen nuestros sentimientos y acciones conscientes.
Una visión científica del mundo que no trate de entender en profundidad el problema de la mente consciente no puede tener pretensiones serias de compleción. La consciencia es parte de nuestro Universo, de modo que cualquier teoría física que no le conceda un lugar apropiado se queda muy lejos de proporcionar una descripción auténtica del mundo.
Claro que, todo conocimiento científico es un de dos filos. Lo que realmente hacemos con nuestro conocimiento científico es otra cuestión. Tratemos de ver dónde pueden llevarnos nuestras visiones de la ciencia y la mente. No siempre hemos sabido utilizar los descubrimientos hechos por los seres de nuestra especie. Acordémonos de la famosa fórmula de Einstein: E = mc2 que, en nuestro triste recuerdo nos trae aquella imagen fatal de la bamba de Hirosima. Es una lástima que, en la Segunda Guerra Mundial, algunos de los mejores físicos del mundo (Planck, Heisenberg y otros, se pusieran al servicio de Hitler). Pero dejemos los malos recuerdos.
La Conciencia dividida

Las de arriba son dos calles de Madrid que, al igual que muchas otras del mundo reflejan logros de la Humanidad que no siempre ha sabido administrar los medios que la Naturaleza les ha proporcionado. De la misma manera, estamos haciendo con la Ciencia que no siempre, sabemos utilizar aquellos descubrimientos que nos podrían llevar a un futuro mejor.
Pensemos que incluso en aquellos países afortunados donde hay una paz próspera y una libertad democrática, los recursos naturales y humanos son malgastados de formas aparentemente absurdas. ¿No es ésta una clara muestra de la estupidez del hombre? Aunque creemos representar el pináculo de la inteligencia en el reino animal, esta inteligencia parece tristemente inadecuada para manejar muchos de los problemas a los que nuestra propia sociedad nos obliga a hacer frente.
Aunque no podemos dejar de reconocer que hemos sido capaces de llegar a conocimientos muy profundos que están situados desde lo más pequeño hasta lo más grande. De átomos y galaxias podemos hablar ahora y contar a quien quiera escuchar como nacen, viven y mueren las estrellas para que nosotros podamos estar aquí.

Pese a todo, no pueden negarse los logros positivos de nuestra inteligencia. Entre dichos logros se encuentran nuestras impresionantes ciencia y tecnología. En realidad, algunos de estos logros son alto cuestionables a largo (o corto) plazo, así lo atestiguan múltiples problemas medioambientales y un genuino temor a una catástrofe mundial inducida por las nuevas tecnologías traídas de la mano por nuestra moderna sociedad (aquí mismo, en éste foro, se ha expresado el temor sobre las consecuencias que traerá el LHC que a primeros del próximo septiembre será puesto en marcha para la partícula de Higgs, y que, según algunos, andar jugando con tan enormes energías pudiera crear un agujero negro que se engulla a la Tierra entera). Os puedo que dicho temor es infundado.
Pero, no podemos mirar para otro lado sin ver que, nuestras tecnologías no sólo nos proporciona una enorme expansión del dominio de nuestro yo físico sino que también amplia nuestras capacidades mentales mejorando en gran medida nuestras habilidades para realizar muchas tareas rutinarias. ¿Qué pasa con las tareas mentales que no son rutinarias, las tareas que requieren inteligencia genuina?

Hormigas inteligentes
A veces me pregunto si podrían ser los Robots la . ¿No existe la posibilidad completamente diferente de una enorme expansión de una capacidad mental, a saber, esa inteligencia electrónica ajena que apenas está empezando a emerger de los extraordinarios avances en tecnología de ordenadores? De hecho, con frecuencia nos dirigimos ya a los ordenadores en busca de asistencia intelectual.

¿Un mundo de Drones? ¿Qué seguridad es esa?
Hay muchas circunstancias en las que la inteligencia humana sin ayuda no resulta nada adecuada para prever las consecuencias probables de acciones alternativas. Tales consecuencias pueden quedar mucho más allá del alcance del poder computacional humano; así pues, cabe esperar que los ordenadores del futuro amplíen enormemente este papel, en la computación pura y dura proporcione una ayuda incalculable para la inteligencia humana.
Pero ¿no cabe la posibilidad de que los ordenadores lleguen finalmente a mucho más que todo esto? Muchos expertos afirman que los ordenadores nos ofrecen, al menos en principio, el potencial para una inteligencia artificial que al final superará a la nuestra. Una vez que los robots controlados por ordenador alcancen el nivel de “equivalencia humana”, entonces no pasará mucho tiempo, argumentan ellos, antes de que superen rápidamente nuestro propio y exiguo nivel. Sólo entonces, afirman estos expertos, tendremos una autoridad con inteligencia, sabiduría y entendimiento suficientes que sea capaz de resolver los problemas de este mundo que ha creado la humanidad.
A todo esto señalan el rapidísimo crecimiento exponencial de la potencia de los ordenadores y basan sus estimaciones en comparación entre la y precisión de los transistores, y la relativa lentitud y poca sólida acción de las neuronas. De hecho, los circuitos electrónicos son ya más de un millón de veces más rápido que el disparo de las neuronas en el cerebro (siendo la velocidad de aproximadamente 109segundos para los transistores y de 13 segundos para las neuronas, y tienen una exactitud cronométrica y una precisión de acción que de ningún modo comparten las neuronas.
El Chip Intel Pentium tiene más de tres millones de de transistores en una “rodaja de silicio” del tamaño aproximado de una uña del pulgar, capaz cada uno de ellos de realizar 113 millones de por segundo.

Se argumenta que el total de neuronas de un cerebro humano (unos cientos de miles de millones) supera absolutamente al número de transistores de un ordenador. Además, existen muchas más conexiones, en promedio, entre neuronas diferentes que las que existen entre los transistores de un ordenador. En particular las células de Purkinje en el cerebelo pueden tener hasta ochenta mil terminaciones sinápticas (uniones entre neuronas), mientras que para un ordenador, el número correspondiente es de tres o cuatro a lo sumo. Además, la mayoría de los transistores de los ordenadores actuales están relacionados solamente con la memoria y no directamente con la acción computacional, mientras que tal acción computacional podría estar mucho más extendida en el caso del cerebro.

Cerebros espintrónicos de increíbles capacidades que, en mucho, podrán superar los de los seresd vivos en el futuro próximo. Si hiciéramos caso de las afirmaciones más extremas de los defensores más locuaces de la IA, y aceptáramos que los ordenadores y los robots guiados por ordenador superarán con el tiempo (quizá en muy poco tiempo) todas las capacidades humanas, entonces los ordenadores serían capaces de hacer muchísimo más que ayudar simplemente a nuestras inteligencias. Podríamos entonces dirigirnos a estas inteligencias superiores en busca de consejo y autoridad en todas las cuestiones de ; ¡y finalmente podrían resolverse los problemas del mundo generados por la humanidad!
Pero parece haber otra consecuencia lógica de estos desarrollos potenciales que muy bien podría producirnos una alarma genuina. ¿No harían estos ordenadores a la largo superfluos a los propios humanos? Si los robots guiados por resultaran ser superiores a nosotros en todos los aspectos, entonces ¿no descubrirían que pueden dirigir el mundo sin ninguna necesidad de nosotros? La propia humanidad se habría quedado obsoleta. Quizá si tenemos suerte, ellos podrían conservarnos como animales de compañía.

Yo, como he dejado claro otras veces. Soy partidario de pensar que, una cosa es la Inteligencia Artificial y otra muy distinta es el pensamiento consciente, muy superior a aquella que trabaja sólo con los suministrados previamente, sin el poder de repentizar una solución que no esté en su programación. Nuestra imaginación si puede hacerlo. ¿Llegarán los robots algún día a pensar por sí mismos, como ahora lo hacemos nosotros?
La cuestión no es nada sencilla y plantea muchas variantes de entre las que de momento, podríamos exponer aquí las propuestas por Roger Penrose y que son las siguientes:

¡¡ Cuidado!! a ser dioses pueden traer consecuencias. Por no ir más lejos, hace unos días pudimos leer sobre la posible vida sintética futura a partír de la levadura. ¡Qué cosas!
- Todo pensamiento es computación; en particular, las sensaciones de conocimiento consciente son provocadas simplemente por la ejecución de computaciones apropiadas.
- El conocimiento es un aspecto de la acción física del cerebro; y si bien cualquier acción física puede ser simulada computacionalmente, la simulación computacional no puede por sí misma provocar conocimiento.
- La acción física apropiada del cerebro provoca conocimiento, pero esta acción física nunca puede ser simulada adecuadamente de forma computacional.
- El conocimiento no puede explicarse en términos físicos, computacionales o cualesquiera otros términos científicos.
Está claro que adentrarnos aquí a ciertas profundidades del pensamiento, no parece adecuado ni al momento ni al lugar, sin embargo, debemos pensar en que, la propia materia parece tener una existencia meramente transitoria puesto que puede transformarse de una forma en otra. Incluso la masa de un cuerpo material , que proporciona una medida física precisa de la cantidad de materia que contiene el cuerpo, puede transformarse en circunstancias apropiadas en pura energía (según E=mc2) de modo que incluso la sustancia material parece ser capaz de transformarse en algo con una actualidad meramente matemática y teórica.

De todas las maneras, por mi parte, me quedo con el punto tercero de los enumerados anteriormente, es un punto de más operacional que el anterior, puesto que afirma que existen manifestaciones externas conscientes (por ejemplo, cerebros) que difieren de las manifestaciones externas de un ordenador: los efectos externos de la consciencia no pueden ser correctamente simulados por un ordenador.

Investigadores de la Universidad Politécnica de Valencia, España, desarrollaron un prototipo que identifica los sentimientos y las emociones de las personas …
¿Permite la Física la posibilidad de una acción que, en principio, sea imposible de simular en un ordenador? La respuesta no está completamente clara, sin embargo, según creo, es que tal acción no computacional tendría que encontrarse en un área de la física que está fuera de las leyes físicas actualmente conocidas.
Claro que, en este simple comentario, no queda claro quien será el vencedor final: Fisicalismo frente a Mentalismo. ¿Seremos tan estúpidos como para poder crear que nos superen en inteligencia hasta el punto de que puedan dominarnos?
Ahí queda la flotando en el aire.
emilio silvera
May
5
La Física y el Tiempo
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en El Tiempo pasa...¿O somos nosotros? ~
Clasificado en El Tiempo pasa...¿O somos nosotros? ~
 Comments (25)
Comments (25)
Modigliani, pintor de un sólo ojo
Para el topólogo, un nudo es una curva continua, cerrada y sin puntos dobles. Esta curva está situada en un espacio de tres dimensiones y se admite que pueda ser deformada, estirada, comprimida, aunque está “prohibido” hacerle cortes. Cuando se puede, a través de diversas manipulaciones, se pasa de un nudo a otro y se dice que son equivalentes. Claro que, algunos se abstraen en cuestiones de otra índole, sí, también son curvas pero, al parecer, no relacionadas.
Un viejo amigo bromeaba diciendo que el Andante en do menor de la Sinfonía Concertante de Mozart conseguía devolverle a su intimidad anímica de partida, y que por eso, en su opinión, plasmaba de forma inefable el tiempo cíclico, o mejor aún, una CTC (“curva de género de tiempo cerrada”). Y transcurridos los doce minutos que dura ese movimiento, volvíamos a escucharlo una vez más. Mientras, discutíamos sin cesar sobre el tiempo, esa abstracción de la Mente que nadie ha sabido explicar.

No es bueno perder la perspectiva
Hay un tiempo para cada cosa. Un tiempo para soñar, inconmensurable, un tiempo para vivir, siempre corto, un tiempo para filosofar, misterioso,…, y un tiempo para la ciencia, sujeto a número.
Me gustaría empezar definiendo el tiempo, pero no sé. Sesudos pensadores, como Platón y Aristóteles, lo ensayaron con brillantez. El tiempo es una imagen móvil de la eternidad. Esta imagen es eterna, pero se mueve según número, dirá Platón en el TIMEO. El tiempo es el número de movimiento según el antes y el después…El tiempo no es movimiento, sino movimiento en tanto en cuanto admite enumeración. El tiempo es una especie de número. El tiempo es obviamente aquello que se cuenta, no aquello con lo cual contamos, escribirá Aristóteles en su FÍSICA.

Alguna vez, en simbiosis con la Naturaleza, podemos sentir como se ha parado el tiempo
Son definiciones muy sugestivas, aunque teñidas de circularidad: movimiento en el tiempo, tiempo a través del movimiento. Agustín de Hipona vio esto claramente. Célebre es asimismo su declaración: Si nemo a me quaerat, scio; si quaerenti explicari velim, nescio (CONFESIONES). En uno de los análisis más penetrantes del tema, sugirió Agustín la Mente como fuente de tiempo: En ti es, mente mía, donde mido los tiempos.
Time is what happens when nothing else happens, afirma Feynman; para a continuación advertir que toda definición del tiempo es necesariamente circular, y que lo importante no es decir qué es el tiempo, sino decir cómo se mide lo que llamamos tiempo. En su enciclopédico tratado sobre la gravitación, Misner, Thorne y Wheeler nos recuerdan de forma sencilla y profunda lo que toda medida del tiempo físico debe cumplir: Time is defined so that motion looks simple.

El tiempo es un concepto inventado por el hombre para ordenar, primero, sus sensaciones y actos, y luego, los fenómenos. Decían los escolásticos: Tempus est ens rationis cum fundamento in re. La primera unidad natural debió ser el día, por la ciclidad conspicua de las salidas del Sol. Los grandes avances científicos y tecnológicos a lo largo de los siglos han estado vinculados a los adelantos en la precisión con que se ha ido midiendo el tiempo. Hoy disponemos de relojes que aseguran un segundo en 20 millones de años, y el paso de la femtoquímica a la astrofísica empieza a ser una realidad.

No pocas veces nos podemos ver perdidos en la vorágine de lo que llamamos tiempo, algo tan enorme que, en realidad, no sabemos lo que es. No lo hemos llegado a comprender, y, por si fuera poco, tampoco sabemos, si en realidad existe.
El tiempo antes de Einstein.
La física nació en torno al tiempo. Las regularidades en los ciclos astrales permitieron al acierto en las predicciones apoyadas en esta periodicidad, y con ello despertó sin duda la confianza del hombre en la racionalidad, llevándole a escoger el cosmos frente al caos.
Breve historia de la medida del tiempo
La longitud de las sombras fue uno de los primeros métodos usados para fijar las horas. En el Museo Egipcio de Berlín hay un fragmento de piedra que posiblemente sea de un reloj de sol de alrededor de 1500 a.C. Los babilonios desarrollaron los relojes de sol, y se dice que el astrónomo Anaximandro de Mileto los introdujo en Grecia en el siglo VI a.C.
En el siglo II a C, Eratóstenes, de la biblioteca de Alejandría, concibió y llevó a cabo la primera medida de las dimensiones de la Tierra de la que se tiene noticia. En el Año Internacional de la Astronomía, una de las actividades que se llevaron a cabo fue, precisamente averiguar el radio terrestre por el mismo método.
Aparte de relojes de sol, en la antigüedad se usaron también relojes de arena, de agua, cirios y lámparas de aceite graduadas.


En la segunda mitad del siglo XIII aparecen los primeros relojes mecánicos. Su precisión era muy baja (10-20%). En el XIV se mejoran, con el invento del escape de rueda catalina, y ya se alcanzan precisiones de 20 a 30 minutos por día (1-2%). Por allá al año 1345 se empieza a dividir las horas en minutos y segundos.
El tiempo físico asoma en el siglo XIV, en el Merton College Oxford y luego en la Universidad de París, con Oresme. Se representa en una línea horizontal, mientras en vertical se disponen las cualidades variables. Son los primeros gráficos de función (en este caso, función del tiempo). La cinemática celeste brinda un buen reloj a través de la segunda ley de Kepler, midiendo tiempos mediante áreas. La ley armónica de Kepler permitirá medirlos a través de longitudes. Galileo desarrolló la cinemática terrestre, y sugirió el reloj de péndulo. A Huygens debemos la técnica de medida del tiempo que ha llegado a nuestros días, y que suministró relojes más precisos y transportables mediante volantes oscilatorios acoplados a resortes de calidad.

Diseño del reloj de péndulo de Huygens, 1656 (imagen de dominio público).
La importancia, no sólo científica sino económica, de disponer de relojes precisos y estables, queda reflejada en el premio ofrecido por el gobierno inglés de la reina Ana en 1714, que dispuso that a reward be settled by Parliament upon such person o persons as shall discover a more certain and practicable method of ascertainig longitude that any yet in practice. La recompensa era de 20, 000 libras para el que presentara un cronómetro capaz de determinar la longitud con error menor de 30´ de arco al término de un viaje a las Indias occidentales, equivalente a mantener el tiempo con error menor de 2 minutos tras seis semanas de viaje. Se la llevó casi medio siglo después el relojero británico John Harrison (1693-1776), con un reloj, conocido como H4, que incorporaba correcciones por variación en la temperatura, y que en un primer viaje de 81 días desde Porstmouth a Puerto Real (Jamaica) en 1761-62 se retrasó 5 s, esto es, de precisión 10⁻⁶ (10; 44).
Después se pasó a los de diapasón, de aquí a los de cuarzo, y hoy los atómicos ofrecen precisiones desde 10⁻¹² – 10⁻¹⁵ (Cs) hasta 10⁻¹⁶ (máser de H).
Una red de relojes atómicos de cesio, sincronizados mediante ondas de radio, velan actualmente por la exactitud de la hora sobre el planeta. Como señala Davies (10), ya no nos sirve como cronómetro el giro de la Tierra alrededor de su eje. Aunque durante siglos ha sido este viejo trompo un magnífico reloj de referencia, la falta de uniformidad de su giro (las mareas, por ejemplo, lo frenan incesantemente y alargan con ello el día en un par de milésimas de segundo por siglo, perceptible para los finos cronómetros actuales), y otras desviaciones estacionales, cuantitativamente similares a estos retrasos seculares, pero irregulares y de signo variable, son circunstancias que en conjunto obligan a añadir al tiempo civil un segundo intercalar cada uno o dos años (el último lo fue el 1 de enero de 1999, a las 0 horas) con el fin de remediar la asincronía entre los tiempos atómicos y los días astronómicos. El día no tiene 86 400 s justos (donde el segundo se define como la duración de 9 192 631 770 períodos de una determinada vibración de los átomos de Cs. Hoy la tecnología alcanza precisiones fabulosas: relojes que en treinta millones de años se desviarían a lo sumo en un diminuto segundo, como el NIST-F1 (Boulder, Colorado).
Por norma general y para mayor exactitud del sistema, dentro del campo visual de cualquier receptor GPS siempre hay por lo menos 8 satélites presentes. Cada uno de esos satélites mide 5 m de largo y pesa 860 kg . La energía eléctrica que requieren para su funcionamiento la adquieren a partir de dos paneles compuestos de celdas solares adosadas a sus costados. Están equipados con un transmisor de señales codificadas de alta frecuencia, un sistema de computación y un reloj atómico de cesio, tan exacto que solamente se atrasa un segundo cada 30 mil años.

La posición que ocupan los satélites en sus respectivas órbitas facilita que el receptor GPS reciba, de forma constante y simultánea, las señales de por lo menos 6 u 8 de ellos, independientemente del sitio donde nos encontremos situado. Mientras más señales capte el receptor GPS, más precisión tendrá para determinar las coordenadas donde se encuentra situado.
Incluso hay relojes de pulsera comerciales (receptores de señales de radio) con precisión de un segundo por millón de años garantizada por un reloj atómico en una lejana estación. La naturaleza de altísima precisión: la estabilidad del púlsar binario b1855+09 puede ser de unas partes en 10¹⁵ o incluso mejor.
El tiempo en Newton:
En los PRINCIPIA, Newton empieza con una renuncia a definir el tiempo: El tiempo, el espacio, el lugar y el movimiento son de todos bien conocidos. Y no los defino. Pero digo que el vulgo no concibe esas cantidades más que por su relación a cosas sensibles. Para evitar ciertos prejuicios que de aquí se originan, es conveniente distinguirlas en absolutas y relativas, verdaderas y aparentes, matemáticas y vulgares.
A continuación, sin embargo, Newton se arrepiente de su primer impulso y aclara: El tiempo absoluto, verdadero y matemático, de suyo y por su propia naturaleza fluye uniformemente sin relación a nada externo y se llama también duración: el tiempo relativo, aparente y vulgar es cualquier medida sensible y externa (exacta o no uniforme) de la duración por medio del movimiento y se usa vulgarmente en lugar del tiempo verdadero: tal como la hora, el día, el mes, el año.

Sabemos del fluir del tiempo por el cambio que se produce en nuestro Universo, en el Mundo, en Nuestras Vidas. Con el paso del Tiempo las cosas cambian y nada permanece. Por eso sabemos que está ahí
¿Qué significa que el tiempo fluye? ¿Qué el tiempo “se mueve en el tiempo”? De nuevo la pescadilla mordiéndose la cola. El absolutismo del tiempo newtoniano recibió encendidas críticas. Leibniz opuso su idea de espacio y tiempos puramente relativos, el primero como un orden de coexistencia, el segundo como un orden de sucesiones de las cosas; ambos, espacio y tiempo, son phœnomena bene fundata. Los argumentos dinámicos con que Newton arropa su tesis de la naturaleza absoluta de la rotación y con ello la de un espacio absoluto, apoyo posterior para el tiempo absoluto, también hallan fuertes objeciones. Para Berkeley esas razones de Newton lo único que muestran es la importancia del giro respecto de las masas lejanas del Universo y no respecto de un espacio absoluto, que él no acepta. Ernst Mach, en la segunda mitad del XIX, insistirá decididamente en este punto de vista, y desde su positivismo acosará los absolutos newtonianos. De “medieval”, “no científico”, “metafísico”, tilda Mach a Newton: No tenemos derecho a hablar de un tiempo “absoluto”: de un tiempo independiente de todo cambio. Tal tiempo absoluto no puede medirse por comparación con ningún movimiento; por tanto no tiene valor práctico ni científico, y nadie tiene derecho a decir que sabe algo de él. Es una concepción metafísica vana.

El tiempo en Einstein:
El tiempo newtoniano, absoluto, el nos es familiar, tuvo que dejar paso al tiempo einsteniano, mutable y relativo, con tantos “ahora” por suceso cuantos estados de movimiento mutuo imaginemos.
El tercero de los trabajo enviados por Albert Einstein (AE) en su Annus Mirabilis de 1905 a Annalen der Physik lleva por título “Zur Elektrodynamik Bewegter Körper” (“Sobre la electrodinámica de los cuerpos en movimiento”). Junto con el quinto, titulado “Ist der Trägheit eines Körpers von seinem Energieinhalt abhängig?” (“¿Depende la inercia de un cuerpo de su contenido de energía?”), constituyen lo que hoy se llama TEORÍA ESPECIAL DE LA RELATIVIDAD.

Velocidad de la luz desde la Tierra a la Luna, situada a más de 380.000 km.
Da Albert Einstein un par de razones para justificar su tercer trabajo:
- La insatisfacción que le produce la asimetría en la descripción maxwelliana de los fenómenos electromagnéticos: la acción entre un conductor y un imán depende solo del movimiento relativo entre ambos, pero la teoría de Maxwell distingue entre el caso de conductor en reposo y el caso de imán en reposo: a) En el primer caso el campo magnético móvil engendra un campo eléctrico, con una energía determinada, que a su vez produce corrientes en el conductor en reposo. b) En el segundo caso, no se produce ningún campo electrónico, sino una fuerza electromotriz en el conductor, sin energía asociada, que engendra una corriente como en el caso anterior.
- La incapacidad de la óptica y del electromagnetismo (EM) para detectar el movimiento respecto del lichtmedium, es decir, de un inercial privilegiado. Esto le sugiere que la óptica y el EM tienen las mismas ecuaciones en todos los inerciales (sistemas en los que las leyes de la mecánica de Newton son las mismas). Y AE eleva esto a un principio, que llama “Prinzip der Relativität”, y le añade un compañero, aparentemente incompatible con él: “La velocidad de la luz en vacío es siempre la misma, con independencia del estado de movimiento del cuerpo emisor”

¿Será ese de arriba el rayo de luz de Einstein, o, por el contrario, será un asteroide que se nos viene encima?
Siendo todavía muy joven, en 1895-1896, ya le preocupaba el EM y la luz, como recordaba en 1955: “Si persiguiéramos a la velocidad de la luz un rayo de luz, veríamos una onda independiente del tiempo. ¡Tal cosa, sin embargo, no existe! Este fue el primer experimento mental, infantil, en relación con la teoría especial de la relatividad”.
Este tercer trabajo de Einstein en 1905 no contiene ninguna referencia a otros trabajos, ni suyos ni de otros (como Lorentz o Poincaré).
Consciente de que su postulado de la constancia de la velocidad de la luz choca frontalmente con la ley galileana de adición de velocidades, Albert Einstein revisa los cimientos de la Física, empezando por definir físicamente y con sumo cuidado el concepto de Gleichzeitigkeit o simultaneidad entre sucesos. Considera un sistema inercial, para el que supone válida la geometría euclidiana para calcular distancias entre objetos estacionarios a través de sus coordenadas respecto de sus ejes cartesianos. Si A, B son dos observadores estacionarios, provistos de relojes iguales, y A (B) manda una señal luminosa a B (A), quien la devuelve sin tardanza a A (B), diremos que el reloj de A está sincronizado con el reloj de B si
t(B) – t(A) = t’(A) – t(B),
donde t(A) es el tiempo marcado por el reloj de A cuando envía la señal a B, t(B) lo que marca el reloj de B al llegarle la señal de A y reemitirla, y t’(A) la lectura del reloj de A al recibir la devolución de B.

No parece el mejor método para medir la velocidad de la luz, el empleado por Galileo. Claro que, en aquellos tiempos…¿Qué se podía hacer?
Supone Albert Einstein que esta definición no lleva a contradicciones, que es en principio posible entre cualquier par de observadores estacionarios en el inercial, y que la relación de sincronización anterior es de equivalencia: Si A está sincronizada con B, también B lo está con A, y si además B lo está con C, también A y C lo están. A esto le siguen ecuaciones que quiero obviar para no dar complejidad al trabajo.
No existe “el” presente
Pasa Albert Einstein a enunciar con precisión el principio de relatividad y el postulado de la constancia de la velocidad de la luz en el vacío:
- Las leyes que rigen los cambios de los sistemas físicos son las mismas en todos los inerciales.
- Todo rayo de luz se mueve en cualquier inercial con una misma velocidad, c, independientemente del movimiento de su fuente.
Como consecuencia, demuestra que el concepto de sincronía, y por ende de simultaneidad, es relativo, no absoluto. La noción de “presente”, “ahora” o cualquier instante determinado depende del referencial inercial.

Algunos incluso hablaron de energía taquiónica
¿Más rápido que la luz?
¿Existen partículas que se muevan con velocidad superior a la de la luz? Sí; por ejemplo, cualquier partícula que lleve en agua, a temperatura entre 0 y 50 ºC, una velocidad ν > c / n, n = 1.3, irá más deprisa en ese medio que los fotones del espectro visible. Lo mismo ocurre con la mayoría de los rayos cósmicos que llegan a la atmósfera; son superlumínicos en relación con la velocidad de la luz en el aire. Precisamente en esta posibilidad de rebasar la velocidad de la luz en un medio reside el efecto Cherenkov.

Lo que no se conocen son taquiones, o partículas que se muevan más deprisa que la luz en el vacío. Si existieran, podrían utilizarse para mandar información al pasado. Violando el orden causa-efecto. Por ello se “decreta” su inexistencia.
En fin, que la velocidad de la luz en el vacío, al menos que sepamos, es infranqueable. Es un límite impuesto por la Naturaleza al que habrá que vencer, no superándolo (que no se puede), sino mediante una artimaña física inteligente que logre burlar dicho límite.
Aparte de algún que otro añadido, el artículo (parcialmente expuesto aquí -se obviaron partes complejas), es del Físico de la Universidad Complutense D. Alberto Galindo Tixaire. Fue publicado en el Volumen 19, número 1 de la Revista Española de Física en 2005 Año Mundial de la Física

En realidad, un Homenaje a Einstein por haber pasado más de un siglo desde aquel acontecimiento memorable de la Relatividad Especial en el año 1.905 y estar a punto de cumplirse otro siglo desde su relatividad general de 1915. Dos acontecimientos que marcaron el camino de la Física y la Cosmología. Hace ahora un par de años que se cumplieron los 100 años desde que Einstein diera al mundo la segunda parte de su Teoría.
emilio silvera
















 Totales: 72.681.851
Totales: 72.681.851 Conectados: 33
Conectados: 33

























