La complejidad del Cerebro…Los caminos de la Mente

          Los cinco sentidos, Hans Makart (1840-1884)

En su obra Materia y memoria, Henri Bergson decía:

“La percepción, en su conjunto, tienen su verdadera razón de ser en la tendencia del cuerpo a moverse”

 

 Nosotros hablamos de los cinco sentidos de los que nos valemos para tener una percepción del mundo que nos rodea. Sabemos, que muchos de los animales que pueblan nuestro planeta tienen algunos de esos sentidos mucho más desarrollados que nosotros, y, sin embargo, es nuestra especie la que prevalece como superior de todas las demás. Nuestras mentes, han llegado a desarrollar un mayor y más completo conjunto de conexiones neuronales que han posibilitado una más amplia consciencia del mundo que nos rodea, de la Naturaleza.

La percepción, los sentidos y los pensamientos… Para poder entender la conciencia como proceso es preciso que entendamos cómo funciona nuestro cerebro, su arquitectura y desarrollo con sus funciones dinámicas. Lo que no está claro es que la conciencia se encuentre causalmente asociada a ciertos procesos cerebrales pero no a otros.

El cerebro humano -hay que reconocerlo-,  es especial; su conectividad, su dinámica, su forma de funcionamiento, su relación con el cuerpo y con el mundo exterior, no se parece a nada que la Ciencia conozca. Tiene un carácter único y ofrecer una imagen fidedigna del cerebro no resulta nada fácil; es un reto tan extraordinario que no estamos preparados para cumplir en este momento. Estamos lejos de ofrecer esa imagen completa, y sólo podemos dar resultados parciales de esta increíble maravilla de la naturaleza.

Nuestro cerebro adulto, con poco más de 1,5 Kg de peso, contiene unos cien mil millones de células nerviosas o neuronas. La parte o capa ondulada más exterior o corteza cerebral, que es la parte del cerebro de evolución más reciente, contiene alrededor de treinta millones de neuronas y un billón de conexiones o sinapsis. Si contáramos una sinapsis cada segundo, tardaríamos 32 millones de años en acabar el recuento. Si consideramos el número posible de circuitos neuronales, tendremos que habérnoslas con cifras hiper-astronómicas. Un 10 seguido de, al menos, un millón de ceros (en comparación, el número de partículas del universo conocido asciende a 10⁷⁹ “tan sólo” un 10 seguido de 79 ceros). ¡A que va a resultar que no somos tan insignificantes!

Con tan enorme cantidad de circuitos neuronales, ¿podremos algún día ser capaces de descifrar todos los secretos de nuestro universo? ¿De qué seremos capaces cuando podamos disponer de un cerebro totalmente evolucionado?

¡Tan frágil y tan fuerte! En tan pequeño conjunto reside el secreto mejor guardado por la Naturaleza que hizo posible, ese asombroso viaje que va, desde la materia inerte hasta los pensamientos. Han sido necesarios dies mil millones de años para que, las estrellas, pudieran fabricar los elementos bioquímicos necesarios para hacer posible tal transición que, por mucho que la queremos comprender…

El límite de lo que podremos conseguir tiene un horizonte muy lejano. Desde hablar o comunicarnos sin palabras sonoras -no es ninguna broma- , a la auto-transportación. Ahora mismo, simplemente con el pensamiento, podemos dar instrucciones a máquinas que obedecen nuestras órdenes. Sí, somos pura energía pensante, el poder de la mente no está totalmente desarrollado y, simplemente es cuestión de tiempo.  Creo que no habrá límite alguno; el cuerpo que ahora nos lleva de un lugar a otro, ya no será necesario, y como los fotones que no tienen masa… ¿Podremos desplazarnos entre las estrellas  a velocidades superlumínicas? Mi imaginación se desboca y va mucho más allá de lo que la razón aconseja.

Creo que estoy corriendo demasiado en el tiempo, volvamos a la realidad. A veces mi mente se dispara. Lo mismo visito mundos extraordinarios con mares luminosos de neón líquido poblados por seres transparentes, que viajo a galaxias muy lejanas pobladas de estrellas de fusión fría circundadas por nubes doradas compuestas de anti-materia en la que, los positrones medio congelados, se mueven lentamente formando un calidoscopio de figuras alucinantes de mil colores. ¡La mente, qué tesoro!

          Es cierto que existen otros mundos y, todos, están dentro de nuestras mentes

Cuando seamos capaces de convertir en realidad todo aquello en lo que podamos pensar, entonces, habremos alcanzado la meta. Para que eso sea una realidad… aún falta y, debemos ser conscientes de que nunca, podremos alcanzarlo todo. Si la Naturaleza y el Universo nos dejo, jugamos con ventaja y con tiempo por delante… ¿Qué se nos puede resistir? Nuestra manera de generar entropía negativa es dejar descendencia, así luchamos contra la desaparición de nuestra especie y de los logros que, durante milenios pudo alcanzar.  Dejamos lo que logramos descubrir a los que nos siguen, ellos a los que vendrán después, y así hasta “el infinito”.

El mundo físico se representa gobernado de acuerdo a leyes matemáticas -fuerzas y constantes universales-. Desde este punto de vista, todo lo que hay en el universo físico está realmente gobernado en todos sus detalles por principios matemáticos, quizá por ecuaciones tales como las que describen nuestras mejores teorías.

Lo más seguro es que la descripción real del mundo físico esté pendiente de matemáticas futuras, aún por descubrir, fundamentalmente distintas de las que ahora tenemos. Llegarán nuevos Gauss, Riemann, Euler, Ramanujan, Cantor…, que con sus frescas y nuevas ideas, transformarán el pensamiento matemático y nuestra manera de ver el mundo.

¿Es, entonces, la Naturaleza matemática? Bueno, yo no me atrevería a negarlo… del todo. Una gran parte sí que lo es

Para llegar a comprenderlo, antes, tendremos que haber descifrado las funciones modulares de los cuadernos perdidos de Ramanujan, o por ejemplo, el verdadero significado del número 137, ése número puro adimensional que encierra los misterios del electrón (e^–)  -electromagnetismo -, de la constante de Planck (h) – el cuanto de acción – y de la luz (c) -la relatividad-, además de otros muchos secretos que nos quedan por desvelar.

Los resultados son lentos, no se avanza con la rapidez que todos deseamos. Poincaré expuso su conjetura para que el mundo la pudiera desvelar y no ha sido posible en más de un siglo, hasta que llegó Perelman para resolverla. Riemann expuso su geometría del espacio curvo, y hasta 60 años más tarde no fue descubierta por Einstein para hacer posible su formulación de la relatividad general, donde describe cómo las grandes masas distorsionan el espacio y el tiempo por medio de la fuerza de gravedad que generan para dibujar la geometría del Universo.

Rebote cuántico de la función de ondas del universo ψ para un espaciotiempo de Friedmann-Robertson-Walker con campo escalar ϕ. v corresponde al volumen del universo en unidades de Planck.  Complejidades como éstas son posibles gracias a los conceptos matemáticos creados por nuestras mentes. Por ejemplo, pensar en las complejas matemáticas topológicas requeridas por la teoría de supercuerdas puede producir incomodidad en muchas personas que, aún siendo físicos, no están tan capacitados para entender tan profundas y complejas  ideas.

Bernhard Riemann introdujo muchas nuevas ideas y fue uno de los más grandes matemáticos. En su corta vida (1.826 – 1.866) propuso innumerables propuestas matemáticas que cambiaron profundamente el curso del pensamiento de los números en el planeta Tierra, como el que subyace en la teoría relativista en su versión general de la gravedad, entre otras muchas (superficie de Riemann, etc.). Riemann les enseñó a todos a considerar las cosas de un modo diferente.

La superficie de Riemann asociada a la función holomorfa “tiene su propia opinión” y decide por sí misma cuál debería ser el, o mejor, su dominio, con independencia de la región del plano complejo que nosotros podamos haberle asignado inicialmente. Durante su corta carrera, Rieman hizo avanzar las matemáticas en muchos campos y, en especial:

El Análisis.

La Teoría de números,

La Geometría, y la

Topología

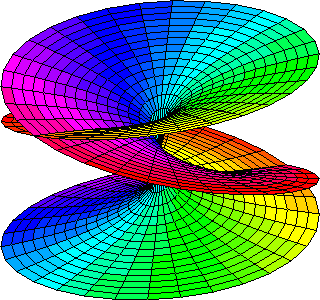
Ahora podemos comprender la complejidad y la belleza de las superficies de Riemann. Este bello concepto desempeña un papel importante en algunos de los intentos modernos de encontrar una nueva base para la física matemática (muy especialmente en la teoría de cuerdas), y al final, seguramente, podremos desvelar  el mensaje que encierra.

El caso de las superficies de Riemann es fascinante, aunque desgraciadamente sólo es para iniciados. Proporcionaron los primeros ejemplos de la noción general de variedad, que es un espacio que puede pensarse “curvado” de diversas maneras, pero que localmente (por ejemplo, en un entorno pequeño de cualquiera de sus puntos), parece un fragmento de espacio euclídeo ordinario.

La esfera de Riemann, superficie de Riemann compacta, el teorema de la aplicación de Riemann, las superficies de Riemann y aplicaciones complejas… He tratado de exponer en unas líneas la enorme importancia de este personaje para las matemáticas en general y la geometría en particular, y,  para la física.

Lo cierto es que, si miramos hacia atrás en el tiempo, nos encontramos con el hecho cierto de que, Einstein pudo formular su bella teoría de la relatividad general gracias a una conferencia que dio Riemann y que, habiendo pedido ayuda a su amigo Marcel Grosmman, éste le mandara una copia en la que, aparecía el Tensor Métrico de Riemann que le dio a Einstein las herramientas de las que carecía.

En escritos anteriores consideramos dos aspectos de la relatividad general de Einstein, a saber, el principio de la relatividad, que nos dice que las leyes de la física son ciegas a la distinción entre reposo y movimiento uniforme; y el principio de equivalencia, que nos dice de qué forma sutil deben modificarse estas ideas para englobar el campo gravitatorio.

Ahora hay que hablar del tercer ingrediente fundamental de la teoría de Einstein, que está relacionada con la finitud de la velocidad de la luz. Es un hecho notable que estos tres ingredientes básicos puedan remontarse a Galileo; en efecto, parece que fue también Galileo el primero que tuvo una expectativa clara de que la luz debería viajar con velocidad finita, hasta el punto de que intentó medir dicha velocidad. El método que propuso (1.638), que implica la sincronización de destellos de linternas entre colinas distantes, era, como sabemos hoy, demasiado tosco. Él no tenía forma alguna de anticipar la extraordinaria velocidad de la luz.

Esta teoría del electromagnetismo de Maxwell tenía la particularidad de que requería que la velocidad de la luz tuviera un valor fijo y definido, que normalmente se conoce como c, y que un unidades ordinarias es aproximadamente 3 × 10⁸ metros por segundo. Parece que tanto Galileo como Newton tenían poderosas sospechas respecto a un profundo papel que conecta la naturaleza de la luz con las fuerzas que mantienen la materia unida.

Pero la comprensión adecuada de estas ideas tuvo que esperar hasta el siglo XX, cuando se reveló la verdadera naturaleza de las fuerzas químicas y de las fuerzas que mantienen unidos los átomos individuales. Ahora sabemos que tales fuerzas tienen un origen fundamentalmente electromagnético (que vincula y concierne a la implicación del campo electromagnético con partículas cargadas) y que la teoría del electromagnetismo es también la teoría de la luz.

Para entender los átomos y la química se necesitan otros ingredientes procedentes de la teoría cuántica, pero las ecuaciones básicas que describen el electromagnetismo y la luz fueron propuestas en 1.865 por el físico escocés James Clark Maxwell, que había sido inspirado por los magníficos descubrimientos experimentales de Michael Faraday unos treinta años antes y que él plasmó en una maravillosa teoría.

             Gracias a la luz, a la radiación electromagnética, podemos saber del universo lejano

Como he dicho antes, la teoría del electromagnetismo de Maxwell tenía la particularidad de que requería que la velocidad de la luz tuviera un valor fijo y definido, que normalmente se conoce como c, y que un unidades ordinarias es aproximadamente 3 × 10⁸ metros por segundo.

Sin embargo, esto nos presenta un enigma si queremos conservar el principio de relatividad. El sentido común nos diría que si se mide que la velocidad de la luz toma el valor concreto c en el sistema de referencia del observador, entonces un segundo observador que se mueva a una velocidad muy alta con respecto al primero medirá que la luz viaja a una velocidad diferente, aumentada o disminuida, según sea el movimiento del segundo observador.

Pero el principio de relatividad exigiría que las leyes físicas del segundo observador (que definen en particular la velocidad de la luz que percibe el segundo observador) deberían ser idénticas a las del primer observador. Esta aparente contradicción entre la constancia de la velocidad de la luz y el principio de relatividad condujo a Einstein (como de hecho, había llevado previamente al físico holandés Hendrick Antón Lorentz y muy en especial al matemático francés Henri Poincaré) a un punto de vista notable por el que el principio de relatividad del movimiento puede hacerse compatible con la constancia de una velocidad finita de la luz.

Baste saber que, como quedó demostrado por Einstein, la luz, independientemente de su fuente y de la velocidad con que ésta se pueda mover, tendrá siempre la misma velocidad en el vacío, c, o 299.792.458 metros por segundo. Cuando la luz atraviesa un medio material, su velocidad se reduce. Precisamente, es la velocidad c el límite alcanzable de la velocidad más alta del universo. Es una constante universal y, como hemos dicho, es independiente de la velocidad del observador y de la fuente emisora.

¿Cómo funciona esto? Sería normal que cualquier persona creyera en la existencia de un conflicto irresoluble entre los requisitos de una teoría como la de Maxwell, en la que existe una velocidad absoluta de la luz, y un principio de relatividad según el cual las leyes físicas parecen las mismas con independencia de la velocidad del sistema de referencia utilizado para su descripción.

¿No podría hacerse que el sistema de referencia se moviera con una velocidad que se acercara o incluso superara a la de la luz? Y según este sistema, ¿no es cierto que la velocidad aparente de la luz no podría seguir siendo la misma que era antes? Esta indudable paradoja no aparece en una teoría, tal como la originalmente preferida por Newton (y parece que también por Galileo), en la que la luz se comporta como partículas cuya velocidad depende de la velocidad de la fuente. En consecuencia, Galileo y Newtonpodían seguir viviendo cómodamente con un principio de relatividad.

Pero semejante imagen de la naturaleza de la luz había entrado en conflicto con la observación a lo largo de los años, como era el caso de observaciones de estrellas dobles lejanas que mostraban que la velocidad de la luz era independiente de la de su fuente. Por el contrario, la teoría de Maxwell había ganado fuerza, no sólo por el poderoso apoyo que obtuvo de la observación (muy especialmente en los experimentos de Heinrich Hertz en 1.888), sino también por la naturaleza convincente y unificadora de la propia teoría, por la que las leyes que gobiernan los campos eléctricos, los campos magnéticos y la luz están todos subsumidos en un esquema matemático de notable elegancia y simplicidad.

En la teoría de Maxwell, la luz toma forma de ondas, no de partículas, y debemos enfrentarnos al hecho de que en esta teoría hay realmente una velocidad fija a la que deben viajar las ondas luminosas. El punto de vista geométrico-espaciotemporal nos proporciona una ruta particularmente clara hacia la solución de la paradoja que presenta el conflicto entre la teoría de Maxwell y el principio de relatividad.

El día que podamos comprender lo que es la luz, habremos logrado secar todas las fuentes de nuestra inmensa ignorancia

Este punto de vista espaciotemporal no fue el que Einstein adoptó originalmente (ni fue el punto de vista de Lorentz, ni siquiera, al parecer, de Poincaré), pero, mirando en retrospectiva, podemos ver la potencia de este enfoque. Por el momento, ignoremos la gravedad y las sutilezas y complicaciones asociadas que proporciona el principio de equivalencia y otras complejas cuestiones, que estimo aburrirían al lector no especialista, hablando de que en el espacio-tiempo se pueden concebir familias de todos los diferentes rayos de luz que pasan a ser familias de líneas de universo, etc.

Baste saber que, como quedó demostrado por Einstein, la luz, independientemente de su fuente y de la velocidad con que ésta se pueda mover, tendrá siempre la misma velocidad en el vacío, c, o 299.792.458 metros por segundo. Cuando la luz atraviesa un medio material, su velocidad se reduce. Precisamente, es la velocidad c el límite alcanzable de la velocidad más alta del universo. Es una constante universal y, como hemos dicho, es independiente de la velocidad del observador y de la fuente emisora.

Aquí, en este mismo trabajo, tenemos un ejemplo de lo que la mente es. Comencé hablando de una cosa y, sin que me diera cuenta, he recorrido caminos que, ni pensaba recorrer cuando comencé a escribir.

¡Qué misterios!

emilio silvera

[?]