Dic
18
Hay que recorrer un largo camino para saber
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en El Universo dinámico ~
Clasificado en El Universo dinámico ~
 Comments (0)
Comments (0)

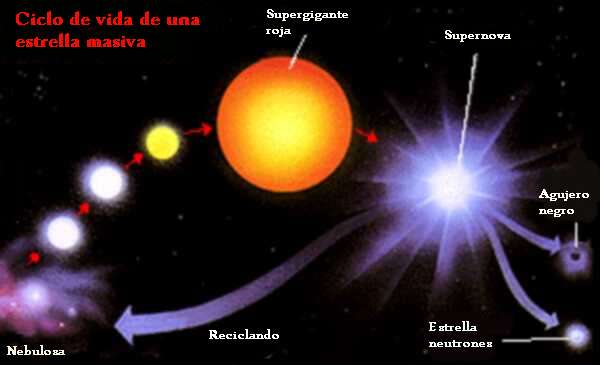
“La masa con la que nace una estrella determina su historia y, sobre todo, la duración de su vida. Llamamos estrellas masivas a todas aquellas estrellas aisladas que explotan como supernovas al final de su existencia debido al colapso gravitatorio. Para que exploten como supernovas deben tener un mínimo de alrededor de ocho masas solares. Estrellas con menos masa pueden explotar, pero no por sí mismas (deben darse otras condiciones). Y hay parámetros secundarios que pueden introducir cambios, pero la masa es determinante.”
El cúmulo estelar RMC 136a, en la Nebulosa de la Tarántula, dentro de la Gran Nube de Magallanes. Credits: ESO/P. Crowther/C.J. Evans
En NGC 3603 los astrónomos pudieron también medir directamente las masas de dos estrellas que pertenecen a un sistema estelar doble, como una validación de los modelos utilizados. Las estrellas A1, B y C en este cúmulo poseen al nacer masas estimadas superiores o cercanas a 150 masas solares
“En cuanto al máximo, el límite está en lo que la naturaleza sea capaz de producir. Hasta hace poco se creía que este límite estaba en torno a monstruos de 150 masas solares, aunque recientes trabajos de investigación y observación lo elevan hasta 300. No obstante, no es un dato seguro ya que, cuanto más masiva es una estrella, menos vive, con lo cual estrellas más grandes serían difíciles de observar.”

Verdaderamente si pudiéramos contemplar de cerca, el comportamiento de una estrella cuando llega el final de su vida, veríamos como es, especialmente intrigante las transiciones de fase de una estrella en implosión observada desde un sistema de referencia externo estático, es decir, vista por observadores exteriores a la estrella que permanecen siempre en la misma circunferencia fija en lugar de moverse hacia adentro con la materia de la estrella en implosión. La estrella, vista desde un sistema externo estático, empieza su implosión en la forma en que uno esperaría.
Al igual que una pesada piedra arrojada desde las alturas, la superficie de la estrella cae hacia abajo (se contrae hacia adentro), lentamente al principio y luego cada vez más rápidamente. Si las leyes de gravedad de Newton hubieran sido correctas, esta aceleración de la implosión continuaría inexorablemente hasta que la estrella, libre de cualquier presión interna, fuera aplastada en un punto de alta velocidad. Pero no era así según las fórmulas relativistas que aplicaron Oppenheimer y Snyder. En lugar de ello, a medida que la estrella se acerca a su circunferencia crítica su contracción se frena hasta hacerse a paso lento. Cuanto más pequeña se hace la estrella, más lentamente implosiona, hasta que se congela exactamente en la circunferencia crítica y, dependiendo de su masa, explosiona como supernova para formar una inmensa nebulosa o, se tranforma en nebulosa planetaria, más pequeña.

La gran erupción de Eta Carinae en la década de 1840 creó la nebulosa del Homúnculo, mostrada aquí en una imagen tomada por el Hubble. Con una longitud ahora de un año-luz, la nube en expansión contiene suficiente material para hacer por lo menos 10 copias de nuestro Sol. Los astrónomos aún no pueden explicar qué causó esta explosión. Crédito: NASA, ESA, y el Hubble SM4 ERO Team
Ahí podemos observar a una estrella muy joven, de dos o tres millones de años que, en un futuro lejano será una gran Supernova. Los procesos que podríamos observar al final de la vida de una estrella gigante… ¡Son fascinantes! Ese punto azulado que vemos envuelto en una masa de gas y polvo, no es otra cosa que la estrella Eta Carinae, una variable luminosa azul hipermasiva. Su masa puede osciular entre las 100 y 150 masas solares y, como el límite para la masa de una estrella está estipulado en 120 masas solares, ésta de arriba, para no ser destruída por su propia radiación, eyecta material al espacio interestelar para descongestionarse.

En la escena que antes explicabámos, por mucho tiempo que nos quedemos esperando y comtemplando el suceso, si uno está en reposo fuera de la estrella (es decir, en reposo en el sistema de referencia externo estático), uno nunca podrá ver que la estrella implosiona a través de la circunferencia crítica. Ese fue el mensaje inequívoco que Oppenheimer y Snyder nos enviaron. Para poder ver eso, habría que estar dentro de la estrella, instalado en la materia que está sufriendo la contracción y, no sabemos porque eso es así.

¿Se debe esta congelación de la implosión a alguna fuerza inesperada de la relatividad general en el interior de la estrella? No, en absoluto, advirtieron Oppenheimer y Snyder. Más bien se debe a la dilatación gravitatoria del tiempo (el frenado del flujo del tiempo) cerca de la circunferencia crítica. Tal como lo ven los observadores estáticos, el tiempo en la superficie de la estrella en implosión debe fluir cada vez más lentamente cuando la estrella se aproxima a la circunferencia crítica; y, consiguientemente, cualquier cosa que ocurre sobre o en el interior de la estrella, incluyendo su implosión, debe aparecer como si el movimiento se frenara poco a poco hasta congelarse.
Por extraño que esto pueda parecer, aún había otra predicción más extrañas de las fórmulas de Oppenheimer y Snyder: si bien es cierto que vista por observadores externos estáticos la implosión se congela en la circunferencia crítica, no se congela en absoluto vista por los observadores que se mueven hacia adentro con la superficie de la estrella. Si la estrella tiene una masa de algunas masas solares y empieza con un tamaño aproximado al del Sol, entonces vista desde su propia superficie implosiona hacia la circunferencia crítica en aproximadamente una hora, y luego sigue implosionando más allá de la criticalidad hacia circunferencias más pequeñas.
Allá por el año 1939, cuando Oppenheimer y Snyder descubrieron estas cosas, los físicos ya se habían acostumbrados al hecho de que el tiempo es relativo; el flujo del tiempo es diferente medido en diferentes sistemas de referencia que se mueven de diferentes formas a través del Universo. Claro que, nunca antes había encontrado nadie una diferencia tan extrema entre sistemas de referencia. Que la implosión se congele para siempre medida en el sistema externo estático, pero continúe avanzando rápidamente superando al punto de congelación medida en el sistema desde la superficie de la estrella era extraordinariamente difícil de comprender. Nadie que estudiara las matemáticas de Oppenheimer y Snyder se sentía cómodo con semejante distorsión extrema del tiempo. Pero ahí estaba, en sus fórmulas. Algunos podían agitar sus brazos con explicaciones heurísticas, pero ninguna explicación parecía muy satisfactoria. No sería completamente entendido hasta finales de los cincuenta.
Fue Wheeler el que discrepó del trabajo de Oppenheimer y Snyder, alegando, con toda la razón que, cuando ellos habían realizado su trabajo, habría sido imposible calcular los detalles de la implosión con una presión realista (presión térmica, presión de degeneración y presión producida por la fuerza nuclear), y con reacciones nucleares, ondas de choque, calor, radiación y expulsión de masa. Sin embargo, los trabajos desde las armas nucleares de los veinte años posteriores proporcionaron justamente las herramientas necesarias.

Presión, reacciones nucleares, ondas de choque, calor radiación y expulsión de masa eran todas ellas características fundamentales de una bomba de hidrógeno; sin ellas, una bomba no explosionaría. A finales de los años cincuenta, Stirling Colgate quedó fascinado por el problema de la implosión estelar. Con el apoyo de Edward Teller, y en colaboración con Richard White y posteriormente Michael May, Colgate se propuso simular semejante implosión en un ordenador. Sin embargo, cometieron un error, mantuvieron algunas de las simplificaciones de Oppenheimer al insistir desde el principio en que la estrella fuera esférica y sin rotación, y, aunque tuvieron en cuenta todos los argumentos que preocupaban a Wheeler, aquello no quedó perfeccionado hasta después de varios años de esfuerzo y, a comienzo de los años sesenta ya estaban funcionando correctamente.
Un día a principio de los años sesenta, John Wheeler entró corriendo en la clase de relatividad de la Universidad de Princeton. Llegaba un poco tarde, pero sonreía con placer. Acababa de regresar de una visita a Livermore donde había visto los resultados de las simulaciones recientes de Colgate y su equipo. Con excitación en su voz dibujó en la pizarra un diagrama tras otro explicando lo que sus amigos de Livermore habían aprendido.

Cuando la estrella en implosión tenía una masa pequeña, desencadenaba una implosión de supernova y formaba una estrella de neutrones precisamente en la forma que Fritz Wicky había especulado treinta años antes. Sin embargo, si la estrella original era más masiva lo que allí se producía (aparte de la explosión supernova) era un agujero negro notablemente similar al altamente simplificado modelo que veinticinco años calcularon Oppenheimer y Snyder. Vista desde fuera, la implosión se frenaba y se quedaba congelada en la circunferencia crítica, pero vista por alguien en la superficie de la estrella, la implosión no se congelaba en absoluto. La superficie de la estrella se contraía a través de la circunferencia crítica y seguía hacia adentro sin vacilación.

Lo cierto fue que allí, por primera vez, se consiguió simular por ordenador la implosión que debía producir agujeros negros. Está claro que la historia de todo esto es mucho más larga y contiene muchos más detalles que me he saltado para no hacer largo el trabajo que, en realidad, sólo persigue explicar a ustedes de la manera más simple posible, el trabajo que cuesta obtener los conocimientos que no llegan (casi nunca) a través de ideas luminosas, sino que, son el resultado del trabajo de muchos.
Hoy, sabemos mucho más de cómo finaliza sus días una estrella y, dependiendo de su masa, podemos decir de manera precisa que clase de Nebulosa formará, que clase de explosión (si la hay) se producirá, y, finalmente, si el resultado de todo ello será una estrella enana blanca que encuentra su estabilidad final por medio del Principio de exclusión de Pauli (en mecánica cuántica)que se aplica a los fermiones pero no a los Bosones (son fermiones los quarks, electrones, protones y neutrones), en virtud del cual dos partículas idénticas en un sistema, como los electrones en un átomo o quarks en un hadrón (protón o neutrón, por ejemplo), no pueden poseer un conjunto idéntico de números cuánticos.

La estrella azul cerca del centro de esta imagen es Zeta Ophiuchi. Cuando se ve en luz visible aparece como una estrella roja relativamente débil rodeada de otras estrellas tenues y sin polvo. Sin embargo, en esta imagen infrarroja tomada con campo amplio por el Explorador Infrared Survey de la NASA, o WISE, un punto de vista completamente diferente emerge. Zeta Ophiuchi es en realidad una muy masiva y caliente estrella azul, brillante que traza su camino a través de una gran nube de polvo y gas interestelar.

Una estrella masiva alejándose de su antiguo compañero se manifiesta haciendo un imponente surco a través de polvo espacial, como si se tratase de la proa de un barco. La estrella, llamada Zeta Ophiuchi, es enorme, con una masa de cerca de 20 veces la de nuestro Sol. En esta imagen, en los que se ha traducido la luz infrarroja a colores visibles que vemos con nuestros ojos, la estrella aparece como el punto azul en el interior del arco de choque. Zeta Ophiuchi orbitó una vez alrededor de una estrella aún más grande. Pero cuando la estrella explotó en una supernova, Zeta Ophiuchi se disparó como una bala. Viaja a la friolera velocidad de 24 kilómetros por segundo arrastrando con ella un conglomerado de polvo que distorsiona la región por la que pasa.
Mientras la estrella se mueve través del espacio, sus poderosos vientos empujan el gas y el polvo a lo largo de su camino en lo que se llama un arco de choque. El material en el arco de choque está tan comprimido que brilla con luz infrarroja que WISE puede captar. El efecto es similar a lo que ocurre cuando un barco cobra velocidad a través del agua, impulsando una ola delante de él. Esta onda de choque queda completamente oculta a la luz visible. Las imágenes infrarrojas como esta son importantes para arrojar nueva luz sobre lo que ocurre en situaciones similares.

Pero, siguiendo con el tema de las implosiones de las estrellas, ¿cuál es la razón por la que la materia no se colapsa, totalmente, sobre sí misma? El mismo principio que impide que las estrellas de neutrones y las estrellas enanas blancas implosionen totalmente y que, llegado un momento, en las primeras se degeneran los neutrones y en las segundas los electrones, y, de esa manera, se frena la compresión que producía la gravedad y quedan estabilizadas gracias a un principio natural que hace que la materia normal sea en su mayor parte espacio vacio también permite la existencia de los seres vivos. El nombre técnico es: El Principio de Exclusión de Pauli y dice que dos fermiones (un tipo de partículas fundamentales) idénticos y con la misma orientación no pueden ocupar simultáneamente el mismo lugar en el espacio. Por el contrario, los bosones (otro tipo de partículas, el fotón, por ejemplo) no se comportan así, tal y como se ha demostrado recientemente por medio de la creación en el laboratorio de los condensados de Bose-Einstein.
¿Cuál es la diferencia?
Los bosones son sociables; les gusta estar juntos. Como regla general, cualquier átomo con un número par de electrones+protones+neutrones es un bosón. Así, por ejemplo, los átomos del sodio ordinario son bosones, y pueden unirse para formar condensados Bose-Einstein.
Izquierda: Los bosones son sociables; los fermiones son antisociales.
Los fermiones, por otro lado, son antisociales. No pueden juntarse en el mismo estado cuántico (por el Principio de Exclusión de Pauli de la mecánica cuántica). Cualquier átomo con un número impar de electrones+protones+neutrones, como el potasio-40, es un fermión.
Pero, estábamos diciendo: “…no pueden poseer un conjunto idéntico de números cuánticos.” A partir de ese principio, sabemos que, cuando una estrella como nuestro Sol deja de fusionar Hidrógeno en Helio que hace que la estrella deje de expandirse y quede a merced de la Gravedad, ésta implosionará bajo el peso de su propia masa, es decir, se contraerá sobre sí misma por la fuerza gravitatoria pero, llegará un momento en el cual, los electrones, debido a ese principio de exclusión de Pauli que les impide estar juntos, se degeneran y se moverán de manera aleatoria con velocidades relativista hasta el punto de ser capaces de frenar la fuerza provocada por la gravedad, y, de esa manera, quedará estabilizada finalmente una estrella enana blanca.

Si hablamos de una estrella supermasiva, su produce la implosión arrojando las capas externas al espacio interestelar mientras que el grueso de la estrella se comprime más y más sin que nada la pueda frenar, aquí no sirve el Principipo de exclusión de Pauli para los fermiones y, es tal la fuerza gravitatoria que se desencadena como consecuencia de que la estrella supergigante no puede seguir fusionando y queda a merce4d de una sola fiuerza: La Gravedad, que ésta, la comprime hasta lo inimaginable para convertir toda aquella ingente masa en una singularidad, es decir, un punto de densidad y energía “infinitas” que ni la luz puede escapar de allí, y, el tiempo se ralentiza y el espacio se curva a su alrededor.

Si la estrella original es más masiva, la degeneración de los electrones no será suficiente para frenar la fuerza gravitatoria y, los electrones se fusionaran con los protones para convertirse en neutrones que, bajo el mismo principio de exclusión sufrirán la degeneración que frenará la fuerza de gravedad quedando entonces una estrella de neutrones. Por último, si la estrella es, aún más masiva, ni la degeneración de los neutrones será suficiente para frenar la inmensa fuerza gravitatoria generada por la masa de la estrella que, continuará la implosión contrayéndose cada vez más hasta desaparecer de nuestra vista convertida en un agujero negro.
¿Qué forma adoptará, qué transición de fase se produce en la materia dentro de una Singularidad?
¡Resulta todo tan complejo!
emilio silvera
















 Totales: 75.519.027
Totales: 75.519.027 Conectados: 43
Conectados: 43























