Dic
27
Sistemas Complejos
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Descubrir y aprender ~
Clasificado en Descubrir y aprender ~
 Comments (0)
Comments (0)
Todos hemos oído hablar, con más o menos frecuencia, de “Sistemas Complejos”, aquí mismo en estas páginas, la palabra sale a relucir con cierta frecuencia y, no me extraña que “la palabreja” cree una barrera, dado que, para muchas personas, “complejo” significa “complicado” y suponen automáticamente que, si un sistema es complicado, será difícil de comprender. La naturaleza posee una fuerte tendencia a estructurarse en forma de entes discretos excitables que interactúan y que se organizan en niveles jerárquicos de creciente complejidad, por ello, los sistemas complejos no son de ninguna manera casos raros ni curiosidades sino que dominan la estructura y función del universo.

Un sistema «complicado» también está formado por varias partes pero las relaciones entre éstas no añaden información adicional. Nos basta con saber cómo funciona cada una de ellas para entender el sistema. En un sistema complejo, en cambio, existen variables ocultas cuyo desconocimiento nos impide analizar el sistema con precisión. Así pues, un sistema complejo, posee más información que la que da cada parte independiente. Para describir un sistema complejo hace falta no sólo conocer el funcionamiento de las partes sino conocer el funcionamiento del sistema completo una vez relacionadas sus partes entre sí.

Claro que, no siempre ese temor a lo difícil y complicado, está justificado y, tal suposición no es, necesariamente correcta. En realidad, un sistema complejo es tan solo un sistema que está formado por varios componentes más sencillos que ejercen entre sí una interacción mutua que, naturalmente, tiene sus consecuencias. Si miramos la imagen de arriba, vemos una inmensa y hermosa Nebulosa que está formada por una serie de “cosas” sencillas como lo son el gas hidrógeno y el polvo interestelar entre otros y, en presencia de energías, la gravedad y otros parámetros, ahí ocurren cosas tales como, el nacimiento de estrellas y la aparición de mundos…entre otras.
Los grandes triunfos de la Ciencia se han logrado, en gran medida, descomponiendo los sistemas complejos en sus componentes simples, es decir, estudiar por partes lo que allí está presente (en caso necesario, como primera aproximación, dando el paso suplementario de pretender que todos los componentes son más sencillos de lo que son en realidad) para llegar a comprender el todo.
En el ejemplo clásico del éxito que ha logrado este planteamiento para conocer el mundo que nos rodea, buena parte de la química puede entenderse mediante un modelo en el que los componentes simples son átomos, y para eso importa poco de qué están formados los núcleos. Ascendiendo un nivel, las leyes que describen el comportamiento del dióxido de Carbono encerrado en una caja pueden entenderse pensando en unas moléculas más o menos esféricas que rebotan unas contra otras y contra las paredes de su contenedor, y poco importa que cada una de estas moléculas esté formada por un átomo de Carbono y dos de Oxígeno unidos entre sí. Ambos sistemas son complejos, en sentido científico, pero fáciles de entender.

Fijémonos, por ejemplo, en el Campo Magnético Terrestre. En esencia, los planetas generan un campo magnético por efecto dinamo. Para ello se requiere que el planeta rote; debe contener una región con un fluido conductor de la electricidad y debe existir convección en dicho fluido. No se puede asegurar pero parece ser que si en la Tierra no hubiese tectónica de placas el transporte convectivo hacia la superficie podría no tener lugar, la dinamo no funcionaría y el campo magnético terrestre sería prácticamente nulo o, al menos, mucho menor que el actual. Sin la protección que nos brinda el campo magnético, la atmósfera podría desaparecer a causa del continuo bombardeo de las partículas de alta energía procedentes del viento solar. Todos estos componentes son estudiados por separado y, más tarde, los juntamos en un todo que nos lleva a la comprensión de este Sistema Complejo.
Claro que la clave para poder llegar al conocimiento del “sistema complejo” consiste en saber elegir los componentes adecuados sencillos que conforman el todo para poder realizar el análisis necesario que nos lleve hasta las respuestas que buscamos. En muchas ocasiones hemos explicado aquí, lo que hay en las Nebulosas como la de arriba y lo que ocurre en ellas para que, finalmente, nazcan estrellas nuevas.
Hermann Minkowski
Hay cuestiones, a un nivel más abstracto del que hemos oído hablar también con cierta frecuencia. Acordaos de que, poco después de que Einstein publicara sus trabajos sobre relatividad especial, el matemático alemán que arriba podéis ver se dio cuenta de que, en cierto modo, el tiempo debía ser considerado como la cuarta coordenada complementaria de las tres coordenadas del espacio. En su discurso de inauguración de la 80 reunión de la Asamblea general alemana de científicos naturales y físicos el 21 de septiembre de 1908 pronunció una célebre frase:
“Las ideas sobre el espacio y el tiempo que deseo mostrarles hoy descansan en el suelo firme de la física experimental, en la cual yace su fuerza. Son ideas radicales. Por lo tanto, el espacio y el tiempo por separado están destinados a desvanecerse entre las sombras y tan sólo una unión de ambos puede representar la realidad”.
Desde entonces el espacio-tiempo cuatridimensional pasó a llamarse espacio de Minkowski. Si empleamos x,y y z para las tres coordenadas del espacio, tomaremos ct para la cuarta coordenada de tiempo, siendo c la velocidad de la luz. Sin embargo debemos multiplicar ct por otro factor que, sin destrozar la armonía del sistema tetradimensional de las coordenadas haga a la coordenada de tiempo físicamente diferente de las tres coordenadas espaciales. La matemática nos suministra precisamente este factor conocido como una “unidad imaginaria” que se designa con el símbolo i (i= raíz cuadrada de -1).
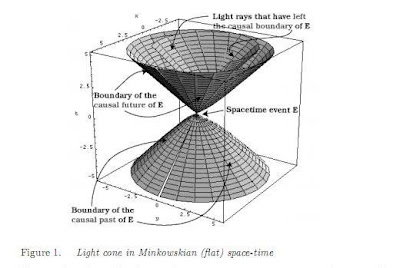 Minkowski
Minkowski- Es un hecho notorio que los procesos que ocurren en el universo observable son irreversibles, mientras que las ecuaciones que expresan las leyes fundamentales de la física son invariantes bajo inversión temporal. La emergencia de la irreversibilidad a partir de la física fundamental ha sido un tema que ha preocupado a físicos, astrónomos y filósofos desde que Boltzmann formulara su famoso teorema “H”.
- ¿Es un sistema complejo un fotón? La propiedad del fotón, de la luz, es que es algo que oscila tan rápidamente que en realidad es como si estuviera en dos sitios a la vez, o sea algo que está pero que no está?
Cómo se entiende algo así
- “¿Tengo que reconocer que está ha sido la incógnita que más me ha costado despejar, todo un desafío a la lógica, a la matemática. Aunque en realidad era sencillo, porque lo cierto es que lo tenía en las narices. ¡Claro! esa es la esencia de nuestra mágica ecuación, e =m.c
2
masa en movimiento
- !,es decir, más de lo mismo. Digamos que la mecánica cuántica en realidad no es más que la Vida llevada a su mínima expresión.
Los números complejos, con una parte real y otra imaginaria, también juegan un papel esencial en los formulismos de la mecánica cuántica. La propia probabilidad de los sucesos cuánticos llega a expresarse en función de números complejos llamados amplitudes de probabilidad. La probabilidad real se halla a partir de estos números, sumando el cuadrado de su parte real y el cuadrado de su parte imaginaria.
Esto nos da una idea de la importancia de los estos números, tanto en la teoria de la relatividad como en la mecánica cuántica y nos ayuda a introducirnos en la teoría de Hartle-Hawking sobre los comienzos del universo, que supone un universo sin límites y con un tiempo imaginario, como se entiende la parte no real de un número complejo.
En cierta forma los ceros y los infinitos que aparecen en la física clásica son suavizados por la mecánica cuántica: La energía más baja en el vacío no es nunca cero, como tampoco es nunca cero la extensión de un punto físico . La existencia del cuanto de acción impide una energía cero del vacío, como impide la medida exacta, a la vez, de una variación de energía y del tiempo asociado a dicha variación.El punto físico menor sería la llamada longitud de Planck, del orden de 10-35 metros, lo que también elimina el infinito que resultaría de considerar las partículas subatómicas como puntuales: su densidad sería infinita y resultarían microscópicos agujeros negros.
Según alguna teoría que circula por ahí, si comenzamos en el momento presente y vamos hacia atrás en el tiempo, lo que aparentemente sería el punto origen de la descripción del tiempo real convencional, la naturaleza del tiempo cambia: la componente imaginaria del tiempo se hace más y más prominente hasta que, en último término, lo que debería ser la singularidad de la teoría clásica se desvanece. El Universo existiría porque es una estructura matemática autoconsistente. Puede imaginarse el tiempo real como una línea que va del principio al final del Universo. Pero también puede considerarse otra dirección del tiempo en ángulo recto al tiempo real. Esta última se denomina la dirección imaginaria del tiempo. En el tiempo imaginario, no habría ninguna singularidad en la que dejaran de regir las leyes de la Ciencia, ni ninguna frontera del Universo tras la cual tuviera que apelarse a Dios. El Universo no sería creado ni destruído. Simplemente existiría. Quizás el tiempo imaginario sea el auténtico tiempo real y lo que llamamos tiempo real sea sólo un producto de nuestra imaginación. En el tiempo real, el Universo tiene un principio y un fin. En el tiempo imaginario no hay singularidades ni límites.

Hartle: “Tiempo imaginario no se refiere a la imaginación: hace referencia a los números complejos. Como demostraron Einstein y Minkowsky, el espacio-tiempo constituye una geometría cuatridimensional. Es posible ir aún más lejos de estos conceptos. Si se miden las direcciones del tiempo utilizando números complejos, se obtiene una simetría total entre espacio y tiempo, que es, matemáticamente, un concepto muy bello y natural”. Don N. Page: ” En la formulación de la ausencia de límites de Hartle-Hawking, el tiempo es imaginario, y en vez de tener un borde es como si se tratara de la superficie del planeta Tierra. Suponiendo tiempo imaginario, el Universo no tuvo comienzo, no tiene límite, es una totalidad en sí mismo”.
He tenido la oportunidad de leer el Libro de Roger Penrose (uno de los físicos actuales más brillantes), titulado, El camino a la realidad, y él nos comenta: “… los números complejos componen una notable unidad con la naturaleza. Es como si la propia naturaleza estuviera tan impresionada por el alcance y consistencia del sistema de los números complejos como lo estamos nosotros, y hubiera confiado a estos números las operaciones detalladas de su mundo en sus escalas más minúsculas”. Se refiere a la mecánica cuántica, pero realmente su importancia se refleja en toda la naturaleza, porque la cosmología, en los primeros instantes del universo se confunde con el mundo microscópico de las partículas elementales.

Claro que, los “Sistemas Complejos” están por todas partes y, tanto ers así que, nosotros mismos somos un buen ejemplo y llevamos con nosotros, el “sistema” más complejo de todos: Nuestro cerebro es, sin dudarlo y hasta donde puede llegar nuestros conocimientos actuales, el más complejo de los sistemas.
Claro que, si hablamos de complejidad de sistemas, el universo sería el mejor de los ejemplos. Con respecto a sus propios patrones, el universo es viejo. El tiempo de vida natural de un mundo gobernado por la gravedad, la relatividad y la mecánica cuántica es el fugaz breve tiempo de Planck. Parece que es mucho más viejo de lo que debería ser.
Pero, pese a la enorme edad del universo en “tics” de Tiempo de Planck, hemos aprendido que casi todo este tiempo es necesario para producir estrellas y los elementos químicos que traen la vida.
![[cerebro-artificial.jpg]](http://4.bp.blogspot.com/_gB8i9RgQMBM/SZPuHenJ6uI/AAAAAAAAHRg/iKaGbui_WMI/s1600/cerebro-artificial.jpg)
La vida que surgió en el planeta Tierra a partir del polvo de estrellas
¿Por qué nuestro universo no es mucho más viejo de lo que parece ser? Es fácil entender por qué el universo no es mucho más joven. Las estrellas tardan mucho tiempo en formarse y producir elementos más pesados que son las que requiere la complejidad biológica. Pero los universos viejos también tienen sus problemas. Conforme para el tiempo en el universo el proceso de formación de estrellas se frena. Todo el gas y el polvo cósmico que constituyen las materias primas de las estrellas habrían sido procesados por las estrellas y lanzados al espacio intergaláctico donde no pueden enfriarse y fundirse en nuevas estrellas. Pocas estrellas hacen que, a su vez, también sean pocos los sistemas solares y los planetas. Los planetas que se forman son menos activos que los que se formaron antes, la entropía va debilitando la energía del sistema para realizar trabajo. La producción de elementos radiactivos en las estrellas disminuirá, y los que se formen tendrán semividas más largas. Los nuevos planetas serán menos activos geológicamente y carecerán de muchos de los movimientos internos que impulsan el vulcanismo, la deriva continental y la elevación de las montañas en el planeta. Si esto también hace menos probable la presencia de un campo magnético en un planeta, entonces será muy poco probable que la vida evolucione hasta formas complejas.

En lugares como este se forman los elementos de la vida
Las estrellas típicas como el Sol, emiten desde su superficie un viento de partículas cargadas eléctricamente que barre las atmósferas de los planetas en órbitas a su alrededor y, a menos que el viento pueda ser desviado por un campo magnético, los posibles habitantes de ese planeta lo podrían tener complicado soportando tal lluvia de radiactividad. En nuestro sistema solar el campo magnético de la Tierra ha protegido su atmósfera del viento solar, pero Marte, que no está protegido por ningún campo magnético, perdió su atmósfera hace tiempo.
Probablemente no es fácil mantener una larga vida en un planeta del Sistema solar. Poco a poco hemos llegado a apreciar cuán precaria es. Dejando a un lado los intentos que siguen realizando los seres vivos de extinguirse a sí mismos, agotar los recursos naturales, propagar infecciones letales y venenos mortales y emponzoñar la atmósfera, también existen serias amenazas exteriores.
¿No es inmensamente complejo todo esto?

En realidad, los Sistemas complejos constituyen y se manifiestan en la inmensa mayoría de los fenómenos observables. Sin embargo, y aquí radica una de sus propiedades más interesantes, la abundancia y diversidad de los sistemas complejos (sean de tipo físicos, químicos, biológicos, sociales, etc.) no implica una innumerable e inclasificable diversidad de conductas dinámicas diferentes. Todo lo contrario, los sistemas complejos poseen propiedades genéricas, independientemente de los detalles específicos de cada sistema o de la base material del mismo.
De esta manera, por ejemplo, una computadora construida con bulbos, otra con transistores y una más con relevadores electromagnéticos; serían capaces de realizar, en principio, las mismas tareas de procesamiento de datos. Podríamos incluso ir mas lejos con este ejemplo y agregar que el sistema nervioso humano posee propiedades tales como memoria difusa y reconocimiento de patrones que funcionan de la misma manera en como funciona una computadora de bulbos o de transistores. Lo que comparten, son una estructura interconectada y formada por elementos individuales (neuronas o circuitos electrónicos) que interactúan para intercambiar información y modificar sus estados internos. Ello hace posible la emergencia de fenómenos globales y colectivos semejantes, sin que los detalles materiales del sistema sean del todo relevantes. De esta manera, es posible identificar propiedades dinámicas similares entre una computadora, el sistema nervioso, el sistema inmunológico, la tectónica de placas, una sociedad de insectos, el crecimiento urbano, las economías de mercado, el tráfico vehicular, etc. a pesar de la aparente disparidad entre estos sistemas.

La aportación fundamental de la ciencia de los sistemas complejos en la tarea de conocer y transformar nuestra realidad, es identificar los principios y fundamentos generales de la operación de dichos sistemas sin importar los detalles particulares de su realización material. Así por ejemplo, podemos imaginar un biólogo del futuro que estudiaría el fenómenos llamado “vida” desde una perspectiva de principios (tal vez leyes?) generales. Tal biólogo tendría conciencia de que el fenómeno “vida” tal y como existe en la Tierra es tan sólo un caso particular de como “la vida” se ha manifestado bajo las condiciones particulares de la Tierra, expresándose bajo la forma de una realización material muy específica (una bioquímica de carbono dominantemente levógira). Sin embargo, este biólogo estaría preparado para identificar el fenómeno “vida” si acaso fuera detectado en otro planeta o parte del universo bajo otras realizaciones materiales especificas, de la misma manera que un físico hoy en día sabe que la ley de gravitación lo mismo es valida para la superficie de la Tierra que para la superficie de Marte o cualquier otra parte del universo. El ejemplo puede ir aún más lejos. Podemos imaginar un sociólogo del futuro que será capaz de identificar los principios generales del fenómeno “social” independientemente de que este ocurra en grupos humanos, animales, microbios, plantas, robots o incluso, si su colega biólogo tiene suerte, en grupos sociales fuera de nuestro planeta.
¿Estaremos capacitados alguna vez determinar las partes “sencillas” de los Sistemas Complejos para llegar a saber?
emilio silvera















 Totales: 75.523.619
Totales: 75.523.619 Conectados: 47
Conectados: 47






















