Bueno, sabemos que sí hay vida en otros mundos, al menos eso nos dice el sentido común al aplicar la lógica y la estadística. Nos queda confirmarlo, cosa que no será fácil debido a las enormes distancias con las que tenemos que bregar, y, mientras las tecnologías del futuro no estén disponibles, nos limitaremos a realizar conjeturas e hipótesis que, más o menos acertadas traten de acercarse a la realidad.

El primero que encontremos podría ser así

Sabemos que todas las Especies que viven en la Tierra están basadas en el Carbono. Si empleamos la lógica, y teniendo en cuenta que el Universo es igual en todas partes en relación a las fuerzas fundamentales y las constantes universales que lo rigen, salvo alguna excepción (que es posible), todos los mundos habitables seguirán el mismo camino evolutivo que la Toerra, y, salvo algunas peculuiaridades, sus habiotantes tendrían que ser parecidos a los que habitan la Tierra.

[?]

En una simulación neuronal sin precedentes, IBM ha logrado simular 500 mil millones de neuronas y 100 billones de sinapsis. Para ello ha utilizado Sequoia, el segundo superordenador más grande del mundo con millón y medio de núcleos. Esto es una proeza computacional, pero tiene poco que ver con la neurociencia. Veamos por qué.

El departamento de Cognitive Computing de IBM en Almaden dirigido por Dharmendra S. Modha lleva unos años realizando asombrosas simulaciones en el contexto del proyecto DARPA SyNAPSE. Como parte de este proyecto, anunció la simulación a la escala del córtex de un ratón, luego de una rata y más tarde de un gato.

El objetivo de este programa es crear un chip neurosináptico que supone una ruptura con la arquitectura tradicional de los ordenadores. Esta arquitectura es la llamada Von Neumann que usan la totalidad de los ordenadores en la actualidad, incluidos móviles y tarjetas. En la arquitectura Von Neumann la memoria está separada del procesador, el hardware del software y los programas están separados de los datos. Ha sido muy exitosa mientras se cumplía la miniaturización de componentes expresada en la ley de Moore: cada dos años se duplica el número de transistores en un espacio dado. El problema es que estamos llegando a los límites del átomo y que la ley dejará de cumplirse.

El chip neurosináptico es una ruptura total con la arquitectura Von Neumann. Se basa en el diseño de las neuronas en las que no hay distinción entre hw y sw, programas y datos, memoria y procesador. El chip consiste en una matriz de neuronas y entre sus cruces se realizan las sinapsis. De este modo, cada sinapsis del chip es hw y sw, proceso y memoria, programa y datos. Dado que todo está distribuido, no es necesaria un miniaturización tan extrema y sobre todo, un reloj tan rápido. Frente a los actuales gigahercios de frecuencia, las neuronas se disparan a un hercio, y en el caso del chip a 8 hercios. Además, los procesadores son clock driven, es decir, actúan bajo la batuta del reloj mientras que las neuronas son event driven, actúan solo si hay actividad que realizar.

Uno de los objetivos es reducir el consumo eléctrico. Un cerebro consume lo que una bombilla pequeña, 20 vatios. Un superordenador consume cientos de megavatios. El nuevo chip tiene un consumo muy reducido. Estos chips están construidos con tecnología de silicio clásica CMOS.

La arquitectura de muchos chips neurosinápticos unidos se ha llamado TrueNorth. Ya existe en desarrollo un chip de 256 neuronas, 1024 axones, y 256×1024 sinapsis.

El chip sin embargo no está en producción masiva. Para seguir trabajando en paralelo al desarrollo, se ha realizado la prueba actual. Para ello se ha usado un simulador llamado Compass. Compass traduce el comportamiento de un chip neurosináptico (no Von Neumann) a un ordenador clásico (Von Neumann). Usando Compass se ha simulado (pdf) el comportamiento de 2.000.000.000 chips. Esto supone 500 mil millones de neuronas y 100 billones de sinapsis, cifras por completo astronómicas. El resultado de la simulación se ha ejecutado 1.542 veces más lento que en tiempo real.

Para realizar la simulación se ha usado el segundo superordenador más grande del mundo, Sequoia un Blue Gene/Q de 96 armarios con 1 millón y medio de núcleos y 1,5 petabytes de memoria. Uno de los objetivos de la simulación es ver el escalado. Un problema habitual es que que cuando añadimos más cores, el sistema no funciona proporcionalmente más rápido. En el extremo, añadir más cores no aumenta el rendimiento: el sistema escala mal. Imagina un camarero atendiendo detrás de la barra. Si hay un segundo camarero, irán más rápido, pero no el doble. Si sigues añadiendo camareros, llegará un momento en que no aumente la eficiencia, incluso se verá reducida. El sistema escala mal. Pues bien, en la simulación realizada el escalado ha sido casi perfecto lo que es muy satisfactorio computacionalmente.

¿Qué tiene esto que ver con la neurociencia y el cerebro? Bien poco. La simulación no imita ningún comportamiento animal ni cognitivo ni humano. Para simular el comportamiento del cerebro, necesitamos saber cómo funciona y eso está lejos de lograrse. Para cuando llegue ese conocimiento debemos tener preparados ordenadores que sean capaces de simularlo y en este contexto se enmarca la presente investigación. Aunque no solo; la idea de diseñar estos nuevos chips es ponerlos en producción en aplicaciones comerciales tradicionales dando una gran potencia con un bajo consumo. La simulación del cerebro deberá esperar aún alguna década.

Fuente: Altioyo

[?]

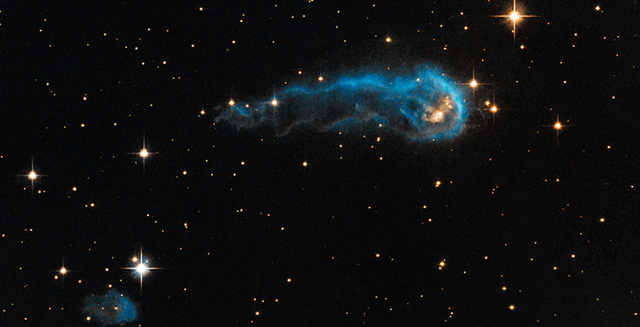
Recreación artística del nudo cósmico en forma de oruga. | NASA

[?]