En 1.949, el físico francés Louis de Broglie, que ganó el premio Nobel, propuso construir un laboratorio europeo de física de partículas. Su idea caló hondo en la comunidad internacional, y tres años tarde, 11 países europeos dieron el visto bueno y el dinero para construir el CERN, inaugurado en Ginebra en 1.954, y al que tanto le debe la física y las Sociedades modernas del mundo.

Los aceleradores de partículas son un gran invento que ha permitido comprobar (hasta se ha podido, al menos) la estructura del átomo. En el acelerador del Fermilab, por ejemplo, un detector de tres pisos de altura que en su momento costó unos ochenta millones de dólares para poder captar electrónicamente los “restos” de la colisión entre un protón y un antiprotón. Aquí la prueba consiste en que decenas de miles de sensores generen un impulso eléctrico cuando pasa una partícula. Todos esos impulsos son llevados a procesadores electrónicos de a través de cientos de miles de cables. Por último, se hace una grabación en carrete de cinta magnética codificada con ceros y unos. La cinta graba las violentas colisiones de los protones y antiprotones, en las que generan unas setenta partículas que salen disparadas en diferentes direcciones dentro de las varias secciones del detector.

 

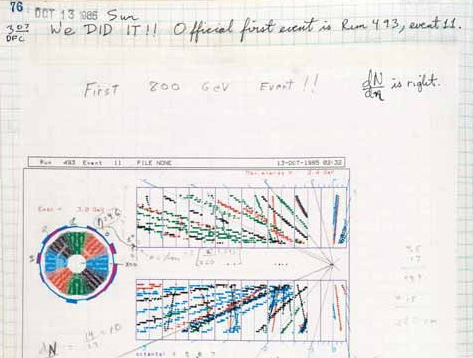
El 13 de octubre de 1985 se produjo la primera colisión protón-antiprotón en el Tevatrón del Fermilab

La ciencia, en la física de partículas, gana confianza en sus conclusiones por duplicación, es decir, un experimento en California se confirma mediante un acelerador de un estilo diferente que funciona en Ginebra con otro equipo distinto, que incluye en cada experimento los controles necesarios y todas las comprobaciones para que puedan confirmar con muchas garantías el resultado finalmente obtenido. Es un proceso largo y muy complejo; la consecuencia de muchos años de investigación de muchos equipos diferentes.

 

No es suficiente con un único resultado. Si muchos, en distintos lugares dan lo mismo…se pueden considerar ciertos

Yo puedo visualizar la estructura interna de un átomo. Puedo hacer que me vengan mentales de nebulosas de “presencia” de electrón alrededor de la minúscula mota del núcleo que atrae esa bruma de la nube electrónica hacia sí. Puedo ver los átomos, los protones y los neutrones, y en su interior, los diminutos quarks enfangados en un mar de neutrones. Claro que todo eso es posible por el hecho de que dicha imagen me es muy familiar. Creo que cada uno construirá sus propias conforme él las vea a partir de las ecuaciones o bien de cómo las formó en su mente a partir de sus lecturas o explicaciones oídas en charlas científicas.

¿Tendrán ellos (los átomos) el secreto de la materia?

Cuando entraron en escena David Politrer, de Harvard, y David Gross y Frank Wilczek, de Pinceton, el panorama de lo que ocurría en el interior del núcleo se aclaró bastante. Ellos, descubrieron algo que llamaron libertad asintótica. Asintótico significa, burdamente, “que se acerca cada vez más, pero no toca nunca”. La interacción fuerte se debilita más y más a medida que un quark se aproxima a otro. Esto significa, paradójicamente, que cuando los quarks están muy juntos se portan casi como si fuesen libres; pero cuando se apartan, las fuerzas se hacen efectivamente mayores. Las distancias cortas suponen energías altas, así que la interacción fuerte se debilita a altas energías. Esto es justo lo contrario de lo que pasa con la fuerza eléctrica. Aún más era que la interacción fuerte necesitase una partícula mensajera, como las otras fuerzas, y en alguna parte le dieron al mensajero el nombre de gluón (del inglés glue, pegamento).

 

A todo esto, llegó Murray Gell-Mann con sus quarks para completar el panorama. Adjudicó a estas diminutas partículas color y sabor (nada que ver con el gusto y los colores reales) y llegó la teoría denominada cromodinámica cuántica. Todo aquello dio mucho que hablar y mucho trabajo a los teóricos y experimentadores, y al en los años ochenta, se había dado ya con todas las partículas de la materia (los quarks y los leptones), y teníamos las partículas mensajeras, o bosones gauge, de las fuerzas, a excepción de la gravedad.

MATERIA
Primera generación	Segunda generación		Tercera generación
u	c		t
d	s		b
Son los quarks up, down, charmed, strange, top y bottom.
Los leptons son:
υe	υμ		υτ
e	μ		τ
FUERZAS
Los bosones gauge:
Fotón		Electromagnetismo
W+, W–, Z0		Interacción débil
Ocho gluones		Interacción

 

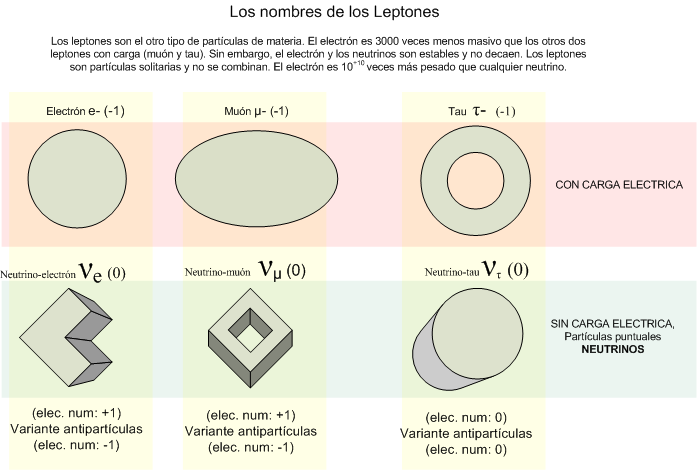
La familia de los leptones está compuesta por el electrón, muón y tau con sus correspondientes neutrinos. Así quedó prácticamente el llamado modelo estándar que describe las partículas que forman la materia conocida y las fuerzas que intervienen e interaccionan con ellas. La gravedad quedó plasmada en la relatividad de Einstein.

¿Por qué es incompleto el modelo estándar? Una carencia es que no se haya visto todavía el quark top; otra, la ausencia de una de las cuatro fuerzas fundamentales, la gravedad. Otro defecto estético es que no es lo bastante ; debería parecerse más a la tierra, aire, fuego y agua de Empédocles. Hay demasiados parámetros y demasiados controles que ajustar. Necesitamos una nueva teoría que sea menos complicada, más sencilla y bella, sin vericuetos intrincados que salvar, con la limpieza y serena majestad de la teoría de la gravedad que, con enorme simpleza y aplicando los principios naturales, trata los temas más profundos del universo. Esperemos que continúe desarrollándose la teoría de cuerdas y que, como parece, incluya todas las fuerzas, todas las partículas y, en fin, todos los parámetros que dan sentido al universo.

Sí, al Modelo Estándar la faltan algunas cosas y le sobran otras, o, al menos, sería necesario explicarlas mejor. La Gravedad no está presente y, hay una veintena de parámetros aleatorios que, como el Bosón de Higgs, no se pueden explicar…aún. La viene de lejos:

El modelo estándar: resumida
Autores	Fechas	Partículas	Fuerza		Comentario
Tales (milesio)	600 a.C.	Agua	No se menciona	8	Fue el primero en explicar el mundo mediante causas naturales. Lógica en lugar de mito.
Empédocles (agrigento)	460 a.C.	Tierra, agua, aire y fuego	Amor y discordia	9	Aportó la idea de que hay múltiples partículas que se combinan para formar toda la materia.
Demócrito (Abdera)	430 a.C.	El átomo indivisible e invisible, o a-tomo	Movimiento violento constante	10	Su modelo requería demasiadas partículas, cada una con una forma diferente, pero su idea básica de que hay un átomo que no puede ser partido sigue siendo la definición básica de partícula elemental.
Isaac Newton (inglés)	1.687	Átomos duros con masa, impenetrables	Gravedad (cosmos); fuerzas desconocidas (átomos)	7	Le gustaban los átomos pero no hizo que su causa avanzase. Su gravedad fue un dolor de cabeza para los peces gordos en la década de 1.990
Roger J. Boscovich (dálmata)	1.760	“ de fuerza” indivisibles y sin forma o dimensión	Fuerzas atractivas y repulsivas que actúan entre	9	Su teoría era incompleta, limitada, pero la idea de que hay partículas de “ nulo”, puntuales, que crean “campos de fuerza”, es esencial en la física moderna.
Michael Faraday (inglés)	1.820	Cargas eléctricas	Electromagnetismo	8’5	Aplicó el atomismo a la electricidad al conjeturar que las corrientes estaban formadas por “corpúsculos de electricidad”, los electrones.
Dimitri Mendeleev (siberiano)	1.870	Más de 50 átomos dispuestos en la tabla periódica de los elementos	No hace cábalas sobre las fuerzas	8’5	Tomó la idea de Dalton y organizó todos los elementos químicos conocidos. En su tabla periódica apuntaba con claridad una estructura más profunda y significativa.
Ernest Rutherford (neozelandés)	1.911	Dos partículas; núcleo y electrón	La fuerza nuclear fuerte más el electromagnetismo. La gravedad	9’5	Al descubrir el núcleo, reveló una nueva simplicidad dentro de todos los átomos de Dalton. El experimentador por excelencia.
Bjorken, Fermi, Friedman, Gell-Mann, Glasgow, Kennedy, Lederman, Peri, Richter, Schwartz, Steinberger, Taylor, Ting, más un reparto de miles.	1.992	Seis quarks y seis leptones, más sus antipartículas. Hay tres colores de quarks	El electromagnetismo, la interacción fuerte y débil: doce partículas que llevan las fuerzas más la gravedad.	?	Demócrito de Abdera ríe.

A todo esto y como he dicho, el quark top está perdido (ya se encontró) y el neutrino tau no se ha detectado directamente (pero experimentos nos han dicho que un neutrino muónico se puede transformar en uno tau), y muchos de los números que nos hacen falta conocer los tenemos de forma imprecisa. Por ejemplo, no sabemos si los neutrinos tienen alguna masa en reposo.

Tenemos que saber cómo la violación de la simetría CP (el proceso que originó la materia) aparece, y lo que es más importante, hemos de introducir un nuevo fenómeno, al que llamamos de Higgs, para preservar las coherencia matemática del modelo estándar. La idea de Higgs y su partícula asociada, el bosón de Higgs, cuenta en todos los problemas que he mencionado antes. Parece, con tantos parámetros imprecisos (19), que el modelo estándar está asentado sobre arenas movedizas.

En realidad, no sabemos si la relatividad y la teoría cuántica, son dos mundos antagónicos que nos empeñamos en unir

Entre los teóricos, el casamiento de la relatividad y la teoría cuántica es el problema central de la física moderna. A los esfuerzos teóricos que se realizan con ese propósito se les llama “supergravedad”, “supersimetría”, “supercuerdas”, “teoría M” o, en último caso, “teoría de todo” o “gran teoría unificada”.

Ahí tenemos unas matemáticas exóticas que ponen de punta hasta los pelos de las cejas de algunos de los mejores matemáticos del mundo (¿y Perelman?; ¿por qué no se ha implicado?). Hablan de 10, 11 y 26 dimensiones, siempre todas ellas espaciales menos una que es la temporal. Vivimos en cuatro: tres de espacio (este-oeste, norte-sur y arriba-abajo) y una temporal. No podemos ni sabemos, o no nos es posible intuir en nuestro cerebro (también tridimensional), ver más dimensiones. Pero llegaron Kaluza y Klein y compactaron en la longitud de Planck las dimensiones que no podíamos ver; ¡problema solucionado! ¿Quién puede ir a la longitud de Planck para verlas?

La puerta de las dimensiones más altas quedó abierta y a los teóricos se les regaló una herramienta maravillosa: el hiperespacio; todo es posible. Hasta el matrimonio de la relatividad general y la mecánica cuántica, allí sí es posible esa soñada teoría de la gravedad cuántica.

 

                      ¡Tiene tantos secretos el Universo! Arriba podrían estar los dos mayores

Así que las teorías se han embarcado a la búsqueda de un objeto audaz: buscan una teoría que describa la simplicidad primigenia que reinaba en el intenso calor del universo en sus primeros tiempos; una teoría carente de parámetros, donde estén presentes todas las respuestas. Todo debe ser contestado a partir de una ecuación básica.

¿Dónde radica el problema?

El problema está en que la única teoría candidata no tiene conexión directa con el mundo de la observación, o no lo tiene todavía si queremos expresarnos con propiedad. La energía necesaria para ello, no la tiene ni el nuevo acelerador de partículas LHC que mencioné en páginas anteriores.

La verdad es que la teoría que ahora tenemos, el modelo estándar, concuerda de manera exacta con todos los a bajar energías y contesta cosas sin sentido a altas energías. ¡Necesitamos algo más avanzado!

Se ha dicho que la función de la partícula de Higgs es la de dar masa a las partículas que carecen de ella, disfrazando así la verdadera simetría del mundo. Cuando su autor lanzó la idea al mundo, resultó además de nueva, muy extraña. El secreto de todo radica en conseguir la simplicidad: el átomo resultó ser complejo, lleno de esas infinitesimales partículas electromagnéticas que bautizamos con el nombre de electrones. Resultó que tenía un núcleo que contenía, a pesar de ser tan pequeño, casi toda la masa del átomo. El núcleo, tan pequeño, estaba compuesto de otros objetos más pequeños aún; los quarks que estaban instalados en nubes de otras partículas llamadas gluones, y ahora queremos profundizando, sospechando que después de los quarks puede haber algo más.

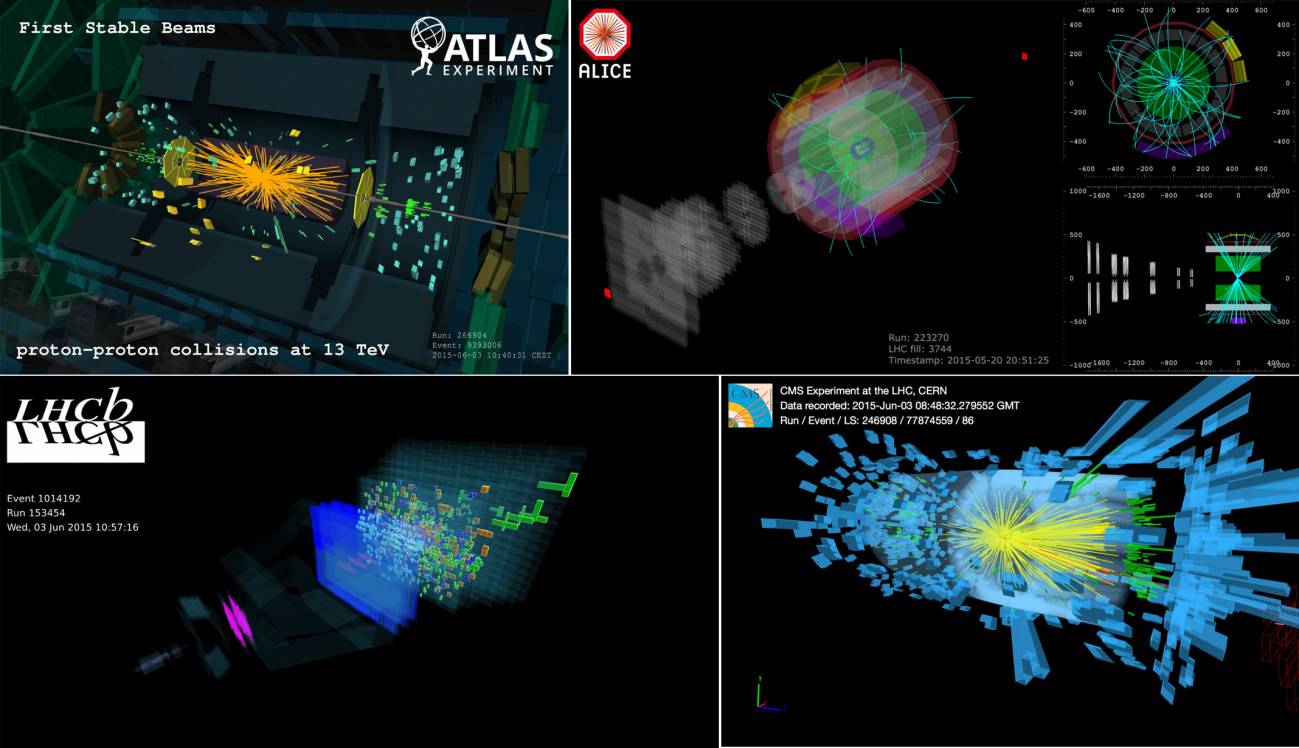
Con los últimos experimentos en el LHC, en busca de la partícula de Higgs, pudimos declaraciones como éstas:

“…confirmaron que durante este año, tal y como se ha anunciado hace semanas, se ha obtenido una auténtica marea de que dejan poco o ningún lugar a dudas sobre la existencia de la partícula que la teoría considera responsable de la masa de todas las demás partículas y sin la que el Universo, sencillamente no existiría tal y como lo conocemos.”

 

 

Bueno, la idea nueva que surgió es que el espacio entero contiene un campo, el campo de Higgs, que impregna el vacío y es el mismo en todas partes, es decir, que si miramos a las estrellas en una noche clara, estamos mirando el campo de Higgs. Las partículas influidas por este campo toman masa. Esto no es por sí mismo destacable, pues las partículas pueden tomar energía de los campos (gauge) de los que hemos comentado: del campo gravitatorio o del electromagnético. Si llevamos un bloque de plomo a lo alto de la , el bloque adquirirá energía potencial a causa de la alteración de su posición en el campo gravitatorio de la Tierra. Como E = mc², ese aumento de la energía potencial equivale a un aumento de la masa, en este caso la masa del sistema Tierra-bloque de plomo. Aquí hemos de añadirle amablemente un poco de complejidad a la venerable ecuación de Einstein: la masa, m, tiene en realidad dos partes; una es la masa en reposo, m₀, la que se mide en el laboratorio cuando la partícula está en reposo. La partícula adquiere la otra parte de la masa en virtud de su movimiento (como los protones en el acelerador de partículas, o los muones, que aumentan varias veces su masa cuando son lanzados a velocidades cercanas a c), o en virtud de su energía potencial de campo. Vemos una dinámica similar en los núcleos atómicos. Por ejemplo, si separamos el protón y el neutrón que componen un núcleo de deuterio, la suma de las masas aumenta.

 

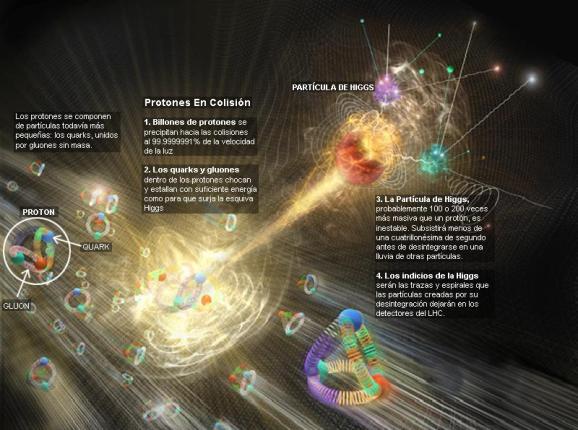
Pero la energía potencial tomada del de Higgs difiere en varios aspectos de la acción de los campos familiares. La masa tomada de Higgs es en realidad masa en reposo. De hecho, en la que quizá sea la versión más apasionante de la teoría del de Higgs, éste genera toda la masa en reposo. Otra diferencia es que la cantidad de masa que se traga del es distinta para las distintas partículas. Los teóricos dicen que las masas de las partículas de nuestro modelo estándar miden con qué intensidad se acoplan éstas al campo de Higgs.

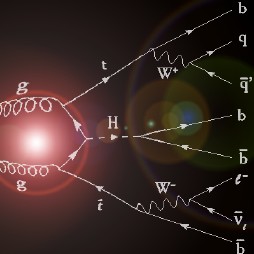
La influencia de Higgs en las masas de los quarks y de los leptones nos recuerda el descubrimiento por Pieter Zeeman, en 1.896, de la división de los niveles de energía de un electrón cuando se aplica un campo magnético al átomo. El campo (que representa metafóricamente el papel de Higgs) rompe la simetría del espacio de la que el electrón disfrutaba.

Hasta ahora no tenemos ni idea de qué reglas controlan los incrementos de masa generados por Higgs (de ahí la expectación creada por el nuevo acelerador de partículas LHC), pero el problema es irritante: ¿por qué sólo esas masas ­­- las masas de los W⁺, W^–, Z⁰, y el up, down, encanto, estraño, top y bottom, así como los leptones – que no forman ningún patrón obvio?

Las masas van desde la del electrón (0’0005 GeV) a la del top, que tiene que ser mayor que 91 GeV. Deberíamos recordar que esta extraña idea (el Higgs) se empleó con mucho éxito para formular la teoría electrodébil (Weinberg-Salam). Allí se propuso el campo de Higgs como una forma de ocultar la unidad de las fuerzas electromagnética y débil. En la unidad hay cuatro partículas mensajeras sin masa – los W⁺, W^–, Z⁰ y el fotón – que llevan la fuerza electrodébil. Además está el campo de Higgs, y rápidamente, los W y Z absorben la esencia de Higgs y se hacen pesados; el fotón permanece intacto. La fuerza electrodébil se fragmenta en la débil (débil porque los mensajeros son muy gordos), y la electromagnética, cuyas propiedades determina el fotón, carente de masa. La simetría se rompe espontáneamente, dicen las teorías. Prefiero la descripción según la cual el Higgs oculta la simetría con su poder dador de masa.

 

Las masas de los W y Z se predijeron con éxito a partir de los parámetros de la teoría electrodébil, y las relajadas sonrisas de los físicos teóricos nos recuerdan que Hooft y Veltman dejaron sentado que la teoría entera está libre de infinitos.

Todos los intentos y los esfuerzos por hallar una pista de cuál era el origen de la masa fallaron. Feynman escribió su famosa : “¿por qué pesa el muón?”. Ahora, por lo menos, tenemos una respuesta parcial, en absoluto completa. Una voz potente y segura nos dice “¡Higgs!”. Durante más de sesenta años los físicos experimentadores se rompieron la cabeza con el origen de la masa, y ahora el de Higgs presenta el problema en un contexto nuevo; no se trata sólo del muón. Proporciona, por lo menos, una fuente común para todas las masas. La nueva feynmaniana podría ser: ¿cómo determina el campo de Higgs la secuencia de masas, aparentemente sin patrón, que da a las partículas de la materia?

La variación de la masa con el estado de movimiento, el cambio de masa con la configuración del sistema y el que algunas partículas (el fotón seguramente, y los neutrinos posiblemente) tengan masa en reposo nula son tres hechos que ponen en entredicho que el concepto de masa sea un atributo fundamental de la materia. Habrá que recordar aquel cálculo de la masa que daba infinito y nunca pudimos resolver; los físicos sólo se deshicieron de él “renormalizándolo”, ese truco matemático que empleam cuando no saben hacerlo bien.

 

                       ¿Sabremos alguna vez cómo adquieren masa las partículas?

Ese es el problema de trasfondo con el que tenemos que encarar el problema de los quarks, los leptones y los vehículos de las fuerzas, que se diferencian por sus masas. Hace que la de Higgs se tenga en pie: la masa no es una propiedad intrínseca de las partículas, sino una propiedad adquirida por la interacción de las partículas y su entorno. ¿Será el efecto frenado en los campoos de Higgs la que le da masa a las partículas? Bueno eso dice nuestro amigo Ramón Máquez.

La idea de que la masa no es intrínseca como la carga o el espín resulta aún más plausible por la idílica idea de que todos los quarks y fotones tendrían masa cero. En ese caso, obedecerían a una simetría satisfactoria, la quiral, en la que los espines estarían asociados para siempre con su dirección de movimiento. Pero ese idilio queda oculto por el fenómeno de Higgs.

Una cosa más; hemos hablado de los bosones gauge y de su espín de una unidad. Hemos comentado también las partículas fermiónicas de la materia (espín de media unidad). ¿Cuál es el pelaje de Higgs? Es un bosón de espín cero. El espín supone una direccionalidad en el espacio, pero el de Higgs da masa a los objetos quiera que estén y sin direccionalidad. Al Higgs se le llama a veces “bosón escalar” (sin dirección) por esa razón.

 

La interacción débil, recordaréis, fue inventada por E. Fermi para describir la desintegración radiactiva de los núcleos, que era básicamente un fenómeno de poca energía, y a medida que la teoría de Fermi se desarrolló, llegó a ser muy precisa a la hora de predecir un enorme número de procesos en el dominio de energía de los 100 MeV. Así que ahora, con las nuevas tecnologías y energías del LHC, las esperanzas son enormes para, por fin, el bosón de Higgs “origen de la masa”… y algunas cosas más.

Hay que responder montones de preguntas: ¿cuáles son las propiedades de las partículas de Higgs? y, lo que es más , ¿cuál es su masa? ¿Cómo reconoceremos una si nos la encontramos en una colisión del LHC? ¿Cuántos tipos hay? ¿Genera el Higgs todas las masas o sólo las hace incrementarse? ¿Cómo podemos más al respecto? Cómo es su partícula, nos cabe esperar que la veremos ahora después de gastar más de 50.000 millones de euros en los elementos necesarios para ello.

También a los cosmólogos les fascina la idea de Higgs, pues casi se dieron de bruces con la necesidad de tener campos escalares que participasen en el complejo proceso de la expansión del universo, añadiendo pues, un peso más a la carga que ha de soportar el Higgs.

 

Existirán los campos de Higgs, o…

 

… sólo será una creación de la mente con su desbordante imaginación

El de Higgs, tal como se lo concibe ahora, se puede destruir con una energía grande, o temperaturas altas. Éstas generan fluctuaciones cuánticas que neutralizan el de Higgs. Por lo tanto, el cuado que las partículas y la cosmología pintan juntas de un universo primitivo puro y de resplandeciente simetría es demasiado caliente para Higgs. Pero cuando la temperatura cae bajo los 10^-5 grados Kelvin o 100 GeV, el Higgs empieza a actuar y hace su generación de masas. Así, por ejemplo, antes del Higgs teníamos unos W, Z y fotones sin masa y la fuerza electrodébil unificada.

El universo se expande y se enfría, y entonces viene el Higgs (que “engorda” los W y Z, y por alguna razón ignora el fotón) y de ello resulta que la simetría electrodébil se rompe.

Tenemos entonces una interacción débil, transportada por los vehículos de la fuerza W⁺, W^–, Z⁰, y por otra parte una interacción electromagnética, llevada por los fotones. Es como si para algunas partículas del de Higgs fuera una especie de aceite pesado a través del que se moviera con dificultad y que les hiciera parecer que tienen mucha masa.  Para otras partículas, el Higgs es como el agua, y para otras, los fotones y quizá los neutrinos, es invisible.

De todas formas, es tanta la ignorancia que tenemos sobre el origen de la masa que nos agarramos como a un clavo ardiendo, en este caso, a la partícula de Higgs, que algunos han llegado a llamar “la partícula divina”.

¡Ya veremos en qué termina todo esto!

 

                                    Sí, dudas hemos tenido todos

Hay otras muchas cuestiones de las que podríamos hablar y, la Física y la Astronomía, siendo mi gran Pasión, ocupa mucho de mi tiempo. La Física, amigos míos, nos dirá como es el “mundo” y digo mundo querinedo significar Naturaleza y Universo. La Física encierra una belleza…, que está presente en:

1. Una simetría unificadora.
2. La capacidad de explicar grandes cantidades de experimentales con las expresiones matemáticas más económicas.

El Modelo Estándar falla en ambos aspectos, mientras que la relatividad los exhibe, ambos, de manera bien patente. Nunca una teoría dijo tanto con tan poco; su sencillez es asombrosa y su profundidad increíble.De hecho, desde que se publicó en 1.915, no ha dejado de dar frutos, y aún no se han obtenido de ella todos los mensajes que contiene.

emilio silvera

LA ESTRELLA DE DAVID, Y LA FÓRMULA GEOMÉTRICA QUE ENLAZA ENTRE SÍ A TODAS LAS LEYES FÍSICAS DEL UNIVERSO

Escribe el doctor Ovidio Pracilio: “Antes de desarrollar en forma geométrica la
maravilla del símbolo mosaico, es necesario formular algunas consideraciones en torno a otro
símbolo, vinculado al anterior, y respecto del cual, según creo, no se ha desentrañado hasta ahora
su verdadero significado.

Me refiero a la llamada “Estrella de David”.

La estrella de David, tal como siempre se trazó, en la figura geométrica que resulta de
dividir una circunferencia en seis partes iguales y unir con líneas rectas en forma alternada los
puntos que dividen esa circunferencia. Esta es la estrella que se conoce y que se usa desde hace
milenios como emblema de la raza judía.

Pero la verdadera estrella llamada de David no es ésa, así trazada con líneas rectas.
La verdadera, la que los mismos judios creo que no conocen, la que tiene relación con
la concepción mosaica de la creación del Mundo, la que se vincula a la Geometría Esferoidal que
la Naturaleza utilizaría para planificar todas sus creaciones, no es una estrella de líneas rectas,
sino una estrella de líneas circulares trazada a compás, y en la cual, en forma análoga a la que se
traza con líneas rectas, la estrella es el resultado de dos triángulos también equiláteros esféricos e
iguales cuyos lados son un tercio del lado del triángulo mayor, y en el interior un exágono con
igual medida por lado. (Véase gráfico).

Existe una única forma, que yo haya logrado, de poder trazar esta estrella de David con

el compás, y es la siguiente:

Trazada una circunferencia, y con la misma medida de su radio, se la divide con el
compás en seis partes iguales. Luego se reduce la abertura del compás disminuyendo el radio en
una setenta-ava parte, y haciendo centro en cada uno de los seis puntos en que se dividió la
circunferencia, se trazan semicírculos que pasarán a una setenta-ava parte de distancia del centro,
semicírculos que, al entrecruzarse, marcarán en la parte central de la circunferencia la estrella de
David de triángulos equiláteros esféricos iguales.

Este gráfico geométrico, por considerarlo la base fundamental de la obra, lo he
colocado en la tapa interna del libro “La Planificación Universal”, y lo vuelvo a reproducir en el
blog de Google debajo anotado, aunque, por razón del tamaño del círculo, se lo omite. Pero es
tan fàcil ejecutarlo con el compás, en la forma indicada, que todo lector que así lo desee puede
confeccionarlo en breves instantes.

No existe otra forma de poder trazar esta estrella con el compás, en la cual sus
triángulos deben ser iguales, y como se ha visto, en dicha forma de hacerlo utilizamos un
número, el 7, su setenta-ava parte, y el 6, del que resulta la estrella. Y lo hemos logrado sin
utilizar ninguna línea recta y usando solamente el compás, como hemos hecho con todos los
gráficos que documentan la obra.

Ahora continúo con la exposición generalizada sobre la concepcióm mosaica de la

Creación del Mundo.

Con una medida cualquiera de compás marquemos una circunferencia, y luego, sin
modificar la medida del compás y haciendo centro en cualquier punto de la circunferencia ya
marcada, tracemos otra circunferencia; luego haciendo centro en el punto en que la primera es
cortada por la segunda, tracemos una tercera, y luego de igual modo una cuarta, una quinta, una
sexta y una séptima. (Ver gráfico).

La última circunferencia, o sea la séptima, corta a la primera en el mismo punto que es
centro de la segunda, vale decir que hemos dividido a la primera circunferencia en seis partes
iguales; la primera está en el centro y es común para las seis, cuyos centros están ubicados sobre
ella a intervalos iguales. Dicho de otro modo, los centros de las seis circunferencias descansan a
intervalos iguales sobre la séptima.

Ya hemos logrado, al hacer esto, una primera aplicación geométrica de la ley mosaica.

Pero debemos continuar para ver cómo funciona la ley.

Observando el gráfico respectivo, vemos que la segunda circunferencia corta no solo a
la circunferencia primera en dos puntos que son los centros de las circunferencias contiguas, sino

que también corta a esas circunferencias en otros dos puntos. A su vez, también las otras
circunferencias cortan a sus contiguas de la misma manera.

Hagamos entonces centro con el compás, y siempre con la misma medida, en esos
nuevos puntos, y marquemos así otras seis circunferencias que cortarà a su vez a sus contiguas y
nos darán nuevos puntos que serán centros de otras circunferencias que podemos seguir
marcando y así hasta el infinito.

Acabamos de marcar así un esquema geométrico que es fundamental, y con el cual
habremos de seguir trabajando, pues de él se parte siempre si es verdad que una única ecuación
matemática (como quería Einstein) o geométrica (como quería Platón) enlaza entre sí a todas
las leyes físicas del Universo, o en otras palabras, si es que el Universo físico es el fruto de una
planificación que utilizó una Geometría perfecta fundada en una ley geométrica igualmente
perfecta como lo es la indicada ley mosaica.

Si observamos la segunda serie de circunferencias que marcamos, veremos que las
seis están agrupadas alrededor de la primera (o sea la séptima) a la que solamente tocan en un
punto, así como entre ellas las contiguas también se tocan solamente en un punto.

He aquí funcionando nuevamente la indicada ley que llamo “mosaica” en homenaje al
gran Moisés. Si las seis que rodean la séptima están llenas y ésta del interior está vacía,
tendremos con ello el símbolo geométrico de la concepción mosaica sobre la creación del
Mundo.

Pero sigamos desentrañando conclusiones de tan maravilloso símbolo. No

conclusiones filosóficas, sino físicas.

Si las seis circunferencias que nos hizo el compás sobre un plano, son simples
representaciones esquemáticas de esferas, tenemos seis esferas llenas rodeando un séptimo
espacio vacio que, de ser ocupado por otra esfera, solo podría serlo por una igual a las otras seis
que la rodean.

Imaginemos ahora, físicamente, que le ocurre a cada esfera llena, en su posición frente
al espacio vacío que hay en el interior. Es indiscutible que tiende a caer en él y ubicarse en el
lugar vacío en el cual se acomodaría exactamente. (Se dice que la Naturaleza tiene horror al
vacío) Pero, ¿qué le impide a cada una de las seis esferas llenas caer en en ese espacio vacío
central? Se lo impiden las dos esferas que le son contiguas, las cuales también quieren caer al
séptimo espacio vacío. Es decir, que ninguna de las seis esferas llenas pueden caer al vacío
central porque mutuamente se lo impiden, debido precisamente a su idéntica predisposición física
a caer al vacío como consecuencia de su pesantez.

Si a una de las esferas le imprimimos movimiento, hará girar a las dos contiguas con
movimiento contrario, y tal movimiento lo podemos propagar al infinito, si es que seguimos
construyendo agrupamientos séxtuples de esferas que rodean un séptimo espacio vacío,
utilizando para ello el esquema geométrico fundamental. (Obsérvese el gráfico correspondiente
en el blog).

Una sola esfera que se mueva hace mover a todas las demás, es decir que el
movimiento se propaga, teóricamente, al infinito (aunque en realidad lo hace hasta donde la
fuerza que genera tal movimiento lo permita) pero sin desplazamiento de lugar de ninguna de las
esferas, las que combinan entre sí sus movimientos girando en sentido contrario las contiguas y
en igual sentido las alternas. Y como las esferas se tocan entre
ellas solamente en un punto (indimensional) y giran rodeadas de vacío, no existiendo rosamiento
y una vez que una fuerza las puso en movimiento seguirán girando perpetuamente si otra fuerza
distinta no modifica su movimiento frenándola o acelerándola.

Si observamos el respectivo gráfico, vemos que el movmiento de las esferas o
partículas esféricas de materia (si la consideramos tales) propagan en línea recta (aunque en todas
direcciones) la ficción de la onda que produce su movimiento, sin que ninguna de ellas se
desplace del lugar. La Física podrá examinar si esta composición geométrica de partículas
esféricas agrupadas en forma séxtuple alrededor de un séptimo espacio vacío puede contribuir a
armonizar las teorìas contradictorias de Newton (clásica corpuscular) y de Huygens (ondulatoria)
o las que ambas se elaboraron posteriormente. “Según Max Planck, la energìa es granular y no
continua y se transmite en haces discretos” (Bernard Jaffe: Michelson y la velocidad de la luz).

Nosotros sigamos con la Geometría Esferoidal.
En el interior de cada una de estas circunferencias que hemos agrupado alrededor de
una séptima, puede ubicarse otro agrupamiento séxtuple de circunferencias alrededor también de

una séptima, por aplicación de la misma ley geométrica, y así sucesivamente podemos continuar
hacia lo infinitamente pequeño.

A su vez, si encaminamos nuestro trabajo geométrico hacia lo grande, vemos que un
agrupamiento séxtuple puede estar contenido en una circunferencia, que forma parte a su vez de
un agrupamiento séxtuple mayor, y así podemos seguir también hacia lo infinitamente grande.
Por otra parte, podemos combinar en variedad infinita agrupamientos pequeños y más
pequeños con grandes y más grandes, siempre que respetemos la ley geométrica fundamental.
Asociando nuevamente estas figuras geométricas con la fìsica, y suponiendo que las
circunferencias son esferas y que tales esferas son éter (admitiendo que el éter existe tal como se
lo ha supuesto por quienes creen en su existencia como materia prima física básica y fundamental
del Universo) tal suposición nos lleva a considerar que el agrupamiento séxtuple de esferas
etéricas que se forman en el interior de una mayor, se produce cuando el éter que forma a ésta se
comprime como resultado de una modificación en la aceleración de su movimiento esferoidal.
Si ello ocurre, el gráfico geométrico nos revela que la totalidad del éter que ocupaba la
esfera mayor se ha condensado en las seis esferas pequeñas del agrupamiento séxtuple que la ha
reemplazado en ese mismo lugar del espacio, y que estas últimas ocupan menos espacio que la
esfera-madre y dejan entre ellas y en el interior del agrupamiento nuevos espacios vacíos. De lo
que resulta que, en igual espacio, comprimiendo igual cantidad de éter, producimos espacio
vacío. Y si queremos condensar más éter por compresión sucesiva en el interior de las seis
esferas del agrupamiento, éstas forman a su vez en el interior de cada una, otras seis esferas más
pequeñas rodeadas de vacío y con un espacio vacío central en el interior del agrupamiento (ley
mosaica).

Marcando en los gráficos geométricos con negro los espacios vacíos interesferoidales
y dejando en blanco el interior de cada esfera que suponemos de éter, resulta como consecuencia
que, a mayor cantidad de esferas o partículas esféricas de éter en igual espacio, corresponde
mayor espacio vacío. (Veansé gráficos en Google: blog:
www.lacienciadeltercermilenio.laplanificacionuniversal.ovidiopracilio).

Ya veremos después cómo esta concepción arquitectural de la materia fundada en el
agrupamiento geométrico esferoidal del éter según lo establece la indicada ley mosaica, nos
llevará inevitablemente a introducir una variante fundamental a la teoría de la gravitación
universal”, expuesta en el blog señalado.

© 2020 – Copyright –Autor: Ovidio Pracilio – Registro: Dante Pracilio. Todos los Derechos Reservados.