¿Universo Estacionario? ¿Y, los elementos?

El Cráneo de Marte en el Cráter Gusev. Imágenes, obtenidas por el robot Spirit, en diferentes emplazamientos y fechas, que muestran calaveras (O al menos eso es lo que parecen)

 

Por muchas razones, el planeta vecino llamó siempre la atención de los pobladores de la Tierra y, con sus “canales” y su misterioso color rojo, despertó nuestra curiosidad y nos llevó a querer saber más de lo que allí pasaba. Algunas de las imágenes que pudimos obtener nos hizo -en ocasiones- pensar en una posible antigua civilización marciana.

Todos hemos visto, en más de una ocasión, imágenes del planeta Marte de regiones dispares y de variado contenido. Marte, el cuarto planeta desde el Sol, aparece marcadamente rojizo cuando se observa a simple vista. Tiene una delgada atmósfera compuesta (en volumen) por alrededor del 95% de dióxido de carbono, 2,7% de Nitrógeno, 1,6% de Argón, 0,1% de Oxígeno, 0,1% de monóxido de carbono y pequeñas trazas variables de vapor de agua. La presión atmosférica en la superficie es de unos 6 mbar. Las temperaturas superficiales pueden variar entre 0 y -125ºC, siendo la media de -50ºC. Es relativamente común la presencia de nubes blancas de vapor de agua condensada o de dióxido de carbono, particularmente cerca del terminador  y en latitudes polares.

Los casquetes polares y las nubes brillantes de Marte

Existen dos casquetes  de hielo de agua permanentes en los polos, que nunca se funden. En invierno éstos aumentan de tamaño al convertirse en casquetes de dióxido de carbono congelado hasta alcanzar los 60º de longitud. Ocurren esporádicamente tormentas de polvo que llegan a cubrir la totalidad del planeta con una neblina amarilla, oscureciendo los accidentes superficiales más familiares.

Así ve la NASA las futuras viviendas de Marte

Paisaje de Syrtis Major

La superficie de Marte es basalto volcánico con un alto contenido en hierro y, su oxidación, es la responsable de su color característico rojo oxido. El accidente oscuro más prominente, Syrtis Major, dirigida hacia el Este con una inclinación menor que 1º.

Dunas activas en Marte

Existen muchas áreas de dunas de arena rodeando las más grandes los casquetes polares y constituyendo los mayores campos de dunas del Sistema Solar.

Imágenes de la NASA muestran “sombras de árboles” sobre la superficie de las dunas en Marte, que en realidad y según explicaron los expertos,  son caminos de arena y extrañas formaciones debidas a la especial conformación del terreno y de las tormentas de arena que allí son frecuentes.

Hace ya bastantes años que en la NASA tuvo lugar una reunión a la que asistieron algunos personajes conocidos como el fallecido Neil Armstrong, Homer Newel, Arthur Clarke y Wernher von Braun entre otros.  El motivo de tal cita no era otro que comentar sobre la posibilidad de ir a Marte e instalar allí una pequeña Colonia Humana que sirviera como punta de lanza para posteriores viajes.

emilio silvera

Siempre hablamos de visitar otros mundos, otros universos y, en ellos, las condiciones físicas no tienen, necesariamente que ser como en el nuestro. Los mundos, como las estrellas y los universos, pueden tener sus propias características dependiendo de muchos factores que lo podrían conformar de manera muy diferente a como lo está nuestro mundo y vemos que se comporta el universo con sus cuatro leyes fundamentales y sus constantes que, en otro universo, podrían ser de otra manera.

Se sospecha que un universo compañero del nuestro está ejerciendo una gran fuerza gravitatoria sobre las galaxias del nuestro que se alejan las unas de las otras a velocidades injustificadas. ¿Será esa fuerza, lo que induce a los cosmólogos a equivocarse y llamarla “materia oscura”?

“Oumuamua, un curioso objeto interestelar observado mientras cruzaba el Sistema Solar, no es una roca desprendida de otras estrellas, sino que se trata del “primer signo de vida inteligente de origen extraterrestre.

El principal catedrático de Astrofísica de la Universidad de Harvard, el israelí-estadounidense Abraham ‘Avi’ Loeb, está convencido de que hay vida inteligente fuera de la Tierra. Esta teoría la sostiene en su libro “Extraterrestre: El primer signo de vida inteligente más allá de la Tierra está en esa imagen de arriba”.

Formas de vida diferentes, estructuras asombrosas y para nosotros desconocidas, y, hasta el Tiempo se podría comportar de diferente manera. Ni negar ni confirmar podemos sobre lo que desconocemos y solo conjeturar y avanzar teorías es nuestra realidad hasta que, en un futuro lejano, podamos constatarlo con hechos.

Si es cierto lo que afirman algunas teorías, entonces existen en realidad un número infinito de universos paralelos, muchos de ellos con diferentes constantes físicas. En algunos de ellos, quizá los protones se desintegran con demasiada rapidez, o las estrellas no pueden fabricar los elementos pesados por encima del hierro, o el Big Crunch tiene lugar demasiado deprisa porque su densidad crítica sobrepasa en mucho a la ideal y no da tiempo a que pueda comenzar la germinación de la vida, y así sucesivamente. De hecho, un número infinito de estos universos paralelos están muertos, sin las leyes físicas que puedan hacer posible la vida tal como la conocemos.

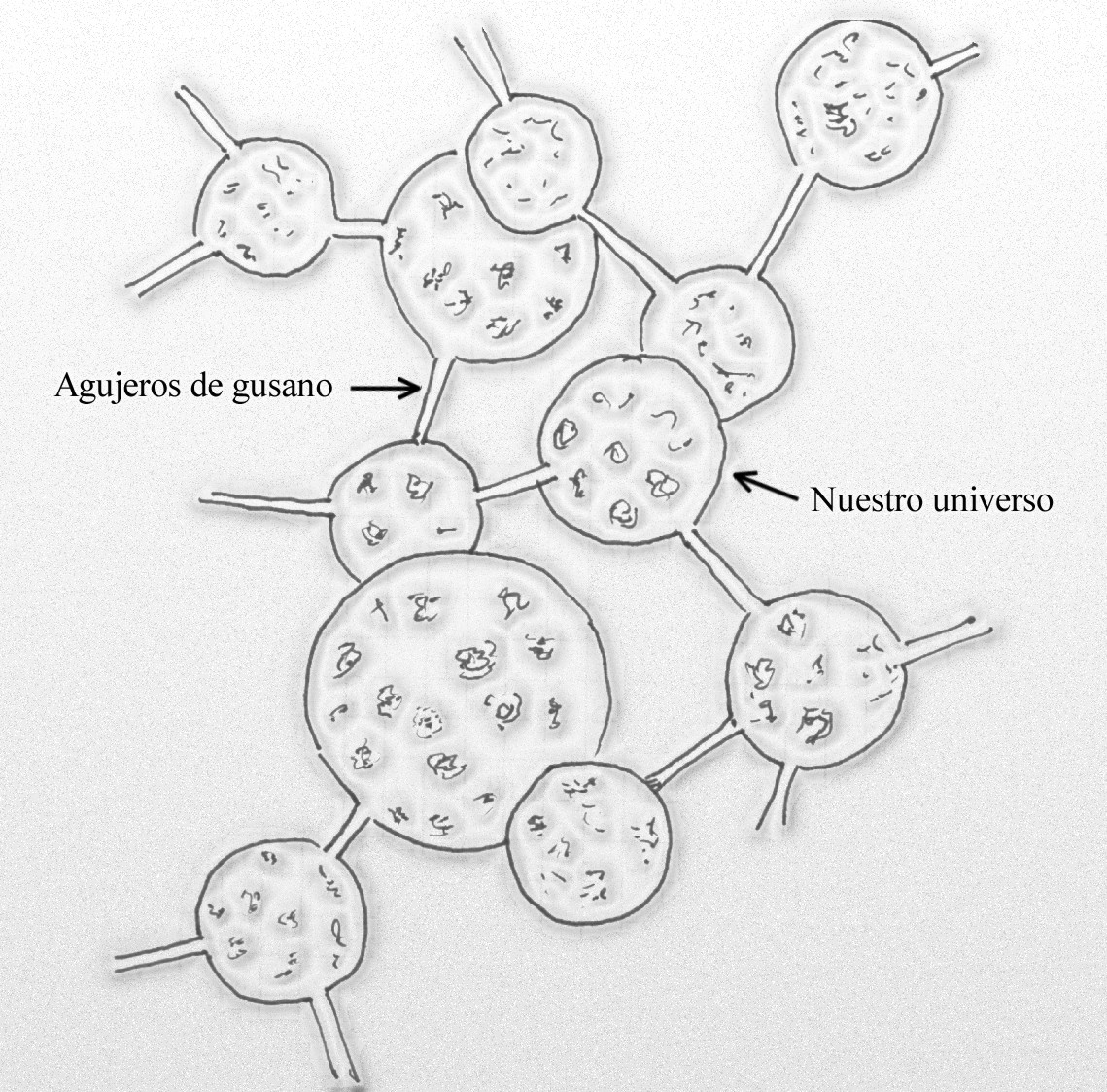
En tal universo paralelo (el nuestro), las leyes de la física eran compatibles con la vida que conocemos. La prueba es que nosotros estamos aquí para tratar esta cuestión. Si esto es cierto, entonces quizá no haya que invocar a Dios para explicar por qué la vida, por preciosa que sea, es posible en nuestro universo. Sin embargo, esto reabre la posibilidad del principio antrópico débil, es decir, que coexistimos con nuestros universos muertos y que el nuestro sea el único compatible para vida.

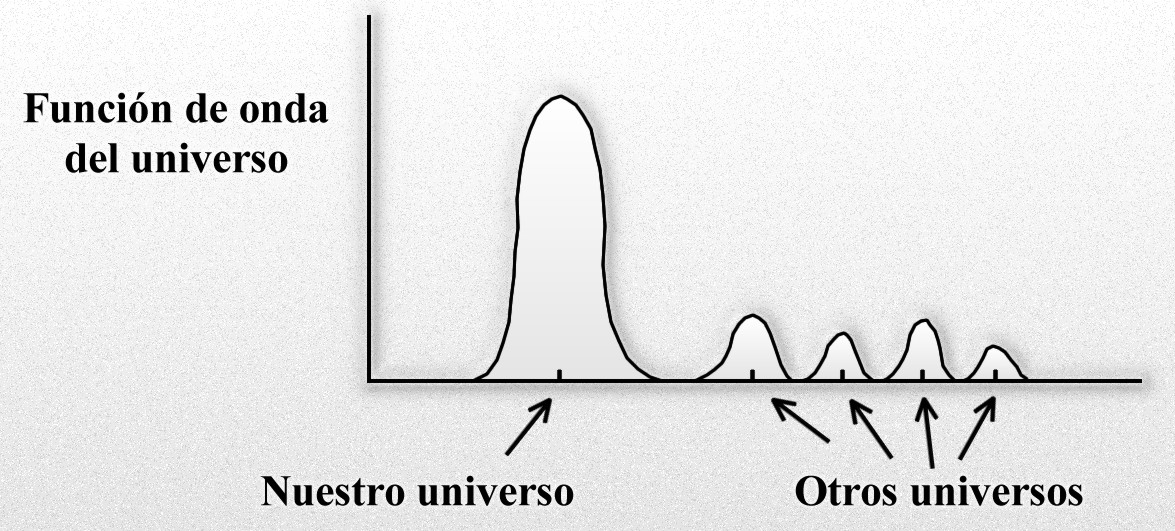
La segunda controversia estimulada por la función de onda del universo de Hawking es mucho más profunda y, de hecho, aun está sin resolver. Se denomina el Gato de Schrödinger. Empezamos con una función de onda que describe el conjunto de todos los universos posibles. Esto significa que el punto de partida de la teoría de Hawking debe ser un conjunto infinito de universos paralelos, la función de onda del universo. El análisis bastante simple de Stephen Hawking, reemplazando la palabra partícula por universo, ha conducido a una revolución conceptual en nuestras ideas sobre la cosmología.

                                                 Función de onda y colapso de la función de onda

La teoría cuántica, recordémoslo, afirma que para todo objeto existe una función de onda que mide la probabilidad de encontrar dicho objeto en un cierto punto del espacio y del tiempo. La teoría cuántica afirma también que nunca se conoce realmente el estado de una partícula hasta que se haya hecho una observación. Antes de que haya una medida, la partícula puede estar en uno de entre una diversidad de estados, descritos por la función de onda de Schrödinger. Por consiguiente, antes de que pueda hacerse una observación o medida, no se puede conocer realmente el estado de la partícula.  De hecho, la partícula existe en un estado ultramundano, una suma de todos los estados posibles, hasta que se hace una medida.

Cuando esta idea fue propuesta por primera vez por Niels Bohr y Werner Heisemberg, Einstein se revolvió contra ella. “¿Existe la luna sólo porque la mira un ratón?“, -o un gato- le gustaba preguntar. Según la teoría cuántica, en su más estricta interpretación, la Luna, antes de que sea observada, no existe realmente tal como la conocemos. “La Luna puede estar, de hecho, en uno cualquiera de entre un número infinito de estados, incluyendo el estado de estar en el cielo, de estar explotando, o de no estar allí en absoluto. Es el proceso de medida que consiste en mirarla el que decide que la Luna está girando realmente alrededor de la Tierra“. Decía Einstein con ironía.

Edwin Schrödinger, autor de la ecuación con su función de onda, se disgustó con estas interpretaciones de su ecuación. Para demostrar lo absurdo de la situación creada, Schrödinger colocó un gato imaginario en una caja cerrada. El gato estaba frente a una pistola, que está conectada a un contador Geiger, que a su vez está conectado a un fragmento de uranio. El átomo de uranio es inestable y sufrirá una desintegración radiactiva. Si se desintegra un núcleo de uranio, será detectado por el contador Geiger que entonces disparará la pistola, cuya bala matará al gato.

Para decidir si el gato está vivo o muerto, debemos abrir la caja y observar al gato. Sin embargo, ¿cuál es el estado del gato antes de que abramos la caja? Según la teoría cuántica, sólo podemos afirmar que el gato esta descrito por una función de onda que describe la suma de un gato muerto y un gato vivo.

Para Schrödinger, la idea de pensar en gatos que no están ni muertos ni vivos era el colmo del absurdo, pero la confirmación experimental de la mecánica cuántica nos lleva inevitablemente a esta conclusión. Hasta el momento, todos los experimentos han verificado, favorablemente, la teoría cuántica.

          Sí, a veces la mecánica cuántica parece tan fantástica como el cuento de Alicia

La paradoja del gato de Schrödinger es tan extraña que uno recuerda a menudo la reacción de Alicia al ver desaparecer el gato de Cheshire en el centro del cuento de Lewis Carroll: “Allí me verás“, dijo el Gato, y desapareció, lo que no sorprendió a Alicia que ya estaba acostumbrada a observar cosas extrañas en aquel lugar fantástico. Igualmente, los físicos durante años se han acostumbrados a ver cosas “extrañas” en la mecánica cuántica.

                  La Mecánica Cuántica y la Mente

Existen varias maneras de abordar esta dificultad de lo incomprensible en mecánica cuántica. En primer lugar, podemos suponer que Dios existe.   Puesto que todas las “observaciones” implican un observador, entonces debe haber alguna “conciencia” en el universo. Algunos físicos como el premio Nobel Eugene Wigner, han insistido en que la teoría cuántica prueba la existencia de algún tipo de conciencia cósmica universal.

La segunda forma de tratar la paradoja es la preferida por la gran mayoría de los físicos en activo: ignorar el problema.

             El físico Richard Feynman dijo en cierta ocasión:

“Creo que es justo decir que nadie comprende la mecánica cuántica. No siga diciéndose a sí mismo, si puede evitarlo, “¿pero cómo puede ser así?” porque usted se meterá “hasta el fondo” en un callejón sin salida del que nadie ha escapado.  Nadie sabe como puede ser eso“. De hecho, a menudo se ha dicho que de todas las teorías propuestas en el siglo XX, la más absurda es la teoría cuántica. Algunos dicen que la única cosa que la teoría tiene a su favor es que “es indudablemente correcta”.

Sin embargo, existe una tercera forma de tratar esta paradoja, denominada teoría de los muchos universos. Esta teoría (como el principio antrópico) no gozó de mucho favor en la última década, pero está siendo revitalizada por la función de onda del universo de Stephen Hawking.

Aunque no siempre, lo más simple tiene que ser lo verdadero. El principio de la Navaja de Ockham es fundamental para el reduccionismo metodológico.

Existe un principio de la física denominado Navaja de Ockham, que afirma que siempre deberíamos tomar el camino más sencillo posible e ignorar las alternativas más complicadas, especialmente si las alternativas no pueden medirse nunca.

Para seguir fielmente el consejo contenido en la Navaja de Ockham , primero hay que tener el conocimiento necesario para poder saber elegir el camino más sencillo, lo que en la realidad, no ocurre. Nos faltan los conocimientos necesarios para hacer las preguntas adecuadas.

¿Quién puede saber lo que ahí fuera existe? ¡Nadie! Sólo podemos imaginarlo en función de cada Mente y de distintas maneras. En tan inconmensurable panorama que nos muestra un Universo (para nosotros) infinito.

Hugo Everett, Bryce DeWitt y ahora Hawking (también otros), han propuesto la teoría de los universos múltiples. En unos universos los protones se desintegran antes haciendo inestable la materia, en otros, el átomo de uranio se desintegra mediante un proceso sin radiaciones, y en otros universos las constantes universales que existen en el nuestro, son totalmente diferentes y no dan posibilidad alguna para la existencia de seres vivos. Está claro que cualquier variación que en principio pudiera parecer sin importancia, como por ejemplo la carga del electrón, podría transformar radicalmente nuestro universo.

Como apuntó el físico Frank Wilczek:

     De la película Troya, el personaje de Elena

“Se dice que la historia del mundo sería totalmente distinto si Helena de Troya hubiera tenido una verruga en la punta de su nariz.”

 

Hasta el momento, se han celebrado varias conferencias internacionales sobre la función de onda del universo. Sin embargo, como ocurre en la teoría de supercuerdas, las matemáticas implicadas en la función de onda del universo, parecen estar más allá de la capacidad de cálculo que cualquier humano en este planeta pudiera resolver, y tendríamos que esperar años antes de que aparezca un individuo genial que pudiera encontrar una solución rigurosa a las ecuaciones de Hawking.

                                Grigori Perelman

Recordemos aquí de nuevo que, precisamente ahora, un siglo más tarde, en el Congreso Internacional de Matemáticas celebrado en Madrid el mes de Agosto de 2.006, se otorgó la Medalla Field (una especie de Nobel de las matemáticas) al matemático ruso Perelman, extraño ser que ni se dignó comparecer a recogerla con el premio, hizo caso omiso. Perelman ha resuelto la conjetura expuesta por Poincaré planteada en 1.904.

La conjetura de Poincaré de 1.904, en el año 2.000, fue catalogada por el Instituto Clan como uno de los siete problemas del milenio. Para hacer un comentario sobre esta conjetura tengo que referirme a la topología, el nivel de las matemáticas donde está ubicada.

      Verdaderamente Perelman es, un extraño personaje, metido en su propio mundo. Viaja en el metro, vive con su madre en un pido de reducido tamaño y, con un canasto recoge setas en el campo.

Las últimas fotos que se conocen de él se las sacaron con un celular en un vagón del metro de Petersburgo. Se está quedando pelado pero las mechas largas y desgreñadas le llegan a los hombros, va en zapatillas sucias, un traje arrugado que le queda corto, sin corbata y con la camisa enteramente desprendida, flaco como un Cristo, la barba igual, la mirada perdida, las uñas largas y sucias y curvadas hacia adentro como garras. El vagón va en dirección sur, a Kúpchino, un barrio de monoblocks donde muere el metro. Todos los vecinos de Kúpchino saben quién es Grisha Perelman y cuál es la puerta del ínfimo departamento que comparte con su madre. Pero ninguno va a decírselo a los periodistas y a los fanáticos de la matemática que cada tanto merodean por ahí.

La topología tienen unas matemáticas endiabladamente complejas

La topología es la geometría de los objetos elásticos o flexibles que cambian de forma pero tienen las mismas propiedades que antes de ser estirados, achatados, etc. Se pueden retorcer pero no cortar ni pegar.

Los topólogos no tienen en cuenta la distancia, puesto que se puede variar al deformar el objeto, sino nociones más sutiles. Los orígenes de la topología se remontan a mediados del siglo XVIII, con los trabajos de Euler en teoría de grafos, que llamó “análisis situs”.

“En Matemáticas, y con más exactitud en topología, la conjetura de Poincaré (también llamada hipótesis de Poincaré) es un resultado sobre la esfera cuatridimensional (la 3-esfera); la hipótesis dejó de ser una conjetura para convertirse en un teorema tras su comprobación en 2003​ por el matemático Grigori Perelman. El teorema sostiene que la esfera cuatridimensional, también llamada 3-esfera o hiperesfera, es la única variedad compacta cuatridimensional en la que todo lazo o círculo cerrado (1-esfera) se puede deformar (transformar) en un punto. Este último enunciado es equivalente a decir que solo hay una variedad cerrada y simplemente conexa de dimensión 3: la esfera cuatridimensional.”​

A finales del siglo XIX y principios del siglo XX, la topología recibió un gran impulso con los trabajos de Poincaré, matemático francés muy influyente en el posterior desarrollo de diversas áreas de las matemáticas y de la física. En particular, en 1.904 planteó la conjetura que lleva su nombre y que no se ha resuelto hasta el siglo XXI. Este problema ha sido un motor para la investigación en topología de todo el siglo pasado y se ha llegado a su resolución con ideas nuevas y apasionantes.

                                                                Henri Poincaré en su estudio trabajando

Para situarnos mejor debemos hablar de las variedades, espacios que tienen una dimensión determinada. Por ejemplo una recta o un circulo son variedades de dimensión uno, puesto que se describen como un parámetro.  El plano o la esfera son ejemplos de variedades bidimensionales, al utilizar dos parámetros para describir sus posiciones. El espacio en que vivimos es una variedad tridimensional, y si le añadimos la dimensión temporal, el espacio-tiempo es una variedad de dimensión cuatro. Ya he comentado en este mismo trabajo cómo las singularidades geométricas, las variedades, fueron introducidas por Riemann a mediados del s.    XIX y constituyeron una herramienta clave para la física del siglo XX. De hecho, la teoría de la relatividad especial de Einstein que fue postulada en 1.905, pero hasta que no incorporó las variedades contenidas en el Tensor métrico de Riemann, no pudo completar la teoría de la relatividad que incluía los espacios curvos.

La pregunta que hizo Poincaré fue la siguiente: ¿Es la esfera la única variedad tridimensional para la cual toda curva se contrae?

Se pasó un siglo entero antes de que un genio de las matemáticas, el extraño Grigori Perelman, pudiera demostrar la conjetura de Poincaré.

De todas las maneras, avanzar en el conocimiento de las cosas no resulta nada fácil, y, aunque el avance es exponencial (cuanto más datos vamos teniendo más rápidamente avanzamos), hay algunos enigmas de la Naturaleza que, de momento, seguirán en la oscuridad de nuestra profunda ignorancia.

emilio silvera