« ¡La Vida! ¿En cuántos planetas estará instalada?

Euclides nos presentaba un universo de espacios planos y, dos mil años más tarde, llegó Riemann y nos habló de un Universo curvo, y, de ese “mundo” curvo se inspiró Einstein en la Relatividad General

Recordemos aquí un extraño caso que surgió el día 10 de Junio de 1.854 con el nacimiento de una nueva geometría: la teoría de dimensiones más altas que fue introducida cuando Georg Friedrich Bernhard Riemann que dio su célebre conferencia en la facultad de la Universidad de Göttingen en Alemania. Aquello fue como abrir de golpe todas las ventanas cerradas durante 2.000 años de una lóbrega habitación que, de pronto, se ve inundada por la luz cegadora de un Sol radiante. Riemann regaló al mundo las sorprendentes propiedades del espacio multidimensional.

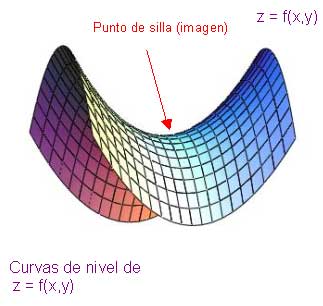
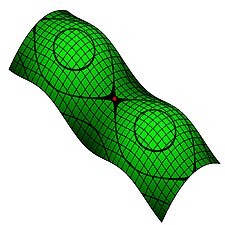
“¿Cuál es exactamente la geometría del universo? ¿Vivimos dentro de una especie de esfera de múltiples dimensiones o se trata más bien de un tejido espaciotemporal que se curva suavemente y sin llegar nunca a cerrarse sobre sí mismo? ¿O puede que incluso no se curve en absoluto y que en realidad habitemos en un universo plano? La cuestión, uno de los mayores interrogantes de la Cosmología, tiene para nosotros implicaciones muy concretas y que van mucho más allá de ser simples cuestiones teóricas. De hecho, la geometría del universo influye de forma decisiva en los objetos que observamos.”

 

 

Ejemplo de variedad de Riemann bidimensional con un sistema de coordenadas ortogonales definido sobre ella, y varias subvariedades curvas de la misma.

El Tensor métrico de Riemann le señalo a Einstein el camino hacia la Relatividad General.

El ensayo de Riemann, de profunda importancia y elegancia excepcional, “sobre las hipótesis que subyacen en los fundamentos de la geometría” derribó pilares de la geometría clásica griega, que habían resistido con éxito todos los asaltos de los escépticos durante dos milenios.

La vieja geometría de Euclides, en la cual todas las figuras geométricas son de dos o tres dimensiones, se venía abajo, mientras una nueva geometría riemanniana surgía de sus ruinas. La revolución riemanniana iba a tener grandes consecuencias para el futuro de las artes y las ciencias. En menos de tres decenios, la “misteriosa cuarta dimensión” influiría en la evolución del arte, la filosofía y la literatura en toda Europa.

Dos mil años más tarde se pasó de la geometría plana de Euclides a la Curva de Riemann

Antes de que hubieran pasado seis decenios a partir de la conferencia de Riemann, Einstein utilizaría la geometría riemanniana tetradimensional para explicar la creación del universo y su evolución mediante su asombrosa teoría de la relatividad general. Ciento treinta años después de su conferencia, los físicos utilizarían la geometría deca-dimensional para intentar unir todas las leyes del universo. El núcleo de la obra de Riemann era la comprensión de las leyes físicas mediante su simplificación al contemplarlas en espacios de más dimensiones.

Contradictoriamente, Riemann era la persona menos indicada para anunciar tan profunda y completa evolución en el pensamiento matemático y físico. Era huraño, solitario y sufría crisis nerviosas. De salud muy precaria que arruinó su vida en la miseria abyecta y la tuberculosis.

Riemann nació en 1.826 en Hannover, Alemania, segundo de los seis hijos de un pobre pastor luterano que trabajó y se esforzó como humilde predicador para alimentar a su numerosa familia que, mal alimentada, tendrían una delicada salud que les llevaría a una temprana muerte. La madre de Riemann también murió antes de que sus hijos hubieran crecido.

A edad muy temprana, Riemann mostraba ya los rasgos que le hicieron famoso: increíble capacidad de cálculo que era el contrapunto a su gran timidez y temor a expresarse en público. Terriblemente apocado era objeto de bromas de otros niños, lo que le hizo recogerse aún más en un mundo matemático intensamente privado que le salvaba del mundo hostil exterior.

Portada de la décimo primera edición de los “Eléments de Geométrie” de A. M. Legendre (1794)

Para complacer a su padre, Riemann se propuso hacerse estudiante de teología, obtener un puesto remunerado como pastor y ayudar a su familia.  En la escuela secundaria estudió la Biblia con intensidad, pero sus pensamientos volvían siempre a las matemáticas. Aprendía tan rápidamente que siempre estaba por delante de los conocimientos de sus instructores, que encontraron imposible mantenerse a su altura. Finalmente, el director de la escuela dio a Riemann un pesado libro para mantenerle ocupado. El libro era la Teoría de números de Adrien-Marie Legendre, una voluminosa obra maestra de 859 páginas, el tratado más avanzado del mundo sobre el difícil tema de la teoría de números. Riemann devoró el libro en seis días.

          Adrien-Marie Legendre

Cuando el director le preguntó: “¿hasta dónde has leído?”, el joven Riemann respondió: “este es un libro maravilloso. Ya me lo sé todo”.

Sin creerse realmente la afirmación de su pupilo, el director le planteó varios meses después cuestiones complejas sobre el contenido del libro, que Riemann respondió correctamente.

                                                                    Universität Göttingen

Con mil sacrificios, el padre de Riemann consiguió reunir los fondos necesarios para que a los 19 años pudiera acudir a la Universidad de Göttingen, donde encontró a Carl Friedrich Gauss, el aclamado por todos “Príncipe de las Matemáticas”, uno de los mayores matemáticos de todos los tiempos. Incluso hoy, si hacemos una selección por expertos para distinguir a los matemáticos más grandes de la Historia, aparecerá indudablemente Euclides, Arquímedes, Newton y Gauss.

Los estudios de Riemann no fueron un camino de rosas precisamente.  Alemania sacudida por disturbios, manifestaciones y levantamientos, fue reclutado en el cuerpo de estudiantes para proteger al rey en el palacio real de Berlín y sus estudios quedaron interrumpidos.

En aquel ambiente, el problema que captó el interés de Riemann fue el colapso que, según el pensaba, suponía la geometría euclidiana, que mantiene que el espacio es tridimensional y “plano” (en el espacio plano, la distancia más corta entre dos puntos es la línea recta; lo que descarta la posibilidad de que el espacio pueda estar curvado, como en una esfera).

Para Riemann, la geometría de Euclides era particularmente estéril cuando se la comparaba con la rica diversidad del mundo. En ninguna parte veía Riemann las figuras geométricas planas idealizadas por Euclides. Las montañas, las olas del mar, las nubes y los torbellinos no son círculos, triángulos o cuadrados perfectos, sino objetos curvos que se doblan y retuercen en una diversidad infinita. Riemann, ante aquella realidad, se rebeló contra la aparente precisión matemática de la geometría griega, cuyos fundamentos, descubrió él, estaban basados en definitiva sobre las arenas movedizas del sentido común y la intuición, no sobre el terreno firme de la lógica y la realidad del mundo.

Euclides nos habló de la obviedad de que un punto no tiene dimensión.  Una línea tiene una dimensión: longitud. Un plano tiene dos dimensiones: longitud y anchura. Un sólido tiene tres dimensiones: longitud, anchura y altura. Y allí se detiene. Nada tiene cuatro dimensiones, incluso Aristóteles afirmó que la cuarta dimensión era imposible. En Sobre el cielo, escribió: “La línea tiene magnitud en una dirección, el plano en dos direcciones, y el sólido en tres direcciones, y más allá de éstas no hay otra magnitud porque los tres son todas”. Además, en el año 150 d. C. el astrónomo Ptolomeo de Alejandría fue más allá de Aristóteles y ofreció, en su libro sobre la distancia, la primera “demostración” ingeniosa de que la cuarta dimensión es imposible.

En realidad, lo único que Ptolomeo demostraba era que era imposible visualizar la cuarta dimensión con nuestros cerebros tridimensionales (de hecho, hoy sabemos que muchos objetos matemáticos no pueden ser visualizados, aunque puede demostrarse que en realidad, existen). Ptolomeo puede pasar a la Historia como el hombre que se opuso a dos grandes ideas en la ciencia: el sistema solar presidido por la Tierra y la cuarta dimensión.

La ruptura decisiva con la geometría euclidiana llegó cuando Gauss pidió a su discípulo Riemann que preparara una presentación oral sobre los “fundamentos de la geometría”. Gauss estaba muy interesado en ver si su discípulo podía desarrollar una alternativa a la geometría de Euclides.

Riemann desarrolló su teoría de dimensiones más altas. Él como algunos artistas, veía el mundo de otra manera.

Finalmente, cuando hizo su presentación oral en 1.854, la recepción fue entusiasta. Visto en retrospectiva, esta fue, sin discusión, una de las conferencias públicas más importantes en la historia de las matemáticas. Rápidamente se entendió por toda Europa la noticia de que Riemann había roto definitivamente los límites de la geometría de Euclides que había regido las matemáticas durante dos milenios.

Riemann creó su tensor métrico para que, a partir de ese momento, otros dispusieran de una poderosa herramienta que les hacía posible expresarse, a partir del famoso teorema de Pitágoras (uno de los grandes descubrimientos de los griegos en matemáticas que establece la relación entre las longitudes de los tres lados de un triángulo rectángulo: afirma que la suma de los cuadrados de los lados menores es igual al cuadrado del lado mayor, la hipotenusa; es decir, si a y b son los longitudes de los dos catetos, y c es la longitud de la hipotenusa, entonces a² + b² = c².  El teorema de Pitágoras, por supuesto, es la base de toda la arquitectura; toda estructura construida en este planeta está basada en él. Claro que, es una herramienta para utilizar en un mundo tridimensional).

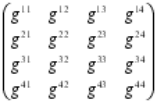
El tensor métrico de Riemann, o N dimensiones, fue mucho más allá y podemos decir que es el teorema para dimensiones más altas con el que podemos describir fenómenos espaciales que no son planos, tales como un remolino causado en el agua o en la atmósfera, como por ejemplo también la curvatura del espacio en presencia de grandes masas. Precisamente, el tensor de Riemann permitió a Einstein formular su teoría de la gravedad y posteriormente lo utilizo Kaluza y Klein para su teoría en la quinta dimensión de la que años más tarde se derivaron las teorías de super-gravedad, supersimetría y, finalmente, las supercuerdas.

Para asombro de Einstein, cuando tuvo ante sus ojos la conferencia de Riemann de 1.854 que le había enviado su amigo Marcel Grossman, rápidamente se dio cuenta de que allí estaba la clave para resolver su problema.  Descubrió que podía incorporar todo el cuerpo del trabajo de Riemann en la reformulación de su principio. Casi línea por línea, el gran trabajo de Riemann encontraba su verdadero lugar en el principio de Einstein de la relatividad general. Esta fue la obra más soberbia de Einstein, incluso más que su celebrada ecuación E = mc². La reinterpretación física de la famosa conferencia de Riemann se denomina ahora relatividad general, y las ecuaciones de campo de Einstein se sitúan entre las ideas más profundas de la historia de la ciencia.

No sería justo reconocer aquí que Riemann, tiene mucho que ver en ese gran logro de Einstein (Relatividad General), y de toda la física en lo que a la geometría de espacios curvos se refiere…

emilio silvera

 « Si la respuesta es…¡El Universo! ¿Cuál es la pregunta?

Seguramente… ¿Qué es lo que todo lo contiene? Los pensamientos también,

 

 

¡Es todo tan complicado! »

La complejidad nos rodea y está presente en la Naturaleza. Nosotros mismos, ¡llevamos consigo tanta!

Hablemos ahora de un personaje singular que, siendo muy buen físico, tuvo que soportar unas condiciones de vida bastante duras y, postergado a una silla mecánica y sin poder expresar sus pensamientos de manera directa, ha tenido que recurrir a tecnologías avanzadas que le permitiera comunicarse con el mundo, desde su mundo que estaba fuera de éste nuestro.

     Hawking con su primera Esposa.

¿Quién no conoce al personaje y no ha leído, al menos, uno de sus libros? Hawking es un pensador arriesgado. Siempre ha estado mucho más dispuesto que la mayoría de sus colegas físicos a emprender el vuelo en direcciones radicalmente nuevas, si dichas direcciones “olían” bien. Un ejemplo es el del Horizonte absoluto en los agujeros negros que “sonaba” bien para él, así que lo aceptó a pesar de su naturaleza radical, y su aceptación tuvo recompensa.

En pocos meses Hawking y James Hartle fueron capaces de derivar, a partir de las leyes de la relatividad general de Einstein, un conjunto de ecuaciones elegantes que describen como el horizonte absoluto se expande y cambia su de manera continua y suave, anticipándose a los residuos o a las ondas gravitatorias que éste engulle o anticipándose a ser atraído por la gravedad de otros cuerpos.

La osadía de éste físico, del personaje, quedó patente cuando realizó aquellas declaraciones que salieron en la prensa y medios de casi todo el mundo:  “El físico británico Stephen Hawking realizó unas curiosas declaraciones el Discovery Channel,  en las que afirmaba que la vida extraterrestre  “casi seguramente sí existe” ,  muy probablemente como vida a nivel celular y en menor medida pero también, como vida inteligente.  Además dice verlo como algo perfectamente racional.

Por  otra parte, aconsejó que los humanos no buscasen (como sucede con el proyecto SETI) mantener relaciones con ellos, ya que algunos podrían ser hostiles y saldríamos perjudicados. A muchos les ha sorprendido que el científico acudiese a la comparación con la llegada de Colón al “Nuevo Mundo” y como afectó a los indígenas. Realmente Hawking, no aludió más que a una teoría del encuentro entre civilizaciones que explica que ante un encuentro entre dos o más civilizaciones,  siempre tiende a perder más, la civilización menos evolucionada (la cual, en un encuentro con una civilización extraterrestre avanzada, sería nuestro caso).”

Sus numerosas publicaciones incluyen La Estructura a Gran Escala del Espacio-tiempo con G. F. R. Ellis, Relatividad General: Revisión en el Centenario de Einstein con W. Israel, y 300 Años de Gravedad, con W. Israel. Stephen Hawking ha publicado tres libros de divulgación: su éxito de ventas “Breve historia del tiempo” (Historia del tiempo: del Big Bang a los agujeros negros), Agujeros negros y pequeños universos y otros ensayos, en 2001 “El universo en una cáscara de nuez”, en 2005 “Brevísima historia del tiempo”, una versión de su libro homónimo adaptada un público más amplio.

Allá por el mes de noviembre de 1970, Stephen Hawking empezó a dar grandes pasos como físico. Ya había hecho varios descubrimientos importantes, pero todavía no era una figura destacada. No pocos nos hemos podido preguntas: ¿Cómo,  con esa grave incapacidad, ha sido capaz Hawking de superar en pensamiento e intuición a sus destacados colegas competidores, personas como Roger Penrose, Werner Israel  y también (entre otros), Yakog Borisovich Zel´dovich?

Ellos pueden hacer uso de sus manos, podían dibujar y hacer esquemas, realizar cálculos con lápiz y papel de muchas páginas de longitud -cálculos de cuyo desarrollo uno registraba muchos resultados complejos intermedios, y luego vuelve atrás, los toma uno a uno y los amplía obtener un resultado final; cálculos que es difícil concebir que alguien sea capaz de hacer en su cabeza. Para comienzos de los años setenta, las manos de Hawking estaban básicamente paralizadas; no podía ya hacer dibujos ni escribir para desarrollar ecuaciones. Su investigación tenía que desarrollarse enteramente en su cabeza.

                                      Miles de personas le despidieron en Cambridge

En marzo de 1959 Hawking se presentó a las convocatorias de becas con el propósito de estudiar Ciencias Naturales en Oxford; consigue una beca, y se licencia en Física en 1962. Desde Oxford, Hawking se trasladó a Cambridge para la investigación en relatividad general y cosmología; unas áreas difíciles alguien con poca base matemática. En aquel tiempo, Hawking había notado que se había vuelto más torpe y físicamente débil, y en la Navidad de 1962 su madre lo convenció para que viese a un médico.

A principios de 1963, pasó dos semanas haciéndose pruebas en el hospital, donde le diagnosticaron una enfermedad neuronal motora: la esclerosis lateral amiotrófica o enfermedad de Lou Gehrig. Su estado se deterioró rápidamente y los médicos le pronosticaron que no viviría lo suficiente para acabar su doctorado. Sin embargo, Hawking escribió:  “Aunque había una sobre mi futuro, descubrí para mi sorpresa que estaba disfrutando la vida en el presente más de lo que lo había hecho antes. Empecé a avanzar en mi investigación”

En su libro “Agujeros negros y pequeños universos” y otros ensayos , editado en 1993, afirmó:  “La ciencia podría afirmar que el universo tenía que haber conocido un comienzo (…) A muchos científicos no les agradó la idea de que el universo hubiese tenido un principio de creación”.  “En el universo primitivo está la respuesta a la pregunta fundamental sobre el origen de todo lo que vemos hoy, incluida la vida”

Puesto que la pérdida de control de sus manos fue lenta, Hawking tuvo tiempo para adaptarse. Ha entrenado su mente poco a poco para pensar de una forma diferente de como lo hacen las mentes de los otros físicos: piensa con nuevos tipos de imágenes intuitivas y ecuaciones mentales que, para él, han reemplazado a las ecuaciones y los dibujos y ecuaciones escritas con papel y lápiz. Las imágenes y las ecuaciones mentales de Hawking han resultado ser más potentes que las viejas imágenes de lápiz y papel para cierto tipo de problemas, y menos potentes para otros, y él a aprendido poco a poco a concentrarse en problemas para los que sus nuevos métodos dan una potencia mayor, una potencia que nadie puede empezar a igualar.

                                           Personaje mediático, ha sido agasajado de mil maneras

Alrededor del año 2004 propuso su nueva teoría acerca de las “simas o agujeros negros” un término que por lo general se aplica a los restos de estrellas que sufrieron un colapso gravitacional después de agotar todo su combustible nuclear. Según Hawking, el universo está prácticamente lleno de “pequeños agujeros negros” y considera que estos se formaron del material original del universo.

Ha declarado acerca del origen del universo:

“En la teoría clásica de la relatividad general […] el principio del universo que debió ser una singularidad de densidad y curvatura del espacio-tiempo infinitas. En esas circunstancias dejarían de regir todas las leyes conocidas de la física (…) Mientras más examinamos el universo, descubrimos que de ninguna manera es arbitrario, sino que obedece ciertas leyes bien definidas que funcionan en diferentes campos. Parece muy razonable suponer que haya principios unificadores, de modo que todas las leyes sean de alguna ley mayor”

 

La discapacidad de Hawking le ha ayudado de otras maneras. Como él mismo ha comentado a menudo, le ha liberado de la responsabilidad de dar clases a los estudiantes universitarios, y por ello ha tenido mucho más tiempo libre para investigar del que han podido tener sus colegas más sanos. Más importante quizá, es que su enfermedad ha mejorado en algunas formas su actitud ante la vida.

Hawking contrajo el ALS en 1963, poco después de que comenzara los estudios de postgrado en la Universidad de Cambridge. El ALS es el global para una variedad de enfermedades neuronales motoras, la mayoría de las cuales llevan rápidamente a la muerte. Creyendo que sólo le quedaban unos pocos años de vida, Hawking perdió inicialmente su entusiasmo por la vida y la física. Sin embargo, para el invierno de 1964-65 se hizo evidente que la suya era una variación extraña de ALS, una variante que mina el control del sistema nervioso central sobre los músculos a lo largo de muchos años de tiempo, y no sólo en unos pocos. Repentinamente la vida le parecía maravillosa. Regreso a la física con mayor vigor y entusiasmo que cuando era un estudiante de licenciatura.

 

Se casó con Jane Wilde, a quien había conocido después de contraer el ALS y de quien se había enamorado durante la primera fase de su enfermedad. El matrimonio de Stephen y Jane (sin ningún género de dudas) fue esencial su éxito y su felicidad en los años sesenta y setenta y entrando en los ochenta.

Hawking ha trabajado en las leyes básicas que gobiernan el Universo. Junto con Roger Penrose mostró que la Teoría General de la Relatividad de Einstein implica que el Espacio y el Tiempo han de tener un principio en el Big Bang y un final dentro de agujeros negros. Semejantes resultados señalan la necesidad de unificar la Relatividad General con la Teoría Cuántica, el otro gran desarrollo científico de la primera mitad del siglo XX. Una consecuencia de tal unificación que él descubrió era que los agujeros negros no eran totalmente negros, sino que podían emitir radiación y eventualmente evaporarse y desaparecer. Otra conjetura es que el universo no bordes o límites en el tiempo imaginario. Esto implicaría que el modo en que el universo empezó queda completamente determinado por las leyes de la ciencia.

Hawking perdió el uso de sus miembros y más tarde, más lentamente, el de su voz. En junio de 1965, él andaba con la ayuda de un bastón y ya su voz era algo temblorosa. En 1970 necesitaba un apoyo de cuatro patas. En 1972 estaba ya confinado en una silla de ruedas motorizada y habría perdido ya, básicamente, la capacidad de escribir, pero aun, con dificultad, podía alimentarse. En 1975 ya no podía alimentarse por sí mismo, y solo las personas muy acostumbradas a su habla podían entenderlo. En 1981, ni las personas más cercanas podían ya entenderlo. En 1985 sus pulmones ya no podían drenar y tuvo que ser sometido a complicadas operaciones. El precio fue alto: perdió completamente su voz. Para compensarlo, adquirió un sintetizador de voz controlado por ordenador con un acento norteamericano por el que él se disculpaba tímidamente. Ver como por ese medio llega a construir las frases es, al menos penoso, no podía producir más de una frase corta por minuto, sin embargo, tales dificultades se ven compensadas cuando, las frases son enunciadas claramente por el sintetizador, y con frecuencia son perlas.

Sí, a pesar de todos los inconvenientes físicos del personaje, ¿Qué duda cabe de que supo, alcanzar la felicidad en su vida privada y triunfó en el ámbito profesional? El mérito de Stephen no siempre es reconocido en toda su grandeza. Sus logros en el campo de la Física son importantes y su historial se puede leer en cualquier .

Él también fue joven como todos nosotros y, a pesar de la enorme prueba que tuvo que superar, ha logrado todo lo que un ser humano puede alcanzar durante una vida tan corta como la que se nos da. Aquí, en este humilde lugar, le hacemos hoy un reconocimiento a todos sus logros y, sobre todo, expresamos nuestra inmensa admiración por el valor demostrado ante la vida, ya que, en sus circunstancias, no todos habrían podido superarla.

Como a él le gusta hacer, de vez en cuando apabulla a sus colegas con ideas que… ¡Son verdaderamente sorprendentes! La última es que ha declarado que: ¡Los agujeros negros no existen! Lástima que en los últimos tiempos lo estén utilizando como objeto de negocio.

¡Qué personaje!

emilio silvera