Nov
1
¡Simetría! Una guía para descubrir
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en General ~
Clasificado en General ~
 Comments (0)
Comments (0)
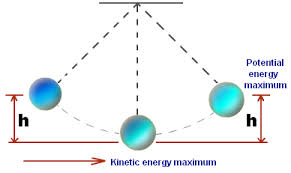
La simetría esférica de los planetas
La simetría es una propiedad universal tanto en la vida corriente, un punto de vista matemático como desde el quehacer de la Física Teórica. En realidad, lo que observamos en la vida corriente es siempre lo repetitivo, lo simétrico, lo que se puede relacionar entre sí por tener algo común.
En un sentido dinámico, la simetría podemos entenderla como lo que se repite, lo reiterativo, lo que tiende a ser igual. Es decir, los objetos que, por mantener la misma geometría, son representativos de otros objetos. En el Caos matemático encontramos concepción de la simetría en el mundo los fractales. Sin embargo, la simetría es mucho más.
Encontramos simetrías en las galaxias espirales, en los cúmulos globulares de estrellas, en las Nebulosas planetarias, y, hasta en los agujeros negros.
Cuando miro en mi diccionario de Física la palabra Simetría, lo que me dice es:
“Conjunto de invariancias de un sistema. Al aplicar una transformación de simetría sobre un sistema, el sistema queda inalterado, la simetría es estudiada matemáticamente usando teoría de grupos. Algunas de las simetrías son directamente físicas. Algunos ejemplos son las reflexiones y las rotaciones en las moléculas y las translaciones en las redes cristalinas. Las simetrías pueden ser discretas (es decir, cuando hay un finito de transformaciones de simetría), como el conjunto de rotaciones de una molécula octaédrica, o continuas (es decir, cuando no hay número finito), como el conjunto de rotaciones de un átomo o núcleo. Existen simetrías más generales y abstractas, como la invariancia CTP y las simetrías asociadas a las teorías gauge.”
Son eminencias niponas de nombres difíciles de pronunciar para nosotros. Estos tres hombres, uno de ellos nacionalizado estadounidense, han sido galardonados con el Premio Nobel de Física. Sus teorías sobre las simetrías rotas.
También podemos hablar de simetría rota y de supersimetrías. Durante los últimos tiempos, los Físicos han elevado los principios de simetría al más alto nivel en la escala de lo que podemos entender por una explicación. Cuando encontramos una Ley propuesta de la Naturaleza, una pregunta se nos viene a la mente: ¿por qué ley? ¿Por qué la relatividad especial y la general? ¿Por qué el electromagnetismo de Maxwell? ¿Por qué las teorías de Yang-Mills de las fuerzas nucleares fuerte y débil?
Claro que, una respuesta de importancia es que, las teorías hacen predicciones que han sido repetidamente conformadas con precisos experimentos, con diversidad de científicos y lugares y que, siempre, en todos los casos, dieron el mismo resultado. Esto, por supuesto, es la base de la confianza esencial que los físicos tienen en esas teorías.
Las partículas son simétricas
Claro que, se deja fuera algo esencial: Los físicos creen también que están en el camino correcto porque, de algún modo que no pueden explicar, tienen la convicción de que son correctas, y las ideas de simetría son esenciales para esa intuición. Se presiente que es correcto que ningún lugar del Universo es especial comparado con cualquier otro lugar del Universo, así que los físicos tienen la confianza de que la simetría de traslación debería estar las simetrías de las leyes de la Naturaleza. Se presiente que es correcto que ningún movimiento a velocidad constante es especial comparado con cualquier otro. De modo que los físicos tienen confianza en que la relatividad especial, al abrazar plenamente la simetría entre todos los observadores con velocidad constante, es una esencial de las leyes de la Naturaleza.
Los hongos atómicos también guardan cierta simetría
Así que las simetrías de la Naturaleza no son meras consecuencias de las leyes de la Naturaleza. Desde nuestra perspectiva moderna, las simetrías son la base de la que manan las leyes y, siendo así (que lo es), cuando un físico observa una simetría, agudiza su atención, ya que, allí, en aquel lugar, podría encontrarse alguna ley de la Naturaleza que siguiendo aquella presencia, se podría .
Más allá de su papel en dar a las leyes que gobiernan las fuerzas de la Naturaleza, las ideas de simetría son vitales para el propio concepto del tiempo. Nadie ha sabido encontrar todavía definición fundamental y definitiva del tiempo. Sin embargo, es indudable que el papel del tiempo en la constitución del cosmos es llevar una especie de de los sucesos y acontecimientos que en el universo ocureren: Nace una estrella, se forma una nueva galaxia, explota una supernova, muere una estrella masiva y surge un agujero negro…
Bueno… ¡No siempre es así!
Reconocemos el transcurrir del tiempo al mirar y ver que, las cosas, no son iguales hoy que lo fueron ayer. Con el transcurrir del tiempo todo cambia y nada permanece. ¿Será el tiempo otra simetría? Debe serlo, ya que, ningún cambio le afecta y, su transcurrir queda inalterado por mucho camino que pudiera haber recorrido y, eso, lo hace diferente de todo lo demás: Todo cambia excepto el tiempo.
Así, tenemos que llegar a la conclusión de que, el concepto de simetría es, para los Físicos, indispensable como punto de referencia en el descubrimiento de las teorías que más tarde, llegan a convertirse en leyes de la Naturaleza al comprobarse que, son inalterables: Otra vez la Simetría. El desarrollo de la moderna teoría cosmológica, por ejemplo, tiene mucho que ver con la simetría. El significado del Tiempo, su aplicabilidad al universo en su conjunto, la forma global del espacio, e incluso el marco subyacente de la relatividad especial, todo descansa sobre fundamentos de simetría.
En la escuela todos aprendemos las famosas leyes de la conservación. La energía se conserva; no se crea ni se destruye, solo se transforma. La materia también se conserva. El movimiento (momento) también. La conservación de estas y otras propiedades son leyes elementales del universo que se observan tanto en las cosas de nuestro día a día, como en las estrellas brillando en los confines del cosmos. No hay explicación de por qué, simplemente es así.
O al menos eso creíamos…
Este año se cumplen 100 años de revelación de una idea extraordinaria. El 23 de Julio de 1918 el mundo conoció un teorema que desbancó la idea de que las leyes de conservación simplemente existen. Gracias a ese descubrimiento, ahora entendemos de dónde vienen y por qué están ahí. Este acontecimiento no solo es notable por su impacto científico, sino por la persona que lo postuló: Emmy Noether.
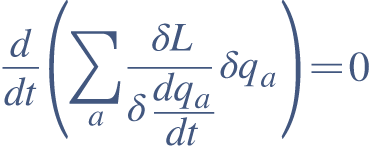
La simetría de las ecuaciones en el espacio implica la conservación de movimiento (momento). La simetría con respecto al tiempo implica la conservación de la energía. La simetría con respecto a rotaciones implica la conservación del momento angular. Y así la conservación de la carga eléctrica, la presión, el color cuántico y otras propiedades tienen simetrías correspondientes de las cuales se originan. Es por esto que el Teorema de Noether es más fundamental que cualquier ley de conservación.
Para entender esta afirmación es importante saber que desde hacía tiempo los académicos habían notado que las ecuaciones que describen la naturaleza exhiben algunas simetrías. Por ejemplo, las ecuaciones de movimiento son simétricas con respecto al espacio, lo cual quiere decir que funcionan igual sin importar el lugar. También son simétricas con respecto el tiempo, es decir que funcionan igual si el experimento se hace hoy, mañana o en mil años.
Emmy Noether se detuvo a reflexionar sobre estas simetrías. ¿Qué implican? En un tour-de-force matemático, utilizando las más avanzadas técnicas que incluyen lagrangianos, teoría de grupos, álgebra abstracta y cálculo, su privilegiada mente logró comprobar rigurosamente, en páginas y páginas de elegantes ecuaciones, que cada simetría del universo necesariamente implica que una cantidad debe permanecer constante.
Durante el último siglo un concepto muy importante en Física, sobre todo en Mecánica Cuántica, ha sido y es el de simetría. Uno de los resultados más bonitos de la Física dice que allá donde hay una simetría hay una cantidad conservada. Es lo que se llama teorema de Noether. De este modo, las leyes de la Física pueden ser iguales bajo una u otra simetría y para cada uno de esos casos se conservará algo. Así por ejemplo, la simetría de traslación temporal corresponde a una cantidad conservada: la energía. También ocurre que las leyes de la física son las mismas bajo unas transformaciones de rotación en el espacio tridimensional y eso significa que se conserva el angular.
Allí donde veámos presente la simetría, debemos prestar atención, ya que, podría ser el indicio de que algo importante se podría derivar de esa simetría presente que, en física, hemos comentado, es un principio de gran importancia.

No podemos olvidarnos que, en la Naturaleza nos encontramos con simetrías por todas partes. La simetría te rodea en la naturaleza. Si dibujas una línea a lo largo del centro de una hoja, vas a ver que la mitad izquierda tiene forma parecida a la derecha. Decimos que las dos mitades de la hoja son simétricas. Si miras las flores, vas a ver que ellas son simétricas.Encontramos simetría en la cara humana y en las hojas de los árbolesLa simetría Biológica del Universo es grandeDeberíamos pararnos a pensar en todo esto y lo que se esconde detrás de la simetría presente por todo el Universo, los físicos dicen que es una razón para descubrir, y, creo que llevan razón.
















 Totales: 74.966.098
Totales: 74.966.098 Conectados: 65
Conectados: 65