Nov
16
Pero…, ¿comprender la Naturaleza? ¿Podremos?
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en General ~
Clasificado en General ~
 Comments (0)
Comments (0)
No siempre podemos dar una explicación cierta de lo que podemos captar con nuestros modernos aparatos tecnológicos que nos traen los más dispares y exóticos objetos y sucesos del espacio “infinito”. Lo cierto es que hemos avanzado y podemos dar alguna que otra explicación (muchas veces aproximada) de lo que ocurre ahí fuera. Sin embargo, hay muchas cosas que se nos escapan y de las que no podemos dar explicación alguna. Las preguntas son más abundantes que las respuestas.
Tratándo de saber, nos sumergimos en los complejos laberintos de las matemáticas, esas estructuras numéricas que el hombre ha sabido inventar para buscar respuestas de lo que no sabe y, partiendo de lineas finitas de puntos relacionados por reglas, pasando por las geometrías, sistemas de recuento como la aritmética de los números enteros, más tarde fracciones, luego decimales y otras estructuras más complejas y grupos y así, sucesivamente y avanzando y subiendo indefinidamente, en una escala ascendente de complejidad que nos ha llevado a matemáticas topológicas cuya inmensa complejidad ponen de punta los pelos de las cejas de los físicos y, todo ello, para buscar una respuesta que no logramos alcanzar.
Y, mientras tanto, el tiempo transcurre inexorable sin que nuestra búsqueda llegue a su fin
Hemos llegado a poder conocer el significado de inmensas y diminutas estructuras que son creadas en el Universo sin cesar. Unas llegan y otras se van, siempre, acompañadas por un tiempo sin fin. Nosotros que tratamos de comprender todo eso, buscamos el significado más profundo de todas esas estructras y, a veces, nos preguntamos cuál de esas estructuras puede describir de una forma completa cómo pudieron surgir los seres conscientes que ahora, tratan de buscar esas respuestas que, tan lejos están para ellos que, en realidad, parecen inalcanzables y, sin embargo…
Hemos podido llegar a tomar axiomas de algunos sistemas lógicos, y luego desarrollamos poco a poco todas las “verdades” que pueden ser deducidas a partir de ellos, utilizando las reglas de deducción prescritas, podemos llegar a vislumbrar una gran madeja de verdades lógicas extendidas ante nosotros. Si esa madeja de verdad nos lleva finalmente a estructuras que puedan describir completamente eso que nosotros llamamos “consciencia”, entonces podríamos decir que “está viva”, en cierto sentido. Claro que, no sabemos en qué sentido lo estaría.
Al no poder llegar a comprender esas estructuras de las que hablamos, nuestra imaginación inagotable en la búsqueda de nuevos caminos que nos conduzcan hasta las respuestas, ha ideado algunas formas y maneras de profundizar y, una de ellas, es la de crear modelos y simulaciones por ordenador, por ejemplo, del proceso mediante el que se forman las estrellas y planetas. Esto es algo que los astrónomos se afanan en hacer. La formación de estrellas es demasiado complicada de entender con todo detalle si utilizamos sólo lápiz y papel y el cálculo humano directo. Se necesita una rápida solución por ordenador de las ecuaciones que la gobiernan.
Algunas de esas simulaciones son extraordinariamente precisas. describen cómo se forman las estrellas y generan descripciones de planetas que encajan muy estrechamente con las observaciones que hacemos a través de nuestros sofísticados telescopios. Algunos científicos entusiastas, sugieren que vayamos más lejos e introduzcamos en el ordenador montones de información sobre bioquímica y geología de modo que podamos seguir las predicciones del ordenador sobre la temprana evolución química de un planeta y su atmósfera. Cuando se hace esto los resultados son muy interesantes.
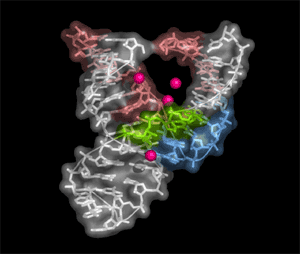
El ordenador describe la formación de moléculas auto-replicantes que empiezan a competir entre sí y a hacer cosas complicadas sobre la superficie joven del planeta. Aparecen hélices de ADN y empiezan a formar las bases de replicantes genéticos. La selección empieza a tener un impacto y los replicantes mejor adaptados se multiplican y mejoran rápidamente, extendiendo sus proyectos por toda la superficie habitable. El programa del ordenador sigue ejecutándose más y más tiempo. Finalmente, parece que algunas estructuras del programa están enviando señales a otras y almacenando información. Han desarrollado un sencillo código y lo que podríamos llamar una aritmética, que se basa en la simetría (octolateral) que poseen los replicantes más grandes. Los programadores están fascinados por este comportamiento, sin haber sospechado nunca que todo eso pudiera surgir de su programa original que ahora, parece haberse transformado, de tal manera que produce la sensación de que “tiene vida propia”.

Esta pequeña fantasía muestra de qué forma es concebible que el comportamiento que podríamos estimar consciente pudiera emerger de una simulación por ordenador. Pero si preguntamos dónde “está” este comportamiento consciente parece que nos vemos empujados a decir que vive en el programa. Es parte del software que se está ejecutando en la máquina. Consiste en una colección de deducciones muy complejas (“teoremas”) que se siguen de las reglas de partida que definen la lógica de la programación. Esta vida “existe” en el formalismo matemático.
En alguna parte he leído que:
“La ilusión de la creación libre de las propiedades de la situación y, por ello, de los fines de la acción, encuentra probablemente una aparente justificación en el círculo, característico de toda simulación condicional que pretende que el habitus sólo puede producir la respuesta objetivamente inscrita en su «fórmula» porque concede a la situación su eficacia de resorte, constituyéndola según sus principios, es decir, haciéndola existir como cuestión pertinente por referencia a una manera particular de interrogar la realidad.”
Y, si eso es así (que lo es), nos podríamos preguntar: ¿Cómo estaremos seguros de las respuestas que obtenemos de programas que realizan las funciones determinadas por las instrucciones que nosotros mismos le hemos dado? Como nosotros no somos infalibles, es lógico pensar que, todo esto nos lleva a obtener respuestas incompletas pero que, cada vez, se acercan más a la realidad.
Pensando en todo esto, caigo en la cuenta de que hay cosas que no podemos explicar. Por ejemplo: Debido a su falta de voluntad para esforzarse con la misma intensidad en el estudio de los clásicos que en el de la ciencia y las matemáticas, Turing suspendió sus exámenes finales varias veces y tuvo que ingresar en la escuela universitaria que eligió en segundo lugar, King’s College, Universidad de Cambridge, en vez de en la que era su primera elección, Trinity. Recibió las enseñanzas de Godfrey Harold Hardy (¿os acordáis, aquel que ayudo a Ramanujan?), un respetado matemático que ocupó la cátedra Sadleirian en Cambridge y que posteriormente fue responsable de un centro de estudios e investigaciones matemáticas de 1931 a 1934.
En 1935 Turing fue nombrado profesor del King’s College. En su memorable estudio “Los números computables, con una aplicación al Entscheidungsproblem” (publicado en 1936), Turing reformuló los resultados obtenidos por Kurt Gödel en 1931 sobre los límites de la demostrabilidad y la computación, sustituyendo al lenguaje formal universal descrito por Gödel por lo que hoy se conoce como Máquina de Turing, unos dispositivos formales y simples. Demostró que dicha máquina era capaz de implementar cualquier problema matemático que pudiera representarse mediante un algoritmo.
Las máquinas de Turing siguen siendo el objeto central de estudio en la teoría de la computación. Turing trabajó desde 1952 hasta que falleció en 1954 en la biología matemática, concretamente en la morfogénesis. Publicó un trabajo sobre esta materia titulado “Fundamentos Químicos de la Morfogénesis” en 1952. Su principal interés era comprender la filotaxis de Fibonacci, es decir, la existencia de los números de Fibonacci en las estructuras vegetales. Utilizó ecuaciones de reacción-difusión que actualmente son cruciales en el campo de la formación de patrones.
Controlar los pensamientos y sensaciones…
Parece increíble como a veces, no podemos controlar los pensamientos y, comienzas a realizar un trabajo que toma sus propios derroteros a medida que avanzas y te llegan nuevas ideas que son producto de los temas que tratas de estructurar. Así, nuestras mentes, como la máquina simuladora de la creación de estrellas, o, del comportamiento de las moléculas en esos mundos imaginados, toman unos derroteros que no siempre podemos explicar. ¿Cómo llegue a Turing?
¡Sabemos tan poco de nosotros mismos! Y, sin embargo, nada nos arredra y buscamos esas respuestas a preguntas que nadie ha sabido contestar como, por ejemplo: ¿Qué es la consciencia? ¿Qué es el Tiempo? ¿Quiénes somos nosotros? ¿Cómo llegamos aquí? ¿Estamos solos en el inmenso Universo?
emilio silvera
Nov
16
¿Qués es la luz? hace 340 años que supimos de su velocidad
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en General ~
Clasificado en General ~
 Comments (0)
Comments (0)
En estos lugares se vivía a base de antorchas y velas para alumbrar los lóbregos pasillos. En la actualidad, esos edificios medievales se alumbran por las noches para el turista.
Está claro que, los estudiosos de la época antigua y medieval estaban por completo a oscuras acerca de la naturaleza de la luz. Especulaban sobre que consistía en partículas emitidas por objetos relucientes o tal vez por el mismo ojo. Establecieron el hecho de que la luz viajaba en línea recta, que se reflejaba en un espejo con un ángulo igual a aquel con el que el rayo choca con el espejo, y que un rayo de luz se inclina (se refracta) cuando pasa del aire al cristal, al agua o a cualquier otra sustancia transparente.

Cuando la luz entra en un cristal, o en alguna sustancia transparente, de una forma oblicua (es decir, en un ángulo respecto de la vertical), siempre se refracta en una dirección que forma un ángulo menor respecto de la vertical. La exacta relación entre el ángulo original y el ángulo reflejado fue elaborada por primera vez en 1.621 por el físico neerlandés Willerbrord Snell. No publicó sus hallazgos y el filósofo francés René Descartes descubrió la ley, independientemente, en 1.637.
Los primeros experimentos importantes acerca de la naturaleza de la luz fueron llevados a cabo por Isaac Newton en 1.666, al permitir que un rayo de luz entrase en una habitación oscura a través de una grieta e las persianas, cayendo oblicuamente sobre una cara de un prisma de cristal triangular. El rayo se refracta cuando entra en el cristal y se refracta aún más en la misma dirección cuando sale por una segunda cara del prisma. (Las dos refracciones en la misma dirección se originan por que los dos lados del prisma de se encuentran en ángulo en vez de en forma paralela, como sería el caso en una lámina ordinaria de cristal.)
Newton y sus experimentos con la luz
Cuando Newton empezó su lucha por establecer un método inductivo correcto en física, estaba trabajando en el campo de la óptica, no en cinemática o en astronomía. En sus primeros años, mucho antes de que los Principia le dieran la fama, llevó a cabo un estudio de la luz y los colores, un estudio que ha sido descrito como “la más excelsa investigación experimental del siglo XVII
Newton atrapó el rayo emergente sobre una pantalla blanca para ver el efecto de la refracción reforzada. Descubrió que, en vez de formar una mancha de luz blanca, el rayo se extendía en una gama de colores: rojo, anaranjado, amarillo, verde, azul, y violeta, en este orden.
Newton dedujo de ello que la luz blanca corriente era una mezcla de varias luces que excitaban por separado nuestros ojos para producir las diversas sensaciones de colores. La amplia banda de sus componentes se denominó spectrum (palabra latina que significa “espectro”, “fantasma”).

Newton llegó a la conclusión de que la luz se componía de diminutas partículas (“corpúsculos”), que viajaban a enormes velocidades.

Le surgieron y se planteó algunas inquietudes cuestiones. ¿Por qué se refractaban las partículas de luz verde más que los de luz amarilla? ¿Cómo se explicaba que dos rayos de luz se cruzaran sin perturbase mutuamente, es decir, sin que se produjeran colisiones entre partículas?
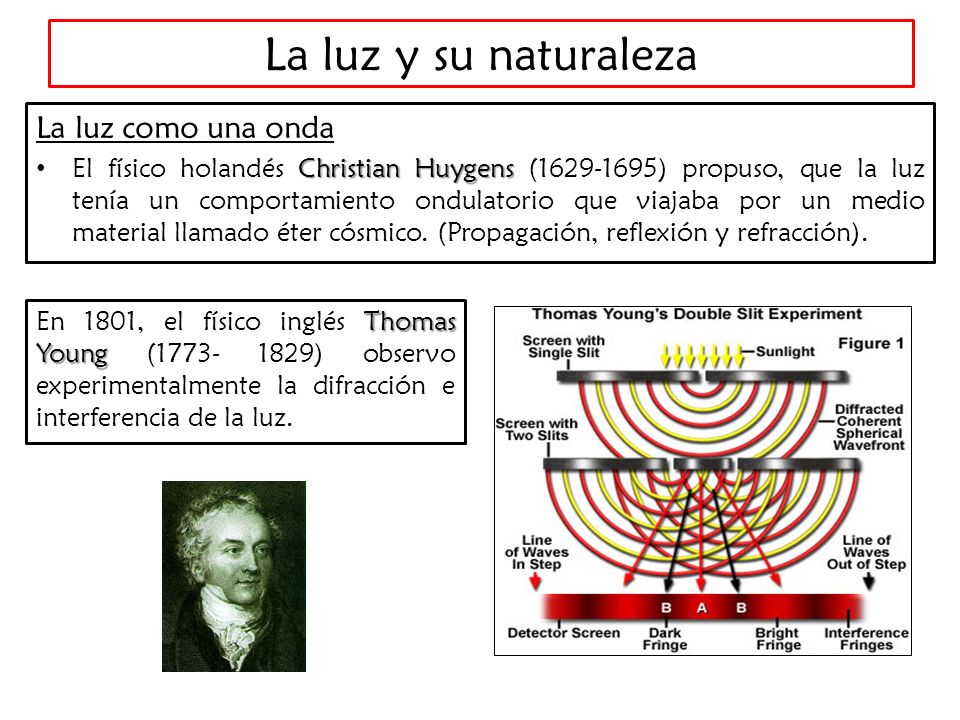
En 1.678, el físico neerlandés Christian Huyghens (un científico polifacético que había construido el primer reloj de péndulo y realizado importantes trabajos astronómicos) propuso una teoría opuesta: la de que la luz se componía de minúsculas ondas. Y si sus componentes fueran ondas, no sería difícil explicar los diversos difracciones de los diferentes tipos de luz a través de un medio refractante, siempre y cuando se aceptara que la luz se movía más despacio en ese medio refractante que en el aire. La cantidad de refracción variaría con la longitud de las ondas: cuanto más corta fuese tal longitud, tanto mayor sería la refracción. Ello significaba que la luz violeta (la más sensible a este fenómeno) debía de tener una longitud de onda mas corta que la luz azul, ésta, más corta que la verde, y así sucesivamente.

Lo que permitía al ojo distinguir los colores eran esas diferencias entre longitudes de onda. Y, como es natural, si la luz estaba integrada por ondas, dos rayos podrían cruzarse sin dificultad alguna. (Las ondas sonoras y las del agua se cruzan continuamente sin perder sus respectivas identidades.)
Pero la teoría de Huyqhens sobre las ondas tampoco fue muy satisfactoria. No explicaba por qué se movían en línea recta los rayos luminosos; ni por qué proyectaban sombras recortadas; ni aclaraba por qué las ondas luminosas no podían rodear los obstáculos, del mismo modo que pueden hacerlo las ondas sonoras y de agua. Por añadidura, se objetaba que si la luz consistía en ondas, ¿cómo podía viajar por el vacío, ya que cruzaba el espacio desde el Sol y las Estrellas? ¿cuál era esa mecánica ondulatoria?

Aproximadamente durante un siglo, contendieron entre sí estas teorías. La teoría corpuscular, de Newton, fue, con mucho, la más popular, en parte, porque la respaldó el famoso nombre de su autor. Pero hacia 1.801, un físico y médico ingles, de nombre Thomas Young, llevó a cabo un experimento que arrastró la opinión pública al campo opuesto. Proyectó un fino rayo luminoso sobre una pantalla, haciéndolo pasar antes por dos orificios casi juntos. Si la luz estuviera compuesta por partículas, cuando los dos rayos emergieran de ambos orificios, formarían presuntamente en la pantalla una región más luminosa donde se superpusieran, y regiones menos brillantes, donde no se diera tal superposición. Pero no fue esto lo que descubrió Young. La pantalla mostró una serie de bandas luminosas, separadas entre sí por bandas oscuras. Pareció incluso que, en esos intervalos de sombra, la luz de ambos rayos contribuía a intensificar la oscuridad.
Primera imagen de una partícula de luz
Sería fácil explicarlo mediante la teoría ondulatoria. La banda luminosa representaba el refuerzo presado por las ondas de un rayo a las ondas del otro. Dicho de otra manera: Entraba “en fase” dos trenes de ondas, es decir, ambos nodos, al unirse, se fortalecían el uno al otro. Por otra parte, las bandas oscuras representaban puntos en que las ondas estaban “desfasadas” porque el vientre de una neutralizaba el nodo de la otra. En vez de aunar sus fuerzas, las ondas se interferían mutuamente, reduciendo la energía luminosa neta a las proximidades del punto cero.
Considerando la anchura de las bandas y la distancia entre los dos edificios por los que surgen ambos rayos, se pudo calcular la longitud de las ondas luminosas, por ejemplo, de la luz roja a la violeta o los colores intermedios. Las longitudes de onda resultaron ser muy pequeñas. Así, la de la luz roja era de unos 0’000075 cm. (Hoy se expresan las longitudes de las ondas luminosas mediante una unidad muy práctica ideada por Angströn. Esta unidad, denominada, en honor a su autor Ángstrom (Á), es la cienmillonésima parte de un centímetro. Así, pues, la longitud de onda de la luz roja equivale más o menos a 7.500 Á, y la de la luz violeta, a 3.900 Å, mientras que las de colores visibles en el espectro oscilan entre ambas cifras.)
La cortedad de estas ondas es muy importante. La razón de que las ondas luminosas se desplacen en línea recta y proyecten sombras recortadas se debe a que todas son incomparablemente más pequeñas que cualquier objeto; pueden contornear un obstáculo sólo si éste no es mucho mayor que la longitud de onda. Hasta las bacterias, por ejemplo, tienen un volumen muy superior de una onda luminosa y, por tanto, la luz puede definir claramente sus contornos bajo el microscopio. Sólo los objetos cuyas dimensiones se asemejan a la longitud de la onda luminosa (por ejemplo, los virus y otras partículas submicroscópicas) son lo suficientemente pequeños como para que puedan ser contorneados por las ondas luminosas.
Un físico francés, Augustin-Jean Fresnel, fue quien demostró por vez primera, en 1.818, que si un objeto es lo suficientemente pequeño, la onda luminosa lo contorneará sin dificultad. En tal caso, la luz determina el llamado fenómeno de “difracción”. Por ejemplo, las finísimas líneas paralelas de una “reja de disfracción” actúan como una serie de minúsculos obstáculos, que se refuerzan entre si. Puesto que la magnitud de la difracción va asociada a la longitud de onda, se produce el espectro. A la inversa, se puede calcular la longitud de onda midiendo la difracción de cualquier color o porción del espectro, así como la separación de las marcas sobre el cristal.
A través de los rayos espectrales se supo de qué estaban hechas las estrellas y los objetos celestes
Fraunhofer exploró dicha reja de difracción con objeto de averiguar sus finalidades prácticas, progreso que suele olvidarse, pues queda eclipsado por su descubrimiento más famoso: los rayos espectrales. El físico americano Henry Augustus Rowlane ideó la reja cóncava y desarrolló técnicas para regularlas de acuerdo con 20.000 líneas por pulgada. Ello hizo posible la sustitución del prisma por el espectroscopio.
Ante tales hallazgos experimentales, más el desarrollo metódico y matemático del movimiento ondulatorio, debido a Fresnel, pareció que la teoría ondulatoria de la luz había arraigado definitivamente, desplazando y relegando para siempre a la teoría corpuscular.

La luz tiene una naturaleza dual: se comporta como onda y partícula. Entre las propiedades de la onda luminosa se incluyen la refracción de la onda cuando …
No sólo se aceptó las existencias de ondas luminosas, sino que también se midió su longitud con una precisión cada vez mayor. Hacia 1.827, el físico francés Jacques Babinet sugirió que se empleara la longitud de onda luminosa (una cantidad física inalterable) como unidad para medir tales longitudes, en vez de las muy diversas unidades ideadas y empleadas por el hombre. Sin embargo, tal sugerencia no se llevó a la práctica hasta 1.880 cuando el físico germano-americano Albert Abraham Michelson inventó un instrumento, denominado “interferómetro”, que podía medir las longitudes de ondas luminosas con una exactitud sin precedentes. En 1.893, Michelson midió la onda de la raya roja en el espectro del cadmio y determinó que su longitud era de 1/1.553.164 m.
Pero la incertidumbre reapareció al descubrirse que los elementos estaban compuestos por isótopos diferentes, cada uno de los cuáles aportaba una raya cuya longitud de onda difería ligeramente de las restantes. En la década de 1.930 se midieron las rayas del criptón 86. Como quiera que este isótopo fuera gaseoso, se podía abordar con bajas temperaturas, para frenar el movimiento atómico y reducir el consecutivo engrosamiento de la raya.
En 1.960, el Comité Internacional de Pesos y Medidas adoptó la raya del criptón 86 como unidad fundamental de longitud. Entonces se restableció la longitud de metro como 1.650.763’73 veces la longitud de onda de dicha raya espectral. Ello aumento mil veces la precisión de las medidas de longitud. Hasta entonces se había medido el antiguo metro patrón con un margen de error equivalente a una millonésima, mientras que en lo sucesivo se pudo medir la longitud de onda con un margen de error equivalente a una milmillonésima.
Ahora, después de todo esto, sabemos algo más sobre la luz.
Pero ¿Qué pasa con su velocidad?
¡Veámoslo!
Está claro que, la luz se desplaza a enormes velocidades. Si pulsamos el interruptor de apagado de la lámpara de nuestro salón, todo queda a oscuras de manera instantánea.
La velocidad del sonido es más lenta, por ejemplo, si vemos a un leñador que está cortando leña en un lugar alejado de nosotros, sólo oiremos los golpes momentos después de que caiga el hacha. Así, pues, el sonido tarda cierto tiempo en llegar a nuestros oídos. En realidad es fácil medir la velocidad de su desplazamiento: unos 1.206 km/h en el aire y a nivel del mar.
Galileo fue el primero en intentar medir la velocidad de la luz. Se colocó en lo alto de una colina, mientras que su ayudante, se situaba en otro lugar alto de la colina vecina; luego sacó una linterna encendida: tan pronto como su ayudante vio la luz, hizo una señal con otra linterna. Galileo repitió el experimento a distancias cada vez mayores, suponiendo que el tiempo requerido por su ayudante para responder mantendría una uniformidad constante, por lo cual, el intervalo entre la señal de su propia linterna y la de su ayudante representaría el tiempo empleado por la luz para recorrer cada distancia. Aunque la idea era lógica, la luz viajaba demasiado aprisa como para que Galileo pudiera percibir las sutiles diferencias con un método tan rudimentario.
Observaciones de Röemer
En 1.676, el astrónomo danés Olau Roemer logró cronometrar la velocidad de la luz a escala de distancias astronómicas. Estudiando los eclipses de Júpiter en sus cuatro grandes satélites, Roemer observó que el intervalo entre eclipses consecutivos era más largo cuando la Tierra se alejaba de Júpiter, y más corto cuado se movía en su órbita hacía dicho astro. Al parecer, la diferencia entre las duraciones del eclipse reflejaba la diferencia de distancias entre la Tierra y Júpiter. Y trataba, pues, de medir la distancia partiendo del tiempo empleado por la luz para trasladarse desde Júpiter hasta la Tierra. Calculando aproximadamente el tamaño de la órbita terrestre y observando la máxima discrepancia en las duraciones del eclipse que, según Roemer, representaba el tiempo que necesitaba la luz para atravesar el eje de al órbita terrestre, dicho astrónomo computó la velocidad de la luz. Su resultado, de 225.000 km/s., parece excelente si se considera que fue el primer intento, y resultó bastante asombroso como para provocar la incredulidad de sus coetáneos.
Sin embargo, medio siglo después se confirmaron los cálculos de Roemer en un campo totalmente distinto. Allá por 1.728, el astrónomo británico James Bradley descubrió que las estrellas parecían cambiar de posición con los movimientos terrestres; y no por el paralaje, sino porque la traslación terrestre alrededor del Sol era una fracción mensurable (aunque pequeña) de la velocidad de la luz. La analogía empleada usualmente es la de un hombre que camina con el paraguas abierto bajo un temporal. Aun cuando las gotas caigan verticalmente, el hombre debe inclinar hacia delante el paraguas, porque ha de abrirse paso entre las gotas.
Cuanto más acelere su paso, tanto más deberá inclinar el paraguas. De manera semejante la Tierra avanza entre los ligeros rayos que caen desde las estrellas, y el astrónomo debe inclinar un poco su telescopio y hacerlo en varias direcciones, de acuerdo con los cambios de la trayectoria terrestre (no olvidemos que nuestro planeta Tierra, es como una enorme nave espacial que nos lleva en un viaje eterno, alrededor del Sol, a la velocidad de 30 km/s. + -) Mediante ese desvío aparente de los astros (“aberración de la luz”), Bradley pudo evaluar la velocidad de la luz y calcularla con gran precisión.
Sus cálculos fueron de 285.000 km/s, bastante más exacto que los de Roemer, pero aún un 5’5% más bajos.
Poco a poco, con medios tecnológicos más sofisticados y más conocimientos matemáticos, los científicos fueron obteniendo medidas más exactas aún, conforme se fue perfeccionando la idea original de Galileo y sus sucesores.
En 1.849, el físico francés Armand-Hippolyte-Louis Fizeau ideó un artificio mediante el cual se proyectaba la luz sobre un espejo situado a 8 km de distancia, que devolvía el reflejo al observador. El tiempo empleado por la luz en su viaje de ida y vuelta no rebasó apenas la 1/20.000 de segundo, por Fizeau logró medirlo colocando una rueda dentada giratoria en la trayectoria del rayo luminoso. Cuando dicha rueda giraba a cierta velocidad, regulada, la luz pasaba entre los dientes y se proyectaba contra el siguiente, al ser devuelta por el espejo; así, Fizeau, colocado tras la rueda, no pudo verla. Entonces se dio más velocidad a la rueda, y el reflejo pasó por la siguiente muesca entre los dientes, sin intercepción alguna. De esa forma, regulando y midiendo la velocidad de la rueda giratoria, Fizeau pudo calcular el tiempo transcurrido y, por consiguiente, la velocidad a que se movía el rayo de luz.
Experimento de Focault
Cuando el espejo gira a una velocidad suficientemente elevada para que el tiempo de que tarda en dar una vuelta sea comparable al tiempo que tarda la luz en ir y volver en su recorrido, la señal luminosa se observa a una distancia fácilmente medible del orificio por el que sale el rayo luminoso.
En estas circunstancias es fácil determinar el ángulo que se ha desviado el rayo. Como se conoce la velocidad de rotación, se determina el tiempo que ha tardado el espejo en girar la mitad de ese ángulo. En este tiempo la luz ha recorrido y de esa cifra se obtiene el valor de la velocidad.
La velocidad del espejo fue de 400 revoluciones por segundo y la distancia entre el espejo giratorio y el espejo fijo era de 5 metros.

Un año más tarde, Jean Foucault (quien realizaría poco después su experimento con los péndulos) precisó más estas medidas empleando un espejo giratorio en ve de una rueda dentada. Entonces se midió el tiempo transcurrido desviando ligeramente el ángulo de reflexión mediante el veloz espejo giratorio. Foucault obtuvo un valor de la velocidad de la luz de 300.883 km/s. También, el físico francés utilizó su método para determinar la velocidad de la luz a través de varios líquidos. Averiguó que era notablemente inferior a la alcanzada en el aire. Esto concordaba también con la teoría ondulatoria de Huyghens.
Interferómetro de Michelson y Morley en reposo respecto al éter luminífero.
Michelson fue más preciso aún en sus medidas. Este autor, durante cuarenta años largos, a partir de 1.879, fue aplicando el sistema Fizeau-Foucault cada vez con mayor refinamiento, para medir la velocidad de la luz. Cuando se creyó lo suficientemente informado, proyectó la luz a través de vacío, en vez de hacerlo a través del aire, pues este frena ligeramente su velocidad, y, empleó para ello tuberías de acero cuya longitud era superior a 1’5 km. Según sus medidas, la velocidad de la luz en el vacío era de 299.730 km/s., (sólo un 0’006% más bajo). Demostraría también que todas las longitudes de ondas luminosas viajan a la misma velocidad en el vacío.

El año luz a razón de 300.000 Km/s es la medida asombrosa para las distancias espaciales
En 1.972, un equipo de investigadores bajo la dirección de Kenneth M. Eveson efectuó unas mediciones aún más exactas y vio que la velocidad de la luz era de 299.727’74 km/seg. Una vez se conoció la velocidad de la luz con semejante precisión, se hizo posible usar la luz, o por lo menos formas de ella, para medir distancias.
Aunque para algunos resulte alto tedioso el tema anterior, no he podido resistirme a la tentación de exponerlo, así podrá saber algo más sobre la luz y, habrán conocido a personajes que hicieron posible el que ahora nosotros, la conozcamos mejor.
Las ondas de luz están presentes en el Espacio Interestelar y mucho más
Podría continuar, hasta el final de este trabajo, hablando de la luz y sus distintas formas o aplicaciones: ondas de luz a través del espacio, de cómo se transmite la luz en el “vacío”, nos llega a través del espacio desde Galaxias situadas a miles de millones de años luz; las líneas de fuerzas electromagnéticas de Faraday y Maxwell de campos eléctricos y magnéticos cambiantes (todo ello explicado en un simple conjunto de cuatro ecuaciones, que describían casi todos los fenómenos referentes a esta materia electromagnética), o de los enigmas aún por descubrir (aunque predichos).
Ahora, en Física, se dice que la luz es una forma de radiación electromagnética a la que el ojo humano es sensible y sobre la cual depende nuestra consciencia visual del universo y sus contenidos.
Sí, el ojo humano puede ver todo objeto en el que incida la luz
Patrón de referencia
En el año 1983, el Bureau Internacional de Poids et Mesures resolvió modificar la definición del metro como unidad de longitud del Sistema Internacional, estableciendo su definición a partir de la velocidad de la luz
El metro como patrón en barras de platino e Iridio
En consecuencia, el mínimo reajuste arbitrario efectuado en la definición del metro, permite que la velocidad de la luz, lógicamente, tenga un valor exacto de 299 792 458 m/s cuando se expresa en metros/segundo. Esta modificación aprovecha de forma práctica una de las bases de la teoría de la relatividad de Einstein: la inmutabilidad de la velocidad de la luz en el vacío, sea cual sea el sistema de referencia utilizado para medirla, convirtiendo esta propiedad en uno de los patrones de los que se deducen otras unidades.
Aparte de todo lo que antes hemos explicado, no sería justo finalizar el trabajo sin exponer aquí que, en 1905, Albert Einstein, inspirado en el cuanto de Planck, realizó un importante avance en el conocimiento de lo que es la luz. Demostró que el Efecto foto-eléctrico sólo podía ser explicado con la hipótesis de que la luz consiste en un chorro de fotones de energía electromagnética discretos.
El conflicto entre la teoría ondulatoria y corpuscular de la luz fue resuelto con la evolución de la teoría cuántica y la mecánica ondulatoria que ha dejado claro que, los electrones y las otras partículas elementales tienen propiedades duales de partículas y onda.
sería mucho más largo, pero creo que está bien con lo dicho.
emilio silvera
Nov
16
Biología de las estrellas
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en General ~
Clasificado en General ~
 Comments (0)
Comments (0)
¿Es viejo el Universo?
Nuevas estrellas, vientos estelares, radiación, energías, estrellas de neutrones o púlsares, agujeros negros, enanas rojas y blancas, ¿estrellas de Quarks? ¿materia oscura? mundos…¿Civilizaciones? ¡El Universo! Lo que todo lo contiene, ahí están presentes todas las cosas que existen y las que tienen que existir… El espacio-tiempo, las fuerzas fundamentales de la Naturaleza…¡La Vida!
Cuando pensamos en la edad y el tamaño del Universo lo hacemos generalmente utilizando medidas de tiempo y espacio como años, kilómetros o años-luz. Como y a hemos visto, estas medidas son extraordinariamente antropomórficas. ¿Por qué medir la edad del Universo con un “reloj” que hace “tic” cada vez que nuestro planeta completa una órbita alrededor de su estrella madre, el Sol? ¿porqué medir su densidad en términos de átomos por metro cúbico? Las respuestas a estas preguntas son por supuesto la misma: porque es conveniente y siempre lo hemos hecho así.
Ésta es una situación en donde resulta especialmente apropiado utilizar las unidades “naturales” la masa, longitud y tiempo de Stoney y Planck, las que ellos introdujeron en la ciencia física para ayudarnos a escapar de la camisa de fuerza que suponía la perspectiva centrada e el ser humano.
Es fácil caer en la tentación de mirarnos el ombligo y no hacerlo al entorno que nos rodea. Muchas más cosas habríamos evitado y habríamos descubierto si por una sola vez hubiésemos dejado el ego a un lado y, en lugar de estar pendientes de nosotros mismos, lo hubiéramos hecho con respecto a la naturaleza que, en definitiva, es la que nos enseña el camino a seguir.
A lo menos una vez al día, el cielo en su parte alta, es iluminado por un gran destello producido por grandes explosiones de rayos gamma. A menudo, esos destellos alcanzan magnitudes superiores a las que pueden ser generadas por todo un conjunto de otros rayos cósmicos y desaparecen posteriormente sin dejar más rastro. Nadie puede predecir cuando volverá a ocurrir la próxima explosión o de que dirección del cielo procederá. Hasta ahora, no contamos con evidencias duras como para asegurar cuáles podrían ser las fuentes precisas de donde provienen esos rayos gamma que observamos en lo alto del cielo, las razones que ocasionan los grandes destellos y la distancia en la cual ocurre el fenómeno.
La edad actual del Universo visible ≈ 1060 tiempos de Planck
Tamaño actual del Universo visible ≈ 1060 longitudes de Planck
La masa actual del Universo visible ≈ 1060 masas de Planck
Vemos así que la bajísima densidad de materia en el Universo es un reflejo del hecho de que:
Densidad actual del Universo visible ≈10-120 de la densidad de Planck
Y la temperatura del espacio, a 3 grados sobre el cero absoluto, es, por tanto
Temperatura actual del Universo visible ≈ 10-30 de la Planck
Desde lo muy pequeño hasta lo muy grande
Estos números extraordinariamente grandes y estas fracciones extraordinariamente pequeñas nos muestran inmediatamente que el Universo está estructurado en una escala sobre humana de proporciones asombrosas cuando la sopesamos en los balances de su propia construcción.
Con respecto a sus propios patrones el Universo es viejo. El tiempo de vida natural de un mundo gobernado por la gravedad, la relatividad y la mecánica cuántica es el fugaz breve tiempo de Planck. Parece que es mucho más viejo de lo que debería ser.
Pero, pese a la enorme edad del Universo en “tics” de Tiempos de Planck, hemos aprendido que casi todo este tiempo es necesario para producir estrellas y los elementos químicos que traen la vida.

En todas las regiones del espacio interestelar donde existen objetos de enormes densidades y estrellas super-masivas se pueden producir sucesos de inmensas energías y, en regiones de gas y polvo de muchos años-luz de diámetro, es donde surgen los Sistemas solares que contienen planetas aptos para la vida.
¿Por qué nuestro Universo no es mucho más viejo de lo que parece ser? Es fácil entender por qué el Universo no es mucho más joven. Las estrellas tardan mucho tiempo en formarse y producir elementos más pesados que son las que requiere la complejidad biológica. Pero los universos viejos también tienen sus problemas. Conforme para el tiempo en el Universo el proceso de formación de estrellas se frena. Todo el gas y el polvo cósmico que constituyen las materias primas de las estrellas habían sido procesados por las estrellas y lanzados al espacio intergaláctico donde no pueden enfriarse y fundirse en nuevas estrellas. Pocas estrellas hacen que, a su vez, también sean pocos los sistemas solares y los planetas. Los planetas que se forman son menos activos que los que se formaron antes, la entropía va debilitando la energía del sistema para realizar trabajo. La producción de elementos radiactivos en las estrellas disminuirá, y los que se formen tendrán semividas más largas. Los nuevos planetas serán menos activos geológicamente y carecerán de muchos de los movimientos internos que impulsan el vulcanismo, la deriva continental y la elevación de las montañas en el planeta. Si esto también hace menos probable la presencia de un campo magnético en un planeta, entonces será muy poco probable que la vida evolucione hasta formas complejas.

Zeta Oph, una colosal estrella cuyo viento estelar deja una huella espectacular en el espacio circundante.
Las estrellas típicas como el Sol, emiten desde su superficie un viento de partículas cargadas eléctricamente que barre los atmósferas de los planetas en órbitas a su alrededor y a menos que el viento pueda ser desviado por un campo magnético, los posibles habitantes de ese planeta lo podrían tener complicado soportando tal lluvia de radiactividad. En nuestro sistema solar el campo magnético de la Tierra ha protegido su atmósfera del viento solar, pero Marte, que no está protegido por ningún campo magnético, perdió su atmósfera hace tiempo.
Probablemente no es fácil mantener una larga vida en un planeta del Sistema solar. Poco a poco hemos llegado a apreciar cuán precaria es. Dejando a un lado los intentos que siguen realizando los seres vivos de extinguirse a sí mismos, agotar los recursos naturales, propagan infecciones letales y venenos mortales y emponzoñar la atmósfera, también existen series amenazas exteriores.
Credit: Emily Lakdawalla/Ted Stryk
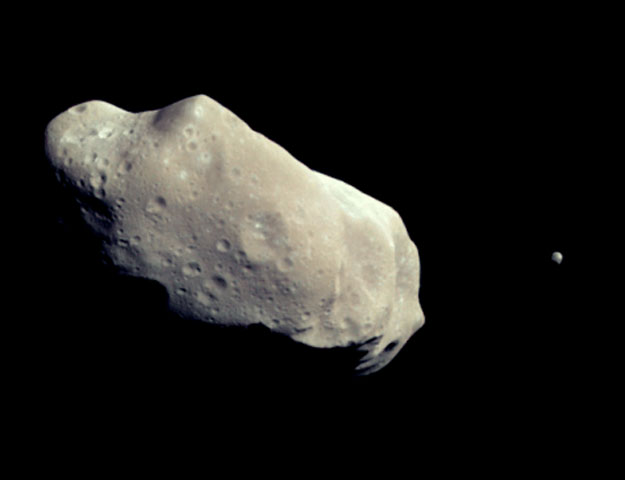
La mayoría de asteroides, incluyendo Vesta, están en el cinturón de asteroides que se sitúa entre Marte y Júpiter. Otros asteroides giran en círculos mas cerca del Sol que de la Tierra, mientras que un gran número de ellos comparten orbitas planetaria. Dada esta gran variedad de asteroides, algunos particularmente extraños han sido descubiertos en los últimos dos siglos desde que el primer asteroide fuera descubierto (Ceres en 1801).
Los movimientos de cometas y asteroides, a pesar de tener la defensa de Júpiter, son una serie y cierta amenaza para el desarrollo y persistencia de vida inteligente en las primeras etapas. Los impactos no han sido infrecuentes en el pasado lejano de la Tierra habiendo tenido efectos catastróficos. Somos afortunados al tener la protección de la luna y de la enorme masa de Júpiter que atrae hacia sí los cuerpos que llegan desde el exterior desviándolos de su probable trayectoria hacia nuestro planeta.
La caída en el Planeta de uno de estos enormes pedruscos podría producir extinciones globales y retrasar en millones de años la evolución, o, por el contrario, evitar que siga cualquier clase de evolución produciendo la extinción total y dejando la Tierra como un planeta muerto.
emilio silvera
Nov
16
¿Viajes en el Tiempo? ¡Otro sueño de la Humanidad!
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en General ~
Clasificado en General ~
 Comments (1)
Comments (1)
En cromodinámica cuántica, la propiedad de libertad asintótica hace que la interacción entre quarks sea más débil cuanto más cerca están unos de otros (confinación de quarks) y la fuerza crece cuando los quarks tratan de separarse, es la única fuerza que crece con la distancia. Los quarks y los gluones están confinados en una región cuyo valor se define por:
R » ћc /L » 10-13 cm
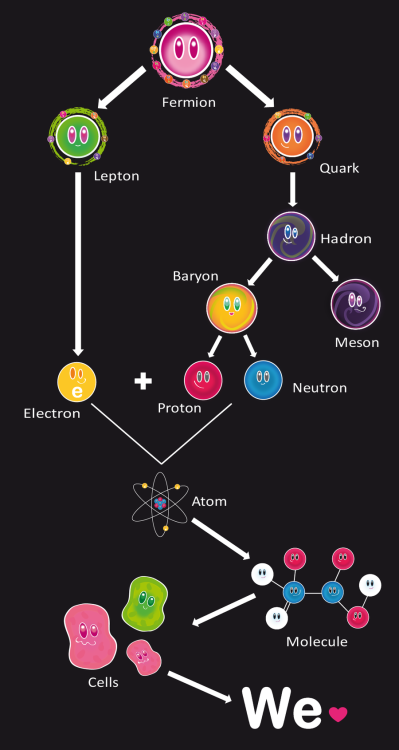

Poder contemplar Quarks libres sólo podría haber sido posible en aquellos primeros momentos, antes de la formación de los hadrónes. En realidad, la única manera de que pudiéramos observar quarks libres, sería en un ambiente con la temperatura del universo primitivo, es la temperatura de desconfinamiento.
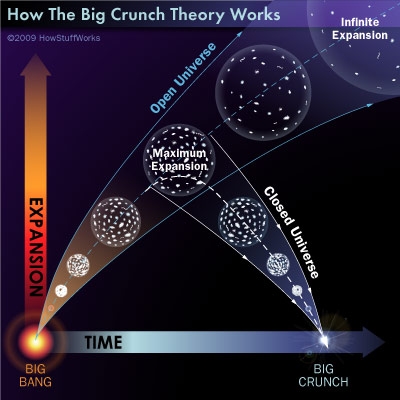
Ahora se cree que el Big Crunch nunca se producirá y que la muerte del Universo será térmica, es decir, una temperatura del cero absoluto que lo paralizará todo, ni los átomos se moverán en ese frío de muerte que dejará un universo congelado donde ni brillaran las estrellas ni estará presente ninguna clase de vida.
En la parte anterior de este mismo trabajo, estaba hablando del Big Crunch y me pasé a otro (los quarks), así que cerremos este capítulo del Big Crunch que está referido a un estado final de un universo cerrado de Friedmann (es decir, uno en el que la densidad excede a la densidad crítica). Dicho universo se expande desde el Big Bang inicial, alcanza un radio máximo, y luego colapsa hacia un Big Crunch, donde la densidad de la materia se vuelve infinita después de que la gravedad haga parar la expansión de las galaxias que, lentamente al principio, y muy rápidamente después, comenzarán a desplazarse en sentido contrario, desandarán el camino para que toda la materia del universo se junte en un punto, formado una singularidad en la que dejaría de existir el espacio-tiempo. Después del Big Crunch debería haber otra fase de expansión y colapso, dando lugar a un universo oscilante. universo que se va y universo que viene.

Pero, ¿y nosotros?, ¿Qué pintamos aquí?
¡Mirado así no parece que seamos gran cosa!
Antes de pasar a otros temas, retomemos el de los viajes en el tiempo y las paradojas que pueden originar.

Una versión de la máquina del tiempo de Thorne consiste en dos cabinas, cada una de las cuales contiene dos placas de metal paralelas. Los intensos cambios eléctricos creados entre cada par de placas de metal paralelas (mayores que cualquier cosa posible con la tecnología actual) rizan el tejido del espacio-tiempo, creando un agujero en el espacio que une las dos cabinas. Una cabina se coloca entonces en una nave espacial y es acelerada a velocidades próximas a la de la luz, mientras que la otra cabina permanece en la Tierra. Puesto que un agujero de gusano puede conectar dos regiones des espacio con tiempos diferentes, un reloj en la cabina de la nave marcha más despacio que un reloj en la cabina de la Tierra. Debido a que el tiempo transcurriría a diferentes velocidades en los dos extremos del agujero de gusano, cualquiera que entrase en un extremo del agujero de gusano sería instantáneamente lanzado al pasado o al futuro.

Viajar al pasado y conocer a personajes famosos a los que contar las novedades científicas. Algunos dicen que el viaje en el Tiempo está prohibido, aunque es posible. Siempre hemos tenido una gran imaginación y, cuando se sabíamos contestar a una cuestión compleja… ¡Inventamos la respuesta!
Normalmente, una de las ideas básicas de la física elemental es que todos los objetos tienen energía positiva. Las moléculas vibrantes, los vehículos que corren, los pájaros que vuelan, los niños jugando tienen todos energía positiva. Por definición, el espacio vacío tiene energía nula. Sin embargo, si podemos producir objetos con “energías negativas” (es decir, algo que tiene un contenido de energía menor que el vacío), entonces podríamos ser capaces de generar configuraciones exóticas de espacio y tiempo en las que el tiempo se curve en un circulo.

Parece que la función de las placas metálicas paralelas consiste en generar la materia o energía exótica necesaria para que las bocas de entrada y salida del agujero de gusano permanezcan abiertas y, como la materia exótica genera energía negativa, los viajeros del tiempo no experimentarían fuerzas gravitatorias superiores a 1g, viajando así al otro extremo de la galaxia e incluso del universo o de otro universo paralelo de los que promulga Stephen Hawking. En apariencia, el razonamiento matemático de Thorne es impecable conforme a las ecuaciones de Einstein.
Normalmente, una de las ideas básicas de la física elemental es que todos los objetos tienen energía positiva. Las moléculas vibrantes, los vehículos que corren, los pájaros que vuelan, los niños jugando tienen todos energía positiva. Por definición, el espacio vacío tiene energía nula. Sin embargo, si podemos producir objetos con “energías negativas” (es decir, algo que tiene un contenido de energía menor que el vacío), entonces podríamos ser capaces de generar configuraciones exóticas de espacio y tiempo en las que el tiempo se curve en un circulo.

Muchas son las máquinas del tiempo que hemos desarrollado en nuestra imaginación
Por el momento, al no ser una propuesta formal, no hay veredicto sobre la máquina del tiempo de Thorne. Su amigo, Stephen Hawking, dice que la radiación emitida en la entrada del agujero sería suficientemente grande como contribuir al contenido de materia y energía de las ecuaciones de Einstein. Esta realimentación de las ecuaciones de Einstein distorsionaría la entrada del agujero de gusano, incluso cerrándolo para siempre. Thorne, sin embargo, discrepa en que la radiación sea suficiente para cerrar la entrada.
Aquí es donde interviene la teoría de supercuerdas. Puesto que la teoría de supercuerdas es una teoría completamente mecanocuántica que incluye la teoría de la relatividad general de Einstein como un subconjunto, puede ser utilizada para calcular correcciones a la teoría del agujero de gusano original.
En principio nos permitiría determinar si la condición AWEC es físicamente realizable, y si la entrada del agujero de gusano permanece abierta para que los viajeros del tiempo puedan disfrutar de un viaje al pasado.
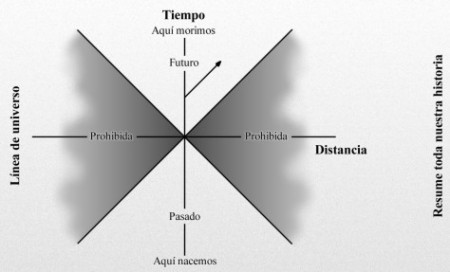
Nuestra línea de universo resume toda nuestra historia, que nacemos hasta que morimos. Cuanto más rápido nos movemos más se inclina la línea de universo. Sin embargo, la velocidad más rápida a la que podemos viajar es la velocidad de la luz. Por consiguiente, una de este diagrama espacio-temporal está “prohibida”; es decir, tendríamos que ir a mayor velocidad que la luz para entrar en esta zona prohibida por la relatividad especial de Einstein, que nos dice que nada en nuestro universo puede viajar a velocidades superiores a c.
Las plantas absorben la energía negativa, se crea masa negativa. Sí, ¿pero dónde está esa energía negativa para viajar en el Tiempo?
Este concepto más bien simple se conoce con un nombre que suena complicado: la condición de energía media débil (average weak energy condition, o AWEC). Como Thorne tiene cuidado en señalar, la AWEC debe ser violada; la energía debe hacerse temporalmente negativa para que el viaje en el tiempo tenga éxito. Sin embargo, la energía negativa ha sido históricamente anatema para los relativistas, que advierten que la energía negativa haría posible la anti-gravedad y un montón de otros fenómenos que nunca se han visto experimentalmente.
Pero Thorne señala al momento que existe una forma de obtener energía negativa, y esto es a través de la teoría cuántica.
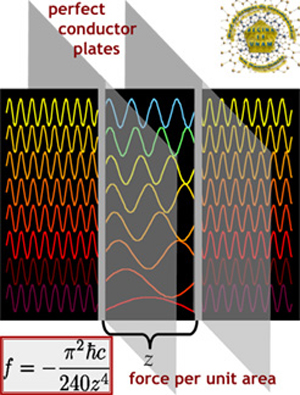
En 1.948, el físico holandés Hendrik Casimir demostró que la teoría cuántica puede crear energía negativa: tomemos simplemente dos placas de metal paralelas y descargadas ordinariamente, el sentido común nos dice que estas dos placas, puesto que son eléctricamente neutras, no ejercen ninguna fuerza entre sí. Pero Casimir demostró que, debido al principio de incertidumbre de Werner Heisenberg, en el vacío que separa estas dos placas existe realmente una agitada actividad, con billones de partículas y antipartículas apareciendo y desapareciendo constantemente. Aparecen a partir de la “nada” y vuelven a desaparecer en el “vacío”. Puesto que son tan fugaces, son, en su mayoría, inobservables, y no violan ninguna de las leyes de la física. Estas “partículas virtuales” crean una fuerza neutra atractiva entre estas dos placas que Casimir predijo que era medible.
Cuando Casimir publicó el artículo, se encontró con un fuerte escepticismo. Después de todo, ¿cómo pueden atraerse dos objetos eléctricamente neutros, violando así las leyes normales de la electricidad clásica? Esto era inaudito. Sin embargo, en 1.985 el físico M. J. Sparnaay observó este efecto en el laboratorio, exactamente como había predicho Casimir. Desde entonces (después de un sin fin de comprobaciones), ha sido bautizado como el efecto Casimir.
Una manera de aprovechar el efecto Casimir mediante grandes placas metálicas paralelas descargadas, sería el descrito para la puerta de entrada y salida del agujero de gusano de Thorne para poder viajar en el tiempo.

Kip Thorne explica a un alumno los misterios y posibilidades de viajar en el Tiempo
Por el momento, al no ser una propuesta formal, no hay veredicto sobre la máquina del tiempo de Thorne. Su amigo, Stephen Hawking, dice que la radiación emitida en la entrada del agujero sería suficientemente grande como para contribuir al contenido de materia y energía de las ecuaciones de Einstein. Esta realimentación de las ecuaciones de Einstein distorsionaría la entrada del agujero de gusano, incluso cerrándolo para siempre. Thorne, sin embargo, discrepa en que la radiación sea suficiente para cerrar la entrada.
Aquí es donde interviene la teoría de supercuerdas. Puesto que la teoría de supercuerdas es una teoría completamente mecanocuántica que incluye la teoría de la relatividad general de Einstein como un subconjunto, puede ser utilizada para calcular correcciones a la teoría del agujero de gusano original.
En principio nos permitiría determinar si la condición AWEC es físicamente realizable, y si la entrada del agujero de gusano permanece abierta para que los viajeros del tiempo puedan disfrutar de un viaje al pasado.

Podríamos ver como se forman las nebulosas y nacen y mueren las estrellas
Antes comentaba algo sobre disfrutar de un viaje al pasado pero, pensándolo bien, no estaría yo tan seguro. Rápidamente acuden a mi mente múltiple paradojas que, de una u otra especie han sido narradas, principalmente por escritores de ciencia-ficción que, por lo general, son los precursores del futuro.
Si viajar en el tiempo finalmente pudiera ser posible, cosas parecidas a esta locura ¡”podrían ocurrir”! I. B. S. Haldane, nos decía:
“La naturaleza no sólo es más extraña de lo que suponemos; es más extraña de lo que podamos suponer”.
emilio silvera















 Totales: 74.933.657
Totales: 74.933.657 Conectados: 62
Conectados: 62