Ene
10
Predicen una explosión que «cambiará el cielo» en 2022
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Astronomía y Astrofísica ~
Clasificado en Astronomía y Astrofísica ~
 Comments (1)
Comments (1)
Ciencia – ABC
Sucederá cuando dos estrellas se fundan en una sola y será perfectamente visible desde la Tierra, sin necesidad de utilizar telescopio alguno. Los autores del estudio hablan de «algo nunca visto hasta ahora»
Un equipo de astrónomos capitaneados por Larry Molnar han predicho que dentro de apenas cinco años, en 2022, se producirá una explosión que será perfectamente visible desde la Tierra, sin necesidad de utilizar telescopio alguno. «Estamos ante una de esas raras ocasiones (una de cada millón de veces) -explica Molnar- en las que podemos predecir una explosión. Será algo nunca visto hasta ahora».
Terminaran fusionándose en una sola estrella
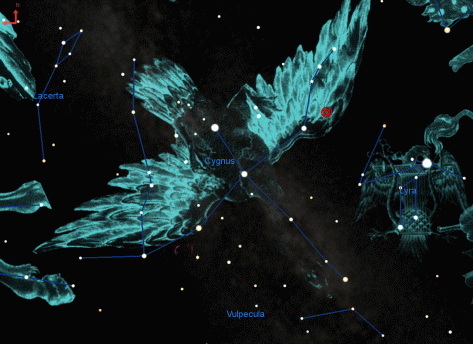
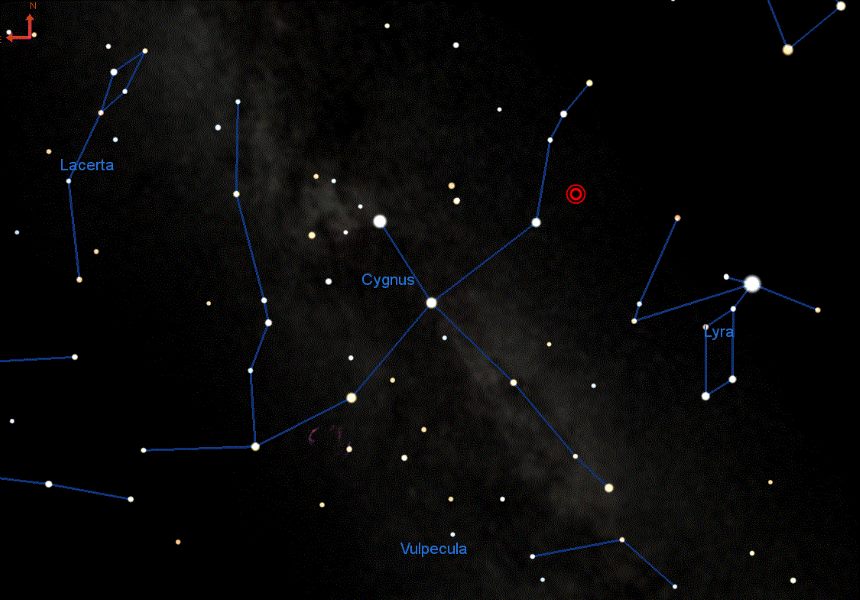
Según la predicción de este científico, se trata de un sistema binario (dos estrellas que orbitan una alrededor de la otra) y que, según los cálculos, se fundirán en una sola en el año 2022, produciendo una explosión catastrófica. En ese momento, la estrella resultante aumentará espectacularmente su brillo y se convertirá, durante un tiempo, en el objeto más brillante del firmamento. La estrella será visible como parte de la constelación del Cisne, y añadirá un nuevo y brillante punto de luz a las estrellas que forman la Cruz del Norte.
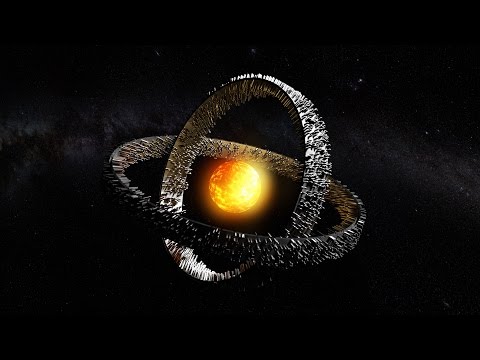
Ilustración crédito de Larry Molnar/Calvin College.
“Es una estrella doble donde una componente pasa delante de la otra generando variaciones del brillo total del sistema. Pero esta binaria mostró otras peculiaridades. Sus componentes están en contacto, es decir que comparten atmósferas y lo están haciendo de manera bastante íntima. Así, se espera que frenen su mutua rotación y terminen fusionándose generando una nova roja.
¿Cuando?, bien, en el año 2022 aproximadamente. Por supuesto que debido a la distancia estamos a salvo de este evento, en el que el sistema puede aumentar su brillo unas 10 mil veces pudiéndose observar a simple vista si las condiciones locales del cielo lo permiten.”
Imagen de V838 Mon. como ejemplo de nova roja. Crédito de NASA, ESA and H.E. Bond (STS
Molnar comenzó a estudiar la estrella KIC 9832227 a finales de 2013. Empezó a hacerlo tras asistir a una conferencia en la que la astrónoma Karen Kinemuchi presentó un estudio sobre los cambios de brillo de esa estrella en particular, dejando abierta la cuestión de si se trataba de una estrella «pulsante» o de un sistema binario. El científico se tomó el asunto como un reto personal y decidió estudiar el objeto en profundidad.
Lo primero que hizo fue observar cómo el color de la estrella se relacionaba con su brillo, lo que le llevó a determinar que se trataba, definitivamente, de un sistema binario. De hecho, descubrió que en realidad se trataba de un sistema binario «de contacto», en el que las dos estrellas del sistema comparten una atmósfera común, como dos cacahuetes que están dentro de a misma cáscara.
A partir de aquí, Molnar explica cómo Daniel Van Noord, estudiante del Calvin College, «logró determinar un periodo orbital muy preciso con los datos del satélite Kepler, y se sorprendió al descubrir que ese periodo era ligeramente inferior al que mostraban los primeros datos del satélite».
Este resultado recordó al astrónomo un estudio publicado previamente por su colega Romuald Tylenda, que mostraba cómo otra estrella (V1309) se estaba comportando justo antes de explotar de forma inesperada en 2008, produciendo una nova roja, uno de los tipos conocidos de explosión estelar. Los registros anteriores a esa explosión mostraban una binaria de contacto, con un período orbital cada vez más corto y a velocidades cada vez mayores. Para Molnar, este patrón de cambios orbitales fue como una “piedra Roseta” que le permitió interpretar los nuevos datos de la estrella que estaba estudiando.
Tomada muy en serio

Molnar observó que los cambios en el período orbital de KIC 9832227 seguían cambiando durante 2013 y 2014, y en 2015 presentó sus resultados ante la Sociedad Astronómica Americana, donde aseguró que había una probabilidad muy alta de que KIC 9832227 siguiera los mismos pasos de V1309. Por supuesto, antes de tomarse su hipótesis completamente en serio, Molnar pasó meses enteros tratando de descartar otros motivos que podrían estar detrás de los cambios detectados en la estrella. «En pocas palabras -explica el investigador- en ese momento pensamos que nuestra hipótesis de la fusión de las dos estrellas debía ser tomada muy en serio, y que deberíamos utilizar los años siguientes para estudiar el acontecimiento a fondo para que, cuando la explosión se produzca, conozcamos con exactitud todos los pasos que llevaron a ella».
“KIC 9832227 es un sistema estelar binario de contacto1 en la constelación de Cygnus, que se encuentra a unos 1.940 (± ~ 30) años luz de distancia. También se identifica como un binario eclipsante con un período orbital de casi 11 horas. En 2017, se predijo que el sistema daría lugar a una fusión en 2022,2 (± 0,6 años), produciendo una nova roja luminosa (LRN) que alcanzaría una magnitud aparente de 2. El LRN debe permanecer visible a simple vista durante aproximadamente un mes. Se predice que la fusión de los dos núcleos estelares dará origen a una nueva estrella más potente y masiva de secuencia principal.”
Por eso, Molnar y sus colegas pasaron todo un año examinando KIC 9832227 en todas las longitudes de onda. Si las predicciones son correctas, será la primera vez que un grupo de astrónomos logra captar el momento en que los dos miembros de un sistema binario de estrellas se fusionan, y estudiar además al detalle lo que sucede durante los años que preceden a la explosión.
Si Molnar tiene razón. el espectáculo está servido para dentro de cinco años. Será entonces cuando, de la negrura del Universo, surgirá un nuevo punto brillante para iluminar nuestras noches.
————————————————————-
Estos eventos son normales en el Universo y, de vez en cuando, los Astrónomos tienen la suerte de localizar uno que pueden observar para ir aprendiendo de cómo ocurren realmente este tipo de encuentros.
Publica: emilio silvera
Ene
10
¡Las matemáticas! ¿El origen?
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en El Origen de las cosas ~
Clasificado en El Origen de las cosas ~
 Comments (2)
Comments (2)
¡Las leyes físicas! A veces sorprendentes,
Si miramos … ¿Qué veremos? La imagen de un objeto se forma en la retina de cada ojo, por tanto tendríamos dos imágenes de un mismo objeto y sin embargo, vemos una sola… Claro que no siempre lo que podemos ver está determinado por la visión de los ojos… ¡La Mente llega más lejos y ve mucho más!

Muescas en el hueso de Ishango, una herramienta de hueso que data del Paleolítico Superior, aproximadamente de unos 35.000 años a. C.
Lo que veremos es que las cosas nunca son como parecen ser a primera vista y, con el tiempo que inexorablemente transcurre, las cosas cambian sin que nada lo pueda evitar y, los saberes del mundo evolucionan tomando siempre el camino de la perfección. Es decir, cada vez se hacen las cosas mejor, se depuran más las técnicas y, con la experiencia llega el conocimiento y la sabiduría.

Los expertos occidentales, por ejemplo, dicen que la autoría del teorema de Pitágoras corresponde a éste. A pesar de que los babilonios habían creado el mismo concepto siglos antes. La razón es que Pitágoras o sus seguidores habían creado la primera demostración de este principio fundamental, mientras que los babilonios no lo hicieron. Es lo mismo que pasó (en tiempos más recientes) con Faraday y Maxwell, el primero descubrió con sus experimentos todos los fundamentos encerrados en la electricidad y el magnetismo y, al no saber exponerlo matemáticamente, tuvo que llegar Maxwell que, con sus ecuaciones vectoriales nos dejara una demostración fundamental del electromagnetismo.
Faraday Maxwell
Los críticos consideran tan la demostración al estilo griego que su inexistencia en las culturas no europeas desacredita, en su opinión, miles de años de trabajos matemáticos. Claro que, en este punto, no todos estamos de acuerdo y, por mi creo que los pueblos no occidentales sí tenían sus demostraciones, mientras que otros dudan de que sea realmente posible “demostrar” cualquier concepto para toda la eternidad y para la totalidad del Universo. Es cierto que eterno…no hay nada pero, en todo el Universo será válida la ecuación E = mc², de la misma manera que 2 + 2 = 4. Hay cosas que ni el Tiempo ni las distancias pueden variar.
La numeración egipcia (escrita) permitía la representación de números mayores que un millón. Utilizaban un sistema aditivo de decimal con jeroglíficos específicos para la unidad y una de las seis primeras potencias de 10.
En la figura podemos ver los símbolos usados para 1, 10, 100 y 1.000. El 10.000 se representaba con un dedo doblado, el 100.000 con un pez y 1.000.000 mediante una figura humana de rodillas y con los brazos alzados.
En un principio escribían los nueve primeros números colocando símbolos de la unidad, uno a continuación de otro; más tarde utilizaron la representación por desdoblamiento mientras los arameos de Egipto usaban un principio ternario (ver tabla).
La nunmeración y sus símbolos fueron variados según los pueblos
El escepticismo es oportuno en toda investigación, pero quien investigue las matemáticas no occidentales se enfrenta a menudo con un gran obstáculo. Expertos que han estudiado los sistemas de numeración de la antigua Etiopía, cuentan que los expertos occidentales se negaron en una ocasión a aceptar que esta civilización africana hubiera desarrollado sus propios números. Los números etíopes se parecen a los números egipcios, que son anteriores, y, en menor medida, a los antiguos números griegos –lo cual no es sorprendente, dada, por una la proximidad geográfica de Etiopía con Egipto y, por otra , la influencia que ejerció Egipto en las matemáticas griegas.
Una serie de cartas escritas por algunos etíopes a personajes griegos y encontradas en Grecia estaban escritas en los dos lenguajes para que las entendieran y, a pesar de ello, algunos “expertos” dudaban que los etíopes hubieran sido capaces de tal sofisticación. Sin embargo, los análisis químicos demostraron que la empleada tenía un color no habitual y los análisis químicos demostraron que la tinta se había fabricado a partir de unas bayas autóctonas de Etiopía.
Nuestro patrimonio matemático y nuestro orgullo occidentales dependen irremediablemente de los logros de la antigua Grecia. Dichos logros se han exagerado tanto que a resulta difícil distinguir qué part3e de la matemática moderna procede de los griegos y cuál es la que su origen en los babilonios, los egipcios, los hindúes, los chinos, los árabes, etc. Sin embargo, si nuestras actuales se basaran exclusivamente en Pitágoras, Euclides, Demócrito, Arquímedes y otros griegos, serían una disciplina bastante deficiente.
En 1908, el historiador de las matemáticas, Rouse Ball escribió:
“La historia de las matemáticas no se puede remontar ciertamente a ninguna ni a ningún período que sean anteriores a la etapa de los griegos jónicos”.
Matemáticas de Mesopotamia Matemática Babilónica
Matemáticas de la India Matemáticas de Egipto
Hoy sabemos que el hombre se extralimitó al ponerle fecha al conocimiento matemático del mundo humano que, como ahora sabemos, viene desde muy lejos en el Tiempo. Aunque las huellas no todas han sobrevivido, si aparecieron tablillas y otros objetos que contenían la prueba de que nuestros antepasados de Mesopotamia, Babilonia, India, Egipto… y otros fueron los precursores de la posterior matemática griega.

En 1952 el historiador Morris Kline escribió:
“Fue en el extraordinariamente propicio suelo de Gracia donde [las matemáticas] garantizaron finalmente una nueva forma de controlar la existencia humana y florecieron espectacularmente durante un breve período de tiempo… Con el declive de la civilización griega la planta quedó aletargada durante unos mil años… [hasta que] esa planta fue llevada de una manera adecuada a Europa y plantada una vez más en el terreno fértil”
De un modo esquemático, se interpreta a menudo el significado de esta afirmación entendiendo que ha habido tres etapas de la de las matemáticas:
- 1. Hacia el año 600 a. C., los antiguos griegos inventaron las matemáticas, que estuvieron desarrollando hasta aproximadamente el año 400 d. C., en el cual desaparecieron de la faz de la Tierra.
- 2. A esto siguió un período oscuro para las matemáticas, que duró más de mil años. Algunos expertos admiten que los árabes mantuvieron vivas las matemáticas griegas durante toda la Edad Media.
- 3. En la Europa del siglo XVI se produce el redescubrimiento de las matemáticas griegas que vuelven a florecer de hasta el momento actual.
Claro que este punto de es muy discutible. Nuestros números modernos -del 0 al 9- se desarrollaron en la India (como ha quedado reseñado en escritos expuestos aquí en tiempos pasados) durante la segunda etapa, el llamado período oscuro de las matemáticas. Las matemáticas existían ya mucho antes de que los griegos construyeran su primer ángulo recto.
Rouse Ball, desconocía las primeras matemáticas hindúes contenidas en los Sulbasutras (las reglas de la cuerda). Escritos en alguna comprendida entre los años 800 y 500 a. C., los Silbasutras demuestran, entre otras cosas, que los indios de este período tenían su propia versión del teorema de Pitágoras así como un procedimiento para obtener la raíz cuadrada de 2 con una precisión de hasta cinco cifras decimales. Los Sulbasutras ponen de manifiesto la existencia de un rico conocimiento geométrico que fue muy a los griegos.
Otro experto nos dice que, la afirmación de Kline es más problemática, ya que ignora un rico conjunto de matemáticas no europeas que fueron desenterradas hacia mediados del siglo XX, incluidas las matemáticas de Mesopotamia, Egipto, China, la India, el mundo árabe y la América precolombina. También existe el problema de los propios griegos –Demócrito, Aristóteles, Heródoto- prodigaron alabanzas a los egipcios, reconociéndolos como sus gurús matemáticos (aunque con distintas palabras). El hecho cierto es que, antes que los griegos fueron muchos los que aportaron su matemático para que ahora nosotros, sepamos de esa imprescindible y necesaria disciplina que nos sirve para construir puentes, para diseñar veloces trenes, para poder calcular las trayectorias de las naces espaciales que van hacia Marte, o, simplemente, para saber cómo funcionan las leyes de la Naturaleza, los átomos que conforman la materia e incluso, saber sobre densidades y energías en las estrellas.
Repasando todos estos hechos, de alguna manera, podemos llegar a entender aquel “Todo es número” de los pitagóricos.
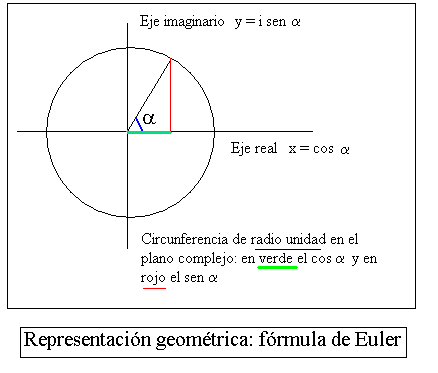
“Relaciona los números imaginarios ( i = raíz cuadrada de ( –1)), con las potencias (número e y logaritmos neperianos ) y con las funciones trigonométricas. Nos la podemos encontrar en cualquier sitio, en cualquier expresión matemática pura o relacionada con algo tan prosaico como las relaciones de impedancias en un circuito de corriente alterna. En la función de onda de la mecánica cuántica o en cualquier expresión de naturaleza ondulatoria o periódica. En la técnica, en la física o en las matemáticas más abstractas ( Roger Penrose reflexiona– en su último libro, en el capítulo sobre las diferenciales complejas – lo que habría disfrutado Euler con todas las maravillas de su fórmula y de los números imaginarios ).”
La más famosa fórmula de Euler. Hay veces en la que no tenemos más opción que asombrarnos de lo que puede discurrir la mente humana. Sobre esta fórmula mágica, alguien dijo:
“Si una aburrida noche de invierno decidieran acudir a un restaurante de las Matemáticas y pidieran una paella con “un poco de todo” o, más precisamente, “un poco de todo lo importante”, probablemente les llevarían a la mesa la ecuación del título. Ésta, a pesar de tratarse de una pura tautología, es muy conocida en la comunidad científica por su simplicidad y casi sobrenatural completitud: contiene en una sola línea de elementos de lo más diverso y de cierta relevancia en la historia de las Matemáticas.”
Leonhard Euler
Está claro que este breve comentario no pretende ser la Historia de las matemáticas que, para ser un fiel reflejo de la realidad, tendría que estar contada en muchos volúmenes llenos de explicaciones, hallazgos y anécdotas y hechos que nos llegaron a través de los descubrimientos realizados a lo largo del tiempo. Sin embargo, si es un apunte interesante de lo que pudo ser. Para cerrar el trabajo he querido traer aquí una fórmula mágica, es debida a Leonhard Euler, nacido en Basilea en el año 1707. Una mente prodigiosa que deslumbraba desde su más tierna juventud en diversas disciplinas, especialmente en Matemáticas. Le llamaron el Rey Midas de las matemáticas.
Fue el precursor de la utilización de la letra
para denotar la base de los logaritmos neperianos.
Popularizó la utilización de la letra
para denotar la razón entre la longitud de una circunferencia y su diámetro.
Introdujo la notación
para
.
Utilizó la letra
para designar a su constante.
Notación sobre lados y ángulos y otras notaciones sobre triángulos.
- Otras notaciones en análisis. Euler también introdujo la notación moderna de las funciones trigonométricas, el símbolo
para denotar un sumatorio y
para denotar logaritmo de
.
- Funciones. Uno de los aportes más importantes (posiblemente el que más) de Euler a la notación matemática fue la utilización de
(usada en los Commentarii de San Petersburgo en 1734-35) como forma para denotar al valor de una función
al aplicarla a un valor
.
Como se puede ver las matemáticas posteriores a Euler no habrían sido las mismas sin las notaciones que nuestro protagonista introdujo, ya que éstas simplificaron de manera significativa la forma de escribir matemáticas.
En el campo de las llamadas Matemáticas Puras, Euler creó de golpe y de manera extraordinaria varias nuevas disciplinas de investigación, apartes de las ya mencionadas, y las desarrolló metódicamente: la teoría de las series infinitas, el álgebra superior y el cálculo de variaciones. Asimismo, Euler determinó, investigando la serie armónica, la constante de su nombre, siendo la más sencilla de las series infinitas que dan el valor de ella: e = 1 + 1/1! + 1/2! + …

La Poesía y la Música han sido eternas compañeras
“Podemos volar hacia el mundo de la poesía y de la música y, nos encontramos cara a cara con la cantidad y el número, en sus ritmos y octavas,…”
Alfred North Whitehead.
emilio silvera
















 Totales: 84.905.099
Totales: 84.905.099 Conectados: 41
Conectados: 41