Las curiosidades de la Física y los números

                                                                       Hardy y Ramanujan

Comentando, sobre Ramanujan y sua cuadernos perdidos, recordé lo que dijo el matemático Richard Askey: “El trabajo de este año, mientras se estaba muriendo, era el equivalente a una vida entera de un matemático muy grande”.

Lo que él consiguió era increíble.  Los matemáticos Jonathan Borwien y Meter Borwein, en relación a la dificultad y la ardua tarea de descifrar los cuadernos perdidos, dijeron: “Que nosotros sepamos nunca se ha intentado una redacción matemática de este alcance o dificultad”.

Por mi parte creo que, Ramanujan, fue un genio matemático muy adelantado a su tiempo y que pasaran algunos años hasta que podamos descifrar al cien por ciento sus trabajos, especialmente, sus funciones modulares que guardan el secreto de la teoría más avanzada de la física moderna,   la única capaz de unir la mecánica quántica y la Gravedad.

                Las misteriosas Funciones Modulares de Ramanujan

La función theta de Ramanujan está definida como:

La siguiente se convierte en la función de Euler, que está estrechamente relacionada con la función eta de Dedekind.

“Ramanujan, trabajando en total aislamiento ( y sin formación, toda su instrucción matemática la consiguió de la lectura de un oscuro y olvidado libro de matemáticas escrito por George Carr), fue capaz de redescubrir por sí mismo lo más valioso de cien años de matemáticas occidentales y de dejarnos una obra, que consta de 4.000 fórmulas en cuatrocientas páginas densamente llenas de teoremas de increíble fuerza pero sin ningún comentario ni demostración. Tenía tal intuición que los teoremas simplemente fluían de su cerebro, sin el menor esfuerzo aparente. Solía decir que las diosas Namakkal le inspiraban la fórmulas en sueños.”

                          

“Los teóricos de cuerdas al intentar manipular los diagramas de lazos KSV ( Kikkawa-Sakita-Virasoro) creados por las cuerdas en interacción encuentran unas extrañas funciones llamadas modulares que aparecen en las ramas más distantes e “inconexas” de las matemáticas((Yutaka Taniyama ( Japón, 1927-1958) observó que cada función modular está relacionada con una curva elíptica. Esto forma la base de la conjetura Taniyama-Shimura que demostró ser una parte importante en la demostración del Último Teorema de Fermat de Andrew Wiles )). Una función que aparece continuamente en la teoría de funciones modulares se denomina función de Ramanujan, en honor al matemático Srinivasa Ramanujan, nacido en 1887 en Erode, India, cerca de Madrás.”

Una serie importante utilizada para obtener dos mil millones de cifras del número Pi (π)

Las matemáticas de Ramanujan son como una sinfonía, la progresión de sus ecuaciones era algo nunca visto, él trabajaba desde otro nivel, los números se combinaban y fluían de su cabeza a velocidad de vértigo y con precisión nunca antes conseguida por nadie.   Tenía tal intuición de las cosas que éstas simplemente fluían de su cerebro.   Quizá no los veía de una manera que sea traducible y el único lenguaje eran los números.

Como saben los físicos, los ” accidentes” no aparecen sin ninguna razón.  Cuando están realizando un cálculo largo y difícil, y entonces resulta de repente que miles de términos indeseados suman milagrosamente cero, los físicos saben que esto no sucede sin una razón más profunda subyacente.  Hoy, los físicos conocen que estos “accidentes” son una indicación de que hay una simetría en juego.  Para las cuerdas, la simetría se denomina simetría conforme, la simetría de estirar y deformar la hoja del Universo de la cuerda.

Aquí es precisamente donde entra el trabajo de Ramanujan.  Para proteger la simetría conforme original contra su destrucción por la teoría cuántica, deben ser milagrosamente satisfechas cierto número de identidades matemáticas que, son precisamente las identidades de la función modular de Ramanujan.  ¡Increíble!   Pero, cierto.

En resumen, he dicho que las leyes de la naturaleza se simplifican cuando se expresan en dimensiones más altas.   Sin embargo, a la luz de la teoría cuántica, debemos corregir algo Este sentido básico de mirar la cuestión.   El enunciado correcto sería ahora:   las leyes de la naturaleza se simplifican cuando se expresan  COHERENTEMENTE en dimensiones más altas.  El añadido de la palabra coherente es crucial.   Esta ligadura nos obliga a utilizar las funciones modulares de Ramanujan, que fijan en diez la dimensión del espacio – tiempo.   Esto, a su vez, puede darnos la clave decisiva para explicar el origen del Universo.

Einstein se preguntaba a menudo si Dios tuvo alguna elección al crear el universo.   Según los teóricos de supercuerdas, una vez que exigimos una unificación de la teoría cuántica y la relatividad general, Dios no tenía elección.  La auto consistencia por sí sola, afirman ellos, debe haber obligado a Dios a crear el universo como lo hizo.

Aunque el perfeccionamiento matemático introducido por la teoría de cuerdas ha alcanzado alturas de vértigo y ha sorprendido a los matemáticos, los críticos de la teoría aún la señalan como su punto más débil.  Cualquier teoría, afirman, debe ser verificable.   Puesto que ninguna teoría definida a la energía de Planck de 10¹⁹ miles de millones de eV es verificable, ¡La teoría de supercuerdas no es realmente una teoría! Y, de momento, parece que la debemos colocar en la estantería de las hipótesis o en la de los Hermosos Sueños.

Un ejemplo es la función de

En matemática y en Física, una función matemática o proceso no perturbativo es uno que no se puede describir con precisión por la teoría de la perturbación .

Así, el principal problema, es teórico más que experimental.  Si fuéramos suficientemente inteligentes, podríamos resolver exactamente la teoría y encontrar la verdadera solución no perturbativa de la teoría. Así lo cree un amigo mío llamado Armando que nos viene a decir que, lo de las altas energías de Planck para verificar la teoría de cuerdas, es una excusa ordenada por la ignorancia. Sin embargo, esto no nos excusa de encontrar algún medio por el que verificar experimentalmente la teoría, debemos esperar señales de la décima dimensión.

              ¿La décima dimensión? Pero, ¿No eran once?

¡Qué extraño sería que la teoría final se descubriera durante nuestra vida! El descubrimiento de las leyes finales de la Naturaleza marcará una discontinuidad en la Historia del intelecto humano, la más abrupta que haya ocurrido desde el comienzo de la ciencia moderna en el siglo XVII. ¿Podemos imaginar ahora como sería?

Steven Weinberg

Pienso en lo que sería una cuerda, esos filamentos que están más allá de los quarks y no me puedo abstraer de pensar en el electrón y el positrón que son notables por sus pequeñas masas (sólo 1/1.836 de la del protón, el neutrón, el antiprotón o antineutrón), y, por lo tanto, han sido denominados leptones (de la voz griega lentos, que significa “delgado”).

  Conocemos su masa y su carga negativa que responden a 9,1093897 (54)x10^-31kg la primera y, 1,602 177 33 (49)x10^-19 culombios, la segunda, y también su radio clásico: r₀ = e²/(mc²) = 2’82×10^-13 cm no se ha descubierto aún ninguna partícula que sea menos cursiva que el electrón (o positrón) y que lleve  una carga eléctrica, sea lo que fuese (sabemos como actúa y cómo medir sus propiedades, pero aun no sabemos qué es), tenga asociada un mínimo de masa, y que esta es la que se muestra en el electrón.

Lo cierto es que, el electrón, es una maravilla en sí mismo.  El Universo no sería como lo conocemos si el electrón (esa cosita “insignificante”), fuese distinto a como es, bastaría un cambio infinitesimal para que, por ejemplo, nosotros no pudiéramos estar aquí ahora.

¡No por pequeño, se es insignificante!

Recordémoslo, todo lo grande está hecho de cosas pequeñas.

En realidad, existen partículas que no tienen en absoluto asociada en ellas ninguna masa (es decir, ninguna masa en reposo).  Por ejemplo, las ondas de luz y otras formas de radiación electromagnéticas se comportan como partículas (Einstein en su efecto fotoeléctrico y De Broglie en la difracción de electrones.

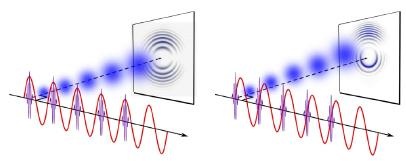
Esta manifestación en forma de partículas de lo que, de ordinario, concebimos como una onda se denomina fotón, de la palabra griega que significa “luz”.

El fotón tiene una masa de 1, una carga eléctrica de 0, pero posee un espín de 1, por lo que es un bosón. ¿Cómo se puede definir lo que es el espín? Los fotones toman parte en las reacciones nucleares, pero el espín total de las partículas implicadas antes y después de la reacción deben permanecer inmutadas (conservación del espín).  La única forma que esto suceda en las reacciones nucleares que implican a los fotones radica en suponer que el fotón tiene un espín de 1. El fotón no se considera un leptón, puesto que este termino se reserva para la familia formada por el electrón, el muón y la partícula Tau con sus correspondientes neutrinos.

Existen razones teóricas para suponer que, cuando las masas se aceleran (como cuando se mueven en órbitas elípticas en torno a otra masa o llevan a cabo un colapso gravitacional), emiten energía en forma de ondas gravitacionales.  Esas ondas pueden así mismo poseer aspecto de partícula, por lo que toda partícula gravitacional recibe el nombre de gravitón.

La fuerza gravitatoria es mucho, mucho más débil que la fuerza electromagnética.  Un protón y un electrón se atraen gravitacionalmente con sólo 1/10³⁹ de la fuerza en que se atraen electromagnéticamente. El gravitón (aún sin descubrir) debe poseer, correspondientemente, menos energía que el fotón y, por tanto, ha de ser inimaginablemente difícil de detectar.

Lo buscan de mil maneras

De todas formas, no creo que, a estas alturas, nadie pueda dudar de la existencia de los gravitones, el bosón mediador de la fuerza gravitatoria.  La masa del gravitón es o, su carga es o, y su espín de 2.  Como el fotón, no tiene antipartícula, ellos mismos hacen las dos versiones.

Tenemos que volver a los que posiblemente son los objetos más misteriosos de nuestro Universo: Los agujeros negros.  Si estos objetos son lo que se dice (no parece que se pueda objetar nada en contrario), seguramente serán ellos los que, finalmente, nos faciliten las respuestas sobre las ondas gravitacionales y el esquivo gravitón.

La colisión de Agujeros negros produce ondas que viajan a la velocidad de la luz

La onda gravitacional emitida por el agujero negro produce una ondulación en la curvatura del espacio-temporal que viaja a la velocidad de la luz transportada por los gravitones.

Hay aspectos de la física que me dejan totalmente sin habla, me obligan a pensar y me transporta de este mundo material nuestro a otro fascinante donde residen las maravillas del Universo.  Hay magnitudes asociadas con las leyes de la gravedad cuántica. La longitud de Planck, es la escala de longitud por debajo de la cual el espacio tal como lo conocemos deja de existir y se convierte en espuma cuántica.  El tiempo de Planck (1/c veces la longitud de Planck o aproximadamente 10^-43 segundos), es el intervalo de tiempo más corto que puede existir; si dos sucesos están separados por menos que esto, no se puede decir cuál sucede antes y cuál después. El área de Planck (el cuadrado de la longitud de Planck, es decir, 2’61×10^-66 cm²) juega un papel clave en la entropía de un agujero negro.

Me llama poderosamente la atención lo que conocemos como las fluctuaciones de vacío, esas oscilaciones aleatorias, impredecibles e in-eliminables de un campo (electromagnético o gravitatorio), que son debidas a un tira y afloja en el que pequeñas regiones del espacio toman prestada momentáneamente energía de regiones adyacentes y luego la devuelven.

Ordinariamente, definimos el vacío como el espacio en el que hay una baja presión de un gas, es decir, relativamente pocos átomos o moléculas.  En ese sentido, un vacío perfecto no contendría ningún átomo o molécula, pero no se puede obtener, ya que todos los materiales que rodean ese espacio tienen una presión de vapor finita.  En un bajo vacío, la presión se reduce hasta 10^-2 pascales, mientras que un alto vacío tiene una presión de 10^-2-10^-7 pascales.  Por debajo de 10^-7 pascales se conoce como un vacío ultraalto.

“Con un diámetro de casi 250 millones de años luz, o un volumen de casi 236 000 Mpc, el vacío de Bootes es uno de los vacíos más grandes que se conocen en el universo, y nos referimos a él como un super-vacío.”

Campo de Yang Mills

No puedo dejar de referirme al vacío theta (vació θ) que, es el estado de vacío de un campo gauge no abeliano (en ausencia de campos fermiónicos y campos de Higgs).

En el vacío theta hay un número infinito de estados degenerados con efecto túnel entre estos estados.  Esto significa que el vacío theta es análogo a una fundón de Bloch en un cristal.

Se puede derivar tanto como un resultado general o bien usando técnicas de instantón.  Cuando hay un fermión sin masa, el efecto túnel entre estados queda completamente suprimido.

Cuando hay campos fermiónicos con masa pequeña, el efecto túnel es mucho menor que para campos gauge puros, pero no está completamente suprimido.

Pero, a todo esto, no perdamos de vista los campos de Higgs, ahí está escondida la gran sorpresa de la Física de éste siglo que, según creo, llegará de la mano del LHC.

emilio silvera

[?]