Ludwig Boltzmann será el protagonista de hoy

Hay ecuaciones que son aparentemente insignificantes por su reducido número de exponentes que, sin embargo, ¡dicen tántas cosas…! En la mente de todos están las sencillas ecuaciones de Einstein y de Planck sobre la energía-masa y la radiación de cuerpo negro. Esa es la belleza de la que hablan los físicos cuando se refieren a “ecuaciones bellas”.

                       Maxwell

Las ecuaciones de Maxwell…,  “y se hizo la luz”

La identidad de Euler: Algunos dijeron de su ecuación: “la expresión matemática más profunda jamás escrita”, “misteriosa y sublime”, “llena de belleza cósmica”, “una explosión cerebral”.

Newton y su segunda ley que, aunque no funcione cuando nos acercamos a velocidades relativistas, rompió la marcha hacia la Gravedad.

Pitágoras y “su” teorema, también debe estar presente como lo está su teorema en las construcciones de todo el mundo y… mucho más.

Schrödinger y su función de onda que tampoco se queda atrás (aunque como la ecuación de Newton, si hablamos de velocidades relativistas…)

Bueno, E = mc², nos lleva a profundidades de la materia antes jamás vistas y nos permite sacar conclusiones como que, en un  gramo de materia está encerrada toda la energía consumida por la Humanidad durante un minuto. ¡Masa y Energía son la misma cosa!

Einstein, con esa ecuación de arriba de la relatividad general, vino a cambiar el mundo y, a partir de entonces, nació la verdadera cosmología. ¡Nos habla de tAntas cosas!

¿Qué decir de la maravillosa fórmula de la entropía de Boltzman?

S = k log W

Creo que hoy, hablaremos de ella. Boltzman con su trabajo e ingenio,  le dio a la Humanidad la herramienta para que pudiera seguir avanzando en el difícil laberinto de la Cienca, es,  sin duda, uno de los físicos más ilustres del siglo XIX.

El trabajo científico desarrollado por Boltzmann en su época crítica de transición que puso el colofón a la física “clásica” –cuya culminación podríamos situar en Maxwell– y antecedió (en pocos años) a la “nueva” física, que podemos decir que comenzó con Max Planck y Einstein. Aunque ciertamente no de la importancia de los dos últimos, la labor científica de Boltzmann tiene una gran relevancia, tanto por sus aportaciones directas (creador junto con “su amigo” Maxwell y Gibbs de la mecánica estadística, aunque sea el formulismo de éste último el que finalmente haya prevalecido; esclarecedor del significado de la entropía, etc.) como por la considerable influencia que tuvo en ilustres físicos posteriores a los que sus trabajos dieron la inspiración, como es el caso de los dos mencionados, Planck y Einstein.

Boltzmann fue un defensor a ultranza del atomismo, polemizando sobre todo con Mach y Ostwald, antiatomistas partidarios de la energética y claros exponentes de la corriente idealista de la física alemana. Tuvo que abandonar su ambiciosa idea de explicar exactamente la irreversibilidad en términos estrictamente mecánicos; pero esta “derrota”, no ocultaré que dolorosa desde el punto de vista personal, le fue finalmente muy productiva, pues de alguna manera fue lo que le llevó al concepto probabilista de la entropía. Estas primeras ideas de Boltzmann fueron reivindicadas y extendidas, en el contexto de la teoría de los sistemas dinámicos inestables, sobre todo por la escuela de Prigogine, a partir de la década de 1970.

                                                                            El joven Boltzmann

La personalidad de Boltzmann   era bastante compleja. Su estado de ánimo podía pasar de un desbordante optimismo al más negro pesimismo en cuestión de unas pocas horas. Era muy inquieto; él decía – medio en serio, medio en broma – que eso se debía a haber nacido en las bulliciosas horas finales de los alegres bailes del Martes de Carnaval, previas a los “duelos y quebrantos” (entonces) del Miércoles de Ceniza.

Su lamentable final, su suicidio en Duino (Trieste) el 5 de septiembre de 1906, muy probablemente no fue ajeno a esa retorcida personalidad, aunque su precaria salud física fue seguramente determinante a la hora de dar el trágico paso hacia el lado oscuro.

Uno de los problemas conceptuales más importantes de la física es cómo hacer compatible la evolución irreversible de los sistemas macroscópicos (el segundo principio de la termodinámica) con la mecánica reversible (las ecuaciones de Hamilton o la ecuación de Schrödinger) de las partículas (átomos o moléculas) que las constituyen. Desde que Boltzmann dedujo su ecuación en 1872, este problema ha dado lugar a muy amplios debates, y el origen de la irreversibilidad es, aún hoy en día, controvertido.

En una de sus primeras publicaciones, Boltzmann obtuvo en 1866 una expresión de la entropía, que había sido definida un año antes por Clausius, basado en conceptos mecánicos. Las limitaciones de este trabajo eran que su aplicación se restringía al estudio de los gases y que el sistema era periódico en el tiempo. Además, Boltzmann no pudo deducir de su definición de entropía la irreversibilidad del segundo principio de la termodinámica de Clausius. En 1868, basándose en las ideas probabilísticas de Maxwell, obtuvo la distribución de equilibrio de un gas de partículas puntuales bajo la acción de una fuerza que deriva de un potencial (distribución de Maxwell-Boltzmann).

                                  En el Universo, considerado como sistema cerrado, la entropía crece y…

En 1.872 publicó la denominada ecuación de Boltzmann para cuya deducción se basó, aparentemente, en ideas mecánicas. Esta ecuación contiene, sin embargo, una hipótesis no mecánica (estadística) o hipótesis del caos molecular, que Boltzmann no apreció como tal, y cuya mayor consecuencia es que, cualquiera que sea la distribución inicial de velocidad de un gas homogéneo diluido fuera del equilibrio, ésta evoluciona irreversiblemente hacia la distribución de velocidad de Maxwell. A raíz de las críticas de Loschmidt (paradoja de la reversibilidad) y Zermelo (paradoja de la recurrencia), Boltzmann acabó reconociendo el carácter estadístico de su hipótesis, y en 1877 propuso una relación entre la entropía S de un sistema de energía constante y el número de estados dinámicos W accesibles al sistema en su espacio de fases; esto es, la conocida ecuación S = k_B ln W, donde k_B es la constante de Boltzmann. En esta nota, se hace una breve descripción de la ecuación de Boltzmann y de la hipótesis del caos molecular.

                            El comportamiento de los gases siempre dio a los físicos en qué pensar

La ecuación de Boltzmann describe la evolución temporal de un gas diluido de N partículas puntuales de masa m contenidas en un volumen V que interaccionan a través de un potencial de par central repulsivo V(r) de corto alcance a. Como simplificación adicional, considérese que sobre las partículas no actúan campos externos. Si f₁(r,v,t) indica la densidad de partículas que en el tiempo t tienen un vector de posición r y velocidad v, que está normalizada en forma:

∫dr ∫dvƒ₁(r,v,t) = N

Su evolución temporal es la suma de dos contribuciones. En ausencia de interacción, las partículas que en el tiempo t tienen vector de posición r y velocidad v se encuentran, después de un intervalo de tiempo Δt, en r + v Δt y tiene la misma velocidad. Como

f₁(r + vΔt,v,t + Δt) = f₁(r,v,t)

en el límite Δt → 0 (2) se escribe:

∂₁ f₁(r,v,t) = – v∂_r f₁(r,v,t)

Que es una ecuación invariante bajo el cambio t → – t y v → – v. La evolución es, por tanto, mecánica.

Se cumplieron más de cien años desde la muerte de Boltzmann y su trabajo sigue siendo recordado. No pienso que Boltzmann creyera en la existencia real de los átomos, pero sí en su utilidad e incluso en su necesidad para comprender las leyes macroscópicas y la evolución irreversible de los fenómenos macroscópicos desde una base más fundamental que el nivel fenomenológico. Pero había quien (con autoridad) no creía ni en la existencia ni en su utilidad. Este debate no era ajeno a las tendencias ideológicas, religiosas y usos sociales de aquella época porque, en general, la ciencia es parte de la cultura y depende del momento histórico que viven los científicos, al fin y al cabo, seres humanos como los demás, influenciables por su entorno en una gran medida.

Por el siglo XIX, e incluso antes, ya se hablaba de “átomos”* y una rudimentaria teoría cinética de los gases gozaba de aceptación y utilidad científica (recordemos los trabajos de Benoulli, Dalton, Laplace, Poisson, Cauchy, Clausius, Krönig… y Maxwell). Pero fue Boltzmann quien definitivamente profundizó en la cuestión, para el estudio del equilibrio y, sobre todo, intentando explicar mecánicamente (mecano-estadísticamente) la evolución termodinámica irreversible y la descripción de los procesos de transporte ligados a ella. Y, nuevamente (por su enorme importancia) no podemos dejar de mencionar la muy singular labor que hicieron Gibbs, Einstein, Planck, Fermi y otros. Sin la motivación ideológica de Boltzmann, Gibbs elaboró una bellísima, útil y hoy dominante formulación (cuerpo de doctrina) de la termodinámica y física estadística.

                     Lorentz

Fue Lorentz quien primero utilizó la ecuación de Boltzmann y lo hizo para describir la corriente eléctrica en sólidos dando un paso significativo por encima del pionero Drude. Lorentz introdujo un modelo opuesto al browniano donde partículas ligeras como viento (electrones) se mueven chocando entre sí y con árboles gordos (tales como iones en una red cristalina); un modelo del que se han hecho estudios de interés tanto físico como matemático. Enskog (inspirándose en Hilbert) y Chapman (inspirándose en Maxwell) enseñaron cómo integrar la ecuación de Boltzmann, abriendo vías a otras diversas aplicaciones (hidrodinámica, propagación del sonido, difusión másica, calor, fricción viscosa, termoelectricidad, etc.). Recordemos que Boltzmann encontró como solución de equilibrio de su ecuación una distribución de velocidades antes descubierta por Maxwell (hoy, como reseñé anteriormente, de Maxwell-Boltzmann), por lo que concluyó que así daba base microscópica mecánica (teorema H mecano-estadístico) al segundo principio de la termodinámica (estrictamente, evolución de un sistema aislado hacia su “desorden” máximo)*.

Está claro que ningún físico que se precie de serlo puede visitar Viena sin visitar el parque Zentralfriedhof para ver la tumba de Boltzmann. Yo sí me pasé por allí. Me senté junto a la tumba; el lugar estaba desierto, y cerrando los ojos traté de conectar con la conciencia del genio. La sensación, extraña y agradable, seguramente fue creada por mi imaginación, pero creo que charlé con él en el interior de mi mente – la fuerza más potente del universo– y aquellos sentimientos, aquel momento, compensaron el esfuerzo del viaje.

En la tumba, sobre una gran lápida de mármol de color blanco con los nombres Ludwig Boltzmann y de los familiares enterrados con él, sobre el busto de Boltzmann, se puede leer la inscripción, a modo de epitafio:

Esta sencilla ecuación es la mayor aportación de Boltzmann y una de las ecuaciones más importantes de la física. El significado de las tres letras que aparecen (aparte la notación del logaritmo) es el siguiente:

• S es la entropía de un sistema.
• W es el número de microestados posibles de sus partículas elementales.
• k es una constante de proporcionalidad que hoy recibe el nombre de Constante de Boltzmann, de valor 1’3805 × 10^-23 J/K (si el logaritmo se toma en la base natural)

S = k log W

¿Qué secretos se encierran aquí? ¿Cómo nos lleva a estos pensamientos?

En esta breve ecuación se encierra la conexión entre el micro-mundo y el macro-mundo, y por ella se reconoce a Boltzmann como el padre de la rama de la física conocida como mecánica estadística.

Como todas las ecuaciones sencilla de gran trascendencia en la física (como la famosa E = mc²), hay un antes y un después de su formulación: sus consecuencias son de un calado tan profundo que cambiaron la forma de entender el mundo, y en particular, de hacer física a partir de ellas. De hecho, la sutileza de la ecuación es tal que hoy, cien años después de la muerte de su creador, se siguen investigando sus nada triviales consecuencias. Creo que lo mismo ocurrirá con α = 2πe²/ħc que, en tan reducido espacio y con tan pocos símbolos, encierra los misterios del electromagnetismo (el electrón), de la constante de Planck (la mecánica cuántica), y de la luz (la relatividad de Einstein), todo ello enterrado profundamente en las entrañas de un número: 137.

Bueno, a pesar de todo lo anterior, Schrödinger nos decía:

“La actitud científica ha de ser reconstruida, la ciencia ha de rehacerse de nuevo”

 

¡Lo grande y lo pequeño! ¡Son tantos los secretos de la Naturaleza!

Siempre hemos tenido consciencia de que en física, había que buscar nuevos paradigmas, nuevos caminos que nos llevaran más lejos. Es bien conocida la anécdota de que a finales del siglo XIX un destacado físico de la época William Thomson (1824-1907) conocido como Lord Kelvin, se atrevió a decir que solo dos pequeñas “nubecillas” arrojaban sombras sobre el majestuoso panorama de conocimiento que había construido la física clásica desde Galileo y Newton hasta ese momento: el resultado del experimento de Michelson-Morley, el cual había fallado en detectar la existencia del supuesto éter luminífero; y la radiación del cuerpo negro, i.e la incapacidad de la teoría electromagnética clásica de predecir la distribución de la energía radiante emitida a diferentes frecuencias emitidas por un radiador idealizado llamado cuerpo negro. Lo que Lord Kelvin no puedo predecir es que al tratar de disipar esas dos “nubecillas”, la física se vería irremediablemente arrastrada a una nueva física: la física moderna fundada sobre dos revoluciones en ciernes: la revolución relativista y la revolución cuántica con dos  científicos como protagonistas: Planck y Albert Einstein. Sin embargo, ha pasado un siglo y seguimos con esas dos únicas guías para continuar el camino y, resultan insuficientes para llegar a la meta que… ¡Está tan lejos!

emilio silvera

[?]

La astronomía es una de las ciencias más antiguas del ser humano, ya que desde la antigüedad las estrellas y los cuerpos de la bóveda celeste han capturado su atención y su curiosidad.

Miramos la historia y nos maravillamos de lo que nuestros antepasados pudieron llegar a conseguir en todas las áreas del saber humano. Se dice con frecuencia que, la Astronomía fue la Ciencia más antigua de todas, ya que, las maravillas del cielo siempre llamaron nuestra atención y despertaron nuestra inmensa curiosidad. Los sucesos que podían observar aquellos seres del pasado, eran fuente de miedo y de mágico asombro que, su ignorancia condujo hasta la divinidad.

Pero el tiempo pasaba, ellos seguían observando y aprendiendo de los hechos que se sucedían una y otra vez y, llegaron a comprender algunas de las cosas que, frecuentemente pasaban. Algunas vez he sentido la tentación de decir que la astronomía del Viejo Mundo estaba más adelantada que la del Nuevo Mundo porque llegaron a introducir el uso de instrumentos en la ciencia de observación de las estrellas. Por supuesto, no había telescopios -esta innovación se debe a Occidente-, pero los astrónomos chinos e islámicos sí que inventaron unos elaborados artilugios de metal para observaciones que realizaron con el propósito de hacer el mapa de los cielos.

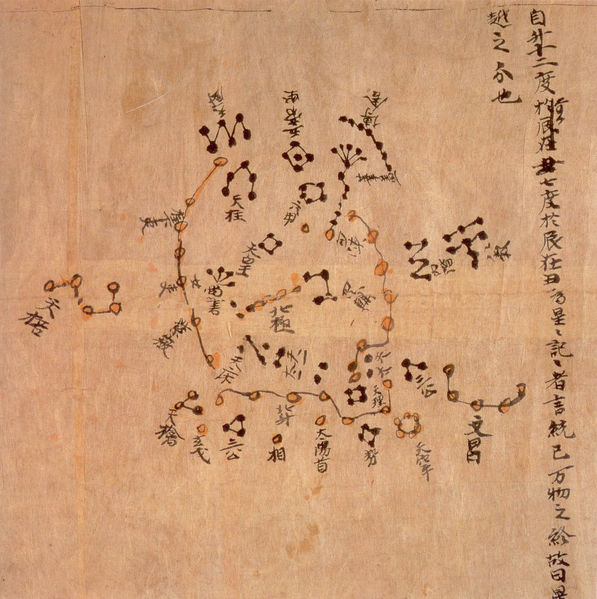
                   El mapa celeste de Dunhuang, uno de los mapas estelares más antiguos de China

Los astrónomos chinos, bajo la protección y administración del gobierno, escrutaban el cielo permanentemente y se convirtieron en los observadores más precisos y persistentes de toda la antigüedad. De hecho, las únicas referencias a algunos fenómenos celestes acontecidos entre los siglos V y X de nuestra era que han llegado a nuestros días proceden de crónicas astronómicas chinas.

Según una estadística reciente se conservan registros de más de diez mil eventos astronómicos entre ellos 270 sobre manchas solares, 300 sobre auroras boreales, 300 sobre meteoritos, 1.600 sobre eclipses de sol, 1.100 sobre eclipses de Luna, 200 sobre ocultaciones lunares, 100 sobre novas y supernovas, 400 sobre lluvias de meteoros y 4.900 sobre meteoros. Además existen cientos de documentos sobre los movimientos de la Luna y los planetas. El descubrimiento en 1967 del púlsar de la Nebulosa del Cangrejo,  relacionada con la nova de 1054 que aparece en los registros chinos, despertó el interés por esta documentación astronómica.

La gran cantidad de observaciones que recopilaron y sus métodos matemáticos fueron unas contribuciones cruciales para el posterior florecimiento de la astronomía entre los hindúes y los musulmanes, así como entre los griegos.

En la limpia atmósfera de Mesopotamia, la Astrología tomó una forma parecida a la de nuestros tiempos. Hace mas de cinco mil años que los sacerdotes-astrólogos de Babilonia se ocuparon en conocer el cielo e identificar a todas las estrellas visibles del firmamento, para ello construyeron observatorios en la llanura que se denominaban zigurats. Existen este tipo de monumentos que datan desde el 2600 a.C. como el que se muestra en la imagen. Aparecen unas tablillas de la Biblioteca de Nínive que tratan de astronomía y astrología babilónicas y caldeas. También registraron en paso del cometa Halley en el año 164 a C.

                                  En la segunda imagen vemos el zigurat de la ciudad de Ur

“El conocimiento de los cielos es heredero de la misma historia del ser humano, pues seguramente desde que el Hombre se dio cuenta del trascurso de las estaciones comenzaron a recopilarse dichos conocimientos que se fueron transmitiendo y ampliando a medida que se sucedían las generaciones ya fueran empíricos,  como consecuencia de la observación, o mitológicos, y después matemáticos. En el firmamento se buscaban presagios de los dioses, que habitaban en el mismo y era el medio que utilizaban como soporte de sus mensajes, a modo de información sobre la conveniencia de desencadenar una guerra o si se avecinaban tiempos de escasez o abundancia…”

Durante más de dos mil años los esfuerzos de los astrónomos de Mesopotamia quedaron olvidados bajo las ruinas de palacios y zigurats en lo que hoy en día es principalmente Irak. Todo lo que se sabía del tema procedía de unos pocos pasajes de la Biblia y de las informaciones dadas por algunos escritores griegos. Pero esas informaciones eran sumamente seductoras. El erudito romano Plinio el Viejo, por ejemplo, escribiò que los babilonios dieron cuenta de sus observaciones de las estrellas en las inscripciones que estuvieron realizando sobre tablillas de barro cocido con previsiones para 720.000 años, un número que duplicó varios siglos más tarde un filósofo griego, Simplicius, llegando a la asombrasa cifra de 1.440.000 años.

A mediados del siglo XIX, los arqueólogos comenzaron a desenterrar en Mesopotamia miles de estas tablillas con inscripciones con escritura cuneiforme. se calcula que cien años más tarde había medio millón de estas tablillas repartidas por los museos de todo el mundo.

En el emplazamiento de la antigua ciudad de Sippar, situada al suroeste en las cercanías de Bagdad, los arqueólogos que realizaban excavaciones allí descubrieron una biblioteca de los últimos tiempos del imperio babilónico en los que se encondia una enorme cantidad de anotaciones astronómicas y ejercicios matemáticos.

                                                                        Piedra de escritura cuneiforme

Los textos traducidos, aunque sólo son una pequeña parte de los descubrimientos, revelan la presencia en Mesopotamia de una astronomía que se remonta al menos hasta el siglo XVIII a. C., fueron los primeros en catalogar las estrellas más brillantes, esbozaron un conjunto rudimentario de constelaciones del zodiaco, reseñaron los movimientos de los cinco planetas visibles (Mercurio, Venus, Marte, Júpiter y Saturno) e hicieron el mapa de los movimientos del Sol y de la Luna con respecto a las constelaciones. Dieron a estas unos nombres que en algunos casos aún nos resultan familiares -Escorpio, Tauro, Leo.

El disco sumerio clasificado como K8538 es una prueba más del avanzado conocimiento astronómico de los sumerios. Es posible que los sumerios fueran el primer pueblo del mundo en desarrollar un calendario basado enteramente en la recurrencia de las fases completas, o sinódicas, de la Luna y también el primero que utilizó los períodos sinódicos de la Luna como la base del año de doce meses, es decir, 360 días.

                         El Disco sumerio K8538

A partir de restos de cimentaciones, se ha querido reconstruir una de las ciudades de babilonia en su época de mayor esplendor y, el resultado ha sido el que arriba podéis contemplar, aunque no fiable del todo, sí que nos habla de avanzados conocimientos para la época. Desde el principio, los babilonios supieron resilver problemas geométricos elementales de una manera algebraica. Optaron por explicar los movimientos de los cuerpos celestes de un modo básicamente temporal, lo contrario de lo que hicieron los griegos, que optaron por la explicación espacial, es decir, geométrica. De esta manera, las notaciones babilónicas -la algebraica y la del valor según la posición- se convirtieron en el fundamento de una astronomía teórica de carácter matemático. Esta astronomía reducía al mínimo los datos empíricos. trató unos fenómenos celestes bastante complicados, descubriendo unas funciones matemáticas sencillas cuya combinación describe éstos fenómenos con inteligencia y elegancia.

                                                     Página del Almagesto de Ptolomeo.

Ptolomeo

(h. 90-h. 168) Astrónomo y geógrafo griego. Su principal obra es el Almagesto, en la que expone su concepción geocéntrica del Universo. El sistema ptolemaico entronca con la tradición aristotélica, fue utilizado por astrónomos árabes y medievales y solo perdió vigencia con la aceptación de las teorías heliocéntricas propuestas por Copérnico.

La influencia babilónica en la astronomía griega, tal como se refleja en el Almagesto, incluía los nombres de muchas constelaciones; el sistema de referencia zodiacal; el grado como unidad básica para la medición de ángulos; observaciones, especialmente de eclipses, que se remontan hasta el comienzo del reinado de Nabonasar en el año 747 a. C., y varios parámetros fundamentales, incluido el valor correspondiente al mes sinódico medio.

Desde que existe sobre la Tierra, el ser humano siempre ha mirado al cielo y, ¿Qué duda nos puede caber? las observaciones astronómicas fueron anteriores a la escritura. El cielo, las estrellas, el espacio la luz… ¡qué maravillas! Los seres humanos se integraron con los sucesos del firmamento en una visión más amplia que los hacía partícipe de acontecimientos mágicos y maravillosos que ocurrían lejos, en las alturas de un espacio inalcanzable pero que, fomentó una firme configuración del cerebro que adquirió nuevas pautas y un sistema de organización que nos llevó más allá de la Tierra al querer saber de los acontecimientos celestes que nos llevó, a nuestro origen, nos transportó hasta las estrellas lejanas que sí, pudimos visitar con nuestras mentes imaginativas que poco a poco, fueron descubriendo los secretos que el Universo escondía.

emilio silvera

[?]

Sí, queridos amigos, el año 2011 fue el elegido como Año Internacional de la mujer científica, ya que, se cumplieron 100 años desde que, Marie Curie obtuviera el Nobel de Química, y, en ella se ha querido simbolizar un homenaje a todas las mujeres que a lo largo de la historia de la Ciencia, han contribuido en uno u otro campo, al saber del mundo.

Hacer aquí una mención pormenorizada de todas ellas, es imposible, y, como el modelo elegido a sido Marie Curie, aquí os dejo un reflejo de quien fue con datos tomados de diferentes fuentes:

                                                                

                    “MARIE CURIE: LA GRAN APORTACIÓN CIENTÍFICA DE LA MUJER

Marie Curie, también conocida como Maria Sklodowska-Curie, fue una química y física polaca, posteriormente nacionalizada francesa. Pionera en el campo de la radioactividad, fue la primera persona en recibir dos premios Nobel (premio Nobel de Física en 1903 y de Química en 1911) y la primera mujer en ser profesora en la Universidad de París.

Todo empezó con la elección del tema de su tesis doctoral. Tras analizarlo con su marido (el físico Pierre Curie), ambos decidieron centrarse en los trabajos del físico Henri Becquerel (al que se le concedió el Nobel de Física, junto con el matrimonio Curie, en 1903), que había descubierto que las sales de uranio transmitían unos rayos de naturaleza desconocida. Este trabajo estaba relacionado con el reciente descubrimiento de los rayos X por parte del físico Wilhelm Röntgen. Marie Curie se interesó por estos trabajos y, con la ayuda de su esposo, decidió investigar la naturaleza de las radiaciones que producían las sales de uranio.

                                                                

[?]