Como no me canso de repetir, el Universo res igual en todas partes, no importa lo alejada que las galaxias puedan estar, en todos ellas, sin excepción, rigen las mismas fuerzas y constantes, nacen y mueren las mismas estrellas que fusionan hidrógeno el elemento número 1 de la Tabla Periódica, hasta el 92 el Uranio que es el último y más complejo no artificial.

Estrellas como el Sol, solo en la Vía Láctea se calculan unos 30.000 millones, y, la mayoría tienen sus propios sistemas planetarios. Lo lógico en esos escenarios es que, alguno de los planetas esté situado en la zona habitable, y, entonces… ¡La Vida estará presente! ¿La forma? Eso será impredecible y depende de muchos factores, aunque eso sí, probablemente estará, como en la Tierra, basadas en el Carbono.

Decía muchas otras cosas, y, sobre todo creía en que todos somos ignorantes de muchas cosas. Nadie podrá saberlo todo sobre todo, y, por eso, aquel gran filósofo decía: ¡Cambiaría, todo lo que se, por la mitad de lo que no se!

René Descartes, filósofo, matemático y físico  francés, considerado el padre de la filosofía moderna, así como uno de los nombres más destacados de la revolución científica. El método científico ( del latín scientia = conocimiento; camino hacia el conocimiento) es un método de investigación usado principalmente en la producción de conocimiento en las ciencias. Para ser llamado científico, un método de investigación debe basarse en la empírica y en la medición, sujeto a los principios específicos de las pruebas de razonamiento.  El método científico es: «un método o procedimiento que ha caracterizado a la ciencia natural desde el siglo XVII, que consiste en la observación sistemática, medición, experimentación, la formulación, análisis y modificación de las hipótesis»

                   ¡Son posibles antas cosas!

Un sistema complejo es un sistema compuesto de partes interrelacionadas que como un conjunto exhiben propiedades y comportamientos no evidentes a partir de la suma de las partes individuales. Las dinámicas del desarrollo son llenos de complejidades.

Sus ecuaciones se exponían en un escaparate de la Quinta Avenida de Nueva York, y, la gente se amontonaban para verlas aunque no entendían nada.

Claro que, siendo todos los indicios muy buenos, para ser serios, no podemos decir aún que las predicciones sean definitivas y comprobables para estar seguros de que la teoría de cuerdas ha levantado realmente el velo de misterio que nos impedía ver las verdades más profundas del universo, sino que con propiedad se podría afirmar que se ha levantado uno de los picos de ese velo y nos permite vislumbrar algo de lo que nos podríamos encontrar.

La teoría de cuerdas, aunque en proceso de elaboración, ya ha contribuido con algunos logros importantes y ha resuelto algún que otro problema primordial como por ejemplo, uno relativo a los agujeros negros, asociado con la llamada entropía de Bekenstein-Hawking, que se había resistido pertinazmente durante más de veinticinco años a ser solucionada con medios más convencionales. Este éxito ha convencido a muchos de que la teoría de cuerdas está en el camino correcto para proporcionarnos la comprensión más profunda posible sobre la forma de funcionamiento del universo, que nos abriría las puertas para penetrar en espacios de increíble belleza y de logros y avances tecnológicos que ahora ni podemos imaginar.

Como he podido comentar en otras oportunidades, Edward Witten, uno de los pioneros y más destacados experto en la teoría de cuerdas, autor de la versión más avanzada y certera, conocida como teoría M, resume la situación diciendo que: “la teoría de cuerdas es una parte de la física que surgió casualmente en el siglo XX, pero que en realidad era la física del siglo XXI“.

Witten, un físico-matemático de mucho talento, máximo exponente y punta de lanza de la teoría de cuerdas, reconoce que el camino que está por recorrer es difícil y complicado. Habrá que desvelar conceptos que aún no sabemos que existen.

El hecho de que nuestro actual nivel de conocimiento nos haya permitido obtener nuevas perspectivas impactantes en relación con el funcionamiento del universo es ya en sí mismo muy revelador y nos indica que podemos estar en el buen camino revelador de la rica naturaleza de la teoría de cuerdas y de su largo alcance. Lo que la teoría nos promete obtener es un premio demasiado grande como para no insistir en la búsqueda de su conformación final.

El universo, la cosmología moderna que hoy tenemos, es debida a la teoría de Einstein de la relatividad general y las consecuencias obtenidas posteriormente por Alexandre Friedmann. El Big Bang, la expansión del universo, el universo plano y abierto o curvo y cerrado, la densidad crítica y el posible Big Crunch que, según parece, nunca será un hecho y, el universo, tendrá una “muerte” térmica, es decir, cuando el alejamiento de las galaxias lo haga más grande, más oscuro y más frío. En el cero absoluto de los -273 ºC, ni los átomos se moverán.

Un comienzo y un final que abarcará miles y miles de millones de años de sucesos universales a escalas cosmológicas que, claro está, nos afectará a nosotros, insignificantes mortales habitantes de un insignificante planeta, en un insignificante sistema solar creado por una insignificante y común estrella.

Pero… ¿somos en verdad tan insignificantes

emilio silvera

[?]

                     No todos vemos el mundo de la misma manera

Nuestra realidad es la que cada uno de nosotros percibimos, entendemos y actuamos de manera diferente en la vida. Cada uno poseemos nuestra propia realidad del mundo y de nosotros mismos. Estamos construidos a base de creencias, y esas creencias son las que influyen de manera decisiva en nuestra realidad y en nuestra conducta, por lo tanto, son las culpables de que consigamos o no nuestros objetivos. Básicamente nuestra realidad está formada por nuestras creencias.

“Nuestra tarea más urgente es dejar de identificarnos con el pensamiento, dejar de estar poseídos por él”     Eso nos aconseja Eckhart Tolle, y, no siempre resulta ser de esa manera, Hay ocasiones en la que, nuestros pensamientos son la guía que nos pueden llevar al buen destino, y, si lo que dice (que no lo aclara) está referido a los pensamientos de los otros, simplemente se trata de discernir dónde radica la verdad, en lo que nos dicen o en lo que nosotros creemos. Claro que, no todos creen siempre en lo correcto.

Lo cierto es que, la única realidad vendrá de los descubrimientos que son desvelados y nos muestran los secretos de la Naturaleza. El problema reside en que no todos, vemos las cosas de la misma manera, 0,,, ¡Es esa la solución?

 

Nosotros los humanos, nunca estamos seguros de nada y, buscando esa seguridad, creamos modelos con los que tratamos de acercarnos más y más a esa realidad que presentimos, y, para ello, encontramos las maneras de aproximarnos a esa realidad “presentida”.

Pero vayamos a algo concreto y pensemos, por ejemplo, en la técnica reiterativa que se utiliza para obtener “soluciones” en casos como el problema de los tres cuerpos (por ejemplo) tiene un inconveniente. A veces no funciona, no siempre podemos decir a priori si va a funcionar o no.

“El problema de los tres cuerpos consiste en determinar, en cualquier instante, las posiciones y velocidades de tres cuerpos, de cualquier masa, sometidos a atracción gravitacional mutua y partiendo de unas posiciones y velocidades dadas (sus condiciones iniciales son 18 valores, consistentes para cada uno de los cuerpos en: sus 3 coordenadas de posición y las tres componentes de su velocidad).”

La técnica que se aplica para “resolver” las ecuaciones diferenciales pertinentes (recordemos que no se pueden resolver analíticamente) implica realizar aproximaciones sucesivas, en las cuales, como es sabido, el primer paso del proceso de cálculo sólo da una solución aproximada; el segundo paso añade (con un poco de suerte) una corrección para obtener una aproximación más precisa de la realidad; el tercer paso nos da una aproximación aún mejor, y así sucesivamente hasta que nos parezca que la aproximación es lo suficientemente buena para el objetivo que nos hayamos propuesto. Pero nunca podremos conseguir con exactitud la “respuesta” que encaja a la perfección con el comportamiento de los objetos del mundo real en lo que se centra nuestro interés en ese determinado momento y sobre ese objetivo en particular.

En la Teoría General de la Relatividad, hay tres tensores que nos interesan para estudiar y especificar la curvatura de un espacio-tiempo curvo: el tensor de Einstein G, el tensor de Ricci y el tensor de Riemann R. El tensor de Einstein es obtenido a partir del tensor de Ricci, y a su vez el tensor de Ricci es obtenido a partir del tensor de Riemann, de modo tal que queremos estudiar y tener muy en claro lo que es el tensor de Riemann puesto que todo lo relacionado con la curvatura en un espacio multi-dimensional deriva de dicho tensor.

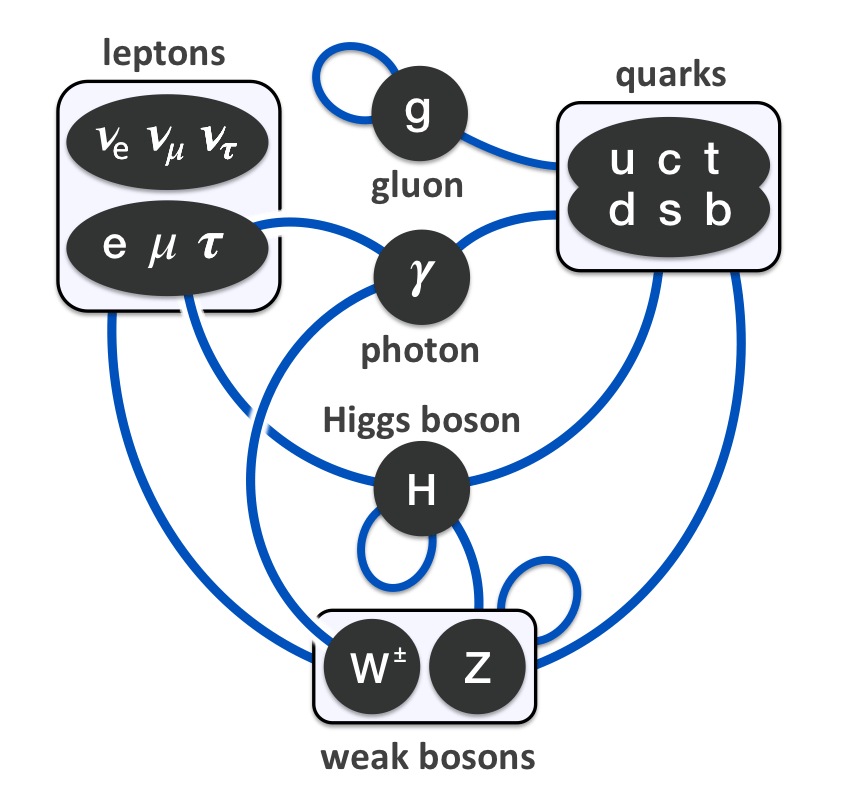
Por ejemplo:

“El modelo de partículas es una teoría cuántica de campos​ desarrollada entre 1970 y 1973 ^{[cita requerida]} basada en las ideas de la unificación y simetrías³​ que describe la estructura fundamental de la materia y el vacío considerando las partículas elementales como entes irreducibles y como ‘cuantos’ de los campos (paquetes de la energía y el impulso de los campos) cuya cinemática está regida por las cuatro interacciones fundamentales conocidas (exceptuando la gravedad, cuya principal teoría, la relatividad general, no encaja con los modelos matemáticos del mundo cuántico). La palabra “modelo” en el nombre viene de la década de 1970 cuando no había suficiente evidencia experimental que confirmara el modelo.​ Hasta la fecha, casi todas las pruebas experimentales de las tres fuerzas descritas por el modelo estándar están de acuerdo con sus predicciones. Sin embargo el modelo estándar no alcanza a ser una teoría completa de las interacciones fundamentales debido a varias cuestiones sin resolver.”

l proceso triple alfa es el proceso por el cual tres núcleos de helio (partículas alfa) se transforman en un núcleo de carbono. Esta reacción nuclear de fusión solo ocurre a velocidades apreciables a temperaturas por encima de 100 000 000 kelvin y en núcleos estelares con una gran abundancia de helio. Fred Hoyle y  William Fowler, ellos conformaron el sistema completo de cómo se fusiona el Carbono en las estrellas.

Así, ninguna idea nos ha llegado de manera instantánea y depurada en todos sus conceptos, sino que, han sido ideas que han tenido que ir siendo depuradas más y más a conseguir esa realidad que buscábamos haciendo que, el esquema encontrado, se parezca lo más posible al mundo que nos rodea y que podemos observar. Esa es, en pocas palabras la historia de la Relatividad de Einstein que juntó muchas ideas  y conceptos para conseguir sus teorías que están muy cercas de lo que el mundo es.

Lo que hacemos es sumar una serie de números -en principio, una serie de números infinitamente larga- A los matemáticos les interesa estas series infinitas para sus propios objetivos, independientemente de la importancia que puedan tener para los estudios del comportamiento de las cosas tales como los planetas que orbitan alrededor del Sol, y conocen una gran cantidad de series infinitas cuyas sumas se comportan lo suficientemente bien como para ofrecer una aproximación cada vez mejor de un número concreto.

Un buen ejemplo lo constituye uno de los procedimientos que se utilizan habitualmente para calcular el valor aproximado de π, el cociente entre la circunferencia de un círculo y su diámetro. Se puede calcular realmente el valor de π/4, con tanta precisión como se desee, sumando la serie numérica:

1 – 1/3 + 1/5 – 1/7 ….

Esto nos da una primera aproximación del valor de π que sería (4 x 1), que no es muy brillante; una segunda aproximación cuyo valor sería 2,6666… (4 x 2/3), que es algo mejor, y que, curiosamente,  se encuentra al otro lado de la respuesta «correcta»; una tercera aproximación que sería 3,46666…, y así sucesivamente. Estas aproximaciones van siendo cada vez mejores y convergen en el verdadero valor de π, en este caso concreto desde ambos lados. Pero el proceso es tedioso -la suma del primer millón de términos de la serie nos da para pi (π) un valor de 3,1415937, que sólo es correcto en sus cinco primeras cinco cifras decimales, Ni obstante, se puede calcular π de este modo hasta el grado de precisión que se desee (hasta alguna cifra de los decimales), si tienes la paciencia necesaria.

Hacemos una parada aquí para dejar una nota que nos dice que  independiente de cualquier otra consideración, lo cierto es que, en matemáticas y la teoría del caos y  entre otros temas. Si hablamos de Pi nos topamos con múltiples sorpresas y él está representado en el diseño de la doble espiral de ADN  el Efecto mariposa y la Torah, entre otras muchísimas cosas que  se escriben con Pi. Es un número misterioso que lo podemos ver por todas partes representado de una u otra manera. Desde la más remota antigüedad, fascinó a los más grandes pensadores.

No pocos están convencidos de la existencia de patrones que se repiten en los distintos órdenes de la vida. Descubrirlos implicaría, nada más y nada menos, que deducir el mundo. Yo no dejaría de lado, en todo esto la Teoría del Caos que podría definirse (¡en forma muy simplona!) como el estudio de sistemas complejos siempre cambiantes. Los resultados que consideramos ´impredecibles´ ocurrirán en sistemas que son sensibles a los cambios pequeños en sus condiciones iniciales. El ejemplo más común es conocido como “el efecto mariposa” “. La teoría supone que el batir de alas de una mariposa en la China durante un determinado período de tiempo podría causar cambios atmosféricos imperceptibles en el clima de New York.

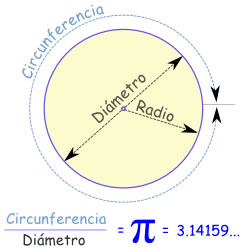
Pi es la decimosexta letra del alfabeto griego y el símbolo que representa el misterio matemático más viejo del mundo: la proporción de la circunferencia de un círculo a su diámetro.

El registro escrito conocido más temprano de la proporción viene del año 1650 antes de Cristo en Egipto, donde un escriba calculó el valor como 3.16 (con un pequeñísimo error). Aunque ahora, nosotros tenemos métodos para calcular los dígitos de pi (3.1415…) sus restos de valor exacto todavía son un misterio.

Desde 1794, cuando se estableció que Pi era irracional e infinita, las personas han estado buscando un patrón en el cordón interminable de números.

Cosa curiosa, Pi puede encontrarse por todas partes, en la astronomía, en la física, en la luz, en el sonido, en el suelo, etc. Algunos cálculos advierten que tendría más de 51 mil millones de dígitos, pero hasta el momento no se ha detectado un patrón discernible que surja de sus números. De hecho, la primera sucesión 123456789 aparece recién cerca de los 500 millones de dígitos en la proporción.

En la actualidad hay algunas computadoras super-poderosas tratando de resolver la cuestión. En el film, la computadora bautizada por Max como Euclides literalmente “estalla” al acercarse a la verdad del cálculo. ¿Y entonces?… Azar, fe, creencias, ciencia, métodos…y siempre un misterio último sin resolver.

¿El hallazgo de patrones será la respuesta? Tal vez por eso los pitagóricos amaban la forma/patrón espiral… porque ella está por todas partes en la naturaleza: en los caracoles, en los cuernos del carnero, en las volutas de humo, en la leche sobre el café, en la cara de un girasol, en las huellas digitales, en el ADN y en la Vía Láctea.

Sí, son muchas las mentes más claras que se han interesado por este fascinante número π. En su libro de 1989 “La nueva mente del emperador”, Roger Penrose comentó sobre las limitaciones en el conocimiento humano con un sorprendente ejemplo: Él conjeturó que nunca más probable es saber si una cadena de 10 7s consecutivo aparece en la expansión digital del número pi . A tan sólo 8 años más tarde, Yasumasa Kanada utiliza una computadora para encontrar exactamente esa cadena, empezando por el dígito de pi …. 17387594880th

Sin embargo, al final, algunos creen que, como todo esta relacionado, sabremos reconocer el mensaje que trata de enviarnos π y que, hasta el momento no hemos sabido comprender. Y, por otra parte, existen otras cuestiones que también estamos tratandode dilucidar para aproximarnos a esa realidad incomprendida que, estando aquí, no podemos ver. Por ejemplo:

Roger Penrose dedicó bastante más tinta en defender  los argumentos de Shadows of Mind que en escribir dicha obra. En una de sus contrarréplicas, publicada en la revista Psyche (Enero, 1996), nos ofrece una de las versiones más claras de su famoso argumento.

Supongamos que todos los métodos de razonamiento matemático humanamente asequibles válidos para la demostración de cualquier tesis están contenidos en el conjunto F. Es más, en F no sólo introducimos lo que entenderíamos como lógica matemática (axiomas y reglas de inferencia) sino todo lo matemáticamente posible para tener un modelo matemático del cerebro que utiliza esa lógica (todos los algoritmos necesarios para simular un cerebro). F es, entonces, el modelo soñado por cualquier ingeniero de AI: un modelo del cerebro y su capacidad para realizar todo cálculo lógico imaginable para el hombre. Y, precisamente, ese es el modelo soñado porque la AI Fuerte piensa que eso es un ser humano inteligente. Así, cabe preguntarse: ¿Soy F? Y parece que todos contestaríamos, a priori, que sí.

                     ¿Es la verdad inalcanzable?

Sin embargo, Roger Penrose, piensa que no, y para demostrarlo utiliza el celebérrimo teorema de Gödel, que venimos a recordar a muy grosso modo: un sistema axiomático es incompleto si contiene enunciados que el sistema no puede demostrar ni refutar (en lógica se llaman enunciados indecidibles). Según el teorema de incompletitud, todo sistema axiomático consistente y recursivo para la aritmética tiene enunciados indecidibles. Concretamente, si los axiomas del sistema son verdaderos, puede exhibirse un enunciado verdadero y no decidible dentro del sistema.

El teorema de incompletitud de Gödel es un resultado matemático que afirma que en cualquier sistema formal lo suficientemente complejo, existen enunciados que son verdaderos pero que no pueden ser demostrados dentro del propio sistema.

El teorema de Gödel o teorema de incompletitud limita las posibilidades de las matemáticas de demostrar fórmulas a través de la deducción. Dibuja el límite a lo que es posible conocer a través de la lógica formal tal y como se plantea en física y otras disciplinas.  Muy resumidamente hablando, el teorema de Gödel viene a decir que «no se puede demostrar cualquier fórmula matemática, aunque sea verdadera». Realmente el teorema de Gödel son dos teoremas que se tratan aquí…

El misterioso número Pi

Si yo soy F, como soy un conjunto de algoritmos (basados en sistemas axiomáticos consistentes y recursivos), contendré algún teorema (proposiciones que se infieren de los axiomas de mi sistema) que es indecidible. Los seres humanos nos damos cuenta, somos conscientes de que ese teorema es indecidible. De repente nos encontraríamos con algo dentro de nosotros mismos con lo que no sabríamos qué hacer. Pero en esto hay una contradicción con ser F, porque F, al ser un conjunto de algoritmos, no sería capaz de demostrar la indecibilidad de ninguno de sus teoremas por lo dicho por Gödel… Una máquina nunca podría darse cuenta de que está ante un teorema indecidible. Ergo, si nosotros somos capaces de descubrir teoremas indecidibles es porque, algunas veces, actuamos mediante algo diferente a un algoritmo: no sólo somos lógica matemática.

Claro que, cómo podría un robot imitar nuestros múltiples, locos  y dispares pensamientos:

• Los Computadores nunca podrán reemplazar la estupidez humana.
• El hombre nace ignorante,  la educación lo idiotiza.
• Una persona inteligente resuelve problemas, el genio los evita.
• Las mujeres consideran que guardar un secreto, es no revelar la fuente.
• Todas las mujeres tienen algo bonito… así sea una prima lejana.
• La felicidad es una lata de atún, pero con el abrelatas un poco distante.
• El único animal que no resiste aplausos es el mosquito.
• El amor está en el cerebro, no en el corazón.
• Definición de nostalgia “es la alegría de estar triste”.
• “Mi segundo órgano favorito es el cerebro”.

Una cosa es imaginar y otra muy distinta… ¡saber!

Vale, ¿y qué consecuencias tiene eso? Para la AI muy graves. Penrose piensa no sólo que no somos computadores sino que ni siquiera podemos tener un computador que pueda simular matemáticamente nuestros procesos mentales. Con esto Penrose no está diciendo que en múltiples ocasiones no utilicemos algoritmos (o no seamos algoritmos) cuando pensemos, sólo dice (lo cual es más que suficiente) que, habrá al menos algunas ocasiones, en las que no utilizamos algoritmos o, dicho de otro modo, hay algún componente en nuestra mente del cual no podemos hacer un modelo matemático, qué menos que replicarlo computacionalmente en un ordenador.

Además el asunto se hace más curioso cuanto más te adentras en él. ¿Cuáles podrían ser esos elementos no computables de nuestra mente? La respuesta ha de ser un rotundo no tenemos ni idea, porque no hay forma alguna de crear un método matemático para saber qué elementos de un sistema serán los indecidibles. Esto lo explicaba muy bien Turing con el famoso problema de la parada:

si tenemos un ordenador que está procesando un problema matemático y vemos que no se para, es decir, que tarda un tiempo en resolverlo, no hay manera de saber si llegará un momento en el que se parará o si seguirá eternamente funcionando (y tendremos que darle al reset para que termine). Si programamos una máquina para que vaya sacando decimales a pi, no hay forma de saber si pi tiene una cantidad de decimales tal que nuestra máquina tardará una semana, seis meses o millones de años en sacarlos todos o si los decimales de pi son infinitos. De esta misma forma, no podemos saber, por definición, qué elementos de nuestra mente son no computables. A pesar de ello, Penrose insiste en que lo no computable en nuestra mente es, nada más y nada menos, que la conciencia, ya que, explica él, mediante ella percibimos la indecibilidad de los teoremas. Es posible, ya que, aunque a priori no pudiéramos saber qué elementos no son decidibles, podríamos encontrarnos casualmente con alguno de ellos y podría ser que fuera la conciencia. Pero, ¿cómo es posible que nuestro cerebro genere conciencia siendo el cerebro algo aparentemente sujeto a computación? Penrose tiene que irse al mundo cuántico, en el que casi todo lo extraño sucede, para encontrar fenómenos no modelizables por las matemáticas y, de paso, resolver el problema del origen físico de la conciencia.

Las neuronas no nos valen. Son demasiado grandes y pueden ser modelizadas por la mecánica clásica. Hace falta algo más pequeño, algo que, por su naturaleza, exprese la incomputabilidad de la conciencia. Penrose se fija en el citoesqueleto de las neuronas formado por unas estructuras llamadas microtúbulos. Este micronivel está empapado de fenómenos cuánticos no computables, siendo el funcionamiento a nivel neuronal, si acaso, una sombra amplificadora suya, un reflejo de la auténtica actividad generadora de conciencia. ¡Qué emocionante! Pero, ¿cómo generan estos microtúbulos empapados de efectos cuánticos la conciencia? Penrose dice que no lo sabe, que ya bastante ha dicho…

O sea señor Penrose, que después de todo el camino hecho, al final, estamos cómo al principio: no tenemos ni idea de qué es lo que genera la conciencia. Sólo hemos cambiado el problema de lugar. Si antes nos preguntábamos cómo cien mil millones de neuronas generaban conciencia, ahora nos preguntamos cómo los efectos cuánticos no computables generan conciencia. Penrose dice que habrá que esperar a que la mecánica cuántica se desarrolle más. Crick o Searle nos dicen que habrá que esperar a ver lo que nos dice la neurología… ¡Pero yo no puedo esperar!

Además, ¿no parece extraño que la conciencia tenga algo que ver con el citoesqueleto de las neuronas? La función del citoesqueleto celular suele ser sustentar la célula, hacerla estable en su locomoción… ¿qué tendrá que ver eso con ser consciente? Claro que en el estado actual de la ciencia igual podría decirse: ¿qué tendrá que ver la actividad eléctrica de cien mil millones de neuronas con que yo sienta que me duele una muela?

     Todo eso está bien pero, ¿Qué es PI?

“Corta 1/9 del diámetro y construye un cuadrado sobre la longitud restante. Este cuadrado tiene el mismo área que el circulo”.

[?]