Ago
30
¿Las estrellas? ¡Sin ellas no estaríamos aquí!
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en General ~
Clasificado en General ~
 Comments (2)
Comments (2)







Es cierto que cuando vemos las cosas con cierta asiduidad y de forma permanente, esa cotidianidad nos hace perder la perspectiva y no pensamos en lo que realmente esas cosas pueden ser y, con las estrellas nos ocurre algo similar, ya que son algo más, mucho más, que simples puntitos luminosos que brillan en la oscuridad de la noche. Una estrella es una gran bola de gas luminoso que, en alguna etapa de su vida, produce energía por la fusión nuclear del hidrógeno para formar helio. El término estrella por tanto, no sólo incluye estrellas como nuestro Sol, que están en la actualidad quemando hidrógeno, sino también protoestrellas, aún no lo suficientemente calientes como para que dicha combustión haya comenzado, y varios tipos de objetos evolucionados como estrellas gigantes y supergigantes, que están quemando otros combustibles nucleares, o las enanas blancas y las estrellas nucleares, que están formadas por combustible nuclear gastado.

Muchos son los ejemplos de estrellas masivas (más de 100 masas solares) que, para no morir, eyectan material al espacio interestelar y siguen viviendo.
Estrellas masivas que expulsan gases, ya que, cuando la masa es muy grande, su propia radiación las puede destruir y, de esta manera, descongestionan la tensión y evitan un final anticipado. Arriba tenéis una estrella super-masiva que ha expulsado gases formando una nebulosa para evitar su muerte, Eta Carinae ha hecho lo mismo. Estas son estrellas que están congestionadas y, sólo la expulsión de material la puede aliviar y conseguir que siga brillando como estrella evitando explotar como supernova.
Se calcula que la masa máxima de una estrella es de unas 120 masas solares, por encima de la cual sería destruida por su propia radiación. La masa mínima es de 0,08 masas solares; por debajo de ella, los objetos no serían lo suficientemente calientes en sus núcleos como para que comience la combustión del hidrógeno, y se convertirían en enanas marrones.

De la misma forma que al calentar una pieza de metal cambia de color, al principio rojo, luego amarillo hasta llegar al blanco, el color de una estrella varia según su temperatura superficial. Las estrellas más frías son las rojas, y las mas calientes las azules. Estos colores suelen percibirse a simple vista, como por ejemplo Antares (la estrella principal de Scorpius) que es de color rojo, o Rigel (en Orión) de color azul. En astronomía se utiliza la escala Kelvin para indicar temperaturas, donde el cero absoluto es -273 grados Celsius.

El diagrama de Hertzsprung-Russell proporcionó a los astrónomos un registro congelado de la evolución de las estrellas, el equivalente astrofísico del registro fósil que los geólogos estudian en los estratos rocosos. Presumiblemente, las estrellas evolucionan de algún modo, pasan la mayor parte de su tiempo en la serie principal (la mayoría de las estrellas en la actualidad, en el brevísimo tiempo que tenemos para observar, se encuentran allí), pero empiezan y terminan su vida en alguna otra parte, entre las ramas o en el mantillo. Por supuesto, no podemos esperar para ver que esto sucede, pues el tiempo de vida, aún de estrellas de vida corta, se mide en millones de años. Hallar la respuesta exigirá conocer la física del funcionamiento estelar.
El progreso en física, mientras tanto, estaba bloqueado por una barrera aparentemente insuperable. Esto era literal: el agente responsable era conocido como la Barrera de Coulomb, y por un tiempo frustró los esfuerzos de los físicos teóricos para comprender cómo la fusión nuclear podía producir energía en las estrellas.
“La barrera de Coulomb, denominado a partir de la ley de Coulomb, nombrada así del físico Charles-Augustin de Coulomb (1736–1806), es la barrera de energía debida a la interacción electrostática que el núcleo atómico debe superar para experimentar una reacción nuclear. Esta barrera de energía es proporcionada por la energía potencial electrostática:
donde:
- k es la constante de Coulomb = 8.9876×109 N m² C−2;
- ε0 es la permeabilidad en el vacío;
- q1, q2 son las cargas de las partículas que interactúan;
- r es el radio de interacción.”
Un valor positivo de U es debido a una fuerza de repulsión, así que las partículas que interactúan están a mayores niveles de energía cuando se acercan. Un valor negativo de la energía potencial U indica un estado de ligadura, debido a una fuerza atractiva. La línea de razonamiento que conducía a esta barrera era impecable. Las estrellas están formadas en su mayor parte por hidrógeno. Esto se hace evidente en el estudio de sus espectros.) El núcleo del átomo de hidrógeno consiste en un sólo protón, y el protón contiene casi toda la masa del átomo. (Sabemos esto por los experimentos de Rutherford explicados aquí en otra ocasión). Por tanto, el protón también debe contener casi toda la energía latente del átomo de hidrógeno.
(Recordemos que la masa es igual a la Energía: E = mc2. (En el calor de una estrella los protones son esparcidos a altas velocidades -el calor significa que las partículas involucradas se mueven rápidamente- y, como hay muchos protones que se apiñan en el núcleo denso de una estrella, deben de tener muchísimos choques. En resumen, la energía del Sol y las estrellas, puede suponerse razonablemente, implica las interacciones de los protones. esta era la base de conjetura de Eddintong de que la fuente de la energía estelar “difícilmente puede ser otra cosa que energía subatómica, la cual, como se sabe, existe en abundancia en toda la materia”.
Hasta ese punto, todo iba bien, la ciencia estaba cerca de identificar la fusión termonuclear como el secreto de la energía solar. Pero aquí era donde intervenía la Barrera de Coulomb. Los protones están cargados positivamente; las partículas de igual carga se repelen entre sí; y este obstáculo parecía demasiado grande para ser superado, aun a la elevada velocidad a la que los protones se agitaban en el intenso calor del centro de las estrellas. De acuerdo con la física clásica, muy raras veces podían dos protones de una estrella ir con la rapidez suficiente para romper las murallas de sus campos de fuerza electromágnéticos y fundirse en un sólo núcleo. Los cálculos decían que la tasa de colisión de protones no podía bastar para mantener las reacciones de fusión. Sin embargo, allí estaba el Sol, con su rostro radiante y sonriente al ver el esfuerzo y las ecuaciones que decían que no podía brillar.
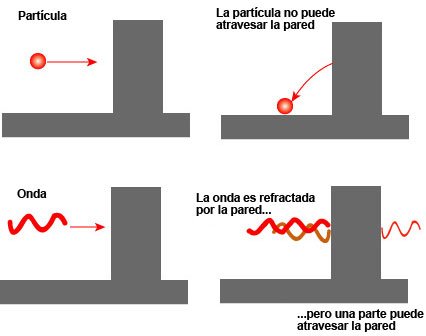

Dejemos aquí este proceso y digamos que, realmente, la mayoría de las veces el protón rebotará en la Barrera de Coulomb, pero de cuando en cuando la atravesará. Este es el “Efecto Túnel Cuántico”; que permite brillar a las estrellas. George Gamow, ansioso de explotar las conexiones entre la astronomía y la nueva física exótica a la que era adepto, aplicó las probabilidades cuánticas a la cuestión de la fusión nuclear en las estrellas y descubrió que los protones pueden superar la Barrera de Coulomb, o casi. El efecto túnel cuántico se hizo cargo de los cálculos de la desalentadora predicción clásica, que establecía la fusión de los protones a sólo una milésima de la tasa necesaria para explicar la energía liberada por el Sol, y la elevó a una décima de la tasa necesaria. Luego se tardó menos de un año para dar cuenta del deficít restante: la solución fue completada en 1929, cuando Robert Atkinson y Fritz Houterman combinaron los hallazgos de Gamow con lo que se ha llamado teoría maxwelliana de la distribución de velocidades. En la distribución maxwelliana hay siempre unas pocas partículas que se mueven mucho más rápidamente que la media y, Robert Atkinson y Fritz Houterman hallaron que estas pocas partículas veloces bastqaban para compensar la diferencia. Finalmente se hizo claro como podía romperse la Barrera de Coulomb suficientemente a menudo para que la fusión nuclear se produjese en las estrellas.

Pero la figura clave en todos estos desarrollos fue Hans Bhete, un refugiado de la Alemania nazi que había estudiado con Fermi en Roma y fue a enseñar en Cornell en EE. UU. Como su amigo Gamow, el joven Bhete era un pensador efervescente y vivaz, con tanto talento que parecía hacer su trabajo como si de un juego se tratara. Aunque no preparado en Astronomía, Bhete era un estudioso de legendaria rapidez. En 1938 ayudó al discípulo de Gamow y Edward Teller, C.L. Critchfield, a calcular una reacción que empezase con la colisión de dos protones podía generar aproximadamente la energía irradiada por el Sol, 3,86 x 1033 ergios por segundo. Así, en un lapso de menos de cuarenta años, la humanidad había progresado de la ignorancia de la existencia misma de los átomos a la comprensión del proceso de fusión termonuclear primaria que suministra energía al Sol.
Pero la reacción protón. protón no era bastante energética para explicar la luminosidad muy superior de estrellas mucho más grandes que el Sol, estrellas como las supergigantes azules de las Pléyades, que ocupan las regiones más altas del diagrama de Herptzsprung-Russell. Bhete puso remedio a esto antes de que terminase aquel el año 1938.



George Gamow Edward Reller
En abril de 1938, Bhete asistió a una conferencia organizada por Gamow y Teller que tenía el objeto de que físicos y astrónomos trabajaran juntos en la cuestión de la generación de energía en las estrellas. “Allí, los astrofísicos nos dijeron a los físicos todo que sabían sobre la constitución interna de las estrellas -recordoba Bhete-. esto era mucho (aunque) habían obtenido todos los resultados sin conocimiento de la fuente específica de energía.” De vuelta a Cornell, Bhete abordó el problema con celeridad y, en cuestión de semanas logró identificar el ciclo del Carbono, la reacción de fusión crítica que da energía a las estrellas que tiene más de una vez y media la masa del Sol.
Bhete que estaba falto de dinero, retiró el artículo que escribió sobre sus hallazgos y que ya tenía entregado en la Revista Physical Review, para entregarlo en un Concurso postulado por la Academia de Ciencias de Nueva York sobre la producción de energía en las estrellas. Por supuesto, Bhete ganó el primer Premio uy se llevó los 500 dolares que le sirvieron para que su madre pudiera emigrar a EE UU. Después lo volvió a llevar a la Revista que lo publicó y, finalmente, se lo publicaron y tal publicación le hizo ganar el Nobel. Por un tiempo, Bhete había sido el único humano que sabía por qué brillan las estrellas.
Cuando miramos al cielo y podemos contemplar extasiados esas maravillas que ahí arriba, en el espacio interestelar están brillando, y, nos da la sensación de que están haciéndonos guiños, como si quisieran mandarnos un mensaje, decirnos algo y nosotros, no pensamos en todo lo que ahí, en esos “puntitos brillantes” se está fraguando. De lo que allí ocurre, depende que los mundos tengan los materiales que en ellos están presentes y, de entre esos materiales, se destacan aquellos que por su química biológica, permiten que se pueda formar la vida a partir de unos elementos que se hicieron en los hornos nucleares de las estrellas.
El Proceso Triple Alfa

El cinturón de Orión, también llamado en algunos países hispanos “los tres reyes magos” o “las tres Marías”, es un conjunto estacionario de estrellas (asterismo) que forma parte de la constelación de Orión, y que está formado por tres estrellas específicas: Alnitak, Alnilam y Mintaka.
Y sí, es curioso que, mirando en la oscura noche como brillan las estrellas del cielo, nos atrae su titilar engañoso (es la atmósfera terrestre la que hace que lo parezca) y su brillo, Sin embargo, pocos llegan a pensar en lo que verdaderamente está allí ocurriendo. Las transformaciones de fase por fusión no cesan. Esta transformación de materia en energía es consecuencia de la equivalencia materia-energía, enunciada por Albert Einstein en su famosa fórmula E=mc2; donde E es la energía resultante, m es la masa transformada en energía, y c es la velocidad de la luz (300 000 kilómetros por segundo). La cantidad de energía que se libera en los procesos de fusión termonuclear es fabulosa. Un gramo de materia transformado íntegramente en energía bastaría para satisfacer los requerimientos energéticos de una familia mediana durante miles de años.
Es un gran triunfo del ingenio humano el saber de qué, están estructuradas las estrellas y qué materiales se están forjando allí, al inmenso calor de sus núcleos. Recuerdo aquí a aquel Presidente de la Real Society de Londres que, en una reunión multitudinaria, llegó a decir:
“Una cosa está clara, nunca podremos saber de qué están hechas las estrellas”.
El hombre se vistió de gloria con la (desde entonces) famosa frase. Creo que nada, con tiempo por delante, será imposible para nosotros.

Poco tiempo después, llegó ohan Franhufer con sus líneas espectrales y echó al traste aquellas palabras
A nuestro planeta sólo llega una ínfima fracción del calor que se genera en el Sol y, sin embargo, es más que suficiente para mantener aquí la vida. El Sol tiene materia que supone la misma que tendrían 300.000 Tierras. Nuestra estrella madre está situada a una UA (150 millones de kilómetros de nosotros) y, todas esas circunstancias y otras muchas, hacen que todo sea tal como lo vemos a nuestro alrededor. Si cualquiera de esos parámetros fuera diferente o variara tan sólo unas fracciones, seguramente la Tierra sería un planeta muerto y, nosotros, no estaríamos aquí. Sin embargo… ¡Estamos! y, gracias a ello, se pueden producir descubrimientos como los que más arriba hemos relatado y han podido y pueden existir personajes de cuyas mentes surgen ideas creadoras que nos llevan a saber cómo son las cosas.
Lo cierto es que, cada día sabemos mejor como funciona ma Naturaleza que, al fin y al cabo, es la que tiene todas las respuestas que necesitamos conocer.
Emilio Silvera V.
Ago
30
Nuestra Imaginación es mucho más rçapida que la luz
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (0)
Comments (0)
Una de las verdades perdidas en la noche de los Tiempos… ¡Es la ATLANTIDA!



¿Cuántas veces habré “visitado” Marte con la Imaginación?
Pero bajemos hasta la realidad y pongamos los pies en el suelo, veamos que cosas pasan por aquí, en nuestro mundo real que, a veces, también resultan tan fantásticas como viajar a Marte con el pensamiento.

Satélite Gravity Probe B. Dedicado a medir la curvatura del campo gravitatorio terrestre debido a la teoría de la relatividad de Einstein. La gravedad ha sido medida y comprobada de muchas maneras pero… ¡Gravedad cuántica! ¿qué es eso? La imaginación anda más rápida que los conocimientos. Sin embargo, así hemos ido avanzando en el transcurrir del Tiempo. Hace algunos miles de años algunos imaginaron la existencia del átomo y de los elementos y, ya sabéis lo que de esas cuestiones sabemos hoy.

La llamada gravedad cuántica trata de fundir en una sola las dos teorías físicas más soberbias con las que contamos, la relatividad general y la mecánica cuántica, que en el estado actual de nuestro conocimiento parecen incompatibles. Su estudio, ahora mismo, es en algunos aspectos análogo a la física de hace cien años, cuando se creía en los átomos, pero se ignaraban los detalles de su estructura.
Desde aquel día en que Kaluza, le escribió a Einstein una carta con su teoría de las cinco dimensiones, en la que unía la Gravedad con el Electromagnetismo, la puerta de las dimensiones más altas quedó abierta y a los teóricos se les regaló una herramienta maravillosa: el hiperespacio; todo es posible. Hasta el matrimonio de la relatividad general y la mecánica cuántica, allí sí es posible encontrar esa soñada teoría de la gravedad cuántica.
Así que las teorías se han embarcado a la búsqueda de un objeto audaz: buscan una teoría que describa la simplicidad primigenia que reinaba en el intenso calor del universo en sus primeros tiempos; una teoría carente de parámetros, donde estén presentes todas las respuestas. Todo debe ser contestado a partir de una ecuación básica.

Claro que saber, lo que el universo es, leyendo una ecuación, por muy ingeniosa que ésta sea y por mucho que la misma pueda abarcar… Parece poco probable. ¿Dónde radica el problema? El problema está en que la única teoría candidata no tiene conexión directa con el mundo de la observación, o no lo tiene todavía si queremos expresarnos con propiedad. La energía necesaria para ello, no la tiene ni el nuevo acelerador de partículas LHC, la máquina más potente del mundo hasta el momento.
La verdad es que la teoría que ahora tenemos, el modelo estándar, concuerda de manera exacta con todos los datos a bajas energías y contesta cosas sin sentido a altas energías. ¡Necesitamos algo más avanzado!

A pesar de su grandeza, se queda corto para que nos pueda decir, lo que necesitamos saber: Si nos habló del Bosón de Higgs, por el momento no está nada mal, y, ahora, en su nueva etapa, seguramente nos dará alguna sorpresa y nos puede desvelar algún que otro secreto de la materia, del universo que presentimos y no podemos ver.
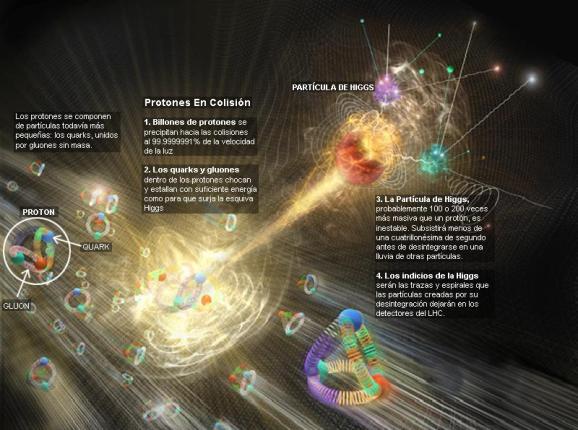
Se dijo que la función de la partícula de Higgs era la de dar masa a las partículas que carecen de ella, disfrazando así la verdadera simetría del mundo. Cuando su autor lanzó la idea a la comunidad científica, resultó además de nueva, muy extraña. El secreto de todo radica en conseguir la simplicidad: el átomo resultó ser complejo, lleno de esas infinitesimales partículas electromagnéticas que bautizamos con el nombre de electrones, y, el núcleo, una parte entre cien mil del total del átomo, resultó ser de una complejidad asombrosa. Allí los nucleones (protones y neutrones) resultaron estar hechos por tripletes de Quarks que, confinados por la fuerza nuclear fuerte, eran rtenidos por los Gluones, los Bosones transmisores de esa fuerza de la naturaleza. Así que un núcleo que contenía, a pesar de ser tan pequeño, casi toda la masa del átomo, cuando fue descubierto en todo su contenido, fue motivo de un gran asombro entre la comunidad científica. El núcleo, tan pequeño, estaba compuesto de otros objetos más pequeños aún; los quarks que estaban instalados en nubes de otras partículas llamadas gluones, y ahora queremos continuar profundizando, sospechando que después de los quarks puede haber algo más.
Nos dicen que existen lugares que llaman los Océanos de Higgs, y, por ellos, circula libremente el dichoso Bosón que, también según nos dicen, proporciona la masa al resto de las partículas. Todo el Universo está permeado por esa especie de sustancia -como el viejo éter- que los griegos llamaban Ilem cósmico y que, a medida que el tiempo avanza, le vamos cambiando el nombre. Pues bien, ahí, en ese “océano” dicen que está el Bosón dador de masas que según parece, descubrieron hace un par de años.
Bueno, la idea nueva que surgió es que el espacio entero contiene un campo, el campo de Higgs, que impregna el vacío y es el mismo en todas partes, es decir, que si miramos a las estrellas en una noche clara, estamos mirando el campo de Higgs. Las partículas influidas por este campo toman masa. Esto no es por sí mismo destacable, pues las partículas pueden tomar energía de los campos (gauge) de los que hemos comentado otras veces, tales como: del campo gravitatorio o del electromagnético.

Si llevamos un bloque de plomo a lo alto de la Torre Eiffel, el bloque adquirirá energía potencial a causa de la alteración de su posición en el campo gravitatorio de la Tierra. Como E = mc2, ese aumento de la energía potencial equivale a un aumento de la masa, en este caso la masa del sistema Tierra-bloque de plomo. Aquí hemos de añadirle amablemente un poco de complejidad a la venerable ecuación de Einstein: la masa, m, tiene en realidad dos partes; una es la masa en reposo, m0, la que se mide en el laboratorio cuando la partícula está en reposo. La partícula adquiere la otra parte de la masa en virtud de su movimiento (como los protones en el acelerador de partículas, o los muones, que aumentan varias veces su masa cuando son lanzados a velocidades cercanas a c) en los aceleradores, o en virtud de su energía potencial de campo. Vemos una dinámica similar en los núcleos atómicos. Por ejemplo, si separamos el protón y el neutrón que componen un núcleo de deuterio, la suma de las masas aumenta.
Pero la energía potencial tomada del campo de Higgs difiere en varios aspectos de la acción de los campos familiares. La masa tomada de Higgs es en realidad masa en reposo. De hecho, en la que quizá sea la versión más apasionante de la teoría del campo de Higgs, éste genera toda la masa en reposo. Otra diferencia es que la cantidad de masa que se traga del campo es distinta para las distintas partículas. Los teóricos dicen que las masas de las partículas de nuestro modelo estándar miden con qué intensidad se acoplan estas al campo de Higgs cuando interaccionan con él.
La influencia de Higgs en las masas de los quarks y de los leptones nos recuerda el descubrimiento por Pieter Zeeman, en 1.896, de la división de los niveles de energía de un electrón cuando se aplica un campo magnético al átomo. El campo (que representa metafóricamente el papel de Higgs) rompe la simetría del espacio de la que el electrón disfrutaba.

Hasta ahora no tenemos ni idea de qué reglas controlan los incrementos de masa generados por Higgs (de ahí la expectación creada -en su momento- por el nuevo acelerador de partículas LHC), pero el problema es irritante: ¿por qué sólo esas masas - las masas de los W+, W–, Z0, y el up, down, encanto, extraño, top y bottom, así como los leptones – que no forman ningún patrón obvio?
Las masas van desde la del electrón (0’0005 GeV) a la del top, que tiene que ser mayor que 91 GeV. Deberíamos recordar que esta extraña idea (el Higgs) se empleó con mucho éxito para formular la teoría electrodébil (Weinberg-Salam). Allí se propuso el campo de Higgs como una forma de ocultar la unidad de las fuerzas electromagnética y débil. En la unidad hay cuatro partículas mensajeras sin masa – los W+, W–, Z0 y el fotón – que llevan la fuerza electrodébil. Además está el campo de Higgs, y rápidamente, los W y Z absorben la esencia de Higgs y se hacen pesados; el fotón permanece intacto. La fuerza electrodébil se fragmenta en la débil (débil porque los mensajeros son muy gordos), y la electromagnética, cuyas propiedades determina el fotón, carente de masa. La simetría se rompe espontáneamente, dicen las teorías. Prefiero la descripción según la cual el Higgs oculta la simetría con su poder dador de masa.
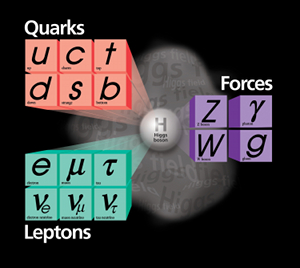
“En la actualidad, prácticamente todos los fenómenos subatómicos conocidos son explicados mediante el modelo estándar, una teoría ampliamente aceptada sobre las partículas elementales y las fuerzas entre ellas. Sin embargo, en la década de 1960, cuando dicho modelo aún se estaba desarrollando, se observaba una contradicción aparente entre dos fenómenos. Por un lado, la fuerza nuclear débil entre partículas subatómicas podía explicarse mediante leyes similares a las del electromagnetismo (en su versión cuántica). Dichas leyes implican que las partículas que actúen como intermediarias de la interacción, como el fotón en el caso del electromagnetismo y las partículas W y Z en el caso de la fuerza débil, deben ser no masivas. Sin embargo, sobre la base de los datos experimentales, los bosones W y Z, que entonces sólo eran una hipótesis, debían ser masivos.
En 1964, tres grupos de físicos publicaron de manera independiente una solución a este problema, que reconciliaba dichas leyes con la presencia de la masa. Esta solución, denominada posteriormente mecanismo de Higgs, explica la masa como el resultado de la interacción de las partículas con un campo que permea el vacío, denominado campo de Higgs. El modelo estándar quedó finalmente constituido haciendo uso de este mecanismo.”
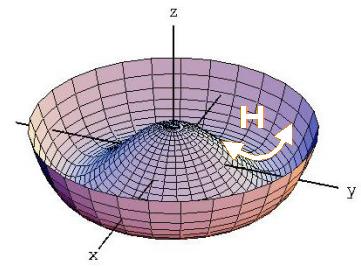
Tampoco el Higgs es una partícula especial porque sea una excitación del del campo de Higgs que nos permita explorar sus propiedades, porque en las teorías sin Higgs o con Higgs compuesto también hay excitaciones del vacío que nos permiten explorar el campo.” Eso nos dicen en el magnifico Blog de Francis (th)E mule Science’s News.
| Partícula | Símbolo | Masa (en GeV/c2) | Carga eléctrica | Espín | Interacción |
|---|---|---|---|---|---|
| Fotón | 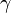 |
0 | 0 | 1 | electromagnética |
| Bosón W | W± | 80,4 | ± 1 | 1 | débil |
| Bosón Z | Z0 | 91,187 | 0 | 1 | débil |
| Gluón | g | 0 | 0 | 1 | fuerte |
Las masas de los W y Z se predijeron con éxito a partir de los parámetros de la teoría electrodébil, y las relajadas sonrisas de los físicos teóricos nos recuerdan que Hooft y Veltman dejaron sentado que la teoría entera está libre de infinitos.
Todos los intentos y los esfuerzos por hallar una pista de cuál era el origen de la masa fallaron. Feynman escribió su famosa pregunta: “¿por qué pesa el muón?”. Ahora, por lo menos, tenemos una respuesta parcial, en absoluto completa. Una voz potente y segura nos dice “¡Higgs!”. Durante más de sesenta años los físicos experimentadores se rompieron la cabeza con el origen de la masa, y ahora el campo de Higgs presenta el problema en un contexto nuevo; no se trata sólo del muón. Proporciona, por lo menos, una fuente común para todas las masas. La nueva pregunta feynmaniana podría ser: ¿cómo determina el campo de Higgs la secuencia de masas, aparentemente sin patrón, que da a las partículas de la materia?
La variación de la masa con el estado de movimiento, el cambio de masa con la configuración del sistema y el que algunas partículas (el fotón seguramente, y los neutrinos posiblemente) tengan masa en reposo nula son tres hechos que ponen en entredicho que el concepto de masa sea un atributo fundamental de la materia. Habrá que recordar aquel cálculo de la masa que daba infinito y nunca pudimos resolver; los físicos sólo se deshicieron de él “renormalizándolo”, ese truco matemático que empleam cuando no saben hacerlo bien.

¿Sabremos alguna vez cómo adquieren masa las partículas?
Ese es el problema de trasfondo con el que tenemos que encarar el problema de los quarks, los leptones y los vehículos de las fuerzas, que se diferencian por sus masas. Hace que la historia de Higgs se tenga en pie: la masa no es una propiedad intrínseca de las partículas, sino una propiedad adquirida por la interacción de las partículas y su entorno.
La idea de que la masa no es intrínseca como la carga o el espín resulta aún más plausible por la idílica idea de que todos los quarks y fotones tendrían masa cero. En ese caso, obedecerían a una simetría satisfactoria, la quiral, en la que los espines estarían asociados para siempre con su dirección de movimiento. Pero ese idilio queda oculto por el fenómeno de Higgs.

Una cosa más; hemos hablado de los bosones gauge y de su espín de una unidad. Hemos comentado también las partículas fermiónicas de la materia (espín de media unidad). ¿Cuál es el pelaje de Higgs? Es un bosón de espín cero. El espín supone una direccionalidad en el espacio, pero el campo de Higgs da masa a los objetos donde quiera que estén y sin direccionalidad. Al Higgs se le llama a veces “bosón escalar” (sin dirección) por esa razón.
La interacción débil, recordaréis, fue inventada por E. Fermi para describir la desintegración radiactiva de los núcleos, que era básicamente un fenómeno de poca energía, y a medida que la teoría de Fermi se desarrolló, llegó a ser muy precisa a la hora de predecir un enorme número de procesos en el dominio de energía de los 100 MeV. Así que ahora, con las nuevas tecnologías y energías del LHC, las esperanzas son enormes para, por fin, encontrar nuevas partículas que puedan despejar algunos interrogantes.
Recuerdo cuando andaban a la caza del Bosón de Higgs y decían “Pero todavía hay que responder montones de preguntas: ¿cuáles son las propiedades de las partículas de Higgs? y, lo que es más importante, ¿cuál es su masa? (Bueno, parece que, en el último experimento apareció se localizó un bosón con ~125 GeV que, según parece, podría ser el esquivo Hihhs)¿Cómo reconoceremos una si nos la encontramos en una colisión del LHC? ¿Cuántos tipos hay? ¿Genera el Higgs todas las masas o sólo las hace incrementarse? ¿Cómo podemos saber más al respecto? Cómo es su partícula, nos cabe esperar que la veremos ahora después de gastar más de 50.000 millones de euros en los elementos necesarios para ello.”
También a los cosmólogos les fascina la idea de Higgs, pues casi se dieron de bruces con la necesidad de tener campos escalares que participasen en el complejo proceso de la expansión del universo, añadiendo pues, un peso más a la carga que ha de soportar el Higgs.
El campo de Higgs, tal como se lo concibe ahora, se puede destruir con una energía grande, o temperaturas altas. Éstas generan fluctuaciones cuánticas que neutralizan el campo de Higgs. Por lo tanto, el cuado que las partículas y la cosmología pintan juntas de un universo primitivo puro y de resplandeciente simetría es demasiado caliente para Higgs. Pero cuando la temperatura cae bajo los 10-5 grados Kelvin o 100 GeV, el Higgs empieza a actuar y hace su generación de masas. Así, por ejemplo, antes del Higgs teníamos unos W, Z y fotones sin masa y la fuerza electrodébil unificada.

No, esto no es el Higgs, es, simplemente, una burbuja multicolor
El universo se expande y se enfría, y entonces viene el Higgs (que “engorda” los W y Z, y por alguna razón ignora el fotón) y de ello resulta que la simetría electrodébil se rompe. Tenemos entonces una interacción débil, transportada por los vehículos de la fuerza W+, W–, Z0, y por otra parte una interacción electromagnética, llevada por los fotones. Es como si para algunas partículas del campo de Higgs fuera una especie de aceite pesado a través del que se moviera con dificultad y que les hiciera parecer que tienen mucha masa. Para otras partículas, el Higgs es como el agua, y para otras, los fotones y quizá los neutrinos, es invisible.
De todas formas, es tanta la ignorancia que tenemos sobre el origen de la masa que nos agarramos como a un clavo ardiendo, en este caso, a la partícula de Higgs, que algunos han llegado a llamar “la partícula divina”. Lo mismo nos pasa con la dichosa “materia oscura” para ocultar lo que no sabemos sobre la expansión del Universo.
¡Ya veremos en qué termina todo esto!




Arriba tenemos nada más y nada menos que: a John Mather, Carlo Rubbia, Martinus Veltman, Gerardus ‘t Hooft at the Lindau Nobel Meetings 2010. Si científicos como ellos no vienen a nuestro rescate, y nos sacan del atolladero en el que estamos inmerso y hasta el cuelo de ignorancia…¡Mal hirán las cosas!
Peter Higgs, de la Universidad de Edimburgo, introdujo la idea en la física de partículas. La utilizaron los teóricos Steven Weinberg y Abdus Salam, que trabajaban por separado, para comprender cómo se convertía la unificada y simétrica fuerza electrodébil, transmitida por una feliz familia de cuatro partículas mensajeras de masa nula, en dos fuerzas muy diferentes: la QED con un fotón carente de masa y la interacción débil con sus W+, W– y Z0 de masa grande. Weinberg y Salam se apoyaron en los trabajos previos de Sheldon Glashow, quien, tras los pasos de Julian Schwinger, sabía sólo que había una teoría electrodébil unificada, coherente, pero no unió todos los detalles. Y estaban Jeffrey Goldstone y Martinus Veltman y Gerard’t Hooft. También hay otros a los que habría que mencionar, pero lo que siempre pasa, quedan en el olvido de manera injusta. Además, ¿cuántos teóricos hacen falta para encender una bombilla? La verdad es que, casi siempre, han hecho falta muchos. Recordemos el largo recorrido de los múltiples detalles sueltos y físicos que prepararon el terreno para que llegara Einstein y pudiera, uniéndolo todo, exponer su teoría relativista.

Lo cierto es que (al menos de momento), la materia y energía oscura, las supercuerdas, y el bosón de Higss, sí son la alfonbra que decía Veltman, aquel físico serío y Premio Nobel que, no confesaba con ciertas ruedas de molino. Él, quería hablar de cosas tamgibles y, tampoco le gustaban las partículas virtuales.
Sobre la idea de Peter Higgs, Veltman, uno de sus arquitectos, dice que es una alfombra bajo la que barremos nuestra ignorancia. Glashow es menos amable y lo llamó retrete donde echamos las incoherencias de nuestras teorías actuales. La objeción principal: que no tenemos la menor prueba experimental. Ahora, por fin, la tendremos con el LHC. El modelo estándar es lo bastante fuerte para decirnos que la partícula de Higgs de menor masa (podría haber muchas) debe “pesar” menor de 1 TeV, ¿por qué?; si tiene más de 1 TeV el modelo estándar se vuelve incoherente y tenemos la crisis de la unitariedad.
Después de todo esto, podríamos llegar a la conclusión de que el campo de Higgs, el modelo estándar y nuestra idea de cómo surgió el universo dependían de que se pudiera encontrar el bosón de Higgs
.Así, hace dos años, utilizando la energía de 7 TeV, por fin dijeron haber encontrado la partícula dadora de masa y, tendrían que explicar un poco más extensamente sus mecanismos y funciones para que, la gente sencilla, llegara a comprender cómo se produce ese “milagro” de que las partículas adquieran su masa al interaccionar con ese campo. El contertulio Ramón Márquez nos dice que es el “Efecto Frenado” el que produce el “milagro”, cuando las partículas deambulan por el campo de Higgs y se frenan con el roce adquiriendo la masa.
Emilio Silvera v.
Ago
30
¿La masa perdida? ¿O no entendemos nada?
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Astronomía y Astrofísica ~
Clasificado en Astronomía y Astrofísica ~
 Comments (0)
Comments (0)
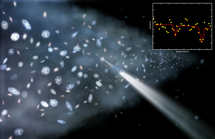
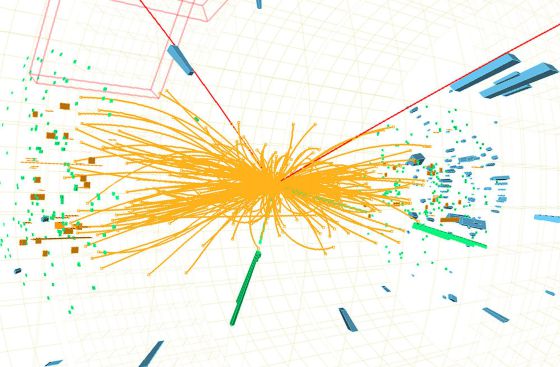
Recreación artística del WHIM en la Pared del Escultor. Fuente: NASA.
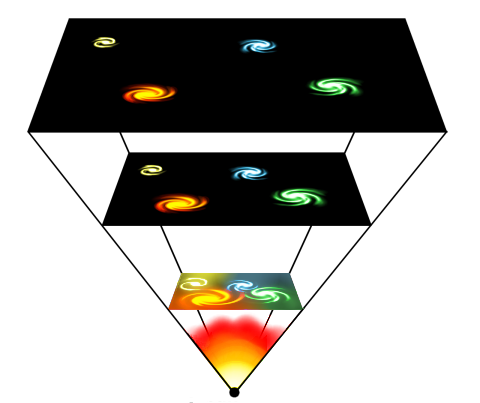
La idea de la masa perdida se introdujo porque la densidad observada de la materia en el universo está cerca del valor crítico (10-29 g/cm3). Sin embargo, hasta comienzo de los ochenta, no hubo una razón teórica firme para suponer que el universo tenía efectivamente la masa crítica. En 1981, Alan Guth, publicó la primera versión de una teoría que desde entonces se ha conocido como “universo inflacionista”. desde entonces la teoría ha sufrido cierto número de modificaciones técnicas, pero los puntos centrales no han cambiado. Lo cierto es que la idea del universo inflacionista, estableció por primera vez una fuerte presunción de que la masa del universo tenía realmente el valor crítico.

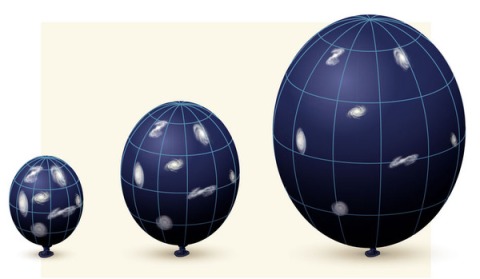
Diagrama de las tres posibles geometrías del universo: cerrado, abierto y plano, correspondiendo a valores del parámetro de densidad Ω0 mayores que, menores que o iguales a 1 respectivamente. En el universo cerrado si se viaja en línea recta se llega al mismo punto, en los otros dos no. ( Ω es lo que los cosmólogos llaman el Omega Negro, es decir, la cantidad de materia que hay en el Universo).
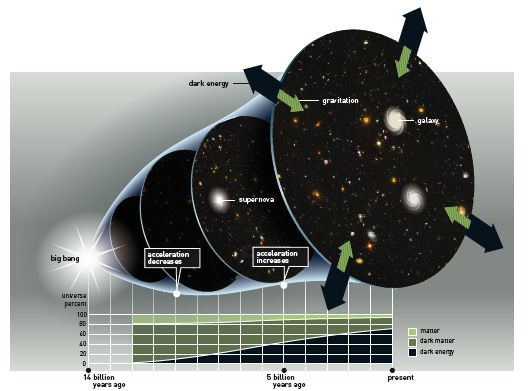
La predicción de Guht viene de las teorías que describen la congelación de la fuerza fuerte en el segundo 10-35 del Big Bang. Entre los muchos otros procesos en marcha en ese tiempo estaba una rápida expansión del universo, un proceso que vino a ser conocido como inflación. Es la presencia de la inflación la que nos lleva a la predicción de que el universo tiene que ser plano.


Se ha tratado de medir la Densidad Crítica del Universo para poder saber en qué clase de universo estamos y, parece que es plano.
Universo cerrado
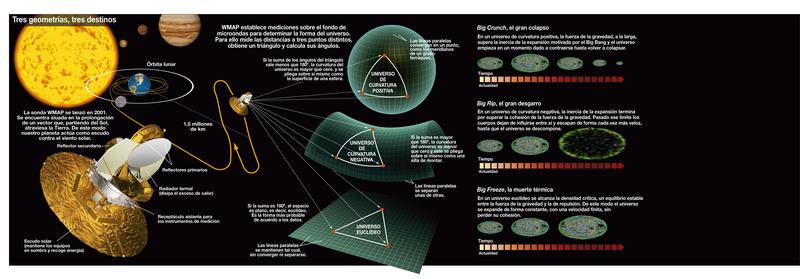
Si Ω>1, entonces la geometría del espacio sería cerrada como la superficie de una esfera. La suma de los ángulos de un triángulo exceden 180 grados y no habría líneas paralelas. Al final, todas las líneas se encontrarían. La geometría del universo es, al menos en una escala muy grande, elíptico.
En un universo cerrado carente del efecto repulsivo de la energía oscura, la gravedad acabará por detener la expansión del universo, después de lo que empezará a contraerse hasta que toda la materia en el universo se colapse en un punto. Entonces existirá una singularidad final llamada el Big Crunch, por analogía con el Big Bang. Sin embargo, si el universo tiene una gran suma de energía oscura (como sugieren los hallazgos recientes), entonces la expansión será grande.
Universo abierto

Si Ω<1, la geometría del espacio es abierta, p.ej., negativamente curvada como la superficie de una silla de montar. Los ángulos de un triángulo suman menos de 180 grados (llamada primera fase) y las líneas paralelas no se encuentran nunca equidistantes, tienen un punto de menor distancia y otro de mayor. La geometría del universo sería hiperbólica.
Incluso sin energía oscura, un universo negativamente curvado se expandirá para siempre, con la gravedad apenas ralentizando la tasa de expansión. Con energía oscura, la expansión no sólo continúa sino que se acelera. El destino final de un universo abierto es, o la muerte térmica” o “Big Freeze” o “Big Rip”, dónde la aceleración causada por la energía oscura terminará siendo tan fuerte que aplastará completamente los efectos de las fuerzas gravitacionales, electromagnéticas y los enlaces débiles.
Universo plano

Si la densidad media del universo es exactamente igual a la densidad crítica tal que Ω=1, entonces la geometría del universo es plana: como en la geometría ecuclidiana, la suma de los ángulos de un triángulo es 180 grados y las líneas paralelas nunca se encuentran.
Sin energía oscura, un universo plano se expande para siempre pero a una tasa continuamente desacelerada: la tasa de expansión se aproxima asintóticamentre a cero. Con energía oscura, la tasa de expansión del universo es inicialmente baja, debido al efecto de la gravedad, pero finalmente se incrementa. El destino final del universo es el mismo que en un universo abierto, la muerte caliente del universo, el “Big Freeze” o el “Big Rip”. En 2005, se propuso la teoría del destino del universo Fermión-Bosón, proponiendo que gran parte del universo estaría finalmente ocupada por condensado de Bose-Einstein y la quasipartícula análoga al fermión, tal vez resultando una implosión. Muchos datos astrofísicos hasta la fecha son consistentes con un universo plano.

La teoría del Big Crunch es un punto de vista simétrico del destino final del Universo. Justo con el Big Bang empezó una expansión cosmológica, esta teoría postula que la densidad media del Universo es suficiente para parar su expansión y empezar la contracción. De ser así, se vería cómo las estrellas tienden a ultravioleta, por efecto Doppler. El resultado final es desconocido; una simple extrapolación sería que toda la materia y el espacio-tiempo en el Universo se colapsaría en una singularidad espaciotemporal adimensional, pero a estas escalas se desconocen los efectos cuánticos necesarios para ser considerados -se aconseja mirar en Gravedad-Cuántica-..
Este escenario permite que el Big Bang esté precedido inmediatamente por el Big Crunch de un Universo precedente. Si esto ocurre repetidamente, se tiene un universo oscilante. El Universo podría consistir en una secuencia infinita de Universos finitos, cada Universo finito terminando con un Big Crunch que es también el Big Bang del siguiente Universo. Teóricamente, el Universo oscilante no podría reconciliarse con la segunda ley de la termodinámica:

la entropía aumentaría de oscilación en oscilación y causaría la muerte caliente. Otras medidas sugieren que el Universo no es cerrado. Estos argumentos indujeron a los cosmólogos a abandonar el modelo del Universo oscilante. Una idea similar es adoptada por el modelo cíclico, pero esta idea evade la muerte caliente porque de una expansión de branas se diluye la entropía acumulada en el ciclo anterior.
Como podéis comprobar por todo lo anteriormente leído, siempre estamos tratando de saber en qué universo estamos y pretendemos explicar lo que pudo pasar desde aquel primer momento que no hemos podido comprender de manera exacta y científicamente autosuficiente para que sea una ley inamovible del nacimiento del universo. Simplemente hemos creado modelos que se acercan de la mejor manera a lo que pudo ser y a lo que podría ser.
Ago
30
¡Cuántas maravillas! Y, nuestra Mente, entre ellas
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (0)
Comments (0)
Parafraseando a Hilbert: ¡Tenemos que saber, y sabremos!
En la tumba de David Hilbert (1862-1943), en el cementerio de Gotinga (Alemania), dice:

“Debemos saber. Sabremos”.
Hilbert nos hacía su planteamiento que era obtener la respuesta a tres importantes preguntas:
- ¿Son las matemáticas completas, es decir cualquier proposición puede ser probada o rechazada?
- ¿Son las matemáticas consistentes, es decir no es posible demostrar algo falso?
- ¿Son las matemáticas decidibles, es decir cualquier proposición se puede demostrar como cierta o falsa tras una secuencia finita de pasos?”








La importancia de la Simetría en la Naturaleza. Y, no digamos de saber emplear la lógica


No sería descabellado decir que las simetrías que vemos a nuestro alrededor, desde un arco iris a las flores y a los cristales, pueden considerarse en última instancia como manifestaciones de fragmentos de la teoría deca-dimensional original. Riemann y Einstein habían confiado en llegar a una comprensión geométrica de por qué las fuerzas pueden determinar el movimiento y la naturaleza de la materia. Por ejemplo, la fuerza de Gravedad generada por la presencia de la materia, determina la geometría del espacio-tiempo.

La teoría de cuerdas plantea que las partículas subatómicas – electrones, fotones, quarks… – no serían puntuales, sino que estados vibracionales en forma de pequeñas cuerdas o filamentos. A veces parece que la ciencia tiene las respuestas a todos los fenómenos que ocurren en nuestro planeta y en el Universo
Dado el enorme poder de sus simetrías, no es sorprendente que la teoría de supercuerdas sea radicalmente diferente de cualquier otro de física. De hecho, fue descubierta casi por casualidad. Muchos físicos han comentado que si este accidente fortuito no hubiese ocurrido, entonces la teoría no se hubiese descubierto hasta bien entrado el siglo XXI. Esto es así porque supone una neta desviación de todas las ideas ensayadas en este siglo. No es una extensión natural de tendencias y teorías populares en este siglo que ha pasado; permanece aparte.
Por el contrario, la teoría de la relatividad general de Einstein tuvo una evolución normal y lógica. En primer lugar, su autor, postula el principio de equivalencia. Luego reformuló principio físico en las matemáticas de una teoría de campos de la gravitación basada en los campos de Faraday y en el tensor métrico de Riemann. Más tarde llegaron las “soluciones clásicas”, tales el agujero negro y el Big Bang. Finalmente, la última etapa es el intento actual de formular una teoría cuántica de la gravedad. Por lo tanto, la relatividad general siguió una progresión lógica, un principio físico a una teoría cuántica.

Geometría → teoría de campos → teoría clásica → teoría cuántica.
Contrariamente, la teoría de supercuerdas ha estado evolucionando hacia atrás su descubrimiento accidental en 1.968. Esta es la razón de que nos parezca extraña y poco familiar, estamos aún buscando un principio físico subyacente, la contrapartida del principio de equivalencia de Einstein.
La teoría nació casi por casualidad en 1.968 cuando dos jóvenes físicos teóricos, Gabriel Veneziano y Mahiko Suzuki, estaban hojeando independientemente libros de matemáticas. Figúrense ustedes que estaban buscando funciones matemáticas que describieran las interacciones de partículas fuertemente interactivas. Mientras estudiaban en el CERN, el Centro Europeo de Física Teórica en Ginebra, Suiza, tropezaron independientemente con la función beta de Euler, una función matemática desarrollada en el S. XIX por el matemático Leonhard Euler. Se quedaron sorprendidos al que la función beta de Euler ajustaba casi todas las propiedades requeridas para describir interacciones fuertes de partículas elementales.
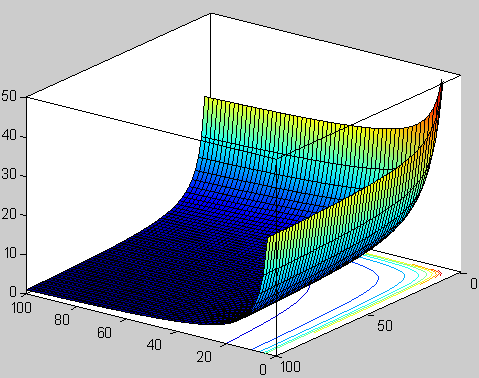
Función beta. Representación de la función valores reales positivos de x e y.
Según he leído, durante un almuerzo en el Lawrence Berkeley Laboratory en California, con una espectacular vista del Sol brillando sobre el puerto de San Francisco, Suzuki le explicó a Michio Kaku mientras almorzaban la excitación de , prácticamente por casualidad, un resultado parcialmente importante. No se suponía que la física se pudiera hacer de ese modo casual.
Tras el descubrimiento, Suzuki, muy excitado, mostró el hallazgo a un físico veterano del CERN. Tras oír a Suzuki, el físico veterano no se impresionó. De hecho le dijo a Suzuki que otro físico joven (Veneziano) había descubierto la misma función unas semanas antes. Disuadió a Suzuki de publicar su resultado. Hoy, esta función beta se conoce con el de modelo Veneziano, que ha inspirado miles de artículos de investigación iniciando una importante escuela de física y actualmente pretende unificar todas las leyes de la física.
Gabriele Veneziano

Mahiko Suzuki
En 1.970, el Modelo de Veneziano-Suzuki (que contenía un misterio), fue parcialmente explicado cuando Yoichiro Nambu, de la Universidad de Chicago, y Tetsuo Goto, de la Nihon University, descubrieron que una cuerda vibrante yace detrás de sus maravillosas propiedades. Así que, como la teoría de cuerdas fue descubierta atrás y por casualidad, los físicos aún no conocen el principio físico que subyace en la teoría de cuerdas vibrantes y sus maravillosas propiedades. El último paso en la evolución de la teoría de cuerdas (y el primer paso en la evolución de la relatividad general) aún está pendiente de que alguien sea capaz de darlo.
Así, Witten dice:
“Los seres humanos en el planeta tierra nunca dispusieron del marco conceptual que les llevara a concebir la teoría de supercuerdas de manera intencionada, surgió por razones del azar, por un feliz accidente. Por sus propios méritos, los físicos c del siglo XX no deberían haber tenido el privilegio de estudiar esta teoría muy avanzada a su tiempo y a su conocimiento. No tenían (ni tenemos mismo) los conocimientos y los prerrequisitos necesarios para desarrollar dicha teoría, no tenemos los conceptos correctos y necesarios.”
¿Se podrá verificar la Teoría de cuerdas? Sicen que se necesitaría la energía de 1019 GeV Lo que no tenemos
Actualmente, como ha quedado dicho en este mismo , Edwar Witten es el físico teórico que, al frente de un equipo de físicos de Princeton, lleva la bandera de la teoría de supercuerdas con aportaciones muy importantes en el desarrollo de la misma. De todas las maneras, aunque los resultados y avances son prometedores, el camino por andar es largo y la teoría de supercuerdas en su conjunto es un edificio con muchas puertas cerradas de las que no tenemos las llaves acceder a su interior y mirar lo que allí nos aguarda.
Ni con colección de llaves podremos abrir la puerta que nos lleve a la Teoría cuántica de la gravedad que, según dicen, subyace en la Teoría M, la más moderna versión de la cuerdas expuesta por E. Witten y que, según contaron los que estuvieron presentes en su presentación, Witten les introdujo en un “universo” fascinante de inmensa belleza que, sin embargo, no puede ser verificado por el experimento.
El problema está en que nadie es lo suficientemente inteligente para resolver la teoría de campos de cuerdas o cualquier otro enfoque no perturbativo de teoría. Se requieren técnicas que están actualmente más allá de nuestras capacidades. Para encontrar la solución deben ser empleadas técnicas no perturbativas, que son terriblemente difíciles. Puesto que el 99 por ciento de lo que conocemos sobre física de altas energías se basa en la teoría de perturbaciones, esto significa que estamos totalmente perdidos a la hora de encontrar la verdadera solución de la teoría.
¿Por qué diez dimensiones?
Uno de los secretos más profundos de la teoría de cuerdas, que aún no es bien comprendido, es por qué está definida sólo en diez, once y veintiséis dimensiones. Si calculamos cómo se rompen y se vuelven a juntar las cuerdas en el espacio N-dimensional, constantemente descubrimos que pululan términos absurdos que destruyen las maravillosas propiedades de la teoría. Afortunadamente, estos términos indeseados aparecen multiplicados por (N-10). Por consiguiente, para hacer que desaparezcan estas anomalías, no tenemos otra elección cuántica que fijar N = 10. La teoría de cuerdas, de hecho, es la única teoría cuántica conocida que exige completamente que la dimensión del espacio-tiempo esté fijada en un único, el diez.
Por desgracia, los teóricos de cuerdas están, por el momento, completamente perdidos explicar por qué se discriminan las diez dimensiones. La respuesta está en las profundidades de las matemáticas, en un área denominada funciones modulares.
Al manipular los diagramas de lazos1 de Kikkawa, Sakita y Virasoro creados por cuerdas en interacción, allí están esas extrañas funciones modulares en las que el 10 aparecen en los lugares más extraños. Estas funciones modulares son tan misteriosas como el hombre que las investigó, el místico del este. Quizá si entendiéramos mejor el trabajo de este genio indio, comprenderíamos por qué vivimos en nuestro universo actual.

Cuando nos asomamos a la Teoría de cuerdas, entramos en un “mundo” lleno de sombras en los que podemos ver brillar, a lo lejos, un resplandor cegador. Todos los físicos coinciden en el hecho de que es una teoría muy prometedora y de la que parece se podrán obtener buenos rendimientos en el futuro pero, de , es imposible verificarla.
El misterio de las funciones modulares podría ser explicado por quien ya no existe, Srinivasa Ramanujan, el hombre más extraño del mundo de los matemáticos. Igual que Riemann, murió antes de cumplir cuarenta años, y Riemann antes que él, trabajó en total aislamiento en su universo particular de números y fue capaz de reinventar por sí mismo lo más valioso de cien años de matemáticas occidentales que, al estar aislado del mundo en las corrientes principales de los matemáticos, le eran totalmente desconocidos, así que los buscó sin conocerlos. Perdió muchos años de su vida en redescubrir matemáticas conocidas.


Dispersas oscuras ecuaciones en sus cuadernos están estas funciones modulares, que figuran entre las más extrañas jamás encontradas en matemáticas. Ellas reaparecen en las ramas más distantes e inconexas de las matemáticas. Una función que aparece una y otra vez en la teoría de las funciones modulares se denomina (como ya he dicho otras veces) hoy día “función de Ramanujan” en su honor. extraña función contiene un término elevado a la potencia veinticuatro.

La magia esconde una realidad
El 24 aparece repetidamente en la obra de Ramanujan. Este es un ejemplo de lo que las matemáticas llaman números mágicos, que aparecen continuamente donde menos se esperan por razones que nadie entiende. Milagrosamente, la función de Ramanujan aparece también en la teoría de cuerdas. El número 24 que aparece en la función de Ramanujan es también el origen de las cancelaciones milagrosas que se dan en la teoría de cuerdas. En la teoría de cuerdas, cada uno de los veinticuatro modos de la función de Ramanujan corresponde a una vibración física de la cuerda. Cuando quiera que la cuerda ejecuta sus movimientos complejos en el espacio-tiempo dividiéndose y recombinándose, deben satisfacerse un gran número de identidades matemáticas altamente perfeccionadas. Estas son precisamente las entidades matemáticas descubiertas por Ramanujan. Puesto que los físicos añaden dos dimensiones más cuando cuentan el número total de vibraciones que aparecen en una teoría relativista, ello significa que el espacio-tiempo debe tener 24 + 2 = 26 dimensiones espacio-temporales.

Comprender este misterioso factor de dos (que añaden los físicos), consideramos un rayo de luz que tiene dos modos físicos de vibración. La luz polarizada puede vibrar, por ejemplo, o bien horizontal o bien verticalmente. Sin embargo, un campo de Maxwell relativista Aµ cuatro componentes, donde µ = 1, 2, 3, 4. Se nos permite sustraer dos de estas cuatro componentes utilizando la simetría gauge de las ecuaciones de Maxwell. Puesto que 4 – 2 = 2, los cuatro campos de Maxwell originales se han reducido a dos. Análogamente, una cuerda relativista vibra en 26 dimensiones. Sin embargo, dos de estos modos vibracionales pueden ser eliminados rompemos la simetría de la cuerda, quedándonos con 24 modos vibracionales que son las que aparecen en la función de Ramanujan.

“En matemática, la función theta de Ramanujan generaliza la forma de las funciones theta de Jacobi, a la vez que conserva sus propiedades generales. En particular, el producto triple de Jacobi se puede escribir elegantemente en términos de la función theta de Ramanujan. La función toma nombre de Srinivasa Ramanujan, y fue su última gran contribución a las matemáticas.”
Como un revoltijo de hilos entrecruzados que son difíciles de seguir, así son las matemáticas de la teoría de cuerdas
Cuando se generaliza la función de Ramanujan, el 24 queda reemplazado por el 8. Por lo tanto, el número crítico para la supercuerda es 8+2=10. Este es el origen de la décima dimensión que exige la teoría. La cuerda vibra en diez dimensiones porque requiere estas funciones de Ramanujan generalizadas para permanecer auto consistente. Dicho de otra manera, los físicos no tienen la menor idea de por qué 10 y 26 dimensiones se seleccionan como dimensión de la cuerda. Es como si hubiera algún tipo de numerología profunda que se manifestara en estas funciones que nadie comprende. Son precisamente estos números mágicos que aparecen en las funciones modulares elípticas los que determinan que la dimensión del espacio-tiempo sea diez.
En el análisis final, el origen de la teoría decadimensional es tan misterioso como el propio Ramanujan. Si alguien preguntara a cualquier físico del mundo por qué la naturaleza debería existir en diez dimensiones, estaría obligado a responder “no lo sé”. Se sabe en términos difusos, por qué debe seleccionarse alguna dimensión del espacio tiempo (de lo contrario la cuerda no puede vibrar de una cuánticamente autoconsistente), pero no sabemos por qué se seleccionan estos números concretos.
Godfrey Harold Hardy
G. H. Hardy, el mentor de Ramanujan, trató de estimar la capacidad matemática que poseía Ramanujan. Concedió a David Hilbert, universalmente conocido y reconocido uno de los mayores matemáticos occidentales del siglo XIX, una puntuación de 80. A Ramanujan le asignó una puntuación de 100. Así mismo, Hardy se concedió un 25.
Por desgracia, ni Hardy ni Ramanujan parecían interesados en la psicología a los procesos de pensamiento mediante los cuales Ramanujan descubría estos increíbles teoremas, especialmente cuando diluvio material brotaba de sus sueños con semejante frecuencia. Hardy señaló:
“Parecía ridículo importunarle sobre como había descubierto o ese teorema conocido, cuando él me estaba mostrando media docena cada día, de nuevos teoremas”.
Hardy recordaba vivamente:
-”Recuerdo una vez que fui a visitarle cuando estaba enfermo en Putney. Yo había tomado el taxi 1.729, y comenté que el numero me parecía bastante feo, y que esperaba que no fuese mal presagio.”
– No. -Replicó Ramanujan postrado en su cama-. Es un número muy interesante; es el número más pequeño expresable una suma de dos cubos en dos formas diferentes.
(Es la suma de 1 x 1 x 1 y 12 x 12 x 12, y la suma de 9 x 9 x 9 y 10 x 10 x 10).
Era capaz de recitar en el acto teoremas complejos de aritmética cuya demostración requeriría un ordenador moderno.
En 1.919 volvió a casa, en la India, donde un año más tarde murió enfermo.
El legado de Ramanujan es su obra, que consta de 4.000 fórmulas en cuatrocientas páginas que llenan tres volúmenes de notas, todas densamente llenas de teoremas de increíble fuerza pero sin ningún comentario o, lo que es más frustrante, sin ninguna demostración. En 1.976, sin embargo, se hizo un nuevo descubrimiento. Ciento treinta páginas de borradores, que contenían los resultados del último año de su vida, fueron descubiertas por casualidad en una caja en el Trinity Collage. Esto se conoce ahora con el de “Cuaderno Perdido” de Ramanujan.

Comentando cuaderno perdido, el matemático Richard Askey dice:
“El de este año, mientras se estaba muriendo, era el equivalente a una vida entera de un matemático muy grande”. Lo que él consiguió era increíble. Los matemáticos Jonathan Borwien y Meter Borwein, en relación a la dificultad y la ardua tarea de descifrar los cuadernos perdidos, dijeron: “Que nosotros sepamos nunca se ha intentado una redacción matemática de este alcance o dificultad”.
Por mi parte creo que, Ramanujan, fue un genio matemático muy adelantado a su tiempo y que pasaran algunos años que podamos descifrar al cien por ciento sus trabajos, especialmente, sus funciones modulares que guardan el secreto de la teoría más avanzada de la física moderna, la única capaz de unir la mecánica quántica y la Gravedad.
Fórmula de Ramanujan determinar los decimales de pi
Las matemáticas de Ramanujan son como una sinfonía, la progresión de sus ecuaciones era algo nunca vísto, él trabajaba otro nivel, los números se combinaban y fluían de su cabeza a velocidad de vértigo y con precisión nunca antes conseguida por nadie. Tenía tal intuición de las cosas que éstas simplemente fluían de su cerebro. Quizá no los veía de una manera que sea traducible y el único lenguaje eran los números.
Como saben los físicos, los “accidentes” no aparecen sin ninguna razón. Cuando están realizando un cálculo largo y difícil, y entonces resulta de repente que miles de términos indeseados suman milagrosamente cero, los físicos saben que esto no sucede sin una razón más profunda subyacente. Hoy, los físicos conocen que estos “accidentes” son una indicación de que hay una simetría en juego. Para las cuerdas, la simetría se denomina simetría conforme, la simetría de estirar y deformar la hoja del Universo de la cuerda.

Nuestro mundo asimétrico contiene hermosas simetrías
Aquí es precisamente donde entra el trabajo de Ramanujan. Para proteger la simetría conforme original contra su destrucción por la teoría cuántica, deben ser milagrosamente satisfechas cierto de identidades matemáticas que, son precisamente las identidades de la función modular de Ramanujan. ¡Increíble! Pero, cierto.

Aunque el perfeccionamiento matemático introducido por la teoría de cuerdas ha alcanzado alturas de vértigo y ha sorprendido a los matemáticos, los críticos de la teoría aún la señalan su punto más débil. Cualquier teoría, afirman, debe ser verificable. Puesto que ninguna teoría definida a la energía de Planck de 1019 miles de millones de eV es verificable, ¡La teoría de cuerdas no es realmente una teoría!
El principal problema, es teórico más que experimental. Si fuéramos suficientemente inteligentes, podríamos resolver exactamente la teoría y encontrar la verdadera solución no perturbativa de la teoría. Sin embargo, esto no nos excusa de encontrar algún medio por el que verificar experimentalmente la teoría, debemos esperar señales de la décima dimensión.

Volviendo a Ramanujan…
Es innegable lo sorprendente de su historia, un muchacho pobre con escasa preparación y arraigado como pocos a sus creencias y tradiciones, es considerado como una de los mayores genios de las matemáticas del siglo XX. Su legado a la teoría de números, a la teoría de las funciones theta y a las series hipergeométricas, además de ser invaluable aún sigue estudiándose por muchos prominentes matemáticos de todo el mundo. Una de sus fórmulas más famosas es la que aparece más arriba en el lugar número 21 de las imágenes expuestas y utilizada para realizar aproximaciones del Pi con más de dos millones de cifras decimales. Otra de las sorprendentes fórmulas descubiertas por Ramanujan es un igualdad en que era “casi” un número entero (la diferencia era de milmillonésimas). De hecho, durante un tiempo se llegó a sospechar que el número era efectivamente entero. No lo es, pero este hallazgo sirvió de base la teoría de los “Cuasi enteros”. A veces nos tenemos que sorprender al comprobar hasta donde puede llegar la mente humana que, prácticamente de “la nada”, es capaz de sondear los misterios de la Naturaleza para dejarlos al descubierto ante nuestros asombros ojos que, se abren como platos ante tales maravillas.
Publica: emilio silvera















 Totales: 75.487.304
Totales: 75.487.304 Conectados: 56
Conectados: 56





























