Monopolos magnéticos

Cuando el LHC se ponía en marcha, algunos hablaron de que se podían crear monopolos magnéticos.

“Desde el punto de vista teórico, uno se siente inclinado a creer que los monopolos han de existir, debido a la belleza matemática de su concepción. Aunque se han hecho varias tentativas de hallarlos, ninguna ha tenido éxito. Debiera deducirse de ello que la belleza matemática en sí no es razón suficiente para que la naturaleza aplique una teoría. Nos queda aún mucho que aprender en la investigación de los principios básicos de la naturaleza.”

 

 

P. A. M. DIRAC, 1981

 

En los años treinta del pasado siglo Paul Dirac realizó unos cálculos teóricos que indicaban que si existieran los monopolos magnéticos, entonces se podría cuantizar fácilmente la carga del electrón. Bastaría que existiera un sólo monopolo magnético en el Universo para que los electrones tuvieran la carga que tienen y no otra.

 

Las imágenes de arriba vinieron acompañada de la noticia siguiente:

 

“Afirman haber podido detectar por primera vez monopolos magnéticos como un estado de la materia que se daría a partir de una disposición especial de los momentos magnéticos dentro de un cristal a baja temperatura.”

 

En realidad, cohabitamos una naturaleza llena de fenómenos enigmáticos. Uno de estos fenómenos es la asimetría insólita que se observaba entre el magnetismo y la electricidad: no hay cargas magnéticas comparables a las cargas eléctricas. Nuestro mundo está lleno de partículas cargadas eléctricamente, como los electrones o los protones, pero nadie ha detectado jamás una carga magnética aislada. El objeto hipotético que la poseería se denomina monopolo magnético.

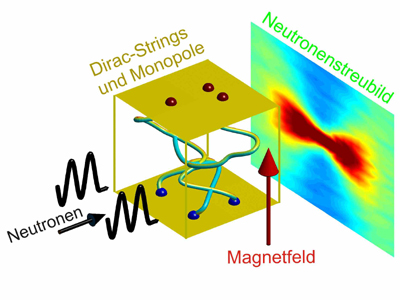
         Montaje experimental. Foto: HZB, D.J.P. Morris y A. Tennant.

El grupo de investigadores dispuso un montaje experimental especial para poder detectar estas cuerdas de Dirac. Hicieron que un chorro de neutrones impactara sobre una muestra a la que aplicaban un campo magnético. En el interior de la muestra se formaban cuerdas de Dirac que dispersaban los neutrones con un patrón específico que delataba su presencia.

La muestra era un cristal de titanato de disprosio. La estructura cristalina de este compuesto tiene una geometría notable, de tal modo que los momentos magnéticos de su interior se organizan en lo que se llama un “espagueti de espines”. El nombre viene de la ordenación de los dipolos, que forman una red de tubos contorsionados (cuerdas) por los que se transporta flujo magnético.

Estos tubos pueden “hacerse visibles” cuando los neutrones interaccionan con ellos; pues los neutrones, aunque no tienen carga eléctrica, sí tienen momento magnético. El patrón de dispersión de los neutrones obtenido es una representación recíproca de las cuerdas de Dirac contenidas en la muestra. Con el campo magnético aplicado los investigadores podían controlar la simetría y orientación de las cuerdas. A temperaturas de entre 0,6 a 2 grados Kelvin los investigadores pudieron ver pruebas de la existencia de monopolos magnéticos (la temperatura suele ser la peor enemiga del magnetismo, pues tiene a desordenarlo todo) en forma de este tipo de cuerdas según se acaba de describir.

En cuestiones como estas de los Monopolos magnéticos, uno puede pensar que los físicos están locos

Además pudieron ver la firma que en la capacidad calorífica dejada el gas de monopolos, viendo que estas cuerdas interaccionan de manera similar a como lo hacen las cargas eléctricas, lo que era de prever para el caso de monopolos magnéticos. En este resultado los monopolos no son partículas, sino que emergen como un estado de la materia, en concreto a partir de un arreglo especial de los dipolos que forman parte del material.

Para hacernos una idea de cómo sería un monopolo magnético si existiera, imaginemos una barra imantada que, como sabemos, posee en cada extremos un «un polo magnético» por el cual se atraen o se repelen. Estos polos son de dos tipos, llamados «norte» y «sur», y se comportan como las cargas eléctricas, positiva y negativa. Esa configuración del campo es un ejemplo de «campo bipolar», y sus líneas de campo no paran: giran y giran interminablemente. Si partimos por la mitad la barra imantada, no tenemos dos polos, el norte y el sur, separados, sino dos imanes. Un polo norte o sur aislado (un objeto con líneas de campo magnético que sólo salgan o que sólo entren) sería un monopolo magnético. De hecho, es imposible aislar una de estas cargas magnéticas. Nunca se ha detectado monopolos magnéticos, es decir partículas que poseyeran una sola carga magnética aislada. Puede que ello se deba a razones no aclaradas, o bien la naturaleza no creó monopolos magnéticos o creó poquísimos.

Todos sabemos que hay cargas eléctricas de distinto signo, tanto positivas como negativas. De este modo podemos reunir unas cuantas cargas de un signo dado en un recinto espacial y ver cómo todas las líneas de campo entran o salen del mismo a través de su superficie. Esto viene dado por la ley de Gauss del campo electrostático, que es una de las leyes de Maxwell. En su forma diferencial se escribe de la siguiente forma:

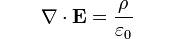Donde E es el campo eléctrico. Mientras que en su forma integral viene dada por:

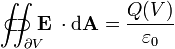O lo que es lo mismo: si sumamos las líneas de campo E que salen y entran en una superficie cerrada nos dará la distribución de carga total encerrada dentro de esa superficie. Para situaciones con geometría esférica este problema es trivial, pues el campo será equivalente al generado por una carga puntual, pero no lo es tanto si es de otro modo. También nos dice que el campo dentro de una esfera hueca cargada es nulo, puesto que cualquier superficie cerrada interior no contiene ninguna carga.

En cambio, los monopolos eléctricos (partículas que llevan carga eléctrica) son muy abundantes. Cada chispa de materia contiene un número increíble de electrones y protones que son auténticos monopolos eléctricos. Podríamos imaginar las líneas de fuerza del campo eléctrico surgiendo de una partícula cargada eléctricamente o convergiendo en ella y empezando o acabando allí. Además, la experiencia ha confirmado la ley de conservación de la carga eléctrica: la carga monopólica eléctrica total de un sistema cerrado no puede crearse ni puede destruirse. Pero en el mundo del magnetismo, no existe nada similar a los monopolos eléctricos, aunque un monopolo magnético sea fácilmente concebible.

La teoría electromagnética unifica la fuerza eléctrica y la fuerza magnética. La fuerza eléctrica es generada por la presencia de cargas eléctricas (el electrón, por ejemplo), mientras que la fuerza magnética surge por el movimiento de estas mismas cargas. El campo magnético de un imán proviene del movimiento de los electrones alrededor de los núcleos de hierro.

James Clerk Maxwell, el físico escocés que unificó matemáticamente los campos magnético y eléctrico en 1864, incluía en sus ecuaciones electromagnéticas fundamentales la existencia de cargas eléctricas, pero no incluyó la posibilidad de cargas magnéticas. Le habría resultado fácil hacerlo; la inclusión, a nivel estético, habría hecho sus ecuaciones bellamente simétricas respecto a la electricidad y el magnetismo. Pero al igual que otros físicos, Maxwell no halló prueba alguna de que hubiera en la naturaleza cargas magnéticas y las excluyó, por principio, de sus ecuaciones. Los físicos consideran desde entonces extraña la asimetría natural de la electricidad y el magnetismo.

El magnetismo es un fenómeno físico por el que los materiales ejercen fuerzas de atracción o repulsión sobre otros materiales.

Siguieron profundizando en sus estudios del campo electromagnético maxwelliano. Sabían que las ecuaciones de Maxwell podían simplificarse si se derivaban matemáticamente los campos eléctrico y magnético de otro campo aún más básico: un campo de medida. El campo de medida electromagnético es el ejemplo primero y más simple de la concepción general de campo de medida que descubrirían mucho después Yang y Mills. Curiosamente, al aplicar las ecuaciones de Maxwell al campo simple de medida, los físicos comprobaron que la ausencia de carga magnética se explicaba matemáticamente. Recíprocamente, pudieron demostrar que la ausencia de carga magnética entrañaba matemáticamente la existencia de un campo de medida. El campo de medida introdujo así una asimetría entre los campos eléctrico y magnético.

    En realidad, ¿Quién sabe lo que puede haber en el Universo? Magnetismo por todas partes

Pero la introducción del campo de medida como estructura subyacente del electromagnetismo se consideraba entonces una novedad matemática, un truco conceptual y no verdadera física. De la idea del campo de medida sacabas exactamente (ninguna carga magnética) lo que ponías en ella (ninguna carga magnética). Luego, en los años veinte, el matemático Hermann Weyl demostró que la incorporación de los campos eléctrico y magnético en la nueva teoría cuántica exigía concretamente una interpretación en términos del campo de medida. Y se empezó así a comprobar que el campo de medida electromagnético era físicamente importante, además de interesante matemáticamente. La mecánica cuántica parecía hecha a la medida de los campos de medida, y, curiosamente, los campos de medida presuponían la ausencia de monopolos magnéticos. Este planteamiento teórico coincidía tan absolutamente con la experiencia que la idea del campo de medida electromagnético se asentó con mucha firmeza. Pero luego, llegó Paul Dirac.

“Uno puede describir la situación diciendo que el matemático juega a un juego en el que él mismo inventa las reglas, mientras que el físico juega a otro en que las reglas vienen fijadas por la naturaleza, pero con el transcurrir del tiempo se hace cada vez más evidente que las reglas que los matemáticos encuentran interesantes son las mismas que ha elegido la naturaleza”.

En 1931, Dirac empezó a examinar las consecuencias físicas de la «belleza matemática» del campo de medida electromagnético en la teoría cuántica. Según él: «Cuando realicé este trabajo, tenía la esperanza de encontrar una explicación de la constante de estructura fina (la constante relacionada con la unidad fundamental de carga eléctrica). Pero no fue así. Las matemáticas llevaban inexorablemente al monopolo.» En contra del punto de vista teórico predominante, Dirac descubrió que la existencia de un campo de medida electromagnético y la teoría cuántica unidas presuponían que en realidad los monopolos magnéticos podían existir… siempre que la unidad fundamental de carga magnética tuviese un valor específico. El valor de la carga magnética que halló Dirac era tan grande que si en realidad existiesen monopolos magnéticos en la naturaleza, tendrían que ser fácilmente detectables, debido a los efectos de sus grandes campos magnéticos.

Para entender mejor las consecuencias de las investigaciones de Dirac imaginemos una barra imantada delgada de kilómetro y medio de longitud, con un campo magnético en cada extremo. En este caso, el campo magnético se parece al de un monopolo magnético porque el imán es muy delgado y los extremos están muy alejados. Pero no es un auténtico monopolo, porque las líneas del campo magnético no terminan realmente en la punta ,del imán; se canalizan a través de éste y surgen por el otro extremo.

Imaginemos luego que un extremo de este delgado imán se extiende hasta el infinito, reduciéndose su grosor matemáticamente a cero. El imán parece ahora una línea matemática, o una cuerda, con un campo magnético radial que brota de su extremo: un auténtico monopolo magnético puntiforme: Pero, ¿y esa cuerda infinitamente delgada (llamada cuerda de Dirac) que canaliza el flujo del campo magnético hasta el infinito? Dirac demostró que si la carga magnética del monopolo, con un valor g, cumplía la ecuación:

ge = n/2

n = 0, ± 1, ± 2…

en la que e es la unidad fundamental de carga eléctrica (una cantidad conocida experimentalmente), la presencia de esa cuerda no podría detectarse nunca físicamente. Según Dirac, la cuerda se convierte entonces sencillamente en un artilugio matemático descriptivo sin realidad física, igual que las coordenadas de los mapas son artilugios matemáticos que utilizamos para describir la superficie de la Tierra, carentes de significado físico. La cuerda de Dirac con un monopolo magnético en la punta era matemáticamente una línea en el espacio, a lo largo de la cual el campo de medida electromagnético no estaba definido. Pero sorprendentemente esta falta de definición no tenía consecuencias mensurables, siempre que la carga del monopolo magnético cumpliese la condición de Dirac. Otra consecuencia más del monopolo de Dirac era que la carga magnética se conservaba rigurosamente como la carga eléctrica.

¿Quién diría, viendo a este niño, que de mayor, desarrollaría un trabajo sobre el electrón que nada tiene que envidiar a las teorías de Einstein? Es Paul Dirac de niño, allá por el año 1907. Después de los importantes trabajos de Dirac, los físicos teóricos aceptaron la posible existencia de monopolos magnéticos, pensando que si ninguna ley física rechazaba su existencia, quizá existiesen.

                  Una ecuación que nos habla del portentoso cerebro humano

Resumiendo, nada se opone, a priori, a la existencia de cargas magnéticas aisladas. Estos monopolos magnéticos producirían una fuerza magnética, mientras que sus movimientos engendrarían una fuerza eléctrica. Pero, por una razón misteriosa, la naturaleza no parece haberse jugado aquí por la simetría, pues creó «monopolos eléctricos» y aparentemente no monopolos magnéticos.

¿Causa problemas esta asimetría, ¿Deberían existir los monopolos magnéticos? La respuesta tradicional de los físicos es: no necesariamente. La teoría sugiere su existencia, pero no la exige, y se acomoda muy bien con su ausencia.

Mas en el marco de la teoría del Big Bang la situación es diferente. En el momento del quiebre. de la simetría de gran unificación, se engendraron cantidades de monopolos magnéticos. Estas partículas, casi tan masivas como las X y las Y, ¡deberían ser tan numerosas como los protones! Masas tan gigantescas deberían poder señalarse fácilmente. ¿Por qué no se dejan percibir por nuestros detectores?

De hecho, con esta masa y esta población, los monopolos magnéticos, si existiesen, otorgarían al universo una densidad bastante superior que la densidad crítica. Bajo su efecto gravitatorio, ¡el universo se habría cerrado hace mucho tiempo! Y ¿de nosotros? Ni hablar…

No están aquí y tanto mejor. Pero, ¿por qué? El problema de los monopolos ausentes es otra de las patologías de las debilidades del Big Bang.

Emilio Silvera

[?]