El paso del tiempo lo cambia todo en todos los ámbitos y niveles

¿Onda o partícula? ¡Ambas a la vez! ¿Cómo es eso?

La luz es tan importante en nuestras vidas que, sin ella, seguramente, no estaríamos aquí. Tampoco podríamos contemplar los bellos paisajes que la Naturaleza nos ofrece por todas partes.

11 de mayo de 1916 – Albert Einstein presenta su Teoría de la Relatividad General que nos trajo una nueva Cosmología.

Es esencialmente la función gamma incompleta

[?]

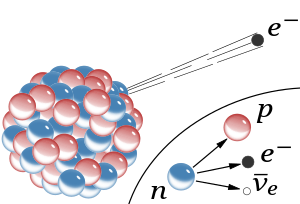
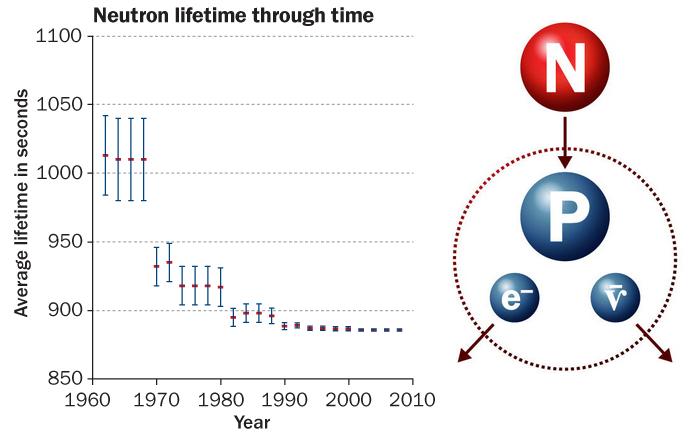
Decaimiento β^– de un núcleo. Se ilustra cómo uno de los neutrones se convierte en un protón a la vez que emite un electrón (β^-) y un antineutrino electrónico.

La desintegración Beta del neutrón está mediada por un Bosón W^–,que transforma uno de sus quarks, y se desintegra en el par electrón-antineutrino. Ahora leamos el reportaje de la Revista “Investigación y Ciencia”, referido a la física de partículas y a unas mediciones efectuadas que no son coincidentes.

“Dos técnicas de precisión arrojan valores distintos para el tiempo que tardan los neutrones en desintegrarse. ¿Se trata de un error experimental, o hay un misterio más profundo?

En síntesis

Un neutrón libre es un neutrón que existe fuera de un núcleo atómico. Mientras que los neutrones pueden ser estables cuando están unidos dentro de los núcleos, los neutrones libres son inestables y se desintegran con una vida media de 886 segundos, unos quince minutos.

Los neutrones libres no son estables: pasados unos 15 minutos, un neutrón se desintegra en un protón, un electrón y un antineutrino. Conocer con exactitud su vida media es clave para abordar varias cuestiones en física y cosmología.

Existen dos métodos para determinar con precisión la vida media de esta partícula. El primero cuenta los neutrones que quedan en un recipiente después de cierto tiempo; el segundo cuenta los protones generados en su desintegración.

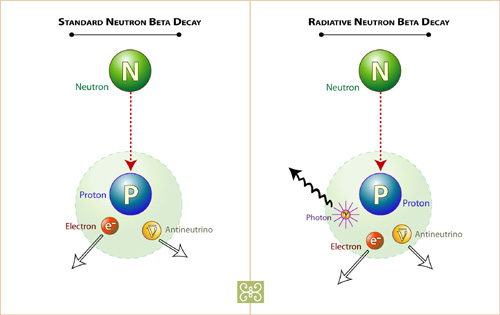
Hace años que una y otra técnica arrojan valores considerablemente dispares. Se cree que la discrepancia obedece a errores sistemáticos en alguno de los experimentos; sin embargo, hasta ahora nadie ha logrado dar con ellos.

Así hemos podido desvelar el secreto de que como se dice antes y se ve en la imagen, el neutrón al desintegrarse sigue este camino:

¹⁴ ₆C → ¹⁴ ₇N + e^–

Este proceso ocurre espontáneamente en neutrones libres, en el transcurso de 885.7(8) s de vida media.

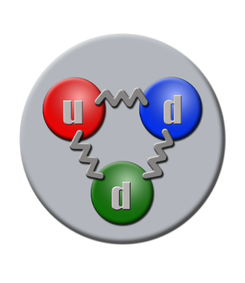
Un neutrón está formado por dos quarks dowm (abajo) y un quark up (arriba), tiene una vida media de 14,761 minutos, es una partícula de la familia de los hadrones en su vertiente bariónica, interacción: con la Gravedad, la nuclear débil y la nuclear fuerte, su símbolo es n, su antipartícula es el antineutrón, la teorizo Rutherford y la descubrió James Chadwick, su masa es de  1,674 927 29(28)×10⁻²⁷ K., la carga eléctrica es cero, espín ½. Se conoce cuando forma parte del átomo por nucleón.

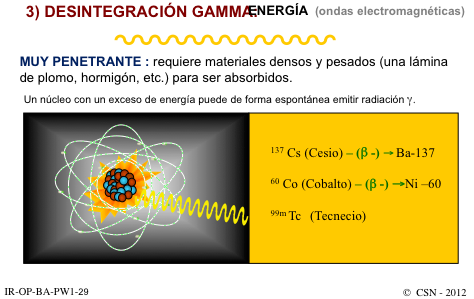
Por suerte para la vida en la Tierra, la mayor parte de la materia no es radiactiva. Aunque no solemos darle demasiada importancia, este hecho no deja de resultar sorprendente, ya que el neutrón (uno de los constituyentes, junto con el protón, de los núcleos atómicos) es propenso a desintegrarse. En el interior de un núcleo típico el neutrón puede vivir durante largo tiempo, pero, aislado, se desintegra en otras partículas en unos 15 minutos. Decimos «unos 15 minutos» para ocultar nuestra ignorancia al respecto, ya que, hasta ahora, no hemos sido capaces de medir con exactitud la vida media de esta partícula.

El neutrón y el protón forman los núcleos de los átomos; el protón es estable (su vida media es superior a 10³² años, según PDG 2012), pero el neutrón es inestable (vía la interacción electrodébil se desintegra en un protón) y aislado su vida media es de solo 880,1 ± 1,1 segundos (14 minutos y 40,1 segundos).

Resolver este «rompecabezas de la vida media del neutrón» no solo supone una cuestión de orgullo para nuestro gremio, el de los físicos experimentales, sino que resulta también vital para comprender mejor las leyes físicas. La desintegración del neutrón constituye uno de los procesos más sencillos en los que interviene la interacción débil, una de las cuatro fuerzas fundamentales de la naturaleza. Para entenderla por completo, hemos de saber cuánto tarda un neutrón aislado en desintegrarse. Por otro lado, la vida media del neutrón condicionó cómo se formaron los elementos químicos más ligeros después de la gran explosión que dio origen a nuestro universo. A los cosmólogos les gustaría poder calcular las abundancias esperadas de los distintos elementos y contrastarlas con los datos obtenidos por los astrofísicos. Un acuerdo apuntalaría nuestras teorías cosmológicas, mientras que una discrepancia indicaría la existencia de fenómenos físicos aún por descubrir. Pero, para poder llevar a cabo dicha comparación, hemos de conocer con exactitud cuánto vive un neutrón antes de desintegrarse.

Hace más de diez años, dos grupos experimentales, uno en Francia y otro en EE.UU., intentaron medir con precisión la vida media del neutrón. Uno de nosotros (Geltenbort) pertenecía al primer equipo, mientras que el otro (Greene) trabajaba en el segundo. Con sorpresa y cierta inquietud, comprobamos que nuestros resultados diferían de manera considerable. Algunos teóricos sugirieron que la discrepancia podría deberse a fenómenos físicos exóticos, como que parte de los neutrones se hubiesen desintegrado en partículas nunca antes observadas. Nosotros, sin embargo, achacamos la diferencia a una razón mucho más mundana: uno de los grupos —o ambos— tenía que haber cometido algún error o sobreestimado la precisión de sus resultados.

Hace poco, el equipo estadounidense completó un largo y concienzudo proyecto para estudiar la principal fuente de error que afectaba a sus mediciones. Lejos de zanjar la cuestión, sus esfuerzos solo confirmaron los resultados previos. Al mismo tiempo, otros investigadores verificaron los resultados del grupo de Geltenbort. Esta discrepancia nos ha dejado más perplejos de lo que ya estábamos, pero no hemos abandonado. Por el momento, ambos equipos y otros físicos experimentales seguimos buscando una respuesta.

CRONOMETRAR NEUTRONES

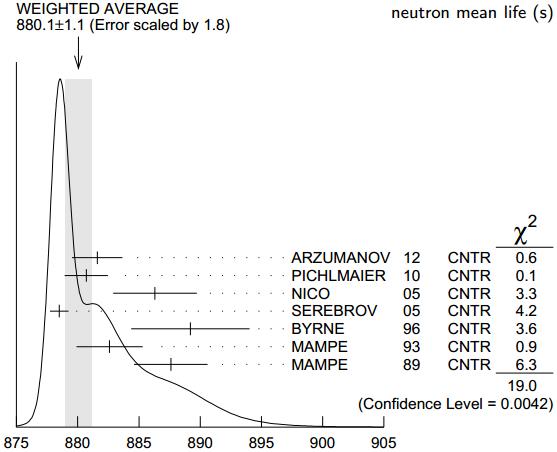
El neutrón y el protón forman los núcleos de los átomos; el protón es estable (su vida media es superior a 10³² años, según PDG 2012), pero el neutrón es inestable (vía la interacción electrodébil se desintegra en un protón) y aislado su vida media es de solo 880,1 ± 1,1 segundos (14 minutos y 40,1 segundos)

En teoría, determinar la vida media del neutrón es sencillo. Entendemos bien la física del proceso y disponemos de las herramientas adecuadas para estudiarlo. Sabemos que, siempre que una partícula pueda desintegrarse en otras de menor masa, acabará haciéndolo si en el proceso se conservan ciertas propiedades, como la carga eléctrica o el espín. En la llamada desintegración beta, un neutrón se transforma en un protón, un electrón y un antineutrino. Las masas de estas tres partículas suman algo menos que la masa del neutrón, pero la carga y el espín totales permanecen idénticos. Entre las cantidades conservadas se incluye la suma de masa y energía, por lo que las tres partículas finales incorporan esa pequeña diferencia de masa en forma de energía cinética.”

Nota: El artículo me ha sido enviado por Don José Gómez, un contertulio y visitante de ésta página que, con buen criterio, apunta que en cuanto a esas diferencias, las pruebas deben ser repetidas en distintos lugares y, si es posible, por distintos científicos también, ya que, en física de partícula, los resultados de un experimento, debe coincidir sin fisuras.

[?]

                        Estructuras Fundamentales de la Naturaleza

Hemos llegado a poder discernir la relación directa que vincula el tamaño, la energía de unión y la edad de las estructuras fundamentales de la Naturaleza. Una molécula es mayor y más fácil de desmembrar que un átomo; lo mismo podemos decir de un átomo respecto al núcleo atómico, y de un núcleo con respecto a los quarks que contiene.

La cosmología  sugiere que esta relación resulta del curso de la historia cósmica, que los quarks se unieron primero, en la energía extrema del big bang original, y que a medida que el Universo se expandió, los protones y neutrones compuestos de quarks se unieron para formar núcleos de átomos, los cuales, cargados positivamente, atrajeron a los electrones cargados con electricidad negativa estableciéndose así como átomos completos, que al unirse formaron moléculas y estas, a su vez, juntas en una inmensa proporción, forman los cuerpos que podemos ver a lo largo y lo ancho de todo el universo. Grandes estructuras y cúmulos y supercúmulos de galaxias que están hechos de la materia conocida como bariónica, es decir, de Quarks y Leptones (todo lo que existe está formado por estas dos partículas).

Si es así, cuanto más íntimamente examinemos la Naturaleza, tanto más lejos hacia atrás vamos en el tiempo.   Alguna vez he puesto el ejemplo de mirar algo que nos es familiar, el dorso de la mano, por ejemplo, e imaginemos que podemos observarlo con cualquier aumento deseado.

Con un aumento relativamente pequeño, podemos ver las células de la piel, cada una con un aspecto tan grande y  complejo como una ciudad, y con sus límites delineados por la pared celular.  Si elevamos el aumento, veremos dentro de la célula una maraña de ribosomas serpenteando y mitocondrias ondulantes, lisosomas esféricos y centríolos, cuyos alrededores están llenos de complejos órganos dedicados a las funciones respiratorias, sanitarias y de producción de energía que mantienen a la célula.

Ya ahí tenemos pruebas de historia.  Aunque esta célula particular solo tiene unos pocos años de antigüedad, su arquitectura se remonta a más de mil millones de años, a la época en que aparecieron en la Tierra las células eucariota o eucarióticas como la que hemos examinado.

Para determinar dónde obtuvo la célula el esquema que le indicó como formarse, pasemos al núcleo y contemplemos los delgados contornos de las macromoléculas de ADN segregadas dentro de sus genes.  Cada una contiene una rica información genética acumulada en el curso de unos cuatro mil millones de años de evolución.

                  Sistema nervioso somático

 Incluye grupos de neuronas que llevan información desde los órganos sensoriales (incluyendo toda la piel) hasta el sistema nervioso central (principalmente hasta el cordón espinal). A estos grupos de neuronas se les llama neuronas sensoriales o aferentes.

                     a. Las neuronas que recogen información directamente de los órganos sensoriales son neuronas especializadas con formas y sensibilidad particular. Por lo regular, estas neuronas tienen abundantes dendritas y axones cortos.

Almacenado en un alfabeto de nucleótidos de  cuatro “letras”- hecho de moléculas de azúcar y fosfatos, y llenos de signos de puntuación, reiteraciones para precaver contra el error, y cosas superfluas acumuladas en los callejones sin salida de la historia evolutiva-, su mensaje dice exactamente cómo hacer un ser humano, desde la piel y los huesos hasta las células cerebrales.

Si elevamos más el aumento veremos que la molécula de ADN está compuesta de muchos átomos, con sus capas electrónicas externas entrelazadas y festoneadas en una milagrosa variedad de formas, desde relojes de arena hasta espirales ascendentes como largos muelles y elipses grandes como escudos y fibras delgadas como puros.  Algunos de esos electrones son recién llegados, recientemente arrancados átomos vecinos; otros se incorporaron junto a sus núcleos atómicos hace más de cinco mil millones de años, en la nebulosa de la cual se formó la Tierra.

Si elevamos el aumento cien mil veces, el núcleo de un átomo de carbono se hinchará hasta llenar el campo de visión.   Tales núcleos átomos se formaron dentro de una estrella que estalló mucho antes de que naciera el Sol.  Si podemos aumentar aún más, veremos los tríos de quarks que constituyen protones y neutrones.

Los quarks han estado unidos desde que el Universo sólo tenía unos pocos segundos de edad

Al llegar a escalas cada vez menores, también hemos entrado en ámbitos de energías de unión cada vez mayores.  Un átomo puede ser desposeído de su electrón aplicando sólo unos miles de electrón-voltios de energía.  Sin embargo, para dispersar los nucleones que forman el núcleo atómico se requieren varios millones de electrón-voltios, y para liberar los quarks que constituyen cada nucleón se necesitaría cientos de veces más energía aún.

Introduciendo el eje de la historia, esta relación da testimonio del pasado de las partículas: las estructuras más pequeñas, más fundamentales están ligadas por niveles de energía mayores porque las estructuras mismas fueron forjadas en el calor del Big Bang.

Nos cuesta asimilar que la evolución de la materia se pudiera elevar (bajo un sin fin de parámetros y transmutaciones muy complejos), hasta alcanzar la consciencia y llegar a generar pensamientos. Parece como si el Universo hubiera sabido que nosotros (también otros seres similares e inteligentes en otros mundos del inmenso Cosmos), teníamos que venir y, para ello, creó sistemas idóneos para la vida como el planeta Tierra y muchos otros de su clase que ofrecen tal cobijo a criaturas vivas.

Los aceleradores de partículas, como los telescopios, funcionen como máquinas del tiempo.  Un telescopio penetra en el pasado en virtud del tiempo que tarda la luz en desplazarse entre las estrellas; un acelerador recrea, aunque sea fugazmente, las condiciones que prevalecían en el Universo primitivo. En la imagen de arriba podemos ver como el Telescopio Espacial Hubble, poco a poco, ha podido ir avanzando hacia atrtás en el tiempo para enseñarnos las imágenes captadas cuando el Universo era muy joven. ¿Podremos algún día fabricar telescopios tan potentes que puedan captar imágenes del universo vecino?

Hemos llegado a dominar técnicas asombrosas que nos facilitan ver aquello que, prohibido para nuestro físico, sólo lo podemos alcanzar mediante sofisticados aparatos que bien nos introduce en el universo microscópico de los átomos, o, por el contrario nos llevan al Universo profundo y nos enseña galaxias situadas a cientos y miles de millones de años-luz de la Tierra.

Cuando vemos esos objetos cosmológicos lejanos, cuando estudiamos una galaxia situada a 100.000 mil años-luz de nosotros, sabemos que nuestros telescopios la pueden captar gracias a que, la luz de esa galaxia, viajando a 300.000 Km/s llegó a nosotros después de ese tiempo, y, muchas veces, no es extraño que el objeto que estamos viendo ya no exista o si existe, que su conformación sea diferente habiéndose transformado en diferentes transiciones de fase que la evolución en el tiempo ha producido.

                    Siempre hemos querido saber lo que hay más allá de lo que el ojo ve

En el ámbito de lo muy pequeño, vemos lo que está ahí en ese momento pero, como se explica más arriba, en realidad, también nos lleva al pasado, a los inicios de cómo todo aquello se formó y con qué componentes que, en definitiva, son los mismos de los que están formadas las galaxias, las estrellas y los planetas, una montaña y un árbol y, cualquiera de nosotros que, algo más evolucionado que todo lo demás, podemos contarlo aquí.

Estas y otras muchas maravillas son las que nos permitirán, en un futuro relativamente cercano, que podamos hacer realidad muchos sueños largamente dormidos en nuestras mentes.

Emilio Silvera Vázquez

[?]