El “mundo” de lo muy pequeño… ¡Es tan extraño!

                 Nube de electrones que rodea al núcleo

Sabemos que los electrones son partículas de la familia de los Leptones, tienen carga negativa, que existen en una nube alrededor del núcleo atómico. Son inimaginablemente pequeños, tan pequeños que se necesita de la mecánica cuántica para explicar su comportamiento peculiar. Sin embargo y a pesar de su pequeñez, son partículas fundamentales del Universo.

Algunas propiedades:

El valor del radio del electrón el SI es 2.817 940 322 7 (19) × 10⁻¹⁵ m.

Muchas veces hemos hablado del electrón que rodea el núcleo, de su carga eléctrica negativa que complementa la positiva de los protones y hace estable al átomo; tiene una masa de solamente 1/1.836 de la del núcleo más ligero (el del hidrógeno). La importancia del electrón es vital en el universo. Simplemente con que su carga fuera distinta en una pequeña fracción… ¡El mundo que nos rodea sería muy diferente! Y, ni la vida estaría presente en el Universo.

   La Ciencia busca, teoriza y experimenta tratando de saber cómo funciona el universo

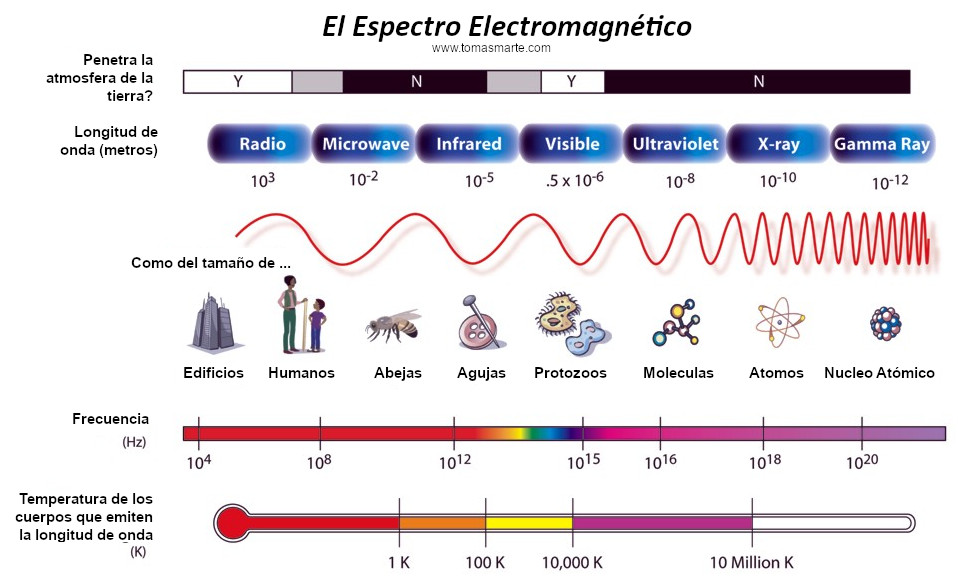
Pero busquemos los “cuantos”. La física del siglo XX empezó exactamente en el año 1900, cuando el físico alemán Max Planck propuso una posible solución a un problema que había estado intrigando a los físicos durante años. Es el problema de la luz que emiten los cuerpos calentados a una cierta temperatura, y también la radiación infrarroja emitida, con menor intensidad, por los objetos más fríos (radiación de cuerpo negro).

Hipótesis cuántica de Planck donde c es la velocidad de la luz en el vacío y k B k B es la constante de Boltzmann, k B = 1,380 × 10 −23 J/K . k B = 1,380 × 10 −23 J/K . La fórmula teórica expresada en la Ecuación 6.11 se denomina ley de radiación de cuerpo negro de Planck.

Estaba bien aceptado entonces que esta radiación tenía un origen electromagnético y que se conocían las leyes de la naturaleza que regían estas ondas electromagnéticas. También se conocían las leyes para el frío y el calor, la así llamada “termodinámica”, o al menos eso parecía. Pero si utilizamos las leyes de la termodinámica para calcular la intensidad de una radiación, el resultado no tiene ningún sentido. Los cálculos nos dicen que se emitiría una cantidad infinita de radiación en el ultravioleta más lejano y, desde luego, esto no es lo que sucede. Lo que se observa es que la intensidad de la radiación muestra un pico a una cierta longitud de onda característica, y que la intensidad disminuye tanto para longitudes mayores como para menores. Esta longitud de onda característica es inversamente proporcional a la temperatura absoluta de objeto radiante (la temperatura absoluta se define por una escala de temperatura que empieza a 273º bajo cero). Cuando a 1.000º C un objeto se pone al “rojo vivo”, el objeto está radiando en la zona de luz visible.

Lo que Planck propuso fue simplemente que la radiación sólo podía ser emitida en paquetes de un tamaño dado. La cantidad de energía de uno de esos paquetes, o cuantos, es inversamente proporcional a la longitud de onda, y por tanto, proporcional a la frecuencia de radiación emitida. La fórmula es E = hν, donde E es la energía del paquete, ν es la frecuencia y h es una nueva constante fundamental de la naturaleza, la constante de Planck. Cuando Planck calculó la intensidad de la radiación térmica imponiendo esta nueva condición, el resultado coincidió perfectamente con las observaciones.

Einstein realizó importantes descubrimientos en el campo fotoeléctrico. Éstos le hicieron merecedor del Premio Nobel de Física en 1922. El efecto fotoeléctrico afirma que un material es capaz de liberar o hacer circular electrones por un material conductor gracias a la energía recibida por un haz de luz.

Poco tiempo después, en 1905, Einstein formuló esta teoría de una manera mucho más tajante: él sugirió que los objetos calientes no son los únicos que emiten radiación en paquetes de energía, sino que toda la radiación consiste en múltiplos del paquete de energía de Planck. El príncipe francés Louis-Victor de Broglie, dándole otra vuelta a la teoría, propuso que no sólo cualquier cosa que oscila tiene energía, sino que cualquier cosa con energía se debe comportar como una “onda” que se extiende en una cierta región del espacio, y que la frecuencia ν de la oscilación verifica la ecuación de Planck. Por lo tanto, los cuantos asociados con los rayos de luz deberían verse como una clase de partículas elementales: el fotón. Todas las demás clases de partículas llevan asociadas  diferentes ondas oscilantes de campos de fuerza, pero esto lo veremos más adelante.

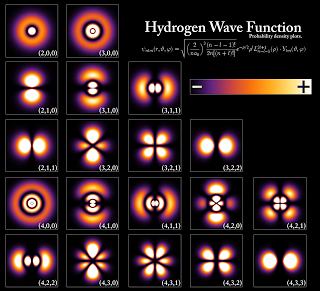
La función de onda de Schrödinger nos acercó a ese mundo infinitesimal

La primera es la imagen obtenida por los físicos en el laboratorio y, la segunda es la Imagen ilustrativa de la dualidad onda-partícula, con la cual se quiere significar cómo un mismo fenómeno puede tener dos percepciones distintas. Lo cierto es que, el mundo de lo muy pequeño es extraño y no siempre lo podemos comprender.

El curioso comportamiento de los electrones en el interior del átomo, descubierto y explicado por el famoso físico danés Niels Bohr, se pudo atribuir a las ondas de de Broglie. Poco después, en 1926, Edwin Schrödinger descubrió cómo escribir la teoría ondulatoria de de Broglie con ecuaciones matemáticas exactas. La precisión con la cual se podían realizar cálculos era asombrosa, y pronto quedó claro que el comportamiento de todos los objetos pequeños quedaba exactamente determinado por las recién descubiertas “ecuaciones de ondas cuánticas”.

Está bien comprobado que la mecánica cuántica funciona de maravilla…, pero, sin embargo, surge una pregunta muy formal: ¿Qué significan realmente estas ecuaciones?, ¿Qué es lo que están describiendo? Cuando Isaac Newton, allá en 1867 formuló cómo debían moverse los planetas alrededor del Sol, estaba claro para todo el mundo qué significaban sus ecuaciones: que los planetas estaban siempre en una posición bien definida des espacio y que sus posiciones y sus velocidades en un momento concreto determinan inequívocamente cómo evolucionarán las posiciones y las velocidades en el tiempo.

Teletransporte y efecto túnel

El electrón está situado en una órbita exterior, llega un fotón energético que choca contra él, el electrón desaparece, y, de inmediato aparece en otra órbita más energética cerca del núcleo. ¿Por dónde hizo el viaje?, ¿Cómo se desplazó de una órbita a otra sin recorrer las distancias que les separan?

Pero para los electrones todo es diferente. Su comportamiento parece estar envuelto en misterio. Es como si pudieran “existir” en diferentes lugares simultáneamente, como si fueran una nube o una onda, y esto no es un efecto pequeño. Si se realizan experimentos con suficiente precisión, se puede determinar que el electrón parece capaz de moverse simultáneamente a lo largo de trayectorias muy separadas unas de otras. ¿Qué puede significar todo esto?

El “universo de las partículas nunca ha sido fácil de comprender y su rica diversidad, nos habla de un vasto “mundo” que se rige por su propias reglas que hemos tenido que ir conociendo y seguimos tratando de saber, el por qué de esos comportamientos extraños y a veces misteriosos. Así, la pregunta anterior, de ¿qué puede significar todo eso?…

La pudo contestar Niels Bohr, de forma tal que,  con su explicación se pudo seguir trabajando, y muchos físicos siguen considerando su respuesta satisfactoria. Se conoce como la interpretación de Copenhague de la mecánica cuántica.

¿Qué es cuantizar?

“A principios del siglo XX la física sufrió dos revoluciones que la cambiaron para siempre. La mayor de ellas, la revolución cuántica, nos hizo ver que objetos matemáticos que dábamos por hecho que poseían existencia física, como, por ejemplo, la trayectoria de las partículas, en realidad de forma precisa no existen en la naturaleza. El principio de indeterminación nos dice que las partículas elementales no son ni ondas ni corpúsculos clásicos, sino unos objetos cuánticos que, en su movimiento, no siguen una trayectoria bien definida. En la teoría que describe el comportamiento de estos objetos, la mecánica cuántica, las variables dinámicas como la posición x o la cantidad de movimiento p no son números reales, sino operadores x^, p^ en un espacio vectorial cuyos elementos son los estados de la partícula cuántica. El principio de indeterminación da lugar a que estos operadores no conmutan, sino que obedecen a la relación de conmutación [x^,p^]=iℏ.

Todo en la naturaleza es cuántico y, por tanto, obedece a los principios de la mecánica cuántica.”

Así se estudia y experimenta en los aceleradores de partículas de qué está hecha la materia. El encontronazo y estallido final, nos descubre nuevas partículas. Estamos tratando de saber que puede existir más allá de los Quarks

Las leyes de la mecánica cuántica han sido establecidas con mucha precisión; permite cómo calcular cualquier cosa que queramos saber. Pero si queremos “interpretar” el resultado, nos encontramos con una curiosa incertidumbre fundamental: que varias propiedades de las partículas pequeñas no pueden estar bien definidas de manera simultánea. Por ejemplo, podemos determinar la velocidad de una partícula con mucha precisión, pero entonces no sabremos exactamente dónde se encuentra; o a la inversa, podemos determinar la posición con precisión, pero entonces su velocidad queda mal definida. Si una partícula tiene espín (rotación alrededor de su eje), la dirección alrededor de la cual está rotando (la orientación del eje) no puede ser definida con gran precisión.

No es fácil explicar de forma sencilla de dónde viene esta incertidumbre, pero existen ejemplos en la vida cotidiana que tienen algo parecido. La altura de un tono y la duración en el tiempo durante el cual oímos el tono tienen una incertidumbre mutua similar. Para afinar un instrumento musical se debe escuchar una nota durante un cierto intervalo de tiempo y compararla, por ejemplo, con un diapasón que debe vibrar también durante un tiempo. Notas muy breves no tienen bien definido el tono.

Para que las reglas de la mecánica cuántica funcionen, es necesario que todos los fenómenos naturales en el mundo de las cosas pequeñas estén regidos por las mismas reglas. Esto incluye a los virus, bacterias e incluso a las personas. Sin embargo, cuando más grande y más pesado es un objeto, más difícil es observar las desviaciones de las leyes del movimiento “clásicas” debidas a la mecánica cuántica. Me gustaría referirme a esta exigencia tan importante y tan peculiar de la teoría con la palabra “holismo”. Esto no es exactamente lo mismo que entienden algunos filósofos por holismo, y que podría definir como “el todo es más que la suma de sus partes”. Si la física nos ha enseñado algo es justo lo contrario. Un objeto compuesto de un gran número de partículas puede ser entendido exactamente si se conocen las propiedades de sus partes (partículas); basta que sepamos sumar correctamente (¡y esto no es nada fácil en mecánica cuántica!). Lo que entiendo por holismo es que, efectivamente, el todo es la suma de las partes, pero sólo se puede hacer la suma si todas las partes obedecen a las mismas leyes. Por ejemplo,  la constante de Planck, h, que es igual a 6’626075… × 10^-34 Julios segundo, debe ser exactamente la misma para cualquier objeto en cualquier sitio, es decir, debe ser una constante universal.

Mucho ha sido el camino andado hasta nuestros tratando de conocer los secretos de la naturaleza que, poco a poco, nos van siendo familiares. Sin embargo, es más el camino que nos queda por recorrer. Es mucho lo que no sabemos y, tanto el micro-mundo como en el vasto mundo de muy grande, hay que cosas que aún, no hemos llegado a comprender.

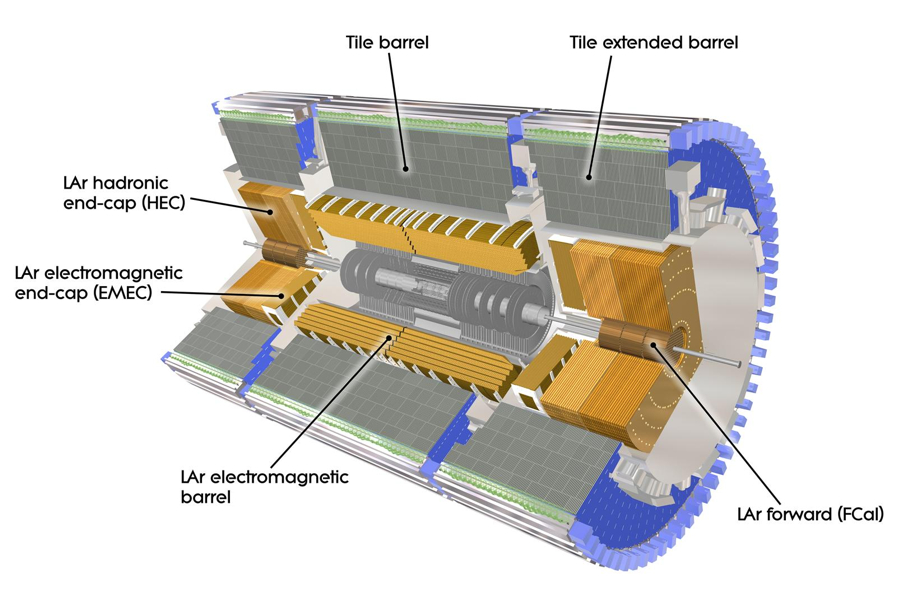
    El detector ATLAS funcionó, y rastrearon las partículas subatómicas…

Las reglas de la mecánica cuántica funcionan tan bien que refutarlas resulta realmente difícil. Los “trucos” ingeniosos descubiertos por Werner Heisenberg, Paul Dirac y muchos otros mejoraron y completaron las reglas generales. Pero Einstein y otros pioneros como Erwin Schrödinger siempre presentaron serias objeciones a esta interpretación. Quizá funcione bien, pero ¿Dónde está exactamente el electrón?, ¿en el punto x o en el punto y? En pocas palabras, ¿Dónde está en realidad?, y ¿Cuál es la realidad que hay detrás de nuestras fórmulas? Si tenemos que creer a Bohr, no tiene sentido buscar tal realidad. Las reglas de la mecánica cuántica, por sí mismas, y las observaciones realizadas con detectores son las únicas realidades de las que podemos hablar.

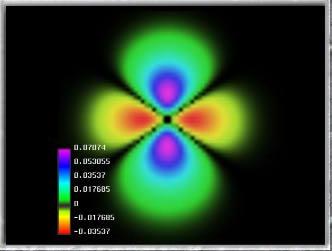
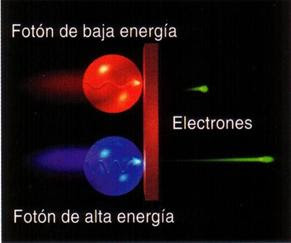
     Es cierto que, localizar y saber en qué punto exacto están esas pequeñas partículas… no es fácil

La mecánica cuántica puede ser definida o resumida así: en principio, con las leyes de la naturaleza que conocemos ahora se puede predecir el resultado de cualquier experimento, en el sentido que la predicción consiste en dos factores: el primer factor es un cálculo definido con exactitud del efecto de las fuerzas y estructuras, tan riguroso como las leyes de Isaac Newton para el movimiento de los planetas en el Sistema Solar; el segundo factor es una arbitrariedad estadística e incontrolable definida matemáticamente de forma estricta. Las partículas seguirán una distribución de probabilidades dadas, primero de una forma y luego de otra. Las probabilidades se pueden calcular utilizando la ecuación de Schrödinger de función de onda (Ψ) que, con muchas probabilidades nos indicará el lugar probable donde se encuentra una partícula en un momento dado.

La teoría de probabilidades se ocupa de asignar un cierto número a cada posible resultado que pueda ocurrir en un experimento aleatorio, con el fin de cuantificar dichos resultados y saber si un suceso es más probable que otro.

Muchos estiman que esta teoría de las probabilidades desaparecerá cuando se consiga la teoría que explique, de forma completa, todas las fuerzas; la buscada teoría del todo, lo que implica que nuestra descripción actual incluye variables y fuerzas que (aún) no conocemos o no entendemos. Esta interpretación se conoce como hipótesis de las variables ocultas.

Albert Einstein, Nathan Rosen y Boris Podolski idearon un “Gedankenexperiment”, un experimento hipotético, realizado sobre el papel, para el cual la mecánica cuántica predecía como resultado algo que es imposible de reproducir en ninguna teoría razonable de variables ocultas. Más tarde, el físico irlandés John Stewar Bell consiguió convertir este resultado en un teorema matemático; el teorema de imposibilidad.

(“El teorema de Bell o desigualdades de Bell se aplica en mecánica cuántica para cuantificar matemáticamente las implicaciones planteadas teóricamente en la paradoja de Einstein-Podolsky-Rosen y permitir así su demostración experimental. Debe su nombre al científico norirlandés John S. Bell, que la presentó en 1964.

Ilustración del test de Bell para partículas de espín 1/2. La fuente produce un par de espín singlete, una partícula se envía a Alicia y otra a Bob. Cada una mide uno de los dos espines posibles.

El teorema de Bell es un meta-teorema que muestra que las predicciones de la mecánica cuántica (MC) no son intuitivas, y afecta a temas filosóficos fundamentales de la física moderna. Es el legado más famoso del físico John S. Bell. El teorema de Bell es un teorema de imposibilidad, que afirma que:

Ninguna teoría física de variables ocultas locales puede reproducir todas las predicciones de la mecánica cuántica.”)

                ¿Cómo saber el número que saldrá cuando lanzamos los dados?

¡¡La mecánica cuántica!!, o, la perplejidad de nuestros sentidos ante lo que ese “universo cuántico” nos ofrece que, generalmente, se sale de lo que entendemos por sentido común. Ahí, en el “mundo” de los objetos infinitesimales, suceden cosas que no siempre podemos comprender. Y, como todo tiene una razón, no dejamos de buscarla en cada uno de aquellos sorprendentes sucesos que en ese lugar se producen. Podríamos llegar a la conclusión de que, la razón está en todo y solo la encontramos una vez que llegamos a comprender, mientras tanto, todo nos resulta extraño, irrazonable, extramundano y, algunas veces…imposible. Sin embargo, ahí está. Dos elementos actúan de común acuerdo para garantizar que no podamos descorrer el velo del futuro, de lo que será después (podemos predecir aproximaciones, nunca certezas), el principal de esos elementos es la ignorancia nunca podremos saber el resultado final de éste o aquél suceso sin tener la certeza de las condiciones iniciales. En la mayoría de los sistemas físicos son, en mayor o menor medida dada su complejidad, del tipo caótico es tal que, el resultado de las interacciones entre elementos es sumamente sensibles a pequeñísimas variaciones de los estados iniciales que, al ser perturbados mínimamente, hacen que el suceso final sea y esté muy alejado del que se creía al comienzo.

Lo que nos lleva a confirmar que el futuro es siempre incierto. ¿Es bueno desconocer lo que nos pasará mañana? Bueno, el Universo cree que sí, y, así lo dispuso.

Emilio Silvera Vázquez

[?]