Feb
25
¡La Física! Esa gran disciplina científica
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (0)
Comments (0)

Universidad Nacional Autónoma de México, Instituto de Astronomía
| Estrellas de Neutrones |
Las estrellas de neutrones son los objetos más densos observables en el Universo. Sólo son superadas por el interior de los hoyos negros, que no es observable. En colisiones relativistas de iones pesados, en RHIC o en el LHC, es posible alcanzar densidades superiores, pero con una enorme densidad de energía (cientos de GeV por nucleón), mientras que la materia en el interior de una estrella de neutrones es altamente degenerada.
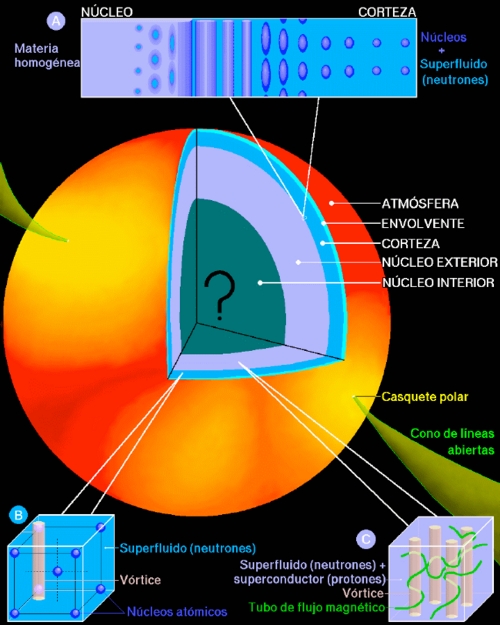
En la Fig. 1 se presenta lo que, teóricamente, consideramos es la estructura de una estrella de neutrones. Con un radio de unos 10 km, el 98% de la masa se encuentra a densidades supra-nucleares en el núcleo de la estrella, mientras que una capa de aproximadamente un kilómetro de espesor, la corteza, está formada de núcleos atómicos. En la superficie tenemos una atmósfera, de unos cuantos centímetros de espesor, donde se forma el espectro térmico que podemos observar. A una densidad ρ ~ 104g cm-3 la materia está totalmente ionizada y cuando ρ ~ 106g cm-3 los electrones forman un gas de Fermi relativista. Dada la enorme energía en este gas de electrones, resulta energéticamente favorable fusionar parte de los electrones con protones, lo que resulta en núcleos cada vez mas ricos en neutrones conforme aumenta la densidad. Cuando ρ ~ 5×1011g cm-3, el número de neutrones es tal que no caben mas en los núcleos. Hemos alcanzado el punto de “goteo” de neutrones, donde además de los núcleos y el gas de electrones, tenemos un gas “libre” de neutrones. Al acercarse a la densidad nuclear, ρ0 ~ 2.8×1014g cm-3 los núcleos se fusionan y entramos al “núcleo” de la estrella (“core” en ingles). En la zona de transición es muy probable que encontremos núcleos no esféricos, muy alargados (“espaguetis”) y bidimensionales (“lasañas”), lo que comúnmente se llama la fase “pasta” (ver recuadro “A” en la Fig. 1). Dadas las altas presiones en la corteza ésta debe ser sólida, muy probablemente en forma cristalina (recuadro “B” en la Fig. 1).
 |
|
| Figura 1. Visión “artística” de una estrella de neutrones. (D. Page, en “Fronteras del Universo”, Ed. M. Peimbert, 2000, Fondo de Cultura Económica) | |
En el núcleo de la estrella, empezamos con un líquido cuántico de neutrones, protones y electrones. Las interacciones débiles, tipo β, como
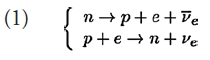
permiten ajustar las densidades nn y np de nucleones. Debido a las diferencias de masas, la primera de estas reacciones ocurre espontáneamente en el vacío mientras que la segunda requiere de energía cinética en el estado inicial. En un medio denso las energías relevantes no son las masas, sino los potenciales químicos de las partículas, los cuales incluyen la masa, la energía cinética de Fermi y la energía potencial. Esta última requiere de un modelo de las interacciones fuertes a densidades supra-nucleares; el equilibrio energético y efecto de las reacciones β, determinan nn y np. El resultado es que a ρ = &rho0 los nucleones se distribuyen en una proporción de 5% de protones por 95% de neutrones, aunque la fracción de protones aumenta con la densidad. Nuevas partículas pueden aparecer a mayores densidades, como hiperones o condensados de mesones (π – o K -). El núcleo interior de la estrella, está marcada en oscuro en la Fig. 1, con un gran signo de interrogación, ya que existe la posibilidad de se alcance la densidad suficiente para inducir desconfinamento de los quarks. Refiero el lector a [1] para más detalles y referencias a los trabajos originales.
Neutrinos
Producidas en explosiones de supernovas, con temperaturas iniciales superiores a los 50 MeV ~ 50×1010 K, las estrellas de neutrones jóvenes se enfrían por emisión de neutrinos, hasta llegar a una edad de unos 100,000 años, a partir de lo cual la pérdida de energía por emisión de fotones térmicos en la superficie empieza a dominar. El proceso de emisión de neutrinos más eficiente es el descrito en la Eq. (1), llamado “Urca directo”, con una emisividad εDUrca ≈ 1027 (T/109 K)6 erg cm-3 s-1.Esto implica que un metro cúbico de materia podría producir una luminosidad (L = 3.8×1033 erg s-1) de neutrinos cuando T=109 K. Sin embargo, la reacción (1) tiene una fuerte limitante: la conservación del momento, la cual requiere un concentración de protones superior al 15%; por lo cual el proceso Urca directo está cinematicamente prohibido. Sin embargo, existen procesos como
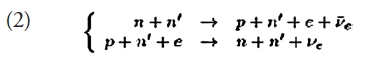
que proporcionan el momento faltante, aquí el neutrón n’ es una partícula del medio. Nótese que el proceso (2), llamado “Urca modificado” por involucrar dos fermiones degenerados, comparado con el proceso (1) es mucho menos eficiente, εMUrca ≈ 1021 (T/109 K)8 erg cm-3 s-1, con una dependencia en la temperatura de la forma T8 en lugar de T6. El proceso (2) es el mecanismo estándar de enfriamiento y el proceso (1) soló actua a densidad altas, es decir en estrellas muy masivas.
Superfluidez y Superconductividad
La teoría BCS de superconductividad está basada en la formación de pares de Cooper y en la aparición de una brecha Δ(T) en elespectro de excitaciones, cuando la interacción entre fermiones es atractiva. La presencia de una brecha y consecuentemente la existencia de pares de Cooper en núcleos fue observada en 1958, poco tiempo después de la formulación de la teoría BCS y es un ingrediente esencial en los modelos de estructura nuclear. Para momentos p<1.5 fm-1 la interacción nuclear n-n o p-p es atractiva en el canal 1S0 (en notación espectroscópica: singlete de espín, momento angular orbital L=0 y J=L+S=0). Esto lleva a predecir que los neutrones deben de formar un superfluido en la corteza interna de una estrella de neutrones mientras que los protones, debido a su baja concentración, formarían un superconductor en el núcleo exterior. En el núcleo de la estrella el momento de Fermi de los neutrones es superior a 1.5 fm-1 y el canal 1S0 se vuelve repulsivo. Sin embargo la formación de pares de Cooper en triplete de espín, en el canal atractivo 3P2, es posible. A mas altas densidades es probable que los hiperones y/o los quarks formen superfluidos/superconductores. El interior de una estrella de neutrones es un paraíso para pares de Cooper, pero el calcular precisamente el tamaño de la brecha Δ(T), y el valor de Tc, es una pesadilla para el físico teórico. El caso del helio-3 es un ejemplo de ello y en el caso del apareamiento 3P2 de los neutrones a densidades supra-nucleares las predicciones para Δ van desde casi 0 hasta más de 5 MeV.
La presencia de una brecha Δ en el espectro de excitaciones implica que cuando T<<Tc estas son fuertemente suprimidas, aproximadamente por un factor de Boltzmann exp (-Δ(T)/T). En consecuencia, el calor específico Cv, así como todos los procesos de emisión de neutrinos en los cuales esta componente apareada participa, están exponencialmente suprimidos. Sin embargo, la transición de fase es de segundo orden, es decir continua. Cuando T ~ Tc, como es bien conocido en el caso de los superfluidos/superconductores terrestres, el calor específico Cv aumenta en un factor del orden 2.5. Otro aspecto del desarrollo progresivo del condensado es el constante rompimiento y formación de pares de Cooper, cuando T ~ Tc , y la posibilidad de que el condensado decaiga en un par neutrino – anti-neutrino:
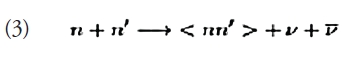
donde <nn´> representa el condensado de pares de Cooper. Este “proceso de Cooper” puede ser mas eficiente que el Urca modificado (2) por mas de un orden de magnitud.
Enfriamiento y Superfluidez
Esta breve descripción permite esbozar el panorama de la evolución térmica de estrellas de neutrones: a partir de su nacimiento se enfrían por emisión de neutrinos y cuando alcanzan edades del orden de 105 años su evolución se determina por la emisión superficial de fotones.
La tasa de emisión de neutrinos es muy sensible a la composición de la materia a densidades supra-nucleares: cualquier cambio a la composición relativa de neutrones a protones resulta en emisividades de neutrinos altísimas y enfriamiento muy rápido. Tenemos un zoológico completo de modelos de materia ultra densa, casi todos prediciendo un enfriamiento rápido. Por otra parte, el enfriamiento rápido puede ser moderado por el apareamiento de las partículas, mientras la brecha, o la temperatura crítica, sea suficientemente grande. Nos encontramos con el problema de la casi imposibilidad de calcular con suficiente precisión el tamaños de las brechas relevantes y el hecho de que la emisión de neutrinos es controlada por estas brecha de manera exponencial. Las dos revisiones [2] y [3] presentan mas detalles sobre los mecanismos de enfriamiento.
Del lado observacional, tenemos una docena de estrellas de neutrones jóvenes con temperaturas estimadas. Sus altas temperaturas superficiales, entre 0.5 y 2×106 K, indican que ningún proceso Urca directo está actuando en ellas, al menos que esté fuertemente suprimido por apareamiento de las partículas que participen en el proceso. El “modelo mínimo” de enfriamiento [4] fue desarrollado con el fin de presentar un punto de referencia con el cual comparar estas observaciones e identificar posibles candidatas a estrellas conteniendo algún tipo de materia “exótica”. Este modelo excluye a priori cualquier forma de materia densa que resulte en enfriamiento rápido, es decir una alta concentración de protones, condensados de mesones, hiperones y quarks desconfinados. Sin embargo considera el efecto de la superconductividad / superfluidez de protones / neutrones, es decir el apareamiento, y el aumento en la emisión de neutrinos por el proceso de Cooper durante la transición de fase. Resulta que los procesos Urca modificados por si mismos no son suficientemente eficientes para explicar la evolución de las estrellas mas frías pero sí se pueden interpretar las observaciones tomando en cuenta el proceso de Cooper, bajo una condición: la temperatura crítica máxima, Tc, para el apareamiento 3P2 de los neutrones debe estar entre 1/2 y 2×109 K [5]. En este rango de valores de Tc el proceso de Cooper domina el enfriamiento a edades entre unos cientos hasta unas decenas de miles de años de edad.
En el caso contrario debemos suponer la presencia de algún tipo de materia extra para entender la evolución de estas estrellas de neutrones jóvenes. En conclusión, hasta hace poco tiempo nos encontrábamos en una situación que requería de alguna nueva pista para poder avanzar.
El Caso de Cas A
Casiopeia A es un remanente de supernova en la constelación de Casiopeia. Por su interés astronómico, la NASA decidió inaugurar el satélite de rayos X Chandra, su “primera luz”, con una imagen de este remanente en agosto del 1999 (ver Fig. 2). ¡En el centro de la imagen apareció la estrella de neutrones, “Cas A”, formada por la supernova! Con una edad de unos 330 años es la estrella de neutrones más joven conocida. Al analizar 10 años de observaciones del remanente, y de su estrella, Craig Heinke y Wynn Ho encontraron que Cas A se había enfriado en un 4% del año 2000 al 2009 [5] y que ¡su flujo se había reducido en un 20%! Esta evolución es inconmpatible con casi todas la predicciones teóricas.
 |
|
| Figura 2. El remanente de supernova Casiopeia A en rayos X: primera luz de Chandra, en agosto del 1999. El punto brillante en su centro es la estrella de neutrones, descubierta en esta observación. (Crédito: NASA/CXC/SAO) | |
La luminosidad térmica de fotones de la estrella es LX ≈ 1034 erg s-1 mientras que la tasa de enfriamiento observada, junto con una estimación del calor específico, requiere que la estrella esté perdiendo energía térmica a una tasa de 1038 erg s-1. ¿Cuál puede ser el agente de enfriamiento que supere al de fotones por 4 órdenes de magnitud? Sólo puede ser la emisión de neutrinos.
Aunque un comportamiento como el de Cas A es sorprendente, había sido descrito teóricamente con anterioridad (ver, e.g., la Fig. 6 en [5] o Fig. 8 en [2]). Después de afinar detalles, la interpretación resulto clara [7,8]: tras un lento enfriamiento previo, la temperatura interna T de Cas A alcanzó, en las últimas décadas, la temperatura crítica de superfluidez de los neutrones, Tc, lo cual disparó la fuerte emisión de neutrinos por el proceso Cooper. La figura 3 ilustra esto con tres modelos: a edades superiores a los 100 años, sin superfluidez (“Tc=0”), el enfriamiento es lento; al contrario, con una Tc demasiado alta (“Tc=109 K” ), el enfriamiento rápido ocurre demasiado temprano y posteriormente el enfriamiento es también lento; mientras que con Tc=5.5×108 K el enfriamiento rápido, pero transitorio, ajusta perfectamente las observaciones. Además de ser, posiblemente, la primera evidencia directa de la existencia de superfluidez a densidades supra-nucleares, esto nos proporciona una “medición” bastante robusta de la temperatura crítica Tc para los neutrones y los detalles del enfriamiento rápido implican también que los protones deben de ser superconductores con una temperatura crítica más alta. Si la interpretación resiste al tiempo, y el enfriamiento continua durante varias décadas como lo predice el modelo, estaríamos viendo en tiempo real una gran concentración de neutrones pasando por la transición de fase de superfluidez.
 |
|
| Figura 3. Tres modelos de enfriamiento, temperatura efectiva “al infinito” Te ∞ vs edad: ver texto para descripción. La estrella marca el valor observado de Cas A y el recuadro detalla el ajuste del modelo con las cinco observaciones de Chandra. (Adaptado de la Ref. [8]) | |
El Futuro: ¿Exótico?
Lo bizarro de un superfluido estelar ha recibido mucha cobertura mediática (ver, e.g., [9]). Sin embargo, lo más importante de estos resultados es que podemos, por lo menos en el caso de Cas A, borrar la zona oscura y el signo “?” en el centro de la Fig. 1. Hace seis meses estábamos todavía caminando en medio de una jungla de modelos, pero sólo uno de ellos parece sobrevivir a la observación del enfriamiento de Cas A que podría ser la “Piedra de Rosetta” de la física de materia ultra-densa. Es ciertamente sólo media piedra: hay evidencias de estrellas que sufren emisión de neutrinos todavía mucho más intensa como son los casos de SAX J1808.4-3658 y 1H 1905+00. Estos dos objetos están en sistemas binarios con acreción transitoria: cuando termina una fase de acreción esperamos ver la superficie caliente de la estrella, estrellas de primera generación como Cas A. Al considerar densidades más altas, alcanzadas en estrellas más masivas, el signo “?” vuelve a aparecer. Sin embargo, el entender con un sorprendente lujo de detalle, la estructura y la evolución de una estrella “mínima” como Cas A, nos abre el camino para identificar más claramente objetos realmente “exóticos”.
Referencias:
[1] Page, D., & Reddy, S., “Dense Matter in Compact Stars: Theoretical Developments and Observational Constraints”, Annu. Rev. Nucl. Part. Sci. 56, 327, (2006)
[2] Yakovlev, D. G., & Pethick, C. J., “Neutron Star Cooling”, Annu. Rev. Astronom. & Astrophys. 42, 169, (2004)
[3] Page, D., Geppert, U., & Weber, F., “The Cooling of Compact Stars”, Nucl. Phys. A 777, 497, (2006), numero especial sobre Nuclear Astrophysics.
[4] Page, D., Lattimer, J. M., Prakash, M., & Steiner, A. W., “Minimal Cooling of Neutron Stars: A New Paradigm”, Astrophys. J. Suppl. 155, 623, (2004).
[5] Page, D., Lattimer, J. M., Prakash, M., & Steiner, A. W., “Neutrino Emission from Cooper Pairs and Minimal Cooling of Neutron Stars”, Astrophys. J. 707, 1131, (2009)
[6] Heinke, C. O., & Ho, W. C. G., “Direct Observation of the Cooling of the Cassiopeia A Neutron Star”, Astrophys. J. Lett. 719, 167, (2010)
[7] Shternin, P. S., Yakovlev, D. G., Heinke, C. O., Ho, W. C. G., & Patnaude, D. J., “Cooling Neutron Star in the Cassiopeia-A Supernova Remnant: Evidence for Superfluidity in the Core”, Mon. Not. Roy. Astron. Soc.: Lett. 412, 108, (2011)
[8] Page, D., Prakash, M., Lattimer, J. M., & Steiner, A. W., “Rapid Cooling of the Neutron Star in Cassiopeia A Triggered by Neutron Superfluidity in Dense Matter”, Phys. Rev. Lett. 106, 081101, (2011)
[9] “Cassiopeia A: NASA’s Chandra Finds Superfluid in Neutron Star’s Core”: http://chandra.harvard.edu/photo/2011/casa/















 Totales: 74.911.676
Totales: 74.911.676 Conectados: 46
Conectados: 46






















