May
18
Sobre la Mecánica Cuántica
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (4)
Comments (4)

La teoría cuántica, recordémoslo, afirma que para todo objeto existe una función de onda que mide la probabilidad de encontrar dicho objeto en un cierto punto del espacio y del tiempo. La teoría cuántica afirma también que nunca se conoce realmente el estado de una partícula hasta que se haya hecho una observación. Antes de que haya una medida, la partícula puede estar en uno de entre una diversidad de estados, descritos por la función de onda de Schrödinger. Por consiguiente, antes de que pueda hacerse una observación o medida, no se puede conocer realmente el estado de la partícula. De hecho, la partícula existe en un estado ultramundano, una suma de todos los estados posibles, hasta que se hace una medida.
Cuando esta idea fue propuesta por primera vez por Niels Bohr y Werner Heisemberg, Einstein se revolvió contra ella. “¿Existe la luna sólo porque la mira un ratón?“, le gustaba preguntar. Según la teoría cuántica, en su más estricta interpretación, la Luna, antes de que sea observada, no existe realmente tal como la conocemos. “La Luna puede estar, de hecho, en uno cualquiera de entre un número infinito de estados, incluyendo el estado de estar en el cielo, de estar explotando, o de no estar allí en absoluto. Es el proceso de medida que consiste en mirarla el que decide que la Luna está girando realmente alrededor de la Tierra“. Decía Einstein con ironía.

Einstein no pensó en la posibilidad de que fuera la Luna la que nos esté mirando
Edwin Schrödinger, autor de la ecuación con su función de onda, se disgustó con estas interpretaciones de su ecuación. Para demostrar lo absurdo de la situación creada, Schrödinger colocó un gato imaginario en una caja cerrada. El gato estaba frente a una pistola, que está conectada a un contador Geiger, que a su vez está conectado a un fragmento de uranio. El átomo de uranio es inestable y sufrirá una desintegración radiactiva. Si se desintegra un núcleo de uranio, será detectado por el contador Geiger que entonces disparará la pistola, cuya bala matará al gato.

Para decidir si el gato está vivo o muerto, debemos abrir la caja y observar al gato. Sin embargo, ¿cuál es el estado del gato antes de que abramos la caja? Según la teoría cuántica, sólo podemos afirmar que el gato está descrito por una función de onda que describe la suma de un gato muerto y un gato vivo.
Para Schrödinger, la idea de pensar en gatos que no están ni muertos ni vivos era el colmo del absurdo, pero la confirmación experimental de la mecánica cuántica nos lleva inevitablemente a esta conclusión. Hasta el momento, todos los experimentos han verificado, favorablemente, la teoría cuántica.
La paradoja del gato de Schrödinger es tan extraña que uno recuerda a menudo la reacción de Alicia al ver desaparecer el gato de Cheshire en el centro del cuento de Lewis Carroll: “Allí me verás“, dijo el Gato, y desapareció, lo que no sorprendió a Alicia que ya estaba acostumbrada a observar cosas extrañas en aquel lugar fantástico. Igualmente, los físicos durante años se han acostumbrados a ver cosas “extrañas” en la mecánica cuántica.
La Mecánica cuántica, es , más fascinante el el Pais de las Maravillas de Alicia
Existen varias maneras de abordar esta dificultad de lo incomprensible en mecánica cuántica. En primer lugar, podemos suponer que Dios existe. Puesto que todas las “observaciones” implican un observador, entonces debe haber alguna “conciencia” en el universo. Algunos físicos como el premio Nobel Eugene Wigner, han insistido en que la teoría cuántica prueba la existencia de algún tipo de conciencia cósmica universal.
La segunda forma de tratar la paradoja es la preferida por la gran mayoría de los físicos en activo: ignorar el problema.
El físico Richard Feynman dijo en cierta ocasión: “Creo que es justo decir que nadie comprende la mecánica cuántica. No siga diciéndose a sí mismo, si puede evitarlo, “¿pero cómo puede ser así?” porque usted se meterá “hasta el fondo” en un callejón sin salida del que nadie ha escapado. Nadie sabe como puede ser eso“. De hecho, a menudo se ha dicho que de todas las teorías propuestas en el siglo XX, la más absurda es la teoría cuántica. Algunos dicen que la única cosa que la teoría tiene a su favor es que “es indudablemente correcta”.
¿Siempre será parte del misterio?
Sin embargo, existe una tercera forma de tratar esta paradoja, denominada teoría de los muchos universos. Esta teoría (como el principio antrópico) no gozó de mucho favor en la última década, pero está siendo revitalizada por la función de onda del universo de Stephen Hawking.
Existe un principio de la física denominado Navaja de Occam, que afirma que siempre deberíamos tomar el camino más sencillo posible e ignorar las alternativas más complicadas, especialmente si las alternativas no pueden medirse nunca.
Para seguir fielmente el consejo contenido en la navaja de Occam, primero hay que tener el conocimiento necesario para poder saber elegir el camino más sencillo, lo que en la realidad, no ocurre. Nos faltan los conocimientos necesarios para hacer las preguntas adecuadas.
Hugo Everett, Bryce DeWitt y ahora Hawking (también otros), han propuesto la teoría de los universos múltiples. En unos universos los protones se desintegran antes haciendo inestable la materia, en otros, el átomo de uranio se desintegra mediante un proceso sin radiaciones, y en otros universos las constantes universales que existen en el nuestro, son totalmente diferentes y no dan posibilidad alguna para la existencia de seres vivos. Está claro que cualquier variación que en principio pudiera parecer sin importancia, como por ejemplo la carga del electrón, podría transformar radicalmente nuestro universo.

Helena de Troya o Helena de Esparta,
Como apuntó el físico Frank Wilczek, uno de los tres ganadores del Nobel de Física de 2004 por la libertad asintótica de los Quarks:
“Se dice que la historia del mundo sería totalmente distinta si Helena de Troya hubiera tenido una verruga en la punta de su nariz.”
Hasta el momento, se han celebrado varias conferencias internacionales sobre la función de onda del universo. Sin embargo, como ocurre en la teoría de supercuerdas, las matemáticas implicadas en la función de onda del universo, parecen estar más allá de la capacidad de cálculo que cualquier humano en este planeta pudiera resolver, y tendríamos que esperar años antes de que aparezca un individuo genial que pudiera encontrar una solución rigurosa a las ecuaciones de Hawking.
Recordemos aquí de nuevo que, precisamente ahora, un siglo más tarde, en el Congreso Internacional de Matemáticas celebrado en Madrid este mes de Agosto de 2.006, se otorgó la Medalla Field (una especie de Nobel de las matemáticas) al matemático ruso Perelman, extraño Ser que no ha comparecido a la cita y la ha rechazado. Perelman ha resuelto la conjetura expuesta por Poincaré planteada en 1.904.
La conjetura de Poincaré de 1.904, en el año 2.000, fue catalogada por el Instituto Planck como uno de los siete problemas del milenio. Para hacer un comentario sobre esta conjetura tengo que referirme a la topología, el nivel de las matemáticas donde está ubicada.
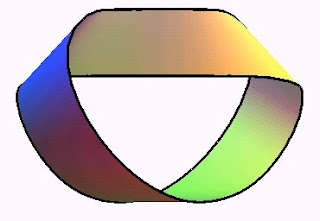
La topología es la geometría de los objetos elásticos o flexibles que cambian de forma pero tienen las mismas propiedades que antes de ser estirados, achatados, etc. Se pueden retorcer pero no cortar ni pegar.
Los topólogos no tienen en cuenta la distancia, puesto que se puede variar al deformar el objeto, sino nociones más sutiles. Los orígenes de la topología se remontan a mediados del siglo XVIII, con los trabajos de Euler en teoría de grafos, que llamó “análisis situs”.
A finales del siglo XIX y principios del siglo XX, la topología recibió un gran impulso con los trabajos de Poincaré, matemático francés muy influyente en el posterior desarrollo de diversas áreas de las matemáticas y de la física. En particular, en 1.904 planteó la conjetura que lleva su nombre y que no se ha resuelto hasta el siglo XXI. Este problema ha sido un motor para la investigación en topología de todo el siglo pasado y se ha llegado a su resolución con ideas nuevas y apasionantes.

Para situarnos mejor debemos hablar de las variedades, espacios que tienen una dimensión determinada. Por ejemplo una recta o un circulo son variedades de dimensión uno, puesto que se describen como un parámetro. El plano o la esfera son ejemplos de variedades bidimensionales, al utilizar dos parámetros para describir sus posiciones. El espacio en que vivimos es una variedad tridimensional, y si le añadimos la dimensión temporal, el espacio-tiempo es una variedad de dimensión cuatro. Ya he comentado en este mismo trabajo cómo las singularidades geométricas, las variedades, fueron introducidas por Riemann a mediados del s. XIX y constituyeron una herra-mienta clave para la física del siglo XX. De hecho, la teoría de la relatividad especial de Einstein fue postulada por Einstein en 1.905, pero hasta que no incorporó las variedades contenidas en el tensor métrico de Riemann, no pudo completar la teoría de la relatividad que incluía los espacios curvos.

La pregunta que hizo Poincaré fue la siguiente: ¿Es la esfera la única variedad tridimensional para la cual toda curva se contrae?
Se pasó un siglo entero antes de que un genio de las matemáticas, el extraño G. Perelman, pudiera demostrar la conjetura de Poincaré. Tan extraño es el personaje que no ha querido venir a España a recibir la medalla Field conquistada con su trabajo reconocido por todos sus colegas y que recibiría de manos del Rey de España. Se desconoce si aceptará el premio en metálico de 1 millón de dólares que lleva consigo dicho triunfo de resolver la conjetura.
Mientras tanto, Perelman ha dejado su trabajo, ha rechazado una cátedra de matemáticas que le ofrecieron en Princeton y junto a su madre, vive en San Petersburgo en una humilde vivienda y compartiendo una miserable pensión de 72 euros al mes. Trabaja aislado y en silencio durante horas encerrado en su mundo y cuando se agota, para relajarse, sale al campo a buscar setas.

Grigori Perelman
PROFESIÓN: PROFESOR EN PARO
EDAD: 50 AÑOS
ORIGEN: SAN PETERSBURGO (RUSIA)
QUÉ HA HECHO: DEMOSTRAR UNA CONJETURA MATEMÁTICA QUE LLEVABA PLANTEADA 100 AÑOS Y RECHAZAR TODO RECONOCIMIENTO.
Es el típico caso del niño superdotado que termina siendo un sabio “raro”, en plan “profesor Tornasol”. En la comunidad matemática es conocido desde hace muchos años por sus brillantes avances y por sus victorias en los “campeonatos matemáticos”. Se lo disputan las universidades de medio mundo y ha dado clase nada menos que en el Massachusetts Institute of Technology. Empezó a trabajar en 2002 sobre la conjetura de Poincaré, planteada por el sabio francés en 1904 y que pudo con los más egregios matemáticos del siglo XX. El Clay Mathematics Institute prometía un millón de dólares a quien lograra demostrarla.
Esta es la vida que ha elegido el hombre que ha sido considerado el más listo del mundo en la actualidad. He repetido prácticamente la historia contada antes en páginas anteriores para que el lector pueda apreciar cómo, de vez en cuando, surgen genios que al estar en posesión de la verdad, desprecian los bienes materiales y se nutren de los verdaderos bienes que alimentan la mente y el espíritu; no dedican su tiempo a cosas que, para ellos, no tienen importancia.
¡Misterios de la vida!
Seguramente, en la mente de personajes como Perelman están escondidas las soluciones que la humanidad necesita par resolver sus problemas. Como Gauss, Riemann, Hamilton, Euler, Ramanujan y tantos otros antes, y ahora Perelman, pronto aparecerán otros que, seguramente, nos darán las respuestas que aún están pendientes, para que podamos plantear la definitiva teoría decadimensional y tengamos las respuestas a tantas preguntas que no han sido contestadas.
Un día Einstein fue conducido a postular la teoría de la relatividad general partiendo de un principio físico, el principio de equivalencia (que la masa gravitatoria y la masa inerte de un objeto son iguales, de modo que todos los cuerpos, por muy grande que sean, caen en la Tierra a la misma velocidad). Sin embargo, no se ha encontrado todavía la contrapartida del principio de equivalencia para la teoría de cuerdas.
Está claro, como dice Witten, que la teoría de cuerdas proporciona, de hecho, un marco lógicamente consistente que engloba la gravedad y la mecánica cuántica, pero el principio análogo al de equivalencia que Einstein encontró para su teoría no ha sido aún encontrado para la teoría de cuerdas.

Representación de cuerdas microscópicas interactuando
¿Tendremos que esperar (como para la solución de la conjetura de Poincaré) cien años para resolver la teoría de supercuerdas? ¡Quién sabe! El problema es muy complejo y encierra muchas cuestiones teóricas que, experimentalmente, no estamos capacitados ni tenemos los medios para poder comprobar. No debemos desanimarnos, el sino de la humanidad, a lo largo de toda su historia, siempre ha sido una constante de ir salvando obstáculos que cuando se presentaban parecían insalvables.
Ahora nuestra esperanza media de vida ronda los 80 años y el tiempo que tenemos por delante (me refiero al tiempo del universo) es muy largo. ¿Qué no seremos capaces de conseguir?
Basta repasar los logros de los últimos 150 años en las distintas ramas del saber humano para asombrarnos de la enorme capacidad de trabajo, sacrificio, inventiva e ingenio de nuestra especie que, sobre todo, tiene ¡¡curiosidad!!
Espero que sigamos así.
emilio silvera
-
Tenemos que cambiar la desigualdad de Heisenberg, el
26 de enero del 2012 a las
2:11
[…] entendido, y tal vez pensó realmente que las razones para el surgimiento de la probabilidad de la mecánica cuántica no eran en el fondo tan diferentes de sus actividades en la física clásica. El cuanto de acción […]
















 Totales: 74.804.604
Totales: 74.804.604 Conectados: 44
Conectados: 44
























el 15 de marzo del 2012 a las 16:37
Amigo Emilio:
En el silencio sigo tu blog y todos los magníficos comentarios que se suscitan en este. Hoy rompo mi silencio por esta vez.
Todo se resume magistralmente en la expresión de arriba:
“Para seguir fielmente el consejo contenido en la navaja de Occam, primero hay que tener el conocimiento necesario para poder saber elegir el camino más sencillo, lo que en la realidad, no ocurre. Nos faltan los conocimientos necesario para hacer las preguntas adecuadas.”
Recuerda que tiempo atrás, manifesté mi convicción de que muchos de los problemas actuales de la física, se resolverán en un periodo de tiempo que ronda los cinco años, y que la balanza se inclinará en favor de Eistein. Cada día estoy más convencido de ello.
Agregaría un comentario escrito en uno de los libros de Roger Penrose hablando de Bob Wald : <<Si realmente crees en la mecánica cuántica, entonces no puedes tomarla en serio.>>
En cuanto a los universo paralelos en mismo Penrose dice: “ He divido los físicos cuánticos en diversas categorías…
En particular, los he clasificado en aquellos que creen y aquellos que son serios.
Un cordial saludo para ti y todos los lectores/ras de tu blog.
el 26 de marzo del 2013 a las 15:24
Las paradojas del gato de schodinger y de las dos rendijas.
La paradoja consiste en suponer que la evolucion temporal de cualqier sistema puede ser descrito por una funcion de onda, lo cual no es cierto; para tener un sistema cuya evolucion temporal sea descrita por una funcion de onda es necesario que el sistema este completamente aislado de cualquier interaccion con el resto del universo; Esta situacion solo pued ser imaginada idealmente puesto que todos los sistemas estan en interaccion con el vacio electromagnetico.
En algunos casos, como por ejemplo un atomo en el estado fundamental, o una particula elemental puede considerarse aislada puesto que no puede interactuar con el vacio; podemos asi describir la evolucion temporal del sistema con la mecanica cuantica.
En el caso del gato de Schodinger el gato es un sistema macroscopico y contiene susbsistemas que tienen interacciones no solo entre ellos sino tambien con el vacio electromagnetico; recuerdese que el gato no esta en equilibrio termodinamico y por lo tanto hay efectos de relajacion. Los procesos de la vida son procesos que mantienen un sistema permanentemente en un estado fuera del equilibrio termodinamico.
Esta paradoja esta relacionada con la paradoja de las rendijas, en esta se lanzan electrones hacia una pantalla, el resultado experimental si las dos rendijas estan abiertas no es igual al resultado de lanzar electrones con una rendija abierta y luego con la otra.
En este caso los electrones se comportan como si pasaran por las dos rendijas a la vez, incompatible con el concepto de particula que tiene la fisica.
En este caso debemos considerar la realidad como un sucesion de eventos o fenomenos, lo que no sea un evento no pertenece a la realidad. En el caso de los electrones tenemos un evento que es la salida del electron de canon de electrones y el proximo evento es la llegada del electron a la pantalla, no tiene sentido preguntarnos por donde paso el electron puesto que su paso de un evento al otro no pertenece a la realidad fisica, aunque este paso de un evento al otro esta condicionado por el ambiente alrededor de el.
el 27 de marzo del 2013 a las 6:39
Amigo mío, sus palabras dejan ver cuán extraña es, la mecánica cuántica.
Saludos.