May
18
Necesitamos teorías más avanzadas
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (0)
Comments (0)
La gravitación y dimensiones extra
“… la línea tiene magnitud en una dirección, el plano en dos direcciones y el sólido en tres direcciones; a parte de éstas, no hay ninguna magnitud porque las tres son todas…”
Eso nos dijo Aristóteles alrededor de 350 años antes de Cristo, y la verdad, es que desde la experiencia cotidiana es difícil refutarlo. Más aún, la existencia de dimensiones extra podría tener consecuencias desastrosas para la estabilidad de las órbitas atómicas y planetarias, sobre todo en el caso de que dichas dimensiones fuesen de un tamaño comparable al del sistema estudiado. En concreto, Paul Ehrenfest en 1.917 demostró que la ley del inverso del cuadrado de la distancia para la fuerza electrostática o gravitatoria se modificaría si hubiera N dimensiones espacial extra, de forma que F ≈ r-2 π. De hecho, ningún experimentado físico realizado hasta la fecha ha revelado la existencia de más de tres dimensiones espaciales, y dicho sea de paso, tampoco más de una dimensión temporal.
Sin embargo, aunque la experiencia ordinaria no necesitase de más de tres más una dimensiones, desde Riemann, Gauss, Ricci y algún otro, el punto de vista matemático permite estudiar de forma consistente la geometría de espacion de dimensión arbitraria que, como digo, lo debemos en gran parte a Bernhard Riemann sobre variedades n-dimensionales (1.854), y ello a pesar de que Ptolomeo propusiera una “demostración” de que una cuarta dimensión espacial no tiene magnitud ni definición posibles (Tratado sobre la distancia, 150 a. C.).
La formulación de la Relatividad Especial de Einstein en 1.905 supuso una revolución en nuestra concepción del espacio y del tiempo, y planteó la cuestión de la dimensionalidad desde una perspectiva completamente nueva. En efecto, en la interpretación geométrica que llevó a cabo Herman Minkowski en 1.909, la teoría de Eintein podía entenderse de forma simple en términos de una variedad espacio-temporal de cuatro dimensiones, en la que a tres dimensiones espaciales se le añadía en pie de igualdad una cuarta, el tiempo, en la forma itc. El espacio y el tiempo pasaron de entenderse como conceptos independientes a formar un entramado único 4-dimensional, en el que las distancias se miden a través de la métrica de Minkowski:
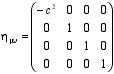
Por su parte, Einstein, lejos de considerar el espacio-tiempo de Minkowski como una mera descripción matemática, lo elevó a la categoría de entidad física con su Teoría General de la Relatividad (RG) de 1.915 al considerarlo como objeto dinámico, cuya geometría, dada por la métrica de Riemann gμυ(x), depende de tener en cuenta en cada punto de su contenido de materia y energía. La curvatura del espacio-tiempo determina la trayectoria de las partículas de prueba que se mueven en él, y por tanto, la teoría proporciona una interpretación geométrica de la interacción gravitatoria.
La unificación del electromagnetismo y la gravitación, mencionada por mí en anteriores trabajos, fue la primera de las teorías con dimensiones extra.
Está claro que a comienzos del siglo pasado, nuestro conocimiento de las interacciones fundamentales se reducía a dos teorías de campos bien establecidas, el electromagnetismo de Maxwell, en pie desde 1.873, y la novedosa Teoría General de la Relatividad para la gravitación, que Einstein comenzara a gestar en 1.907 y publicara en 1.915. No es por tanto de extrañar que el atractivo de la teoría de Einstein provocara en muchos, incluido el propio Einstein, el impulso de buscar una generalización de la misma, que incluyera también a la teoría de Maxwell, en una descripción geométrica unificada.
Con ese único objetivo, se tomaron varios caminos que, si bien no llegaron al destino deseado, permitieron realizar descubrimientos trascendentales que marcaría la evolución de la física teórica hasta nuestros días.
El primero de estos caminos fue propuesto por Hermann Weyl en 1.918. En la Relatividad General, el espacio-tiempo se considera como una variedad pseudo-Riemanniana métrica, esto es, en la que, aunque la orientación de un vector transportado paralelamente de un punto a otro depende del camino seguido, su norma es independiente del transporte. Esta independencia de la norma disgustaba a Weyl que propuso reemplazar el tensor métrico gμυ por una clase de métricas conformemente equivalentes [gμυ] (esto es, equivalentes bajo cambios de escala gμυ → λ gμυ), y el transporte paralelo por otro que respetara esa estructura conforme. Esto se conseguía introduciendo un nuevo campo, Aμ, que al cambiar de representante de la clase de equivalencia [gμυ], se transformaba precisamente como el potencial vector de la teoría de Maxwell:
Aμ → Aμ + ∂μλ
Este tipo de transformación es lo que Weyl denominó trasformación de “gauge”, en el sentido de cambio de longitud. En propias palabras de Weyl en una carta dirigida a Einstein en 1.918, con su teoría había conseguido “… derivar la electricidad y la gravitación de una fuente común…“. La respuesta de Einstein no se hizo esperar:
“Aunque su idea es muy elegante, tengo que declarar francamente que, en mi opinión, es imposible que la teoría se corresponda con la naturaleza.”
La objeción de Einstein se basaba en el hecho de que en la propuesta de Weyl, el ritmo de avance de los relojes también dependería del camino seguido por éstos, lo cual entraría en contradicción, por ejemplo, con la estabilidad de los espectros atómicos.
Aunque la teoría de Weyl fue abandonada rápidamente, en ella se introducía por primera vez el concepto de simetría gauge. Varias décadas más tarde, con el desarrollo de las teorías gauge no abelianas por Yang Mills (1.954), y del Modelo Estándar de las partículas elementales, se comprobó que la misma noción de invarianza subyacía en la descripción del resto de interacciones fundamentales (electrodébiles y fuertes).
El segundo camino en la búsqueda de la unificación comenzó un año antes de la publicación de la Relatividad General. En 1.914 Gunnar Nordström propuso una teoría en cinco dimensiones que unificaba el electromagnetismo con la gravitación de Newton. La aparición de la Teoría de la Relatividad General hizo olvidar la teoría de Nordström, pero no la idea de la unificación a través de dimensiones extra.
Kaluza
Así estaban las cosas cuando en 1.919 recibió Einstein un trabajo de Theodor Kaluza, un privatdozent* en la Universidad de Königsberg, en el que extendía la Relatividad General a cinco dimensiones. Kaluza consideraba un espacio con cuatro dimensiones, más la correspondiente dimensión temporal y suponía que la métrica del espacio-tiempo se podía escribir como:
![]()
Donde ![]() con μ,υ = 1, 2, 3, 4, corresponde a la métrica 4-dimensional del espacio-tiempo de la RG, Aμ proporciona el campo electromagnético, Φ es un campo escalar conocido posteriormente como dilatón, y α = √(2k) es la constante de acoplo relacionada con la constante de Newton k. Kaluza demostró que las ecuaciones de Einstein en cinco dimensiones obtenidas de esta métrica y linealizadas por los campos, se reducían a las ecuaciones de Einstein ordinarias (en cuatro dimensiones) en vacío, junto con las ecuaciones de Maxwell para Aμ, siempre que se impusiera la condición cilíndrica, esto es, que la métrica
con μ,υ = 1, 2, 3, 4, corresponde a la métrica 4-dimensional del espacio-tiempo de la RG, Aμ proporciona el campo electromagnético, Φ es un campo escalar conocido posteriormente como dilatón, y α = √(2k) es la constante de acoplo relacionada con la constante de Newton k. Kaluza demostró que las ecuaciones de Einstein en cinco dimensiones obtenidas de esta métrica y linealizadas por los campos, se reducían a las ecuaciones de Einstein ordinarias (en cuatro dimensiones) en vacío, junto con las ecuaciones de Maxwell para Aμ, siempre que se impusiera la condición cilíndrica, esto es, que la métrica ![]() no dependiera de la quinta coordenada.
no dependiera de la quinta coordenada.
El trabajo de Kaluza impresionó muy positivamente a Einstein: “Nunca había caído en la cuenta de lograr una teoría unificada por medio de un cilindro de cinco dimensiones… A primera vista, su idea me gusta enormemente…” (carta de Einstein a Kaluza en 1.919, en abril).
Este hecho resulta sorprendente si consideramos que el trabajo de Nordström fue publicado cinco años antes. Por motivos desconocidos, en el mes de mayo de 1.919, Einstein rebajó su entusiasmo inicial: “Respeto en gran medida la belleza y lo atrevido de su idea, pero comprenderá que a la vista de las objeciones actuales no pueda tomar parte como originalmente se planeó“. Einstein retuvo el trabajo de T. Kaluza durante dos años, hasta que en 1.921 fue presentado por él mismo ante la Academia Prusiana. Hasta 1.926 Einstein guardó silencia acerca de la teoría en cinco dimensiones.
Klein
Ese mismo año, Oskar Klein publicaba un trabajo sobre la relación entre la teoría cuántica y la relatividad en cinco dimensiones. Uno de los principales defectos del modelo de Kaluza era la interpretación física de la quinta dimensión. La condición cilíndrica impuesta ad hoc hacía que ningún campo dependiera de la dimensión extra, pero no se justificaba de manera alguna.
Klein propuso que los campos podrían depender de ella, pero que ésta tendría la topología de un círculo con un radio muy pequeño, lo cual garantizaría la cuantización de la carga eléctrica. Su diminuto tamaño, R5 ≈ 8×10-31 cm, cercano a la longitud de Planck, explicaría el hecho de que la dimensión extra no se observe en los experimentos ordinarios, y en particular, que la ley del inverso del cuadrado se cumpla para distancias r » R5. Pero además, la condición de periodicidad implica que existe una isometría de la métrica bajo traslaciones en la quinta dimensión, cuyo grupo U(1), coincide con el grupo de simetría gauge del electromagnetismo.
Por último, imponiendo que el dilatón es una constante, Klein demostró que las ecuaciones de movimiento reproducen las ecuaciones completas de Einstein y Maxwell. Esta forma de tratar la dimensión extra, bautizada posteriormente como el paradigma de la compactificación, había logrado superar los obstáculos iniciales: “… parece que la unión de la gravitación y la teoría de Maxwell se consigue de una forma completamente satisfactoria con la teoría de cinco dimensiones” (carta de Einstein a Lorentz en 1.927), y de hecho, ha sido la única forma consistente de introducir dimensiones extra hasta fechas más recientes.
El propio Einstein había comenzado a trabajar en la teoría de Kaluza con su ayudante Jacob Grommer y en 1.922 publicó un primer trabajo sobre existencia de soluciones esféricamente simétricas, con resultado negativo. Más tarde, en 1.927 presentó ante la Academia Prusiana dos trabajos en los que reobtenía los resultados de Klein. Su infructuosa búsqueda de una teoría de campo unificada le haría volver cada pocos años a la teoría en cinco dimensiones durante el resto de su vida. Los resultados de Klein sobre la cuantización de la carga eléctrica pueden entenderse fácilmente considerando el desarrollo en modos de Fourier de los campos con respecto a la dimensión periódica:
![]()
La ecuación de ondas en cinco dimensiones puede reescribirse como:
![]()
Donde Dμ es una derivada covariante con respecto a transformaciones generales de coordenadas y con respecto a transformaciones gauge con una carga qn = nk/R5. Vemos por tanto que el campo en cinco dimensiones se descompone en una torre infinita de modos 4-dimensionales Ψn(x) con masas mn2 = n2/R52, en unidades naturales ћ = c = 1, y carga qn (modos de Kaluza-Klein).
Puesto que el radio de compactificación es tan pequeño, el valor típico de las masas será muy elevado, cercano a la masa de Planck Mp = k-12 = 1’2 × 1019 GeV*, y por tanto, a las energías accesibles hoy día (y previsiblemente, tampoco en un futuro cercano – qué más quisieran E. Witten y los perseguidores de las supercuerdas -), únicamente el modo cero n = 0 será relevante. Esto plantea un serio problema para la teoría, pues no contendría partículas ligeras cargadas como las que conocemos.
¿Y si llevamos a Kaluza-Klein a dimensiones superiores para unificar todas las interacciones?
La descripción de las interacciones débiles y fuertes a través de teorías gauge no abelianas mostró las limitaciones de los modelos en cinco dimensiones, pues éstas requerirían grupos de simetría mayores que el del electromagnetismo. En 1.964 Bryce de UIT presentó el primer modelo de tipo Kaluza-Klein-Yang-Mills en el que el espacio extra contenía más de una dimensión.
El siguiente paso sería construir un modelo cuyo grupo de isometría contuviese el del Modelo Estándar SU(3)c × SU(2)l × U(1)y, y que unificara por tanto la gravitación con el resto de las interacciones.
Edward Witten demostró en 1.981 que el número total de dimensiones que se necesitarían sería al menos de once. Sin embargo, se pudo comprobar que la extensión de la teoría a once dimensiones no podía contener fermiones quirales, y por tanto sería incapaz de describir los campos de leptones y quarks.
Por otra parte, la supersimetría implica que por cada bosón existe un fermión con las mismas propiedades. La extensión supersimétrica de la Relatividad General es lo que se conoce como supergravedad (supersimetría local).
Unos años antes, en 1.978, Cremmer, Julia y Scherk habían encontrado que la supergravedad, precisamente en once dimensiones, tenía propiedades de unicidad que no se encontraban en otras dimensiones. A pesar de ello, la teoría no contenía fermiones quirales, como los que conocemos, cuando se compactaba en cuatro dimensiones. Estos problemas llevaron a gran parte de los teóricos al estudio de otro programa de unificación a través de dimensiones extra aún más ambicioso, la teoría de cuerdas.
emilio silvera
* Profesor sin plaza ni salario, salvo honorarios según las clases impartidas. Volver
* ![]() del orden de 10-8 Kg = 1011 GeV; es la masa de una partícula cuya longitud de onda compton es igual a la longitud de Planck. Volver
del orden de 10-8 Kg = 1011 GeV; es la masa de una partícula cuya longitud de onda compton es igual a la longitud de Planck. Volver















 Totales: 74.955.705
Totales: 74.955.705 Conectados: 61
Conectados: 61






















