Oct
25
Relatividad – Supergravedad – Cuerdas…
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en General ~
Clasificado en General ~
 Comments (2)
Comments (2)
Relatividad – Supergravedad – Cuerdas…
La fuerza gravitatoria la describió magníficamente Einstein en su teoría general de la relatividad, donde explica cómo los campos gravitatorios curvan el espacio-tiempo en presencia de grandes cuerpos de materia, tales como planetas, estrellas y galaxias. Su ecuación de campo se presenta como sigue.
Eik = 8π G/CA Tik
Donde el tensor Eik es la curvatura de Einstein, una ecuación diferencial de segundo orden en términos del tensor métrico gik, y Tik es el tensor de tensión-energía. La constante de acoplamiento se da en términos de π, c es la velocidad de la luz y G la constante gravitacional. De esta ecuación se deducen otras muchas que han dado lugar a múltiples conexiones y es asombroso que esta ecuación, que introduce mínimas correcciones en las fórmulas de la geometría euclídea, recoja casi todas las ecuaciones conocidas de la física macroscópica. La relatividad de Einstein está dividida en dos partes; la especial con su contenido de E = mc2, cómo la velocidad de la luz c puede ralentizar el tiempo y cuando esta velocidad tiene al infinito, de ella se derivan la ley newtoniana de la gravitación, la ecuación de Poisson (y por tanto el carácter atractivo de las fuerzas gravitatorias), las ecuaciones de la mecánica de fluidos (ecuación de continuidad y ecuaciones de Euler), las leyes de la conservación de la masa y el momento, el carácter euclídeo del espacio, etc.
Igualmente se derivan todas las leyes de conservación relativista, y que la existencia de campos gravitatorios y de masa sólo es posible cuando el espacio tiene dimensión mayor que dos. Más aún, si se supone que el espacio tiene dimensión 4 (las tres que vemos diariamente más una pequeñísima dimensión circular extra, aproximadamente del tamaño de la llamada longitud de Planck: 10–33 cm), de la ecuación de Einstein se deducen la teoría clásica del electromagnetismo: las ecuaciones de Maxwell (y por tanto la ley de Coulomb), la conservación de la carga y la ley de Lorentz. ¡Una maravilla!
Tan enorme fue el impacto causado en el mundo de la física por las ecuaciones de campo de Einstein que sus colegas al estudiarla, calcularla, profundizar y sumergirse en su enorme contenido, pudieron derivar artículos relacionados sobre agujeros negros, agujeros de gusano, contracción de Lorentz, cosmología, cuadrimomento, lente gravitacional, energía cinética, energía en reposo, espacio de Minkowski, dilatación del tiempo, efecto Doppler relativista, ondas gravitatorias, paradoja de Bell, paradoja de los gemelos, principio de Mach, tensor de Ricci, tensor tensión-energía, tensor de Riemann, teoría general de la relatividad, teoría especial de la relatividad, tiempo propio, transformación de Lorentz, velocidad de la luz y sus efectos, viajes en el tiempo… Aún hoy, un siglo después de la publicación de su primera teoría relativista, Einstein, allá donde esté, sonríe al ver cómo tanto la espacial como la general traen de cabeza a sus colegas. Incluso en el desarrollo de la moderna teoría de supercuerdas surge como por arte de magia la ecuación de Einstein.
La gravedad actúa sobre la masa de las partículas, mientras que todas las demás fuerzas actúan sobre algo que llamamos “carga”. La diferencia es que la carga depende muy ligeramente del grado de amplificación de nuestro microscopio, mientras que la masa (recordemos E = mc2) está conectada con la energía, y si tratamos de localizar una partícula en un volumen menor entonces, de acuerdo con las leyes de la mecánica cuántica, ahí habrá movimiento (llamada energía de movimiento o energía mecánica) que aumenta por el mismo hecho de enfocar sobre ella el microscopio electrónico que con su luz transmite fotones a la partícula que tratamos de localizar (principio de incertidumbre), y ésta es la razón de que a distancias menores corresponden energías mayores, y por lo tanto, también masa mayores. Cuando las distancias son tan pequeñas que los movimientos se hacen relativistas (esto es, alcanzar velocidades cercanas a la de la luz) los efectos de la fuerza gravitatoria comienzan a aumentar gradualmente en comparación con las demás fuerzas; sin embargo, aún son increíblemente débiles y tienen un largo camino por recorrer hasta poder competir en intensidad con las otras fuerzas.
Entremos en campo de gravedad que de forma paulatina aumentan la fuerza y nos diga sus efectos:
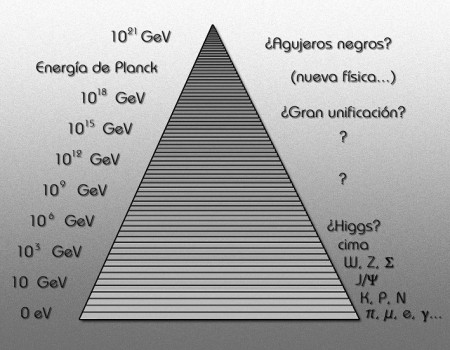
Aquí hemos llegado a una región de la física de partículas donde la energía (por partícula) es mucho mayor que la que actualmente podemos estudiar en nuestros laboratorios. Claro que especulamos, pero con los datos de los que disponemos, la realidad estará muy cerca de la expuesta en el gráfico.
En la zona más alta (último tramo) del dibujo se encuentran los misterios por resolver; allí la fuerza gravitatoria es enormemente elevada. Se encuentra en ese lugar misterioso que nadie conoce que está después de pasar el horizonte de sucesos de un agujero negro, ¡la singularidad!, donde el espacio y el tiempo dejan de existir.
La frontera se encuentra en ese lugar en que las masas o las energías superan 1019 veces la masa del protón, y esto implica que estamos mirando a estructuras con un tamaño de unos 10–33 cm. Esta masa la conocemos con el nombre de masa de Planck, y a la distancia correspondiente la llamamos distancia de Planck; expresada en gramos es de 22 microgramos, que es la masa de un grano muy pequeño de azúcar. Esto signifia que si tratamos de localizar una partícula con la precisión de una longitud de Planck (Lp = Gћ/c3 = 10–33 cm), las fluctuaciones cuánticas darán tanta energía que su masa será tan grande como la masa de Planck, y los efectos de la fuerza gravitatoria entre partículas sobrepasará los de cualquier otra fuerza. Es decir, para estas partículas la gravedad es una interacción fuerte.
Si la gravedad llega a ser una interacción fuerte, será un verdadero desastre, todo lo que conocemos acerca de la naturaleza será inválido en la escala de Planck; allí la física es otra. La teoría de Einstein funciona a la perfección acerca de la naturaleza de la fuerza de gravedad. Parte de un principio muy fundamental, uno que prácticamente tiene que ser correcto: la gravedad es una propiedad del espacio y el tiempo mismos. El espacio y el tiempo están “curvados”. Por curvados quiero decir exactamente lo que le sucede a un trozo de papel cuando se humedece: se deforma y no hay manera de alisarlo con la plancha. La fuerza gravitatoria es la responsable de semejante rugosidad en el espacio y el tiempo.
Cuando más cerca estamos de la longitud de Planck más fuerte es la necesidad de aplicar las leyes de la mecánica cuántica a esas arrugas del espacio-tiempo. Mientras las arrugas sean pequeñas, sabemos hacerlo y así obtenemos una teoría conocida como gravedad cuántica. Esta teoría predice la existencia de los ya mencionados gravitones, partículas elementales con espín 2 y pasa 0; así como el fotón es para el electromagnetismo, el gravitón es para la fuerza gravitatoria: su bosón transportador de la fuerza.
Conforme seguimos acercándonos a la longitud de Planck, más rugoso se vuelve el espacio-tiempo, simplemente porque las arrugas más pequeñas se hacen más pronunciadas que las grandes. Las incertidumbres usuales, típicas de la mecánica cuántica, harán que las arrugas sean más borrosas. Y si tratamos de ir más allá de la longitud de Planck, todo funciona mal. La curvatura y la incertidumbre llegan a ser tan grandes que la noción de “distancia entre dos puntos” deja de tener sentido, porque no hay reglas para medir que se ajusten a este espacio de 0’000000000000000000000000000000001 cm. El espacio y el tiempo mismos se vuelven magnitudes inútiles. La definición matemática de los que “significa” el espacio y el tiempo depende de la definición de “distancia entre dos puntos”. Esto probablemente implica que antes de encontrar una descripción útil del mundo subplanckiano tendremos que cambiar completamente todo lo que sabemos de física, que por cierto, es lo que le pasó al mismo Max Planck cuando formuló su teoría del cuanto de acción, h, origen de la mecánica cuántica.
Si entramos en el terreno de la teoría llamada de la “supergravedad”, nos encontramos con una construcción matemática muy complicada que consigue combinar la supersimetría con la fuerza gravitatoria. En esta teoría, sus partículas se transforman en otras con diferente espín. Realmente se está modificando no sólo en sus propiedades “internas” tales como la carga y la extrañeza, sino en las espacio-temporales.
Aunque un gran número de físicos en todo el mundo pusieron su esfuerzo en esta teoría, tardaron, dada su enorme complejidad, varios años en obtener una formulación cerrada.
La versión “N = 8” es la teoría de supergravedad más complicada y seguramente la más interesante también. Cada supermultiplete debe contener todos los valores de espín entre 0 y 2. Para ser precisos, si se considera el movimiento de rotación alrededor de un eje en una dirección fija del espacio, el espín debe cambiar desde -2 a 2 en ocho pasos de media unidad. Pero también debe haber un único gravitón (cuyo espín relativo a un eje fijo es siempre 2 o -2), ya que en la teoría de Einstein sólo se permite un tipo de fuerza gravitatoria, y por lo tanto sólo puede haber un supermultiplete “N = 8”.
Un rasgo atractivo de esta teoría es que no está permitido ningún otro tipo de partícula, y que este único supermultiplete contiene tantas especies de partículas que pueden explicar todas las existentes. Aquí tenemos de nuevo un ejemplo de teoría que no admite ni permite extensiones ni adiciones. Alrededor de 1980 se extendió el entusiasmo por esta construcción. ¿Habrá por fin alcanzado la física su meta con esta teoría? ¿Es la teoría global de la cual se derivan todas las fuerzas y todas las partículas?
A principios de la década de los 60, Richard Feynman estaba entre los primeros científicos que intentaron diseñar una teoría cuántica consistente de la gravedad. Feynman descubrió sus “partículas fantasmas”, partículas que no existen realmente pero que parecen emerger como estados intermedios de un cálculo para determinar el efecto de intercambios múltiples del gravitón. Este trabajo pionero fue continuado por el americano Bryce de Witt y Stanley Mandelstam, y los rusos Ludwig Faddeev, Victor Popov, Efim Fradkin, Andrei Slavnov y otros. Las partículas fantasmas de Feynman ahora son partículas del equipo estándar de todas las teorías de partículas.
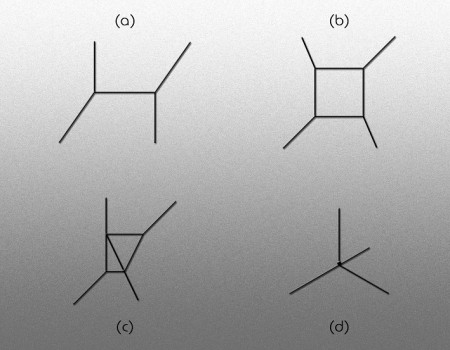
Gerard’t Hooft y Veltman aprendieron cómo renormalizar la teoría de Yang-Mills y de inmediato entraron en la discusión sobre la gravedad. Lo que descubrieron fue que los primeros efectos de los intercambios múltiples del gravitón (ver diagramas a continuación), se puede calcular sin ambigüedad, si sólo se consideran los gravitones. Pero si se les permite interaccionar con otro tipo de partículas, o se las partículas mediadoras forman dos o más lazos interconectados, (figura b), aparecen las primeras dificultados: se tienen que introducir más y más fuerzas infinitas para calcular dentro de un resultado final finito y con sentido. Pero estas fuerzas contador conducen por sí mismas a infinitos aún peores cuando se incluyen en los lazos y las cosas crecen fuera de control. Esto es lo que se conoce como una teoría no renormalizable; se desboca sin que se pueda controlar en infinitos que no llevan a ninguna parte.
a) Es el caso más simple de intercambio de partícula. Aquí los efectos de la mecánica cuántica son todavía mínimos.
b) Intercambio múltiple en único lazo cerrado
c) Diagrama de dos lazos cerrados. En la gravedad cuántica estos intercambios únicamente dan efectos finitos si se introduce una nueva interacción finita del tipo d, pero si se introduce la interacción en uno de los vértices de b o c surgen complicaciones que no se pueden controlar.
¿Qué pasa entonces con la supergravedad? Aquí, al principio, las cosas parecen mucho mejores, e incluso al nivel de tres lazos nada parece ir mal. Los entusiastas afirmaban que esto podía ser una coincidencia y que la teoría final de todas las fuerzas estaba a la vista. Una teoría de todas las fuerzas… ¿podemos imaginar una cosa tan grande? Albert Einstein persiguió ese sueño durante los últimos 30 años de su vida sin lograrlo. Claro que, entonces no se conocían tantos datos como se conocen hoy, y el paradójico que muchos de esos nuevos datos hayan salido, precisamente, de sus ecuaciones de campo de la relatividad general. Esa que nos explica cómo en presencia de grandes masas y energías, el tiempo y el espacio se curvan.
Es curioso que llegados a un punto de la mecánica cuántica, ése que es menor que la distancia de Planck, en ese reino, el espacio y el tiempo dejan de existir. Llegados a un punto de la relatividad general, ése que nos dice que existen singularidades que están en el centro de los agujeros negros, allí donde la gravedad se hace infinita, el espacio y el tiempo dejan de existir.
emilio silvera
















 Totales: 83.532.605
Totales: 83.532.605 Conectados: 61
Conectados: 61























el 9 de febrero del 2014 a las 7:07
Sabemos que el espacio y tiempo al menos necesitan una linea para que existan, pero tal linea nace de la conexion de un punto, tal punto, segun Poincare es una esfera tridimensional. Necesitamos darle esencia matematica a su existencia de tal punto para poder comprender su comportamiento fisico.
el 10 de febrero del 2014 a las 5:49
Precisamente eso es, lo que desde hace mucho tiempo estamos tratando de hacer.
Saludos.