Siempre hablamos de visitar otros mundos, otros universos y, en ellos, las condiciones físicas no tienen, necesariamente, que ser como en el nuestro. Los mundos, como las estrellas y los universos, pueden tener sus propias características dependiendo de muchos factores que lo podrían conformar de manera muy diferente a como lo está nuestro mundo y vemos que se comporta el universo con sus cuatro leyes fundamentales y sus constantes que, en otro universo, podrían ser de otra manera.

Formas de vida diferentes, estructuras asombrosas y para nosotros desconocidas, y, hasta el Tiempo se podría comportar de diferente manera. Un universo en el que las constantes fuesen diferentes y las fuerzas fundamentales que lo rigen sean de otra manera, y, también existe la posibilidad de que no se expanda, o, que… (Cualquier escenario que ni podemos imaginar).

Si es cierto lo que afirman algunas teorías, entonces existen en realidad un número infinito de universos paralelos, muchos de ellos con diferentes constantes físicas. En algunos de ellos, quizá los protones se desintegran con demasiada rapidez, o las estrellas no pueden fabricar los elementos pesados por encima del hierro, o el Big Crunch tiene lugar demasiado deprisa porque su densidad crítica sobrepasa en mucho a la ideal y no da tiempo a que pueda comenzar la germinación de la vida, y así sucesivamente. De hecho, un número infinito de estos universos paralelos están muertos, sin las leyes físicas que puedan hacer posible la vida tal como la conocemos.

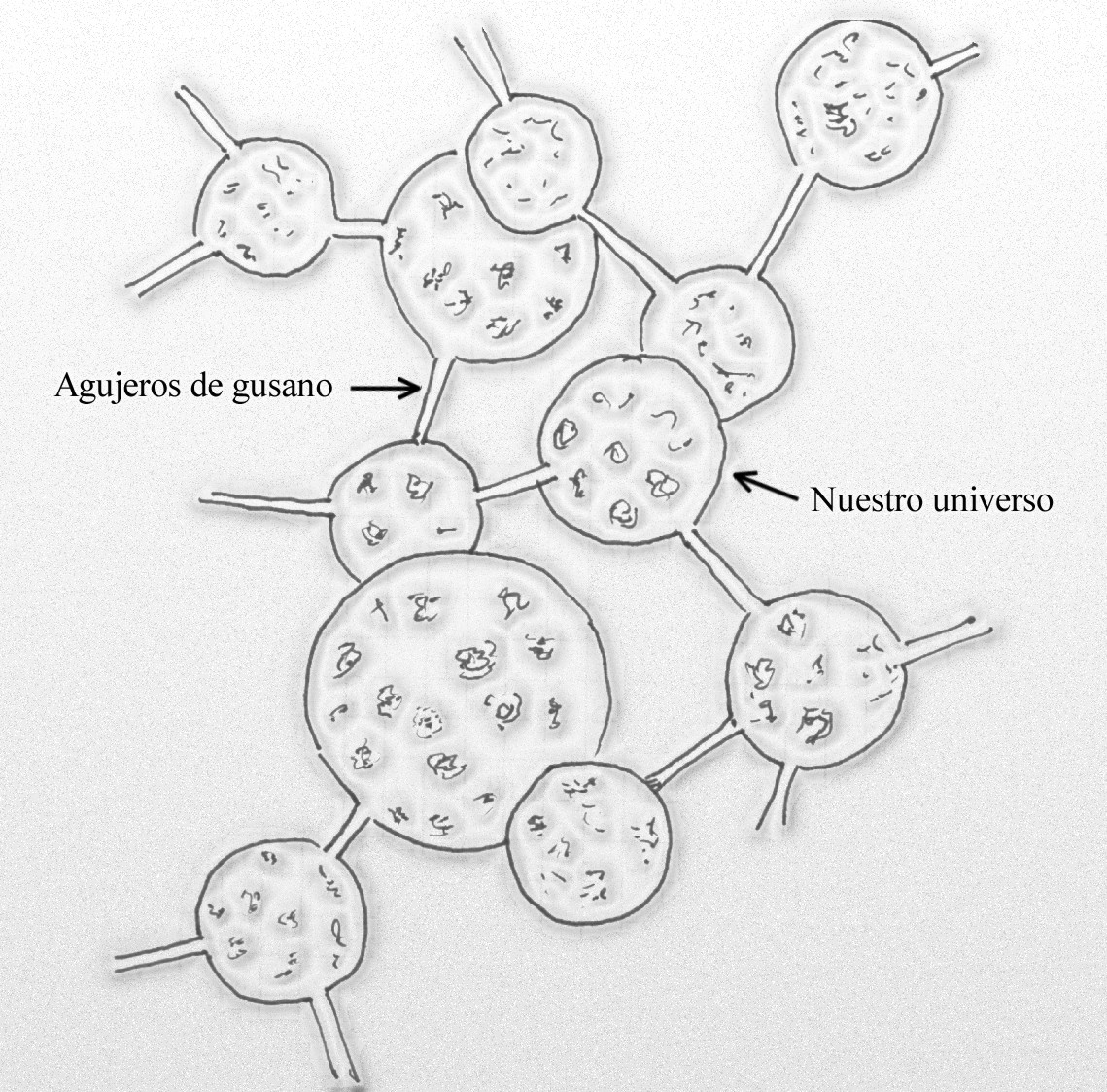
En tal universo paralelo (el nuestro), las leyes de la física eran compatibles con la vida que conocemos. La prueba es que nosotros estamos aquí para tratar esta cuestión. Si esto es cierto, entonces quizá no haya que invocar a Dios para explicar por qué la vida, por preciosa que sea, es posible en nuestro universo. Sin embargo, esto reabre la posibilidad del principio antrópico débil, es decir, que coexistimos con nuestros universos muertos y que el nuestro sea el único compatible para vida.

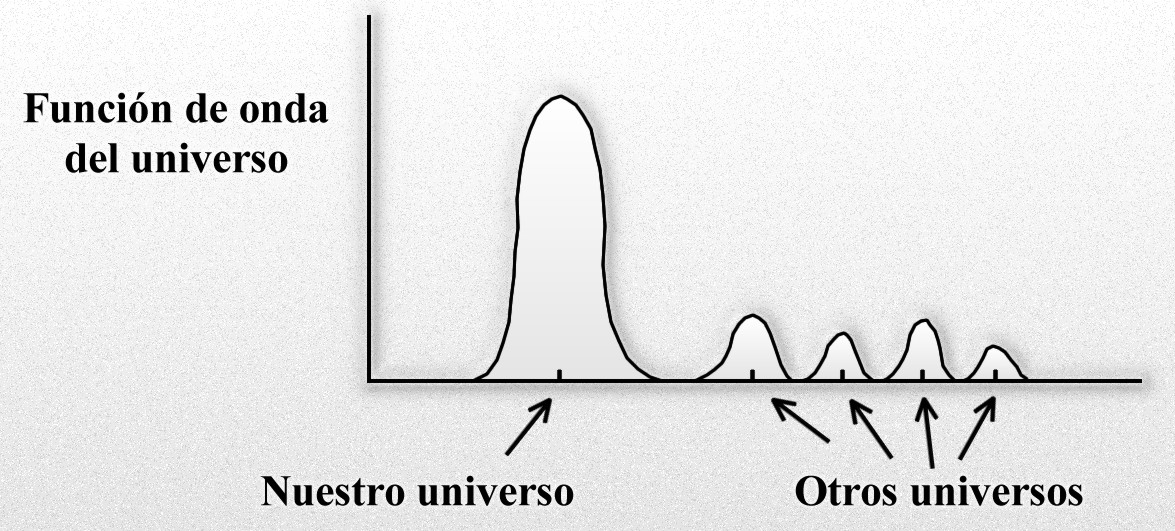
La segunda controversia estimulada por la función de onda del universo de Hawking es mucho más profunda y, de hecho, aun está sin resolver. Se denomina el Gato de Schrödinger. Empezamos con una función de onda que describe el conjunto de todos los universos posibles. Esto significa que el punto de partida de la teoría de Hawking debe ser un conjunto infinito de universos paralelos, la función de onda del universo. El análisis bastante simple de Stephen Hawking, reemplazando la palabra partícula por universo, ha conducido a una revolución conceptual en nuestras ideas sobre la cosmología.

La teoría cuántica, recordémoslo, afirma que para todo objeto existe una función de onda que mide la probabilidad de encontrar dicho objeto en un cierto punto del espacio y del tiempo.

La teoría cuántica afirma también que nunca se conoce realmente el estado de una partícula hasta que se haya hecho una observación. Antes de que haya una medida, la partícula puede estar en uno de entre una diversidad de estados, descritos por la función de onda de Schrödinger. Por consiguiente, antes de que pueda hacerse una observación o medida, no se puede conocer realmente el estado de la partícula.  De hecho, la partícula existe en un estado ultramundano, una suma de todos los estados posibles, hasta que se hace una medida.

Cuando esta idea fue propuesta por primera vez por Niels Bohr y Werner Heisenberg, Einstein se revolvió contra ella. “¿Existe la luna sólo porque la mira un ratón?“, -o un gato- le gustaba preguntar. Según la teoría cuántica, en su más estricta interpretación, la Luna, antes de que sea observada, no existe realmente tal como la conocemos. “La Luna puede estar, de hecho, en uno cualquiera de entre un número infinito de estados, incluyendo el estado de estar en el cielo, de estar explotando, o de no estar allí en absoluto. Es el proceso de medida que consiste en mirarla el que decide que la Luna está girando realmente alrededor de la Tierra“. Decía Einstein con ironía.

Edwin Schrödinger, autor de la ecuación con su función de onda, se disgustó con estas interpretaciones de su ecuación. Para demostrar lo absurdo de la situación creada, Schrödinger colocó un gato imaginario en una caja cerrada. El gato estaba frente a una pistola, que está conectada a un contador Geiger, que a su vez está conectado a un fragmento de uranio. El átomo de uranio es inestable y sufrirá una desintegración radiactiva. Si se desintegra un núcleo de uranio, será detectado por el contador Geiger que entonces disparará la pistola, cuya bala matará al gato.

Para decidir si el gato está vivo o muerto, debemos abrir la caja y observar al gato. Sin embargo, ¿cuál es el estado del gato antes de que abramos la caja? Según la teoría cuántica, sólo podemos afirmar que el gato esta descrito por una función de onda que describe la suma de un gato muerto y un gato vivo.

Para Schrödinger, la idea de pensar en gatos que no están ni muertos ni vivos era el colmo del absurdo, pero la confirmación experimental de la mecánica cuántica nos lleva inevitablemente a esta conclusión. Hasta el momento, todos los experimentos han verificado, favorablemente, la teoría cuántica.

        Sí, a veces la mecánica cuántica parece tan fantástica como el cuento de Alicia

La paradoja del gato de Schrödinger es tan extraña que uno recuerda a menudo la reacción de Alicia al ver desaparecer el gato de Cheshire en el centro del cuento de Lewis Carroll: “Allí me verás“, dijo el Gato, y desapareció, lo que no sorprendió a Alicia que ya estaba acostumbrada a observar cosas extrañas en aquel lugar fantástico. Igualmente, los físicos durante años se han acostumbrados a ver cosas “extrañas” en la mecánica cuántica.

Existen varias maneras de abordar esta dificultad de lo incomprensible en mecánica cuántica. En primer lugar, podemos suponer que Dios existe.   Puesto que todas las “observaciones” implican un observador, entonces debe haber alguna “conciencia” en el universo. Algunos físicos como el premio Nobel Eugene Wigner, han insistido en que la teoría cuántica prueba la existencia de algún tipo de conciencia cósmica universal.

La segunda forma de tratar la paradoja es la preferida por la gran mayoría de los físicos en activo: ignorar el problema.

El físico Richard Feynman dijo en cierta ocasión: “Creo que es justo decir que nadie comprende la mecánica cuántica. No siga diciéndose a sí mismo, si puede evitarlo, “¿pero cómo puede ser así?” porque usted se meterá “hasta el fondo” en un callejón sin salida del que nadie ha escapado.  Nadie sabe como puede ser eso“. De hecho, a menudo se ha dicho que de todas las teorías propuestas en el siglo XX, la más absurda es la teoría cuántica. Algunos dicen que la única cosa que la teoría tiene a su favor es que “es indudablemente correcta”.

Sin embargo, existe una tercera forma de tratar esta paradoja, denominada teoría de los muchos universos. Esta teoría (como el principio antrópico) no gozó de mucho favor en la última década, pero está siendo revitalizada por la función de onda del universo de Stephen Hawking.

Aunque no siempre, lo más simple tiene que ser lo verdadero. El principio de la Navaja de Ockham es fundamental para el reduccionismo metodológico.

Existe un principio de la física denominado Navaja de Ockham, que afirma que siempre deberíamos tomar el camino más sencillo posible e ignorar las alternativas más complicadas, especialmente si las alternativas no pueden medirse nunca.

Para seguir fielmente el consejo contenido en la navaja de Ockham , primero hay que tener el conocimiento necesario para poder saber elegir el camino más sencillo, lo que en la realidad, no ocurre. Nos faltan los conocimientos necesarios para hacer las preguntas adecuadas.

¿Quién puede saber lo que ahí fuera existe? ¡Nadie! Sólo podemos imaginarlo en función de cada Mente y de distintas maneras. Lo que sí es seguro es que, más allá de nuestro Universo existen más “cosas” de las que ni podemos imaginar.

Hugo Everett, Bryce DeWitt y después Hawking (también otros), han propuesto la teoría de los universos múltiples. En unos universos los protones se desintegran antes haciendo inestable la materia, en otros, el átomo de uranio se desintegra mediante un proceso sin radiaciones, y en otros universos las constantes universales que existen en el nuestro, son totalmente diferentes y no dan posibilidad alguna para la existencia de seres vivos. Está claro que cualquier variación que en principio pudiera parecer sin importancia, como por ejemplo la carga del electrón, podría transformar radicalmente nuestro universo.

Como apuntó el físico Frank Wilczek:

La Helena de Troya de la película

“Se dice que la historia del mundo sería totalmente distinto si Helena de Troya hubiera tenido una verruga en la punta de su nariz.”

Hasta el momento, se han celebrado varias conferencias internacionales sobre la función de onda del universo. Sin embargo, como ocurre en la teoría de supercuerdas, las matemáticas implicadas en la función de onda del universo, parecen estar más allá de la capacidad de cálculo que cualquier humano en este planeta pudiera resolver, y tendríamos que esperar años antes de que aparezca un individuo genial que pudiera encontrar una solución rigurosa a las ecuaciones del añorado Hawking.

Recordemos aquí de nuevo que, precisamente ahora, un siglo más tarde, en el Congreso Internacional de Matemáticas celebrado en Madrid el mes de Agosto de 2.006, se otorgó la Medalla Field (una especie de Nobel de las matemáticas) al matemático ruso Perelman, extraño ser que ni se dignó comparecer a recogerla con el premio, hizo caso omiso. Perelman ha resuelto la conjetura expuesta por Poincaré planteada en 1.904.

La conjetura de Poincaré de 1.904, en el año 2.000, fue catalogada por el Instituto Clan como uno de los siete problemas del milenio. Para hacer un comentario sobre esta conjetura tengo que referirme a la topología, el nivel de las matemáticas donde está ubicada.

En el Año Internacional de las matemáticas, reunidos en Madrid y presididos por el Rey de España, todos esperaban la llegada del genio Grigori Perelman, le entregarían el premio de un millón de dólares por haber resuelto uno de los 7 problemas matemáticos del milenio. No apareció a recogerlo y desapareció sin dejar rastro.

El personaje vive dentro de su propio mundo, opinaba que toda aquella gente no merecía que le explicara algo que no entenderían.

Vive en una pequeña casa de 60 m/2 con su madre y sale al campo a coger setas

Las últimas fotos que se conocen de él se las sacaron con un celular en un vagón del metro de Petersburgo. Se está quedando pelado pero las mechas largas y desgreñadas le llegan a los hombros, va en zapatillas sucias, un traje arrugado que le queda corto, sin corbata y con la camisa enteramente desprendida, flaco como un Cristo, la barba igual, la mirada perdida, las uñas largas y sucias y curvadas hacia adentro como garras. El vagón va en dirección sur, a Kúpchino, un barrio de monoblocks donde muere el metro. Todos los vecinos de Kúpchino saben quién es Grisha Perelman y cuál es la puerta del ínfimo departamento que comparte con su madre. Pero ninguno va a decírselo a los periodistas y a los fanáticos de la matemática que cada tanto merodean por ahí.

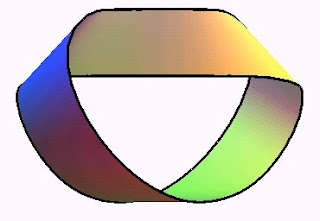
    La topología tienen unas matemáticas endiabladamente complejas

La topología es la geometría de los objetos elásticos o flexibles que cambian de forma pero tienen las mismas propiedades que antes de ser estirados, achatados, etc. Se pueden retorcer pero no cortar ni pegar.

Los topólogos no tienen en cuenta la distancia, puesto que se puede variar al deformar el objeto, sino nociones más sutiles. Los orígenes de la topología se remontan a mediados del siglo XVIII, con los trabajos de Euler en teoría de grafos, que llamó “análisis situs”.

A finales del siglo XIX y principios del siglo XX, la topología recibió un gran impulso con los trabajos de Poincaré, matemático francés muy influyente en el posterior desarrollo de diversas áreas de las matemáticas y de la física. En particular, en 1.904 planteó la conjetura que lleva su nombre y que no se ha resuelto hasta el siglo XXI. Este problema ha sido un motor para la investigación en topología de todo el siglo pasado y se ha llegado a su resolución con ideas nuevas y apasionantes.

                             Henri Poincaré en su estudio trabajando

Para situarnos mejor debemos hablar de las variedades, espacios que tienen una dimensión determinada. Por ejemplo una recta o un circulo son variedades de dimensión uno, puesto que se describen como un parámetro.  El plano o la esfera son ejemplos de variedades bidimensionales, al utilizar dos parámetros para describir sus posiciones. El espacio en que vivimos es una variedad tridimensional, y si le añadimos la dimensión temporal, el espacio-tiempo es una variedad de dimensión cuatro. Ya he comentado en este mismo trabajo cómo las singularidades geométricas, las variedades, fueron introducidas por Riemann a mediados del s.    XIX y constituyeron una herra-mienta clave para la física del siglo XX. De hecho, la teoría de la relatividad especial de Einstein fue postulada por Einstein en 1.905, pero hasta que no incorporó las variedades contenidas en el tensor métrico de Riemann, no pudo completar la teoría de la relatividad que incluía los espacios curvos.

La pregunta que hizo Poincaré fue la siguiente: ¿Es la esfera la única variedad tridimensional para la cual toda curva se contrae?

Se pasó un siglo entero antes de que un genio de las matemáticas, el extraño G. Perelman, pudiera demostrar la conjetura de Poincaré.

De todas las maneras, avanzar en el conocimiento de las cosas no resulta nada fácil, y, aunque el avance es exponencial (cuanto más datos vamos teniendo más rápidamente avanzamos), hay algunos enigmas de la Naturaleza que, de momento, seguirán en la oscuridad de nuestra profunda ignorancia.

Emilio Silvera Vázquez

[?]

No son pocas las Organizaciones que operan alrededor de todo este tinglado del falso “Cambio Climático”. Viven de subvenciones de los grandes capitales a los que interesa este movimiento para imponer a la población una serie de normas que los tenga controlados y, al mismo tiempo, les produzcan a ellos grandes beneficios. Incluso lo de las vacunas del Covid-19 sospecho que fue un movimiento de “algunos” para hacer el gran negocio de miles de millones. Desde que apareció los primeros síntomas de la Pandemia, hasta que se pusieron a la venta las vacunas, no había tiempo material de que hubieran hecho las suficientes pruebas y cumplidos con todos los requisitos que la Ley exige antes de dar vía libre al medicamente. Sin embargo, el permiso se obtuvo con el beneplácito de los Gobiernos que firmaron un documento liberando de responsabilidad a las farmacéuticas por las consecuencias derivadas de las “vacunas” que no han sido pocas y, entre ellas, el de la destrucción del sistema inmune, ya que, dichas “vacunas” tenían hasta grafeno.

No son pocas las muertes de personas consecuencia de esas vacunas, algunos de las fallecidos y perjudicados son famosos y alguna cantante de primera fila que ha quedado imposibilitada para mover los músculos. Además nos quieren prohibir comer carne y consumir insectos… ¡Qué puñetas está pasando! ¿Hasta cuando soportaremos todos estos abusos?

¡Valiente montaje! Solo hay que darse una vuelta por el Pasado para comprobar que los cambios climáticos han sido cosa natural en la Historia de la Tierra. El hombre no tiene la capacidad de cambiar absolutamente nasa, y, cierto es que, en el ámbito comarcal puede crear alguna que otra contaminación con sus actividades pero… ¡A nivel mundial!

Del 7 al 18 de diciembre de 2009, se celebraron en Copenhague (Dinamarca) las reuniones correspondientes a la 15. ª Conferencia de las Partes de la Convención Marco de las Naciones Unidas sobre el Cambio Climático

Tienen avionetas fumigando para deshacer las nubes y que no llueva (miramos al cielo y vemos esas rayas blancas provocadas con materiales que destrozan las nubes), los Gobiernos de la Agenda 2030 lo autorizan perjudicando a las personas para conseguir sus fines bastardos.

Betelgeuse, una estrella moribunda 1.000 veces mayor que el sol podría y `podría estallar muy pronto.                 

Si resbalas te darás un golpe

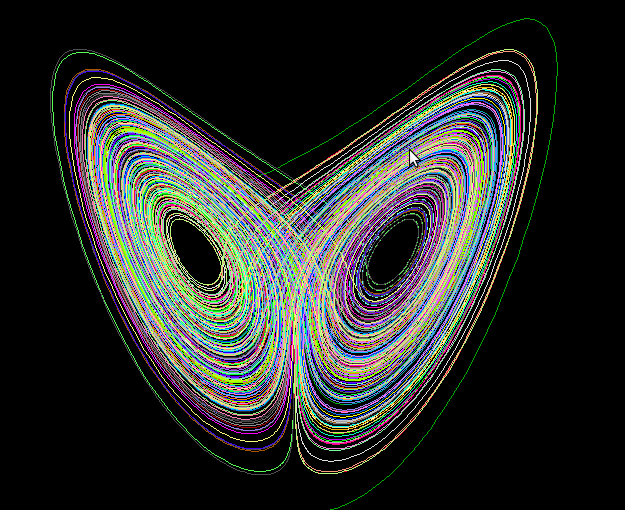
La Teoría del Caos una rama de las matemáticas, la física y otras ciencias que trata ciertos tipos de sistemas dinámicos, es decir aquellos sistemas cuyo estado evoluciona con el tiempo, con la particularidad de ser muy sensibles a las variaciones en las condiciones iniciales. Pequeñas variaciones en dichas condiciones iniciales pueden implicar grandes diferencias en el comportamiento futuro, haciendo  complicada la predicción a largo plazo.

                        El aleteo de una mariposa puede provocar un Tsunami al otro lado del mundo

                                          El problema de los tres cuerpos 

                                                              La famosa conjetura de pOINCARÉ

                                                                El efecto mariposa

En la Asamblea de Matemáticas celebrada en Madrid, se negó a coger el premio de un millón de dolores

[?]

“Un sistema complejo está compuesto por varias partes interconectadas o entrelazadas cuyos vínculos crean información adicional no visible ante el observador como resultado de las interacciones entre elementos. y, así pues, un sistema complejo, posee más información que la que da cada parte independiente.”

Todos hemos oído hablar, con más o menos frecuencia, de “Sistemas Complejos”, aquí mismo en estas páginas, la palabra sale a relucir con cierta frecuencia y, no me extraña que “la palabreja” cree una barrera, dado que, para muchas personas, “complejo” significa “complicado” y suponen automáticamente que, si un sistema es complicado, será difícil de comprender. La naturaleza posee una fuerte tendencia a estructurarse en forma de entes discretos excitables que interactúan y que se organizan en niveles jerárquicos de creciente complejidad, por ello, los sistemas complejos no son de ninguna manera casos raros ni curiosidades sino que dominan la estructura y función del universo.

    La Tierra como sistema es un conjunto de cosas separadas que conforma una gran complejidad

Claro que, no siempre ese temor a lo difícil y complicado, está justificado y, tal suposición no es, necesariamente correcta. En realidad, un sistema complejo es tan solo un sistema que está formado por varios componentes más sencillos que ejercen entre sí una interacción mutua que, naturalmente, tiene sus consecuencias. Si miramos la imagen de arriba, vemos una inmensa y hermosa Nebulosa que está formada por una serie de “cosas” sencillas como lo son el gas hidrógeno y el polvo interestelar entre otros y, en presencia de energías, la gravedad y otros parámetros, ahí ocurren cosas tales como, el nacimiento de estrellas y la aparición de mundos…entre otras.

Los grandes triunfos de la Ciencia se han logrado, en gran medida, descomponiendo los sistemas complejos en sus componentes simples, es decir, estudiar por partes lo que allí está presente (en caso necesario, como primera aproximación, dando el paso suplementario de pretender que todos los componentes son más sencillos de lo que son en realidad) para llegar a comprender el todo.

En el ejemplo clásico del éxito que ha logrado este planteamiento para conocer el mundo que nos rodea, buena parte de la química puede entenderse mediante un modelo en el que los componentes simples son átomos, y para eso importa poco de qué están formados los núcleos. Ascendiendo un nivel, las leyes que describen el comportamiento del dióxido de Carbono encerrado en una caja pueden entenderse pensando en unas moléculas más o menos esféricas que rebotan unas contra otras y contra las paredes de su contenedor, y poco importa que cada una de estas moléculas esté formada por un átomo de Carbono y dos de Oxígeno unidos entre sí. Ambos sistemas son complejos, en sentido científico, pero fáciles de entender.

Fijémonos, por ejemplo, en el Campo Magnético Terrestre. En esencia, los planetas generan un campo magnético por efecto dinámo. Para ello se requiere que el planeta rote; debe contener una región con un fluido conductor de la electricidad y debe existir convección en dicho fluido. No se puede asegurar pero parece ser que si en la Tierra no hubiese tectónica de placas el transporte convectivo hacia la superficie podría no tener lugar, la dinamo no funcionaría y el campo magnético terrestre sería prácticamente nulo o, al menos, mucho menor que el actual. Sin la protección que nos brinda el campo magnético, la atmósfera podría desaparecer a causa del continuo bombardeo de las partículas de alta energía procedentes del viento solar. Todos estos componentes son estudiados por separado y, más tarde, los juntamos en un todo que nos lleva a la comprensión de este Sistema Complejo.

Claro que la clave para poder llegar al conocimiento del “sistema complejo” consiste en saber elegir los componentes adecuados sencillos que conforman el todo para poder realizar el análisis necesario que nos lleve hasta las respuestas que buscamos. En muchas ocasiones hemos explicado aquí, lo que hay en  las  Nebulosas como la de arriba y lo que ocurre en ellas para que, finalmente, nazcan estrellas nuevas.

Hay cuestiones, a un nivel más abstracto del que hemos oído hablar también con cierta frecuencia. Acordaos de que, poco después de que Einstein publicara sus trabajos sobre relatividad especial, el matemático alemán que arriba podéis ver se dio cuenta de que, en cierto modo, el tiempo debía ser considerado como la cuarta coordenada complementaria de las tres coordenadas del espacio. En su discurso de inauguración de la 80 reunión de la Asamblea general alemana de científicos naturales y físicos el 21 de septiembre de 1908 pronunció una célebre frase:

“Las ideas sobre el espacio y el tiempo que deseo mostrarles hoy descansan en el suelo firme de la física experimental, en la cual yace su fuerza. Son ideas radicales. Por lo tanto, el espacio y el tiempo por separado están destinados a desvanecerse entre las sombras y tan sólo una unión de ambos puede representar la realidad”.

Desde entonces el espacio-tiempo cuatridimensional pasó a llamarse espacio de Minkowski. Si empleamos x,y y z para las tres coordenadas del espacio, tomaremos ct para la cuarta coordenada de tiempo, siendo c la velocidad de la luz. Sin embargo debemos multiplicar ct por otro factor que, sin destrozar la armonía del sistema tetradimensional de las coordenadas haga a la coordenada de tiempo físicamente diferente de las tres coordenadas espaciales. La matemática nos suministra precisamente este factor conocido como una “unidad imaginaria” que se designa con el símbolo i (i= raíz cuadrada de -1).

“Es un hecho notorio que los procesos que ocurren en el universo observable son irreversibles, mientras que las ecuaciones que expresan las leyes fundamentales de la física son invariantes bajo inversión temporal. La emergencia de la irreversibilidad a partir de la física fundamental ha sido un tema que ha preocupado a físicos, astrónomos y filósofos desde que Boltzmann formulara su famoso teorema “H”.

¿Es un sistema complejo un fotón? La propiedad del fotón, de la luz, es que es algo que oscila tan rápidamente que en realidad es como si estuviera en dos sitios a la vez, o sea algo que está pero que no está ?

Cómo se entiende algo así

“¿Tengo que reconocer que está ha sido la incógnita que más me ha costado despejar, todo un desafío a la lógica, a la matemática. Aunque en realidad era sencillo, porque lo cierto es que lo tenía en las narices. ¡Claro! esa es la esencia de nuestra mágica ecuación, e =m.c

²

, ¡”

masa en movimiento

!,es decir, más de lo mismo. Digamos que la mecánica cuántica en realidad no es más que la Vida llevada a su mínima expresión.

Los números complejos, con una parte real y otra imaginaria, también juegan un papel esencial en los formulismos de la mecánica cuántica. La propia probabilidad de los sucesos cuánticos llega a expresarse en función de números complejos llamados amplitudes de probabilidad. La probabilidad real se halla a partir de estos números, sumando el cuadrado de su parte real y el cuadrado de su parte imaginaria.

Esto nos da una idea de la importancia de los estos números, tanto en la teoría de la relatividad como en la mecánica cuántica y nos ayuda a introducirnos en la teoría de Hartle-Hawking sobre los comienzos del universo, que supone un universo sin límites y con un tiempo imaginario, como se entiende la parte no real de un número complejo.

En cierta forma los ceros y los infinitos que aparecen en la física clásica son suavizados por la mecánica cuántica: La energía más baja en el vacío no es nunca cero, como tampoco es nunca cero la extensión de un punto físico . La existencia del cuanto de acción impide una energía cero del vacío, como impide la medida exacta, a la vez, de una variación de energía y del tiempo asociado a dicha variación.El punto físico menor sería la llamada longitud de Planck, del orden de 10^-35 metros, lo que también elimina el infinito que resultaría de considerar las partículas subatómicas como puntuales: su densidad sería infinita y resultarían microscópicos agujeros negros.

                         En este Universo nuestro… ¡Todo cambia a medida que el Tiempo pasa!

Según alguna teoría que circula por ahí, si comenzamos en el momento presente y vamos hacia atrás en el tiempo, lo que aparentemente sería el punto origen de la descripción del tiempo real convencional, la naturaleza del tiempo cambia: la componente imaginaria del tiempo se hace más y más prominente hasta que, en último término, lo que debería ser la singularidad de la teoría clásica se desvanece. El Universo existiría porque es una estructura matemática auto-consistente. Puede imaginarse el tiempo real como una línea que va del principio al final del Universo.

                         El Principio y el final: El BIg Bang y la muerte térmica del Universo

Pero también puede considerarse otra dirección del tiempo en ángulo recto al tiempo real. Esta última se denomina la dirección imaginaria del tiempo. En el tiempo imaginario, no habría ninguna singularidad en la que dejaran de regir las leyes de la Ciencia, ni ninguna frontera del Universo tras la cual tuviera que apelarse a Dios. El Universo no sería creado ni destruido. Simplemente existiría. Quizás el tiempo imaginario sea el auténtico tiempo real y lo que llamamos tiempo real sea sólo un producto de nuestra imaginación. En el tiempo real, el Universo tiene un principio y un fin. En el tiempo imaginario no hay singularidades ni límites.

Tiempo imaginario no se refiere a la imaginación: hace referencia a los números complejos. Como demostraron Einstein y Minkowsky, el espacio-tiempo constituye una geometría cuatridimensional. Es posible ir aún más lejos de estos conceptos. Si se miden las direcciones del tiempo utilizando números complejos, se obtiene una simetría total entre espacio y tiempo, que es, matemáticamente, un concepto muy bello y natural”. Don N. Page: ” En la formulación de la ausencia de límites de Hartle-Hawking, el tiempo es imaginario, y en vez de tener un borde es como si se tratara de la superficie del planeta Tierra. Suponiendo tiempo imaginario, el Universo no tuvo comienzo, no tiene límite, es una totalidad en sí mismo.

He tenido la oportunidad de leer el Libro de Roger Penrose (uno de los físicos actuales más brillantes), titulado,  El camino a la realidad, y él nos comenta:  “… los números complejos componen una notable unidad con la naturaleza. Es como si la propia naturaleza estuviera tan impresionada por el alcance y consistencia del sistema de los números complejos como lo estamos nosotros, y hubiera confiado a estos números las operaciones detalladas de su mundo en sus escalas más minúsculas”. Se refiere a la mecánica cuántica, pero realmente su importancia se refleja en toda la naturaleza, porque la cosmología, en los primeros instantes del universo se confunde con el mundo microscópico de las partículas elementales.

Claro que, los “Sistemas Complejos” están por todas partes y, tanto ers así que, nosotros mismos somos un buen ejemplo y llevamos con nosotros, el “sistema” más complejo de todos: Nuestro cerebro es, sin dudarlo y hasta donde puede llegar nuestros conocimientos actuales, el más complejo de los sistemas.

Claro que, si hablamos de complejidad de sistemas, el universo sería el mejor de los ejemplos. Con respecto a sus propios patrones, el universo es viejo. El tiempo de vida natural de un mundo gobernado por la gravedad, la relatividad y la mecánica cuántica es el fugaz breve tiempo de Planck.  Parece que es mucho más viejo de lo que debería ser.

Pero, pese a la enorme edad del universo en “tics” de Tiempo de Planck,  hemos aprendido que casi todo este tiempo es necesario para producir estrellas y los elementos químicos que traen la vida.

                                       La vida que surgió en el planeta Tierra a partir del polvo de estrellas

¿Por qué nuestro universo no es mucho más viejo de lo que parece ser? Es fácil entender por qué el universo no es mucho más joven. Las estrellas tardan mucho tiempo en formarse y producir elementos más pesados que son las que requiere la complejidad biológica. Pero los universos viejos también tienen sus problemas. Conforme para el tiempo en el universo el proceso de formación de estrellas se frena. Todo el gas y el polvo cósmico que constituyen las materias primas de las estrellas habrían sido procesados por las estrellas y lanzados al espacio intergaláctico donde no pueden enfriarse y fundirse en nuevas estrellas.

Pocas estrellas hacen que, a su vez, también sean pocos los sistemas solares y los planetas. Los planetas que se forman son menos activos que los que se formaron antes, la entropía va debilitando la energía del sistema para realizar trabajo. La producción de elementos radiactivos en las estrellas disminuirá, y los que se formen tendrán semividas más largas. Los nuevos planetas serán menos activos geológicamente y carecerán de muchos de los movimientos internos que impulsan el vulcanismo, la deriva continental y la elevación de las montañas en el planeta. Si esto también hace menos probable la presencia de un campo magnético en un planeta, entonces será muy poco probable que la vida evolucione hasta formas complejas.

                          Estos son los escenarios en los que se formaron  los elementos de la vida

Las estrellas típicas como el Sol, emiten desde su superficie un viento de partículas cargadas eléctricamente que barre las atmósferas de los planetas en órbitas a su alrededor y, a menos que el viento pueda ser desviado por un campo magnético, los posibles habitantes de ese planeta lo podrían tener complicado soportando tal lluvia de radiactividad. En nuestro sistema solar el campo magnético de la Tierra ha protegido su atmósfera del viento solar, pero Marte, que no está protegido por ningún campo magnético, perdió su atmósfera hace tiempo.

Probablemente no es fácil mantener una larga vida en un planeta del Sistema solar. Poco a poco hemos llegado a apreciar cuán precaria es. Dejando a un lado los intentos que siguen realizando los seres vivos de extinguirse a sí mismos, agotar los recursos naturales, propagar infecciones letales y venenos mortales y emponzoñar la atmósfera, también existen serias amenazas exteriores.

¿No es inmensamente complejo todo esto?

                                            Una galaxia es un gran sistema cerrado

En realidad, los Sistemas complejos constituyen y se manifiestan en la inmensa mayoría de los fenómenos observables. Sin embargo, y aquí radica una de sus propiedades más interesantes, la abundancia y diversidad de los sistemas complejos (sean de tipo físicos, químicos, biológicos, sociales, etc.) no implica una innumerable e inclasificable diversidad de conductas dinámicas diferentes. Todo lo contrario, los sistemas complejos poseen propiedades genéricas, independientemente de los detalles específicos de cada sistema o de la base material del mismo.

Primera generacion (1945-1956)                               Las computadores del Presente

De esta manera, por ejemplo, una computadora construida con bulbos, otra con transistores y una más con relevadores electromagnéticos; serían capaces de realizar, en principio, las mismas tareas de procesamiento de datos. Podríamos incluso ir mas lejos con este ejemplo y agregar que el sistema nervioso humano posee propiedades tales como memoria difusa y reconocimiento de patrones que funcionan de la misma manera en como funciona una computadora de bulbos o de transistores. Lo que comparten, son una estructura interconectada y formada por elementos individuales (neuronas o circuitos electrónicos) que interactúan para intercambiar información y modificar sus estados internos. Ello hace posible la emergencia de fenómenos globales y colectivos semejantes, sin que los detalles materiales del sistema sean del todo relevantes.

De esta manera, es posible identificar propiedades dinámicas similares entre una computadora, el sistema nervioso, el sistema inmunológico, la tectónica de placas, una sociedad de insectos, el crecimiento urbano, las economías de mercado, el tráfico vehicular, etc. a pesar de la aparente disparidad entre estos sistemas.

La aportación fundamental de la ciencia de los sistemas complejos en la tarea de conocer y transformar nuestra realidad, es identificar los principios y fundamentos generales de la operación de dichos sistemas sin importar los detalles particulares de su realización material. Así por ejemplo, podemos imaginar un biólogo del futuro que estudiaría el fenómenos llamado “vida” desde una perspectiva de principios (tal vez leyes?) generales.

Tal biólogo tendría conciencia de que el fenómeno “vida” tal y como existe en la Tierra es tan sólo un caso particular de como “la vida” se ha manifestado bajo las condiciones particulares de la Tierra, expresándose bajo la forma de una realización material muy específica (una bioquímica de carbono dominantemente levógira). Sin embargo, este biólogo estaría preparado para identificar el fenómeno “vida” si acaso fuera detectado en otro planeta o parte del universo bajo otras realizaciones materiales especificas, de la misma manera que un físico hoy en día sabe que la ley de gravitación lo mismo es valida para la superficie de la Tierra que para la superficie de Marte o cualquier otra parte del universo.

No sabemos lo que ahí fuera nos podremos encontrar en un futuro lejano

El ejemplo puede ir aún más lejos. Podemos imaginar un sociólogo del futuro que será capaz de identificar los principios generales del fenómeno “social” independientemente de que este ocurra en grupos humanos, animales, microbios, plantas, robots o incluso, si su colega biólogo tiene suerte, en grupos sociales fuera de nuestro planeta.

¿Estaremos capacitados alguna vez para determinar las partes “sencillas” de los Sistemas Complejos para llegar a saber?

emilio silvera

[?]

El telescopio Hubble capta el «combate» entre David y Goliat, dos galaxias enfrentadas

La mayor está engullendo a la menor, pero la gravedad está cambiando el interior de ambas

                 Dos galaxias en fusión: la barrada NGC 1512 y la enana NGC 1510 – ESA/Hubble, NASA

Cuando dos galaxias están demasiado cerca, comienza el lento proceso de fusión. Giran una en torno a la otra, como si estuvieran bailando, aunque otros podrían decir que más bien se están midiendo y preparándose para un combate. Sea como sea, al final de este complejo proceso habrá cambiado la distribución de gas, estrellas y planetas, y en ocasiones los agujeros negros supermasivos de su interior se habrán tragado a una buena parte de la galaxia vecina.

El telescopio espacial Hubble ha fotografiado uno de estos combates, que lleva 400 millones de años ocurriendo entre una pequeña galaxia, llamada NGC 1510, y una colosal galaxia barrada, llamada NGC 1512, ambas situadas a 30 millones de años luz de la Tierra. La imagen muestra a dos galaxias de tamaño muy desigual, como David y Goliat, unidas por la gravedad y sufriendo por ello cambios muy sutiles en su apariencia. (Aquí puedes leer un artículo sobre el sombrío pasado de la galaxia NGC 1512).

La fotografía muestra otras cosas muy curiosas. Por ejemplo, la barra de NGC 1512 es como un canal de suministro de combustible cósmico, que va inyectando gas desde el exterior al interior de la galaxia y facilitando así el nacimiento de nuevas estrellas en el corazón de esta gran galaxia, en una zona que el telescopio capta en color azul. Ese criadero estelar, que ocupa una pequeña fracción de toda la galaxia, tiene un diámetro de cerca de 2.400 años luz.

Según los astrofísicos, tanto la barra como esta zona de nacimiento de estrellas son el resultado de la riña cósmica entre las dos galaxias.

NGC 1512 tiene una segunda zona de creación de estrellas más tranquila, en el enorme anillo de su parte externa. Esta zona está repleta de hidrógeno ionizado, donde enormes cantidades de este gas primigenio son bombardeadas por la radiación de estrellas vecinas recién nacidas, que hacen que el gas brille de forma muy vistosa.

Más allá de este anillo exterior, la gran galaxia tiene varios brazos, con forma de zarcillo, que llegan a envolver a la galaxia pequeña y que le someten a una intensa presión gravitacional.

En consecuencia, el gas y el polvo de la pequeña galaxia se ha arremolinado y ha comenzado a favorecer un proceso de nacimiento de estrellas muy rápido y aún más intenso que el de NGC 1512. Por eso, la pequeña David brilla con el característico azul de los lugares donde hay estrellas calientes y recién nacidas.

Pero aún hay algo más. Parte de los brazos espirales de la gran galaxia NGC 1512 en realidad le fueron arrancados a una antigua galaxia hoy desaparecida. Esta fue sencillamente desgarrada, tal como está ocurriendo ahora con NGC 1510. Por eso, se puede decir que NGC 1512 es toda una galaxia caníbal.

En conjunto, estas imágenes muestran que la interacción de galaxias, incluso si tienen un tamaño muy distinto, afecta profundamente a su funcionamiento interno e incluso activa el nacimiento de nuevas estrellas. Esto parece ser un fenómeno clave en la evolución del Universo.

[?]

La erupción del Volcan Cabulco ha obligado a la evacuación de miles de personas. Estas imágenes nos hablan de la indefensión a la que estamos sometidos cuando la Naturaleza habla y se recicla evolucionando con el transcurrir del tiempo. Las placas tectónicas son dinámicas y producen catástrofes naturalez que no podemos dominar.

Veamos algunas imágenes del suceso.

Cuando la Naturzleza bosteza… ¡Nosotros a temblar!

Sólo deseamos desde aquí que la buena gente afectada por el suceso, regresen a sus hogares lo antes posible. La catástrofe que afecta a una parte infinitesimal de la población del mundo, es, sin embargo, una gran tragedia para esos pocos afectados que, en no pocas ocasiones, ven como les cambia la vida.

¡Estamos con ellos!

emilio silvera

Fuente de las imágenes: El diario La Razón.

[?]