Feb
6
La verdadera Historia de la Teoría del Caos
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Caos y Complejidad ~
Clasificado en Caos y Complejidad ~
 Comments (3)
Comments (3)
Quizás sea la mejor muestra de complejidad que existe en el Universo

“Es la peor noticia posible para aquellos que esperan avances importantes en la cumbre climática que se celebró en Copenhague. Uno de los científicos más destacados de la teoría del cambio climático, Phil Jones, se veía obligado a presentar su dimisión temporal como director de la Unidad de Investigación Climática de la Universidad de East Anglia, en Norwich, Inglaterra, tras ser acusado de manipular datos sobre los efectos del cambio climático para exagerar su impacto.”
¿Qué iría buscando con tal comportamiento? Cuando se hacen cosas así, dichos comportamientos están aconsejados por intereses particulares que no siempre se pueden confesar. No está bien manipular datos para que el gran público tenga una idea iquivocada de la verdadera situación de las cosas.

¿Os acordáis de aquella vez que Mark Twain tuvo que decir:
“Las noticias sobre mi muerte han sido exageradas”.
Bueno, pues hasta ahí llegan para vender.
Los Medios de Comunicación, no siempre son fieles “comunicadores” y, para realzar las noticias, las expresan con un grado extra de exaltación, o, licencia poética que, distorsiona la realidad de lo que realmente deberían comunicar, y, no pocas veces, tal hecho se debe a que (sobre todo en noticias relativas a cuestiones científicas) no se elige a la persona debidamente preparada y adecuada a la noticia que se quiere ofrecer al público. Si la noticia se ha dado de manera equívoca, el científico redactor debe enmendar lo que se dijo con miras a llamar la atención o conseguir alguna subvención.
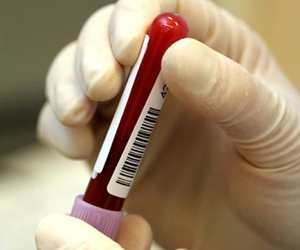
“Desde la década de los 80 el Síndrome de Inmunodeficiencia Humana (SIDA) se ha considerado una de las peores enfermedades de nuestra época, para la que, según se creía hasta hace poco, parecía no existir cura.
Desde hace bien poco tiempo, sin embargo, se han dado a conocer ciertos hallazgos que podrían acabar por fin con este mal. Primero fue el caso de un niño en Estados Unidos a quien por el tratamiento médico recibido fue posible erradicar todo rastro posiblemente peligroso de VIH con el que había nacido. Después el Instituto Pasteur de París anunció que 14 adultos habían logrado controlar la acción del virus.”
Así, de manera comedida y reflejando la realidad es como deben darse siempre las noticias sin levantar espectativas falsas en uno u otro sentido.

Betelgeuse que es una supergigante roja, sólo tiene 20 veces la masa del Sol y su tamaño 600 veces mayor
Escribo esto a partir de un artículo leído en la prensa diaria que, tratando de hablar de exóticos objetos que existen en el Universo, llegan a hablarnos de estrellas masivas con 600 veces la masa del Sol, y, tal barbaridad, nos lleva a pensar que, para hacer un reportaje o comentario de estos temas, los diferentes medios, deberían acudir a personas versadas en lo que están tratando, y, de esa manera, además de quedar mucho mejor, evitarían el ridículo de publicar las cosas alejadas de la realidad. La masa máxima que se considera para una estrella viene a ser de 120 masas solares, ya que, cuando su masa es mayor, la propia radiación la destruye. Pueden existir algunas estrellas que sobrepasen ese límite de las 120 masas solares pero, están continuamente eyectando material al espacio para descongestionarse y no explotar.

Eta Carinae es una estrella que posiblemente pueda tener más de 120 masas solares pero, como podéis contemplar en la imagen, está envuelta en una Nebulosa que ella misma ha generado al estar, continuamente eyectando material al espacio y evitar así su propia muerte.
Buscando en mi documentación, un buen ejemplo de lo que digo, por suerte, me encuentro con un artículo escrito por Don Carlos Miguel Madrid Casado del Departamento de Lógica y Filosofía de la Ciencia en la Facultad de Filosofía de la Universidad Complutense de Madrid, dónde nos deja un claro ejemplo de lo que no debiera ser. Aquí os lo dejo.
“Edward Lorenz (1917-2008): ¿Padre de la Teoría del Caos?

El miércoles de 16 de abril de 2008, a los 90 años de edad, moría Edward Norton Lorenz. Los periódicos de medio mundo pronto se hicieron eco de la noticia. Todos los obituarios recogieron que había muerto “el Padre de la Teoría del Caos”. Lorenz, escribían, fue el primero en reconocer el comportamiento caótico de ciertos sistemas dinámicos, como el atmosférico. El estudio de este comportamiento altamente inestable y errático le condujo, continuaban, a formular una de las principales características de lo que hoy se llama “caos determinista”: la dependencia sensible a las condiciones iniciales, popularmente conocida como “efecto mariposa”. Lorenz, concluían, fue el artífice de la tercera revolución científica del siglo XX, después de la Teoría de la Relatividad y la Mecánica Cuántica.

Una de la mayores carácterísticas de un Sistema inestable es que tiene una gran dependencia de las condiciones iniciales. De un sistema del que se conocen sus ecuaciones características, y con unas condiciones iniciales fijas, se puede conocer exactamente su evolución en el tiempo. Pero en el caso de los sistemas caóticos, una mínima diferencia en esas condiciones hace que el sistema evolucione de manera totalmente distinta e impredecible.


Las condiciones iniciales de un sistema implican que las condiciones finales sean tal como, de manera inevitable serán. Es decir, su condición inicial nos dice cuál será su condición final. Desde su nacimiento nos está diciendo como será su “muerte”.
De todo sistema del que se conocen sus ecuaciones características, y con unas condiciones iniciales fijas, se puede conocer exactamente su evolución en el tiempo. Pero en el caso de los sistemas caóticos, una mínima diferencia en esas condiciones hace que el sistema evolucione de manera totalmente distint
Pero, veamos, ¿ha sido realmente Edward Lorenz el “creador” de la Teoría del Caos? ¿O acaso su papel de estrella protagonista se debe más bien a una inusitada alianza entre mérito y fortuna? El propósito de esta nota es ofrecer una panorámica de la Historia de la Teoría del Caos que complique su nacimiento y enriquezca su evolución, sacando a la luz la figura de ciertos científicos que el gran talento de Lorenz ha ensombrecido y ocultado.Comenzamos nuestra panorámica retrocediendo hasta los tiempos de la Revolución Científica. El intento por comprender las trayectorias planetarias observadas por Kepler condujo a Newton a modelarlas matemáticamente, siguiendo la estela de Galileo. Newton formuló sus leyes de una forma matemática que relacionaba entre sí las magnitudes físicas y sus ritmos de cambio. Las leyes físicas quedaron expresadas como ecuaciones diferenciales. Estudiar un fenómeno físico y hallar las ecuaciones diferenciales que las gobernaban eran las dos caras de la misma moneda.

Desde el siglo XVII, toda la naturaleza –sólidos, fluidos, sonido, calor, luz, electricidad- fue modelada mediante ecuaciones diferenciales. Ahora bien, una cosa era dar con las ecuaciones del fenómeno en cuestión y otra, bien distinta, resolverlas. La teoría de las ecuaciones diferenciales lineales fue desarrollada por completo en poco tiempo. No así la teoría gemela, la teoría de las ecuaciones diferenciales no lineales.
Uno de los problemas no lineales que trajo de cabeza a físicos y matemáticos fue el problema de los n cuerpos de la Mecánica Celeste: dados n cuerpos de distintas masas bajo atracción gravitacional mutua, se trataba de determinar el movimiento de cada uno de ellos en el espacio. Newton resolvió geométricamente el problema de los dos cuerpos en los Principia. Posteriormente, Bernoulli y Euler lo resolvieron analíticamente con todo detalle. Sin embargo, no ocurrió así con el problema de los tres cuerpos. Newton sabia que, cuando un tercer cuerpo entraba en escena, el problema no era fácilmente resoluble, y que esto traía serias consecuencias para la cuestión de la estabilidad del Sistema Solar (que, a fin de cuentas, en la época, pasaba por ser un sistema de siete cuerpos). Aunque débiles en comparación con la fuerza de atracción del Sol, las fuerzas gravitatorias entre los planetas no eran ni mucho menos despreciables, por cuanto a la larga podían desviar algún planeta de su órbita e incluso, en el límite, expulsarlo fuera del Sistema Solar.

El matemático suizo Leonhard Euler
Las fuerzas interplanetarias podían estropear las bellas elipses keplerianas, sin que fuera posible predecir el comportamiento del Sistema Solar en un futuro lejano. En Motu corporum in gyrum, Newton afirmaba que los planetas no se mueven exactamente en elipses ni recorren dos veces la misma órbita, y reconocía que definir estos movimientos para todo futuro excedía con mucho la fuerza entera del intelecto humano. Si el Sistema Solar se iba desajustando, era necesaria una solución drástica: la Mano de Dios tenía que reconducir cada planeta a su elipse, reestableciendo la armonía. Este Deus ex machina newtoniano provocó, como es bien sabido, la ira de Leibniz, para quien Dios no podía ser un relojero tan torpe.

Tiempo después, Laplace creyó explicar las anomalías orbitales que preocuparon a Newton como meras perturbaciones que sólo dependían de la Ley de Gravitación y tendían a compensarse en el transcurso del tiempo. Así, al presentar su Mecánica Celeste a Napoleón, exclamó que Dios no era una hipótesis necesaria en su sistema del mundo. Sin embargo, en sus ecuaciones del sistema Sol-Júpiter-Saturno (problema de los tres cuerpos), Laplace despreció un término matemático que creía muy pequeño pero que, en contra de lo por él supuesto, podía crecer rápidamente y sin límite, hasta desestabilizar el Sistema Solar.
Muchos físicos y matemáticos decimonónicos dedicaron sus esfuerzos a dar una respuesta completa al problema de los tres cuerpos y a la cuestión de la estabilidad del Sistema Solar. Entre ellos, uno de los personajes clave en la configuración de la Teoría del Caos: Henri Poincaré.

Henri Poincaré
En 1855, los matemáticos europeos tuvieron noticia de que un importante concurso internacional iba a ser convocado bajo el auspicio de Oscar II, rey de Suecia y Noruega, para celebrar su sesenta aniversario en el trono. Se ofrecía un sustancioso premio al matemático capaz de resolver el problema de los tres cuerpos y, de este modo, avanzar en el estudio de la estabilidad del Sistema Solar. Alentado por la competencia, Poincaré procedió a sintetizar muchas de sus ideas acerca del estudio cualitativo o topológico de las ecuaciones diferenciales no lineales. El Jurado declaró ganador a Poincaré por una compleja resolución del problema restringido de los tres cuerpos, en que un planeta ligero se mueve bajo la atracción gravitatoria de dos estrellas iguales que giran una alrededor de la otra describiendo dos elipses confinadas en un mismo plano. Sin embargo, el artículo de Poincaré contenía un error y una tirada completa de la prestigiosa revista Acta Mathemática hubo de ser destruida.
A toda prisa, Poincaré revisó su trabajo y descubrió que, en verdad, no podía probarse la estabilidad del sistema, porque su dinámica no seguía pauta regular alguna. Su revisión del problema contiene una de las primeras descripciones del comportamiento caótico en un sistema dinámico. Poincaré fue, desde luego, el abuelo de la Teoría del Caos. Además, a partir de entonces, Poincaré contribuyó como pocos, a popularizar la idea de que existen sistemas deterministas cuya predicción a largo plazo resulta imposible. En Ciencia y Método, escribía: “Puede suceder que pequeñas diferencias en las condiciones iniciales produzcan algunas muy grandes en los estados finales. Un pequeño error al inicio engendrará un enorme error al final. La predicción se vuelve imposible”.

Otros también trataron el tema y profundizaron en los secretos de la Naturaleza
¡Caramba! Medio siglo antes que Lorenz, Poincaré se había topado con… ¡el efecto mariposa! Aún más: el genial matemático francés señaló que el tiempo meteorológico hacía gala de esta clase de inestabilidad y apuntó qué dificultades se derivarían para la predicción meteorológica. En su labor divulgadora no estuvo solo: su compatriota Pierre Duhem difundió las investigaciones de Poincaré y, también, de Jacques Hadamard, quien fue pionero en demostrar matemáticamente que, para cierto sistema dinámico hoy conocido como el Billar de Hadamard, un pequeño cambio en las condiciones iniciales provoca un notable cambio en la posterior evolución del sistema.

Durante el primer cuarto del siglo XX, la influencia de Poincaré no desapareció y se dejó notar en los trabajos de George David Birkhoff a propósito de las características cualitativas y topológicas de los sistemas dinámicos. Tampoco puede olvidarse el papel de Stephen Smale, que ganaría la Medalla Fields –el Premio Nobel de los matemáticos- en 1966 por sus contribuciones a la Teoría de los Sistemas Dinámicos. Mediado el siglo XX, este topólogo continuó la senda trazada por Poincaré t Birkhoff, y descubrió la Herradura de Smale, que pasa por ser el mecanismo topológico que da lugar al caos (efecto mezcla).

George David Birkhoff
Simultáneamente, cruzando el telón de acero, existía otra fértil tradición: la Escuela Rusa. En la U. R. S. S., los físicos y matemáticos habían heredado de Alexander Liapunov sus influyentes nociones acerca de la estabilidad del movimiento de los sistemas dinámicos. Si Poincaré se había ocupado de la teoría de la estabilidad desde una perspectiva cualitativa, Liapunov lo hizo cuantitativamente (exponentes de Liapunov). Recogiendo el testigo de ambos, Kolmogorov y Arnold se concentraron en el estudio de la estabilidad de los sistemas dinámicos de la Dinámica Celeste. Durante la guerra fría, los principales resultados de los matemáticos soviéticos fueron traducidos al inglés y dados a conocer al resto de matemáticos, europeos y norteamericanos, gracias al providencial trabajo de Solomon Lefschetz.
Y en éstas, apareció Lorenz… En 1963, este matemático y meteorólogo, antiguo alumno de Birkhoff en Harvard, estaba trabajando en el pronóstico del tiempo en el MIT. Estudiando la convección en la atmósfera, Lorenz planteó un modelo matemático formado por tres ecuaciones diferenciales ordinarias para describir el movimiento de un fluido bajo la acción de un gradiente térmico. Mientras buscaba soluciones numéricas con la ayuda de una computadora, se encontró –al volver de tomar una taza de café- con que se producía un dramático comportamiento inestable, caótico. Lorenz se había topado por casualidad con el fenómeno de la sensibilidad a las condiciones iniciales, que hacía de su sistema algo en la práctica impredecible. En efecto, tras establecer las propiedades básicas del flujo, Lorenz reparó en que una pequeña variación en las condiciones iniciales ocasionaba estados finales completamente diferentes. Lorenz había descubierto, tomando prestada la indeleble metáfora que forjaría más tarde, el efecto mariposa: el aleteo de una mariposa en Brasil puede ocasionar un tornado en Texas. Ahora bien, sería el matemático norteamericano Guckenheimer el que, allá por los años 70, acuñara la expresión “dependencia sensible a las condiciones iniciales”.

Lorenz publicó su hallazgo en una revista de meteorología, en un artículo titulado Deterministic Nonperiodic Flow, en que citaba expresamente a Poincaré y Birkhoff (aunque desconocía las ideas del primero sobre predicciones meteorológicas), pero que pasó prácticamente desapercibido. Sólo Stephen Smale y James Jorke –el introductor del término caos en la literatura científica- reconocieron las repercusiones filosóficas de la investigación de Lorenz y la dieron a conocer. Si Edward Lorenz ofreció a la comunidad científica el paradigma de sistema dinámico caótico continuo, el zoólogo Robert May dio a conocer en su artículo Simple Mathematical Models with Complicated Dynamics el paradigma del sistema dinámico caótico discreto: la aplicación logística.
A finales de los 70 y principios de los 80, la exploración de aplicaciones de la Teoría del Caos comenzó a dar sus frutos más allá de las simulaciones en las pantallas de ordenador. Entre los fenómenos físicos estudiados destaca, sin duda, la transición a la turbulencia en los fluidos, cuyo estudio contaba con el precedente que suponía el artículo On the nature of turbulence de David Ruelle y Floris Takens, quiénes introdujeron la noción de atractor extraño. Paralelamente, el físico Mitchell Feigenbaum descubrió heurísticamente ciertas constantes universales que caracterizan la transición del movimiento periódico al movimiento caótico, dando inicio a una de las ramas más prometedoras de la Teoría del Caos a día de hoy: la Teoría de la Bifurcación.

En resumidas cuentas, a comienzos del siglo XXI, la Teoría del Caos se nos aparece como la ciencia fisicomatemática que estudia el comportamiento aperiódico e inestable en sistemas deterministas no lineales. Mientras que la revolución relativista fue, prácticamente, fruto de un único hombre (Albert Einstein), y la revolución cuántica lo fue de apenas un puñado (Planck, Bhor, Heisenberg, Schrödinger, Dirac), la revolución del caos determinista es, en cambio, obra de múltiples. La Teoría del Caos es hija tanto de matemáticos (Poincaré, Hadamard, Birkhoff, Smale, Yorke…) como de físicos, biólogos y otros tantos científicos de campos dispares (Lorenz, May, Feigenbaum…). Atribuir su paternidad únicamente a un hombre, aun cuando sea Lorenz, es una simplificación excesiva. Lorenz fue, por así decirlo uno de los muchos padres.”
Hasta aquí el artículo que el Señor Madrid Casado escribió y fue publicado en el número 3 del volumen 22 de la Revista Española de Física en 2008. (salvo algunas imágenes y apuntes propios, en esencia, el artículo es del Señor Madrid Casado).

El trabajo está bien y nos introduce en la historia de la Teoría del Caos desde sus raíces, y, lo único en lo que podemos disentir del autor es, en el hecho cierto de que, Einstein, autor de la relatividad, también se apoyó en muchos (Mach, Maxwell, Lorentz, -en la primera parte, y, sobre todo en Riemann, en la segunda), aunque eso no le quita ni una pizca del mérito que tiene como científico que supo aunar muchos conocimientos dispersos, unirlos en una sola entidad y hacer ver al mundo lo que allí había. Y, por otra parte, al hablar de la Mecánica Cuántica, excluye a Einstein que, en verdad (aunque la combatió) fue uno de sus padres en aquellos primeros momentos, su trabajo sobre el Efecto Fotoeléctrico (que le dio el Nobel de Física) así lo demuestra. Por otra parte, no habría estado de más y de pasada, comentar que Poincaré fue el autor de la “Conjetura” que lleva su nombre y que ha estado ahí 100 años sin que nadie la resolviera hasta que llegó, un matemático extraño, llamado Perelman (ruso) que sin tener el premio que ofrecían al ganador, puso en Internet la solución. Este personaje, no acudió a la cita en Madrid, donde se celebraba el Año Internacional de las Matemáticas y el rey le entregaría la Medalla Field. Todos se quedaron esperando y él, que vicía con su madre en un apartamento de 65 m2, estaba con su cestita al brazo cogiendo setas en el campo.
De todo esto podemos obtener la consecuencia de que, todo tiene otra historia detrás, y, si profundizamos, la podemos descubrir para conocer de manera completa y precisa, el transcurso de los hechos y los personajes que en ellos tomaron parte.
emilio silvera
Oct
14
La verdadera Historia de la Teoría del Caos
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Caos y Complejidad ~
Clasificado en Caos y Complejidad ~
 Comments (0)
Comments (0)
“Un equipo de astrónomos ha identificado en la constelación de Acurio, a 900 años luz de nuestro planeta, la que posiblemente es la estrella enana blanca más fría y débil jamás detectada. Este antiguo remanente estelar, el estado final de un astro como nuestro Sol, es tan frío que su carbono se ha cristalizado, formando en el espacio un diamante del tamaño de la Tierra y con una masa similar a la de nuestro Sol.
Esta gigantesca joya cósmica «es un objeto muy notable», afirma David Kaplan, profesor de la Universidad de Wisconsin-Milwaukee. «Estas cosas deben estar por ahí, pero son tan débiles que son muy difíciles de encontrar».

“Es la peor noticia posible para aquellos que esperan avances importantes en la cumbre climática que se celebró en Copenhague. Uno de los científicos más destacados de la teoría del cambio climático, Phil Jones, se veía obligado a presentar su dimisión temporal como director de la Unidad de Investigación Climática de la Universidad de East Anglia, en Norwich, Inglaterra, tras ser acusado de manipular datos sobre los efectos del cambio climático para exagerar su impacto.”
¿Qué iría biuscando con tal comportamiento?

¿Os acordáis de aquella vez que Mark Twain tuvo que decir: “Las noticias sobre mi muerte han sido exageradas”. Bueno, pues hasta ahí llegan para vender
Los Medios de Comunicación, no siempre son fieles “comunicadores” y, para realzar las noticias, las expresan con un grado extra de exaltación, o, licencia poética que, distorsiona la realidad de lo que realmente deberían comunicar, y, no pocas veces, tal hecho se debe a que (sobre todo en noticias relativas a cuestiones científicas) no se elige a la persona debidamente preparada y adecuada a la noticia que se quiere ofrecer al público. Si la noticia se ha dado de manera equívoca, el científico redactor debe enmendar lo que se dijo con miras a llamar la atención o conseguir alguna subvención.
Escribo esto a partir de un artículo leído en la prensa diaria que, tratando de hablar de exóticos objetos que existen en el Universo, llegan a hablarnos de estrellas masivas con 600 veces la masa del Sol, y, tal barbaridad, nos lleva a pensar que, para hacer un reportaje o comentario de estos temas, los diferentes medios, deberían acudir a personas versadas en lo que están tratando, y, de esa manera, además de quedar mucho mejor, evitarían el ridículo de publicar las cosas alejadas de la realidad.
Buscando en mi documentación, un buen ejemplo de lo que digo, por suerte, me encuentro con un artículo escrito por Don Carlos Miguel Madrid Casado del Departamento de Lógica y Filosofía de la Ciencia en la Facultad de Filosofía de la Universidad Complutense de Madrid, dónde nos deja un claro ejemplo de lo que no debiera ser. Aquí os lo dejo.
“Edward Lorenz (1917-2008): ¿Padre de la Teoría del Caos?

El miércoles de 16 de abril de 2008, a los 90 años de edad, moría Edward Norton Lorenz. Los periódicos de medio mundo pronto se hicieron eco de la noticia. Todos los obituarios recogieron que había muerto “el Padre de la Teoría del Caos”. Lorenz, escribían, fue el primero en reconocer el comportamiento caótico de ciertos sistemas dinámicos, como el atmosférico. El estudio de este comportamiento altamente inestable y errático le condujo, continuaban, a formular una de las principales características de lo que hoy se llama “caos determinista”: la dependencia sensible a las condiciones iniciales, popularmente conocida como “efecto mariposa”. Lorenz, concluían, fue el artífice de la tercera revolución científica del siglo XX, después de la Teoría de la Relatividad y la Mecánica Cuántica.

Una de la mayores carácterísticas de un Sistema inestable es que tiene una gran dependencia de las condiciones iniciales. De un sistema del que se conocen sus ecuaciones características, y con unas condiciones iniciales fijas, se puede conocer exactamente su evolución en el tiempo. Pero en el caso de los sistemas caóticos, una mínima diferencia en esas condiciones hace que el sistema evolucione de manera totalmente distinta e impredecible.
ndencia de las condiciones iniciales. De un siste del que se conocen sus ecuaciones características, y con unas condiciones iniciales fijas, se puede conocer exactamente su evolución en el tiempo. Pero en el caso de los sistemas caóticos, una mínima diferencia en esas condiciones hace que el sistema evolucione de manera totalmente distint
condiciones iniciales. De un siste del que se conocen sus ecuaciones características, y con unas condiciones iniciales fijas, se puede conocer exactamente su evolución en el tiempo. Pero en el caso de los sistemas caóticos, una mínima diferencia en esas condiciones hace que el sistema evolucione de manera totalmente distint
Pero, veamos, ¿ha sido realmente Edward Lorenz el “creador” de la Teoría del Caos? ¿O acaso su papel de estrella protagonista se debe más bien a una inusitada alianza entre mérito y fortuna? El propósito de esta nota es ofrecer una panorámica de la Historia de la Teoría del Caos que complique su nacimiento y enriquezca su evolución, sacando a la luz la figura de ciertos científicos que el gran talento de Lorenz ha ensombrecido y ocultado.Comenzamos nuestra panorámica retrocediendo hasta los tiempos de la Revolución Científica. El intento por comprender las trayectorias planetarias observadas por Kepler condujo a Newton a modelarlas matemáticamente, siguiendo la estela de Galileo. Newton formuló sus leyes de una forma matemática que relacionaba entre sí las magnitudes físicas y sus ritmos de cambio. Las leyes físicas quedaron expresadas como ecuaciones diferenciales. Estudiar un fenómeno físico y hallar las ecuaciones diferenciales que las gobernaban eran las dos caras de la misma moneda.

Desde el siglo XVII, toda la naturaleza –sólidos, fluidos, sonido, calor, luz, electricidad- fue modelada mediante ecuaciones diferenciales. Ahora bien, una cosa era dar con las ecuaciones del fenómeno en cuestión y otra, bien distinta, resolverlas. La teoría de las ecuaciones diferenciales lineales fue desarrollada por completo en poco tiempo. No así la teoría gemela, la teoría de las ecuaciones diferenciales no lineales.
Uno de los problemas no lineales que trajo de cabeza a físicos y matemáticos fue el problema de los n cuerpos de la Mecánica Celeste: dados n cuerpos de distintas masas bajo atracción gravitacional mutua, se trataba de determinar el movimiento de cada uno de ellos en el espacio. Newton resolvió geométricamente el problema de los dos cuerpos en los Principia. Posteriormente, Bernoulli y Euler lo resolvieron analíticamente con todo detalle. Sin embargo, no ocurrió así con el problema de los tres cuerpos. Newton sabia que, cuando un tercer cuerpo entraba en escena, el problema no era fácilmente resoluble, y que esto traía serias consecuencias para la cuestión de la estabilidad del Sistema Solar (que, a fin de cuentas, en la época, pasaba por ser un sistema de siete cuerpos). Aunque débiles en comparación con la fuerza de atracción del Sol, las fuerzas gravitatorias entre los planetas no eran ni mucho menos despreciables, por cuanto a la larga podían desviar algún planeta de su órbita e incluso, en el límite, expulsarlo fuera del Sistema Solar.

El matemático suizo Leonhard Euler
Las fuerzas interplanetarias podían estropear las bellas elipses keplerianas, sin que fuera posible predecir el comportamiento del Sistema Solar en un futuro lejano. En Motu corporum in gyrum, Newton afirmaba que los planetas no se mueven exactamente en elipses ni recorren dos veces la misma órbita, y reconocía que definir estos movimientos para todo futuro excedía con mucho la fuerza entera del intelecto humano. Si el Sistema Solar se iba desajustando, era necesaria una solución drástica: la Mano de Dios tenía que reconducir cada planeta a su elipse, reestableciendo la armonía. Este Deus ex machina newtoniano provocó, como es bien sabido, la ira de Leibniz, para quien Dios no podía ser un relojero tan torpe.

Tiempo después, Laplace creyó explicar las anomalías orbitales que preocuparon a Newton como meras perturbaciones que sólo dependían de la Ley de Gravitación y tendían a compensarse en el transcurso del tiempo. Así, al presentar su Mecánica Celeste a Napoleón, exclamó que Dios no era una hipótesis necesaria en su sistema del mundo. Sin embargo, en sus ecuaciones del sistema Sol-Júpiter-Saturno (problema de los tres cuerpos), Laplace despreció un término matemático que creía muy pequeño pero que, en contra de lo por él supuesto, podía crecer rápidamente y sin límite, hasta desestabilizar el Sistema Solar.
Muchos físicos y matemáticos decimonónicos dedicaron sus esfuerzos a dar una respuesta completa al problema de los tres cuerpos y a la cuestión de la estabilidad del Sistema Solar. Entre ellos, uno de los personajes clave en la configuración de la Teoría del Caos: Henri Poincaré.

Henri Poincaré
En 1855, los matemáticos europeos tuvieron noticia de que un importante concurso internacional iba a ser convocado bajo el auspicio de Oscar II, rey de Suecia y Noruega, para celebrar su sesenta aniversario en el trono. Se ofrecía un sustancioso premio al matemático capaz de resolver el problema de los tres cuerpos y, de este modo, avanzar en el estudio de la estabilidad del Sistema Solar. Alentado por la competencia, Poincaré procedió a sintetizar muchas de sus ideas acerca del estudio cualitativo o topológico de las ecuaciones diferenciales no lineales. El Jurado declaró ganador a Poincaré por una compleja resolución del problema restringido de los tres cuerpos, en que un planeta ligero se mueve bajo la atracción gravitatoria de dos estrellas iguales que giran una alrededor de la otra describiendo dos elipses confinadas en un mismo plano. Sin embargo, el artículo de Poincaré contenía un error y una tirada completa de la prestigiosa revista Acta Mathemática hubo de ser destruida.

A toda prisa, Poincaré revisó su trabajo y descubrió que, en verdad, no podía probarse la estabilidad del sistema, porque su dinámica no seguía pauta regular alguna. Su revisión del problema contiene una de las primeras descripciones del comportamiento caótico en un sistema dinámico. Poincaré fue, desde luego, el abuelo de la Teoría del Caos. Además, a partir de entonces, Poincaré contribuyó como pocos, a popularizar la idea de que existen sistemas deterministas cuya predicción a largo plazo resulta imposible. En Ciencia y Método, escribía: “Puede suceder que pequeñas diferencias en las condiciones iniciales produzcan algunas muy grandes en los estados finales. Un pequeño error al inicio engendrará un enorme error al final. La predicción se vuelve imposible”.
¡Caramba! Medio siglo antes que Lorenz, Poincaré se había topado con… ¡el efecto mariposa! Aún más: el genial matemático francés señaló que el tiempo meteorológico hacía gala de esta clase de inestabilidad y apuntó qué dificultades se derivarían para la predicción meteorológica. En su labor divulgadora no estuvo solo: su compatriota Pierre Duhem difundió las investigaciones de Poincaré y, también, de Jacques Hadamard, quien fue pionero en demostrar matemáticamente que, para cierto sistema dinámico hoy conocido como el Billar de Hadamard, un pequeño cambio en las condiciones iniciales provoca un notable cambio en la posterior evolución del sistema.

Durante el primer cuarto del siglo XX, la influencia de Poincaré no desapareció y se dejó notar en los trabajos de George David Birkhoff a propósito de las características cualitativas y topológicas de los sistemas dinámicos. Tampoco puede olvidarse el papel de Stephen Smale, que ganaría la Medalla Fields –el Premio Nobel de los matemáticos- en 1966 por sus contribuciones a la Teoría de los Sistemas Dinámicos. Mediado el siglo XX, este topólogo continuó la senda trazada por Poincaré t Birkhoff, y descubrió la Herradura de Smale, que pasa por ser el mecanismo topológico que da lugar al caos (efecto mezcla).

George David Birkhoff
Simultáneamente, cruzando el telón de acero, existía otra fértil tradición: la Escuela Rusa. En la U. R. S. S., los físicos y matemáticos habían heredado de Alexander Liapunov sus influyentes nociones acerca de la estabilidad del movimiento de los sistemas dinámicos. Si Poincaré se había ocupado de la teoría de la estabilidad desde una perspectiva cualitativa, Liapunov lo hizo cuantitativamente (exponentes de Liapunov). Recogiendo el testigo de ambos, Kolmogorov y Arnold se concentraron en el estudio de la estabilidad de los sistemas dinámicos de la Dinámica Celeste. Durante la guerra fría, los principales resultados de los matemáticos soviéticos fueron traducidos al inglés y dados a conocer al resto de matemáticos, europeos y norteamericanos, gracias al providencial trabajo de Solomon Lefschetz.
Y en éstas, apareció Lorenz… En 1963, este matemático y meteorólogo, antiguo alumno de Birkhoff en Harvard, estaba trabajando en el pronóstico del tiempo en el MIT. Estudiando la convección en la atmósfera, Lorenz planteó un modelo matemático formado por tres ecuaciones diferenciales ordinarias para describir el movimiento de un fluido bajo la acción de un gradiente térmico. Mientras buscaba soluciones numéricas con la ayuda de una computadora, se encontró –al volver de tomar una taza de café- con que se producía un dramático comportamiento inestable, caótico. Lorenz se había topado por casualidad con el fenómeno de la sensibilidad a las condiciones iniciales, que hacía de su sistema algo en la práctica impredecible. En efecto, tras establecer las propiedades básicas del flujo, Lorenz reparó en que una pequeña variación en las condiciones iniciales ocasionaba estados finales completamente diferentes. Lorenz había descubierto, tomando prestada la indeleble metáfora que forjaría más tarde, el efecto mariposa: el aleteo de una mariposa en Brasil puede ocasionar un tornado en Texas. Ahora bien, sería el matemático norteamericano Guckenheimer el que, allá por los años 70, acuñara la expresión “dependencia sensible a las condiciones iniciales”.

Lorenz publicó su hallazgo en una revista de meteorología, en un artículo titulado Deterministic Nonperiodic Flow, en que citaba expresamente a Poincaré y Birkhoff (aunque desconocía las ideas del primero sobre predicciones meteorológicas), pero que pasó prácticamente desapercibido. Sólo Stephen Smale y James Jorke –el introductor del término caos en la literatura científica- reconocieron las repercusiones filosóficas de la investigación de Lorenz y la dieron a conocer. Si Edward Lorenz ofreció a la comunidad científica el paradigma de sistema dinámico caótico continuo, el zoólogo Robert May dio a conocer en su artículo Simple Mathematical Models with Complicated Dynamics el paradigma del sistema dinámico caótico discreto: la aplicación logística.
A finales de los 70 y principios de los 80, la exploración de aplicaciones de la Teoría del Caos comenzó a dar sus frutos más allá de las simulaciones en las pantallas de ordenador. Entre los fenómenos físicos estudiados destaca, sin duda, la transición a la turbulencia en los fluidos, cuyo estudio contaba con el precedente que suponía el artículo On the nature of turbulence de David Ruelle y Floris Takens, quiénes introdujeron la noción de atractor extraño. Paralelamente, el físico Mitchell Feigenbaum descubrió heurísticamente ciertas constantes universales que caracterizan la transición del movimiento periódico al movimiento caótico, dando inicio a una de las ramas más prometedoras de la Teoría del Caos a día de hoy: la Teoría de la Bifurcación.

En resumidas cuentas, a comienzos del siglo XXI, la Teoría del Caos se nos aparece como la ciencia fisicomatemática que estudia el comportamiento aperiódico e inestable en sistemas deterministas no lineales. Mientras que la revolución relativista fue, prácticamente, fruto de un único hombre (Albert Einstein), y la revolución cuántica lo fue de apenas un puñado (Planck, Bhor, Heisenberg, Schrödinger, Dirac), la revolución del caos determinista es, en cambio, obra de múltiples. La Teoría del Caos es hija tanto de matemáticos (Poincaré, Hadamard, Birkhoff, Smale, Yorke…) como de físicos, biólogos y otros tantos científicos de campos dispares (Lorenz, May, Feigenbaum…). Atribuir su paternidad únicamente a un hombre, aun cuando sea Lorenz, es una simplificación excesiva. Lorenz fue, por así decirlo uno de los muchos padres.”
Hasta aquí el artículo que el Señor Madrid Casado escribió y fue publicado en el número 3 del volumen 22 de la Revista Española de Física en 2008.

El trabajo está bien y nos introduce en la historia de la Teoría del Caos desde sus raíces, y, lo único en lo que podemos disentir del autor es, en el hecho cierto de que, Einstein, autor de la relatividad, también se apoyó en muchos (Mach, Maxwell, Lorentz, -en la primera parte, y, sobre todo en Riemann, en la segunda), aunque eso no le quita ni una pizca del mérito que tiene como científico que supo aunar muchos conocimientos dispersos, unirlos en una sola entidad y hacer ver al mundo lo que allí había. Y, por otra parte, al hablar de la Mecánica Cuántica, excluye a Einstein que, en verdad (aunque la combatió) fue uno de sus padres en aquellos primeros momentos, su trabajo sobre el Efecto Fotoeléctrico (que le dio el Nobel de Física) así lo demuestra. Por otra parte, no habría estado de más y de pasada, comentar que Poincaré fue el autor de la “Conjetura” que lleva su nombre y que ha estado ahí 100 años sin que nadie la resolviera hasta que llegó, un matemático extraño, llamado Perelman (ruso) que sin tener el premio que ofrecían al ganador, puso en Internet la solución. Este personaje, no acudió a la cita en Madrid, donde se celebraba el Año Internacional de las Matemáticas y el rey le entregaría la Medalla Field. Todos se quedaron esperando y él, que vicía con su madre en un apartamento de 65 m2, estaba con su cestita al brazo cogiendo setas en el campo.
De todo esto podemos obtener la consecuencia de que, todo tiene otra historia detrás, y, si profundizamos, la podemos descubrir para conocer de manera completa y precisa, el transcurso de los hechos y los personajes que en ellos tomaron parte.
emilio silvera
Jun
17
El colapso del núcleo de las estrellas
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Caos y Complejidad ~
Clasificado en Caos y Complejidad ~
 Comments (3)
Comments (3)

En la imagen podemos contemplar lo que se clasifica NGC 3603, es un cúmulo abierto de estrellas en una vasta región estelar, rodeada de una región H II (una enorme nube de gas y plasma en el que constantemente están naciendo estrellas), situado en el brazo espiral Carina de la Vía Láctea, a unos 20.000 -luz de distancia en la constelación de Carina. Es uno de los jóvenes cúmulos de estrellas más luminosas e impresionante en la Vía Láctea, y la concentración más densa de estrellas muy masivas conocidas en la galaxia. Se estima que se ha formado hace alrededor de un millón de años. Las estrellas azules calientes en el núcleo son responsables de la fuerte radiación ultravioleta y los vientos estelares, tallando una gran cavidad en el gas.

NGC 3603 alberga miles de estrellas de todo : la mayoría tienen masas similares o menores a la de nuestro Sol, pero las más espectaculares son algunas de las estrellas muy masivas que están cerca del final de sus vidas. Ahí están presentes algunas estrellas supergigantes que se agolpan en un volumen de menos de un año luz cúbico, se han localizado en la misma zona a tres llamadas Wolf-Rayet, estrellas muy brillantes y masivas que expulsan grandes cantidades de material antes de convertirse en supernovas.
Una de estas estrellas (NGC 3603-A1), una estrella doble azul que orbita alrededor de la otra una vez cada 3,77 días, es la estrella más masiva conocida hasta en la Vía Láctea. La más masiva de estas dos estrellas tiene una masa estimada de 116 masas solares, mientras que su compañera tiene una masa de 89 masas solares.

Las estrellas supermasivas cuando colapsan forman extrañas y, a veces, fantásticas imágenes que podemos captar por nuestros más sofisticados telescopios. Hace veinte años, los astrónomos fueron testigos de uno de los más brillantes explosiones estelares en más de 400 años. La supernova titánica, llamada SN 1987A, ardió con la fuerza de 100 millones de soles varios meses después de su descubrimiento el 23 de febrero de 1987.
Las observaciones de SN 1987A, hechas en los últimos 20 por el Telescopio Espacial Hubble de NASA / ESA y muchos otros grandes telescopios terrestres y espaciales, han servido para cambiar la perspectiva que los astrónomos tenían de cómo las estrellas masivas terminan sus vidas.Estudiando estos sucesos sus comienzos se pueden ver los detalles más significativos del acontecimiento, cosa que, estuadinado los remanentes de supernovas muy antiguas no se podían ver.

Arriba podemos contemplar observaciones realizadas en distintas fechas que nos muestran la evolución de los anillos de SN 1987 A

El clúster abierto NGC 3603 contiene a Sher 25, una super gigante B1a que inevitablemente morirá en un masivo suceso supernova en los próximos 20,000 . ¡Esto emitirá una luz tan potente que competirá en el cielo con el planeta Venus! Un detalle muy emocionante es que Sher 25 presenta anillos similares a los que dejó la supernova SN 1987 A.
Cuando colapsa el núcleo de una estrella, ocurre en la formación de una estrella de neutrones, es preciso que la estrella esté evolucionada hasta el punto de que su núcleo esté compuesto completamente por hierro, que se niega a ser quemado en reacciones nucleares, no se puede producir la fusión y, por tanto, no produce la energía suficiente como soportar la inmensa fuerza de gravedad que propia masa de la estrella genera y que, solamente era frenada por la energía que produce la fusión nuclear que tiende a expandir la estrella, mientras que la gravedad tiende a contraerla.
El núcleo entonces se contrae, liberando energía potencial gravitatoria, se rompen los núcleos de los átomos de hierro en sus protones y sus neutrones constiituyentes. A medida que aumenta la densidad, los protones se combinan con los electrones para formar neutrones. El colapso sólo se detiene la presión de degeneración del gas de neutrones compensa el empuje hacia adentro de la Gravedad. El proceso completo hasta que se la estrella de neutrones dura de un segundo.

Otra perspectiva del remanente de la supernova por colapso de núcleo SN 1987A.
Han sido muy variados los grupos de astrónomos investigadores que han realizado observaciones durante largos períodos de tiempo llevar a cabo la no fácil tarea de comprender cómo se forman las estrellas de neutrones y púlsares cuando estrellas masivas llegan al final de sus vidas y finalizan el proceso de la fusión nuclear, momento en el que -como explicaba antes- la estrella se contrae, implosiona sobre sí misma, se produce la explosión supernova y queda el remanente formado por material más complejo en forma de gases que han sido expulsados por la estrella en este proceso final en el que, las capas exteriores de la estrella, forman una nebulosa y la estrella en sí misma, al contraerse y hacerse más densa, es decir de 1017 kg/m3.
Se ha podido llegar a saber que las supernovas por colapso de núcleo suelen ocurrir en los brazos de galaxias espirales, así como también en las regiones HII, donde se concentran regiones de formación estelar. Una de las consecuencias de esto es que las estrellas, con masas a partir de 8 veces la masa del Sol, son las estrellas progenitoras de estos estos sucesos cósmicos. También es muy interesante y se está estudiando cómo se forman los inmensos campos magnéticos alreddor de estas estrellas de neutrones y púlsares que se conviertan en magnétares.

Cuando hace unos pocos años se descubrió la estrella de neutrones SGR0418, poco podían pensar los astrónomos que su funcionamiento alteraría todas las teorías existentes ahora acerca del funcionamiento de los magnétares. Sin embargo es así, ya que funciona como uno de éstos y no como sería propio de su condicción. Este hallazgo obliga a la ciencia a replantearse las teorías que se manejaban hasta ahora acerca del origen y evolución de los magnétares.
El “universo” de los procesos que siguen al colapso de los núcleos de las estrellas masivas es fascinante. Así, cuando se un púlsar que es una estrella de neutrones que gira sobre sí misma a una gran velocidad y tambien una fuente de ondas de radio que vibran con periodos regulares, este de estrellas tan extrañas son fruto -como antes decía- de una supernova o por consecuencías de la acreción de materia en estrellas enanas blancas en sistemas binarios. Una enana blanca que también es muy masiva, si tiene una estrella compañera cercana, genera mucha fuerza gravitatoria comienza a tirar del material de la estrella vecina y se lo queda hasta tal punto que, se transforma en una estrella de neutrones en una segunda etapa en la que se producen nuevos procesos de implosión.
La densidad de estas estrellas es increiblemente grande, tanto que un cubo de arena lleno del material de una estrella de neutrones tendría un peso parecido al de la montaña mas grande de la tierra, el monte . Los púlsares fueron descubiertos en 1970 y hasta solo se conece unas 300 estrellas de este tipo. Sin embargo, se calcula que sólo en nuestra Galaxia podrían ser un millón. La rápida rotación de los pùlsares los mantiene fuertemente magnetizados y sus rotaciones vertiginosas generan y son inmensas fuentes de electricidad. Llegan a producir mil millones de millones de voltios. Cuando nustros aparatos los observan y estudian detectan intensos haces de radiación en toda la gama del espectro (radio, luz, rayos X, Gamma).
Imagen de rayos-X en falso color de la región del cielo alrededor de SGR 1627-41 obtenida con XMM-Newton. La emisión indicada en rojo procede de los restos de una estrella masiva que estalló. Cubre una región más extendida de lo que se deducía anteriormente de las observaciones de radio, alrededor del SGR. Esto sugiere que la estrella que estalló fue el progenitor del magnetar. Crédito: ESA/XMM-Newton/EPIC (P. Esposito et al.)
Por ahora se conoce que de cada diez supernovas una se convierte en magnetar, si la supernova posee 6 y 12 masas solares, se convierte en una estrella de neutrones de no más de 10 a 20 km de diámetro. En el caso de las estrellas supermasivas de decenas de masas solares, el resultado es muy diferente y nos encontramos con los agujeros negros, esos monstruos del espacio devoradores de materia.

una estrella supermasiva muere, las consecuencias energéticas son inmensas. Ahí, en esa explosión se producen transiciones de fase que producen materiales pesados y complejos. En una supernova, en orden decreciente tenemos la secuencia de núcleos H, He, O, C, N, Fe, que coincide bastante bien con una ordenación en la tabla periódica de elementos.

La explosión de una estrella gigante y supermasiva hace que brille más que la propia galaxia que la acoge y, en su ese tránsito de estrella a púlsar o agujero negro, se forman elementos que, el oro o el platino, se riegan por el espacio interestelar en las inmensas nebulosas de las que, más tarde, naceran nuevas estrellas y nuevos mundos.
Pero está claro que todo el proceso estelar evolutivo inorgánico nos condujo el simple gas y polvo cósmico a la formación de estrellas y nebulosas solares hasta los planetas, la Tierra en particular, en cuyo medio ígneo describimos la formación de las estructuras de los silicatos, desplegándose con ello una enorme diversidad de composiciones, formas y colores, asistiéndose, por primera vez en la historia de la materia, a unas manifestaciones que contrastan con las que hemos mencionado en relación al proceso de las estrellas. Porque, en última instancia, debemos ser conscientes de un hecho cierto: En las estrellas se ¡ “fabrican los materiales que darán lugar al surgir de la vida”!.

El remanente estelar después de la explosiòn puede ser muy variado
Es posible que lo que nosotros llamamos materia inerte, no lo sea tanto, y, puede que incluso tenga memoria que transmite por medios que no sabemos reconocer. Esta clase de materia, se alía con el tiempo y, en momento adopta una forma predeterminada y de esa manera sigue evolucionando hasta llegar a su máximo ciclo o nivel en el que, de “materia inerte” llega a la categoría de “materia viva”, y, por el camino, ocupará siempre el lugar que le corresponda. No olvidemos de aquel sabio que nos dijo: “todas las cosas son”. El hombre, con aquellas sencillas palabras, elevó a todas las cosas a la categoría de ¡SER!
¿No os pensar que nosotros estemos hechos, precisamente, de lo que llamamos materia inerte?
Claro que, el mundo inorgánico es sólo una del inmenso mundo molecular. El resto lo constituye el mundo orgánico, que es el de las moléculas que contienen carbono y otros átomos y del que quedan excluidos, por convenio y características especiales, los carbonatos, bicarbonatos y carburos metálicos, los cuales se incluyen en el mundo inorgánico.
Según expliqué muchas veces, los quarks u y d se hallan en el seno de los nucleones (protones y neutrones) y, por tanto, en los núcleos atómicos. Hoy día, éstos se consideran una subclase de los hadrones. La composición de los núcleos (lo que en química se llama análisis cualitativo) es extraordinariamente sencilla, ya que como es sabido, constan de neutrones y protones que se pueden considerar como unidades que dentro del núcleo mantienen su identidad. Tal simplicidad cualitativa recuerda, por ejemplo, el caso de las series orgánicas, siendo la de los hidrocarburos saturados la más conocida. Recordad que su fórmula general es CnH2n+2, lo que significa que una molécula de hidrocarburo contiene n átomos de carbono (símbolo C) y (2n+2) átomos de hidrógeno (símbolo H).
Bueno, otra vez, como tantas veces me pasa, me desvío del camino que al principio del me propuse seguir y me pierdo en las elucubraciones que imaginan mis pensamientos. Mejor lo dejamos aquí.
emilio silvera
Jul
6
¡La complejidad! Si la miramos por parte…desaparece
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Caos y Complejidad ~
Clasificado en Caos y Complejidad ~
 Comments (26)
Comments (26)
Todos hemos oído hablar, con más o menos frecuencia, de “Sistemas Complejos”, aquí mismo en estas páginas, la palabra sale a relucir con cierta frecuencia y, no me extraña que “la palabreja” cree una barrera, dado que, para muchas personas, “complejo” significa “complicado” y suponen automáticamente que, si un sistema es complicado, será difícil de comprender. La naturaleza posee una fuerte tendencia a estructurarse en forma de entes discretos excitables que interactúan y que se organizan en niveles jerárquicos de creciente complejidad, por ello, los sistemas complejos no son de ninguna manera casos raros ni curiosidades sino que dominan la estructura y función del universo.

Claro que, no siempre ese temor a lo difícil y complicado, está justificado y, tal suposición no es, necesariamente correcta. En realidad, un sistema complejo es tan solo un sistema que está formado por varios componentes más sencillos que ejercen entre sí una interacción mutua que, naturalmente, tiene sus consecuencias. Si miramos la imagen de arriba, vemos una inmensa y hermosa Nebulosa que está formada por una serie de “cosas” sencillas como lo son el gas hidrógeno y el polvo interestelar entre otros y, en presencia de energías, la gravedad y otros parámetros, ahí ocurren cosas tales como, el nacimiento de estrellas y la aparición de mundos…entre otras.
Los grandes triunfos de la Ciencia se han logrado, en gran medida, descomponiendo los sistemas complejos en sus componentes simples, es decir, estudiar por partes lo que allí está presente (en caso necesario, como primera aproximación, dando el paso suplementario de pretender que todos los componentes son más sencillos de lo que son en realidad) para llegar a comprender el todo.
En el ejemplo clásico del éxito que ha logrado este planteamiento para conocer el mundo que nos rodea, buena parte de la química puede entenderse mediante un modelo en el que los componentes simples son átomos, y para eso importa poco de qué están formados los núcleos. Ascendiendo un nivel, las leyes que describen el comportamiento del dióxido de Carbono encerrado en una caja pueden entenderse pensando en unas moléculas más o menos esféricas que rebotan unas contra otras y contra las paredes de su contenerdor, y poco importa que cada una de estas moléculas esté formada por un átomo de Carbono y dos de Oxígeno unidos entre sí. Ambos sistemas son complejos, en sentido científico, pero fáciles de entender.

Fijémonos, por ejemplo, en el Campo Magnético Terrestre. En esencia, los planetas generan un campo magnético por efecto dinámo. Para ello se requiere que el planeta rote; debe contener una región con un fluido conductor de la electricidad y debe existir convección en dicho fluido. No se puede asegurar pero parece ser que si en la Tierra no hubiese tectónica de placas el transporte convectivo hacia la superficie podría no tener lugar, la dinamo no funcionaría y el campo magnético terrestre sería prácticamente nulo o, al menos, mucho menor que el actual. Sin la protección que nos brinda el campo magnético, la atmósfera podría desaparecer a causa del continuo bombardeo de las partículas de alta energía procedentes del viento solar. Todos estos componentes son estudiados por separado y, más tarde, los juntamos en un todo que nos lleva a la comprensión de este Sistema Complejo.
Claro que la clave para poder llegar al conocimiento del “sistema complejo” consiste en saber elegir los componentes adecuados sencillos que conforman el todo para poder realizar el análisis necesario que nos lleve hasta las respuestas que buscamos. En muchas ocasiones hemos explicado aquí, lo que hay en las Nebulosas como la de arriba y lo que ocurre en ellas para que, finalmente, nazcan estrellas nuevas.
Hermann Minkowski
Hay cuestiones, a un nivel más abstracto del que hemos oído hablar también con cierta frecuencia. Acordaos de que, poco después de que Einstein publicara sus trabajos sobre relatividad especial, el matemático alemán que arriba podeis ver se dio cuenta de que, en cierto modo, el tiempo debía ser considerado como la cuarta coordenada complementaria de las tres coordenadas del espacio. En su discurso de inauguración de la 80 reunión de la Asamblea general alemana de científicos naturales y físicos el 21 de septiembre de 1908 pronunció una célebre frase:
“Las ideas sobre el espacio y el tiempo que deseo mostrarles hoy descansan en el suelo firme de la física experimental, en la cual yace su fuerza. Son ideas radicales. Por lo tanto, el espacio y el tiempo por separado están destinados a desvanecerse entre las sombras y tan sólo una unión de ambos puede representar la realidad”.
Desde entonces el espacio-tiempo cuatridimensional pasó a llamarse espacio de Minkowski. Si empleamos x,y y z para las tres coordenadas del espacio, tomaremos ct para la cuarta coordenada de tiempo, siendo c la velocidad de la luz. Sin embargo debemos multiplicar ct por otro factor que, sin destrozar la armonía del sistema tetradimensional de las coordenadas haga a la coordenada de tiempo físicamente diferente de las tres coordenadas espaciales. La matemática nos suministra precisamente este factor conocido como una “unidad imaginaria” que se designa con el símbolo i (i= raíz cuadrada de -1).
 Minkowski
Minkowski
“Es un hecho notorio que los procesos que ocurren en el universo observable son irreversibles, mientras que las ecuaciones que expresan las leyes fundamentales de la física son invariantes bajo inversión temporal. La emergencia de la irreversibilidad a partir de la física fundamental ha sido un tema que ha preocupado a físicos, astrónomos y filósofos desde que Boltzmann formulara su famoso teorema “H”.

- ¿Es un sistema complejo un fotón? La propiedad del fotón, de la luz, es que es algo que oscila tan rápidamente que en realidad es como si estuviera en dos sitios a la vez, o sea algo que está pero que no está?
Cómo se entiende algo así
- “¿Tengo que reconocer que está ha sido la incógnita que más me ha costado despejar, todo un desafío a la lógica, a la matemática. Aunque en realidad era sencillo, porque lo cierto es que lo tenía en las narices. ¡Claro! esa es la esencia de nuestra mágica ecuación, e =m.c2, ¡”
masa en movimiento
- !,es decir, más de lo mismo. Digamos que la mecánica cuántica en realidad no es más que la Vida llevada a su mínima expresión.
Los números complejos, con una parte real y otra imaginaria, también juegan un papel esencial en los formulismos de la mecánica cuántica. La propia probabilidad de los sucesos cuánticos llega a expresarse en función de números complejos llamados amplitudes de probabilidad. La probabilidad real se halla a partir de estos números, sumando el cuadrado de su parte real y el cuadrado de su parte imaginaria.
Esto nos da una idea de la importancia de los estos números, tanto en la teoria de la relatividad como en la mecánica cuántica y nos ayuda a introducirnos en la teoría de Hartle-Hawking sobre los comienzos del universo, que supone un universo sin límites y con un tiempo imaginario, como se entiende la parte no real de un número complejo.
En cierta forma los ceros y los infinitos que aparecen en la física clásica son suavizados por la mecánica cuántica: La energía más baja en el vacío no es nunca cero, como tampoco es nunca cero la extensión de un punto físico . La existencia del cuanto de acción impide una energía cero del vacío, como impide la medida exacta, a la vez, de una variación de energía y del tiempo asociado a dicha variación.El punto físico menor sería la llamada longitud de Planck, del orden de 10-35 metros, lo que también elimina el infinito que resultaría de considerar las partículas subatómicas como puntuales: su densidad sería infinita y resultarían microscópicos agujeros negros.
Según alguna teoría que circula por ahí, si comenzamos en el momento presente y vamos hacia atrás en el tiempo, lo que aparentemente sería el punto origen de la descripción del tiempo real convencional, la naturaleza del tiempo cambia: la componente imaginaria del tiempo se hace más y más prominente hasta que, en último término, lo que debería ser la singularidad de la teoría clásica se desvanece. El Universo existiría porque es una estructura matemática autoconsistente. Puede imaginarse el tiempo real como una línea que va del principio al final del Universo. Pero también puede considerarse otra dirección del tiempo en ángulo recto al tiempo real. Esta última se denomina la dirección imaginaria del tiempo. En el tiempo imaginario, no habría ninguna singularidad en la que dejaran de regir las leyes de la Ciencia, ni ninguna frontera del Universo tras la cual tuviera que apelarse a Dios. El Universo no sería creado ni destruído. Simplemente existiría. Quizás el tiempo imaginario sea el auténtico tiempo real y lo que llamamos tiempo real sea sólo un producto de nuestra imaginación. En el tiempo real, el Universo tiene un principio y un fin. En el tiempo imaginario no hay singularidades ni límites.

Hartle: “Tiempo imaginario no se refiere a la imaginación: hace referencia a los números complejos. Como demostraron Einstein y Minkowsky, el espacio-tiempo constituye una geometría cuatridimensional. Es posible ir aún más lejos de estos conceptos. Si se miden las direcciones del tiempo utilizando números complejos, se obtiene una simetría total entre espacio y tiempo, que es, matemáticamente, un concepto muy bello y natural”. Don N. Page: ” En la formulación de la ausencia de límites de Hartle-Hawking, el tiempo es imaginario, y en vez de tener un borde es como si se tratara de la superficie del planeta Tierra. Suponiendo tiempo imaginario, el Universo no tuvo comienzo, no tiene límite, es una totalidad en sí mismo”.
He tenido la oportunidad de leer el Libro de Roger Penrose (uno de los físicos actuales más brillantes), titulado, El camino a la realidad, y él nos comenta: “… los números complejos componen una notable unidad con la naturaleza. Es como si la propia naturaleza estuviera tan impresionada por el alcance y consistencia del sistema de los números complejos como lo estamos nosotros, y hubiera confiado a estos números las operaciones detalladas de su mundo en sus escalas más minúsculas”. Se refiere a la mecánica cuántica, pero realmente su importancia se refleja en toda la naturaleza, porque la cosmología, en los primeros instantes del universo se confunde con el mundo microscópico de las partículas elementales.

Claro que, los “Sistemas Complejos” están por todas partes y, tanto ers así que, nosotros mismos somos un buen ejemplo y llevamos con nosotros, el “sistema” más complejo de todos: Nuestro cerebro es, sin dudarlo y hasta donde puede llegar nuestros conocimientos actuales, el más complejo de los sistemas.
Claro que, si hablamos de complejidad de sistemas, el universo sería el mejor de los ejemplos. Con respecto a sus propios patrones, el universo es viejo. El tiempo de vida natural de un mundo gobernado por la gravedad, la relatividad y la mecánica cuántica es el fugaz breve tiempo de Planck. Parece que es mucho más viejo de lo que debería ser.
Pero, pese a la enorme edad del universo en “tics” de Tiempo de Planck, hemos aprendido que casi todo este tiempo es necesario para producir estrellas y los elementos químicos que traen la vida.
![[cerebro-artificial.jpg]](http://4.bp.blogspot.com/_gB8i9RgQMBM/SZPuHenJ6uI/AAAAAAAAHRg/iKaGbui_WMI/s1600/cerebro-artificial.jpg)
La vida que surgió en el planeta Tierra a partir del polvo de estrellas
¿Por qué nuestro universo no es mucho más viejo de lo que parece ser? Es fácil entender por qué el universo no es mucho más joven. Las estrellas tardan mucho tiempo en formarse y producir elementos más pesados que son las que requiere la complejidad biológica. Pero los universos viejos también tienen sus problemas. Conforme para el tiempo en el universo el proceso de formación de estrellas se frena. Todo el gas y el polvo cósmico que constituyen las materias primas de las estrellas habrían sido procesados por las estrellas y lanzados al espacio intergaláctico donde no pueden enfriarse y fundirse en nuevas estrellas. Pocas estrellas hacen que, a su vez, también sean pocos los sistemas solares y los planetas. Los planetas que se forman son menos activos que los que se formaron antes, la entropía va debilitando la energía del sistema para realizar trabajo. La producción de elementos radiactivos en las estrellas disminuirá, y los que se formen tendrán semividas más largas. Los nuevos planetas serán menos activos geológicamente y carecerán de muchos de los movimientos internos que impulsan el vulcanismo, la deriva continental y la elevación de las montañas en el planeta. Si esto también hace menos probable la presencia de un campo magnético en un planeta, entonces será muy poco probable que la vida evolucione hasta formas complejas.

En lugares como este se forman los elementos de la vida
Las estrellas típicas como el Sol, emiten desde su superficie un viento de partículas cargadas eléctricamente que barre las atmósferas de los planetas en órbitas a su alrededor y, a menos que el viento pueda ser desviado por un campo magnético, los posibles habitantes de ese planeta lo podrían tener complicado soportando tal lluvia de radiactividad. En nuestro sistema solar el campo magnético de la Tierra ha protegido su atmósfera del viento solar, pero Marte, que no está protegido por ningún campo magnético, perdió su atmósfera hace tiempo.
Probablemente no es fácil mantener una larga vida en un planeta del Sistema solar. Poco a poco hemos llegado a apreciar cuán precaria es. Dejando a un lado los intentos que siguen realizando los seres vivos de extinguirse a sí mismos, agotar los recursos naturales, propagar infecciones letales y venenos mortales y emponzoñar la atmósfera, también existen serias amenazas exteriores.
¿No es inmensamente complejo todo esto?
En realidad, los sistemas complejos constituyen y se manifiestan en la inmensa mayoría de los fenómenos observables. Sin embargo, y aquí radica una de sus propiedades más interesantes, la abundancia y diversidad de los sistemas complejos (sean de tipo físicos, químicos, biológicos, sociales, etc.) no implica una innumerable e inclasificable diversidad de conductas dinámicas diferentes. Todo lo contrario, los sistemas complejos poseen propiedades genéricas, independientemente de los detalles específicos de cada sistema o de la base material del mismo. De esta manera, por ejemplo, una computadora construida con bulbos, otra con transistores y una más con relevadores electromagnéticos; serían capaces de realizar, en principio, las mismas tareas de procesamiento de datos. Podríamos incluso ir mas lejos con este ejemplo y agregar que el sistema nervioso humano posee propiedades tales como memoria difusa y reconocimiento de patrones que funcionan de la misma manera en como funciona una computadora de bulbos o de transistores. Lo que comparten, son una estructura interconectada y formada por elementos individuales (neuronas o circuitos electrónicos) que interactúan para intercambiar información y modificar sus estados internos. Ello hace posible la emergencia de fenómenos globales y colectivos semejantes, sin que los detalles materiales del sistema sean del todo relevantes. De esta manera, es posible identificar propiedades dinámicas similares entre una computadora, el sistema nervioso, el sistema inmunológico, la tectónica de placas, una sociedad de insectos, el crecimiento urbano, las economías de mercado, el tráfico vehicular, etc. a pesar de la aparente disparidad entre estos sistemas.

La aportación fundamental de la ciencia de los sistemas complejos en la tarea de conocer y transformar nuestra realidad, es identificar los principios y fundamentos generales de la operación de dichos sistemas sin importar los detalles particulares de su realización material. Así por ejemplo, podemos imaginar un biólogo del futuro que estudiaría el fenómenos llamado “vida” desde una perspectiva de principios (tal vez leyes?) generales. Tal biólogo tendría conciencia de que el fenómeno “vida” tal y como existe en la Tierra es tan sólo un caso particular de como “la vida” se ha manifestado bajo las condiciones particulares de la Tierra, expresándose bajo la forma de una realización material muy específica (una bioquímica de carbono dominantemente levógira). Sin embargo, este biólogo estaría preparado para identificar el fenómeno “vida” si acaso fuera detectado en otro planeta o parte del universo bajo otras realizaciones materiales especificas, de la misma manera que un físico hoy en día sabe que la ley de gravitación lo mismo es valida para la superficie de la Tierra que para la superficie de Marte o cualquier otra parte del universo. El ejemplo puede ir aún más lejos. Podemos imaginar un sociólogo del futuro que será capaz de identificar los principios generales del fenómeno “social” independientemente de que este ocurra en grupos humanos, animales, microbios, plantas, robots o incluso, si su colega biólogo tiene suerte, en grupos sociales fuera de nuestro planeta.
¿Estaremos capacitados alguna vez determinar las partes “sencillas” de los “Sistemas Complejos” para llegar a saber?
emilio silvera
Jun
5
El “mundo” que nos rodea
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Caos y Complejidad ~
Clasificado en Caos y Complejidad ~
 Comments (4)
Comments (4)
No siempre sabemos ver el mundo que nos rodea. El que miremos no significa que estemos viendo lo que realmente hay delante de nuestros ojos y, muchas veces, no son los ojos los únicos que pueden “ver” lo que hay más allá de lo que la vista puede alcanzar. Anoche, hasta una hora avanzada, estuve releyendo el Libro “Así de Simple” de John Gribbin, y, pareciéndome interesante os saqué un pequeño resumen del comienzo. Aquí os lo dejo.
El mundo que nos rodea parece ser un lugar complicado. Aunque hay algunas verdades sencillas que parecen eternas (las manzanas caen siempre hacia el suelo y no hacia el cielo; el Sol se levanta por el este, nunca por el oeste), nuestras vidas, a pesar de las modernas tecnologías, están todavía, con demasiada frecuencia, a merced de los complicados procesos que producen cambios drásticos y repentinos. La predicción del tiempo atmosférico tiene todavía más de arte adivinatorio que de ciencia; los terremotos y las erupciones volcánicas se producen de manera impredecible y aparentemente aleatorias; las fluctuaciones de la economía siguen ocasionando la bancarrota de muchos y la fortuna de unos pocos.

Sobre la posición de la salida del sol

Desde la época de Galileo (más o menos, a comienzos del siglo XVII) la ciencia ha hecho progresos –enormes-, ignorando en gran medida estas complejidades y centrándose en cuestiones sencillas, intentando explicar por qué las manzanas caen al suelo y por qué el Sol se levanta por el este. Los avances fueron de hecho tan espectaculares que hacia mediados del siglo XX ya se había dado respuesta a todas las cuestiones sencillas. Conceptos tales como la teoría general de la relatividad y la mecánica cuántica explicaron el funcionamiento global del universo a escalas muy grandes y muy pequeñas respectivamente, mientras el descubrimiento de la estructura del ADN y el modo en que éste se copia de una generación a otra hizo que la propia vida, así como la evolución, parecieran sencillas a nivel molecular. Sin embargo, persistió la complejidad del mundo a nivel humano –al nivel de la vida-. La cuestión más interesante de todas, la que planteaba cómo la vida pudo haber surgido a partir de la materia inerte, siguió sin respuesta.
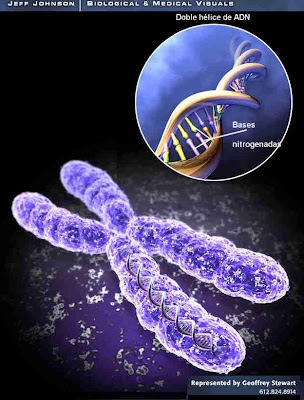
Un descubrimiento así no podía dejar al mundo indiferente. En unos años el mundo científico se puso al día y la revolución genética cambió los paradigmas establecidos. Mucha gente aún no está preparada para aceptar el comienzo de una era poderosa en la que el ser humano tiene un control de sí mismo mayor al habitual. Había nacido la Ingeniería genética.
No debe extrañarnos que sea precisamente a escala humana donde se den las características más complejas del universo. Las que se resisten más a rendirse ante los métodos tradicionales de la investigación científica. Realmente, es posible que seamos lo más complejo que existe en el universo. La razón es que, a escalas más reducidas, entidades tales como los átomos se comportan individualmente de un modo relativamente sencillo en sus interacciones mutuas, y que las cosas complicadas e interesantes surgen, cuando se unen muchos átomos de maneras complicadas e interesantes, para formar organismos tales como los seres humanos.
Pero este proceso no puede continuar indefinidamente, ya que, si se unen cada vez más átomos, su masa total aumenta hasta tal punto que la Gravedad aplasta toda la estructura importante y la aniquila. Un átomo, o incluso una molécula tan simple como la del agua, es algo más sencillo que un ser humano, porque tiene poca estructura interna; una estrella, o el interior de un planeta, es también algo más sencillo que un ser humano porque la gravedad aplasta cualquier estructura hasta aniquilarla. Esta es la razón por la cual la ciencia puede decirnos más sobre el comportamiento de los átomos y el funcionamiento interno de las estrellas o los planetas que sobre el modo en que las personas nos comportamos.
Sí, hemos podido llegar a conocer lo que ocurre en el Sol, y sabemos de sus procesos interiores y exteriores, de las ráfagas de partículas que en sus épocas activas, nos envía continuamente hacía la superficie del planeta y, que no sólo provoca esas bonitas Auroras, sino que, su intensa radiación y magnetismo incide en todos los atilugios que tenemos para leer los datos de… ¡tántas cosas!
Cuando los problemas sencillos se rindieron ante el empuje de la investigación, fue algo natural que los científicos abordaran rompecabezas más complicados que iban asociados con sistemas complejos, para que por fin fuera posible comenzar a comprender el funcionamiento del mundo a una escala más humana compleja y, para ello, hubo que esperar hasta la década de 1960, que fue cuando aparecieron los poderosos y rápidos (para lo que se estilaba en aquella época) ordenadores electrónicos. Estos nuevos inventos empezaron a ser conocidos por un público más amplio entre mediados y finales de la década de 1980, primero con la publicación del libro, ahora convertido en un clásico, Order out of Chaos, de Ilya Prigogine e Isabelle Stergers, y luego, con Chaos, de James Gleick.

Las personas sencillas que, aunque tengan una educación aceptable, no están inmersas en el ámbito de la ciencia, cuando oyen hablar de Complejidad y Caos en esas áreas, sienten, de primeras, una especie de rechazo por aquello que (ellos creen) no van a comprender. Sin embargo, la cuestión no es tan difícil como a primera vista pudiera parecer, todo consiste en tener la posibilidad de que alguien, de manera “sencilla” (dentro de lo posible), nos explique las cosas dejando a un lado las matemáticas que, aunque describen de manera más amplia y pura aquellos conceptos que tratamos, también es verdad que, no siempre, están al alcance de todos. Un conocimiento básico de las cosas más complicadas, es posible. También la relatividad general y la mecánica cuántica, se consideraron, cuando eran nuevas, como unas ideas demasiado difíciles para que cualquiera las entendiera, salvo los expertos –pero ambas se basan en conceptos sencillos que son inteligibles para cualquier persona lega en la materia, siempre que esté dispuesta a aceptar su parte matemática con los ojos cerrados-. E la misma manera, el Caos y la Complejidad, también pueden ser entendidos y, si tenemos la suerte de tener un buen interlocutor que nos sepa explicar, aquellos conceptos básicos sobre los que se asientan tanto el Caos como la Complejidad, veremos maravillados como, de manera natural, la luz se hace en nosotros y podemos entender lo que antes nos parecía inalcanzable.

Se cree que las galaxias se han formado por la acumulación gravitacional de gas, algún tiempo después de la época de la recombinación. Las nubes de gas podrían haber comenzado a formar estrellas, quizás como resultado de las colisiones mutuas. El tipo de galaxia generado podría depender del ritmo al que el gas era transformado en estrellas, formándose las elípticas cuando el gas se convertía rápidamente en estrellas, y las espirales si la transformación de estrellas era lo suficientemente lenta como para permitir crecer de forma significativa un disco de gas. Lo cierto es que, hasta la fecha, nadie sabe explicar cómo se pudieron formar las galaxias a pesar de la expansión de Hubble. ¿Qué fuerza estaba allí presente para retener la materia?

Nubes moleculares en Orión que son los materiales primigenios para complejidades futuras
Las galaxias evolucionan al convertir progresivamente su gas remanente en estrellas, si bien no existe probablemente una evolución entre las diferentes tipos de la clasificación del conocido sistema de Hubble. No obstante, algunas galaxias elípticas pudieron haberse creado por la colisión y posterior fusión de dos galaxias espirales.
NGC 5426 y NGC 5427 son dos galaxias espirales de tamaños similares involucradas en una danza espectacular. No es seguro que esta interacción culmine en una colisión y a la larga en la fusión de las dos galaxias, aunque éstas ya han sido ya afectadas. Conocidas ambas con el nombre de Arp 271, su danza perdurará por decenas de millones de años, creando nuevas estrellas como resultado de la mutua atracción gravitacional entre las galaxias, un tirón observable en el borde de las estrellas que ya conectan a ambas. Ubicada a 90 millones de años-luz de distancia hacia la constelación de Virgo (la Virgen), el par Arp 271 tiene unos 130.000 años-luz de extensión. Fue descubierta originalmente en 1785 por William Herschel. Muy posiblemente nuestra Vía Láctea sufrirá una colisión similar en unos cinco mil millones de años más con la galaxia vecina Andrómeda, que ahora está ubicada a cerca de 2,6 millones de años-luz de la Vía Láctea.
Sí, mirando las imagenes nos da la sensación de cierto Caos y Complejidad
Tenemos que entender que, algunos sistemas (“sistema” no es más que una palabra de la jerga científica para asignar cualquier cosa, como un péndulo que oscila, o el sistema solar, o el agua que gotea de un grifo) son muy sensibles a sus condiciones de partida, de tal modo que una diferencia mínima en el “impulso” inicial que les damos ocasiona una gran diferencia en cómo van a acabar, y existe una retroalimentación, de manera que lo que un sistema hace afecta a su propio comportamiento. Así, a primera vista, parece que la guía es sencilla y, nos puede parecer mentira que así sea. Sin embargo, esa es la premisa que debemos tener en cuenta. Nos podríamos preguntar: ¿Es realmente verdad, que todo este asunto del Caos y de la Complejidad se basaba en dos ideas sencillas –la sensibilidad de un sistema a sus condiciones de partida, y la retroalimentación-¿ La respuesta es que sí.
 La mayor parte de los objetos que pueden verse en el cielo nocturno son estrellas, unos pocos centenares son visibles a simple vista. Una estrella es una bola caliente principalmente compuesta por hidrógeno gaseoso. El Sol es un ejemplo de una estrella típica y común. La gravedad impide que el gas se evapore en el espacio y la presión, debida a la alta temperatura de la estrella, y la densidad impiden que la bola encoja. En el corazón de la estrella, la temperatura y la densidad son lo suficientemente altas para sustentar a las reacciones de fusión nuclear, y la energía, producida por estas reacciones, hace su camino a la superficie y la irradia al espacio en forma de calor y luz. Cuando se agota el combustible de las reacciones de fusión, la estructura de la estrella cambia. El proceso de producir elementos, cada vez más pesados, a partir de los más livianos y de ajustar la estructura interna para balancear gravedad y presión, es llamado evolución estelar.
La mayor parte de los objetos que pueden verse en el cielo nocturno son estrellas, unos pocos centenares son visibles a simple vista. Una estrella es una bola caliente principalmente compuesta por hidrógeno gaseoso. El Sol es un ejemplo de una estrella típica y común. La gravedad impide que el gas se evapore en el espacio y la presión, debida a la alta temperatura de la estrella, y la densidad impiden que la bola encoja. En el corazón de la estrella, la temperatura y la densidad son lo suficientemente altas para sustentar a las reacciones de fusión nuclear, y la energía, producida por estas reacciones, hace su camino a la superficie y la irradia al espacio en forma de calor y luz. Cuando se agota el combustible de las reacciones de fusión, la estructura de la estrella cambia. El proceso de producir elementos, cada vez más pesados, a partir de los más livianos y de ajustar la estructura interna para balancear gravedad y presión, es llamado evolución estelar.
Observar una estrella a través del telescopio permite conocer muchas de sus importantes propiedades. El color de una estrella es un indicador de su temperatura y ésta, a su vez, depende de una combinación entre la masa de la estrella y su fase evolutiva. Usualmente, las observaciones también permiten encontrar la luminosidad de la estrella o la tasa con la cual ella irradia energía, en forma de calor y luz.
Todas las estrellas visibles a simple vista forman parte de nuestra galaxia, la Vía Láctea. La Vía Láctea es un sistema compuesto por unos cien mil millones de estrellas, junto con una considerable cantidad de material interestelar. La galaxia tiene forma de un disco chato sumergido en un halo débil y esférico. La gravedad impide que las estrellas se escapen y, sus movimientos, hacen que el sistema no colapse. La Vía Láctea no posee un límite definido, la distribución de las estrellas decrece gradualmente con distancias crecientes del centro. El SDSS detecta estrellas más de un millón de veces más débiles que las que podemos ver a simple vista, lo suficientemente lejos para ver la estructura de la Vía Láctea.

De algún modo, esto es como decir que “todo lo que hay” sobre la teoría especial de la relatividad es que la velocidad de la luz es la misma para todos los observadores. Sin embargo, la complejidad de la estructura que se levanta sobre este hecho sencillo resulta asombrosa y requiere algunos conocimientos matemáticos para poder apreciarla plenamente. Claro que, eso no quita para que, un buen comunicador le pueda transmitir a otras personas mediante explicaciones sencillas lo esencial de la relatividad especial y general y también, sobre la esencia de la mecánica cuántica, y, de la misma manera, podríamos hablar del Caos y de la Complejidad. Debemos ser conscientes de que, el Caos, puede surgir a partir del Orden y que, la Complejidad, siempre llega a través de la sencillez de un comienzo. Podemos estar al borde del Caos y, de manera milagrosa ver que, también a partir de él surge la normalidad y lo nuevo que, no en pocas ocasiones pueden ser nuevas formas de vida. De la misma manera, las transformaciones de los elementos sencillos, bajo ciertas condiciones, llegan a adquirir una complejidad inusitada que, de alguna manera, es necesaria para que, en este mundo que nos rodea, existan seres que, como nosotros, sean el ejemplo más real y de más alto nivel que está presente en el Universo. Y, de la misma manera que nosotros estamos aquí, en un minúsculo sistema solar habitando un pequeño planeta que reúne todas las condiciones necesarias para la vida, de la misma forma digo, estarán poblados otros muchos planetas de otros muchos sistemas solares repartidos por nuestra Galaxia y por las otras que, a cientos de miles pululan por el Universo, y, todos esos seres “racionales”, se preguntaran las mismas cosas que nosotros y estarán interesados en descubrir los mismos misterios, los mismos secretos de la Naturaleza que, presintiendo que existen, tienen la intuición de que serán las respuestas esperadas para solucionar muchos de los problemas e inseguridades que ahora, en nuestro tiempo, nos aquejan.
Claro que, la mente nunca descansa. Acordaos de Aristarco de Samos que, en el siglo III a. C., ya anunció que la Tierra orbitaba alrededor del Sol y, Copérnico, que se llevó el premio, no lo dijo hasta el año 1543. Esto nos viene a demostrar que, a pesar de la complejidad del mundo, lo realmente complejo está en nosotros, en nuestras mentes que, presienten lo que pueda ser, intuyen el por qué de las cosas, fabrican pensamientos que, mucho más rápidos que la luz, llegan a las galaxias lejanas y, con los ojos de la mente pueden, atisbar aquellas cosas de las que, en silencio, ha oído hablar a su intuición dentro de su mente siempre atenta a todo aquello que puede ser una novedad, una explicación, un descubrimiento.

Vista de la Tierra y el Sol de la órbita (la imagen de la tierra tomada de http://visibleearth.nasa.gov)
Ahora estamos centrados en el futuro aquí en la Tierra pero, sin dejar de la mano ese futuro que nos espera en el espacio exterior. Es pronto aún para que el hombre vaya a las estrellas pero, algún día, ese será su destino y, desde ya, debe ir preparándose para esa aventura que sólo está a la espera de tener los medios tecnológicos necesarios para hacerla posible. Mientras tanto, jugamos con las sondas espaciales que enviamos a planetas vecinos para que, nos vayan informando de lo que están hechos aquellos mundos –grandes y pequeños- que, en relativamente poco tiempo, serán visitados por nuestra especie para preparar el salto mayor.
emilio silvera
















 Totales: 75.162.292
Totales: 75.162.292 Conectados: 47
Conectados: 47
























