Abr
18
La maravilla de… ¡los cuantos!
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (0)
Comments (0)

Es una magnitud fundamental llamada cuanto de acción y es el Ser de la Mecánica Cuántica. Planck lo llamó “cuanto” y lo simbolizó con la letra h.
La Física del siglo XX empezó exactamente en el año 1900, cuando el físico alemán Max Planck propuso una posible solución a un problema que había estado intrigando a los físicos durante años. Es el problema de la luz que emiten los cuerpos calentados a una cierta temperatura, y también la radiación infrarroja emitida, con menos intensidad, por los objetos más fríos. Planck escribió un artículo de ocho páginas y el resultado fue que cambió el mundo de la física y aquella páginas fueron la semilla de la futura ¡mecánica cuántica! que, algunos años más tardes, desarrollarían físicos como Einstein (Efecto fotoeléctrico), Heisenberg (Principio de Incertidumbre), Feynman, Bhor, Schrödinger, Dirac…
La expresión radiación se refiere a la emisión continua de energía de la superficie de todos los cuerpos. Los portadores de esta energía son las ondas electromagnéticas producidas por las vibraciones de las partículas cargadas que forman parte de los átomos y moléculas de la materia. La radiación electromagnética que se produce a causa del movimiento térmico de los átomos y moléculas de la sustancia se denomina radiación térmica o de temperatura.

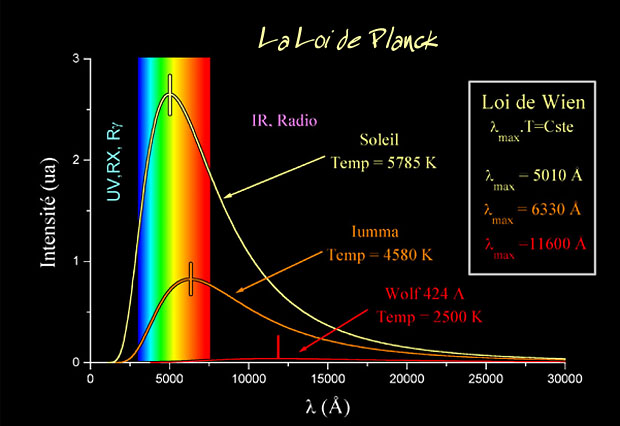
Ley de Planck para cuerpos a diferentes temperaturas.
Estaba bien aceptado entonces que esta radiación tenía un origen electromagnético y que se conocían las leyes de la naturaleza que regían estas ondas electromagnéticas. También se conocían las leyes para el frío y el calor, la así llamada “termodinámica”, o al menos eso parecía.
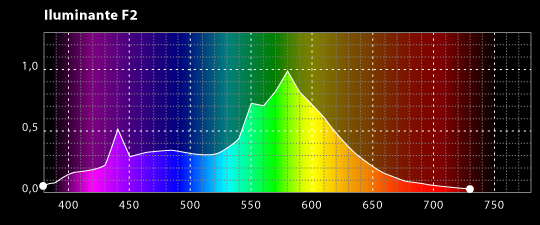
Pero si usamos las leyes de la termodinámica para calcular la intensidad de la radiación, el resultado no tiene ningún sentido. Los cálculos nos dicen que se emitiría una cantidad infinita de radiación en el ultravioleta más lejano, y, desde luego, esto no es lo que sucede. Lo que se observa es que la intensidad de la radiación muestra un pico o una cierta longitud de onda característica, y que la intensidad disminuye tanto para longitudes mayores como para longitudes menores. Esta longitud característica es inversamente proporcional a la temperatura absoluta del objeto radiante (la temperatura absoluta se define por una escala de temperatura que empieza a – 273,15 ºC bajo cero). Cuando a 1.000 ºC un objeto se pone al “rojo vivo”, el objeto está radiando en la zona de la luz visible.

Acero al “rojo vivo”, el objeto está radiando en la zona de la luz visible.
Lo que Planck propuso fue simplemente que la radiación sólo podía ser emitida en paquetes de un tamaño dado. La cantidad de energía de uno de esos paquetes, o cuantos, es inversamente proporcional a la longitud de onda y, por lo tanto, proporcional a la frecuencia de la radiación emitida. La sencilla fórmula es:
E = hv
Donde E es la energía del paquete, v es la frecuencia y h es una nueva constante fundamental de la naturaleza, la constante de Planck. Cuando Planck calculó la intensidad de la radiación térmica imponiendo esta nueva condición, el resultado coincidió perfectamente con las observaciones.
Poco tiempo después, en 1905, Einstein formuló esta teoría de una manera mucho más tajante: el sugirió que los objetos calientes no son los únicos que emiten radiación en paquetes de energía, sino que toda la radiación consiste en múltiplos del paquete de energía de Planck.
El príncipe francés Louis Victor de Broglie, dándole otra vuelta a la teoría, que no sólo cualquier cosa que oscila tiene una energía, sino que cualquier cosa con energía se debe comportar como una “onda” que se extiende en una cierta dirección del espacio, y que la frecuencia, v, de la oscilación verifica la ecuación de Planck. Por lo tanto, los cuantos asociados con los rayos de luz deberían verse como una clase de partículas elementales: el fotón. Todas las demás clases de partículas llevan asociadas diferentes ondas oscilatorias de campos de fuerza.

Es curioso el comportamiento de los electrones en el interior del átomo, descubierto y explicado por el famoso físico danés Niels Bohr, se pudo atribuir a las ondas de De Broglie. Poco después, en 1926, Edwin Schrödinger descubrió como escribir la teoría ondulatoria de De Broglie con ecuaciones matemáticas exactas. La precisión con la cual se podían realizar los cálculos era asombrosa, y pronto quedó claro que el comportamiento de todos los objetos pequeños quedaba exactamente determinado por las recién descubiertas “ecuaciones de onda cuántica”.

No hay duda de que la Mecánica Cuántica funciona maravillosamente bien. Sin embargo, surge una pregunta muy formal: ¿qué significan realmente esas ecuaciones?, ¿qué es lo que están describiendo? Cuando Isaac Newton, allá por el año 1687, formuló cómo debían moverse los planetas alrededor del Sol, estaba claro para todo el mundo lo que significaban sus ecuaciones: que los planetas están siempre en una posición bien definida en el espacio y que sus posiciones y sus velocidades en un momento concreto determinan inequívocamente cómo evolucionarán las posiciones y las velocidades con el tiempo.
Pero para los electrones todo esto es muy diferente. Su comportamiento parece estar envuelto en la bruma. Es como si pudieran “existir” en diferentes lugares simultáneamente, como si fueran una nube o una onda, y esto no es un efecto pequeño. Si se realizan experimentos con suficiente precisión, se puede determinar que el electrón parece capaz de moverse simultáneamente a lo largo de trayectorias muy separadas unas de otras. ¿Qué puede significar todo esto?

Niels Bohr consiguió responder a esta pregunta de forma tal que con su explicación se pudo seguir trabajando y muchos físicos siguen considerando su respuesta satisfactoria. Se conoce como la “interpretación de Copenhague” de la Mecánica Cuántica. En vez de decir que el electrón se encuentra en el punto x o en el punto y, nosotros hablamos del estado del electrón. Ahora no tenemos el estado “x” o el estado “y”, sino estados “parcialmente x” o “parcialmente y. Un único electrón puede encontrarse, por lo tanto, en varios lugares simultáneamente. Precisamente lo que nos dice la Mecánica Cuántica es como cambia el estado del electrón según transcurre el tiempo.
Un “detector” es un aparato con el cual se puede determinar si una partícula está o no presente en algún lugar pero, si una partícula se encuentra con el detector su estado se verá perturbado, de manera que sólo podemos utilizarlo si no queremos estudiar la evolución posterior del estado de la partícula. Si conocemos cuál es el estado, podemos calcular la probabilidad de que el detector registre la partícula en el punto x.

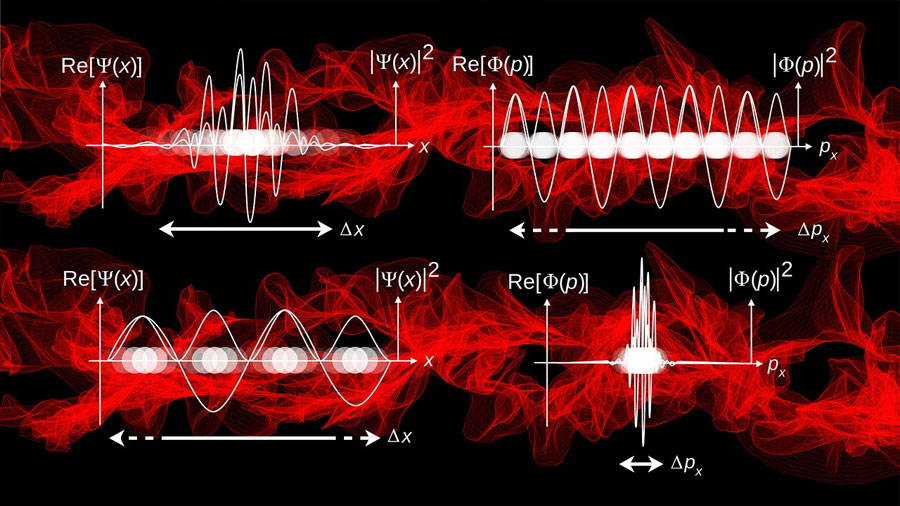
Las leyes de la Mecánica Cuántica se han formulado con mucha precisión. Sabemos exactamente como calcular cualquier cosa que queramos saber. Pero si queremos “interpretar” el resultado, nos encontramos con una curiosa incertidumbre fundamental: que varias propiedades de las partículas pequeñas no pueden estar bien definidas simultáneamente. Por ejemplo, podemos determinar la velocidad de una partícula con mucha exactitud, pero entonces no sabremos exactamente dónde se encuentra; o, a la inversa. Si una partícula tiene “espín” (rotación alrededor de su eje), la dirección alrededor de la cual está rotando (la orientación del eje) no puede ser definida con gran precisión.
No es fácil explicar con sencillez de dónde viene esta incertidumbre, pero hay ejemplos en la vida cotidiana que tienen algo parecido. La altura de un tono y la duración en el tiempo durante el cual oímos el tono tienen una incertidumbre mutua similar.

¿Onda o partícula? ¡Ambas a la vez! ¿Cómo es eso?
Para que las reglas de la Mecánica Cuántica funcionen, es necesario que todos los fenómenos naturales en el mundo de las cosas pequeñas estén regidos por las mismas reglas. Esto incluye a los virus, bacterias e incluso a las personas. Sin embargo, cuanto más grande y más pesado es un objeto más difícil es observar las desviaciones de las leyes del movimiento “clásicas” debidas a la mecánica cuántica.
Me gustaría referirme a esta exigencia tan importante y tan peculiar de la teoría con la palabra “holismo”. Esto no es exactamente lo mismo que entienden algunos filósofos por “holismo”, y que se podría definir como “el todo es más que la suma de las partes”.
Bien, si la Física nos ha enseñado algo, es justamente lo contrario: un objeto compuesto de un gran número de partículas puede ser entendido exactamente si se conocen las propiedades de sus partes (las partículas): basta que uno sepa sumar correctamente (¡y esto no es nada fácil en mecánica cuántica!). Lo que yo entiendo por holismo es que, efectivamente, el todo es la suma de las partes, pero sólo se puede hacer la suma si todas las partes obedecen a las mismas leyes.
Por ejemplo, la constante de Planck, h = 6,626075…x 10 exp. -34 julios segundo, debe ser exactamente la misma para cualquier objeto en cualquier sitio, es decir, debe ser una constante universal.
Las reglas de la mecánica cuántica funcionan tan bien que refutarlas resulta realmente difícil. Los trucos ingeniosos descubiertos por Werner Heisenberg, Paul Dirac y muchos otros mejoraron y completaron las reglas generales. Pero Einstein y otros pioneros tales como Edwin Schrödinger, siempre presentaron serias objeciones a esta interpretación.
Quizá funcione bien, pero ¿dónde está exactamente el electrón, en el punto x o en el punto y? Em pocas palabras, ¿dónde está en realidad?, ¿cuál es la realidad que hay detrás de nuestras fórmulas? Si tenemos que creer a Bohr, no tiene sentido buscar tal realidad. Las reglas de la mecánica cuántica, por sí mismas, y las observaciones realizadas con detectores son las únicas realidades de las que podemos hablar.
Hasta hoy, muchos investigadores coinciden con la actitud pragmática de Bohr. Los libros de historia dicen que Bohr demostró que Einstein estaba equivocado. Pero no son pocos, incluyéndome a mí, los que sospechamos que a largo plazo el punto de vista de Einstein volverá: que falta algo en la interpretación de Copenhague. Las objeciones originales de Einstein pueden superarse, pero aún surgen problemas cuando uno trata de formular la mecánica cuántica para todo el Universo (donde las medidas no se pueden repetir) y cuando se trata de reconciliar las leyes de la mecánica cuántica con las de la Gravitación… ¡Infinitos!
La mecánica cuántica y sus secretos han dado lugar a grandes controversias, y la cantidad de disparates que ha sugerido es tan grande que los físicos serios ni siquiera sabrían por donde empezar a refutarlos. Algunos dicen que “la vida sobre la Tierra comenzó con un salto cuántico”, que el “libre albedrío” y la “conciencia” se deben a la mecánica cuántica: incluso fenómenos paranormales han sido descritos como efectos mecano-cuánticos.
Yo sospecho que todo esto es un intento de atribuir fenómenos “ininteligibles” a causas también “ininteligibles” (como la mecánica cuántica) dónde el resultado de cualquier cálculo es siempre una probabilidad, nunca una certeza.
Claro que, ahí están esas teorías más avanzadas y modernas que vienen abriendo los nuevos caminos de la Física y que, a mi no me cabe la menor duda, más tarde o más temprano, podrá explicar con claridad esas zonas de oscuridad que ahora tienen algunas teorías y que Einstein señalaba con acierto.
¿No es curioso que, cuando se formula la moderna Teoría M, surjan, como por encanto, las ecuaciones de Einstein de la Relatividad General? ¿Por qué están ahí? ¿Quiere eso decir que la Teoría de Einstein y la Mecánica Cuántica podrán al fin unirse en pacifico matrimonio sin que aparezcan los dichosos infinitos?
Bueno, eso será el origen de otro trabajo que también, cualquier día de estos, dejaré aquí para todos ustedes.
Emilio Silvera Vázquez
Abr
17
¡El límite de las teorías!
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (20)
Comments (20)
Presentado en la XIX Edición del

Siempre andamos a vueltas con las teorías, y, tenemos que ser conscientes que las teorías tienen unos límites que están bien determinados. Veamos:
Longitud de Planck: valor = 1.616255(18)×10−35 m7.
Masa de Planck: valor = 2.176434(24)×10−8 kg.
Tiempo de Planck: valor = 5.391247(60)×10−44 s.
Temperatura de Planck: valor = 1.416784(16)×1032 K.
Planck consideró sólo las unidades basadas en las constantes universales G, h, c, y kB para llegar a unidades naturales para longitud, tiempo, masa y temperatura. Sus definiciones difieren de las modernas en un factor de 2π, porque las definiciones modernas utilizan ℏ en lugar de h

¿Cuáles son los límites de la teoría cuántica y de la teoría de la relatividad general de Einstein? Afortunadamente, hay una respuesta simple y las unidades de Planck nos dicen cuales son.

Y precisamente esta constante es el segundo motivo por el que no encuentras los muebles en una posición diferente cada vez que entras en el salón.
Supongamos que tomamos toda la masa del universo visible y determinamos su longitud de onda cuántica. Podemos preguntarnos en qué momento esta longitud de onda cuántica del universo visible superará su tamaño. La respuesta es: cuando el universo sea más pequeño en tamaño que la longitud de Planck, es decir, 10-33 centímetros, más joven que el tiempo de Planck 10ˉ⁴³ segundos y supere la temperatura de Planck de 1032 grados. Las unidades de Planck marcan la frontera de aplicación de nuestras teorías actuales. Para comprender en que se parece el mundo a una escala menor que la longitud de Planck tenemos que comprender plenamente cómo se entrelaza la incertidumbre cuántica con la gravedad. Para entender lo que podría haber sucedido cerca del suceso que estamos tentados a llamar el principio del universo, o el comienzo del tiempo, tenemos que penetrar la barrera de Planck. Las constantes de la naturaleza marcan las fronteras de nuestro conocimiento existente y nos dejan al descubierto los límites de nuestras teorías.

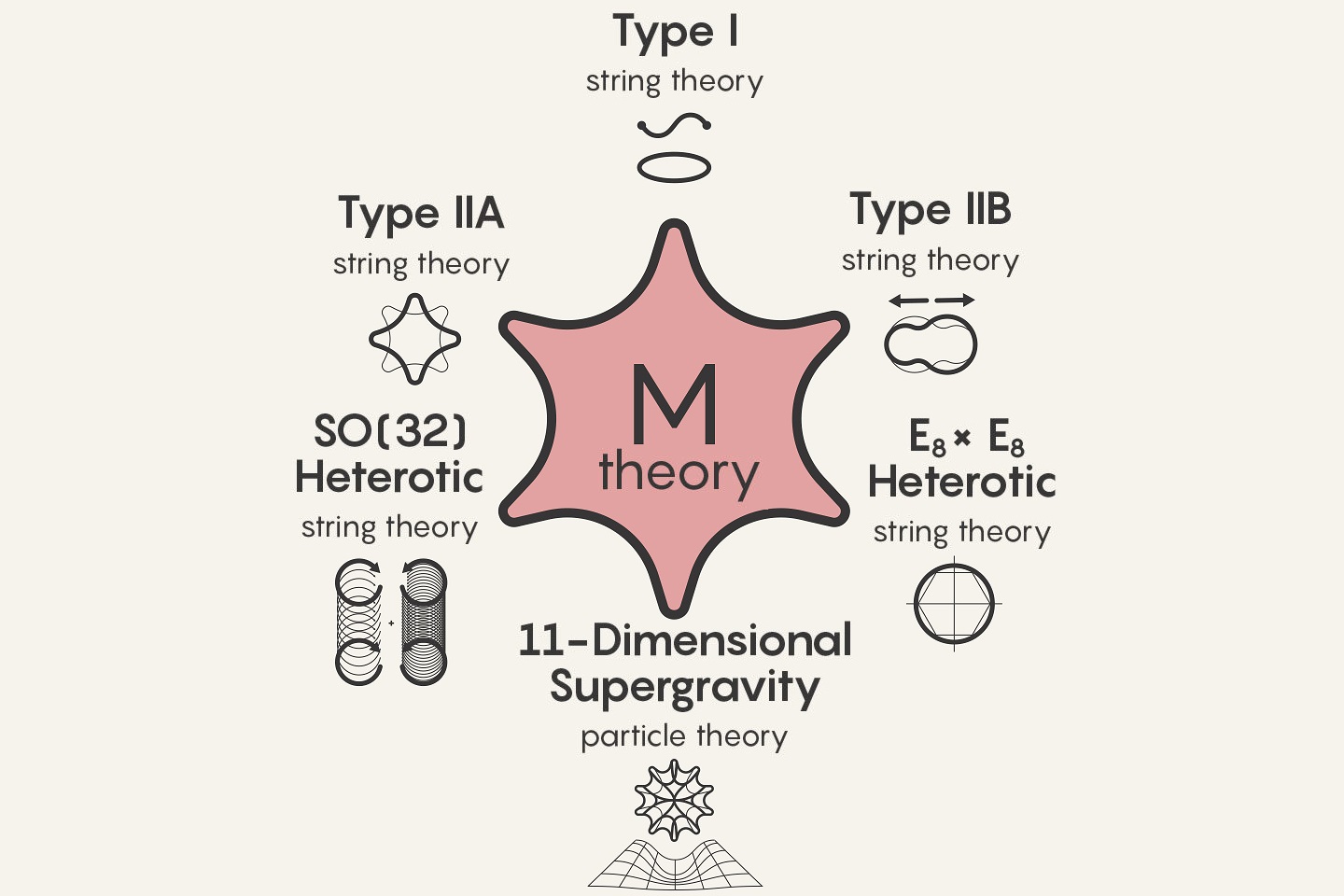
La Gravedad Cuántica, el eslabón perdido para comprender la evolución del Universo. Los físicos teóricos la han encontrado, ellos saben que dicha teoría subyace en la Teoría de Supercuerdas que, desgraciadamente, es inverificable… ¡Por el momento! Se cree que llegar hasta las cuerdas requeriría disponer de la energía de Planck (1019 GeV).
Siendo cierto que en la actualidad no podemos verificar la Teoría de cuerdas, también lo es que, según todos los indicios, en esa Teoría puede subyacer esa otra Teoría Cuántica de la Gravedad, todos sabemos que cuando se juntan la Cuántica de Planck y la Gravedad de Einstein… ¡Aquello hecha chispas! Surgen los infinitos que no se pueden re-normalizar.
Resulta que, cuando los teóricos de las cuerdas trabajan con las ecuaciones de campo de esa teoría, sin que nadie las llame, allí aparecen las ecuaciones de campo de la Relatividad General, ¡por qué será? El viejo Einstein, socarrón, con su cachimba entre los dientes, allá donde se pueda encontrar, estará sonriendo atento a lo que vendrá.
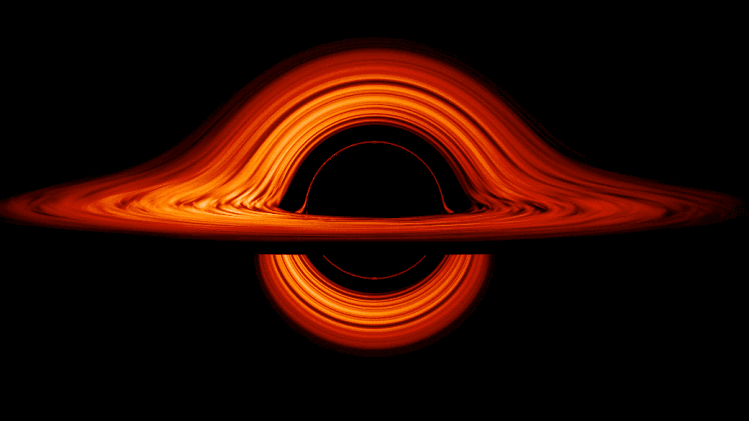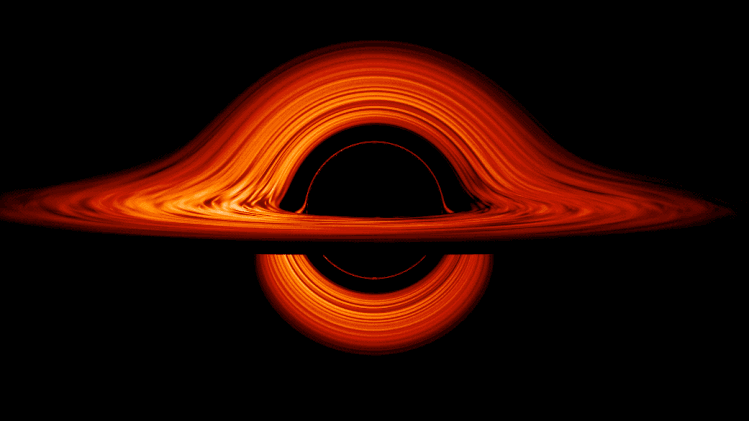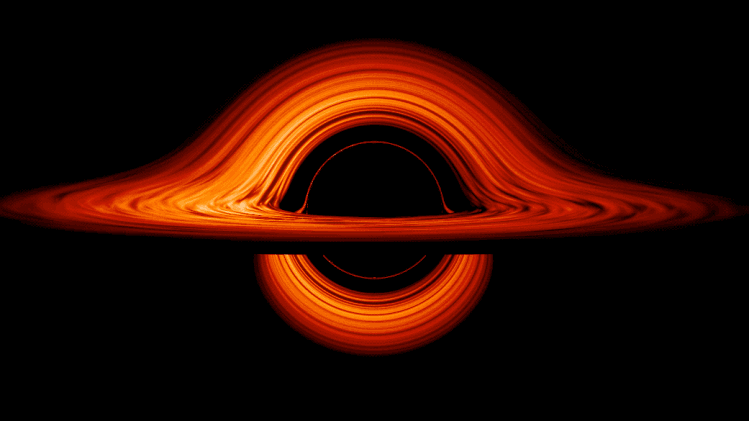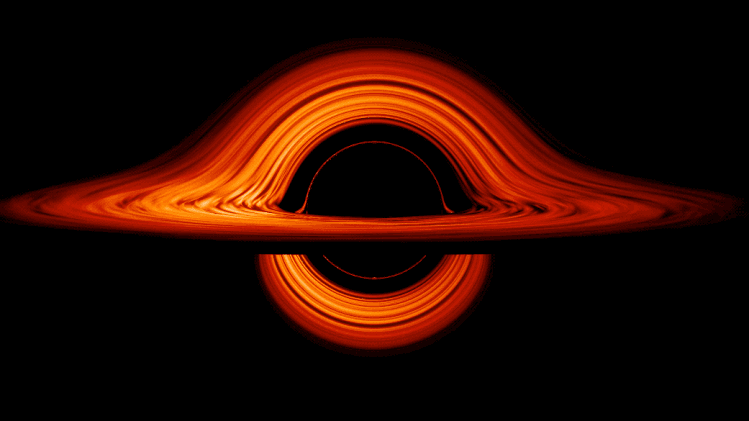
Sí, al ,menos se cree que, el límite de la información está en el horizonte de sucesos de un agujero negro, donde se pierde de forma permanente.
En los intentos más recientes de crear una teoría nueva para describir la naturaleza cuántica de la gravedad ha emergido un nuevo significado para las unidades naturales de Planck. Parece que el concepto al que llamamos “información” tiene un profundo significado en el universo. Estamos habituados a vivir en lo que llamamos “la edad de la información”.

La información puede ser empaquetada en formas electrónicas, enviadas rápidamente y recibidas con más facilidad que nunca antes. Nuestra evolución en el proceso rápido y barato de la información se suele mostrar en una forma que nos permite comprobar la predicción de Gordon Moore, el fundador de Intel, llamada ley de Moore, en la que, en 1.965, advirtió que el área de un transistor se dividía por dos aproximadamente cada 12 meses. En 1975 revisó su tiempo de reducción a la mitad hasta situarlo en 24 meses. Esta es “la ley de Moore” cada 24 meses se obtiene una circuiteria de ordenador aproximadamente el doble, que corre a velocidad doble, por el mismo precio, ya que, el coste integrado del circuito viene a ser el mismo, constante.
Representación gráfica de la obtención experimental de la constante de Planck
Los límites últimos que podemos esperar para el almacenamiento y los ritmos de procesamiento de la información están impuestos por las constantes de la naturaleza. En 1981, el físico israelí, Jacob Bekenstein, hizo una predicción inusual que estaba inspirada en su estudio de los agujeros negros. Calculó que hay una cantidad máxima de información que puede almacenarse dentro de cualquier volumen. Esto no debería sorprendernos. Lo que debería hacerlo es que el valor máximo está precisamente determinado por el área de la superficie que rodea al volumen, y no por el propio volumen. El número máximo de bits de información que puede almacenarse en un volumen viene dado precisamente por el cómputo de su área superficial en unidades de Planck. Supongamos que la región es esférica. Entonces su área superficial es precisamente proporcional al cuadrado de su radio, mientras que el área de Planck es proporcional a la longitud de Planck al cuadrado, 10-66 cm2. Esto es muchísimo mayor que cualquier capacidad de almacenamiento de información producida hasta ahora. Asimismo, hay un límite último sobre el ritmo de procesamiento de información que viene impuesto por las constantes de la naturaleza.
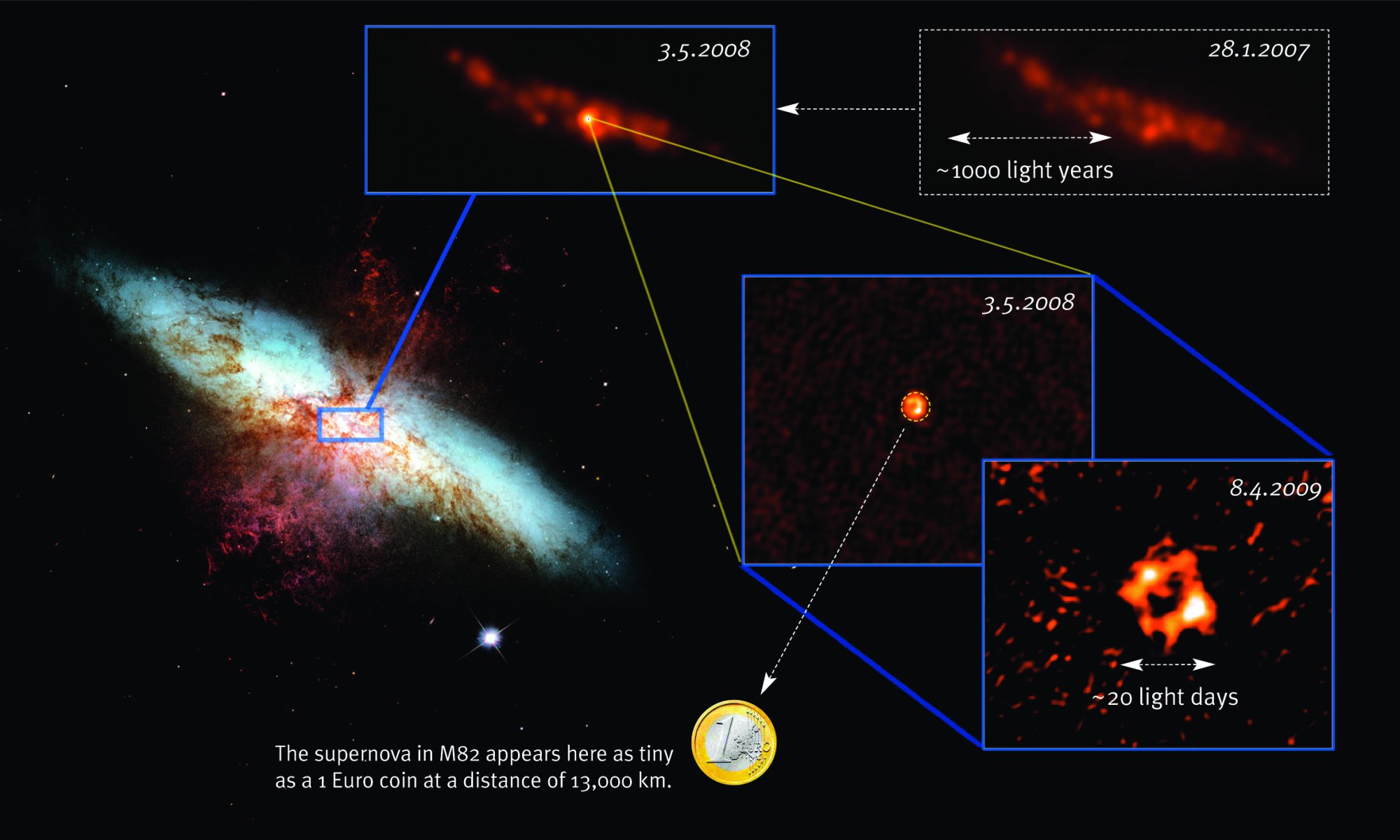

No debemos descartar la posibilidad de que seamos capaces de utilizar las unidades de Planck-Stoney para clasificar todo el abanico de estructuras que vemos en el universo, desde el mundo de las partículas elementales hasta las más grandes estructuras astronómicas. Este fenómeno se puede representar en un gráfico que recree la escala logarítmica de tamaño desde el átomo a las galaxias. Todas las estructuras del universo existen porque son el equilibrio de fuerzas dispares y competidoras que se detienen o compensan las unas a las otras; la atracción y la repulsión. Ese es el equilibrio de las estrellas donde la repulsión termonuclear tiende a expandirla y la atracción (contracción) de su propia masa tiende a comprimirla; así, el resultado es la estabilidad de la estrella. En el caso del planeta Tierra, hay un equilibrio entre la fuerza atractiva de la gravedad y la repulsión atómica que aparece cuando los átomos se comprimen demasiado juntos. Todos estos equilibrios pueden expresarse aproximadamente en términos de dos números puros creados a partir de las constantes e, h, c, G y mprotón.
Desde el vuelo del colibrí, hasta u huracán, erupción volcánica, un Tsunami… 0, un embarazo… ¡Todo es energía!
En nuestro Universo todo es energía y el resultado de dos fuerzas contrapuestas que, al ser iguales en potencia, equilibran el todo y hace posible la estabilidad que podemos contemplar en las estrellas y en los átomos.
| α = 2πe2 / hc ≈ 1/137 |
| αG = (Gmp2)2 / hc ≈ 10-38 |
La Constante física que carece de dimensiones, es decir, un número puro sin unidades asociadas, eso es, una constante adimensional. Su valor numérico es independiente del sistema de unidades que se utilice. Un amuestra es el número 137, el de Alfa, la Constante de estructura fina.
La identificación de constantes adimensionales de la naturaleza como a (alfa) y aG, junto con los números que desempeñan el mismo papel definitorio para las fuerzas débil y fuerte de la naturaleza, nos anima a pensar por un momento en mundos diferentes del nuestro. Estos otros mundos pueden estar definidos por leyes de la naturaleza iguales a las que gobiernan el universo tal como lo conocemos, pero estarán caracterizados por diferentes valores de constantes adimensionales. Estos cambios numéricos alterarán toda la fábrica de los mundos imaginarios. Los átomos pueden tener propiedades diferentes. La gravedad puede tener un papel en el mundo a pequeña escala. La naturaleza cuántica de la realidad puede intervenir en lugares insospechados.
Lo único que cuenta en la definición del mundo son los valores de las constantes adimensionales de la Naturaleza (así lo creían Einstein y Planck). Si se duplica el valor de todas las masas no se puede llegar a saber, porque todos los números puros definidos por las razones de cualquier par de masas son invariables.

Nunca nadie ha explicado el valor numérico de ninguna de las constantes de la naturaleza. ¿Recordáis el 137? Ese número puro, adimensional, que guarda los …
Cuando surgen comentarios de números puros y adimensionales, de manera automática aparece en mi mente el número 137. Ese número encierra más de lo que estamos preparados para comprender; me hace pensar y mi imaginación se desboca en múltiples ideas y teorías. Einstein era un campeón en esta clase de ejercicios mentales que él llamaba “libre invención de la mente”. El gran físico creía que no podríamos llegar a las verdades de la naturaleza sólo por la observación y la experimentación. Necesitamos crear conceptos, teorías y postulados de nuestra propia imaginación que posteriormente deben ser explorados para averiguar si existe algo de verdad en ellos.
Para poner un ejemplo de nuestra ignorancia poco tendríamos que buscar, tenemos a mano miles de millones.

Hablamos de portales cuánticos, fluctuaciones de vacío… Cuerdas y de Taquiones pero…
Un gran Físico nos decía:
“Todos los físicos del mundo, deberían tener un letrero en el lugar más visible de sus casas, para que al mirarlo, les recordara lo que no saben. En el cartel sólo pondría esto: 137. Ciento treinta y siete es el inverso de algo que lleva el nombre de constante de estructura fina”.
Este número guarda relación con la posibilidad de que un electrón emita un fotón o lo absorba. La constante de estructura fina responde también al nombre de “alfa” y sale de dividir el cuadrado de la carga del electrón, por el producto de la velocidad de la luz y la constante de Planck. Tanta palabrería y numerología no significan otra cosa sino que ese solo numero, 137, encierra los misterios del electromagnetismo (el electrón, e–), la relatividad (la velocidad de la luz, c), y la teoría cuántica (la constante de Planck, h).
¡Sabemos tan poco! ¡Son tantas las preguntas que no tienen respuestas! Pocas dudas nos podrían caber si nos propusieran cambiar, todo lo que sabemos por la mitad de lo que ignoramos. Y, como decía el sabio:
“Cuanto más profundizo en el saber de las cosas, más consciente soy delo poco que se. Mis conocimientos son limitados, mi ignorancia infinita.”
Sócrates lo simplificaba con su: “Solo se que no se nada!.
Emilio Silvera Vázquez
Abr
1
Sí, a pesar de todo, algunas cosas no cambian
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (33)
Comments (33)
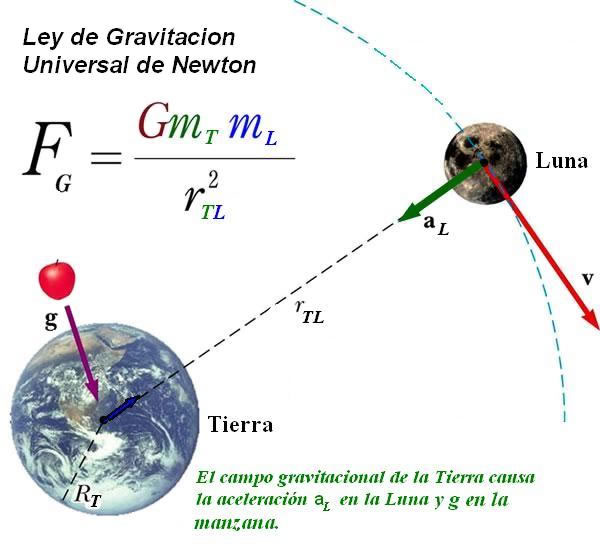
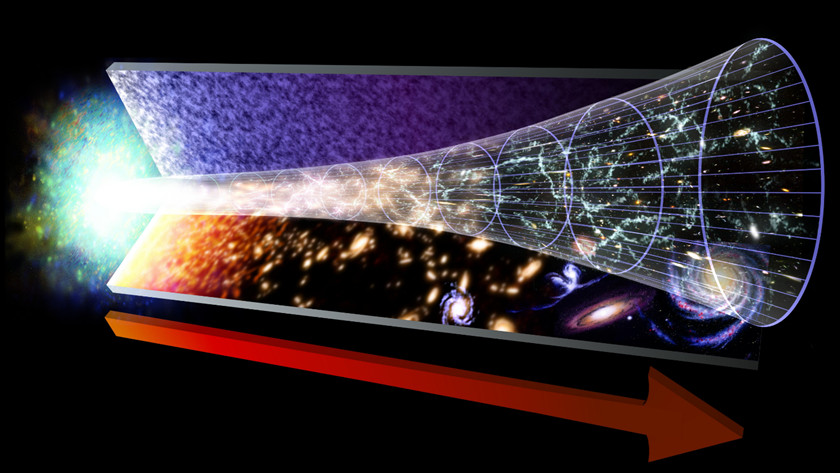


Esos números que representan a las Constantes de la Naturaleza que apareen considerando elementos y codifican secretos profundamente escondidos de la Naturaleza, y, entre esos parámetros naturales, se encuentran la Constante de la Gravitación universal (G), la de la velocidad de la luz en el vacío (c), la Constante de Planck (h), y, también, la Constante de Estructura Fina (α), entre otras.
La Física de los Primeros Principios a la que aludía Aristóteles (La Metafísica)
La Física de Aristóteles: Naturaleza, principios y causas.
Lo que sucede primero, no es necesariamente el principio. Antes de ese “Principio”, suceden algunas cosas que nosotros no hemos podido o sabido percibir. Sin embargo, hay cosas que no cambian nunca.
¿Qué decir de las fluctuaciones cuántics?
Hace tiempo, los sucesos que constituían historias eran las irregularidades de la experiencia. Sabemos que lo que no cambia son las Constantes de la Naturaleza pero, tampoco cambia el Amor de una madre por un hijo, la salida y la puesta del Sol, nuestra curiosidad, y otras muchas cosas que conviven con nosotros en lo cotidiano.
Poco a poco, los científicos llegaron a apreciar el misterio de la regularidad y lo predecible del mundo. Pese a la concatenación de movimientos caóticos e impredecibles de átomos y moléculas, nuestra experiencia cotidiana es la de un mundo que posee una profunda consistencia y continuidad. Nuestra búsqueda de la fuente de dicha consistencia atendía primero a las leyes de la Naturaleza que son las que gobiernan como cambian las cosas. Sin embargo, y al mismo tiempo, hemos llegado a identificar una colección de números misteriosos arraigados en la regularidad de la apariencia. Son las Constantes de la Naturaleza que, como la carga y la masa del electrón o la velocidad de la luz, le dan al Universo un carácter distintivo y lo singulariza de otros que podríamos imaginar. Todo esto, unifica de una vez nuestro máximo conocimiento y también, nuestra infinita ignorancia.
Mar
26
¿Pueden llegarnos mensajes del futuro?
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (5)
Comments (5)
Investigadores proponen una solución a algunos problemas de la Física Cuántica, y se refieren a los viajes en el tiempo o la paradoja del abuelo.

Las curvas temporales abiertas podrían resolver muchos problemas de la Física – NPJ QUANTUM INFORMATION
Un grupo internacional de investigadores, liderados por la Universidad de Singapur, acaba de demostrar que numerosos problemas de la Física Cuántica, hoy por hoy irresolubles, podrían solucionarse fácilmente con un ordenador cuántico que viajara a través de “curvas temporales abiertas”. El trabajo, que ha levantado gran expectación en la comunidad científica, se publica en la revista Nature Quantum Information.
IBM prepara el primer ordenador cuántico. La máquina podría resolver problemas que las computadoras actuales ni se pueden plantear. Cuando esté completada su configuración podrá dar millones de respuestas a un problema planteado en fracciones de segundo.
Hace ya una década que el físico Dave Bacon, que en la actualidad trabaja para Google, demostró que la mejor forma de resolver rápidamente todo un grupo de problemas de la Física (llamados NP-completo) y que traían de cabeza a los matemáticos, era utilizando un ordenador cuántico que se desplazara a través del tiempo. ¿La razón? El hipotético ordenador de Bacon podría moverse con libertad a través de una serie de “curvas cerradas de tiempo”, atajos en el tejido espaciotemporal que se curvan sobre sí mismos. La relatividad general en efecto, permite que dichos caminos puedan existir a través de las contorsiones en el espacio-tiempo que conocemos como agujeros de gusano.
Imaginamos cosas que….
¿Pero para qué enviar un mensaje en el tiempo y bloquearlo después para que nadie pueda leer su contenido? Sencillamente porque el procedimiento podría ser la clave que se necesitaba para resolver problemas que, actualmente, no tienen solución alguna. Y es que incluso un mensaje “sin abrir” puede resultar tremendamente útil, especialmente si los científicos “entrelazan” el mensaje con algún otro sistema antes de enviarlo.
Confirman el entrelazamiento cuántico gracias a la luz de una estrella
“Ahora, una nueva investigación internacional dirigida por David Kaiser, del Instituto Tecnológico de Massachusetts (MIT) en Cambridge, Estados Unidos, en la que han participado físicos de la Universidad de Viena en Austria, y de otras entidades, han resuelto un fallo en uno de los test de la desigualdad de Bell, conocido como libertad de elección (Freedom-of-Choice Loophole). Al resolver este fallo, han conseguido una sólida demostración del entrelazamiento cuántico, según se informa en un comunicado. Los resultados se han publicado en la revista Physical Review Letters.”
Como se sabe, el entrelazamiento cuántico es un efecto extraño que es posible solo en el mundo de la Física subatómica, y consiste en una suerte de “comunicación instantánea” entre partículas que, como si fueran hermanos gemelos diminutos, “saben” al instante lo que le ha sucedido a las demás partículas entrelazadas y reaccionan al instante, sin importar la distancia que las separe. Y lo que proponen los investigadores es precisamente eso, crear un entrelazamiento entre el mensaje enviado a través del tiempo y el sistema del laboratorio. Una correlación que podría alimentar y potenciar la computación cuántica.

Sin embargo, las curvas temporales cerradas conllevan no pocos problemas. En general, los físicos creen que, aunque son teóricamente posibles, algo debe de estar evitando que ese tipo de desplazamientos temporales se produzcan en la Naturaleza. De otra forma, argumentan, podrían darse todo tipo de paradojas, entre ellas la clásica de que alguien podría viajar al pasado y matar a su abuelo, impidiendo así su propia existencia.


Y no solo es la familia la que estaría amenazada por unos viajes así. En efecto, romper el flujo temporal, dejando a un lado el principio de causalidad (un acontecimiento causa otro, que causa otro, y otro…) también puede tener consecuencias para la propia Física cuántica. A lo largo de las dos décadas pasadas los investigadores han mostrado hasta la saciedad que los principios mismos sobre los que se basa la Física Cuántica se quiebran en pedazos ante la presencia de curvas temporales cerradas. Por ejemplo, se puede quebrar el principio de incertidumbre, que establece la imposibilidad de conocer al mismo tiempo determinados pares de magnitudes físicas de una partícula (como la velocidad y el momento). O incluso dejar a un lado el Teorema de no Clonación, que dice que los estados cuánticos no se pueden copiar y que constituye uno de los pilares más sólidos de la Mecánica Cuántica.
Evitar las paradojas

De Historias referidas a Viajes en el Tiempo hemos podido ver muchas en películas fantásticas
Sin embargo, el nuevo trabajo muestra que un ordenador cuántico sería capaz de resolver problemas hasta ahora irresolubles si en vez de por curvas cerradas, se desplazara a través de “curvas temporales abiertas”, que no crean los problemas de causalidad anteriormente descritos. Esto se debe a que dichas curvas no permiten la interacción directa con cualquier cosa en el propio pasado del objeto: las partículas viajeras del tiempo (o, para ser más exactos, los datos que contienen) nunca interaccionarían con sí mismas.
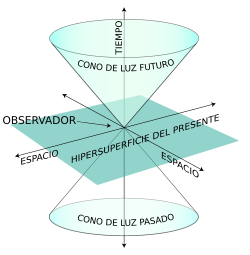
En la Teoría de la Relatividad se admite un espacio tetradimensional, con tres coordenadas espaciales y una temporal. Como no es posible representar en nuestra realidad semejante espacio de cuatro dimensiones, realizaremos una aproximación representando por un plano el espacio tridimensional, más una coordenada temporal. Las soluciones temporales abiertas para expresar la evolución de un punto sería una gráfica del tipo:
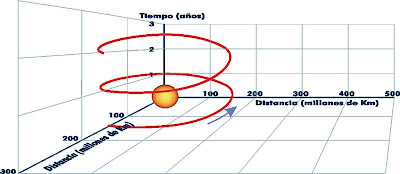
Para Mila Gu, de la Universidad de Singapur y director de la investigación, de esta forma “evitamos las paradojas clásicas, como la de los abuelos, aunque seguimos consiguiendo todos esos resultados extraños”.
“Cada vez que presentamos la idea -afirma por su parte Jayne Thompson, coautor de la investigación- todo el mundo dice que no hay forma de que esto pueda tener un efecto”. Pero sí que la hay. Las partículas enviadas de esta forma a través de un bucle temporal pueden, de hecho, ganar un enorme poder de “super computación”, incluso si jamás interactúan con nada del pasado. “La razón se debe a que algunos datos se almacenan en las correlaciones de entrelazado: y esto es precisamente lo que estamos aprovechando”, asegura Thompson.
Por imaginar…. ¡Que no quede!
Sin embargo, no todos los físicos piensan que estas líneas de tiempo abiertas tengan más posibilidades de manifestarse en el Universo físico que las líneas cerradas. Y pueden que tengan razón. Uno de los principales argumentos en contra de la existencia de curvas temporales cerradas es que nadie, que sepamos, nos ha visitado nunca desde el futuro. Un argumento que, por lo menos, no es válido con las curvas temporales abiertas, ya que en ellas cualquier mensaje procedente del futuro resultaría bloqueado.
Emilio Silvera Vázquez
Mar
24
La Vida de las partículas
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (0)
Comments (0)
:format(jpg)/f.elconfidencial.com%2Foriginal%2Fd1c%2Fb60%2F633%2Fd1cb60633b738916a9a7eab75c82cf6a.jpg)

La Mente: Ese misterio

Una vez que fuimos conscientes de SER, pudimos discernir del por qué de las cosas, asombrados miramos los fenómenos naturales, el día y la noche, la lluvia y la tormenta, los relámpagos. el Sol abrasador, el frío y la nieve, el desborde de los ríos, el Mar y los océanos, las plantas y las flores, los frutos silvestre, la madera de los árboles, la tierra y el agua…
:format(jpg):quality(99):watermark(f.elconfidencial.com/file/bae/eea/fde/baeeeafde1b3229287b0c008f7602058.png,0,275,1)/f.elconfidencial.com/original/c2c/bba/036/c2cbba0360bd68d82954bfe903c67083.jpg)
La mente humana es tan compleja que no todos ante la misma cosa vemos lo mismo. Nos enseñan figuras y dibujos y nos piden que digamos (sin pensarlo) la primera cosa que nos sugiere. De entre diez personas, sólo coinciden tres, los otros siete divergen en la apreciación de lo que el dibujo o la figura les sugiere. Un paisaje puede ser descrito de muy distintas maneras según quién lo pueda contar.

Solo el 1% de las formas de vida que han vivido en la Tierra están ahora presentes, el 99%, por una u otra razón se han extinguido. Sin embargo, ese pequeño tanto por ciento de la vida actual, supone unos cinco millones de especies según algunas estimaciones. La Tierra acoge a todas esas especies u palpita de vida que prolifera por doquier. Hay seres vivos por todas partes y por todos los rincones del inmenso mosaico de ambientes que constituye nuestro planeta encontramos formas de vida, cuyos diseños parecen hechos a propósito para adaptarse a su hábitat, desde las profundidades abisales de los océanos hasta las más altas cumbres, desde las espesas selvas tropicales a las planicies de hielo de los casquetes polares. Se ha estimado la edad de 3.800 millones de años desde que aparecieron los primeros “seres vivos” sobre el planeta (dato de los primeros microfósiles). Desde entonces no han dejado de aparecer más y más especies, de las que la mayoría se han ido extinguiendo. Desde el siglo XVIII en que Carlos Linneo propuso su Systema Naturae no han cesado los intentos por conocer la Biodiversidad…, de la que por cierto nuestra especie, bautizada como Homo sapiens por el propio Linneo, es una recién llegada de apenas 200.000 años.

Ahora, hablaremos de la vida media de las partículas elementales (algunas no tanto). Cuando hablamos del tiempo de vida de una partícula nos estamos refiriendo al tiempo de vida media, una partícula que no sea absolutamente estable tiene, en cada momento de su vida, la misma probabilidad de desintegrarse. Algunas partículas viven más que otras, pero la vida media es una característica de cada familia de partículas.
También podríamos utilizar el concepto de “semivida”. Si tenemos un gran número de partículas idénticas, la semivida es el tiempo que tardan en desintegrarse la mitad de ese grupo de partículas. La semivida es 0,693 veces la vida media.

Si miramos una tabla de las partículas más conocidas y familiares (fotón, electrón muón tau, la serie de neutrinos, los mesones con sus piones, kaones, etc., y, los Hadrones bariones como el protón, neutrón, lambda, sigma, psi y omega, en la que nos expliquen sus propiedades de masa, carga, espín, vida media (en segundos) y sus principales maneras de desintegración, veríamos como difieren las unas de las otras.


Algunas partículas tienen una vida media mucho más larga que otras. De hecho, la vida media difiere enormemente. Un neutrón por ejemplo, vive 10¹³ veces más que una partícula Sigma⁺, y ésta tiene una vida 10⁹ veces más larga que la partícula sigma cero. Pero si uno se da cuenta de que la escala de tiempo “natural” para una partícula elemental (que es el tiempo que tarda su estado mecánico-cuántico, o función de ondas, en evolucionar u oscilar) es aproximadamente 10ˉ²⁴ segundos, se puede decir con seguridad que todas las partículas son bastantes estables. En la jerga profesional de los físicos dicen que son “partículas estables”.
¿Cómo se determina la vida media de una partícula? Las partículas de vida larga, tales como el neutrón y el muón, tienen que ser capturadas, preferiblemente en grandes cantidades, y después se mide electrónicamente su desintegración. Las partículas comprendidas entre 10ˉ¹⁰ y 10ˉ⁸ segundos solían registrarse con una cámara de burbujas, pero actualmente se utiliza con más frecuencia la cámara de chispas. Una partícula que se mueve a través de una cámara de burbujas deja un rastro de pequeñas burbujas que puede ser fotografiado. La Cámara de chispas contiene varios grupos de de un gran número de alambres finos entrecruzados entre los que se aplica un alto voltaje. Una partícula cargada que pasa cerca de los cables produce una serie de descargas (chispas) que son registradas electrónicamente. La ventaja de esta técnica respecto a la cámara de burbujas es que la señal se puede enviar directamente a una computadora que la registra de manera muy exacta.

Una partícula eléctricamente neutra nunca deja una traza directamente, pero si sufre algún tipo de interacción que involucre partículas cargadas (bien porque colisionen con un átomo en el detector o porque se desintegren en otras partículas), entonces desde luego que pueden ser registradas. Además, realmente se coloca el aparato entre los polos de un fuerte imán. Esto hace que la trayectoria de las partículas se curve y de aquí se puede medir la velocidad de las partículas. Sin embargo, como la curva también depende de la masa de la partícula, es conveniente a veces medir también la velocidad de una forma diferente.

Una colisión entre un prtón y un antiprotón registrada mediante una cámara de chispas del experimento UA5 del CERN.
En un experimento de altas energías, la mayoría de las partículas no se mueven mucho más despacio que la velocidad de la luz. Durante su carta vida pueden llegar a viajar algunos centímetros y a partir de la longitud media de sus trazas se puede calcular su vida. Aunque las vidas comprendidas entre 10ˉ¹³ y 10ˉ²⁰ segundos son muy difíciles de medir directamente, se pueden determinar indirectamente midiendo las fuerzas por las que las partículas se pueden transformar en otras. Estas fuerzas son las responsables de la desintegración y, por lo tanto, conociéndolas se puede calcular la vida de las partículas, Así, con una pericia ilimitada los experimentadores han desarrollado todo un arsenal de técnicas para deducir hasta donde sea posible todas las propiedades de las partículas. En algunos de estos procedimientos ha sido extremadamente difícil alcanzar una precisión alta. Y, los datos y números que actualmente tenemos de cada una de las partículas conocidas, son los resultados acumulados durante muchísimos años de medidas experimentales y de esa manera, se puede presentar una información que, si se valorara en horas de trabajo y coste de los proyectos, alcanzaría un precio descomunal pero, esa era, la única manera de ir conociendo las propiedades de los pequeños componentes de la materia.
Que la mayoría de las partículas tenga una vida media de 10ˉ⁸ segundos significa que son ¡extremadamente estables! La función de onda interna oscila más de 10²² veces/segundo. Este es el “latido natural de su corazón” con el cual se compara su vida. Estas ondas cuánticas pueden oscilar 10ˉ⁸ x 10²², que es 1¹⁴ o 100.000.000.000.000 veces antes de desintegrarse de una u otra manera. Podemos decir con toda la seguridad que la interacción responsable de tal desintegración es extremadamente débil.

Se habla de ondas cuánticas y también, de ondas gravitacionales. Las primeras han sido localizadas y las segundas están siendo perseguidas.
Aunque la vida de un neutrón sea mucho más larga (en promedio un cuarto de hora), su desintegración también se puede atribuir a la interacción débil. A propósito, algunos núcleos atómicos radiactivos también se desintegran por interacción débil, pero pueden necesitar millones e incluso miles de millones de años para ello. Esta amplia variación de vidas medias se puede explicar considerando la cantidad de energía que se libera en la desintegración. La energía se almacena en las masas de las partículas según la bien conocida fórmula de Einstein E = Mc². Una desintegración sólo puede tener lugar si la masa total de todos los productos resultantes es menor que la masa de la partícula original. La diferencia entre ambas masas se invierte en energía de movimiento. Si la diferencia es grande, el proceso puede producirse muy rápidamente, pero a menudo la diferencia es tan pequeña que la desintegración puede durar minutos o incluso millones de años. Así, lo que determina la velocidad con la que las partículas se desintegran no es sólo la intensidad de la fuerza, sino también la cantidad de energía disponible.


Si no existiera la interacción débil, la mayoría de las partículas serían perfectamente estables. Sin embargo, la interacción por la que se desintegran las partículas π°, η y Σ° es la electromagnética. Se observará que estas partículas tienen una vida media mucho más corta, aparentemente, la interacción electromagnética es mucho más fuerte que la interacción débil.
Durante la década de 1950 y 1960 aparecieron tal enjambre de partículas que dio lugar a esa famosa anécdota de Fermi cuando dijo: “Si llego a adivinar esto me hubiera dedicado a la botánica.”
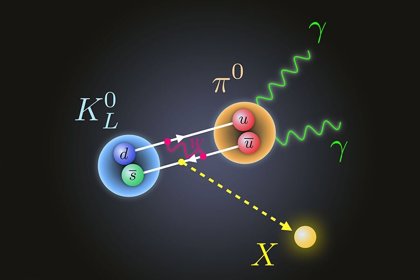
Si la vida de una partícula es tan corta como 10-23 segundos, el proceso de desintegración tiene un efecto en la energía necesaria para producir las partículas ante de que se desintegre. Para explicar esto, comparemos la partícula con un diapasón que vibra en un determinado modo. Si la “fuerza de fricción” que tiende a eliminar este modo de vibración es fuerte, ésta puede afectar a la forma en la que el diapasón oscila, porque la altura, o la frecuencia de oscilación, está peor definida. Para una partícula elemental, esta frecuencia corresponde a su energía. El diapasón resonará con menor precisión; se ensancha su curva de resonancia. Dado que para esas partículas extremadamente inestable se miden curvas parecidas, a medida se las denomina resonancias. Sus vidas medias se pueden deducir directamente de la forma de sus curvas de resonancia.

Bariones Delta. Un ejemplo típico de una resonancia es la delta (∆), de la cual hay cuatro especies ∆ˉ, ∆⁰, ∆⁺ y ∆⁺⁺(esta última tiene doble carga eléctrica). Las masas de las deltas son casi iguales 1.230 MeV. Se desintegran por la interacción fuerte en un protón o un neutrón y un pión.
Existen tanto resonancias mesónicas como bariónicas . Las resonancias deltas son bariónicas. Las resonancias deltas son bariónicas. (También están las resonancias mesónicas rho, P).

Las resonancias parecen ser solamente una especie de versión excitada de los Hadrones estable. Son réplicas que rotan más rápidamente de lo normal o que vibran de diferente manera. Análogamente a lo que sucede cuando golpeamos un gong, que emite sonido mientras pierde energía hasta que finalmente cesa de vibrar, una resonancia termina su existencia emitiendo piones, según se transforma en una forma más estable de materia.
Por ejemplo, la desintegración de una resonancia ∆ (delta) que se desintegra por una interacción fuerte en un protón o neutrón y un pión, por ejemplo:
∆⁺⁺→р + π⁺; ∆⁰→р + πˉ; o п+π⁰
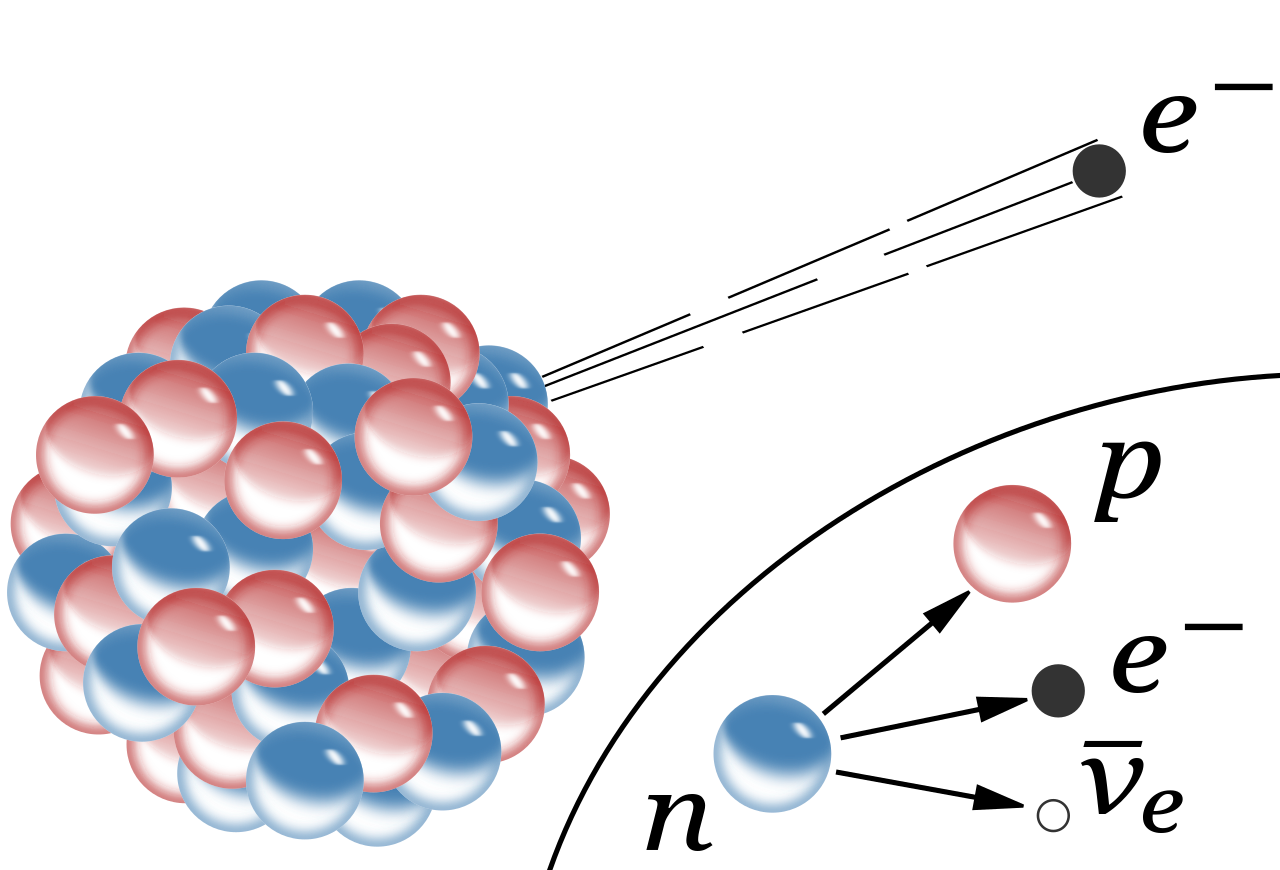
En la desintegración de un neutrón, el exceso de energía-masa es sólo 0,7 MeV, que se puede invertir en poner en movimiento un protón, un electrón y un neutrino. Un Núcleo radiactivo generalmente tiene mucha menos energía a su disposición.
El estudio de los componentes de la materia tiene una larga historia en su haber, y, muchos son los logros conseguidos y muchos más los que nos quedan por conseguir, ya que, nuestros conocimientos de la masa y de la energía (aunque nos parezca lo contrario), son aún bastante limitados, nos queda mucho por descubrir antes de que podamos decir que dominamos la materia y sabemos de todos sus componentes. Antes de que eso llegue, tendremos que conocer, en profundidad, el verdadero origen de la Luz que esconde muchos secretos que tendremos que desvelar.

Esperemos que con los futuros experimentos del LHC y de los grandes Aceleradores de partículas del futuro, se nos aclaren algo las cosas y podamos avanzar en el perfeccionamiento del Modelo Estándar de la Física de Partículas que, como todos sabemos es un Modelo incompleto que no contiene a todas las fuerzas de la Naturaleza y, cerca de una veintena de sus parámetros son aleatorios y no han sido explicados. Uno de ellos, el Bosón de Higgs, dicen que ha sido encontrado. Sin embargo, a mí particularmente me quedan muchas dudas al respecto.
Emilio Silvera Vázquez
















 Totales: 75.487.844
Totales: 75.487.844 Conectados: 73
Conectados: 73























 valor = 1.616255(18)×10−35 m7.
valor = 1.616255(18)×10−35 m7. valor = 2.176434(24)×10−8 kg.
valor = 2.176434(24)×10−8 kg. valor = 5.391247(60)×10−44 s.
valor = 5.391247(60)×10−44 s. valor = 1.416784(16)×1032 K.
valor = 1.416784(16)×1032 K.





![La METAFÍSICA de Aristóteles - [RESUMEN fácil + VÍDEOS y EJERCICIO]](https://cdn0.unprofesor.com/es/posts/7/1/5/la_metafisica_de_aristoteles_517_orig.jpg)