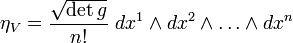Jul
3
La física de partículas y las interacciones fundamentales
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (1)
Comments (1)
El hombre se ha preguntado durante largo tiempo, “¿de qué está hecho el mundo?” Demócrito de Abdera nos hablaba del “átomo” y Empédocles de “elemenmtos”, otros, se referían a la sustancia cósmica a la que llamaban Ylem, aquella “semilla” primera que daría lugar a la venida de la materia. ¿No será el Ylem, lo que hoy llaman materia oscura?
Ahora sabemos que, no sólo nuestro mundo, sino todo el inmenso Universo, está hecho de pequeños objetos infinitesimales a las que hemos denominado partículas sub-atómicas y que forman varias familias. Unas son más elementales que otras y según, a qué familia pertenezcan, atienden o se rigen por una u otra fuerza elemental.
“Esquema de principios de siglo XX para un átomo de helio, mostrando dos protones (en rojo), dos neutrones (en verde) y dos electrones.”

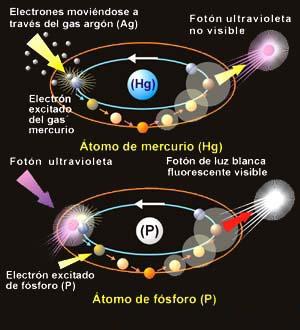
Son los constituyentes fundamentales de toda la materia del Universo (por lo menos de toda la materia conocida y que podemos detectar formando estrellas y mundos, galaxias o seres vivos). Hemos podido llegar a saber que, de esas briznas de materia se forman los núcleos que, rodeados de electrones conforman los átomos de la materia.

Los grupos de átomos conforman las moléculas que son las unidades fundamentales de los compuestos químicos pero, comencemos por los núcleos atómicos:

Muchas son las veces que aquí mismo he podido explicar, que los quarks u y d se hallan en el interior de los nucleones y, por tanto, su habitat está en los núcleos atómicos donde se encuentran confinados y, en realidad, no intervienen directamente en las propiedades de los núcleos. Sin embargo, no podemos olvidar que la fuerza nuclear fuerte está ahí reteniendo a los Quarks por medio de losGgluones y, eso hace que, el núcleo sea estable.
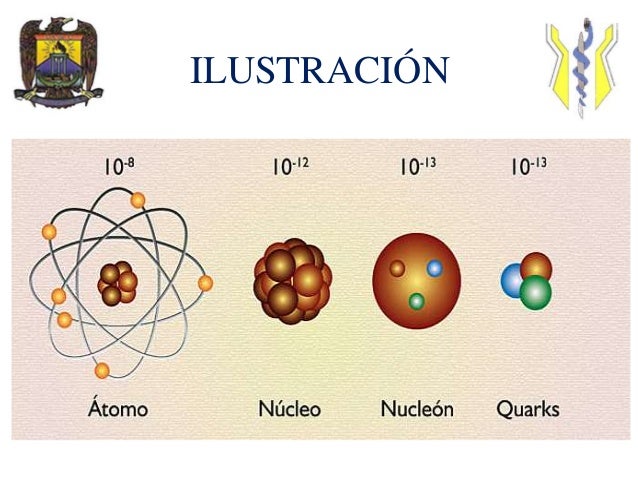
Los núcleos atómicos constituyen un tipo de materia que, aisladamente, de forma individual (si exceptuamos el protón), siempre están en ambientes muy energéticos, por ejemplo, en el interior de las estrellas. En nuestro entorno terráqueo, es raro encontrar núcleos aislados, sino parcial o totalmente confinados dentro de los átomos.
Sabemos que el número de especímenes atómicos es limitado, existiendo ciertas razones para suponer que hacia el número atómico 173 los correspondientes núcleos serían inestables, no por razones intrínsecas de inestabilidad “radiactiva” nuclear, sino por razones relativistas. Ya señalé en otros escritos que, el número de especies atómicas, naturales y artificiales, es de unos pocos miles, en cambio, el número de moléculas conocidas hasta ahora comprenden unos pocos millones de especímenes, aumentando continuamente el número de ellas gracias a la síntesis que se lleva a cabo en numerosos laboratorios repartidos por todo el mundo.
Una molécula es una estructura, con individualidad propia, constituida por un conjunto de núcleos y sus electrones. La molécula más sencilla es la de Hidrógeno que tiene dos electrones, hasta las más complejas como las de las proteínas, con muchos miles de ellos, existen toda una gama de varios millones. Esta extraordinaria variedad de especies moleculares contrasta con la de las especies nucleares e incluso atómicas.
Molécula de Agua
Silicio
Desde el punto de vista de la información, las especies moleculares la poseen en mucho mayor grado que las nucleares o atómicas. Dejando aparte los núcleos, la información que soportan los átomos se podría atribuir a la distribución de su carga eléctrica, y en particular a los electrones más débilmente ligados. Concretando un poco más, se podría admitir que la citada información la aportan los orbitales atómicos, pues son precisamente estos orbitales los que introducen diferencias “geométricas” entre los diferentes electrones “corticales”.
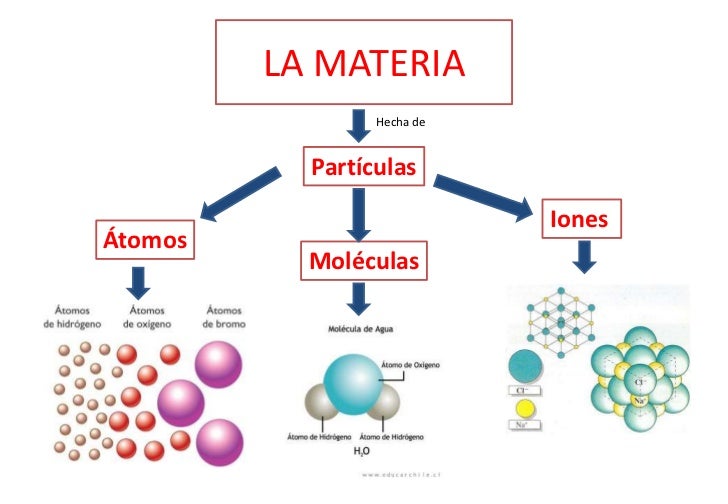
Las partículas forman átomos, los átomos moléculas y las moléculas sustancias y cuerpos que están hechos por la diversa variedad de elementos que conforma la materia conocida y que, en definitiva, sólo son Quarks y Leptones-

“Durante el paso del tiempo una de las mayores incógnitas de la humanidad es saber de qué estamos hechos. Muchas filosofías antiguas creían eran un conjunto de elementos como el agua, el aire, el fuego y la tierra por mencionar algunos. Hoy en día los físicos creen que estamos formados por doce partículas fundamentales los quarks y leptones.”
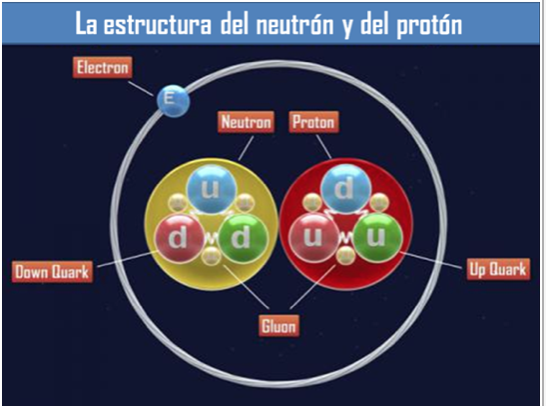
Con los Quarks formados en tripletes se forman los protones y neutrones que son los nucleones situados en el núcleo de los átomos (Hadrones de la rama barionica), otros hadrones llamados mesones están hechos de un Quarks y un antiquark y sus funciones son otras.
Los quarks y leptones como partículas fundamentales (se cree) no tienen infraestructura y no se puede descomponer en partículas más pequeñas. Estos interactúan a través de cuatro fuerzas para formar así el universo que lo conocemos hoy en día.
Partículas mediadoras de la fuerza nuclear débil

La primera imagen que se logró de la partícula de luz: El Fotón, la partícula mediadora de todas las interacciones electromagnéticas del Universo.
Los Quarks están confinados dentro de los nucleones (Protones y Neutrones= retenidos por la partícula mediadora llamada Gluón (en la segunda imagen se ve la muestra).

El esquivo Gravitón (si existe), no ha podido ser encontrado, se cree que al ser la Gravedad la más débil de las cuatro fuerzas fundamentales su partícula mediadora el Gravitón es de escala infinitesimal y difícil de detectar.
Estas doce partículas elementales a su vez están mediadas por los intercambios de otro tipo de partículas que pueden referirse como mediadores de fuerza, de estos se conocen cuatro tipos: el “gluón”, “fotón”, “gravitón” y “bosones débiles”. Aunque en realidad, el gravitón aún no ha sido confirmado experimentalmente , pero muchos físicos asumen que existe este mediador.
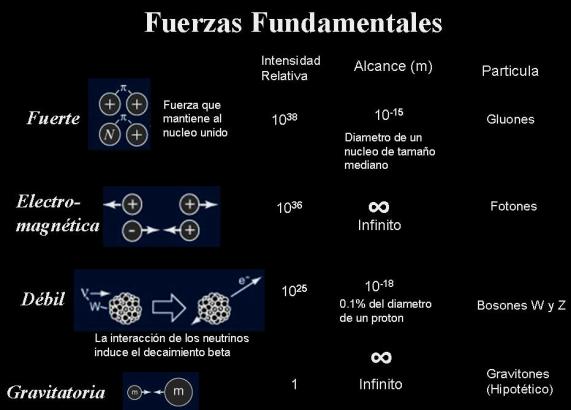
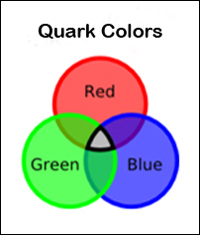
Como un núcleo y un electrón que se atraen entre sí debido a sus cargas eléctricas, los quarks se combinan entre sí por sus cargas de color . La fuerza que la mayoría de los físicos creen que los quarks son los bloques de construcción fundamentales que componen el universo, no se ha observado un quark aislado por sí mismo. Esto es debido a la naturaleza a fuerte es una fuerza que actúa entre cargas de color. Al igual que hay dos tipos de cargas eléctricas, hay tres tipos de cargas de color “rojo”, “azul” y “verde”, análogos a los colores primarios de la luz.
Ahora bien si conoces la teoría de los colores elementales de la luz , se puede recordar que la superposición de los tres colores elementales termina con el blanco. Esta es la razón por la cual un protón y un neutrón están formados por tres quarks. En un protón y un neutrón, un quark tiene un color rojo, otro tiene un color azul y la tercera uno tiene unie ha tenido éxito en aislar un quark, a este fenómeno se llama el confinamiento quark.
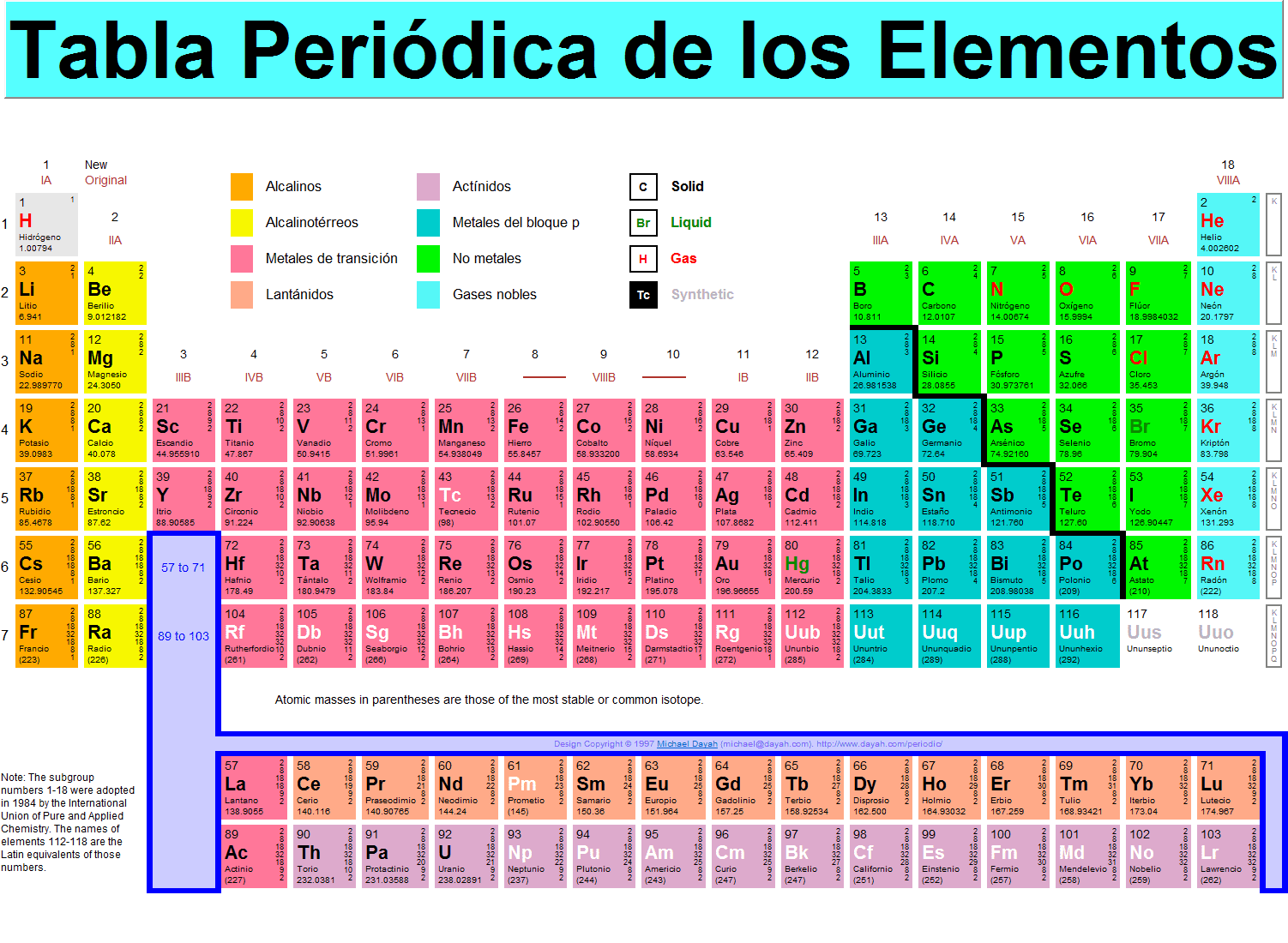
“La tabla periódica de los elementos es una disposición de los elementos químicos en forma de tabla, ordenados por su número atómico (número de protones),2 por su configuración de electrones y sus propiedades químicas. Este ordenamiento muestra tendencias periódicas, como elementos con comportamiento similar en la misma columna.
Dmitri Mendeléyev publicó en 1869 la primera versión de tabla periódica que fue ampliamente reconocida. La desarrolló para ilustrar tendencias periódicas en las propiedades de los elementos entonces conocidos, al ordenar los elementos basándose en sus propiedades químicas,7 si bien Julius Lothar Meyer, trabajando por separado, llevó a cabo un ordenamiento a partir de las propiedades físicas de los átomos.8 Mendeléyev también pronosticó algunas propiedades de elementos entonces desconocidos que anticipó que ocuparían los lugares vacíos en su tabla. Posteriormente se demostró que la mayoría de sus predicciones eran correctas cuando se descubrieron los elementos en cuestión.”
“De los elementos con número atómico entre 1 hasta 92, todos a excepción de cuatro (43Tc, 61Pm, 85At, y 87Fr) se pueden detectar fácilmente en ciertas cantidades en la Tierra, teniendo una vida estable, o unos isótopos de vida media relativamente larga, o se generan como subproductos del uranio. Todos los elementos con gran número atómico tienen una probabilidad alta de haber sido generados de forma artificial, otros son extremadamente raros y por lo tanto han sido descubiertos mediante investigaciones científicas, y otros por el contrario no han existido anteriormente, como el plutonio y el neptunio, de los cuales ninguno tiene existencia natural sobre la tierra.
Todos ellos son radiactivos, con una vida media más corta que la edad de la Tierra, de esta forma es posible que estos elementos, estuvieran presentes en la formación de la tierra. Las trazas de neptunio y plutonio aparecen solo durante las pruebas de las bombas atómicas explotadas en la atmósfera. Tanto el Np como el Pu generados proceden de captura de neutrones en el uranio con dos reacciones posteriores de decaimiento beta.”
“La mayoría de los elementos generados de forma artificial se pueden obtener como elemento sintético vía reacciones nucleares o acelerador de partículas. La vida media de estos elementos suele decrecer con el número atómico.
“Algunos isótopos de los elementos níquel (Ni), cobre (Cu) y zinc (Zn). Como en la mayoría de las tablas de isótopos, los elementos se organizan de abajo hacia arriba según su número atómico creciente, y los isótopos de izquierda a derecha según su masa creciente. Color negro: isótopos estables; azul: isótopos emisores de partículas beta; rojo: isótopos emisores de partículas beta.”
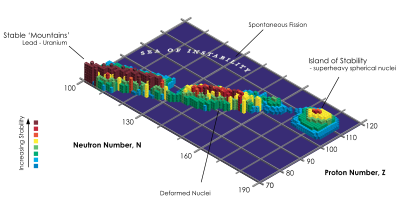
Existen, no obstante excepciones, que incluyen el dubnio y algunos isótopos del curio. El químico Glenn T. Seaborg (Premio Nobel de Química) llegó a crear leyes empíricas capaces de predecir estas anomalías. Todas ellas se categorizan en lo que viene a denominarse como “isla de estabilidad”. Los elementos transuránicos no descubiertos todavía, o que no han sido denominados de forma oficial, emplearán la nomenclatura indicada por la IUPAC. A pesar de ello la denominación de algunos elementos transuránicos en el pasado y hoy en día son fuentes de controversia.·
Lista de los elementos transuránicos
- 93 neptunio Np
- 94 plutonio Pu
- 95 americio Am
- 96 curio Cm
- 97 berkelio Bk
- 98 californio Cf
- 99 einstenio Es
- 100 fermio Fm
- 101 mendelevio Md
- 102 nobelio No
- 103 lawrencio Lr
- elementos transactínidos
- 104 rutherfordio Rf
- 105 dubnio Db
- 106 seaborgio Sg
- 107 bohrio Bh
- 108 hassio Hs
- 109 meitnerio Mt
- 110 darmstadtio Ds
- 111 roentgenio Rg
- 112 copernicio Cn
- 113 nihonio Nh
- 114 flerovio Fl
- 115 moscovio Mc
- 116 livermorio Lv
- 117 teneso Ts
- 118 oganesón Og
- Podemos finalizar para decir que, la materia, esconde muchos secretos que aún, debemos desvelar.
Emilio silvera
Jun
18
¡Increíble mecánica cuántica!
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (16)
Comments (16)

Representación aproximada del átomo de Helio, en el núcleo los protones están representados en rojo y los neutrones en azul. Si lo pudiéramos ver, el núcleo también es simétricamente esférico. En realidad, ese minúsculo granito másico formado por los nucleones (protones y neutrones, que a su vez están formados por quarks inmersos en una nube de gluones), es la verdadera materia, el resto, podríamos decir que son espacios vacíos en los que, los electrones cirdulan a increíbles velocidades formando un campo magnético que hace que el átomo nos parezca enteramente compacto.

El núcleo central que contiene casi toda la masa del átomo y es rodeado por una nube de electrones que, con su carga eléctrica negativa, compensan la positiva de los protones dando estabilidad al átomo

“¿Es esta una galaxia o dos? Esta pregunta salió a la luz en 1950 cuando el astrónomo Arthur Hoag se topó con este inusual objeto extragaláctico. En el exterior hay un anillo dominado por brillantes estrellas azules, mientras que cerca del centro se encuentra una bola de estrellas mucho más rojas que probablemente sean mucho más antiguas. Entre los dos hay una brecha que parece casi completamente oscura. Se desconoce cómo se formó el Objeto de Hoag,”
Todos los objetos que podemos contemplar en el Universo, como la galaxia anillo de la imagen, están formados de pequeñas partículas sub-atómicas de tamaño infinitesimal, los Quarks y los Leptones que son las partículas constituyentes de la materia. Los Quarks se juntan en tripletes (2 up y 1 down, conforman los protones, y, 2 down y 1 up los neutrones) Los Quarks están confinados dentro de los hadrones (nucleones) por una “nube” de Gluones, los Bosones intermediarios de la fuerza nuclear fuerte..
Todo esto queda bien explicado en el Midelo Estándar de la Física de Partículas que incluye tres de las cuatro fuerza. La fuerxza de la Gravedad no quiere juntarse con estas tres. En el gráfico de arriba podéis ver la representación de los Quarks, los Leptones y en vertical los Bosonbes intermediarios de las fuerzas.
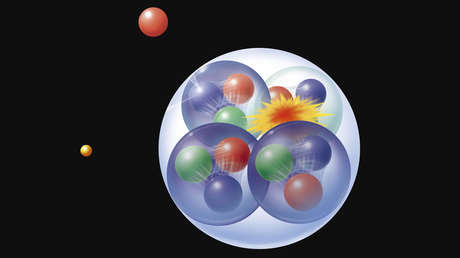
“Científicos confirman al fin que protones y neutrones no tienen la misma estructura dentro de un átomo que fuera de él”
En el centro del átomo pues, se encuentra un pequeño grano compacto aproximadamente 100.000 veces más pequeño que el propio átomo: el núcleo atómico. Su masa, e incluso más aún su carga eléctrica, determinan las propiedades del átomo del cual forma parte.

Debido a la solidez del núcleo parece que los átomos, que dan forma a nuestro mundo cotidiano, son intercambiables entre sí, e incluso cuando interaccionan entre ellos para formar sustancias químicas (los elementos). Pero el núcleo, a pesar de ser tan sólido, puede partirse. Si dos átomos chocan uno contra el otro con gran velocidad podría suceder que los núcleos llegaran a chocar entre sí y entonces, o bien se rompen en trozos, o se funden liberando en el proceso partículas sub-nucleares. La nueva física de la primera mitad del siglo XX estuvo dominada por los nuevos acertijos que estas partículas planteaban.
Viajando a velocidades cercanas a la de la luz, dos partículas pueden chocar de forma violenta y, de ellas, surgen otras partículas más elementales de las que estan conformadas las primeras. Un protón está hecho de dos Quarks up y un Quark down, mientras que un neutrón, está hecho de dos Quarks down y un Quark up.
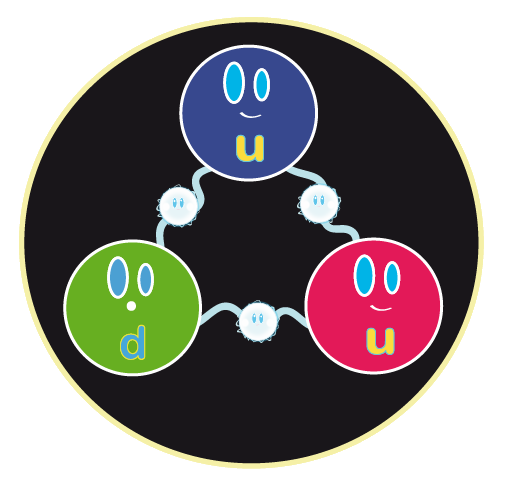
Los Quarks están confinados por los Gluones que no les permite separarse (libertad asintótica). Es la fuerza nuclear fuerte que funciona como un muelle de acero: Su lo estiramos pone ás resistencia, así, cuando los Quarks se quieren separar la fuerza aumenta y los retiene.
Fuerza Fuerte y Fuerza Débil
Pero tenemos la mecánica cuántica; ¿es que no es aplicable siempre?, ¿cuál es la dificultad? Desde luego, la mecánica cuántica es válida para las partículas subatómicas, pero hay más que eso. Las fuerzas con que estas partículas interaccionan y que mantienen el núcleo atómico unido son tan fuertes que las velocidades a las que tienen que moverse dentro y fuera del núcleo están cerca de la velocidad de la luz, c, que es de 299.792,458 Km/s.
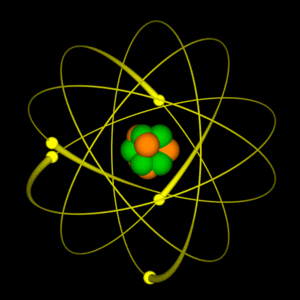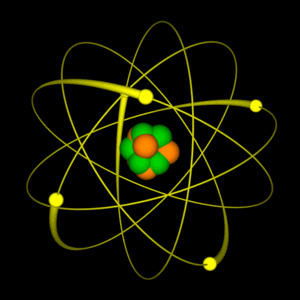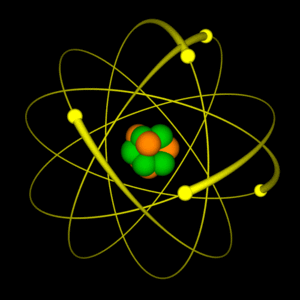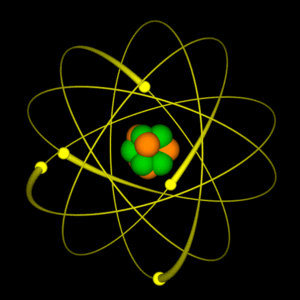
Cuando tratamos con velocidades tan altas se necesita una segunda modificación a las leyes de la física del siglo XIX; tenemos que contar con la teoría de la relatividad especial de Einstein.
Esta teoría también fue el resultado de una publicación de Einstein de 1905. en esta teoría quedaron sentadas las bases de que el movimiento y el reposo son conceptos relativos, no son absolutos, como tampoco habrá un sistema de referencia absoluto con respecto al cual uno pueda medir la velocidad de la luz.
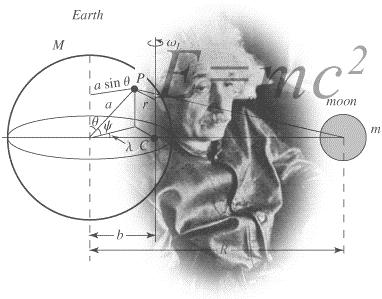
Pero había más cosas que tenían que ser relativas. En esta teoría, la masa y la energía también dependen de la velocidad, como lo hacen la intensidad del campo eléctrico y del magnético. Einstein descubrió que la masa de una partícula es siempre proporcional a la energía que contienen, supuesto que se haya tenido en cuenta una gran cantidad de “energía en reposo” de una partícula cualquiera, como se denota a continuación:
E = M x c2
Esto es, si la masa M se define por la ley de Newton F = M x a.
Como la velocidad de la luz es muy grande, esta ecuación sugiere que cada partícula debe almacenar una cantidad enorme de energía, y en parte esta predicción fue la que hizo que la teoría de la relatividad tuviese tanta importancia para la física (¡y para todo el mundo!). Para que la teoría de la relatividad también sea autoconsistente tiene que ser holista, esto es, que todas las cosas y todo el mundo obedezcan a las leyes de la relatividad. No son sólo los relojes los que se atrasan a grandes velocidades, sino que todos los procesos animados se comportan de la forma tan inusual que describe esta teoría cuando nos acercamos a la velocidad de la luz.

La despedida El recibimiento
El Hermano Astronáuta viajó a la velocidad de la luz y su Tiempo transcurrió más lento que el del gemelo que lo esperó en la Tierra.
El corazón humano es simplemente un reloj biológico y latirá a una velocidad menor cuando viaje en un vehículo espacial a velocidades cercanas a la de la luz. Este extraño fenómeno conduce a lo que se conoce como la “paradoja de los gemelos”, sugerida por Einstein, en la que dos gemelos idénticos tienen diferente edad cuando se reencuentran después de que uno haya permanecido en la Tierra mientras que el otro ha viajado a velocidades relativistas.

La fuerza gravitatoria crea las mareas, mantiene unidos los planetas alrefedor del Sol, las estrellas en las Galaxias, y, nuestros pies pegados al suelo del planeta para que podamos caminar.
Einstein comprendió rápidamente que las leyes de la gravedad también tendrían que ser modificadas para que cumplieran el principio relativista. Para poder aplicar el principio de la relatividad a la fuerza gravitatoria, el principio tuvo que ser extendido de la siguiente manera: no sólo debe ser imposible determinar la velocidad absoluta del laboratorio, sino que también es imposible distinguir los cambios de velocidad de los efectos de una fuerza gravitatoria.
La fuerza de Gravedad incide en todos los objetos celestes, y, hasta la luz, se ve afectada cuando interacciona con cuerpos muy densos como se ha podido comprobar en multitud ee ocasiones. Ne encantaría saber como funciona en verdad la Gravedad, esa fuerza misteriosa que mantiene unidos los planetas alrededor del Sol y a nosotros sobre la superficie terrestre
Einstein comprendió que la consecuencia de esto era que la gravedad hace al espacio-tiempo lo que la humedad a una hoja de papel: deformar la superficie con desigualdades que no se pueden eliminar. Hoy en día se conocen muy bien las matemáticas de los espacios curvos, pero en el época de Einstein el uso de estas nociones matemáticas tan abstractas para formular leyes físicas era algo completamente nuevo, y le llevó varios años encontrar la herramienta matemática adecuada para formular su teoría general de la relatividad que describe cómo se curva el espacio en presencia de grandes masas como planetas y estrellas.

Cuatro imágenes del mismo cuásar rodean una galaxia en un típico espejismo topológico
En vez de ser plano e infinito, el universo podría estar replegado en sí mismo y nuestra percepción distorsionada por rayos luminosos que se multiplican. Como en un espejismo. Algún día sabremos, como es, en realidad nuestro Universo.

La Teoría de un Universo espejo
Einstein tenía la idea en su mente desde 1907 (la relatividad especial la formuló en 1905), y se pasó 8 años buscando las matemáticas adecuadas para su formulación.
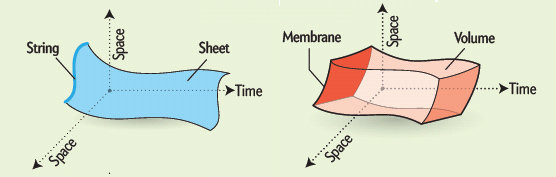
Eso permite hacer que el espacio tenga estructura de Variedad de Riemann y en él pueda definirse la llamada forma de volumen que es la n-forma siguiente:
En esas condiciones el hipervolumen de una región Ω (con frontera suficientemente regular) viene definida por la integral:
Pero dejemos la complejidad matemática y volvamos a la hisotoria que se cuenta con palabras sencillas.
Leyendo el material enviado por un amigo al que pidió ayuda (Marcel Grossman), Einstein quedó paralizado. Ante él, en la primera página de una conferencia dada ante el Sindicato de Carpinteros, 60 años antes por un tal Riemann, tenía la solución a sus desvelos: el tensor métrico de Riemann, que le permitiría utilizar una geometría espacial de los espacios curvos que explicaba su relatividad general.

De la lección de Riemann se deduce que en espacios multidimensionales se crea el principio de que el espacio múltiple (de más dimensiones) unifica las leyes de la naturaleza encajándolas en el tensor métrico como piezas de un rompecabezas N-dimensional. Riemann anticipó otro desarrollo de la física; fue uno de los primeros en discutir espacios múltiples y conexos, o agujeros de gusano.

La carga positiva de los protones es compensada por la negativa de los electrones
No está mal que en este punto recordemos la fuerza magnética y gravitatoria que nos puede ayudar a comprender mejor el comportamiento de las partículas subatómicas. El electromagnetismo, decíamos al principio, es la fuerza con la cual dos partículas cargadas eléctricamente se repelen (si sus cargas son iguales) o se atraen (si tienen cargas de signo opuesto).
La interacción magnética es la fuerza que experimenta una partícula eléctricamente cargada que se mueve a través de un campo magnético. Las partículas cargadas en movimiento generan un campo magnético como, por ejemplo, los electrones que fluyen a través de las espiras de una bobina.+

Un electrón y un protón se atraen de dos maneras, por un lado a causa de que el primero tiene carga eléctrica positiva y el segundo negativa, y ya se sabe que cargas contrarias se atraen. Por el otro, a causa de sus propias masas, como efecto de la fuerza de la gravedad. Se puede calcular que la atracción causada por las cargas eléctricas es aproximadamente “10 elevado a 40” veces mayor que la atracción gravitatoria.


Las fuerzas magnéticas y eléctricas están entrelazadas. En 1873, James Clerk Maxwell consiguió formular las ecuaciones completas que rigen las fuerzas eléctricas y magnéticas, descubiertas experimentalmente por Michael Faraday. Se consiguió la teoría unificada del electromagnetismo que nos vino a decir que la electricidad y el magnetismo eran dos aspectos de una misma cosa.
La interacción es universal, de muy largo alcance (se extiende entre las estrellas), es bastante débil. Su intensidad depende del cociente entre el cuadrado de la carga del electrón y 2hc (dos veces la constante de Planck por la velocidad de la luz). Esta fracción es aproximadamente igual a 1/137’036…, o lo que llamamos α y se conoce como constante de estructura fina.
La fuerza de Gravedad y la electromagnética tienen alcance infinitos (Se debilitan con la distancia)
En general, el alcance de una interacción electromagnética es inversamente proporcional a la masa de la partícula mediadora, en este caso, el fotón, sin masa.
También antes hemos comentado sobre la interacción gravitatoria de la que Einstein descubrió su compleja estructura y la expuso al mundo en 1915 con el nombre de teoría general de la relatividad, y la relacionó con la curvatura del espacio y el tiempo. Sin embargo, aún no sabemos cómo se podrían reconciliar las leyes de la gravedad y las leyes de la mecánica cuántica (excepto cuando la acción gravitatoria es suficientemente débil).

La curvatura del espacio-tiempo se produce por la gravedad que incide y está presente
La teoría de Einstein nos habla de los planetas y las estrellas del cosmos. La teoría de Planck, Heisemberg, Schrödinger, Dirac, Feynman y tantos otros (también el mismo Einstein aportó su granito de arena), nos habla del comportamiento del átomo, del núcleo, de las partículas elementales en relación a estas interacciones fundamentales. La primera se ocupa de los cuerpos muy grandes y de los efectos que causan en el espacio y en el tiempo; la segunda de los cuerpos muy pequeños y de su importancia en el universo atómico. Cuando hemos tratado de unir ambos mundos se produce una gran explosión de rechazo. Ambas teorías son (al menos de momento) irreconciliables.
Todo esto es posible por la Fuerza de la Gravedad que mantiene junto los elementos
- La interacción gravitatoria actúa exclusivamente sobre la masa de una partícula.
- La gravedad es de largo alcance y llega a los más lejanos confines del universo conocido.
- Es tan débil que, probablemente, nunca podremos detectar esta fuerza de atracción gravitatoria entre dos partículas elementales. La única razón por la que podemos medirla es debido a que es colectiva: todas las partículas (de la Tierra) atraen a todas las partículas (de nuestro cuerpo) en la misma dirección.

El gravitón hace tiempo que se ríe de nosotros…y se esconde donde no lo podamos ver.
Hablamos de la partícula mediadora, el hipotético gravitón. Aunque aún no se ha descubierto experimentalmente, sabemos lo que predice la mecánica cuántica: que tiene masa nula y espín 2.
La ley general para las interacciones es que, si la partícula mediadora tiene el espín par, la fuerza entre cargas iguales es atractiva y entre cargas opuestas repulsiva. Si el espín es impar (como en el electromagnetismo) se cumple a la inversa.
Pero antes de seguir profundizando en estas cuestiones hablemos de las propias partículas subatómicas, para lo cual la teoría de la relatividad especial, que es la teoría de la relatividad sin fuerza gravitatoria, es suficiente.
Si viajamos hacia lo muy pequeño tendremos que ir más allá de los átomos, que son objetos voluminosos y frágiles comparados con lo que nos ocupará a continuación: el núcleo atómico y lo que allí se encuentra. Los electrones, que ahora vemos “a gran distancia” dando vueltas alrededor del núcleo, son muy pequeños y extremadamente robustos. El núcleo está constituido por dos especies de bloques: protones y neutrones. El protón (del griego πρώτος, primero) debe su nombre al hecho de que el núcleo atómico más sencillo, que es el hidrógeno, está formado por un solo protón. Tiene una unidad de carga positiva. El neutrón recuerda al protón como si fuera su hermano gemelo: su masa es prácticamente la misma, su espín es el mismo, pero en el neutrón, como su propio nombre da a entender, no hay carga eléctrica; es neutro.
Nos gustaría saber si existe algo más allá de los Quarks, esas infinitesimales partículas “elementales” que conforman protones y neutrones.
La masa de estas partículas se expresa en una unidad llamada mega-electrón-voltio o MeV, para abreviar. Un MeV, que equivale a 106 electrón-voltios, es la cantidad de energía de movimiento que adquiere una partícula con una unidad de carga (tal como un electrón o un protón) cuando atraviesa una diferencia de potencial de 106 (1.000.000) voltios. Como esta energía se transforma en masa, el MeV es una unidad útil de masa para las partículas elementales.

La mayoría de los núcleos atómicos contienen más neutrones que protones. Los protones se encuentran tan juntos en el interior de un núcleo tan pequeño que se deberían repeles entre sí fuertemente, debido a que tienen cargas eléctricas del mismo signo. Sin embargo, hay una fuerza que los mantiene unidos estrechamente y que es mucho más potente e intensa que la fuerza electromagnética: la fuerza o interacción nuclear fuerte, unas 102 veces mayor que la electromagnética, y aparece sólo entre hadrones para mantener a los nucleones confinados dentro del núcleo. Actúa a una distancia tan corta como 10-15 metros.
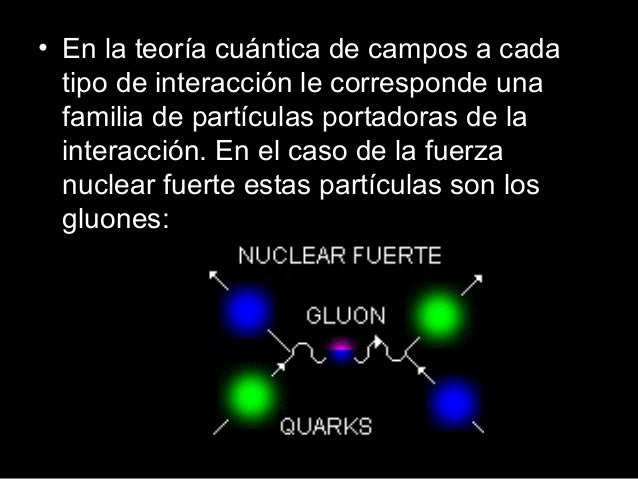
La interacción fuerte está mediada por el intercambio de mesones virtuales, 8 gluones que, como su mismo nombre indica (glue en inglés es pegamento), mantiene a los protones y neutrones bien sujetos en el núcleo, y cuanto más se tratan de separar, más aumenta la fuerza que los retiene, que crece con la distancia, al contrario que ocurre con las otras fuerzas.
Toda la materia del Universo (la Bariónica), emite radiación, es decir, emite energía por medio de fotones, por medio de luz que impregna todos los acontecimientos de transiciones de fase de los objetos y de las fuerzas que conocemos en las que están presentes la emisión y absorción de fotones.
La luz es una manifestación del fenómeno electromagnético y está cuantizada en “fotones”, que se comportan generalmente como los mensajeros de todas las interacciones electromagnéticas. Así mismo, como hemos dejado reseñado en el párrafo anterior, la interacción fuerte también tiene sus cuantos (los gluones). El físico japonés Hideki Yukawa (1907 – 1981) predijo la propiedad de las partículas cuánticas asociadas a la interacción fuerte, que más tarde se llamarían piones. Hay una diferencia muy importante entre los piones y los fotones: un pión es un trozo de materia con una cierta cantidad de “masa”. Si esta partícula está en reposo, su masa es siempre la misma, aproximadamente 140 MeV, y si se mueve muy rápidamente, su masa parece aumentar en función E = mc2. Por el contrario, se dice que la masa del fotón en reposo es nula. Con esto no decimos que el fotón tenga masa nula, sino que el fotón no puede estar en reposo. Como todas las partículas de masa nula, el fotón se mueve exclusivamente con la velocidad de la luz, 299.792’458 Km/s, una velocidad que el pión nunca puede alcanzar porque requeriría una cantidad infinita de energía cinética. Para el fotón, toda su masa se debe a su energía cinética.
En física moderna, el fotón es la partícula elemental responsable de las manifestaciones cuánticas del fenómeno electromagnético. Es la partícula portadora de todas las formas de radiación electromagnética, incluyendo a los rayos gamma, los rayos X, la luz ultravioleta, la luz visible, la luz infrarroja, las microondas, y las ondas de radio.
El fotón tiene una masa invariante cero,y viaja en el vacío con una velocidad constante c. Como todos los cuantos, el fotón presenta tanto propiedades corpusculares como ondulatorias (“dualidad onda-corpúsculo”). Se comporta como una onda en fenómenos como la refracción que tiene lugar en una lente, o en la cancelación por interferencia destructiva de ondas reflejadas; sin embargo, se comporta como una partícula cuando interacciona con la materia para transferir una cantidad fija de energía.
La luz, ese fenómeno natural que nos tiene guardadas muchas sorpresas. Está hecho de fotones, el cuanto de luz, y, le da respuesta al campo gravitatorio de un agujero negro que la engulle, y, si no tiene masa, ¿cómo ocurre eso? ¡sabemos tan poco! (de algunas cosas). Como antes decía, la luz es algo que aún no hemos llegado a comprender en toda su magnitud y, desde luego, esconde secretos que debemos desvelar si pretendemos conocer, de verdad, el Universo.
Representación esquemática de la forma en que el átomo de mercurio (Hg) emite fotones de luz. utravioleta, invisibles para el ojo humano y como el átomo de fósforo (P) los convierte en fotones de luz blanca visible, tal como ocurre en el interior del tubo de una lámpara fluorescente.
Los físicos de partículas suelen encontrarse en sus vidas profesionales con el inconveniente de que aquello con lo que trabajan es tan sumamente pequeño que se vuelve indetectable tanto para el ojo humano como para los más avanzados sistemas de microscopía. Es cierto que en la actualidad se pueden conseguir imágenes en las que se distinguen átomos individuales cuando estos son lo suficientemente grandes, pero de ahí a poder visualizar un sólo protón, o un aún más pequeño electrón, hay un escalón insalvable para la técnica actual.
Los experimentos en el LHC han dejado al descubierto muchos misterios
¿Cómo pueden, pues, los físicos saber que aquello con lo que trabajan no es un mero ente creado por su mente? ¿Cómo se pueden asegurar de que las partículas subatómicas existen en realidad? La respuesta es obvia: a través de su interacción con otras partículas o con otro sistema físico; y un ejemplo extraordinario de ello es el que se puede contemplar en una cámara de niebla.
Los físicos experimentales buscaban partículas elementales en las trazas de los rayos cósmicos que pasaban por estos aparatos “cámaras de niebla”. Así encontraron una partícula coincidente con la masa que debería tener la partícula de Yukawa, el pión, y la llamaron mesón (del griego medio), porque su masa estaba comprendida entre la del electrón y la del protón. Pero detectaron una discrepancia que consistía en que esta partícula no era afectada por la interacción fuerte, y por tanto, no podía ser un pión. Actualmente nos referimos a esta partícula con la abreviatura μ y el nombre de muón, ya que en realidad era un leptón, hermano gemelo del electrón, pero con 200 veces su masa.
Antes de seguir veamos las partículas elementales de vida superior a 10-20 segundos que eran conocidas en el año 1970.
| Nombre | Símbolo | Masa (MeV) | Carga | Espín | Vida media (s) |
| Fotón | γ | 0 | 0 | 1 | ∞ |
| Leptones (L = 1, B = 0) | |||||
| Electrón | e– | 0’5109990 | – | ½ | ∞ |
| Muón | μ– | 105’6584 | – | ½ | 2’1970 × 10-6 |
| Tau | τ | ||||
| Neutrino electrónico | νe | ~ 0 | 0 | ½ | ~ ∞ |
| Neutrino muónico | νμ | ~ 0 | 0 | ½ | ~ ∞ |
| Neutrino tauónico | ντ | ~ 0 | 0 | ½ | ~ ∞ |
| Mesones (L = 0, B = 0) | |||||
| Pión + | π+ | 139’570 | 2’603 × 10-8 | ||
| Pión – | π– | 139’570 | 2’603 × 10-8 | ||
| Pión 0 | π0 | 134’976 | 0’84 × 10-16 | ||
| Kaón + | k+ | 493’68 | 1’237 × 10-8 | ||
| Kaón – | k– | 493’68 | 1’237 × 10-8 | ||
| Kaón largo | kL | 497’7 | 5’17 × 10-8 | ||
| Kaón corto | kS | 497’7 | 0’893 × 10-10 | ||
| Eta | η | 547’5 | 0 | 0 | 5’5 × 10-19 |
| Bariones (L = 0, B = 1) | |||||
| Protón | p | 938’2723 | + | ½ | ∞ |
| Neutrón | n | 939’5656 | 0 | ½ | 887 |
| Lambda | Λ | 1.115’68 | 0 | ½ | 2’63 × 10-10 |
| Sigma + | Σ+ | 1.189’4 | + | ½ | 0’80 × 10-10 |
| Sigma – | Σ– | 1.1974 | – | ½ | 7’4× 10-20 |
| Sigma 0 | Σ0 | 0 | ½ | 1’48 × 10-10 | |
| Ksi 0 | Ξ0 | 1.314’9 | 0 | ½ | 2’9 × 10-10 |
| Ksi – | Ξ– | 1.321’3 | – | ½ | 1’64 × 10-10 |
| Omega – | Ω– | 1.672’4 | – | 1½ | 0’82 × 10-10 |
¡Y hay muchas más…!
Recomendamos visitar la lista “oficial” en http://pdg.lbl.gov/
Para cada leptón y cada barión existe la correspondiente antipartícula, con exactamente las mismas propiedades a excepción de la carga que es la contraria. Por ejemplo, el antiprotón se simboliza con y el electrón con e+. Los mesones neutros son su propia antipartícula, y el π+ es la antipartícula del π–, al igual que ocurre con k+ y k–. El símbolo de la partícula es el mismo que el de su antipartícula con una barra encima. Las masas y las vidas medias aquí reflejadas pueden estar corregidas en este momento, pero de todas formas son muy aproximadas.
Nunca me cansaré de mirar ésta maravilla que, no por pequeña, deja de ser de lo más importante del Universo. De hecho, todo lo que conocemos está conformado por estos infinitesimales objetos. Todo lo grande está hecho de cosas pequeñas.
Los símbolos que se pueden ver algunas veces, como s (extrañeza) e i (isoespín) están referidos a datos cuánticos que afectan a las partículas elementales en sus comportamientos. En la física de partículas, el isospín (espín isotópico o espín isobárico) es un número cuántico relacionado a la interacción fuerte y aplicado a las interacciones del neutrón y del protón. El isospín fue introducido por Werner Hesinmberg para explicar muchas simetrías.
Debo admitir que todo esto tiene que sonar algo misterioso. Es difícil explicar estos temas por medio de la simple palabra escrita sin emplear la claridad que transmiten las matemáticas, lo que, por otra parte, es un mundo secreto para el común de los mortales, y ese lenguaje es sólo conocido por algunos privilegiados que, mediante un sistema de ecuaciones pueden ver y entender de forma clara, sencilla y limpia, todas estas complejas cuestiones.
Estamos huecos y vibramos. Los electrones van a toda prisa; parece que dan siete mil billones (7.000.000.000.000.000 = 7×1015) revoluciones por segundo. A esa increíble velocidad casi puede decirse que cada electrón está simultáneamente en todos los puntos de su órbita. Tienen que ir así de rápidos para generar la suficiente fuerza centrífuga que contrarreste la también fortísima fuerza de atracción eléctrica del núcleo (los protones tienen carga positiva, los electrones negativa).
Si hablamos del espín (o, con más precisión, el momento angular, que es aproximadamente la masa por el radio por la velocidad de rotación) se puede medir como un múltiplo de la constante de Planck, h, dividido por 2π. Medido en esta unidad y de acuerdo con la mecánica cuántica, el espín de cualquier objeto tiene que ser o un entero o un entero más un medio. El espín total de cada tipo de partícula – aunque no la dirección del mismo – es fijo.

El electrón, por ejemplo, tiene espín ½. Esto lo descubrieron dos estudiantes holandeses, Samuel Gondsmit (1902 – 1978) y George Uhlenbeck (1900 – 1988), que escribieron sus tesis conjuntamente sobre este problema en 1972. Fue una idea audaz que partículas tan pequeñas como los electrones pudieran tener espín, y de hecho, bastante grande. Al principio, la idea fue recibida con escepticismo porque la “superficie del electrón” se tendría que mover con una velocidad 137 veces mayor que la de la luz, lo cual va en contra de la teoría de la relatividad general en la que está sentado que nada en el universo va más rápido que la luz, y por otra parte, contradice E=mc2, y el electrón pasada la velocidad de la luz tendría una masa infinita. Hoy día, sencillamente, tal observación es ignorada, toda vez que el electrón carece de superficie.
ENTRE FERMIONES Y BOSONES
Lo que vemos arriba son nubes compuestas por dos isótopos de litio: la de la izquierda está formada a partir de bosones, mientras que la de la derecha está formada a partir de fermiones. A medida que baja la temperatura, los bosones se apilan unos sobre otros, pero los fermiones se mantienen separados, ya sabeis, el Principio de exclusión de Pauli.

Las nubes de átomos se muestran a tres temperaturas diferentes: 810, 510 y 240 nano-Kelvin. Un nano-Kelvin es una temperatura extremadamente fría – es una milmillonésima de grado sobre el cero absoluto, que es -460 grados Fahrenheit. Cuando la temperatura es más fría, uno puede ver que el gas de bosones, que se muestra a la izquierda, se funde en una nube compacta, mientras que el tamaño de los gases de fermiones se estabiliza a un tamaño específico.
La degeneración de los electrones hace que, una estrella como el Sol, al final de su vida, se convierta en una enana blanca en el centro de una Nebulosa Planetaria

Cualquiera de ellas podría ser el Sil dentro de 5.000 millones de años
Esto ilustra el principio de la “degeneración de Fermi”, en que los fermiones no se puede condensar aún más, debido a una ley de la mecánica cuántica – el principio de exclusión de Pauli – que mantiene fermiones idénticos de ocupar el mismo espacio al mismo tiempo. El mismo efecto se estabiliza estrellas enanas blancas contra el colapso bajo su propia atracción gravitatoria, después de haber reducido su núcleo que en principio adquiriera una dimensión definitiva, a los que no estarán ajenos los elementos que son bosones como aportante de una sección mucho mas reducida a igual masa.
La mecánica cuántica nos muestra el extraño y fascinante “universo” de lo muy pequeño. Allí suceden cosas que contradicen el sentido común y que, la naturaleza nos dice que es el menos común de los sentidos.

Si estos son los sentidos, ¿dónde está el llamado “sentido común? ¿Nos indica Einstein su morada?

Sí, ese debe ser el sitio en el que debería estar
Sigamos. Las partículas con espín entero se llaman bosones, y las que tienen espín entero más un medio se llaman fermiones. Consultado los valores del espín en la tabla anterior podemos ver que los leptones y los bariones son fermiones, y que los mesones y los fotones son bosones. En muchos aspectos, los fermiones se comportan de manera diferente de los bosones.
Los fermiones tienen la propiedad de que cada uno de ellos requiere su propio espacio: dos fermiones del mismo tipo no pueden ocupar o estar en el mismo punto, y su movimiento está regido por ecuaciones tales que se evitan unos a otros. Curiosamente, no se necesita ninguna fuerza para conseguir esto. De hecho, las fuerzas entre los fermiones pueden ser atractivas o repulsivas, según las cargas. El fenómeno por el cual cada fermión tiene que estar en un estado diferente se conoce como el principio de exclusión de Pauli. Cada átomo está rodeado de una nube de electrones, que son fermiones (espín ½). Si dos átomos se aproximan entre sí, los electrones se mueven de tal manera que las dos nubes se evitan una a otra, dando como resultado una fuerza repulsiva. Cuando aplaudimos, nuestras manos no se atraviesan pasando la uno a través de la otra. Esto es debido al principio de exclusión de Pauli para los electrones de nuestras manos que, de hecho, los de la izquierda rechazan a los de la derecha.
En contraste con el característico individualismo de los fermiones, los bosones se comportan colectivamente y les gusta colocarse todos en el mismo lugar. Un láser, por ejemplo, produce un haz de luz en el cual muchísimos fotones llevan la misma longitud de onda y dirección de movimiento. Esto es posible porque los fotones son bosones.

Son muchas las maravillas que existen en ese universo de lo pequeño que, en definitiva, es lo que hace que pueda existir lo grande.
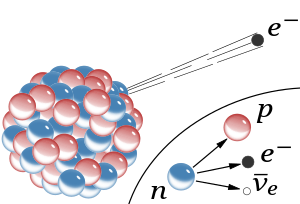
Cuando hemos hablado de las fuerzas fundamentales que, de una u otra forma, interaccionan con la materia, también hemos explicado que la interacción débil es la responsable de que muchas partículas y también muchos núcleos atómicos exóticos sean inestables. La interacción débil puede provocar que una partícula se transforme en otra relacionada, por emisión de un electrón y un neutrino. Enrico Fermi, en 1934, estableció una fórmula general de la interacción débil, que fue mejorada posteriormente por George Sudarshan, Robert Marschak, Murray Gell-Mann, Richard Feynman y otros. La fórmula mejorada funciona muy bien, pero se hizo evidente que no era adecuada en todas las circunstancias.

Richard Feinman, Físico de nacimiento
En 1970, de las siguientes características de la interacción débil sólo se conocían las tres primeras:
- La interacción actúa de forma universal sobre muchos tipos diferentes de partículas y su intensidad es aproximadamente igual para todas (aunque sus efectos pueden ser muy diferentes en cada caso). A los neutrinos les afecta exclusivamente la interacción débil.
- Comparada con las demás interacciones, ésta tiene un alcance muy corto.
- La interacción es muy débil. Consecuentemente, los choques de partículas en los cuales hay neutrinos involucrados son tan poco frecuentes que se necesitan chorros muy intensos de neutrinos para poder estudiar tales sucesos.
- Los mediadores de la interacción débil, llamados W+, W– y Z0, no se detectaron hasta la década de 1980. al igual que el fotón, tienen espín 1, pero están eléctricamente cargados y son muy pesados (esta es la causa por la que el alcance de la interacción es tan corto). El tercer mediador, Z0, que es responsable de un tercer tipo de interacción débil que no tiene nada que ver con la desintegración de las partículas llamada “corriente neutra”, permite que los neutrinos puedan colisionar con otras partículas sin cambiar su identidad.
A partir de 1970, quedó clara la relación de la interacción débil y la electromagnética (electrodébil de Weinberg-Salam).
Abdus Salam (1926-1996)
Físico paquistaní, conocido por sus aportaciones a la comprensión de las interacciones de las partículas elementales. Asistió al Colegio del Gobierno en Lahore y recibió el doctorado en matemáticas y física por la Universidad de Cambridge en 1952. Dio clases en ambas instituciones antes de ser profesor de física teórica en el Colegio Imperial de Ciencias y Tecnología de la Universidad de Londres en 1957, y fue nombrado director del Centro Internacional de Física Teórica de Trieste, Italia, cuando se fundó en 1964. En 1967, junto con el físico estadounidense Steven Weinberg, Salam ofreció una denominada hipótesis de unificación que incorporaba los hechos conocidos sobre las fuerzas electromagnética y nuclear débil.
cunndo se contrastó, la hipótesis mantuvo su vigencia, al contrario de otras muchas hipótesis alternativas.

Steven Weinberg
La interacción fuerte (como hemos dicho antes) sólo actúa entre las partículas que clasificamos en la familia llamada de los hadrones, a los que proporciona una estructura interna complicada. Hasta 1972 sólo se conocían las reglas de simetría de la interacción fuerte y no fuimos capaces de formular las leyes de la interacción con precisión.

Como apuntamos, el alcance de esta interacción no va más allá del radio de un núcleo atómico ligero (10-13 cm aproximadamente). La interacción es fuerte. En realidad, la más fuerte de todas y hace posible mantener estable los átomos para que el Universo sea tal como lo conocemos. Es tan fascinante el mundo de la mecánica cuántica que, la verdadera pena es que aún no lo podamos comprender (del todo) y que mantenga regiones plagadas de oscuridad en las que no hemos podido entrar por falta de esa “luz cegadora” tan necesaria y que, los humanos, llamamos inteligencia.
La fuente del artículo es variada pero, el armazón principal es de Gerard ´t Hooft, el físico premio Nobel de 1999 que, con su manera de ver la Naturaleza de las partículas, abrió nuevos caminos y nos dejó ideas como esa teoría del “universo holográfico”.
¡Es tanto lo que no sabemos!
emilio silvera
Jun
5
El vacío superconducto – La máquina de Higgs-Kibble
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (11)
Comments (11)
El vacío superconductor – La máquina de Higgs-Kibble II

Lo único que no resulta ser lo mismo cuando se mira a través del microscopio (o, en la jerga de la física teórica, cuando se realiza una transformación de escala) es la masa de la partícula. Esto se debe a que el alcance de la fuerza parece mayor a través del microscopìo y, por lo tanto, la masa de la partícula parece ser menor. Nótese que esta situación es la opuesta a la que se presenta en vida corriente donde un grano de arena parece mayor -¿más pesado, por lo tanto?- cuando se observa con un microscopio.

Granos de arena vistos al microscopio
Una consecuencia de todo esto es que en una teoría de Yang-Mills el termino de masa parece desaparecer cuando se realiza una transformación de escala, lo que implica que a través del microscopio se recupera la invariancia gauge. Esto es lo que causa la dificultad con la que se enfrentó Veltman. ¿Se puede observar directamente el potencial vector de Yang-Mills? Parece que puede observa4rse en el mundo de las cosas grandes, pero no en el mundo de lo pequeño. Esto es una contradicción y es una raz´`on por la que ese esquema nunca ha podido funcionar adecuadamente.

En 2009, la empresa canadiense D-Wave Systems, conjuntamente con la NASA, desarrolló un ordenador cuántico de 128 cubits. Rainer contiene 128 dispositivos físicos (pequeños aros de metal niobidio) que a muy baja temperatura actúan como sistemas cuánticos con dos niveles (es decir, cubits) como consecuencia de la superconductividad.
¡Había una salida! Pero ésta procede de una rama muy diferente de la física teórica, la física de los metales a muy bajas temperaturas. A esas temperaturas, los “fenómenos cuánticos” dan lugar a efectos muy sorprendentes, que se describen con teorías cuánticas de campos, exactamente iguales a las que se utilizan en la física de partículas elementales. La física de partículas elementales no tienen nada que ver con la física de bajas temperaturas, pero las matemáticas son muy parecidas.

La primera imagen del átomo de Hidrógeno
En algunos materiales, el “campo” que se hace importante a temperaturas muy bajas podría ser el que describe cómo los átomos oscilan alrededor de sus posiciones de equilibrio, o el que describe a los electrones en este tipo de material. A temperaturas muy baja nos encontramos con los “cuantos” de esos campos. Por ejemplo, el “fonón” es el cuanto del sonido. Su comportamiento recuerda al fotón, el cuanto de la luz, salvo que los números son muy diferentes: los fonones se propagan con la velocidad del sonido, a cientos o quizá miles de metros por segundo, y los fotones lo hacen a la velocidad de la luz que es de 300.000 km/s, ¡aproximadamente un millón de veces más deprisa! Las partículas elementales en las que estamos interesados generalmente tienen velocidades cercanas a las de la luz.

El fonon es la partícula elemental del sonido, como el foton lo es en la luz...
Uno de los “fenómenos cuánticos” más espectaculares que tienen lugar en los materiales muy fríos es la llamada sup-erconductividad, fenómeno consistente en el hecho de que la resistencia que presenta ese material al paso de la corriente eléctrica se hace cero. Una de las consecuencias de ese estado es que el material no admite la más mínima diferencia de potencial eléctrico, porque ésta sería inmediatamente neutralizada por una corriente eléctrica “ideal”. El material tampoco admite la presencia de campos magnéticos porque, de acuerdo con las ecuaciones de Maxwell, la creación del campo magnético está asociada con una corriente eléctrica inducida, que al no encontrar resistencia neutralizaría completamente el campo magnético. Por lo tanto, en el interior de un superconductor no se puede crear ni un campo electrónico ni magnético. Esta situación sólo cambia si las corrientes inducidas son muy elevadas, como ocurre cuando se somete el superconductor a los campos de imanes muy potentes y que perturban el material. No siendo capaz de resistir una fuerza tan brutal, pierde la súper-conductividad y se rinde permitiendo la existencia de un campo magnético en su interior.

¿Pero, qué tiene que ver un superconductor con las partículas elementales? Bien, un material superconductor se puede entender como un sistema en el cual el campo electromagnético es un campo de muy corto alcance. Está siendo apantallado y, sin embargo, es un campo de Maxwell, un campo gauge. ¡Esto es lo que hace interesante un superconductor para alguien que quiera describir la interacción débil entre partículas como una teoría gauge! ¡Qué característica tan bella de la física teórica! Se pueden comparar dos mundos completamente diferentes simplemente porque obedecen a las mismas ecuaciones matemáticas.
¿Cómo funciona un superconductor? La verdadera causa de este fenómeno peculiar la descubrieron John Bardeen, Leon N. Cooper y John R. Schrieffer por lo que recibieron el premio Nobel en 1972). Los electrones de un trozo sólido de material tienen que reunir al mismo tiempo dos condiciones especiales para dar lugar a la superconductividad: la primera es apareamiento y la segunda condensación de Bose.
“Apareamiento” significa que los electrones forman pares y actúan en pares, y los que producen la fuerza que mantiene los pares unidos son los fonones. En cada par, los electrones rotan alrededor de su propio eje, pero en direcciones opuestas, de manera que el par (llamado “par de Cooper”), en su conjunto, se comporta como si no tuviera rotación (“momento angular”). Así, un par de Cooper se comporta como una “partícula” con espín 0 y carga eléctrica.
La “condensación de Bose” es un fenómeno típicamente mecánico-cuántico. Sólo se aplica a partículas con espín entero (bosones). Al igual que los lemmings, los bosones se agrupan juntos en el estado de menor energía posible, Recuérdese que a los bosones les gusta hacer a todos la misma cosa. En este estado todavía se puede mover, pero no pueden perder más energía y, en consecuencia, no sufren ninguna resistencia a su movimiento. Los pares de Cooper se mueven libremente, de manera que pueden crear corrientes eléctricas que no encuentran ninguna resistencia. Un fenómeno parecido tiene lugar en el helio líquido a muy bajas temperaturas. Aquí los átomos de helio forman una condensación de Bose y el líquido que forman puede fluir a través de los agujeros más pequeños sin la más mínima resistencia.
Condensado de Bose-Einstein
Como los electrones por separado tienen espín ⅟₂ no pueden sufrir una condensación de Bose. Las partículas cuyo espín es igual a un entero más un medio (fermiones) tienen que estar en estados cuánticos diferentes debido al principio de exclusión de Pauli. Esta es la razón por la que la superconductividad sólo se puede producir cuando se forman pares. Sí, comprendo que estas afirmaciones le sugerirán varias preguntas y me disculpo por adelantado, pero de nuevo he traducido fórmulas a palabras, lo que implica que el razonamiento pueda parecer poco satisfactorio. ¡Simplemente tome esto como una cierta “lógica cuántica” difícil de manejar! Fueron el belga François Englert, el americano Robert Brout y el inglés Peter Higgs los que descubrieron que la superconductividad podría ser importante para las partículas elementales. Propusieron un modelo de partículas elementales en el cual partículas eléctricamente cargadas, sin espín, sufrían una condensación de Bose. Esta vez, sin embargo, la condensación no tenía lugar en el interior de la materia sino el vacío. Las fuerzas entre las partículas tenían que ser elegidas de tal manera que se ahorrara más energía llenando el vacío de estas partículas que dejándolo vacío. Estas partículas no son directamente observables, pero podríamos sentir el estado, en cuyo espacio y tiempo están moviéndose las partículas de Higgs (como se las conoce ahora) con la mínima energía posible, como si el espacio tiempo estuviera completamente vacío.

Haber encontrado el bosón de Higgs puede resolver el misterio de la composición de masa de todos los objetos. Esta masa está presente en las partículas subatómicas y sin ellas la materia sólida no podría existir. El bosón de Higgs está relacionado a un campo energético, que se llama el campo de Higgs, el mismo que está presente en todo el universo de igual forma como el agua inunda una piscina. Es formando parte de ese campo, que las diversas partículas, como los protones, neutrones, electrones y otras, adquieren su masa. Las partículas más pequeñas encuentran menos dificultades para desplazarse, y las más grandes lo hacen con mayor dificultad. De todas las maneras, quedan muchas por explicar. Fandila nos prguntaba que,dónde adquiere su masa el mismo Bosón de Higgs?
Las partículas de Higgs son los cuantos del “campo de Higgs”. Una característica de este campo es que su energía es mínima cuando el campo tiene una cierta intensidad, y no cuando es nulo. Lo que observamos como espacio vacío no es más que la configuración de campo con la menor energía posible. Si pasamos de la jerga de campos a la de partículas, esto significa que el espacio vacío está realmente lleno de partículas de Higgs que han sufrido una condensación Bose”.
Este espacio vacío tiene muchas propiedades en común con el interior de un superconductor. El campo electromagnético aquí también es de corto alcance. Esto está directamente relacionado con el hecho de que, en tal mundo, el fotón tiene una cierta masa en reposo.
Y aún tenemos una simetría gauge completa, es decir, la invariancia gauge no se viola en ningún sitio. Y así, sabemos cómo transformar un fotón en una partícula “con masa” sin violar la invariancia gauge. Todo lo que tenemos que hacer es añadir estas partículas de Higgs a nuestras ecuaciones.

La razón por la que el efecto de invariancia gauge en las propiedades del fotón es tan diferente ahora es que las ecuaciones están completamente alteradas por la presencia del campo de Higgs en nuestro estado vacío. A veces se dice que “el estado vacío rompe la simetría espontáneamente”. Esto no es realmente correcto, pero el fenómeno está muy relacionado con otras situaciones en las que se produce espontáneamente una rotura de simetría.
Higgs sólo consideró campos electromagnéticos “ordinarios”, pero, desde luego, sabemos que el fotón ordinario en un vacío auténtico no tiene masa en reposo. Fue Thomas Kibble el que propuso hacer una teoría de Yang-Mills superconductora de esta forma, simplemente añadiendo partículas sin espín, con carga de Yang-Mills en vez de carga ordinaria, y suponer que estas partículas podían experimentar una condensación de Bose. Entonces el alcance de las interacciones de Yang-Mills se reduce y los fotones de Yang-Mills se convierten en partículas con espín igual a 1 y masa distinta de cero.

La discontinuidad manifiesta junto con la invariancia de escala (autosemejanza), que presenta la energía de las fluctuaciones del vacío cuántico. Las consecuencias de la existencia del cuanto mínimo de acción fueron revolucionarios para la comprensión del vacío. Mientras la continuidad de la acción clásica suponía un vacío plano, estable y “realmente” vacío, la discontinuidad que supone el cuanto nos dibuja un vacío inestable, en continuo cambio y muy lejos de poder ser considerado plano en las distancias atómicas y menores. El vacío cuántico es de todo menos vacío, en él la energía nunca puede quedar estabilizada en valor cero, está fluctuando sobre ese valor, continuamente se están creando y aniquilando todo tipo de partículas, llamadas por eso virtuales, en las que el producto de su energía por el tiempo de su existencia efímera es menor que el cuanto de acción. Se llaman fluctuaciones cuánticas del vacío y son las responsables de que exista un campo que lo inunda todo llamado campo de punto cero.
Algunos físicos proponen una controvertida teoría en la que un extraño tipo de materia, el Singlet de Higgs, se movería hacia el pasado o el futuro en el LHC. ¡Qué imaginación! Claro que, puestos a imaginar…

Bien sabido es que mientras más profundizamos en el conocimiento de los secretos del mundo que nos rodea, más interrogantes y misterios sin resolver se nos muestran. Cada vez que abrimos una puerta, llegamos a una habitación que tiene otras muchas por abrir. Es la búsqueda incesante del hombre, su insoslayable afán por saber el por qué, el cómo y el cuándo de todas las cosas.
¿Estaremos entrando en una especie de locura?
Bueno…
Por su parte, el científico británico Peter Higgs, de 80 años, que dio su nombre a la llamada “partícula divina” en 1964, afirmó que cree que su Bosón seríaá hallado gracias al Gran Colisionador. “Creo que es bastante probable” dijo pocas horas después de que entrara en funcionamiento el gigantesco acelerador. Y, según parece, se está saliendo con la suya.

De todas las maneras, estaría bien saber, a ciencia cierta, cómo es el campo de Higgs del que toman la masa todas las partículas, y conocer, mediante que sistema se transfieren la masa, o, si cuando las partículas entran en el campo de Higgs e interracionan con él, es el efecto frenado el que les otorga la masa como nos dice nuestro amigo Ramón Marques en su teoría.
emilio silvera
Jun
3
¡La Física! Los Caminos de la Naturaleza.
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (12)
Comments (12)
Einstein se preguntaba a menudo si Dios tuvo alguna elección al crear el universo. Según los teóricos de supercuerdas, una vez que exigimos una unificación de la teoría cuántica y la relatividad general, Dios no tenía elección. La auto-consistencia por sí sola, afirman ellos, debe haber obligado a Dios a crear el universo como lo hizo (todo ello partiendo de la base de que “Dios” estaba allí cuando se produjo el acontecimiento)-

Tenemos tantas dudas que a veces recurrimos a lo divino que, siendo cosa de fe, poco tiene que ver con la ciencia
Escuchar a E. Wittin hablar sobre Física, puede ser un viaje alucinante que nos lleve hacia el futuro que está por llegar. Él es el autor de la Teoría M de cuerdas en la que ha unificado todas las versiones de supersimetría, supergravedad, cuerda heterótica, supercuerdas y demás. Se avanza sin descanso pero, seguimos sin poder verificar de forma experimental. Se dice que esta teoría esta adelantada a su tiempo.
Aunque el perfeccionamiento matemático introducido por la teoría de cuerdas ha alcanzado alturas de vértigo y ha sorprendido a los matemáticos, los críticos de la teoría aún la señalan como su punto más débil. Cualquier teoría, afirman, debe ser verificable. Puesto que ninguna teoría definida a la energía de Planck de 1019 miles de millones de eV es verificable, ¡la teoría de supercuerdas no es realmente una teoría!

Con esa simple fçormula, Planck no dijo la energía que se necesitaba para verificar la teoría de cuerdad, es decir 1019 GeV, y, desgraciadamente, esa energía, de momento, no es de este mundo.
¡Es todo tan complejo! La topología nos dará algunas respuestas y, seguramente, las funciones modulares de Ramunujan también podría tener el derecho a voto en esto de la teoría de cuerdas.
May
21
Tan sencillo y tan complejo
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (0)
Comments (0)

Nunca podremos dejar de maravillarnos ante las “cosas” que puede realizar la Naturaleza para conseguir sus fines. y, como dice Leonard Susskind, para comprender la realidad en sus niveles más elementales, basta con conocer el comportamiento de dos elementos: el electrón y el fotón. Todo el argumento de la Electrodinámica Cuántica gira en torno a un proceso fundamental:
¡La emisión de un único fotón por un único electrón!
Cuando el movimiento de un electrón es alterado súbitamente, puede responder desprendiendo un fotón. La emisión de un fotón es el suceso básico de la mecánica cuántica.
“Cuando un electrón se encuentra en un nivel de energía elevado, tiende a caer espontáneamente a un nivel de energía inferior con la subsiguiente emisión de luz. … El proceso contrario, aquel en el que el fotón se absorbe induciendo la subida de un electrón a un nivel de energía superior, se llama absorción estimulada.”
Toda la luz visible que vemos, así como las ondas de radio, la radiación infrarroja y los rayos X, está compuesta de fotones que han sido emitidos por electrones, ya sea en el Sol, el filamento de una bombilla, una antena de radio o un aparato de rayos.
Claro que, los electrones no son las únicas partículas que pueden emitir fotones. Cualquier partícula eléctricamente cargada puede hacerlo, incluido el protón. Esto significa que los fotones pueden saltar entre dos protones o incluso entre un protón y un electrón. Este hecho es de enorme importancia para toda la ciencia y la vida en general. El intercambio continuo de fotones entre el núcleo y los electrones atómicos proporciona la fuerza que mantiene unido el átomo.

Sin estos fotones saltarines, el átomo se desharía y toda la materia dejararía de existir, y, no podemos olvidar que, también nosotros, los seres vivos… ¡Somos materia!
Decía que la Naturaleza hace las cosas más inverosímiles y de la manera más económica posible y, ha sabido crear esos objetos pequeñitos (infinitesimales como lo son las partículas subatómicas) que ha agrupado en familias. Los electrones son de la Familia de los Leptones y son fermiones, mientras que los fotones pertenecen a la familia de los Bosones. Los primeros no quieren estar juntos y se repelen cuando andan cerca los unos de los otros, mientras que los segundos, están encantados de la vida cuando se juntan muchos, de hecho, la Luz es un conjunto de fotones que, realmente, ilumina nuestras vidas.
Veamos el Efecto fotoeléctrico
El fenómeno del efecto fotoeléctrico es una forma de mostrar el carácter corpuscular de la radiación electromagnética al interactuar la radiación y la materia, para lo cual se requiere fotoconductividad que hace referencia al aumento de la conductividad eléctrica de la materia o en diodos provocada por la luz y la presencia del efecto fotovoltaico que implica una transformación parcial de la energía luminosa en energía eléctrica.
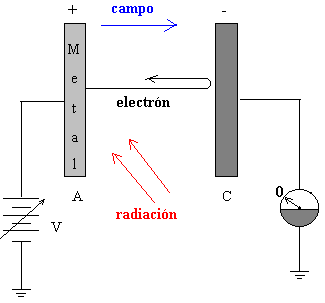
Para que ocurra el efecto fotoeléctrico descubierto por Heinrich Hertz en 1887 (Que Einstein desarrolló en su famoso trabajo de 1.905 que le valió el Nóbel de Física de 1.923), se observa la liberación de los electrones de enlaces de átomos y moléculas de la sustancia bajo acción de la luz: visible, infrarroja y ultravioleta; en sus experimentos halla un arco que se forma entre dos electrodos conectados a alta tensión alcanzando distancias mayores cuando se ilumina con luz ultravioleta que cuando se deja en la oscuridad.
Se caracteriza por:
El experimento consiste en colocar una placa metálica en un recipiente de vidrio al cual que se ha realizado un vacio, existe otra placa que hace de colectar de partículas cargadas. Al hacer incidir un haz monocromático de radiación electromagnética se produce un desprendimiento de electrones de ella. Si se presenta una diferencia de potencial positivo entre el colector y la placa los electrones serán acelerados hacia él y se registrará una corriente: fotocorriente; sin embargo si se aplica un potencial negativo al colector, los fotoelectrones serán repelidos y llegarán solamente los que alcancen una energía mayor que el potencial.

La energía mínima necesaria para arrancar un electrón (trabajo de extracción) de una lámina de plata es 7,52 10-19 J.
Es así que ∅ es la energía mínima necesaria para que un electrón escape del metal.
















 Totales: 74.207.845
Totales: 74.207.845 Conectados: 38
Conectados: 38























![g = \sum_{i,j=1}^n g_{ij} \ dx^i \otimes dx^j, \qquad \qquad [g_{ij}] = \begin{pmatrix} g_{11} & g_{12} & ... & g_{1n} \\ g_{21} & g_{22} & ... & g_{2n} \\ \vdots & \vdots & \vdots & \vdots \\ g_{n1} & g_{n2} & ... & g_{nn} \end{pmatrix}](http://upload.wikimedia.org/wikipedia/es/math/7/c/0/7c0413a55aadd47d534382c6fdcb8df3.png)