May
22
¿Qué habrá más allá del Modelo Estándar de la Física de Partículas?
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (0)
Comments (0)

“Inicialmente, se presenta, de modo simplificado, el Modelo Estándar como una teoría sofisticada que identifica las partículas elementales y sus interacciones. Después, en el ámbito de esa teoría, se enfocan aspectos –el vacuo no es vacío; partículas desnudas y vestidas; materia oscura y viento oscuro; materia y antimateria; el campo y el bosón de Higgs; neutrinos oscilantes– que pueden ser motivadores desde el punto de vista de la enseñanza y del aprendizaje de la Física. Finalmente, se discute la probable superación de esa teoría por otra más completa.”
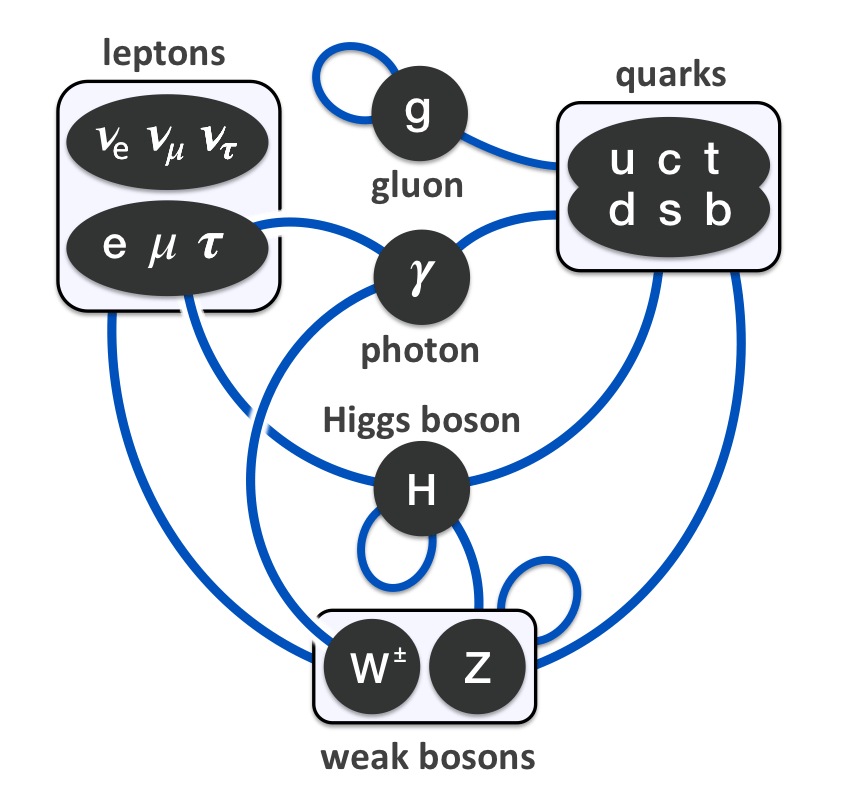
“… el Modelo Estándar es, en la historia, la más sofisticada teoría matemática sobre la naturaleza. A pesar de la palabra “modelo” en su nombre, el Modelo Estándar es una teoría comprensiva que identifica las partículas básicas y especifica cómo interactúan. Todo lo que pasa en nuestro mundo (excepto los efectos de la gravedad) es resultado de las partículas del Modelo Estándar interactuando de acuerdo con sus reglas y ecuaciones.”
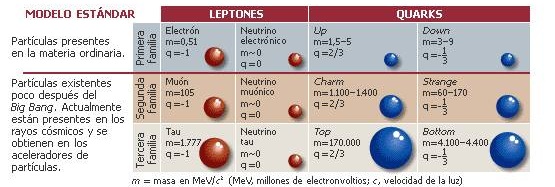


“La teoría de cuerdas es un intento por unificar estos dos mundos en un modelo matemático que funcione en todas las escalas. Pero ocurrió algo no muy deseable. En un breve espacio de tiempo surgieron 5 versiones distintas del modelo, lo que le restó credibilidad. La Teoría-M es una nueva proposición postulada por Edward Witten que unifica esas cinco teorías de las Supercuerdas. Cada una de las versiones de la teoría de cuerdas serían una proyección del del modelo M, del mismo modo que un cilindro proyecta sombras de diferentes formas dependiendo de la dirección de la luz (perdiendo una dimensión).”
La Física actual busca una teoría más amplia que el modelo estándar . Una teoría que dé una descripción completa, unificada y consistente de la estructura fundamental del universo. ¿Será la compleja Teoría de cuerdas,que integra también la interacción gravitatoria?
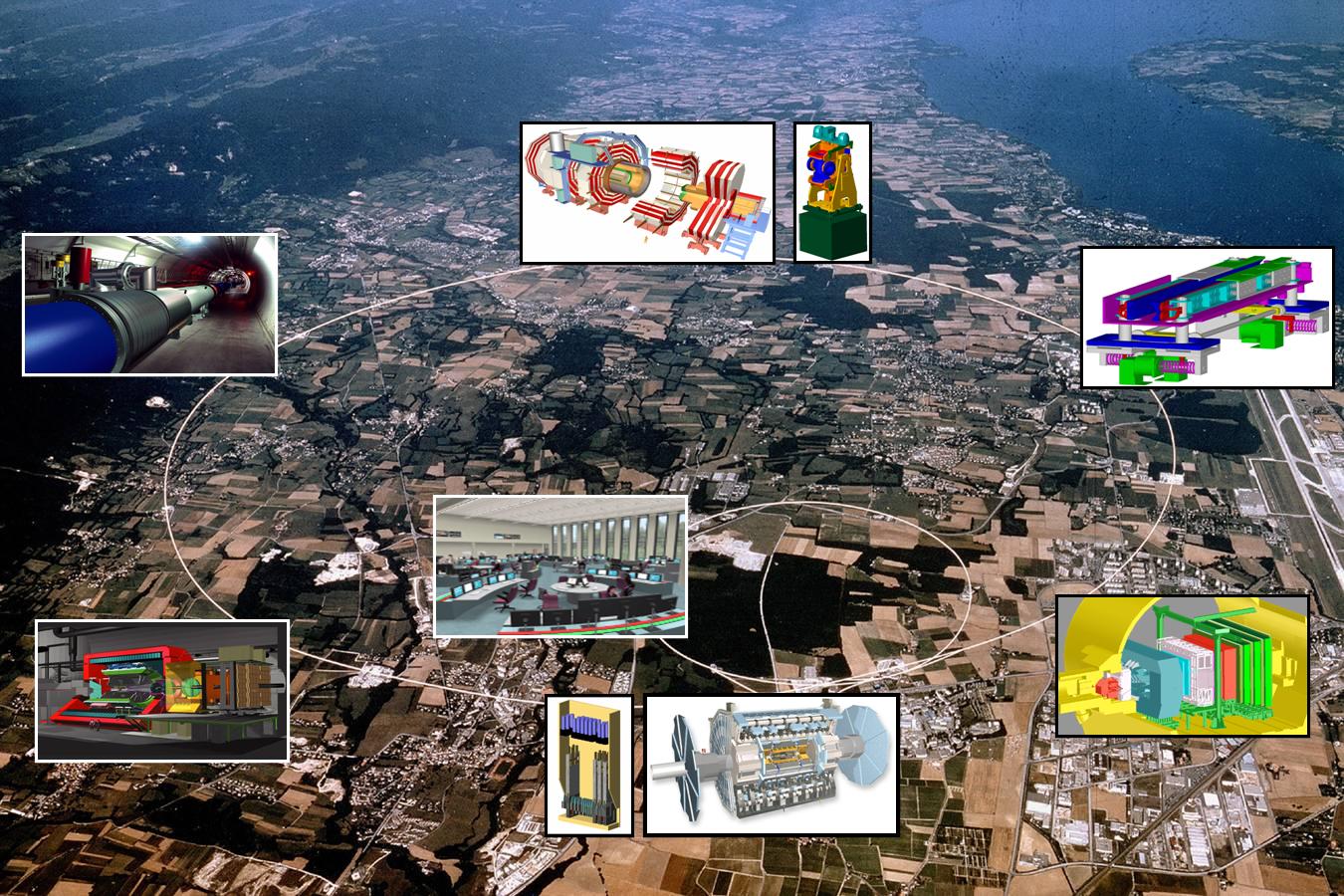
El modelo estándar es una poderosa herramienta pero no cumple todas las expectativas; no es un modelo perfecto. En primer lugar, podríamos empezar por criticar que el modelo tiene casi veinte constantes que no se pueden calcular. Desde luego, se han sugerido numerosas ideas para explicar el origen de todos estos parámetros o números inexplicables y sus valores, pero el problema de todas estas teorías es que los argumentos que dan nunca han sido enteramente convincentes. ¿Por qué se iba a preocupar la naturaleza de una fórmula mágica si en ausencia de tal fórmula no hubiera contradicciones? Lo que realmente necesitamos es algún principio fundamental nuevo, tal como el principio de la relatividad, pero no queremos abandonar todos los demás principios que ya conocemos. Ésos, después de todo, han sido enormemente útiles en el descubrimiento del modelo estándar. El mejor lugar para buscar un nuevo principio es precisamente donde se encuentran los puntos débiles de la presente teoría y, construímos máquinas como el LHC para que nos diga lo que no sabemos.
Solo en máquinas inmensas se puede llegar a desentrañar los secretos de la materia
Una regla universal en la física de partículas es que para partículas con energías cada vez mayores, los efectos de las colisiones están determinados por estructuras cada vez más pequeñas en el espacio y en el tiempo. El modelo estándar es una construcción matemática que predice sin ambigüedad cómo debe ser el mundo de las estructuras aún más pequeñas. Pero existen varias razones para sospechar que sus predicciones pueden, finalmente (cuando podamos emplear más energía en un nivel más alto), resultar equivocadas.
Vistas a través del microscopio, las constantes de la naturaleza parecen estar cuidadosamente ajustadas sin ninguna otra razón aparente que hacer que las partículas parezcan lo que son. Hay algo muy erróneo aquí. Desde un punto de vista matemático no hay nada que objetar, pero la credibilidad del modelo estándar se desploma cuando se mira a escalas de tiempo y longitud extremadamente pequeñas, o lo que es lo mismo, si calculamos lo que pasaría cuando las partículas colisionan con energías extremadamente altas. ¿Y por qué debería ser el modelo válido hasta aquí? Podrían existir muchas clases de partículas súper pesadas que no han nacido porque se necesitan energías aún inalcanzables. ¿Dónde está la partícula de Higgs? ¿Cómo se esconde de nosotros el gravitón?

Parece que el Modelo estándar no admite la cuarta fuerza y tendremos que buscar más profundamente, en otras teorías que nos hablen y describan además de las partículas conocidas de otras nuevas que están por nacer y que no excluya la Gravedad. Ese es el Modelo que necesitamos para conocer mejor la Naturaleza.
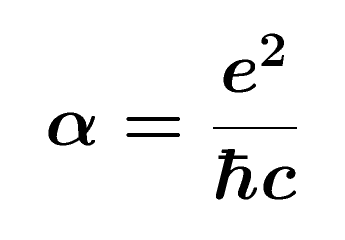
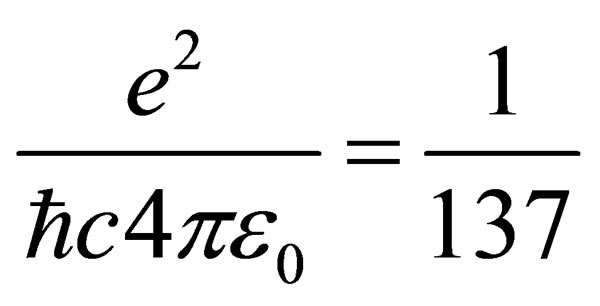
Claro que las cosas no son tan sencilla y si deseamos evitar la necesidad de un delicado ajuste de las constantes de la naturaleza, creamos un nuevo problema: ¿cómo podemos modificar el modelo estándar de tal manera que el ajuste fino no sea necesario? Está claro que las modificaciones son necesarias, lo que implica que muy probablemente haya un límite más allá del cual el modelo tal como está deja de ser válido. El modelo estándar no será nada más que una aproximación matemática que hemos sido capaces de crear, de forma que todos los fenómenos que hemos observado hasta el presente están reflejados en él, pero cada vez que se pone en marcha un aparato más poderoso, tenemos que estar dispuestos a admitir que puedan ser necesarias algunas modificaciones del modelo para incluir nuevos datos que antes ignorábamos.
Más allá del modelo estándar habrá otras respuestas que nos lleven a poder hacer otras preguntas que en este momento, no sabemos ni plantear por falta de conocimientos. Si no conociéramos que los protonesestán formados por Quarks, ¿cómo nos podríamos preguntar si habrá algo más allá de los Quarks?
El gobierno de Estados Unidos, después de llevar gastados miles de millones de dólares, suspendió la construcción del supercolisionador superconductor de partículas asestando un duro golpe a la física de altas energías, y se esfumó la oportunidad para obtener nuevos datos de vital importancia para el avance de este modelo, que de momento es lo mejor que tenemos.
Se han estado inventando nuevas ideas, como la supersimetría y el technicolor. Los astrofísicos estarán interesados en tales ideas porque predicen una gran cantidad de nuevas partículas superpesadas, y también varios tipos de partículas que interaccionan ultradébilmente, los technipiones. Éstas podrían ser las WIMP’s (Weakly Interacting Massive Particles, o Partículas Masivas Débilmente Interactivas) que pueblan los huecos entre las galaxias, y serían así las responsables de la masa perdida que los astrofísicos siguen buscando y llaman “materia oscura”.

Que aparezcan “cosas” nuevas y además, imaginarlas antes, no es fácil. Recordemos cómo Paul Dirac se sintió muy incómodo cuando en 1931 dedujo, a partir de su ecuación del electrón, que debería existir una partícula con carga eléctrica opuesta. Esa partícula no había sido descubierta y le daba reparo perturbar la paz reinante en la comunidad científica con una idea tan revolucionaria, así que disfrazó un poco la noticia: “Quizá esta partícula cargada positivamente, tan extraña, sea simplemente el protón”, sugirió. Cuando poco después se identificó la auténtica antipartícula del electrón (el positrón) se sorprendió tanto que exclamó: “¡Mi ecuación es más inteligente que su inventor!”. Este último comentario es para poner un ejemplo de cómo los físicos trabajan y buscan caminos matemáticos mediante ecuaciones de las que, en cualquier momento (si están bien planteadas), surgen nuevas ideas y descubrimientos que ni se podían pensar. Así pasó también con las ecuaciones de Einstein de la relatividad general, donde Schwarzschild dedujo la existencia de los agujeros negros.
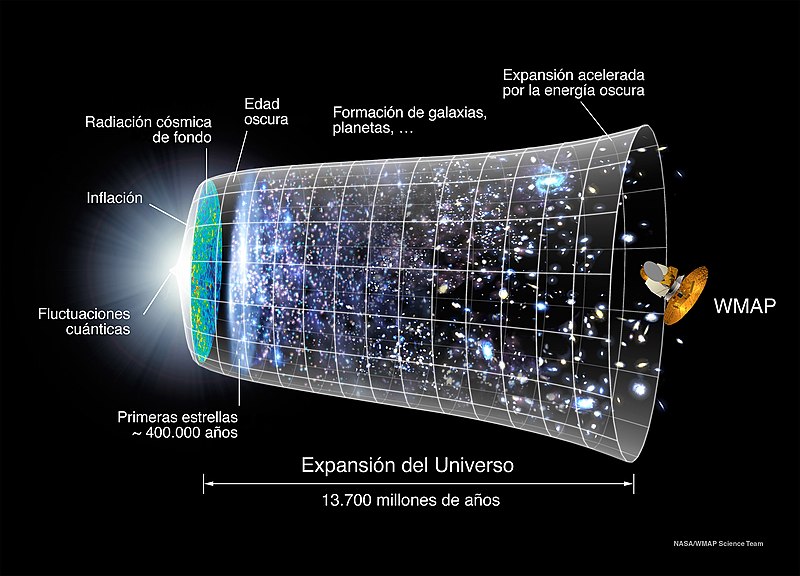
Se piensa que al principio del comienzo del tiempo, cuando surgió el Big Bang, las energías eran tan altas que allí reinaba la simetría total; sólo había una sola fuerza que todo lo englobaba. Más tarde, a medida que el universo se fue expandiendo y enfriando, surgieron las cuatro fuerzas que ahora conocemos y que todo lo rigen. Tenemos los medios, en los supercolisionadores de partículas, para viajar comenzando por 1.000 MeV, hasta finalizar en cerca de 1019 MeV, que corresponde a una escala de longitudes de aproximadamente 10–30 cm. Howard Georgi, Helen Quinn y Steven Weinberg descubrieron que ésta es la región donde las tres constantes de acoplamiento gauge se hacen iguales (U(1), SU(2) y SU(3)); resultan ser lo mismo. ¿Es una coincidencia que las tres se hagan iguales simultáneamente? ¿Es también una coincidencia que esto suceda precisamente en esa escala de longitud? Faltan sólo tres ceros más para alcanzar un punto de retorno. Howard Georgi y Sheldon Glashow descubrieron un modelo genuinamente unificado en el dominio de energías de 1019 MeV tal que, cuando se regresa de allí, espontáneamente surgen las tres fuerzas gauge tal como las conocemos. De hecho, ellos encontraron el modelo; la fórmula sería SU(5), que significa que el multiplote más pequeño debe tener cinco miembros.


Materia y Energía Oscura… Un Misterio…Sin resolver.
Y, a todo esto, ¿dónde está esa energía oculta? ¿Y donde la materia? Podemos suponer que la primera materia que se creo en el Universo fue la que llamamos (algún nom,bre había que ponerle) “Materia Oscura”, esa clase de Ilem o sustancia primera del Universo que mejor sería llamarla invisible, ya que, de no ser así, difícil sería explicar cómo se pudieron formar las primeras estrellas y galaxias de nuestro Universo, ¿dónde está el origen de la fuerza de Gravedad que lo hizo posible, sino en esa materia escondida?
¡Lo dicho! Necesitamos saber, y, deseo que de una vez por todas, se cumpla lo que dejó dicho Hilbert en su tumba de Gotinga (Alemania): “Tenemos que saber, ¡sabremos!. Pero…
¡Que sea pronto!
emilio silvera
May
4
¡La Luz! ¡La Mecánica Cuántica! Nuestro Universo
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (3)
Comments (3)

Cuando en nuestro Universo quedaron libres los fotones… ¡Se hizo la Luz!
En alguna parte he podido leer que para comprender la realidad en sus niveles más elementales, basta con conocer el comportamiento de dos infinitesimales objetos: el electrón y el fotón. Todo el argumento de la QED [electrodinámica cuántica] gira en torno a un proceso fundamental: la emisión de un único fotón por un único electrón.
Cuando el movimiento de un electrón es alterado súbitamente, puede responder desprendiendo un fotón. La emisión de un fotón es el suceso básico de la mecánica cuántica:

Un equipo de científicos lograron filmar por primera vez un electrón en movimiento gracias a una tecnología reciente que genera pulsos cortos e intensos de luz láser.
Toda la luz visible que vemos, así como las ondas de radio, la radiación infrarroja y los rayos X, está compuesta de fotones que han sido emitidos por electrones, ya sea en el Sol, el filamento de una bombilla, una antena de radio o un aparato de rayos.
Los electrones no son las únicas partículas que pueden emitir fotones. Cualquier partícula eléctricamente cargada puede hacerlo, incluido el protón. Esto significa que los fotones pueden saltar entre dos protoneso incluso entre un protón y un electrón. Este hecho es de enorme importancia para toda la ciencia y la vida en general. El intercambio continuo de fotones entre el núcleo y los electrones atómicos proporciona la fuerza que mantiene unido al átomo. Sin estos fotones saltarines, el átomo se desharía y toda la materia dejaría de existir.
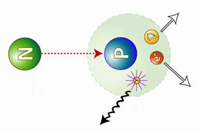 |
Se ha conseguido observar por primera vez la desintegración radiativa del neutrón.
Dentro de los núcleos de los átomos hay neutrones y protones. En condiciones normales y mientras que están ahí los neutrones son estables. Sin embargo los neutrones libres son inestables, tienen una vida media de unos 10 minutos, y se desintegran produciendo un protón un electrón y un antineutrino. Pero los físicos nucleares teóricos predijeron que una de cada mil veces los neutronesdecaerían en todas esas partículas y además en un fotón.
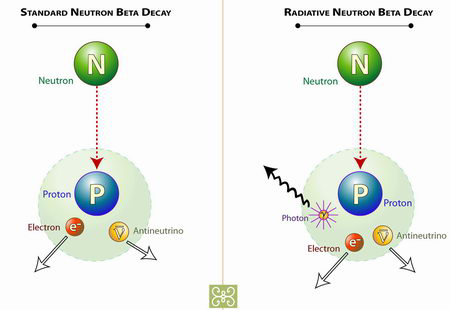
Típicamente el neutrón decae en un protón, un antineutrino y un electrón. Muy raramente lo hace radiativamente emitiendo además un fotón. Diagrama: Zina Deretsky, National Science Foundation.
Mientras que un electrón pertenece al grupo de partículas llamadas fermiones, los fotones pertenecen a la familia de los bosones. Intentemos comprender esta película que es la intermediaria de todas las formas de radiación electromagnética.
…protagonizada por bosones…
Los fermiones hacen posible la materia “al estilo tradicional”, mientras que los bosones son elementos muy raros desde la forma de pensar a que estamos acostumbrados el común de los mortales. Para no complicarnos, la tabla periódica de elementos existe porque los fermiones no pueden “ser iguales”: no pueden solaparse uno sobre otro y se repelen si los obligamos. Es lo que damos por hecho cuando hablamos de materia, que cada pedazo de ésta ocupa su lugar y tiene sus propias cualidades.
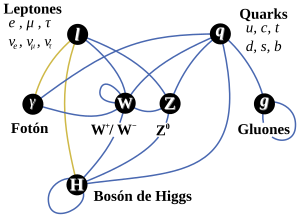
Toda la materia que conocemos, la que forma las estrellas y los mundos y las galaxias, esa que llamamos luminosa o bariónica, la que emite radiación, está hecha de Leptones y Quarks, partículas que son Fermiones, y, esas otras partículas intermediarias de las cuatro fuerzas fundamentales, son las que pertenecen a la familia de los Bosones, tales como el Fotón, las W+, W- y Zº, los Gluones y el Gravitón.

Los bosones carecen de este sentido de la individualidad que tienen los Fermiones, digamos que poseen “alma grupal” y, en su estado más puro, todos forman una misma “superpartícula”.
Para entenderlo mejor, conviene recordar que las partículas no son bolitas como nos siguen enseñando en la escuela, sino que más allá de esta imagen existen como ondas o, al menos, sus funciones se equiparan al comportamiento de una onda.
En la década de 1920, Albert Einstein y el hindú Satyendra Nath Bose pronosticaron un quinto estado de la materia: el condensado de Bose-Einstein (BEC), el cual fue conseguido en laboratorio en 1995, algo que le valió el premio Nobel de 2001 a los científicos que lo lograron.
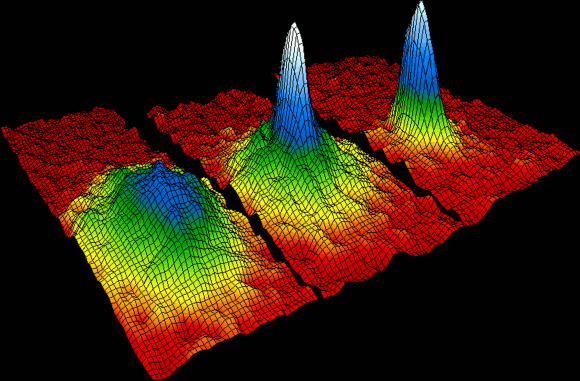
Un condensado de Bose-Einstein es un estado de la materia que se da en ciertos materiales a muy baja temperatura. En este estado de la materia, todos los átomos que lo constituyen se encuentran en el nivel de mínima energía, denominado estado fundamental. Descubierto en 1924 para los fotones por el indio Bose y por Einstein, no fue obtenido en laboratorio hasta 1995 por Cornell y Wieman al enfriar átomos a pocos nanokelvin por encima del cero absoluto. El condensado de Bose-Einstein fue la “molécula del año” según la revista Science en 1995 ya que se trata de un sistema cuántico macroscópico similar a una molécula pero con millones de átomos. Un átomo en un gas se mueve a una velocidad de unos unos 1000 km/h (unos 300 m/s) pero un condensado de Bose-Einstein se mueve a sólo 1 cm/s. Un condensado de Bose-Einstein es respecto a la materia ordinaria, como la luz de un láser es respecto a la de una bombilla. Gracias a ello se puede fabricar un láser de átomos, que en lugar de producir un haz de luz como un láseróptico, produce un haz (coherente) de átomos. En 1997 Ketterle fabricó el primer láser de átomos que producía un haz de átomos de sodio.
Cuando ciertas formas de materia [bosones] se enfrían hasta casi el cero absoluto, sus átomos se ponen en el estado de energía más baja, de modo que todos sus átomos vibran al unísono y se hacen coherentes. Las funciones de onda de todos los átomos se solapan, de manera que, en cierto sentido, un BEC [condensado de Bose-Einstein] es como un “superátomo” gigante en donde todos los átomos individuales vibran al unísono.
Al enfriar los átomos, su velocidad disminuye hasta que las longitudes de onda de cada uno de ellos se vuelven casi planas, superponiéndose unas a otras para formar una única onda que los describe a todos.

Así que un BEC se forma cuando los átomos en un gas sufren la transición de comportarse como “bolas de billar” al estilo de la física clásica, a comportarse como una onda gigante de materia al estilo de mecánica cuántica:
Si creamos dos BECs y los colocamos juntos, no se mezclan como gases ordinarios ni rebotan como lo harían dos sólidos. Donde los dos BECs se superponen, ellos “interfieren” como las ondas: delgadas capas paralelas de materia son separadas por capas delgadas de espacio vacío. El patrón se forma porque las dos ondas se suman donde sus crestas coinciden, y se cancelan donde una cresta se encuentra con un valle — a lo cual llamamos interferencia “constructiva” y “destructiva” respectivamente. El efecto es similar al de dos ondas que se superponen cuando dos piedras son lanzadas a un lago.
…ambientada en el vacío…
Y ahora, retrocedamos un poco más en este asunto del misterio que nos ocupa. Gracias a la tecnología láser, la física ha podido comprobar el extremo poder de la luz. Los láseres pueden hacer que las partículas virtuales se vuelvan reales. Pero, primero, aclaremos conceptos…
Las “Partículas virtuales”son partículas fundamentales que están constantemente surgiendo aparentemente de la nada y permanecen en el espacio-tiempo la friolera de una milésima de trillonésima de segundo –una cantidad que se forma poniendo una veintena de ceros a la derecha de la coma—. A pesar de denominarse “virtuales”, sus efectos son muy reales: la constante agitación de este burbujeo cuántico de partículas hace que el vacío tenga energía. Y esto es algo que afecta a la realidad, pues en ésta las fuerzas de atracción y repulsión dependen de la masa, y la masa no es sino energía expresada en unidades diferentes: E=mc².

Partículas virtuales que surgen de la NADA. Claro que, en la NADA no debe haber…¡Nada! Pero hay
En el uso corriente la palabra vacío significa espacio vacío, espacio del que se ha extraído todo el aire, vapor de agua u otro material. Eso es también lo que significa para un físico experimental que trabaja con tubos de vacío y bombas de vacío. Pero para un físico teórico, el término vacío tiene muchas más connotaciones. Significa una especie de fondo en el que tiene lugar el resto de la física. El vacío representa un potencial para todas las cosas que pueden suceder en ese fondo. Significa una lista de todas las partículas elementales tanto como de las constantes de la Naturaleza que se pondrían de manifiesto mediante experimentos en dicho vacío. En resumen, significa un ambiente en el que las leyes de la física toman una forma particular. Un vacío diferente significa leyes de la física diferentes; cada punto en el paisaje representa un conjunto de leyes que son, con toda probabilidad, muy diferentes de las nuestras pero que son, en cualquier caso, posibilidades consistentes. El modelo estándar es meramente un punto en el paisaje de posibilidades.

La energía del vacío es, por tanto, la suma total de las energías de todas las partículas posibles. Es la llamada “energía oscura” que hace que el universo se expanda, haciendo frente a la atracción de la gravedad, y que proporciona alrededor del 80% de la materia-energía al universo –un 26% es “materia oscura”, y sólo un 4% es la materia conocida hasta el momento—.
Pero, ¿cómo una partícula virtual se convierte en real? Es decir, ¿cómo queda “atrapada” en el espacio-tiempo de forma más estable?

¡Los fotones de Yang-Mills adquieren su masa y el principio gauge se sigue cumpliendo! Al principio esta visión no mereció la atención que merecía. Por una parte, la gente pensó que el modelo era feo. El principio gauge estaba ahí, pero ya no era el tema central. El “Campo de Higgs” había sido puesto ahí “a propósito” y la “partícula de Higgs”, en sí misma, no era una “partícula gauge”
La Teoría de la Sipersimetría establece que, por cada partícula de materia, nace una gemela de antimateria. La antimateria es igual que la materia, pero con carga opuesta. Por ejemplo, el electrón tiene carga negativa, y su partícula de antimateria, el positrón, positiva. Materia y antimateria se aniquilan mutuamente pero, por algún motivo aún no aclarado, la simetría se rompió en algún momento, surgiendo más materia que antimateria, de ahí que nuestro universo, materia, pueda existir.
Pero hay algo más en todo esto. Y para ello, la luz es la clave.

Controlar los estados cuánticos macroscópicos de osciladores micromecánicos no es fácil; hacerlo con luz (fotones) requiere el acoplamiento coherente entre …
Una de los modelos teóricos elaborados para superar la visión de la gravedad de Einstein indica que los fotones de los rayos gamma de alta energía viajarían algo más despacio que los de baja energía, lo que viola el axioma del sabio alemán acerca de que toda radiación electromagnética, desde las ondas radio hasta los rayos gamma, viajan en el vacío a la misma velocidad (la de la luz). Sin embargo, no ha sido verificado mediante experimento, con lo cual, Einstein sigue teniendo razón.
… protagonizada por la “luz” como la propia …
Ya en los años 30, los físicos predijeron que un campo eléctrico muy fuerte, que no es sino un espacio alterado por la actividad de un montón de fotones coordinados, podría impulsar a las partículas virtuales con carga opuesta en diferentes direcciones, impidiendo que la materia y la antimateria se aniquilen.

Según el efecto de creación de pares, un fotón con energía suficiente, lo que equivale a tener el doble de la energía que posee un electrón en reposo, da lugar a una pareja de electrón y positrón.
Aunque esto ya se consiguió en los años 90 a pequeña escala, gracias al desarrollo de la tecnología láserlos científicos creen que estarán cerca de conseguir crear materia “en serie” mediante este proceso en unos pocos años.

Sabemos desde 1932, que un fotón gama con suficiente energía, puede formar un par de antipartículas, al interactuar con un átomo masivo, como el plomo. Pero el problema no termina, sino que, el electrónformado por un rayo gama, no interactúa con este tipo de fotón (gama), sino uno de luz visible,
Por otra parte, una vez que existen las partículas, los fotones interactúan sin cesar con ellas, siendo absorbidos y emitidos por las mismas de manera ininterrumpida.
Y de ello nace el movimiento gracias al cual todo existe en el espacio-tiempo. Sin movimiento, nuestra realidad desaparecería.
La carencia de masa de un fotón está ligada a su movimiento. Para que un cuerpo alcance la velocidad de la luz, su masa ha de ser cero. Y, como Einstein explicó en su día, la luz se mueve siempre a la velocidad de la luz. Si pretendemos que un fotón se pare, en lugar de ralentizarse observaremos que desaparece. Y, como se ha dicho al principio, si estos “fotones saltarines” desaparecieran, toda la materia dejaría de existir.
Su esencia es el movimiento y su misión, según parece, hacer girar la rueda de la existencia.
Ello es así debido al impacto de los fotones sobre las partículas elementales. La energía transmitida por un fotón es inversamente proporcional a su longitud de onda. Cuanto menos longitud de onda, más energía. Así, un fotón de luz visible tiene la energía suficiente para hacer reaccionar a un bastón de la retina. Si nos movemos en el espectro electromagnético, los fotones con longitud de onda ultravioleta pueden expulsar a los electrones de los átomos. Más allá, los rayos gamma pueden romper protones y neutrones…
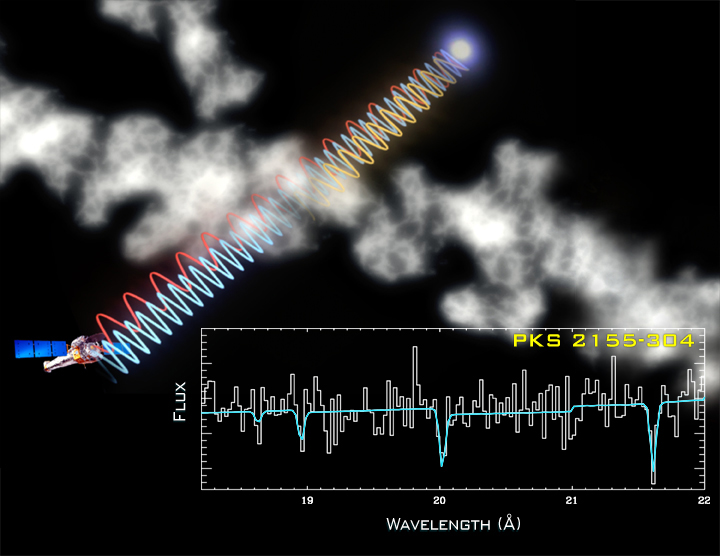
Y ahora, vayamos al meollo de la cuestión e indaguemos en la cita con que se iniciaba este artículo: ¿qué hace que los electrones absorban y emitan fotones? Esto, en otros términos, vendría a ser lo mismo que preguntarnos: ¿por qué existe nuestro universo?
…con un misterio: el 137…
¿Qué determina el momento exacto en que un electrón emite un fotón? La física cuántica dice que nada lo hace, pues la Naturaleza es caprichosa en sus niveles más elementales. Aunque no es caótica en extremo, sólo probabilística.
A diferencia de la física newtoniana, la mecánica cuántica nunca predice el futuro en función del pasado. En su lugar, ofrece reglas muy precisas para computar la probabilidad de varios resultados alternativos de un experimento.
Y la probabilidad de que un electrón emita o absorba un fotón es la constante de estructura fina. El valor de esa constante es 1/137.

En otras palabras, sólo un afortunado electrón de cada 137 emite un fotón. Este es el significado de alfa: es la probabilidad de que un electrón, cuando se mueve a lo largo de su trayectoria, emita caprichosamente un fotón.
El inverso de la constante de estructura fina es 137. Desde su descubrimiento, éste número ha traído de cabeza a los grandes científicos.
No puedo recordar si fue Richard Feynman o León Lederman, quien sugirió que todos los físicos pusiesen un cartel en sus despachos o en sus casas que les recordara cuánto es lo que no sabemos. En el cartel no pondría nada más que esto: 137. Ciento treinta y siete es el inverso de algo que lleva el nombre de constante de estructura fina. Este número guarda relación con la probabilidad de que un electrónemita o absorba un fotón. La constante de estructura fina responde también al nombre de alfa, y sale de dividir el cuadrado de la carga del electrón por el producto de la velocidad de la luz y la constante de Planck. Tanta palabra no significa otra cosa sino que ese solo número, 137, encierra los meollos del electromagnetismo (el electrón), la relatividad (la velocidad de la luz) y la teoría cuántica (la constante de Planck). Menos perturbador sería que la relación entre todos estos importantes conceptos hubiera resultado ser un uno o un tres o quizás un múltiplo de pi. Pero ¿137?
![]()
… es un número que determina la fuerza de una interacción) y equivale a 1/137,03599911.
“Lo más notable de este notable número es su adimensionalidad. La velocidad de la luz es de unos 300.000 kilómetros por segundo. Abraham Lincoln medía 1,98 metros. La mayoría de los números vienen con dimensiones. Pero resulta que cuando uno combina las magnitudes que componen alfa, ¡se borran todas las unidades! El 137 está solo: se exhibe desnudo a donde va. Esto quiere decir que a los científicos de Marte, o a los del decimocuarto planeta de la estrella Sirio, aunque usen Dios sabe qué unidades para la carga y la velocidad y qué versión de la constante de Planck, también les saldrá 137. Es un número puro.”
(Leon Ledderman, La partícula divina)
Uno de los padres de la mecánica cuántica, Wolfgang Pauli, se obsesionó tanto con este número que dijo que, de poder hacerle una pregunta a Dios, sería esta: “¿Por qué 137?”
Gracias a su gran amistad con Carl G. Jung, Pauli conoció el mundo “alternativo” de los estudios sobre la psique y accedió a la tradición esotérica que ha acompañado al hombre desde el principio de los tiempos. Es así como supo que 137 se aproxima al valor correspondiente al ángulo áureo. Esto es, la versión circular del número áureo o φ (phi).

Sin fotones… ¡El Universo sería inestable, sería otro universo diferente!
En realidad, el ángulo de oro es, más o menos, 137,5º, y está presente en todo proceso natural donde se dé una combinación de espirales. Así, por ejemplo, las hojas de una planta surgen a lo largo del tallo cada 137,5º, pues así se logra la mayor eficiencia de espacio y de captación de la luz solar, ya que únicamente con éste ángulo es posible evitar que ninguna hoja obstaculice a las demás en la toma de luz sin que existan espacios muertos o vacíos.
Esta semejanza entre los valores de la constante de estructura fina y el ángulo áureo llevó a la doctora Raji Heyrovska a buscar el ángulo áureo en el universo atómico (véase versión en español de su estudio).
Que esto sea así no debería extrañarnos, pues si el número áureo es una constante en toda la Naturaleza, su versión angular es la apropiada para estar presente en el universo cuántico, donde, recordemos, los elementos básicos de la realidad se reducen a funciones de onda.
…y un final místico.
Los fotones no tienen masa ni carga eléctrica. Sin embargo, pueden “extraer” del vacío partículas con masa y carga, tanto negativa como positiva.
Más allá de la matería y la energía, del tiempo y del espacio, el concepto de función de onda nos introduce en una realidad abstracta de donde surge todo.Y si, como hemos dicho, a menor longitud de onda mayor energía, también es posible afirmar que, en eso que David Bohm llamaba “orden implicado”, cuanto menor es la longitud de una onda cuántica, mayor es la presencia de masa en el espacio-tiempo.
Para la física, las matemáticas se han mostrado como la realidad que subyace a la materia. Todo se puede reducir a números, entidades que forman y organizan el espacio-tiempo. En este nivel de realidad, ni la materia ni la energía existen como tales, sino que demuestran ser el resultado de la interacción de entidades abstractas.

En esta pasión por los números, no podemos evitar recordar la versión cabalística de la filosofía perenne. Para la Kabbalah, lo divino responde a la “Nada”, ya que lo trascendente no puede ser aprehendido desde nuestra posición en el mundo finito.
En el momento de la Creación, la luz infinita se habría divido, quedando encerrada en conductos que, al romperse, producen la materia y, en definitiva, la fractura de la unidad primordial de la luz.
Esta materia o qelippot, en el sentido de “conchas” o caparazones que “encierran” la luz y rompen la armonía unitaria de la luz, es el origen del mundo, de su finitud y causa del mal en la realidad no-divina. El mundo creado es así una fractura de la harmonía de la luz que crea la diferenciación y la tensión entre unas cosas y otras: este es el origen del mal, de la falta de armonía que debe recuperarse en el curso de la historia.
La Kabbalah enseña, según esto, el camino para desarrollar la Vasija interior donde recibir la Luz, la cual, según va llenando dicha vasija, nos acerca a la unidad del Espíritu. Es así que la Luz, al tiempo que “absorbida” por el alma, puede ser “proyectada” en el mundo mediante los actos del hombre trascendido.
Que la luz ha sido usada por todos los movimientos espirituales para referirse a lo divino es algo que a nadie se le escapa. La imagen que la Kabbalah ofrece aquí no es muy diferente de la que podríamos encontrar en textos rosacruces o en escritos orientales, entre otros.
Sin embargo, si esta vez he preferido usar el hermetismo hebreo es, como he mencionado, por su pasión hacia los números. Y es que el valor numérico para el término hebreo de “kabbalah” (cuya traducción es “recepción”) es…
como muchos ya sabrán…
Efectivamente…
137.

Ciencia y tradición hermética unidas por un número que, en ambas, define la interacción entre luz y materia.
Cosas…
Luz que, también en ambos casos, procede de la Nada.
Decía Jung que el espacio y el tiempo son conceptos hipostasiados, fenómenos que hemos decidido convertir en reales. La física teórica y la consolidación de la mecánica cuántica han dejado claro, a lo largo de las últimas décadas, que toda esta realidad por la que combatimos, matamos, morimos, odiamos, repudiamos, humillamos, codiciamos, envidiamos o ansiamos consiste, simplemente, en Nada.
Nada…

Una ilusión de la psique por la que renunciamos a indagar en el misterio de la Vida y nuestra experiencia momentánea en el espacio-tiempo se convierte en un vagar ausentes, asumiendo que todo es un sinsentido.
A veces, en momentos de bajón, me pregunto si no será por eso por lo que, casi cien años después, nos siguen diciendo que la física cuántica es muy complicada para que lleguemos a entenderla…
Lo más triste, sin embargo, es que lo aceptamos…
Todo esto lo he leido o aprendido de gente que son más sabias que yo, ideas que tienen sus fuentes en trabajos realizados con la misión y el propósito de desvelar los secretos de la Naturaleza para saber, como es el Universo.
Lo conseguiremos alguna ve?
emilio silvera
May
4
Velocidades inimaginables
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (0)
Comments (0)

En el centro del átomo se encuentra un pequeño grano compacto aproximadamente 100.000 veces más pequeño que el propio átomo: el núcleo atómico. Su masa, e incluso más aún su carga eléctrica, determinan las propiedades del átomo del cual forma parte.
Debido a la solidez del núcleo parece que los átomos, que dan forma a nuestro mundo cotidiano, son intercambiables entre sí, e incluso cuando interaccionan entre ellos para formar sustancias químicas (los elementos). Pero el núcleo, a pesar de ser tan sólido, puede partirse. Si dos átomos chocan uno contra el otro con gran velocidad podría suceder que los núcleos llegaran a chocar entre sí y entonces, o bien se rompen en trozos, o se funden liberando en el proceso partículas subnucleares. La nueva física de la primera mitad del siglo XX estuvo dominada por los nuevos acertijos que estas partículas planteaban.
Pero tenemos la mecánica cuántica; ¿es que no es aplicable siempre?, ¿cuál es la dificultad? Desde luego, la mecánica cuántica es válida para las partículas subatómicas, pero hay más que eso. Las fuerzas con que estas partículas interaccionan y que mantienen el núcleo atómico unido son tan fuertes que las velocidades a las que tienen que moverse dentro y fuera del núcleo están cerca de la velocidad de la luz, c, que es de 299.792’458 Km/s. Cuando tratamos con velocidades tan altas se necesita una segunda modificación a las leyes de la física del siglo XIX; tenemos que contar con la teoría de la relatividadespecial de Einstein.
Esta teoría también fue el resultado de una publicación de Einstein de 1905. en esta teoría quedaron sentadas las bases de que el movimiento y el reposo son conceptos relativos, no son absolutos, como tampoco habrá un sistema de referencia absoluto con respecto al cual uno pueda medir la velocidad de la luz.
Pero había más cosas que tenían que ser relativas. En este teoría, la masa y la energía también dependen de la velocidad, como lo hacen la intensidad del campo eléctrico y del magnético. Einstein descubrió que la masa de una partícula es siempre proporcional a la energía que contienen, supuesto que se haya tenido en cuenta una gran cantidad de energía en reposo de una partícula cualquiera, como se denota a continuación:

E = mc2
Como la velocidad de la luz es muy grande, esta ecuación sugiere que cada partícula debe almacenar una cantidad enorme de energía, y en parte esta predicción fue la que hizo que la teoría de la relatividad tuviese tanta importancia para la física (¡y para todo el mundo!). Para que la teoría de la relatividad también sea autoconsistente tiene que ser holista, esto es, que todas las cosas y todo el mundo obedezcan a las leyes de la relatividad. No son sólo los relojes los que se atrasan a grandes velocidades, sino que todos los procesos animados se comportan de la forma tan inusual que describe esta teoría cuando nos acercamos a la velocidad de la luz. El corazón humano es simplemente un reloj biológico y latirá a una velocidad menor cuando viaje en un vehículo espacial a velocidades cercanas a la de la luz. Este extraño fenómeno conduce a lo que se conoce como la “paradoja de los gemelos”, sugerida por Einstein, en la que dos gemelos idénticos tienen diferente edad cuando se reencuentran después de que uno haya permanecido en la Tierra mientras que el otro ha viajado a velocidades relativistas.

Einstein comprendió rápidamente que las leyes de la gravedad también tendrían que ser modificadas para que cumplieran el principio relativista.
Para poder aplicar el principio de la relatividad a la fuerza gravitatoria, el principio tuvo que ser extendido de la siguiente manera: no sólo debe ser imposible determinar la velocidad absoluta del laboratorio, sino que también es imposible distinguir los cambios de velocidad de los efectos de una fuerza gravitatoria.
Einstein comprendió que la consecuencia de esto era que la gravedad hace al espacio-tiempo lo que la humedad a una hoja de papel: deformar la superficie con desigualdades que no se pueden eliminar. Hoy en día se conocen muy bien las matemáticas de los espacios curvos, pero en el época de Einstein el uso de estas nociones matemáticas tan abstractas para formular leyes físicas era algo completamente nuevo, y le llevó varios años encontrar la herramienta matemática adecuada para formular su teoría general de la relatividad que describe cómo se curva el espacio en presencia de grandes masas como planetas y estrellas.
Einstein tenía la idea en su mente desde 1907 (la relatividad especial la formuló en 1905), y se pasó 8 años buscando las matemáticas adecuadas para su formulación.
El Tensor métrico de Riemann se podría adaptar a las necesidades de la búsqueda estableciendo la multiplicidad de dimensiones que la teoría requería para su desarrollo.
Leyendo el material enviado por un amigo al que pidió ayuda, Einstein quedó paralizado. Ante él, en la primera página de una conferencia dada ante el Sindicato de Carpinteros, 60 años antes por un tal Riemann, tenía la solución a sus desvelos: el tensor métrico de Riemann, que le permitiría utilizar una geometría espacial de los espacios curvos que explicaba su relatividad general.
No está mal que en este punto recordemos la fuerza magnética y gravitatoria que nos puede ayudar a comprender mejor el comportamiento de las partículas subatómicas.
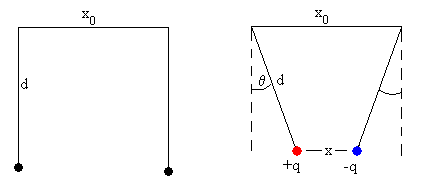
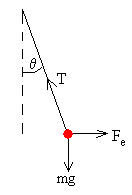
Las cargas de distinto signo se atraen, acercándose a una distancia x. Los hilos forman un ángulo θ con la vertical. Obviamos las ecuaciones de una larga explicación.
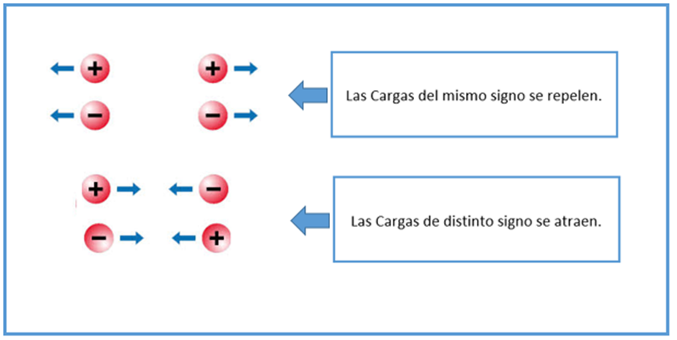
El electromagnetismo, decíamos al principio, es la fuerza con la cual dos partículas cargadas eléctricamente se repelen (si sus cargas son iguales) o se atraen (si tienen cargas de signo opuesto).
La interacción magnética es la fuerza que experimenta una partícula eléctricamente cargada que se mueve a través de un campo magnético. Las partículas cargadas en movimiento generan un campo magnético como, por ejemplo, los electrones que fluyen a través de las espiras de una bobina.
Las fuerzas magnéticas y eléctricas están entrelazadas. En 1873, James Clerk Maxwell consiguió formular las ecuaciones completas que rigen las fuerzas eléctricas y magnéticas, descubiertas experimentalmente por Michael Faraday. Se consiguió la teoría unificada del electromagnetismo que nos vino a decir que la electricidad y el magnetismo eran dos aspectos de una misma cosa.
La interacción es universal, de muy largo alcance (se extiende entre las estrellas), es bastante débil. Su intensidad depende del cociente entre el cuadrado de la carga del electrón y 2hc (dos veces la constante de Planck por la velocidad de la luz). Esta fracción es aproximadamente igual a 1/137’036…, o lo que llamamos α y se conoce como constante de estructura fina.

Campo eléctrico de cargas puntuales.
En general, el alcance de una interacción electromagnética es inversamente proporcional a la masa de la partícula mediadora, en este caso, el fotón, sin masa.
También antes hemos comentado sobre la interacción gravitatoria de la que Einstein descubrió su compleja estructura y la expuso al mundo en 1915 con el nombre de teoría general de la relatividad, y la relacionó con la curvatura del espacio y el tiempo. Sin embargo, aún no sabemos cómo se podrían reconciliar las leyes de la gravedad y las leyes de la mecánica cuántica (excepto cuando la acción gravitatoria es suficientemente débil).
La teoría de Einstein nos habla de los planetas y las estrellas del cosmos. La teoría de Planck, Heisemberg, Schrödinger, Dirac, Feynman y tantos otros, nos habla del comportamiento del átomo, del núcleo, de las partículas elementales en relación a estas interacciones fundamentales. La primera se ocupa de los cuerpos muy grandes y de los efectos que causan en el espacio y en el tiempo; la segunda de los cuerpos muy pequeños y de su importancia en el universo atómico. Cuando hemos tratado de unir ambos mundos se produce una gran explosión de rechazo. Ambas teorías son (al menos de momento) irreconciliables.

- La interacción gravitatoria actúa exclusivamente sobre la masa de una partícula.
- La gravedad es de largo alcance y llega a los más lejanos confines del universo conocido.
- Es tan débil que, probablemente, nunca podremos detectar esta fuerza de atracción gravitatoria entre dos partículas elementales. La única razón por la que podemos medirla es debido a que es colectiva: todas las partículas (de la Tierra) atraen a todas las partículas (de nuestro cuerpo) en la misma dirección.

La partícula mediadora es el hipotético gravitón. Aunque aún no se ha descubierto experimentalmente, sabemos lo que predice la mecánica cuántica: que tiene masa nula y espín 2.
La ley general para las interacciones es que, si la partícula mediadora tiene el espín par, la fuerza entre cargas iguales es atractiva y entre cargas opuestas repulsiva. Si el espín es impar (como en el electromagnetismo) se cumple a la inversa.
Pero antes de seguir profundizando en estas cuestiones hablemos de las propias partículas subatómicas, para lo cual la teoría de la relatividad especial, que es la teoría de la relatividad sin fuerza gravitatoria, es suficiente.
Si viajamos hacia lo muy pequeño tendremos que ir más allá de los átomos, que son objetos voluminosos y frágiles comparados con lo que nos ocupará a continuación: el núcleo atómico y lo que allí se encuentra. Los electrones, que ahora vemos “a gran distancia” dando vueltas alrededor del núcleo, son muy pequeños y extremadamente robustos. El núcleo está constituido por dos especies de bloques: protones y neutrones. El protón (del griego πρώτος, primero) debe su nombre al hecho de que el núcleo atómico más sencillo, que es el hidrógeno, está formado por un solo protón. Tiene una unidad de carga positiva. El neutrón recuerda al protón como si fuera su hermano gemelo: su masa es prácticamente la misma, su espín es el mismo, pero en el neutrón, como su propio nombre da a entender, no hay carga eléctrica; es neutro.

La masa de estas partículas se expresa en una unidad llamada mega-electrón-voltio o MeV, para abreviar. Un MeV, que equivale a 106 electrón-voltios, es la cantidad de energía de movimiento que adquiere una partícula con una unidad de carga (tal como un electrón o un protón) cuando atraviesa una diferencia de potencial de 106 (1.000.000) voltios. Como esta energía se transforma en masa, el MeV es una unidad útil de masa para las partículas elementales.
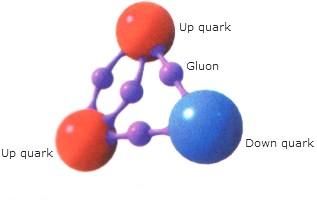
La mayoría de los núcleos atómicos contienen más neutrones que protones. Los protones se encuentran tan juntos en el interior de un núcleo tan pequeño que se deberían repelerse entre sí fuertemente, debido a que tienen cargas eléctricas del mismo signo. Sin embargo, hay una fuerza que los mantiene unidos estrechamente y que es mucho más potente e intensa que la fuerza electromagnética: la fuerza o interacción nuclear fuerte, unas 102 veces mayor que la electromagnética, y aparece sólo entre hadronespara mantener a los nucleones confinados dentro del núcleo. Actúa a una distancia tan corta como 10-15 metros, o lo que es lo mismo, 0’000000000000001 metros.
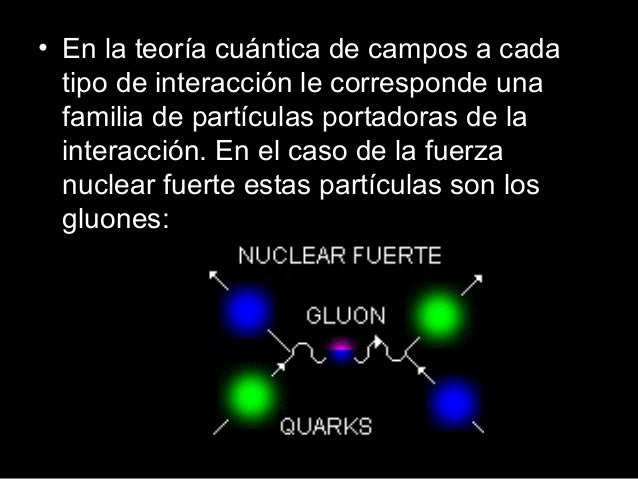
La interacción fuerte está mediada por el intercambio de mesones virtuales, 8 gluones que, como su mismo nombre indica (glue en inglés es pegamento), mantiene a los protones y neutrones bien sujetos en el núcleo, y cuanto más se tratan de separar, más aumenta la fuerza que los retiene, que crece con la distancia, al contrario que ocurre con las otras fuerzas.
La luz es una manifestación del fenómeno electromagnético y está cuantizada en “fotones”, que se comportan generalmente como los mensajeros de todas las interacciones electromagnéticas. Así mismo, como hemos dejado reseñado en el párrafo anterior, la interacción fuerte también tiene sus cuantos (los gluones). El físico japonés Hideki Yukawa (1907 – 1981) predijo la propiedad de las partículas cuánticas asociadas a la interacción fuerte, que más tarde se llamarían piones. Hay una diferencia muy importante entre los piones y los fotones: un pión es un trozo de materia con una cierta cantidad de “masa”. Si esta partícula está en reposo, su masa es siempre la misma, aproximadamente 140 MeV, y si se mueve muy rápidamente, su masa parece aumentar en función E = mc2. Por el contrario, se dice que la masa del fotón en reposo es nula. Con esto no decimos que el fotón tenga masa nula, sino que el fotón no puede estar en reposo. Como todas las partículas de masa nula, el fotón se mueve exclusivamente con la velocidad de la luz, 299.792’458 Km/s, una velocidad que el pión nunca puede alcanzar porque requeriría una cantidad infinita de energía cinética. Para el fotón, toda su masa se debe a su energía cinética.

Los físicos experimentales buscaban partículas elementales en las trazas de los rayos cósmicos que pasaban por aparatos llamados cámaras de niebla. Así encontraron una partícula coincidente con la masa que debería tener la partícula de Yukawa, el pión, y la llamaron mesón (del griego medio), porque su masa estaba comprendida entre la del electrón y la del protón. Pero detectaron una discrepancia que consistía en que esta partícula no era afectada por la interacción fuerte, y por tanto, no podía ser un pión. Actualmente nos referimos a esta partícula con la abreviatura μ y el nombre de muón, ya que en realidad era un leptón, hermano gemelo del electrón, pero con 200 veces su masa.
Antes de seguir veamos las partículas elementales de vida superior a 10-20 segundos que eran conocidas en el año 1970.
| Nombre | Símbolo | Masa (MeV) | Carga | Espín | Vida media (s) |
| Fotón | γ | 0 | 0 | 1 | ∞ |
| Leptones (L = 1, B = 0) | |||||
| Electrón | e– | 0’5109990 | – | ½ | ∞ |
| Muón | μ– | 105’6584 | – | ½ | 2’1970 × 10-6 |
| Tau | τ | ||||
| Neutrino electrónico | νe | ~ 0 | 0 | ½ | ~ ∞ |
| Neutrino muónico | νμ | ~ 0 | 0 | ½ | ~ ∞ |
| Neutrino tauónico | ντ | ~ 0 | 0 | ½ | ~ ∞ |
| Mesones (L = 0, B = 0) | |||||
| Pión + | π+ | 139’570 | 2’603 × 10-8 | ||
| Pión – | π– | 139’570 | 2’603 × 10-8 | ||
| Pión 0 | π0 | 134’976 | 0’84 × 10-16 | ||
| Kaón + | k+ | 493’68 | 1’237 × 10-8 | ||
| Kaón – | k– | 493’68 | 1’237 × 10-8 | ||
| Kaón largo | kL | 497’7 | 5’17 × 10-8 | ||
| Kaón corto | kS | 497’7 | 0’893 × 10-10 | ||
| Eta | η | 547’5 | 0 | 0 | 5’5 × 10-19 |
| Bariones (L = 0, B = 1) | |||||
| Protón | p | 938’2723 | + | ½ | ∞ |
| Neutrón | n | 939’5656 | 0 | ½ | 887 |
| Lambda | Λ | 1.115’68 | 0 | ½ | 2’63 × 10-10 |
| Sigma + | Σ+ | 1.189’4 | + | ½ | 0’80 × 10-10 |
| Sigma – | Σ– | 1.1974 | – | ½ | 7’4× 10-20 |
| Sigma 0 | Σ0 | 0 | ½ | 1’48 × 10-10 | |
| Ksi 0 | Ξ0 | 1.314’9 | 0 | ½ | 2’9 × 10-10 |
| Ksi – | Ξ– | 1.321’3 | – | ½ | 1’64 × 10-10 |
| Omega – | Ω– | 1.672’4 | – | 1½ | 0’82 × 10-10 |
Para cada leptón y cada barión existe la correspondiente antipartícula, con exactamente las mismas propiedades a excepción de la carga que es la contraria. Por ejemplo, el antiprotón se simboliza con y el electrón con e+. Los mesones neutros son su propia antipartícula, y el π+ es la antipartícula del π–, al igual que ocurre con k+ y k–. El símbolo de la partícula es el mismo que el de su antipartícula con una barra encima. Las masas y las vidas medias aquí reflejadas pueden estar corregidas en este momento, pero de todas formas son muy aproximadas.
Los símbolos que se pueden ver algunas veces, como s (extrañeza) e i (isoespín) están referidos a datos cuánticos que afectan a las partículas elementales en sus comportamientos.

En mecánica cuántica se utilizan símbolos que explican dentro de complicadas ecuaciones cuestiones que, con palabras serían más difícil de explicar.
Debo admitir que todo esto tiene que sonar algo misterioso. Es difícil explicar estos temas por medio de la simple palabra escrita sin emplear la claridad que transmiten las matemáticas, lo que, por otra parte, es un mundo secreto para el común de los mortales, y ese lenguaje es sólo conocido por algunos privilegiados que, mediante un sistema de ecuaciones pueden ver y entender de forma clara, sencilla y limpia, todas estas complejas cuestiones.
Si hablamos del espín (o, con más precisión, el momento angular, que es aproximadamente la masa por el radio por la velocidad de rotación) se puede medir como un múltiplo de la constante de Planck, h, dividido por 2π. Medido en esta unidad y de acuerdo con la mecánica cuántica, el espín de cualquier objeto tiene que ser o un entero o un entero más un medio. El espín total de cada tipo de partícula – aunque no la dirección del mismo – es fijo.
El electrón, por ejemplo, tiene espín ½. Esto lo descubrieron dos estudiantes holandeses, Samuel Gondsmit (1902 – 1978) y George Uhlenbeck (1900 – 1988), que escribieron sus tesis conjuntamente sobre este problema en 1972. Fue una idea audaz que partículas tan pequeñas como los electronespudieran tener espín, y de hecho, bastante grande. Al principio, la idea fue recibida con escepticismo porque la “superficie del electrón” se tendría que mover con una velocidad 137 veces mayor que la de la luz, lo cual va en contra de la teoría de la relatividad general en la que está sentado que nada en el universo va más rápido que la luz, y por otra parte, contradice E=mc2, y el electrón pasada la velocidad de la luz tendría una masa infinita.
Hoy día, sencillamente, tal observación es ignorada, toda vez que el electrón carece de superficie.
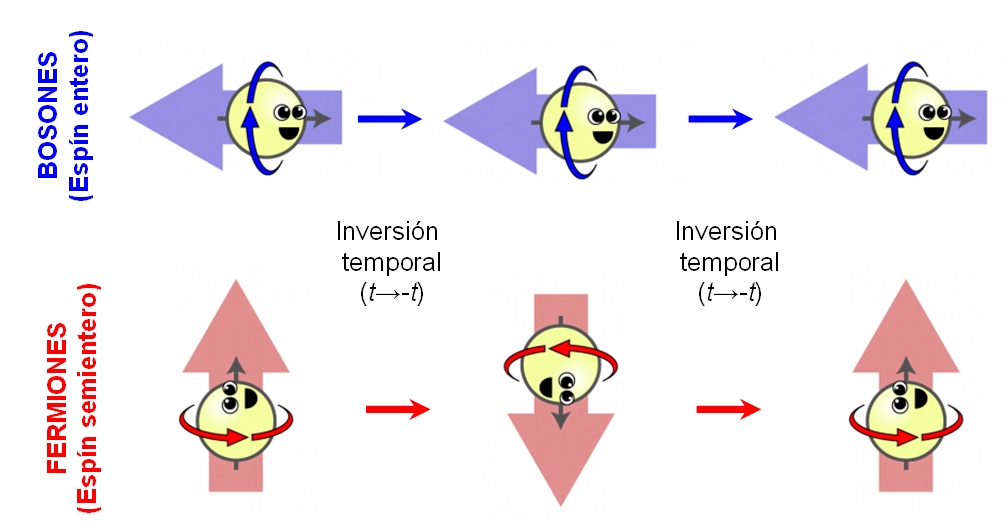
Las partículas con espín entero se llaman bosones, y las que tienen espín entero más un medio se llaman fermiones. Consultado los valores del espín en la tabla anterior podemos ver que los leptones y los bariones son fermiones, y que los mesones y los fotones son bosones. En muchos aspectos, los fermionesse comportan de manera diferente de los bosones. Los fermiones tienen la propiedad de que cada uno de ellos requiere su propio espacio: dos fermiones del mismo tipo no pueden ocupar o estar en el mismo punto, y su movimiento está regido por ecuaciones tales que se evitan unos a otros. Curiosamente, no se necesita ninguna fuerza para conseguir esto. De hecho, las fuerzas entre los fermiones pueden ser atractivas o repulsivas, según las cargas. El fenómeno por el cual cada fermión tiene que estar en un estado diferente se conoce como el principio de exclusión de Pauli. Cada átomo está rodeado de una nube de electrones, que son fermiones (espín ½). Si dos átomos se aproximan entre sí, los electrones se mueven de tal manera que las dos nubes se evitan una a otra, dando como resultado una fuerza repulsiva. Cuando aplaudimos, nuestras manos no se atraviesan pasando la uno a través de la otra. Esto es debido al principio de exclusión de Pauli para los electrones de nuestras manos que, de hecho, los de la izquierda rechazan a los de la derecha.
En contraste con el característico individualismo de los fermiones, los bosones se comportan colectivamente y les gusta colocarse todos en el mismo lugar. Un láser, por ejemplo, produce un haz de luz en el cual muchísimos fotones llevan la misma longitud de onda y dirección de movimiento. Esto es posible porque los fotones son bosones.
Cuando hemos hablado de las fuerzas fundamentales que, de una u otra forma, interaccionan con la materia, también hemos explicado que la interacción débil es la responsable de que muchas partículas y también muchos núcleos atómicos exóticos sean inestables. La interacción débil puede provocar que una partícula se transforme en otra relacionada, por emisión de un electrón y un neutrino. Enrico Fermi, en 1934, estableció una fórmula general de la interacción débil, que fue mejorada posteriormente por George Sudarshan, Robert Marschak, Murray Gell-Mann, Richard Feynman y otros. La fórmula mejorada funciona muy bien, pero se hizo evidente que no era adecuada en todas las circunstancias.
En 1970, de las siguientes características de la interacción débil sólo se conocían las tres primeras:
- La interacción actúa de forma universal sobre muchos tipos diferentes de partículas y su intensidad es aproximadamente igual para todas (aunque sus efectos pueden ser muy diferentes en cada caso). A los neutrinos les afecta exclusivamente la interacción débil.
- Comparada con las demás interacciones, ésta tiene un alcance muy corto.
- La interacción es muy débil. Consecuentemente, los choques de partículas en los cuales hay neutrinos involucrados son tan poco frecuentes que se necesitan chorros muy intensos de neutrinos para poder estudiar tales sucesos.
- Los mediadores de la interacción débil, llamados W+, W– y Z0, no se detectaron hasta la década de 1980. al igual que el fotón, tienen espín 1, pero están eléctricamente cargados y son muy pesados (esta es la causa por la que el alcance de la interacción es tan corto). El tercer mediador, Z0, que es responsable de un tercer tipo de interacción débil que no tiene nada que ver con la desintegración de las partículas llamada “corriente neutra”, permite que los neutrinos puedan colisionar con otras partículas sin cambiar su identidad.
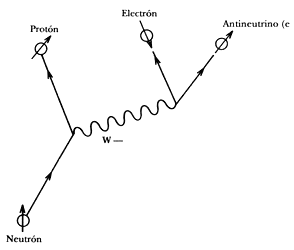
A partir de 1970, quedó clara la relación de la interacción débil y la electromagnética (electrodébil de Weinberg-Salam).
La interacción fuerte (como hemos dicho antes) sólo actúa entre las partículas que clasificamos en la familia llamada de los hadrones, a los que proporciona una estructura interna complicada. Hasta 1972 sólo se conocían las reglas de simetría de la interacción fuerte y no fuimos capaces de formular las leyes de la interacción con precisión.
Como apuntamos, el alcance de esta interacción no va más allá del radio de un núcleo atómico ligero (10-13 cm aproximadamente).
La interacción es fuerte. En realidad, la más fuerte de todas.
Lo dejaré aquí, en verdad, eso que el Modelo Estándar de la Física, es feo, complejo e incompleto y, aunque hasta el momento es una buena herramienta con la que trabajar, la verdad es que, se necesita un nuevo modelo más avanzado y que incluya la Gravedad.
Veremos que nos trae la nueva etapa del LHC que busca los componentes de la “materia oscura”.
emilio silvera
Abr
20
Maravillas de la Física
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (1)
Comments (1)

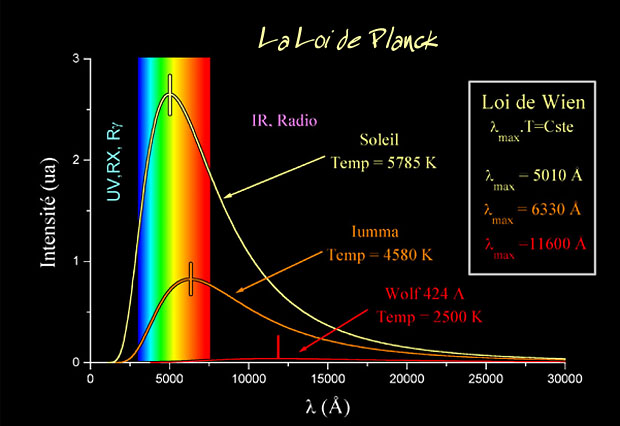
La Física del siglo XX empezó exactamente en el año 1900, cuando el físico alemán Max Planck propuso una posible solución a un problema que había estado intrigando a los físicos durante años. Es el problema de la luz que emiten los cuerpos calentados a una cierta temperatura, y también la radiación infrarroja emitida, con menos intensidad, por los objetos más fríos. Planck escribió un artículo de ocho páginas y el resultado fue que cambió el mundo de la física y aquella páginas fueron la semilla de la futura ¡mecánica cuántica! que, algunos años más tardes, desarrollarían físicos como Einstein (Efecto fotoeléctrico), Heisenberg (Principio de Incertidumbre), Feynman, Bhor, Schrödinger, Dirac…
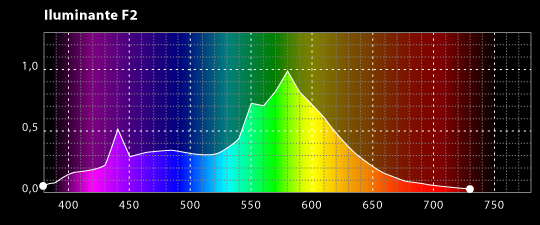
La expresión radiación se refiere a la emisión continua de energía de la superficie de todos los cuerpos. Los portadores de esta energía son las ondas electromagnéticas producidas por las vibraciones de las partículas cargadas que forman parte de los átomos y moléculas de la materia. La radiación electromagnética que se produce a causa del movimiento térmico de los átomos y moléculas de la sustancia se denomina radiación térmica o de temperatura.

Ley de Planck para cuerpos a diferentes temperaturas.
Estaba bien aceptado entonces que esta radiación tenía un origen electromagnético y que se conocían las leyes de la naturaleza que regían estas ondas electromagnéticas. También se conocían las leyes para el frío y el calor, la así llamada “termodinámica”, o al menos eso parecía.

Pero si usamos las leyes de la termodinámica para calcular la intensidad de la radiación, el resultado no tiene ningún sentido. Los cálculos nos dicen que se emitiría una cantidad infinita de radiación en el ultravioleta más lejano, y, desde luego, esto no es lo que sucede. Lo que se observa es que la intensidad de la radiación muestra un pico o una cierta longitud de onda característica, y que la intensidad disminuye tanto para longitudes mayores como para longitudes menores. Esta longitud característica es inversamente proporcional a la temperatura absoluta del objeto radiante (la temperatura absoluta se define por una escala de temperatura que empieza a 273 ºC bajo cero). Cuando a 1.000 ºC un objeto se pone al “rojo vivo”, el objeto está radiando en la zona de la luz visible.

Acero al “rojo vivo”, el objeto está radiando en la zona de la luz visible.

Lo que Planck propuso fue simplemente que la radiación sólo podía ser emitida en paquetes de un tamaño dado. La cantidad de energía de uno de esos paquetes, o cuantos, es inversamente proporcional a la longitud de onda y, por lo tanto, proporcional a la frecuencia de la radiación emitida. La sencilla fórmula es:
E = hv
Donde E es la energía del paquete, v es la frecuencia y h es una nueva constante fundamental de la naturaleza, la constante de Planck. Cuando Planck calculó la intensidad de la radiación térmica imponiendo esta nueva condición, el resultado coincidió perfectamente con las observaciones.

Poco tiempo después, en 1905, Einstein formuló esta teoría de una manera mucho más tajante: el sugirió que los objetos calientes no son los únicos que emiten radiación en paquetes de energía, sino que toda la radiación consiste en múltiplos del paquete de energía de Planck.

El príncipe francés Louis Victor de Broglie, dándole otra vuelta a la teoría, que no sólo cualquier cosa que oscila tiene una energía, sino que cualquier cosa con energía se debe comportar como una “onda” que se extiende en una cierta dirección del espacio, y que la frecuencia, v, de la oscilación verifica la ecuación de Planck. Por lo tanto, los cuantos asociados con los rayos de luz deberían verse como una clase de partículas elementales: el fotón. Todas las demás clases de partículas llevan asociadas diferentes ondas oscilatorias de campos de fuerza.
Es curioso el comportamiento de los electrones en el interior del átomo, descubierto y explicado por el famoso físico danés Niels Bohr, se pudo atribuir a las ondas de De Broglie. Poco después, en 1926, Edwin Schrödinger descubrió como escribir la teoría ondulatoria de De Broglie con ecuaciones matemáticas exactas. La precisión con la cual se podían realizar los cálculos era asombrosa, y pronto quedó claro que el comportamiento de todos los objetos pequeños quedaba exactamente determinado por las recién descubiertas “ecuaciones de onda cuántica”.

No hay duda de que la Mecánica Cuántica funciona maravillosamente bien. Sin embargo, surge una pregunta muy formal: ¿qué significan realmente esas ecuaciones?, ¿qué es lo que están describiendo? Cuando Isaac Newton, allá por el año 1687, formuló cómo debían moverse los planetas alrededor del Sol, estaba claro para todo el mundo lo que significaban sus ecuaciones: que los planetas están siempre en una posición bien definida en el espacio y que sus posiciones y sus velocidades en un momento concreto determinan inequívocamente cómo evolucionarán las posiciones y las velocidades con el tiempo.
Pero para los electrones todo esto es muy diferente. Su comportamiento parece estar envuelto en la bruma. Es como si pudieran “existir” en diferentes lugares simultáneamente, como si fueran una nube o una onda, y esto no es un efecto pequeño. Si se realizan experimentos con suficiente precisión, se puede determinar que el electrón parece capaz de moverse simultáneamente a lo largo de trayectorias muy separadas unas de otras. ¿Qué puede significar todo esto?
Niels Bohr consiguió responder a esta pregunta de forma tal que con su explicación se pudo seguir trabajando y muchos físicos siguen considerando su respuesta satisfactoria. Se conoce como la “interpretación de Copenhague” de la Mecánica Cuántica. En vez de decir que el electrón se encuentra en el punto x o en el punto y, nosotros hablamos del estado del electrón. Ahora no tenemos el estado “x” o el estado “y”, sino estados “parcialmente x” o “parcialmente y. Un único electrón puede encontrarse, por lo tanto, en varios lugares simultáneamente. Precisamente lo que nos dice la Mecánica Cuántica es como cambia el estado del electrón según transcurre el tiempo.
Un “detector” es un aparato con el cual se puede determinar si una partícula está o no presente en algún lugar pero, si una partícula se encuentra con el detector su estado se verá perturbado, de manera que sólo podemos utilizarlo si no queremos estudiar la evolución posterior del estado de la partícula. Si conocemos cuál es el estado, podemos calcular la probabilidad de que el detector registre la partícula en el punto x.

Las leyes de la Mecánica Cuántica se han formulado con mucha precisión. Sabemos exactamente como calcular cualquier cosa que queramos saber. Pero si queremos “interpretar” el resultado, nos encontramos con una curiosa incertidumbre fundamental: que varias propiedades de las partículas pequeñas no pueden estar bien definidas simultáneamente. Por ejemplo, podemos determinar la velocidad de una partícula con mucha exactitud, pero entonces no sabremos exactamente dónde se encuentra; o, a la inversa. Si una partícula tiene “espín” (rotación alrededor de su eje), la dirección alrededor de la cual está rotando (la orientación del eje) no puede ser definida con gran precisión.
No es fácil explicar con sencillez de dónde viene esta incertidumbre, pero hay ejemplos en la vida cotidiana que tienen algo parecido. La altura de un tono y la duración en el tiempo durante el cual oímos el tono tienen una incertidumbre mutua similar.

¿Onda o partícula? ¡Ambas a la vez! ¿Cómo es eso?
Para que las reglas de la Mecánica Cuántica funcionen, es necesario que todos los fenómenos naturales en el mundo de las cosas pequeñas estén regidos por las mismas reglas. Esto incluye a los virus, bacterias e incluso a las personas. Sin embargo, cuanto más grande y más pesado es un objeto más difícil es observar las desviaciones de las leyes del movimiento “clásicas” debidas a la mecánica cuántica.
Me gustaría referirme a esta exigencia tan importante y tan peculiar de la teoría con la palabra “holismo”. Esto no es exactamente lo mismo que entienden algunos filósofos por “holismo”, y que se podría definir como “el todo es más que la suma de las partes”.
Bien, si la Física nos ha enseñado algo, es justamente lo contrario: un objeto compuesto de un gran número de partículas puede ser entendido exactamente si se conocen las propiedades de sus partes (las partículas): basta que uno sepa sumar correctamente (¡y esto no es nada fácil en mecánica cuántica!). Lo que yo entiendo por holismo es que, efectivamente, el todo es la suma de las partes, pero sólo se puede hacer la suma si todas las partes obedecen a las mismas leyes.
Por ejemplo, la constante de Planck, h = 6,626075…x 10 exp. -34 julios segundo, debe ser exactamente la misma para cualquier objeto en cualquier sitio, es decir, debe ser una constante universal.
Las reglas de la mecánica cuántica funcionan tan bien que refutarlas resulta realmente difícil. Los trucos ingeniosos descubiertos por Werner Heisenberg, Paul Dirac y muchos otros mejoraron y completaron las reglas generales. Pero Einstein y otros pioneros tales como Edwin Schrödinger, siempre presentaron serias objeciones a esta interpretación.
Quizá funcione bien, pero ¿dónde está exactamente el electrón, en el punto x o en el punto y? Em pocas palabras, ¿dónde está en realidad?, ¿cuál es la realidad que hay detrás de nuestras fórmulas? Si tenemos que creer a Bohr, no tiene sentido buscar tal realidad. Las reglas de la mecánica cuántica, por sí mismas, y las observaciones realizadas con detectores son las únicas realidades de las que podemos hablar.

Hasta hoy, muchos investigadores coinciden con la actitud pragmática de Bohr. Los libros de historia dicen que Bohr demostró que Einstein estaba equivocado. Pero no son pocos, incluyéndome a mí, los que sospechamos que a largo plazo el punto de vista de Einstein volverá: que falta algo en la interpretación de Copenhague. Las objeciones originales de Einstein pueden superarse, pero aún surgen problemas cuando uno trata de formular la mecánica cuántica para todo el Universo (donde las medidas no se pueden repetir) y cuando se trata de reconciliar las leyes de la mecánica cuántica con las de la Gravitación… ¡Infinitos!
La mecánica cuántica y sus secretos han dado lugar a grandes controversias, y la cantidad de disparates que ha sugerido es tan grande que los físicos serios ni siquiera sabrían por donde empezar a refutarlos. Algunos dicen que “la vida sobre la Tierra comenzó con un salto cuántico”, que el “libre albedrío” y la “conciencia” se deben a la mecánica cuántica: incluso fenómenos paranormales han sido descritos como efectos mecanocuánticos.

Yo sospecho que todo esto es un intento de atribuir fenómenos “ininteligibles” a causas también “ininteligibles” (como la mecánica cuántica) dónde el resultado de cualquier cálculo es siempre una probabilidad, nunca una certeza.
Claro que, ahí están esas teorías más avanzadas y modernas que vienen abriendo los nuevos caminos de la Física y que, a mi no me cabe la menor duda, más tarde o más temprano, podrá explicar con claridad esas zonas de oscuridad que ahora tienen algunas teorías y que Einstein señalaba con acierto.
¿No es curioso que, cuando se formula la moderna Teoría M, surjan, como por encanto, las ecuaciones de Einstein de la Relatividad General? ¿Por qué están ahí? ¿Quiere eso decir que la Teoría de Einstein y la Mecánica Cuántica podrán al fin unirse en pacifico matrimonio sin que aparezcan los dichosos infinitos?
Bueno, eso será el origen de otro comentario que también, cualquier día de estos, dejaré aquí para todos ustedes.
emilio silvera
Abr
20
¡Fluctuaciones de vacío! ¿Que son?
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (0)
Comments (0)
Un fuerte campo gravitatorio puede inducir un efecto desbocado en las fluctuaciones cuánticas que se producen en el espacio, aparentemente vacío, …
En física cuántica, la fluctuación cuántica es un cambio temporal en la cantidad de energía en un punto en el espacio como resultado del Principio de Incertidumbre que imaginó Werner Heisenberg. De acuerdo a una formulación de este principio energía y tiempo se relacionan de la siguiente forma:
Esto significa que la conservación de la energía puede parecer violada, pero sólo por breves lapsos. Esto permite la creación de pares partícula-antipartícula de partículas virtuales. El efecto de esas partículas es medible, por ejemplo, en la carga efectiva del electrón, diferente de su carga “desnuda”. En una formulación actual, la energía siempre se conserva, pero los estados propios del Hamiltoniano no son los mismos que los del operador del número de partículas, esto es, si está bien definida la energía del sistema no está bien definido el número de partículas del mismo, y viceversa, ya que estos dos operadores no conmutan.

Las fluctuaciones del vacío entre una esfera y una superficie plana
En un estudio realizado por un equipo de físicos con avanzados aparatos, han hallado un resultado del que nos dicen:
“La materia se construye sobre fundamentos frágiles. Los físicos acaban de confirmar que la materia, aparentemente sustancial, es en realidad nada más que fluctuaciones en el vació cuántico. Los investigadores simularon la frenética actividad que sucede en el interios de los protones y neutrones, que como sabéis son las partículas que aportan casi la totalidad de la masa a la materia común.
Cada protón (o neutrón) se compone de tres quarks – véase ilustración – pero las masas individuales de estos quarks apenas comprenden el 1% del total de la masa del protón¿Entonces de dónde sale el resto? La teoría sostiene que esta masa es creada por la fuerza que mantiene pegados a los quarks, y que se conoce como fuerza nuclear fuerte. En términos cuánticos, la fuerza fuerte es contenida por un campo de partículas virtuales llamadas gluones, las cuales irrumpen aleatoriamente en la existencia para desaparecer de nuevo. La energía de estas fluctuaciones del vacío debe sumarse a la masa total del neutróny del protón.”
Tiene y encierra tantos misterios la materia que estamos aún y años-luz de y conocer sobre su verdadera naturaleza. Es algo que vemos en sus distintas formas materiales que configuran y conforman todo lo material desde las partículas elementales hasta las montañas y los océanos. Unas veces está en estado “inerte” y otras, se eleva hasta la vida que incluso, en ocasiones, alcanza la consciencia de SER. Sin embargo, no acabamos de dilucidar de dónde viene su verdadero origen, su esencia, lo que era antes de “ser” materia. ¿Existe acaso una especie de sustancia cósmica anterior a la materia? Y, si realmente existe esa sustancia… ¿Dónde está?
Claro que hemos llegado a saber que las llamadas fluctuaciones del vacío son oscilaciones aleatorias, impredecibles e ineliminables de un campo de fuerza (electromagnético o gravitatorio) que son debidas a un “tira y afloja” en el que pequeñas regiones del espacio toman prestada, momentáneamente, energía de regiones adyacentes y luego las devuelven. Pero…
– ¿Qué regiones adyacentes?
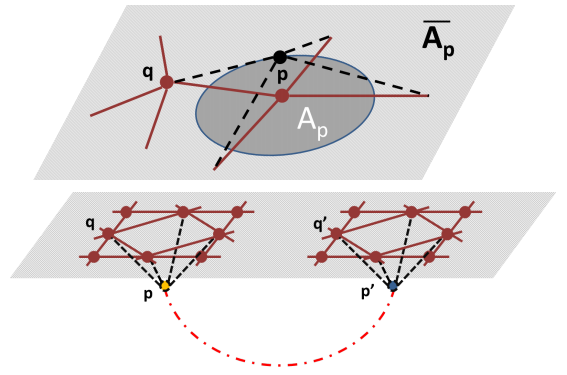
“No sabemos de qué está hecho el espacio a nivel cuántico. Pero no importa, pues podemos describir dichos elementos de espacio y sus relaciones usando un grafo de espacios de Hilbert. El famoso Sean Carroll y su colega Chun Jun Cao usan esta idea para ilustrar cómo podrían emerger algunas propiedades del espacio. Por desgracia todavía no han logrado que emerja el tiempo, ni el espaciotiempo descrito por la relatividad de Einstein.”
Acaso universos paralelos, acaso deformaciones del espacio-tiempo a escalas microscópicas, micros agujeros negros que pasan a ser agujeros blancos salidos de estas regiones o campos de fuerza que no podemos ver pero sí sentir, y, en última instancia, ¿por qué se forman esas partículas virtuales que de inmediato se aniquilan y desaparecen antes de que puedan ser capturadas? ¿Qué sentido tiene todo eso?

Las consecuencias de la existencia del cuanto mínimo de acción fueron revolucionarios para la comprensión del vacío. Mientras la continuidad de la acción clásica suponía un vacío plano, estable y “realmente” vacío, la discontinuidad que supone el cuanto nos dibuja un vacío inestable, en continuo cambio y muy lejos de poder ser considerado plano en las distancias atómicas y menores. El vacío cuántico es de todo menos vacío, en él la energía nunca puede quedar estabilizada en valor cero, está fluctuando sobre ese valor, continuamente se están creando y aniquilando todo tipo de partículas, llamadas por eso virtuales, en las que el producto de su energía por el tiempo de su existencia efímera es menor que el cuanto de acción. Se llaman fluctuaciones cuánticas del vacío y son las responsables de que exista un que lo inunda todo llamado campo de punto cero.
Pero volvamos de nuevo a las fluctuaciones de vacío, que al igual que las ondas “reales” de energía positiva, están sujetas a las leyes de la dualidad onda/partícula; es decir, tienen tanto aspectos de onda como aspectos de partícula.

“El vacío es una sustancia. Las fluctuaciones cuánticas de energía cero del estado de vacío del campo electromagnético se pueden medir de forma indirecta.”
Las ondas fluctúan de forma aleatoria e impredecible, con energía positiva momentáneamente aquí, energía negativa momentáneamente allí, y energía cero en promedio. El aspecto de partícula está incorporado en el concepto de partículas virtuales, es decir, partículas que pueden nacer en pares (dos partículas a un tiempo), viviendo temporalmente de la energía fluctuacional tomada prestada de regiones “vecinas” del , y que luego se aniquilan y desaparecen, devolviendo la energía a esas regiones “vecinas”. Si hablamos de fluctuaciones electromagnéticas del vacío, las partículas virtuales son fotones virtuales; en el caso de fluctuaciones de la gravedad en el vacío, son gravitones virtuales.
De las llamadas fluctuaciones de vacío pueden surgir, partículas virtuales y quién sabe que cosas más… Hasta un nuevo Universo.

Son muchas las preguntas que no tienen respuestas
Parece que las fluctuaciones ocurren en cualquier lugar, pero que, son tan minúsculas que ningún observador o experimentador las ha detectado de una manera franca hasta la fecha y, se sabe que están ahí por experimentos que lo han confirmado. Estas fluctuaciones son más poderosas cuanto menos escala se considera en el espacio y, por debajo de la longitud de Planck-Wheeler las fluctuaciones de vacío son tan enormes que el espacio tal como lo conocemos “pareciera estar hirviendo” para convertirse en una especie de espuma cuántica que parece que en realidad, cubre todo el espacio “vacío cuántico” que sabemos que está ahí y es el campo del que surgen esas partículas virtuales que antes mencionaba.

¿Espuma cuántica? Si profundizamos mucho en la materia… Podríamos ver otro universo distinto al nuestro. Las cosas miles de millones de veces más pequeñas que en nuestro mundo cotidiano, no parecen las mismas cosas.
Hay magnitudes asociadas con las leyes de la gravedad cuántica. La longitud de Planck-Wheeler, ![]() es la escala de longitud por debajo de la cual el tal como lo conocemos deja de existir y se convierte en espuma cuántica. El tiempo de Planck-Wheeler (1/c veces la longitud de Planck-Wheeler o aproximadamente 10-43 segundos), es el intervalo de tiempo más corto que puede existir; si dos sucesos están separados por menos que esto, no se puede decir cuál sucede antes y cuál después. El área de Planck-Wheeler (el cuadrado de la longitud de Planck-Wheeler, es decir, 2,61×10-66cm2) juega un papel clave en la entropía de un agujero negro. ¡Qué locura!
es la escala de longitud por debajo de la cual el tal como lo conocemos deja de existir y se convierte en espuma cuántica. El tiempo de Planck-Wheeler (1/c veces la longitud de Planck-Wheeler o aproximadamente 10-43 segundos), es el intervalo de tiempo más corto que puede existir; si dos sucesos están separados por menos que esto, no se puede decir cuál sucede antes y cuál después. El área de Planck-Wheeler (el cuadrado de la longitud de Planck-Wheeler, es decir, 2,61×10-66cm2) juega un papel clave en la entropía de un agujero negro. ¡Qué locura!
Como tantas veces hemos comentado, los trabajos que se han realizado sobre poder construir una teoría cuántica de la gravedad nos llevan a un sorprendente de implicaciones. Por un lado, sólo se ha podido conceptuar a la gravedad cuántica, siempre y cuando, el universo tenga más de cuatro dimensiones. Además, se llega a considerar que en la era de Planck, tanto el universo como la gravedad pudieron ser una sola cosa compacta estructurada por objetos cuánticos infinitamente diminutos, como los que suponemos que conforman las supercuerdas. A esta escala, el mismísimo espaciotiempo estaría sometido a imprescindibles fluctuaciones muy semejantes a las que causan las partículas al nacer y desaparecer de la existencia en el espacio-tiempo ordinario. Esta noción ha conducido a los teóricos a describir el universo de la era cuántica como una especie de extremadamente densa y agitada espuma que pudo haber contenido las vibrantes cuerdecillas que propugnan los cosmólogos cuerdistas.
Los físicos especulan que el cosmos ha crecido a desde una «nada» primigenia que al nacer comenzó el principio del tiempo y que, en ese parto, contenía toda la materia y toda la energía.

En física como en todas las demás disciplinas científicas, los conocimientos avanzan y las teorías que sostuvieron los cimientos de nuestros conocimientos se van haciendo viejas y van teniendo que ser reforzadas con las nuevas y más poderosas “vigas” de las nuevas ideas y los nuevos hallazgos científicos que hacen posible ir perfeccionando lo que ya teníamos.
Recientemente se han alzado algunas voces contra el Principio de Incertidumbre de Heisenberg. He podido leer en un artíoculo de la prestigiosa Revista Nature, un artículo del premio Nobel de Física Gerald ´t Hoofft, en el que propone que la naturaleza probabilistica de la mecánica cuántica, desaparecería a la escala de Planck, en la que el comportamiento de la materia sería determinista; a longitudes mayores, energías más pequeñas.
El mundo de lo muy pequeño (el micro espacio), a nivel atómico y subatómico, es el dominio de la física cuántica, así nunca podríamos saber, de acuerdo m con el principio de incertidumbre, y, en un momento determinado, la posición y el estado de una partícula. Este estado podría ser una función de la escala espacio-temporal. A esta escala tamaños todo sucede demasiado deprisa para nosotros.

El “universo cuántico” nada es lo que parece a primera vista, allí entramos en otro mundo que en nada, se parece al nuestro
Cuando hablamos de la mecánica cuántica, tenemos mirar un poco hacia atrás en el tiempo y podremos darnos del gran impacto que tuvo en el devenir del mundo desde que, en nuestras vidas, apareció el átomo y, más tarde, sus contenidos. Los nombres de Planck, Einstein, Bohr, Heisenberg, Schrödinger, Pauli, Bardeen, Roentgen, Dirac y muchos otros, se pudieron a la cabeza de la lista de las personas más famosas. Aquel primer premio Nobel de Física otorgado en 1900 a Roentgen por descubrir los rayos X, en el mismo año llegaría el ¡cuanto! De Planck que inspiró a Einstein para su trabajo sobre el Efecto fotoeléctrico que también, le valdría el Nobel, y, a partir de ese momento, se desencadenó una especie de alucinante por saber sobre el átomo, sus contenidos, y, de qué estaba hecha la materia.
La conocida como Paradoja EPR y los conceptos de Tiempo y , presente, pasado y futuro.
“Nadie ha resuelto la paradoja del gato de Schrödinger, ni la paradoja de Einstein-Podolsky-Rosen. El principio de incertidumbre no se ha explicado y se asume como un dogma, lo mismo pasa con el spin. El spin no es un giro pero es un giro. Aquí hay un desafío al pensamiento humano. ¡Aquí hay una aventura del pensamiento!”
Fueron muchas las polémicas desatadas a cuenta de las aparentes incongruencias de la moderna Mecánica Cuántica. La paradoja de Einstein-Podolsky-Rosen, denominada “Paradoja EPR”, trata de un experimento mental propuesto por Albert Einstein, Boris Podolsky y Nathan Rosen en 1935. Es relevante, pues pone de manifiesto un problema aparente de la mecánica cuántica, y en las décadas siguientes se dedicaron múltiples esfuerzos a desarrollarla y resolverla.
A Einstein (y a muchos otros científicos), la idea del entrelazamiento cuántico le resultaba extremadamente perturbadora. Esta particular característica de la mecánica cuántica permite preparar estados de dos o más partículas en los cuales es imposible obtener útil sobre el estado total del sistema haciendo sólo mediciones sobre una de las partículas.

Por otro lado, en un entrelazado, manipulando una de las partículas, se puede modificar el estado total. Es decir, operando sobre una de las partículas se puede modificar el estado de la otra a distancia de manera instantánea. Esto habla de una correlación entre las dos partículas que no tiene paralaje en el mundo de nuestras experiencias cotidianas. Cabe enfatizar pues que cuando se mide el estado de una partícula, enseguida sabemos el estado de la otra, lo cual aparentemente es instantáneo, es decir, sin importar las distancias a las que se encuentren las partículas, una de la otra, ambas saben instantáneamente el estado de la otra.
El experimento planteado por EPR consiste en dos partículas que interactuaron en el pasado y que quedan en un estado entrelazado. Dos observadores reciben cada una de las partículas. Si un observador mide el momento de una de ellas, sabe cuál es el momento de la otra. Si mide la posición, gracias al entrelazamiento cuántico y al principio de incertidumbre, puede la posición de la otra partícula de forma instantánea, lo que contradice el sentido común.

Animación que muestra dos átomos de oxígeno fusionándose para formar una molécula de O2 en su estado cuántico fundamental. Las nubes de color representan los orbitales atómicos. Los orbitales 2s y 2p de cada átomo se combinan para formar los orbitales σ y π de la molécula, que la mantienen unida. Los orbitales 1s, más interiores, no se combinan y permiten distinguir a cada núcleo. Lo que ocurre a escalas tan pequeñas es fascienante.
Si nos pudiéramos convertir en electrones, por ejemplo, sabríamos dónde y cómo estamos en cada momento y podríamos ver asombrados, todo lo que estaba ocurriendo a nuestro alrededor que, entonces sí, veríamos transcurrir a un ritmo más lento del que podemos detectar en los electrones desde nuestro macroestado espacio temporal. El electrón, bajo nuestro punto de vista se mueve alrededor del núcleo atómico a una velocidad de 7 millones de km/h.
A medida que se asciende en la escala de tamaños, hasta el tiempo se va ajustando a esta escala, los objetos, a medida que se hacen mayores se mueven más despacio y, además, tienen más duración que los pequeños objetos infinitesimales del micro mundo cuántico. La vida media de un neutron es de unos 15 minutos, por ejemplo, mientras que la vida media de una estrellas se puede contar en miles de millones de años.
En nuestra macroescala, los acontecimientos y ,los objetos se mueven a velocidades que a nosotros nos parecen normales. Si se mueven con demasiada lentitud nos parece que no se mueven. Así hablamos de escala de tiempo geológico, para referirnos al tiempo y velocidad de la mayor parte de los acontecimientos geológicos que afectan a la Tierra, el tiempo transcurre aquí en millones de años y nosotros ni lo apreciamos; nos parece que todo está inmóvil. Nosotros, los humanos, funcionamos en la escala de años (tiempo biológico).

El Tiempo Cosmológico es aún mucho más dilatado y los objetos cósmicos (mundos, estrellas y galaxias), tienen una mayor duración aunque su movimiento puede ser muy rápido debido a la inmensidad del espacio universal en el que se mueven. La Tierra, por ejemplo, órbita alrededor del Sol a una velocidad media de 30 Km/s., y, el Sol, se desplaza por la Galaxia a una velocidad de 270 km/s. Y, además, se puede incrementar el tiempo y el espacio en su andadura al estar inmersos y ligados en una misma maya elástica.
Así, el espacio dentro de un átomo, es muy pequeño; dentro de una célula, es algo mayor; dentro de un animal, mayor aún y así sucesivamente… hasta llegar a los enormes espaciosa que separan las estrellas y las galaxias en el Universo.

Distancias astronómicas separan a las estrellas entre sí, a las galaxias dentro del cúmulo, y a los cúmulos en los supercúmulos.
Las distancias que separan a los objetos del Cosmos se tienen que medir con unidades espaciales, tal es su inmensa magnitud que, nuestras mentes, aunque podamos hablar de ellas de manera cotidiana, en realidad, no han llegado a asimilarlas.Y, a todo ésto, los físicos han intentado con denuedo elaborar una teoría completa de la gravedad que incluya la mecánica cuántica. Los cálculos de la mayoría de las teorías propuesta de la «gravedad cuántica» arrojan numerosos infinitos. Los físicos no están seguros si el problema es técnico o conceptual. No obstante, incluso prescindiendo de una teoría completa de gravedad cuántica, se puede deducir que los efectos de la teoría cuántica, habrían cruciales durante los primeros 10-43 segundos del inicio del universo, cuando éste tenía una densidad de 1093 gramos por centímetro cúbico y mayor. (El plomo sólido tiene una densidad de aproximadamente diez gramos por centímetro cúbico.) Este período, que es el que corresponde a la era de Planck, y a su estudio se le llama cosmología cuántica. Como el universo en su totalidad habría estado sujeto a grandes incertidumbres y fluctuaciones durante la era de Planck o era cuántica, con la materia y la energía apareciendo y desapareciendo de un vacío en grandes cantidades, el concepto de un principio del universo podría no tener un significado bien definido. En todo caso, la densidad del universo durante este período es de tal magnitud que escapa a nuestra comprensión. Para propósitos prácticos, la era cuántica podría considerarse el estado inicial, o principio, del universo. En consecuencia, los procesos cuánticos ocurridos durante este período, cualquiera sea su naturaleza, determinaron las iniciales del universo.

Una cosa nos ha podido quedar clara: Los científicos para lograr conocer la estructura del universo a su escala más grande, deben retroceder en el tiempo, centrando sus teorías en el momento en que todo comenzó. Para ello, como todos sabéis, se han formulado distintas teorías unificadoras de las cuatro fuerzas de la naturaleza, con las cuales se han modelado acontecimiento y en el universo primitivo casi a todo lo largo del camino hasta el principio. Pero cómo se supone que debió haber habido un «antes», aparece una barrera que impide ir más allá de una frontera que se halla fijada a los 10-43 [s] después del Big Bang, un instante conocido como «momento de Planck», en homenaje al físico alemán Max Planck.

Esta barrera existe debido a que antes del momento de Planck, durante el período llamado la «era de Planck o cuántica», se supone que las cuatro fuerza fundamentales conocidas de la naturaleza eran indistinguibles o se hallaban unificadas , que era una sola fuerza. Aunque los físicos han diseñado teorías cuánticas que unen tres de las fuerzas, una por una, a través de eras que se remontan al momento de Planck, hasta ahora les ha prácticamente imposible armonizar las leyes de la teoría cuántica con la gravedad de la relatividad de Einstein, en un sólo modelo teórico ampliamente convincente y con posibilidades claras de ser contrastado en experimentos de laboratorio y, mucho menos, con observaciones.
Y después de todo ésto, sólo una caso me queda clara: ¡Lo poco que sabemos! A pesar de la mucha imaginación que ponemos en las cosas que creemos conocer.
emilio silvera
















 Totales: 74.216.189
Totales: 74.216.189 Conectados: 34
Conectados: 34