May
17
Partículas, antipartículas, fuerzas…
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (8)
Comments (8)
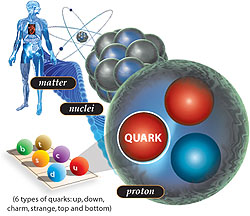
Bajo la “definición basada en quarks y leptones”, las partículas elementales y compuestas formadas de quarks (en púrpura) y leptones (en verde) serían la “materia”; mientras los bosones “izquierda” (en rojo) no serían materia. Sin embargo, la energía de interacción inherente a partículas compuestas (por ejemplo, gluones, que implica a los neutrones y los protones) contribuye a la masa de la materia ordinaria.

Esquema de una aniquilación electrón-positrón.
Ya hemos descrito en trabajos anteriores las dos familias de partículas elementales: Quarks y Leptones. Pero hasta ahí, no se limita la sociedad del “universo” infinitesimal. Existen además las antifamilias. A quarks y electrones se asocian, por ejemplo, antiquarks y antielectrones. A cada partícula, una antipartícula.
Uno de los primeros éxitos de la teoría relativista del campo cuántico fue la predicción de las anti-partículas: nuevos cuantos que eran la imagen especular de las partículas ordinarias. Las antipartículas tienen la misma masa y el mismo spin que sus compañeras las partículas ordinarias, pero cargas inversas. La antipartícula del electrón es el positrón, y tiene, por tanto, carga eléctrica opuesta a la del electrón. Si electrones y positrones se colocan juntos, se aniquilan, liberando la energía inmensa de su masa según la equivalencia masa-energía einsteniana.

¿Cómo predijeron los físicos la existencia de antipartículas? Bueno, por la «interpretación estadística» implicaba que la intensidad de un campo determinaba la probabilidad de hallar sus partículas correspondientes. Así pues, podemos imaginar un campo en un punto del espacio describiendo la creación o aniquilación de sus partículas cuánticas con una probabilidad concreta. Si esta descripción matemática de la creación y aniquilación de partículas cuánticas se inserta en el marco de la teoría relativista del campo cuántico, no podemos contar con la posibilidad de crear una partícula cuántica sin tener también la de crear un nuevo género de partícula: su antipartícula. La existencia de antimateria es imprescindible para una descripción matemáticamente coherente del proceso de creación y aniquilación según la teoría de la relatividad y la teoría cuántica.

La misteriosa sustancia
conocida como “materia oscura” puede ser en realidad una ilusión, creada por la interacción gravitacional entre partículas de corta vida de materia y antimateria. Un mar hirviente de partículas en el espacio puede crear la gravedad repulsiva.

Algunas no se paran en barra, y, por sobresalir y obtener unos minutos de gloria, son capaces de cualquier cosa. El verdadero físico, ante este cartel, quedó asombrado y se preopueso investigar de quá iba todo aquello.
“Investigando un poco, la historia, hasta donde puedo determinarla, es que Alejandro Gallardo es un estudiante de la Facultad de Ingeniería de la UNAM, que está (o quiźa estaba) por presentar su examen de grado en estos días (sin ningún sinodal del área de gravitación) y que tiene alguna relación con la sociedad de astrónomos aficionados que ostensiblemente organizaba la conferencia. Desde hace al menos diez años labora en un intento de describir una fuerza de repulsión gravitatoria usando álgebra elemental, falsando así tanto la gravedad Newtoniana como la Relatividad General. En esto es similar a innumerables personas que hacen ciencia marginal o pseudociencia (entendida como algo que no es ciencia pero que pretende hacerse pasar por ciencia).”

Puede ser posible que las cargas gravitacionales en el vacío cuántico podrían proporcionar una alternativa a la “materia oscura”. La idea se basa en la hipótesis de que las partículas y antipartículas tienen cargas gravitacionales de signo opuesto. Como consecuencia, los pares de partícula-antipartícula virtuales en el vacío cuántico y sus dipolos de forma gravitacional (una carga gravitacional positivos y negativos) pueden interactuar con la materia bariónica para producir fenómenos que se suele atribuir a la materia oscura. Fue el físico del CERN, Dragan Slavkov Hajdukovic, quien propuso la idea, y demostró matemáticamente que estos dipolos gravitacionales podrían explicar las curvas de rotación de las galaxias observadas sin la materia oscura en su estudio inicial. Sin embargo, señaló que quedaba mucho por hacer.
Pero sigamos con la cuántica…

El pionero en comprender que era necesario que existiesen antipartículas fue el físico teórico Paul Dirac, que hizo varías aportaciones importantes a la nueva teoría cuántica. Fue él quien formuló la ecuación relativista que lleva hoy su nombre, y a la que obedece el campo electrónico; constituye un descubrimiento comparable al de las ecuaciones del campo electromagnético de Maxwell. Cuando resolvió su ecuación, Dirac se encontró con que además de describir el electrón tenía soluciones adicionales que describían otra partícula con una carga eléctrica opuesta a la del electrón. ¿Qué significaría aquello? En la época en que Dirac hizo esta observación, no se conocían más partículas con esta propiedad que el protón. Dirac, que no deseaba que las partículas conocidas proliferasen, decidió que las soluciones adicionales de su ecuación describían el protón.
“La llamada ecuación de Dirac es la versión relativista de la ecuación de ondas de la mecánica cuántica y fue formulada por Paul Dirac en 1928. Da una descripción de las partículas elementales de espín ½, como el electrón, y es completamente consistente con los principios de la mecánica cuántica y de la teoría de la relatividad especial. Además de dar cuenta del espín, la ecuación predice la existencia de antimateria.”
Pero, tras un análisis más meticuloso, se hizo evidente que las partículas que describían las soluciones adicionales tenían que tener exactamente la misma masa que el electrón. Quedaba así descartado el protón, cuya masa es por lo menos, 1.800 veces mayor que la del electrón. Por tanto, las soluciones adicionales tenían que corresponder a una partícula completamente nueva de la misma masa que el electrón, pero de carga opuesta: ¡El antielectrón! Esto quedó confirmado a nivel experimental en 1932 cuando Carl Anderson, físico del Instituto de Tecnología de Calífornia, detectó realmente el antielectrón, que hoy se llama positrón.

Antes de empezar, debemos recordar que el Premio Nobel de Física de 1936 se repartió a partes iguales entre Victor Franz Hess y Carl David Anderson. Merece la pena leer la Nobel Lecture de Carl D. Anderson, “The production and properties of positrons,” December 12, 1936, quien nos explica que en esta imagen un “electrón” de 63 MeV atraviesa un placa de plomo de 6 mm y emerge con una energía de 23 MeV, pero lo hace con la curvatura “equivocada” como si fuera una partícula de carga positiva, como si fuera un protón pero con la masa de un electrón. La Nobel Lecture muestra muchas otras fotografías de positrones y electrones. Anderson afirma: “The present electron theory of Dirac provides a means of describing many of the phenomena governing the production and annihilation of positrons.”

Por otro lado, el Premio Nobel de Física de 1933 se repartió a partes iguales entre Erwin Schrödinger y Paul Adrien Maurice Dirac. También vale la pena leer la Nobel Lecture de Paul A. M. Dirac, “Theory of electrons and positrons,” December 12, 1933, aunque no cuente la historia de su descubrimiento, afirma que su ecuación predice el “antielectrón” de soslayo: ”There is one other feature of these equations which I should now like to discuss, a feature which led to the prediction of the positron.” (fuente: Francis (th)E mule Science’s News).


La aparición de las antipartículas cambió definitivamente el modo de pensar de los físicos respecto a la materia. Hasta entonces, se consideraba la materia permanente e inmutable. Podían alterarse las moléculas, podían desintegrarse los átomos en procesos radiactivos, pero los cuántos fundamentales se consideraban invariables. Sin embargo, tras el descubrimiento de la antimateria realizado por Paul Dirac hubo que abandonar tal criterio. Heisenberg lo expresaba así:

“Creo que el hecho de que Dirac haya descubierto partículas y antipartículas, ha cambiado toda nuestra visión de la física atómica… creo que, hasta entonces, todos los físicos habían concebido las partículas elementales siguiendo los criterios de la filosofía de Demócrito, es decir, considerando esas partículas elementales como unidades inalterables que se hallan en la naturaleza como algo dado y son siempre lo mismo, jamás cambian, jamás pueden transmutarse en otra cosa. No son sistemas dinámicos, simplemente existen en sí mismas. Tras el descubrimiento de Dirac, todo parecía distinto, porque uno podía preguntar: ¿por qué un protón no podría ser a veces un protón más un par electrón-positrón, etc.?… En consecuencia, el problema de la división de la materia había adquirido una dimensión distinta.”
Dado que la antimateria tiene la misma masa que la materia, es decir son de la misma magnitud y signo (la definición de masa es positiva siempre), el efecto gravitacional de la antimateria no debe ser distinto de la materia, es decir, siempre sera un efecto atractivo. Pero, ¿acaso no importa la equivalencia establecida de antipartícula viajando al futuro = partícula viajando al pasado?

Existe un “universo” que se nos escapa de la comprensión
La respuesta es sí. Dicha equivalencia proviene de algo llamado simetría CPT (Charge-Parity-Time), y nos dice que la equivalencia entre las partículas y antipartículas no solo corresponde a realizar una transformación sobre la carga, sino también sobre la paridad y el tiempo. La carga no afecta la gravedad, pero la paridad y el tiempo si la afectan. En otras palabras, al modificarse el tiempo (poner el tiempo al reves) y el espacio (la paridad es “girar” el espacio), estamos alterando el espacio-tiempo, y como la teoría general de la relatividad lo afirma, es la geometría de este el que determina la gravedad.
El carácter mutable de la materia se convirtió en piedra angular de la nueva física de partículas. El hecho de que partículas y antipartículas puedan crearse juntas a partir del vacío si se aporta energía suficiente, no sólo es importante para entender cómo se crean las partículas en aceleradores de alta energía, sino también para entender los procesos cuánticos que se produjeron en el Big Bang.
Como ya lo hemos expresado, el conocimiento que se obtuvo sobre la existencia de antifamilias de partículas o familias de antipartículas es una consecuencia de la aplicación de la teoría relativista del campo cuántico, para cada partícula existe una partícula que tiene la misma masa pero cuya carga eléctrica (y otras llamadas cargas internas) son de signo opuesto. Estas son las antipartículas. Así, al conocido electrón, con carga negativa, le corresponde un «electrón positivo» como antipartícula, llamado positrón, descubierto en 1932. El antiprotón, descubierto en 1956, tiene la misma masa que el protón, pero carga eléctrica negativa de igual valor. El fotón, que no tiene masa ni carga eléctrica, puede ser considerada su propia antipartícula.
Un agujero negro es un objeto que tiene tres propiedades: masa, espin y carga eléctrica. La forma del material en un agujero negro no se conoce, en parte porque está oculta para el universo externo, y en parte porque, en teoría, el material continuaría colapsando hasta tener radio cero, punto conocido como Singularidad, de densidad infinita.

Un agujero negro tiene tres propiedades: masa, espín y carga eléctrica. La forma del material de un agujero negro no se conoce, en parte porque está oculta para el universo externo, y en parte porque, en teoría, el material continuaría colapsando hasta tener radio cero, punto conocido como singularidad, de densidad infinita.

La luz (fotones), no son una onda distinta que un electrón o protón, etc.

1°- “No se dispersan”, no son más pequeñas, como las ondas del agua (olitas) cuando tiramos una piedrita, a medida que se alejan de su centro; sino que en el caso de la luz son menos partículas, pero son siempre el mismo tipo de onda (determinada frecuencia), igual tamaño.
2°- Las ondas con más energía son más grandes, los fotones al igual que las partículas son más pequeñas, contra toda lógica (contracción de Lorentz).
3°- No necesitan de un medio material para desplazarse. Viajan en el vacío. El medio que usan para viajar, es el mismísimo espacio.
4°- Su cualidad de onda no es diferente de las partículas. Lo podemos ver en la creación de pares y la cualidad de onda de las partículas, etc. En ningún momento la partícula, es una cosa compacta (ni una pelotita), siempre es una onda, que no se expande. En la comparación con la ola, sería como un “montón” o un “pozo” de agua, con una dirección, lo que conocemos como ecuación de Schrödinger. En ningún momento la partícula, es una pelotita; la ola sobre el agua, no es un cuerpo que se mueve sobre el agua, no es un montón de agua que viene (aunque parece), sino una deformación del agua. Así la partícula, no es un montón de algo, sino una deformación del espacio.

La curvatura está relacionadas con la probabilidad de presencia, no es una bolita que está en uno de esos puntos, sino que es una onda en esa posición. El fotón es una onda que no necesita de un medio material para propagarse, se propaga por el espacio vacío. Así como una onda de sonido es una contracción-expansión del medio en que se propaga, el fotón es una contracción-expansión del espacio (del mismísimo espacio), razón por la cual entendemos que el espacio se curva, se contrae y expande. La rigidez del medio, da la velocidad de la deformación (velocidad de la onda), en el caso de la rigidez del espacio da una velocidad “c”.Esta onda por causa de la contracción del tiempo (velocidad “c”), no se expande, sino que se mantiene como en su origen (para el observador ), como si fuese una “burbuja”, expandida o contraída, en cada parte, positiva-negativa
Cada partícula está caracterizada por un cierto número de parámetros que tienen valores bien definidos: su masa, carga eléctrica, spin o rotación interna y otros números, conocidos como cuánticos. Estos parámetros son tales que, en una reacción, su suma se mantiene y sirve para predecir el resultado. Se dice que hay conservación de los números cuánticos de las partículas. Así, son importantes el número bariónico, los diversos números leptónicos y ciertos números definidos para los quarks, como la extrañeza, color, etc. Estos últimos y sus antipartículas tienen cargas eléctricas (± 1/3 o ± 2/3) y números bariónicos (±1/3) fraccionarios. No todos los números asociados a cada partícula han sido medidos con suficiente precisión y no todas las partículas han sido detectadas en forma aislada, por lo menos de su ligamento, como el caso de
los quarks
De los Quarks y de los gluones.
Los gluones son una especie de «partículas mensajeras» que mantienen unidos a los quarks. Su nombre proviene del término inglés “glue”, que significa pegamento, en español quizás podría ser gomón. Ahora, en cuanto a los quarks, ya hicimos referencia de ellos anteriormente. Pero recordemos aquí, que fueron descubiertos en 1964 por Murray Gell-Mann, como los componentes más reducidos de la materia. Hasta entonces se pensaba que los átomos consistían simplemente en electrones rodeando un núcleo formado por protones y electrones.
En estado natural, quarks y gluones no tienen libertad. Pero si se eleva la temperatura a niveles 100.000 veces superiores, como se ha hecho en aceleradores de partículas, a la del centro del Sol, se produce el fenómeno del desconfinamiento y por un brevísimo tiempo quedan libres. En ese preciso momento aparece lo que se suele llamar plasma, «una sopa de quarks y gluones» que equivale al estado en que se podría haber encontrado la naturaleza apenas una milésima de segundo luego del Big Bang.
Recientemente se ha descubierto un nuevo estado de la materia, esta vez a niveles muy altos de energía, que los científicos han denominado Plasma Gluón-Quark. La transición ocurre a temperaturas alrededor de cien mil millones de grados y consiste en que se rompen las fuertes ligaduras que mantienen unidos los quarks dentro de los núcleos atómicos. Los protones y neutrones están formados, cada uno, por 3 quarks que se mantienen unidos gracias a los gluones (El gluón es la partícula portadora de interacción nuclear fuerte, fuerza que mantiene unida los núcleos atómicos). A temperaturas superiores se vence la fuerza nuclear fuerte y los protones y neutrones se dividen, formando esta sopa denominada plasma Gluón-Quark.

Pero por ahora aquí, nos vamos a quedar con los quarks al natural. Normalmente, los quarks no se encuentra en un estado separados, sino que en grupos de dos o tres. Asimismo, la duración de las vidas medias de las partículas, antes de decaer en otras, es muy variable (ver tablas).
Por otra parte, las partículas presentan una o más de las siguientes interacciones o fuerzas fundamentales entre ellas. Por un lado se tiene la gravitación y el electromagnetismo, conocidas de la vida cotidiana. Hay otras dos fuerzas, menos familiares, que son de tipo nuclear y se conocen como interacciones fuertes y débiles.
La gravitación afecta a todas las partículas, es una interacción universal. Todo cuerpo que tiene masa o energía está sometido a esta fuerza. Aunque es la más débil de las interacciones, como las masas son siempre positivas y su alcance es infinito, su efecto es acumulativo. Por ello, la gravitación es la fuerza más importante en cosmología.

Los campos magnéticos están presentes por todo el Universo
La fuerza electromagnética se manifiesta entre partículas con cargas eléctricas. A diferencia de las demás, puede ser de atracción (entre cargas de signos opuestos) o de repulsión (cargas iguales). Esta fuerza es responsable de la cohesión del átomo y las moléculas. Mantiene los objetos cotidianos como entidades con forma propia. Un vaso, una piedra, un auto, el cuerpo humano. Es mucho más fuerte que la gravitación y aunque es de alcance infinito, las cargas de distinto signo se compensan y sus efectos no operan a grandes distancias. Dependiendo de las circunstancias en que actúen, estas interacciones pueden manifestarse como fuerzas eléctricas o magnéticas solamente, o como una mezcla de ambos tipos.
La Fuerza Nuclear Débil: otra fuerza nuclear, considerada mucho más débil que la Fuerza Nuclear Fuerte. El fenómeno de decaimiento aleatorio de la población de las partículas subatómicas (la radioactividad) era difícil de explicar hasta que el concepto de esta fuerza nuclear adicional fue introducido.
La interacción nuclear débil es causa de la radioactividad natural y la desintegración del neutrón. Tiene un rol capital en las reacciones de fusión del hidrógeno y otros elementos en el centro de las estrellas y del Sol. La intensidad es débil comparada con las fuerzas eléctricas y las interacciones fuertes. Su alcance es muy pequeño, sólo del orden de 10-15 cm.
La interacción fuerte es responsable de la cohesión de los núcleos atómicos. Tiene la intensidad más elevada de todas ellas, pero es también de corto alcance: del orden de 10-13 cm. Es posible caracterizar las intensidades de las interacciones por un número de acoplamiento a, sin dimensión, lo que permite compararlas directamente:
Fuerte as = 15
Electromagnéticas a = 7,3 x 10-3
Débil aw 3,1 x 10-12
Gravitacional aG = 5,9 x 10-39
Por otro lado, la mecánica cuántica considera que la interacción de dos partículas se realiza por el intercambio de otras llamadas «virtuales». Tienen ese nombre porque no son observables: existen por un tiempo brevísimo, tanto más corto cuanto mayor sea su masa, siempre que no se viole el principio de incertidumbre de Heisenberg de la teoría cuántica (que en este contexto dice que el producto de la incertidumbre de la energía por el tiempo de vida debe ser igual o mayor que una constante muy pequeña). Desaparecen antes de que haya tiempo para que su interacción con otras partículas delate su existencia.
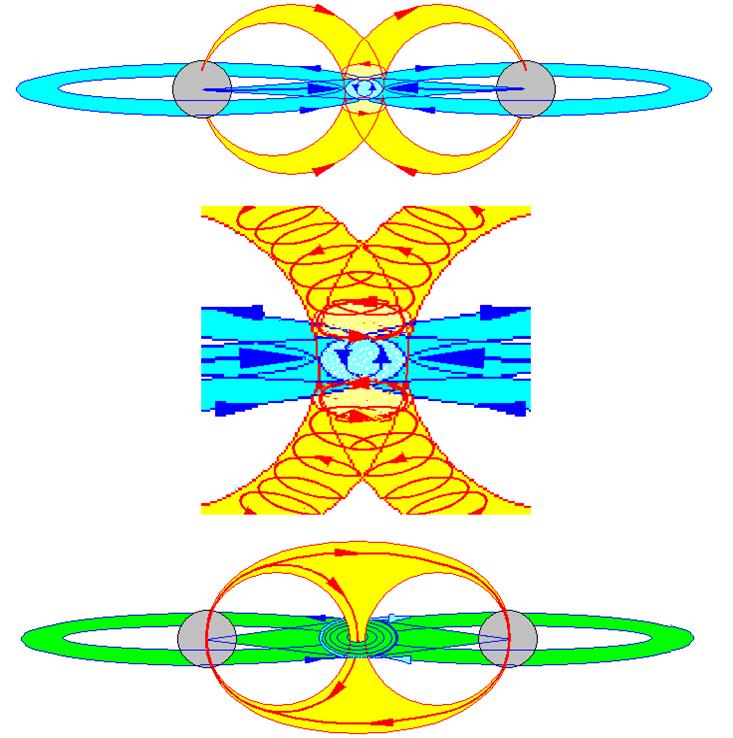
El fotón virtual común se desplaza hacia la partícula menos energética.
Dos partículas interactúan al emitir una de ellas una partícula virtual que es absorbida por la otra. Su emisión y absorción cambia el estado de movimiento de las originales: están en interacción. Mientras menos masa tiene la partícula virtual, más lejos llega, mayor es el rango de la interacción. El alcance de la interacción es inversamente proporcional a la masa de la partícula portadora o intermedia. Por ejemplo, la partícula portadora de la fuerza electromagnética es el fotón, de masa nula y, por lo tanto, alcance infinito. La interacción gravitacional también tiene alcance infinito y debe corresponder a una partícula de masa nula: se le denomina gravitón. Naturalmente tiene que ser neutro. (Aún no ha sido vistos ni en pelea de perros).
Como ya hicimos mención de ello, a las fuerzas nucleares se les asocian también partículas portadoras. Para la interacción débil estas partículas se llaman bosones intermedios, expresados como W+, W- y Zº (neutro). El W- es antipartícula del W+. Los W tienen masas elevadas comparadas con las otras partículas elementales. Lo de bosones les viene porque tienen spin entero, como el fotón y el gravitón, que también los son, pero que tienen masas nulas. Las fuerzas fuertes son mediadas por unas partículas conocidas como gluones, de los cuales habría ocho. Sin embargo, ellos no tienen masa, pero tienen algunas de las propiedades de los quarks, que les permiten interactuar entre ellos mismos. Hasta ahora no se han observado gluones propiamente tal, ya que lo que mencionamos en párrafos anteriores corresponde a un estado de la materia a la que llamamos plasma. Claro está, que es posible que un tiempo más se puedan detectar gluones libres cuando se logre aumentar, aún más, la temperatura, como está previsto hacerlo en el acelerador bautizado como “Relativistic Heavy Ion Collider”, empotrado en Estados Unidos de Norteamérica.
TABLA DE LAS PRINCIPALES PROPIEDADES DE LAS PARTÍCULAS PORTADORAS DE LAS INTERACCIONES FUNDAMENTALES
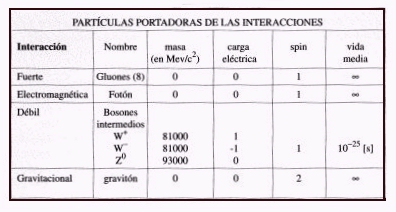
Una partícula y su antipartícula no pueden coexistir si están suficientemente cerca como para interactuar. Si ello ocurre, ellas se destruyen mutuamente: hay aniquilación de las partículas. El resultado es radiación electromagnética de alta energía, formada por fotones gamma. Así, si un electrón está cercano a un positrón se aniquilan en rayos gamma. Igual con un par protón-antiprotón muy próximos.
La reacción inversa también se presenta. Se llama «materialización o creación de partículas» de un par partícula-antipartícula a partir de fotones, pero se requieren condiciones físicas rigurosas. Es necesario que se creen pares partícula-antipartícula y que los fotones tengan una energía mayor que las masas en reposo de la partículas creadas. Por esta razón, se requieren fotones de muy alta energía, de acuerdo a la relación de Einstein E=mc2 . Para dar nacimiento a electrones/positrones es necesario un campo de radiación de temperaturas mayores a 7×109 °K. Para hacer lo mismo con pares protón/antiprotón es necesario que ellas sean superiores a 2×1012 °K. Temperaturas de este tipo se producen en los primeros instantes del universo.

Se detectan grandes emisiones de rayos gamma en explosiones supernovas y otros objetos energéticos
Los rayos gamma están presentes en explosiones de supernovas, colisión de estrellas de neutrones… Todos los sucesos de altas energías los hace presente para que nuestros ingenios los detecten y podamos conocer lo que la materia esconde en lo más profundo de sus “entrañas”. Aún no hemos podido conocer en profundidad la materia ni sabemos, tampoco, lo que realmente es la luz.
emilio silvera
May
15
Algunos desarrollos de la Física Teórica…Son notables
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (10)
Comments (10)
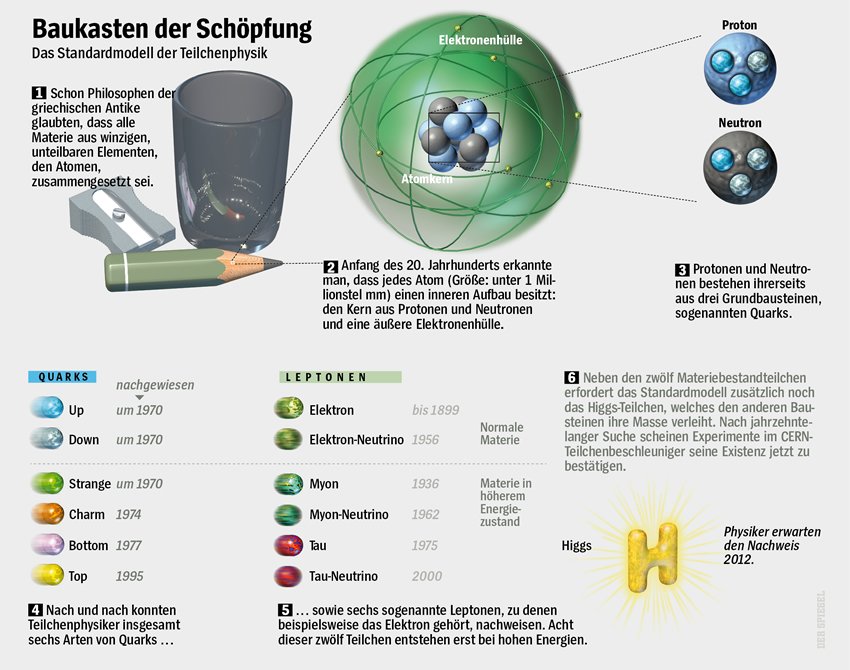
Hasta hace muy pocos años la Gravitación y la Mecánica Cuántica eran dos campos de la Física Teórica que utilizaban metodologías muy distintas y que estaban prácticamente desconectados entre sí. Por una parte, la interacción gravitatoria está descrita por la Teoría de la Relatividad General de Einstein, que es una teoría clásica (es decir, no cuántica) en la que la Gravedad se representa como una propiedad geométrica del espacio y del tiempo. Por otro lado, gobierna el mundo de las partículas atómicas y subatómicas. Su generalización relativista (la Teoría Cuántica de Campos) incorpora los principios de la Teoría Especial Relativista y, junto con el principio gauge, ha permitido construir con extraordinario éxito el llamado Modelo Estándar de la Física de las Partículas Elementales.

Con sus 20 parámetros aleatorios (parece que uno de ellos ha sido hallado -el bosón de Higgs-), el Modelo estándar de la física de partículas que incluye … sólo tres de las cuatro fuarzas fundamentales. La Gravedad se niega a juntarse con las otras fuerzas.
La interacción electromagnética, por ejemplo, es la responsable de las fuerzas que controlan la estructura atómica, reacciones químicas y todos los fenómenos electromagnéticos. Puede explicar las fuerzas entre las partículas cargadas, pero al contrario que las interacciones gravitacionales, pueden ser tanto atractivas como repulsivas. Algunas partículas neutras se desintegran por interacciones electromagnéticas. La interacción se puede interpretar tanto como un modelo clásico de fuerzas (ley de Coulomb) como por el intercambio de unos fotones virtuales. Igual que en las interacciones gravitatorias, el hecho de que las interacciones electromagnéticas sean de largo alcance significa que tiene una teoría clásica bien definida dadas por las ecuaciones de Maxwell. La teoría cuántica de las interacciones electromagnéticas se describe con la electrodinámica cuántica, que es una forma sencilla de teoría gauge.

El electromagnetismo está presente por todo el Universo
La interacción fuerte es unas 102 veces mayor que la interacción electromagnética y, como ya se dijo antes, aparece sólo entre los hadrones y es la responsable de las fuerzas entre nucleones que confiere a los núcleos de los átomos su gran estabilidad. Actúa a muy corta distancia dentro del núcleo (10-15 metros) y se puede interpretar como una interacción mediada por el intercambio de mesones virtuales llamados Gluones. Está descrita por una teoría gauge llamada Cromodinámica cuántica.
Las teorías gauge explican satisfactoriamente la dinámica de las interacciones electromagnéticas, fuertes y débiles en un gran rango de distancias. Sin embargo, a pesar que la Teoría General de la Relatividad puede formularse como una teoría gauge, todos los intentos de introducir en ella de manera completamente satisfactoria los principios de la Mecánica Cuántica, han fracasado. No obstante, los desarrollos realizados en el marco de la Teoría de Cuerdas en los últimos años han dado lugar a una convergencia, al menos metodológica, entre estos dos campos de la Física Fundamental.

Lo cierto es que buscamos incansables para saber de qué está hecho el “mundo”
La piedra angular de esta inesperada conexión es la llamada correspondencia gravedad/teoría gauge. En su forma más genérica dicha correspondencia afirma que la dinámica de ciertas teorías cuánticas de campos sin gravedad puede ser descrita por medio de una teoría gravitatoria en un espacio-tiempo que contiene al menos una dimensión adicional.
Para poder comprender con claridad los orígenes y las consecuencias de tan sorprendente relación entre teorías tan diferentes, es interesante recordar como fue descubierta en el contexto de la Teoría de Cuerdas. la Teoría de cuerdas tiene su origen en los años 60-70 como un intento de describir los hadrones(partículas elementales que experimentan interacción fuerte) como estados de una cuerda en movimiento.
¡Teoría de cuerdas! (¿)
La longitud de la cuerda se puede identificar con el tamaño del hadrón y sería del orden del fermi (10-15metros). Sin embargo, al analizar en detalle el espectro de modos de vibración de las cuerdas cerradas se descubrió que estas contienen una partícula de espín 2 y masa nula…(¿el gravitón?) que no se corresponde con ningún hadrón y que, en cambio, se identifica de manera natural con el gravitón (el cuanto fundamental de la interacción gravitatoria). De esta forma la Teoría de Cuerdas pasó de ser considerada una teoría de las interacciones fuertes a ser una posible teoría de unificación de las cuatro interacciones fundamentales de la Naturaleza a una escala mucho más pequeña: La longitud de Planck(10-35 metros).
La longitud de Planck se define como:
donde c es la velocidad de la luz en el vacío, G es la constante de gravitación universal, y  es la Constante de Planck racionalizada o reducida.
es la Constante de Planck racionalizada o reducida.
Una consecuencia sorprendente del estudio cuántico de la cuerda es que ésta debe propagarse en un espacio-tiempo de diez dimensiones. La métrica de dicho espacio-tiempo está también fuertemente constreñida. De hecho, la consistencia mecano-cuántica del movimiento de la cuerda en un espacio curvo impone que la métrica de este debe satisfacer unas ecuaciones que, en el límite en el que la longitud de la cuerda se considera muy pequeña, se reducen a las ecuaciones de Einstein de la relatividad general. Así pues, las ecuaciones fundamentales de la gravedad clásica en diez dimensiones se puede obtener de la dinámica cuántica de la cuerda.

En los años noventa se descubrió que el espectro de la Teoría de Cuerdas contiene, además de los modos de vibración asociados a las diferentes partículas, otros estados que están extendidos a lo largo de varias dimensiones espacio-temporales. Dichos espacios se denominan Branas y son paredes de dominio en el espacio-tiempo diez-dimensional que corresponden a estados no-perturbativos de la Teoría de Cuerdqas similares a los solitones de las teorías cuánticas de campo. En particular, las denominadas Dp-Branas son objetos que pueden estar extendidos a lo largo de p dimensiones espaciales y una temporal para 0 ≤ p ≤ 9. Uno puede imaginárselas como hiperplanos (p+1)-dimensionales. En particular la D3-Branas están extendidas a lo largo de cuatro dimensiones (tres espaciales y una temporal).
Claro, todo es pura conjetura (hasta que no sea verificado de forma experimental). Increíblemente el mundo de las branas es tan colosalmente extraño como lo es el infinitecimal mundo de las partículas cuánticas, con la salvedad de que, al tratar de objetos aún más pequeños, es decir aquellos que posiblemente existan más allá de los Quarks, la fascinación sube de tono al toparnos con un universo de cosas “imposibles”, bueno, mejor alejado de lo que nos dice el sentido común que (está visto), no es el mejor de los sentidos.
Las D-branas aparecen en muchas discusiones modernas relacionadas con las cuerdas (por ejemplo, en la entropía de los agujeros negros). Suelen tratarse como si fueran objetos clásicos que yacen dentro del espacio-tiempo completo 1 + 9 (o 1 + 10) dimensiones. La “D” viene de “Dirichlet”, por analogía con el tipo de problema de valor de frontera conocido como un problema de Dirichlet, en el que hay una frontera de género tiempo sobre la que se especifican datos (según Peter G. Lejeune Dirichlet, un eminente matemático francés que vivió entre 1.805 y 1.859).
No resulta fácil para nosotros imaginar el Mundo Brana
Las D-Branas son objetos dinámicos que pueden moverse, deformarse y cambiar de estado interno. Una de sus características fundamentales es que este último está caracterizado por un campo gauge que viv3e en su interior. Así podremos decir que las D-Branas albergan teorías de gauge en su seno. Esta es una realización novedosa de la simwetría gauge que está en la base de la correspondencia gravedad/teoría gauge. Además, dado que la Teoría de Cuerdas es una teoría gravitatoria, cualquier objeto masivo (y en particular las D-Branas) tiene asociado una métrica que describe la distorsión gravitatoria del espacio-tiempo en torno a él. En el caso de las D-Branas estas métricas son fáciles de encontrar y son similares a la clásica solución de Schwazschild de la relatividad general. En 1997 el joven físico argentino Juan Maldacena sugirió utilizar esta solución de gravedad para describir la teoría gauge que vive en las D-Branas.
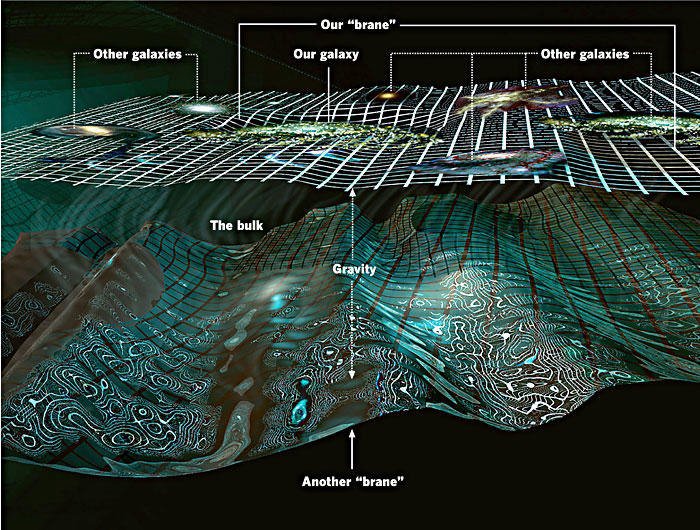
¿Podría ser nuestro universo una membrana flotando en un espacio de más dimensiones, que se rompe muchas veces en un universo circundante? Según una rama de la teoría de las cuerdas llamada braneword, hay una gran cantidad de dimensiones extra de espacio, y aunque la gravedad puede llegar a salir, nosotros estamos confinados a nuestro propio universo “brana”, con sólo tres dimensiones. Neil Turok, de la Universidad de Cambridge en el Reino Unido, y Paul Steinhardt, de la Universidad de Princeton en Nueva Jersey, EE.UU., han trabajado en cómo el Big Bang se podría haber provocado cuando nuestro universo se enfrentó violentamente con otro. Se repite el enfrentamiento, produciendo un nuevo Big Bang de vez en cuando, por lo que si el modelo del universo cíclico es correcto, el cosmos puede ser inmortal. ¡Por imaginar que no quede!
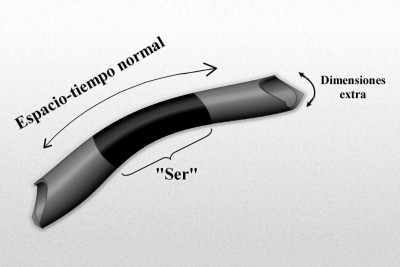
Sólo vamos a ser conscientes de dimensiones extra allí donde inciden directamente sobre las D-brana en la que “vivimos”. Más que una imagen de tipo “espacio cociente” que evoca la analogía de Kaluza-Kleinoriginal: El gráfico representa un modelo de manguera de un espacio-tiempo de dimensiones más altas de tipo Kaluza-Klein, donde la longitud, o mejor, la dimensión a lo largo de la longitud de la manguera representa el 4-espacio-tiempo normal, y la dimensión alrededor de la manguera representa la dimensión extra “pequeñas” (quizá escala de Planck). Imaginemos un “ser” que habite en este mundo, que rebasa estas dimensiones extra “pequeñas”, y por ello no es realmente consciente de ellas.
En la propuesta de Maldacena de las dos descripciones (gauge y gravitatoria) son duales y complementarias entre sí. En principio nos puede parecer confusa la afirmación de que la gravedad juega un papel relevante en la física de la teoría gauge. En los cursos de física nosm enseñan que la gravedad es mucho más débil que las otras fuerzas, y que, por lo tanto, su efecto es despreciable salvo a distancias realmente pequeñas o masas realmente grandes. Para resolver esta paradoja hay que tener en cuenta que la gravedad de la que estamos hablando no es la de nuestro universo aproximadamente plano y (posiblemente) con una pequeña constante cosmológica positiva, sino que se trata de una teorìa auxiliar en más de cuatro dimensiones y con constante cosmológica negativa.
Para seguir explicando el tema, mucho tendríamos que escribir. Sin embargo, quede aquí esta entrada que, al menos, puede despertar alguna curiosidad en los lectores que, aconsejados por lo leido, busquen más sobre el tema que, sin duda alguna, llega a ser fascinante.
Fuente: Muchos de los párrafos aquí insertos, han sido transcritos de un trabajo de Alfon V Ramallo del Departamento de Física de Partículas de la Universidad de Santiago de Compostela.
PD.

Aclaración: Cuando mencionamos una teoría gauge, lo estamos haciendo de cualquiera de las teorías cuánticas de campos creadas para explicar las interacciones fundamentales. Una teoría gauge requiere un grupo de simetría para los campos y los potenciales (el grupo gauge). En el caso de la electrodinámica, el grupo es abeliano, mientras que las teorías gauge para las interacciones fuertes y débiles utilizan grupos no abelianos. Las teorías gauge no abelianas son conocidas como teorías de Yang-Mills. esta diferencia explñica por qué la electrodinámica cuántica es una teoría mucho más simple que la cromodinámica cuántica, que describe las interacciones fuertes, y la teoría electrodébil, que es la teoría unificada de las interacciones débiles y las electromagnéticas. En el caso de la Gravedad Cuántica, el Grupo Gauge es mucho más complicado que los grupos gauge tanto de las interacciones fuertes como de las débiles.
¡La Física! ¡Qué complejidad!
emilio silvera
May
13
El “universo” de las partículas I
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (0)
Comments (0)
¿Qué no será capaz de inventar el hombre para descubrir los misterios de la naturaleza?
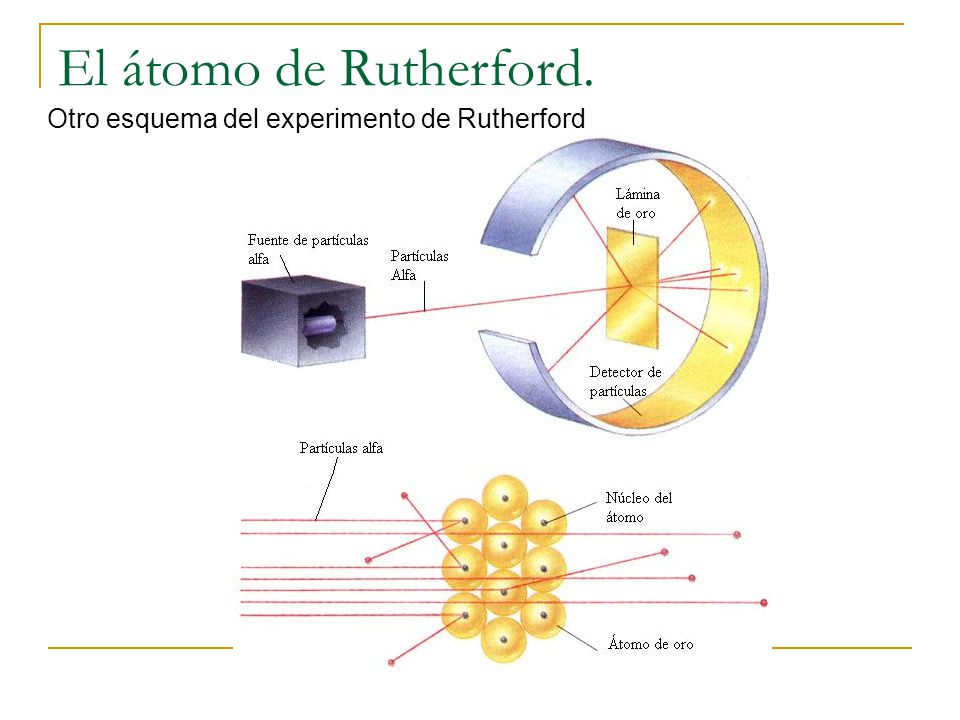
Ha pasado mucho tiempo desde que Rutherford identificara la primera partícula nuclear (la partícula alfa). El camino ha sido largo y muy duro, con muchos intentos fallidos antes de ir consiguiendo los triunfos (los únicos que suenan), y muchos han sido los nombres que contribuyen para conseguir llegar al conocimiento que actualmente tenemos del átomo y del núcleo; los electrones circulando alrededor del núcleo, en sus diferentes niveles, con un núcleo compuesto de protones y neutrones que, a su vez, son constituidos por los quarks allí confinados por los gluones, las partículas mediadoras de la fuerza nuclear fuerte. Pero, ¿qué habrá más allá de los quarks?, ¿las supercuerdas vibrantes? Algún día se sabrá.
Partículas
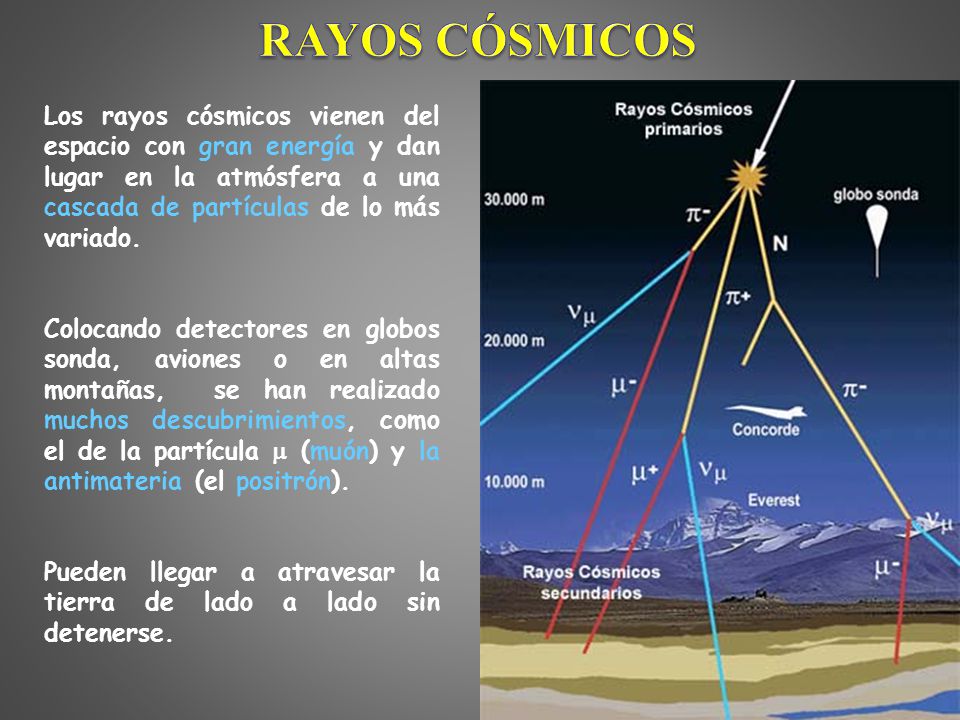
El universo de las partículas es fascinante. Cuando las partículas primarias chocan con átomos y moléculas en el aire, aplastan sus núcleos y producen toda clase de partículas secundarias. En esta radiación secundaria (aún muy energética) la que detectamos cerca de la Tierra, por los globos enviados a la atmósfera superior, han registrado la radiación primaria.
El físico estadounidense Robert Andrews Millikan, que recogió una gran cantidad de información acerca de esta radiación (y que le dio el nombre de rayos cósmicos), decidió que debería haber una clase de radiación electromagnética. Su poder de penetración era tal que, parte del mismo, atravesaba muchos centímetros de plomo. Para Millikan, esto sugería que la radiación se parecía a la de los penetrantes rayos gamma, pero con una longitud de onda más corta.

Otros, sobre todo el físico norteamericano Holly Compton, no estaban de acuerdo en que los rayos cósmicos fuesen partículas. Había un medio para investigar este asunto; si se trataba de partículas cargadas, deberían ser rechazadas por el campo magnético de la Tierra al aproximarse a nuestro planeta desde el espacio exterior. Compton estudió las mediciones de la radiación cósmica en varias latitudes y descubrió que en realidad se curvaban con el campo magnético: era más débil cera del ecuador magnético y más fuerte cerca de los polos, donde las líneas de fuerza magnética se hundían más en la Tierra.
Las partículas cósmicas primarias, cuando entran en nuestra atmósfera, llevan consigo unas energías fantásticas, muy elevadas. En general, cuanto más pesado es el núcleo, más raro resulta entre las partículas cósmicas. Núcleos tan complejos como los que forman los átomos de hierro se detectaron con rapidez; en 1.968, otros núcleos como el del uranio. Los núcleos de uranio constituyen sólo una partícula entre 10 millones. También se incluirán aquí electrones de muy elevada energía.

Ahora bien, la siguiente partícula inédita (después del neutrón) se descubrió en los rayos cósmicos. A decir verdad, cierto físico teórico había predicho ya este descubrimiento. Paul Adrien Dirac había aducido, fundándose en un análisis matemático de las propiedades inherentes a las partículas subatómicas, que cada partícula debería tener su antipartícula (los científicos desean no sólo que la naturaleza sea simple, sino también simétrica). Así pues, debería haber un antielectrón, salvo por su carga que sería positiva y no negativa, idéntico al electrón; y un antiprotón, con carga negativa en vez de positiva.
En 1.930, cuando Dirac expuso su teoría, no llamó demasiado la atención en el mundo de la ciencia. Pero, fiel a la cita, dos años después apareció el antielectrón. Por entonces, el físico americano Carl David Anderson trabajaba con Millikan en un intento por averiguar si los rayos cósmicos eran radiación electromagnética o partículas. Por aquellas fechas, casi todo el mundo estaba dispuesto a aceptar las pruebas presentadas por Compton, según las cuales, se trataría de partículas cargadas; pero Millikan no acababa de darse por satisfecho con tal solución.

Anderson se propuso averiguar si los rayos cósmicos que penetraban en una cámara de ionización se curvaban bajo la acción de un potente campo magnético. Al objeto de frenar dichos rayos lo suficiente como para detectar la curvatura, si la había, puso en la cámara una barrera de plomo de 6’35 mm de espesor. Descubrió que, cuando cruzaba el plomo, la radiación cósmica trazaba una estela curva a través de la cámara; y descubrió algo más. A su paso por el plomo, los rayos cósmicos energéticos arrancaban partículas de los átomos de plomo. Una de esas partículas dejó una estela similar a la del electrón. ¡Allí estaba, pues, el antielectrón de Dirac! Anderson le dio el nombre de positrón. Tenemos aquí un ejemplo de radiación secundaria producida por rayos cósmicos. Pero aún había más, pues en 1.963 se descubrió que los positrones figuraban también entre las radiaciones primarias.
Abandonado a sus propios medios, el positrón es tan estable como el electrón (¿y por qué no habría de serlo si el idéntico al electrón, excepto en su carga eléctrica?). Además, su existencia puede ser indefinida. Ahora bien, en realidad no queda abandonado nunca a sus propios medios, ya que se mueve en un universo repleto de electrones. Apenas inicia su veloz carrera (cuya duración ronda la millonésima de segundo), se encuentra ya con uno.

Así, durante un momento relampagueante quedaron asociados el electrón y el positrón; ambas partículas girarán en torno a un centro de fuerza común. En 1.945, el físico americano Arthur Edwed Ruark sugirió que se diera el nombre de positronio a este sistema de dos partículas, y en 1.951, el físico americano de origen austriaco Martin Deutsch consiguió detectarlo guiándose por los rayos gamma característicos del conjunto.
Pero no nos confundamos, aunque se forme un sistema positronio, su existencia durará, como máximo, una diezmillonésima de segundo. El encuentro del electrón-positrón provoca un aniquilamiento mutuo; sólo queda energía en forma de radiación gamma. Ocurre pues, tal como había sugerido Einstein: la materia puede convertirse en energía y viceversa. Por cierto, que Anderson consiguió detectar muy pronto el fenómeno inverso: desaparición súbita de rayos gamma para dar origen a una pareja electrón-positrón. Este fenómeno se llama producción en pareja. Anderson compartió con Hess el premio Nobel de Física de 1.936.

Poco después, los Joliot-Curie detectaron el positrón por otros medios, y al hacerlo así realizaron, de paso, un importante descubrimiento. Al bombardear los átomos de aluminio con partículas alfa, descubrieron que con tal sistema no sólo se obtenían protones, sino también positrones. Cuando suspendieron el bombardeo, el aluminio siguió emitiendo positrones, emisión que sólo con el tiempo se debilitó. Aparentemente habían creado, sin proponérselo, una nueva sustancia radiactiva. He aquí la interpretación de lo ocurrido según los Joliot-Curie: cuando un núcleo de aluminio absorbe una partícula alfa, la adición de los dos protones transforma el aluminio (número atómico 13) en fósforo (número atómico 15). Puesto que las partículas alfa contienen cuatro nucleones en total, el número masivo se eleva 4 unidades, es decir, del aluminio 27 al fósforo 31. Ahora bien, si al reaccionar se expulsa un protón de ese núcleo, la reducción en una unidad de sus números atómicos y masivos hará surgir otro elemento, o sea, el silicio 30.
Puesto que la partícula alfa es el núcleo del helio, y un protón es el núcleo del hidrógeno, podemos escribir la siguiente ecuación de esta reacción nuclear:
aluminio 27 + helio 4 = silicio 30 + hidrógeno 1
Nótese que los números másicos se equilibran:
27 + 4 = 30 + 1
Adentrarse en el universo de las partículas que componen los elementos de la tabla periódica, y en definitiva, la materia conocida, es verdaderamente fantástico.
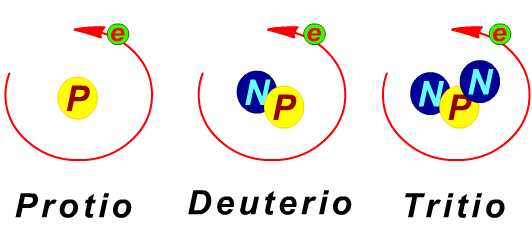
Tan pronto como los Joliot-Curie crearon el primer isótopo radiactivo artificial, los físicos se lanzaron en tropel a producir tribus enteras de ellas. En realidad, las variedades radiactivas de cada elemento en la tabla periódica son producto de laboratorio. En la moderna tabla periódica, cada elemento es una familia con miembros estables e inestables, algunos procedentes de la naturaleza, otros sólo del laboratorio. Por ejemplo, el hidrógeno presenta tres variedades: en primer lugar, el corriente, que tienen un solo protón. En 1.932, el químico Harold Urey logró aislar el segundo. Lo consiguió sometiendo a lenta evaporación una gran cantidad de agua, de acuerdo con la teoría de que los residuos representarían una concentración de la forma más pesada del hidrógeno que se conocía, y, en efecto, cuando se examinaron al espectroscopio las últimas gotas de agua no evaporadas, se descubrió en el espectro una leve línea cuya posición matemática revelaba la presencia de hidrógeno pesado.
El núcleo de hidrógeno pesado está constituido por un protón y un neutrón. Como tiene un número másico de 2, el isótopo es hidrógeno. Urey llamó a este átomo deuterio (de la voz griega deutoros, “segundo”), y el núcleo deuterón. Una molécula de agua que contenga deuterio se denomina agua pesada, que tiene puntos de ebullición y congelación superiores al agua ordinaria, ya que la masa del deuterio es dos veces mayor que la del hidrógeno corriente. Mientras que ésta hierve a 100º C y se congela a 0º C, el agua pesada hierve a 101’42º C y se congela a 3’79º C. El punto de ebullición del deuterio es de -23’7º K, frente a los 20’4º K del hidrógeno corriente. El deuterio se presenta en la naturaleza en la proporción de una parte por cada 6.000 partes de hidrógeno corriente. En 1.934 se otorgó a Urey el premio Nobel de Química por su descubrimiento del deuterio.

El deuterio resultó ser una partícula muy valiosa para bombardear los núcleos. En 1.934, el físico australiano Marcus Lawrence Edwin Oliphant y el austriaco P. Harteck atacaron el deuterio con deuterones y produjeron una tercera forma de hidrógeno, constituido por un protón y dos neutrones. La reacción se planteó así:
hidrógeno 2 + hidrógeno 2 = hidrógeno 3 + hidrógeno 1
Este nuevo hidrógeno superpesado se denominó tritio (del griego tritos, “tercero”); su ebullición a 25º K y su fusión a 20’5º K.
Como es mi costumbre, me desvío del tema y sin poderlo evitar, mis ideas (que parecen tener vida propia), cogen los caminos más diversos. Basta con que se cruce en el camino del trabajo que realizo un fugaz recuerdo; lo sigo y me lleva a destinos distintos de los que me propuse al comenzar. Así, en este caso, me pasé a la química, que también me gusta mucho y está directamente relacionada con la física; de hecho son hermanas: la madre, las matemáticas, la única que finalmente lo podrá explicar todo.
emilio silvera
May
13
El “universo” de las Partículas II
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (0)
Comments (0)
Estamos hablando de las partículas y no podemos dejar a un lado el tema del movimiento rotatorio de las mismas. Usualmente se ve cómo la partícula gira sobre su eje, a semejanza de un trompo, o como la Tierra o el Sol, o nuestra galaxia o, si se me permite decirlo, como el propio universo. En 1.925, los físicos holandeses George Eugene Uhlenbeck y Samuel Abraham Goudsmit aludieron por primera vez a esa rotación de las partículas. Éstas, al girar, generan un minúsculo campo electromagnético; tales campos han sido objeto de medidas y exploraciones, principalmente por parte del físico alemán Otto Stern y el físico norteamericano Isaac Rabi, quienes recibieron los premios Nobel de Física en 1.943 y 1.944 respectivamente, por sus trabajos sobre dicho fenómeno.

Esas partículas (al igual que el protón, el neutrón y el electrón), que poseen espines que pueden medirse en números mitad, se consideran según un sistema de reglas elaboradas independientemente, en 1.926, por Fermi y Dirac; por ello, se las llama y conoce como estadísticas Fermi-dirac. Las partículas que obedecen a las mismas se denominan fermiones, por lo cual el protón, el electrón y el neutrón son todos fermiones.
Hay también partículas cuya rotación, al duplicarse, resulta igual a un número par. Para manipular sus energías hay otra serie de reglas, ideadas por Einstein y el físico indio S. N. Bose. Las partículas que se adaptan a la estadística Bose-Einstein son bosones, como por ejemplo la partícula alfa.
Las reglas de la mecánica cuántica tienen que ser aplicadas si queremos describir estadísticamente un sistema de partículas que obedece a reglas de esta teoría en vez de los de la mecánica clásica. En estadística cuántica, los estados de energía se considera que están cuantizados. La estadística de Bose-Einstein se aplica si cualquier número de partículas puede ocupar un estado cuántico dad. Dichas partículas (como dije antes) son bosones, que tienden a juntarse.
Los bosones tienen un momento angular nh/2π, donde n es 0 o un entero, y h es la constante de Planck. Para bosones idénticos, la función de ondas es siempre simétrica. Si sólo una partícula puede ocupar un estado cuántico, tenemos que aplicar la estadística Fermi-Dirac y las partículas (como también antes dije) son los fermiones que tienen momento angular (n + ½)h / 2π y cualquier función de ondas de fermiones idénticos es siempre antisimétrica. La relación entre el espín y la estadística de las partículas está demostrada por el teorema espín-estadística.

En un espacio de dos dimensiones es posible que haya partículas (o cuasipartículas) con estadística intermedia entre bosones y fermiones. Estas partículas se conocen con el nombre de aniones; para aniones idénticos, la función de ondas no es simétrica (un cambio de fase de +1) o antisimétrica (un cambio de fase de -1), sino que interpola continuamente entre +1 y -1. Los aniones pueden ser importantes en el análisis del efecto Hall cuántico fraccional y han sido sugeridos como un mecanismo para la superconductividad de alta temperatura.

Debido al principio de exclusión de Pauli, es imposible que dos fermiones ocupen el mismo estado cuántico (al contrario de lo que ocurre con los bosones). La condensación Bose-Einstein es de importancia fundamental para explicar el fenómeno de la superfluidez. A temperaturas muy bajas (del orden de 2×10-7K) se puede formar un condensado de Bose-Einstein, en el que varios miles de átomos dorman una única entidad (un superátomo). Este efecto ha sido observado con átomos de rubidio y litio. Como ha habréis podido suponer, la condensación Bose-Einstein es llamada así en honor al físico Satyendra Nath Bose (1.894 – 1.974) y a Albert Einstein. Así que, el principio de exclusión de Pauli tiene aplicación no sólo a los electrones, sino también a los fermiones; pero no a los bosones.
Si nos fijamos en todo lo que estamos hablando aquí, es fácil comprender cómo forma un campo magnético la partícula cargada que gira, pero ya no resulta tan fácil saber por qué ha de hacer lo mismo un neutrón descargado. Lo cierto es que cuando un rayo de neutrones incide sobre un hierro magnetizado, no se comporta de la misma forma que lo haría si el hierro no estuviese magnetizado. El magnetismo del neutrón sigue siendo un misterio; los físicos sospechan que contiene cargas positivas y negativas equivalente a cero, aunque por alguna razón desconocida, logran crear un campo magnético cuando gira la partícula.

Particularmente creo que, si el neutrón tiene masa, si la masa es energía (E = mc2), y si la energía es electricidad y magnetismo (según Maxwell), el magnetismo del neutrón no es tan extraño, sino que es un aspecto de lo que en realidad es materia. La materia es la luz, la energía, el magnetismo, en definitiva, la fuerza que reina en el universo y que está presente de una u otra forma en todas partes (aunque no podamos verla).
Sea como fuere, la rotación del neutrón nos da la respuesta a esas preguntas:
¿Qué es el antineutrón? Pues, simplemente, un neutrón cuyo movimiento rotatorio se ha invertido; su polo sur magnético, por decirlo así, está arriba y no abajo. En realidad, el protón y el antiprotón, el electrón y el positrón, muestran exactamente el mismo fenómeno de los polos invertidos.
Es indudable que las antipartículas pueden combinarse para formar la antimateria, de la misma forma que las partículas corrientes forman la materia ordinaria.
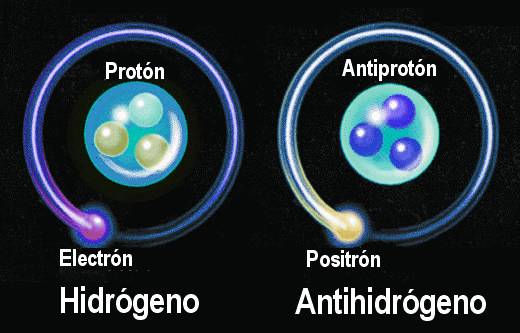
La primera demostración efectiva de antimateria se tuvo en Brookhaven en 1.965, donde fue bombardeado un blanco de berilio con 7 protones BeV y se produjeron combinaciones de antiprotones y antineutrones, o sea, un antideuterón. Desde entonces se ha producido el antihelio 3, y no cabe duda de que se podría crear otros antinúcleos más complicados aún si se abordara el problema con más interés.
Pero, ¿existe en realidad la antimateria? ¿Hay masas de antimateria en el universo? Si las hubiera, no revelarían su presencia a cierta distancia. Sus efectos gravitatorios y la luz que produjeran serían idénticos a los de la materia corriente. Sin embargo, cuando se encontrasen las masas de las distintas materias, deberían ser claramente perceptibles las reacciones masivas del aniquilamiento mutuo resultante del encuentro. Así pues, los astrónomos observan especulativamente las galaxias, para tratar de encontrar alguna actividad inusual que delate interacciones materia-antimateria.
No parece que dichas observaciones fuesen un éxito. ¿Es posible que el universo esté formado casi enteramente por materia, con muy poca o ninguna antimateria? Y si es así, ¿por qué? Dado que la materia y la antimateria son equivalente en todos los aspectos, excepto en su oposición electromagnética, cualquier fuerza que crease una originaría la otra, y el universo debería estar compuesto de iguales cantidades de la una y de la otra.

Aquí detectaron lograron encontrar la anti-materia por primera vez
Este es el dilema. La teoría nos dice que debería haber allí antimateria, pero las observaciones lo niegan, no lo respaldan. ¿Es la observación la que falla? ¿Y qué ocurre con los núcleos de las galaxias activas, e incluso más aún, con los quásares? ¿Deberían ser estos fenómenos energéticos el resultado de una aniquilación materia-antimateria? ¡No creo! Ni siquiera ese aniquilamiento parece ser suficiente, y los astrónomos prefieren aceptar la noción de colapso gravitatorio y fenómenos de agujeros negros, como el único mecanismo conocido para producir la energía requerida.
Con esto de la antimateria me ocurre igual que con el hecho, algunas veces planteado, de la composición de la materia en lugares lejanos del universo. “Ha caído una nave extraterrestre y nuestros científicos han comprobado que está hecha de un material desconocido, casi indestructible”. Este comentario se ha podido oír en alguna película de ciencia ficción. Podría ser verdad (un material desconocido), sin embargo, no porque la nave esté construida por una materia distinta, sino porque la aleación es distinta y más avanzada a partir de los materiales conocidos del universo. En cualquier parte del universo, por muy lejana que pueda estar, rigen los mismos principios y las mismas fuerzas: la materia y la energía son las mismas en cualquier parte. Lo único que puede diferir es la forma en que se utilice, el tratamiento que se le pueda dar, y sobre todo, el poseer el conocimiento y la tecnología necesarios para poder obtener el máximo resultado de las propiedades que dicha materia encierra, porque, en última instancia, ¿es en verdad inerte la materia?

El experimento Alpha para el estudio de la antimateria – Maximilien Brice / CERN
Todo lo que podemos ver en el Universo, sin excepción, está hecho de materia. Tiene y encierra tantos misterios la materia que estamos aún a años luz de saber y conocer sobre su verdadera naturaleza. Nos podríamos preguntar miles de cosas que no sabríamos contestar. Nos maravillan y asombran fenómenos naturales que ocurren ante nuestros ojos, pero que tampoco sabemos, en realidad, a qué son debidas. Sí, sabemos ponerles etiquetas como la fuerza nuclear débil, la fisión espontánea que tiene lugar en algunos elementos como el protactinio o el torio, y con mayor frecuencia, en los elementos que conocemos como transuránidos.

A medida que los núcleos se hacen más grandes, la probabilidad de una fisión espontánea aumenta. En los elementos más pesados de todos (einstenio, fermio y mendelevio), esto se convierte en el método más importante de su ruptura, sobrepasando a la emisión de partículas alfa. ¡Parece que la materia está viva! Son muchas las cosas que desconocemos, y nuestra curiosidad nos empuja continuamente a buscar esas respuestas.
El electrón y el positrón son notables por sus pequeñas masas (sólo 1/1.836 de la del protón, el neutrón, el antiprotón o el antineutrón), y por lo tanto, han sido denominados leptones (de la voz griega leptos, que dignifica “delgado”).
Aunque el electrón fue descubierto en 1.897 por el físico británico Joseph John Thomson (1.856 – 1.940), el problema de su estructura, si la hay, aún no está resuelto. Conocemos su masa y su carga negativa que responden a 9’1093897 (54) × 10-31 Kg la primera, y 1’60217733 (49) × 10-19 culombios la segunda, y también su radio clásico r0 igual a e2/(mc2) = 2’82 × 10-13 cm. No se ha descubierto aún ninguna partícula que sea menos masiva que el electrón (o positrón) y que lleve una carga eléctrica, sea la que fuese (sabemos cómo actúa y cómo medir sus propiedades, pero aún no sabemos qué es), que tenga asociada un mínimo de masa.
Lo cierto es que el electrón es una maravilla en sí mismo. El universo no sería como lo conocemos si el electrón fuese distinto a como es; bastaría un cambio infinitesimal para que, por ejemplo, nosotros no pudiéramos estar aquí ahora.

Muchos granos de arena conforman la inmensa playa
¡No por pequeño se el insignificante!
Recordémoslo, todo lo grande está hecho de cosas pequeñas. En realidad, existen partículas que no tiene asociada ninguna masa en absoluto, es decir, ninguna masa en reposo. Por ejemplo, las ondas de luz y otras formas de radiación electromagnética se comportan como partículas (Einstein en su efecto fotoeléctrico y De Broglie en la difracción de electrones*). Esta manifestación en forma de partículas de lo que, de ordinario, concebimos como una onda, se denomina fotón, de la palabra griega que significa “luz”.
El fotón tiene una masa de 1, una carga eléctrica de 0, pero posee un espín de 1, por lo que es un bosón. ¿Cómo se puede definir lo que es el espín? Los fotones toman parte en las reacciones nucleares, pero el espín total de las partículas implicadas antes y después de la reacción deben permanecer inmutadas (conservación del espín). La única forma de que esto suceda en las reacciones nucleares que implican a los fotones radica en suponer que el fotón tiene un espín de 1. El fotón no se considera un leptón, puesto que este término se reserva para la familia formada por el electrón, el muón y la partícula tau, con sus correspondiente neutrinos: υe, υμ y υτ.

Existen razones teóricas para suponer que cuando las masas se aceleran (como cuando se mueven en órbitas elípticas en torno a otra masa o llevan a cabo un colapso gravitacional), emiten energía en forma de ondas gravitaciones. Esas ondas pueden, así mismo, poseer aspecto de partícula, por lo que toda partícula gravitacional recibe el nombre de gravitón.
La forma gravitatoria es mucho, mucho más débil que la fuerza electromagnética. Un protón y un electrón se atraen gravitacionalmente con sólo 1/1039 de la fuerza en que se atraen electromagnéticamente. El gravitón (aún sin descubrir) debe poseer, correspondientemente, menos energía que el fotón, y por tanto, ha de ser inimaginablemente difícil de detectar.

No será fácil detectar gravitones
De todos modos, el físico norteamericano Joseph Weber emprendió en 1.957 la formidable tarea de detectar el gravitón. Llegó a emplear un par de cilindros de aluminio de 153 cm de longitud y 66 de anchura, suspendidos de un cable en una cámara de vacío. Los gravitones (que serían detectados en forma de ondas) desplazarían levemente esos cilindros, y se empleó un sistema para detectar el desplazamiento que llegase a captar la cienbillonésima parte de un centímetro. Las débiles ondas de los gravitones, que proceden del espacio profundo, deberían chocar contra todo el planeta, y los cilindros separados por grandes distancias se verán afectados de forma simultánea. En 1.969, Weber anunció haber detectado los efectos de las ondas gravitacionales. Aquello produjo una enorme excitación, puesto que apoyaba una teoría particularmente importante (la teoría de Einstein de la relatividad general). Desgraciadamente, nunca se pudo comprobar mediante las pruebas realizadas por otros equipos de científicos que duplicaron el hallazgo de Weber.
En cualquier caso, no creo que a estas alturas alguien pueda dudar de la existencia de los gravitones, el bosón mediador de la fuerza gravitatoria. La masa del gravitón es 0, su carga es 0, y su espín es 2. Como el fotón, no tiene antipartícula; ellos mismos hacen las dos versiones.
emilio silvera
May
12
Velocidades inimaginables
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (3)
Comments (3)

En el centro del átomo se encuentra un pequeño grano compacto aproximadamente 100.000 veces más pequeño que el propio átomo: el núcleo atómico. Su masa, e incluso más aún su carga eléctrica, determinan las propiedades del átomo del cual forma parte. Debido a la solidez del núcleo parece que los átomos, que dan forma a nuestro mundo cotidiano, son intercambiables entre sí, e incluso cuando interaccionan entre ellos para formar sustancias químicas (los elementos). Pero el núcleo, a pesar de ser tan sólido, puede partirse. Si dos átomos chocan uno contra el otro con gran velocidad podría suceder que los núcleos llegaran a chocar entre sí y entonces, o bien se rompen en trozos, o se funden liberando en el proceso partículas subnucleares. La nueva física de la primera mitad del siglo XX estuvo dominada por los nuevos acertijos que estas partículas planteaban.

Pero tenemos la mecánica cuántica; ¿es que no es aplicable siempre?, ¿cuál es la dificultad? Desde luego, la mecánica cuántica es válida para las partículas subatómicas, pero hay más que eso. Las fuerzas con que estas partículas interaccionan y que mantienen el núcleo atómico unido son tan fuertes que las velocidades a las que tienen que moverse dentro y fuera del núcleo están cerca de la velocidad de la luz, c, que es de 299.792’458 Km/s. Cuando tratamos con velocidades tan altas se necesita una segunda modificación a las leyes de la física del siglo XIX; tenemos que contar con la teoría de la relatividadespecial de Einstein.

Esta teoría también fue el resultado de una publicación de Einstein de 1905. en esta teoría quedaron sentadas las bases de que el movimiento y el reposo son conceptos relativos, no son absolutos, como tampoco habrá un sistema de referencia absoluto con respecto al cual uno pueda medir la velocidad de la luz.
Pero había más cosas que tenían que ser relativas. En este teoría, la masa y la energía también dependen de la velocidad, como lo hacen la intensidad del campo eléctrico y del magnético. Einstein descubrió que la masa de una partícula es siempre proporcional a la energía que contienen, supuesto que se haya tenido en cuenta una gran cantidad de energía en reposo de una partícula cualquiera, como se denota a continuación:
E = mc2

Como la velocidad de la luz es muy grande, esta ecuación sugiere que cada partícula debe almacenar una cantidad enorme de energía, y en parte esta predicción fue la que hizo que la teoría de la relatividadtuviese tanta importancia para la física (¡y para todo el mundo!). Para que la teoría de la relatividadtambién sea autoconsistente tiene que ser holista, esto es, que todas las cosas y todo el mundo obedezcan a las leyes de la relatividad. No son sólo los relojes los que se atrasan a grandes velocidades, sino que todos los procesos animados se comportan de la forma tan inusual que describe esta teoría cuando nos acercamos a la velocidad de la luz. El corazón humano es simplemente un reloj biológico y latirá a una velocidad menor cuando viaje en un vehículo espacial a velocidades cercanas a la de la luz. Este extraño fenómeno conduce a lo que se conoce como la “paradoja de los gemelos”, sugerida por Einstein, en la que dos gemelos idénticos tienen diferente edad cuando se reencuentran después de que uno haya permanecido en la Tierra mientras que el otro ha viajado a velocidades relativistas.
Einstein comprendió rápidamente que las leyes de la gravedad también tendrían que ser modificadas para que cumplieran el principio relativista.

La formulación de newton es bien conocida, en la segunda imagen que se representan en este esquema dos partículas que se acercan entre sí siguiendo un movimiento acelerado. La interpretación newtoniana supone que el espacio-tiempo es llano y que lo que provoca la curvatura de las líneas de universo es la fuerza de interacción gravitatoria entre ambas partículas. Por el contrario, la interpretación einsteiniana supone que las líneas de universo de estas partículas son geodésicas (“rectas”), y que es la propia curvatura del espacio tiempo lo que provoca su aproximación progresiva.
Para poder aplicar el principio de la relatividad a la fuerza gravitatoria, el principio tuvo que ser extendido de la siguiente manera: no sólo debe ser imposible determinar la velocidad absoluta del laboratorio, sino que también es imposible distinguir los cambios de velocidad de los efectos de una fuerza gravitatoria.

Einstein comprendió que la consecuencia de esto era que la gravedad hace al espacio-tiempo lo que la humedad a una hoja de papel: deformar la superficie con desigualdades que no se pueden eliminar. Hoy en día se conocen muy bien las matemáticas de los espacios curvos, pero en el época de Einstein el uso de estas nociones matemáticas tan abstractas para formular leyes físicas era algo completamente nuevo, y le llevó varios años encontrar la herramienta matemática adecuada para formular su teoría general de la relatividad que describe cómo se curva el espacio en presencia de grandes masas como planetas y estrellas.
Einstein tenía la idea en su mente desde 1907 (la relatividad especial la formuló en 1905), y se pasó 8 años buscando las matemáticas adecuadas para su formulación.
Leyendo el material enviado por un amigo al que pidió ayuda, Einstein quedó paralizado. Ante él, en la primera página de una conferencia dada ante el Sindicato de Carpinteros, 60 años antes por un tal Riemann, tenía la solución a sus desvelos: el tensor métrico de Riemann, que le permitiría utilizar una geometría espacial de los espacios curvos que explicaba su relatividad general.

Desde que se puso en órbita el telescopio espacial de rayos gamma Fermi, el 11 de junio de 2008, ha detectado poblaciones enteras de objetos nunca antes vistos. El último hallazgo de Fermi afecta al púlsar J1823-3021A, avistado en 1994 con el radiotelescopio Lovell, en Inglaterra. Un equipo internacional de expertos se ha dado cuenta de que esta estrella pulsante emite rayos gamma y gracias a Fermi ha podido caracterizar sus inusuales propiedades. Los resultados de su investigación se publican en el último número de Science. Lo cierto es que han descubierto el púlsar de milisegundos más joven y con la fuerza magnética más potente

No está mal que en este punto recordemos la fuerza magnética y gravitatoria que nos puede ayudar a comprender mejor el comportamiento de las partículas subatómicas.
El electromagnetismo, decíamos al principio, es la fuerza con la cual dos partículas cargadas eléctricamente se repelen (si sus cargas son iguales) o se atraen (si tienen cargas de signo opuesto).
La interacción magnética es la fuerza que experimenta una partícula eléctricamente cargada que se mueve a través de un campo magnético. Las partículas cargadas en movimiento generan un campo magnético como, por ejemplo, los electrones que fluyen a través de las espiras de una bobina.
Las fuerzas magnéticas y eléctricas están entrelazadas. En 1873, James Clerk Maxwell consiguió formular las ecuaciones completas que rigen las fuerzas eléctricas y magnéticas, descubiertas experimentalmente por Michael Faraday. Se consiguió la teoría unificada del electromagnetismo que nos vino a decir que la electricidad y el magnetismo eran dos aspectos de una misma cosa.
La interacción es universal, de muy largo alcance (se extiende entre las estrellas), es bastante débil. Su intensidad depende del cociente entre el cuadrado de la carga del electrón y 2hc (dos veces la constante de Planck por la velocidad de la luz). Esta fracción es aproximadamente igual a 1/137’036…, o lo que llamamos α y se conoce como constante de estructura fina.
En general, el alcance de una interacción electromagnética es inversamente proporcional a la masa de la partícula mediadora, en este caso, el fotón, sin masa.
También antes hemos comentado sobre la interacción gravitatoria de la que Einstein descubrió su compleja estructura y la expuso al mundo en 1915 con el nombre de teoría general de la relatividad, y la relacionó con la curvatura del espacio y el tiempo. Sin embargo, aún no sabemos cómo se podrían reconciliar las leyes de la gravedad y las leyes de la mecánica cuántica (excepto cuando la acción gravitatoria es suficientemente débil).

La teoría de Einstein nos habla de los planetas y las estrellas del cosmos. La teoría de Planck, Heisemberg, Schrödinger, Dirac, Feynman y tantos otros, nos habla del comportamiento del átomo, del núcleo, de las partículas elementales en relación a estas interacciones fundamentales. La primera se ocupa de los cuerpos muy grandes y de los efectos que causan en el espacio y en el tiempo; la segunda de los cuerpos muy pequeños y de su importancia en el universo atómico. Cuando hemos tratado de unir ambos mundos se produce una gran explosión de rechazo. Ambas teorías son (al menos de momento) irreconciliables.
- La interacción gravitatoria actúa exclusivamente sobre la masa de una partícula.
- La gravedad es de largo alcance y llega a los más lejanos confines del universo conocido.
- Es tan débil que, probablemente, nunca podremos detectar esta fuerza de atracción gravitatoria entre dos partículas elementales. La única razón por la que podemos medirla es debido a que es colectiva: todas las partículas (de la Tierra) atraen a todas las partículas (de nuestro cuerpo) en la misma dirección.

La partícula mediadora es el hipotético gravitón. Aunque aún no se ha descubierto experimentalmente, sabemos lo que predice la mecánica cuántica: que tiene masa nula y espín 2.
La ley general para las interacciones es que, si la partícula mediadora tiene el espín par, la fuerza entre cargas iguales es atractiva y entre cargas opuestas repulsiva. Si el espín es impar (como en el electromagnetismo) se cumple a la inversa.
Pero antes de seguir profundizando en estas cuestiones hablemos de las propias partículas subatómicas, para lo cual la teoría de la relatividad especial, que es la teoría de la relatividad sin fuerza gravitatoria, es suficiente.

Si viajamos hacia lo muy pequeño tendremos que ir más allá de los átomos, que son objetos voluminosos y frágiles comparados con lo que nos ocupará a continuación: el núcleo atómico y lo que allí se encuentra. Los electrones, que ahora vemos “a gran distancia” dando vueltas alrededor del núcleo, son muy pequeños y extremadamente robustos. El núcleo está constituido por dos especies de bloques: protones y neutrones. El protón (del griego πρώτος, primero) debe su nombre al hecho de que el núcleo atómico más sencillo, que es el hidrógeno, está formado por un solo protón. Tiene una unidad de carga positiva. El neutrón recuerda al protón como si fuera su hermano gemelo: su masa es prácticamente la misma, su espín es el mismo, pero en el neutrón, como su propio nombre da a entender, no hay carga eléctrica; es neutro.
La masa de estas partículas se expresa en una unidad llamada mega-electrón-voltio o MeV, para abreviar. Un MeV, que equivale a 106 electrón-voltios, es la cantidad de energía de movimiento que adquiere una partícula con una unidad de carga (tal como un electrón o un protón) cuando atraviesa una diferencia de potencial de 106 (1.000.000) voltios. Como esta energía se transforma en masa, el MeV es una unidad útil de masa para las partículas elementales.

La mayoría de los núcleos atómicos contienen más neutrones que protones. Los protones se encuentran tan juntos en el interior de un núcleo tan pequeño que se deberían repeles entre sí fuertemente, debido a que tienen cargas eléctricas del mismo signo. Sin embargo, hay una fuerza que los mantiene unidos estrechamente y que es mucho más potente e intensa que la fuerza electromagnética: la fuerza o interacción nuclear fuerte, unas 102 veces mayor que la electromagnética, y aparece sólo entre hadronespara mantener a los nucleones confinados dentro del núcleo. Actúa a una distancia tan corta como 10-15 metros, o lo que es lo mismo, 0’000000000000001 metros.
La interacción fuerte está mediada por el intercambio de mesones virtuales, 8 gluones que, como su mismo nombre indica (glue en inglés es pegamento), mantiene a los protones y neutrones bien sujetos en el núcleo, y cuanto más se tratan de separar, más aumenta la fuerza que los retiene, que crece con la distancia, al contrario que ocurre con las otras fuerzas.
La luz es una manifestación del fenómeno electromagnético y está cuantizada en “fotones”, que se comportan generalmente como los mensajeros de todas las interacciones electromagnéticas. Así mismo, como hemos dejado reseñado en el párrafo anterior, la interacción fuerte también tiene sus cuantos (los gluones). El físico japonés Hideki Yukawa (1907 – 1981) predijo la propiedad de las partículas cuánticas asociadas a la interacción fuerte, que más tarde se llamarían piones. Hay una diferencia muy importante entre los piones y los fotones: un pión es un trozo de materia con una cierta cantidad de “masa”. Si esta partícula está en reposo, su masa es siempre la misma, aproximadamente 140 MeV, y si se mueve muy rápidamente, su masa parece aumentar en función E = mc2. Por el contrario, se dice que la masa del fotón en reposo es nula. Con esto no decimos que el fotón tenga masa nula, sino que el fotón no puede estar en reposo. Como todas las partículas de masa nula, el fotón se mueve exclusivamente con la velocidad de la luz, 299.792’458 Km/s, una velocidad que el pión nunca puede alcanzar porque requeriría una cantidad infinita de energía cinética. Para el fotón, toda su masa se debe a su energía cinética.

Los físicos experimentales buscaban partículas elementales en las trazas de los rayos cósmicos que pasaban por aparatos llamados cámaras de niebla. Así encontraron una partícula coincidente con la masa que debería tener la partícula de Yukawa, el pión, y la llamaron mesón (del griego medio), porque su masa estaba comprendida entre la del electrón y la del protón. Pero detectaron una discrepancia que consistía en que esta partícula no era afectada por la interacción fuerte, y por tanto, no podía ser un pión. Actualmente nos referimos a esta partícula con la abreviatura μ y el nombre de muón, ya que en realidad era un leptón, hermano gemelo del electrón, pero con 200 veces su masa.
Antes de seguir veamos las partículas elementales de vida superior a 10-20 segundos que eran conocidas en el año 1970.
| Nombre | Símbolo | Masa (MeV) | Carga | Espín | Vida media (s) |
| Fotón | γ | 0 | 0 | 1 | ∞ |
| Leptones (L = 1, B = 0) | |||||
| Electrón | e– | 0’5109990 | – | ½ | ∞ |
| Muón | μ– | 105’6584 | – | ½ | 2’1970 × 10-6 |
| Tau | τ | ||||
| Neutrino electrónico | νe | ~ 0 | 0 | ½ | ~ ∞ |
| Neutrino muónico | νμ | ~ 0 | 0 | ½ | ~ ∞ |
| Neutrino tauónico | ντ | ~ 0 | 0 | ½ | ~ ∞ |
| Mesones (L = 0, B = 0) | |||||
| Pión + | π+ | 139’570 | 2’603 × 10-8 | ||
| Pión – | π– | 139’570 | 2’603 × 10-8 | ||
| Pión 0 | π0 | 134’976 | 0’84 × 10-16 | ||
| Kaón + | k+ | 493’68 | 1’237 × 10-8 | ||
| Kaón – | k– | 493’68 | 1’237 × 10-8 | ||
| Kaón largo | kL | 497’7 | 5’17 × 10-8 | ||
| Kaón corto | kS | 497’7 | 0’893 × 10-10 | ||
| Eta | η | 547’5 | 0 | 0 | 5’5 × 10-19 |
| Bariones (L = 0, B = 1) | |||||
| Protón | p | 938’2723 | + | ½ | ∞ |
| Neutrón | n | 939’5656 | 0 | ½ | 887 |
| Lambda | Λ | 1.115’68 | 0 | ½ | 2’63 × 10-10 |
| Sigma + | Σ+ | 1.189’4 | + | ½ | 0’80 × 10-10 |
| Sigma – | Σ– | 1.1974 | – | ½ | 7’4× 10-20 |
| Sigma 0 | Σ0 | 0 | ½ | 1’48 × 10-10 | |
| Ksi 0 | Ξ0 | 1.314’9 | 0 | ½ | 2’9 × 10-10 |
| Ksi – | Ξ– | 1.321’3 | – | ½ | 1’64 × 10-10 |
| Omega – | Ω– | 1.672’4 | – | 1½ | 0’82 × 10-10 |


Para cada leptón y cada barión existe la correspondiente antipartícula, con exactamente las mismas propiedades a excepción de la carga que es la contraria. Por ejemplo, el antiprotón se simboliza con y el electrón con e+. Los mesones neutros son su propia antipartícula, y el π+ es la antipartícula del π–, al igual que ocurre con k+ y k–. El símbolo de la partícula es el mismo que el de su antipartícula con una barra encima. Las masas y las vidas medias aquí reflejadas pueden estar corregidas en este momento, pero de todas formas son muy aproximadas.
Los símbolos que se pueden ver algunas veces, como s (extrañeza) e i (isoespín) están referidos a datos cuánticos que afectan a las partículas elementales en sus comportamientos.
Debo admitir que todo esto tiene que sonar algo misterioso. Es difícil explicar estos temas por medio de la simple palabra escrita sin emplear la claridad que transmiten las matemáticas, lo que, por otra parte, es un mundo secreto para el común de los mortales, y ese lenguaje es sólo conocido por algunos privilegiados que, mediante un sistema de ecuaciones pueden ver y entender de forma clara, sencilla y limpia, todas estas complejas cuestiones.

Si hablamos del espín (o, con más precisión, el momento angular, que es aproximadamente la masa por el radio por la velocidad de rotación) se puede medir como un múltiplo de la constante de Planck, h, dividido por 2π. Medido en esta unidad y de acuerdo con la mecánica cuántica, el espín de cualquier objeto tiene que ser o un entero o un entero más un medio. El espín total de cada tipo de partícula – aunque no la dirección del mismo – es fijo.
El electrón, por ejemplo, tiene espín ½. Esto lo descubrieron dos estudiantes holandeses, Samuel Gondsmit (1902 – 1978) y George Uhlenbeck (1900 – 1988), que escribieron sus tesis conjuntamente sobre este problema en 1972. Fue una idea audaz que partículas tan pequeñas como los electronespudieran tener espín, y de hecho, bastante grande. Al principio, la idea fue recibida con escepticismo porque la “superficie del electrón” se tendría que mover con una velocidad 137 veces mayor que la de la luz, lo cual va en contra de la teoría de la relatividad general en la que está sentado que nada en el universo va más rápido que la luz, y por otra parte, contradice E=mc2, y el electrón pasada la velocidad de la luz tendría una masa infinita.
Hoy día, sencillamente, tal observación es ignorada, toda vez que el electrón carece de superficie.
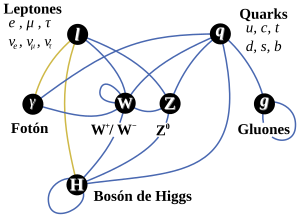
En la segunda imagen podemos ver los signos del fotón, las W+, W– y Zº, así como el Gluon y por último, el reciente Bosón de Higgs. Cada una de estas partículas representan intermediación en las cuatro fuerzas fundamentales de la Naturaleza: El fotón las radiaciones electromagnéticas (la luz entre ellas), la W y Zº la fuerza nuclear electrodébil, los gluones la nuclear fuerte, el Bosón de Higgs que dicen proporciona la masa de las partíuclas, y, ausente está el gravitón, intermediario de la Gravedad que no ha podido ser hallado.
Las partículas con espín entero se llaman bosones, y las que tienen espín entero más un medio se llaman fermiones. Consultado los valores del espín en la tabla anterior podemos ver que los leptones y los bariones son fermiones, y que los mesones y los fotones son bosones. En muchos aspectos, los fermionesse comportan de manera diferente de los bosones. Los fermiones tienen la propiedad de que cada uno de ellos requiere su propio espacio: dos fermiones del mismo tipo no pueden ocupar o estar en el mismo punto, y su movimiento está regido por ecuaciones tales que se evitan unos a otros. Curiosamente, no se necesita ninguna fuerza para conseguir esto. De hecho, las fuerzas entre los fermiones pueden ser atractivas o repulsivas, según las cargas. El fenómeno por el cual cada fermión tiene que estar en un estado diferente se conoce como el principio de exclusión de Pauli. Cada átomo está rodeado de una nube de electrones, que son fermiones (espín ½). Si dos átomos se aproximan entre sí, los electrones se mueven de tal manera que las dos nubes se evitan una a otra, dando como resultado una fuerza repulsiva. Cuando aplaudimos, nuestras manos no se atraviesan pasando la uno a través de la otra. Esto es debido al principio de exclusión de Pauli para los electrones de nuestras manos que, de hecho, los de la izquierda rechazan a los de la derecha.
En contraste con el característico individualismo de los fermiones, los bosones se comportan colectivamente y les gusta colocarse todos en el mismo lugar. Un láser, por ejemplo, produce un haz de luz en el cual muchísimos fotones llevan la misma longitud de onda y dirección de movimiento. Esto es posible porque los fotones son bosones.
Cuando hemos hablado de las fuerzas fundamentales que, de una u otra forma, interaccionan con la materia, también hemos explicado que la interacción débil es la responsable de que muchas partículas y también muchos núcleos atómicos exóticos sean inestables. La interacción débil puede provocar que una partícula se transforme en otra relacionada, por emisión de un electrón y un neutrino. Enrico Fermi, en 1934, estableció una fórmula general de la interacción débil, que fue mejorada posteriormente por George Sudarshan, Robert Marschak, Murray Gell-Mann, Richard Feynman y otros. La fórmula mejorada funciona muy bien, pero se hizo evidente que no era adecuada en todas las circunstancias.
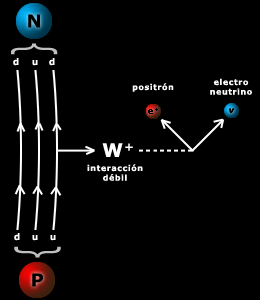
Uno de los protones se transmuta en un neutrón por medio de la interacción débil, transformando un quark “up”, en “down”. Este proceso consume energía (el neutrón tiene ligeramente más masa que..
En 1970, de las siguientes características de la interacción débil sólo se conocían las tres primeras:
- La interacción actúa de forma universal sobre muchos tipos diferentes de partículas y su intensidad es aproximadamente igual para todas (aunque sus efectos pueden ser muy diferentes en cada caso). A los neutrinos les afecta exclusivamente la interacción débil.
- Comparada con las demás interacciones, ésta tiene un alcance muy corto.
- La interacción es muy débil. Consecuentemente, los choques de partículas en los cuales hay neutrinos involucrados son tan poco frecuentes que se necesitan chorros muy intensos de neutrinos para poder estudiar tales sucesos.
- Los mediadores de la interacción débil, llamados W+, W– y Z0, no se detectaron hasta la década de 1980. al igual que el fotón, tienen espín 1, pero están eléctricamente cargados y son muy pesados (esta es la causa por la que el alcance de la interacción es tan corto). El tercer mediador, Z0, que es responsable de un tercer tipo de interacción débil que no tiene nada que ver con la desintegración de las partículas llamada “corriente neutra”, permite que los neutrinos puedan colisionar con otras partículas sin cambiar su identidad.
A partir de 1970, quedó clara la relación de la interacción débil y la electromagnética (electrodébil de Weinberg-Salam).
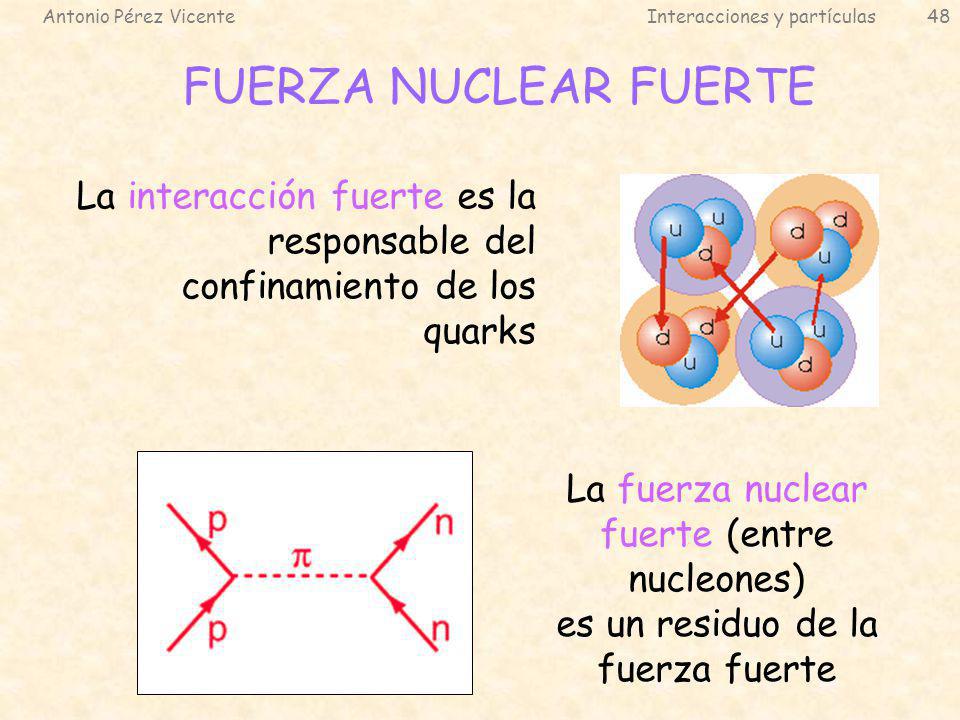
La interacción fuerte (como hemos dicho antes) sólo actúa entre las partículas que clasificamos en la familia llamada de los hadrones, a los que proporciona una estructura interna complicada. Hasta 1972 sólo se conocían las reglas de simetría de la interacción fuerte y no fuimos capaces de formular las leyes de la interacción con precisión.

Como apuntamos, el alcance de esta interacción no va más allá del radio de un núcleo atómico ligero (10-13 cm aproximadamente).
La interacción es fuerte. En realidad, la más fuerte de todas.
Lo dejaré aquí, en verdad, eso que el Modelo Estándar de la Física, es feo, complejo e incompleto y, aunque hasta el momento ha sido una buena herramienta con la que trabajar, la verdad es que, se necesita un nuevo modelo más avanzado y que incluya la Gravedad.
Existen esperanzas de que el LHC empleando energías más elevadas, nos pueda dar alguna sorpresa y encuentre objetos largamente perseguidos.
emilio silvera
















 Totales: 75.724.543
Totales: 75.724.543 Conectados: 57
Conectados: 57