Oct
20
Los Quarks invisibles
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (1)
Comments (1)
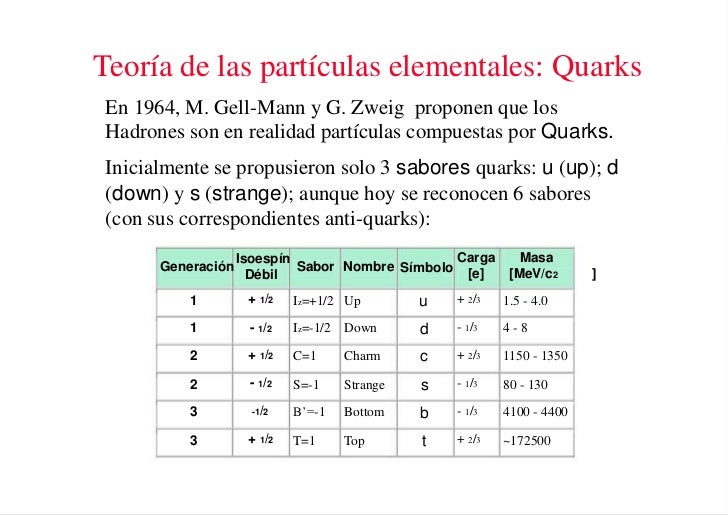
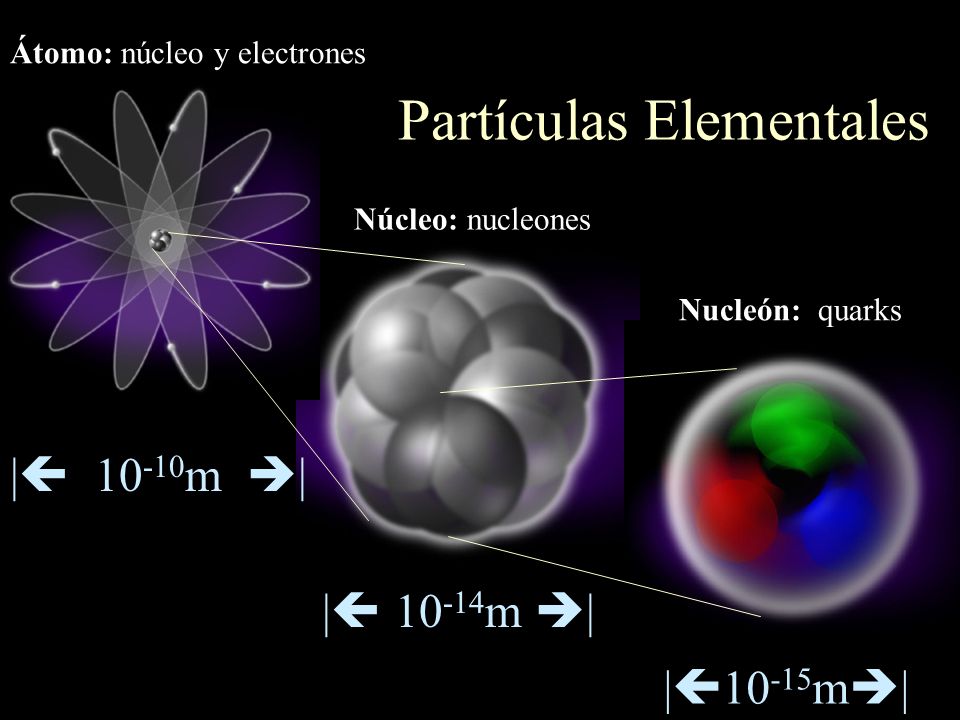
Una vez que se ha puesto orden entre las numerosas especies de partículas, se puede reconocer una pauta. Igual que Dimitri Ivanovich Mendeleev descubrió el sistema periódico de los elementos químicos en 1869, así también se hizo visible un sistema similar para las partículas. Esta pauta la encontraron independientemente el americano Murray Gell-Mann y el israelí Yuval Ne’eman. Ocho especies de mesones, todos con el mismo espín, u ocho especies de bariones, con el mismo espín, se podían reagrupar perfectamente en grupos que llamaremos multipletes. El esquema matemático correspondiente se llama SU(3). Grupletes de ocho elementos forman un octete “fundamental”. Por esta razón Gell-Mann llamó a esta teoría el “óctuplo camino”. Lo tomó prestado del budismo de acuerdo con el cual el camino hacia el nirvana es el camino óctuplo.
Rueda del dharma.
El Noble Camino Óctuple es considerado, según el budismo, como la vía que lleva al cese del sufrimiento. Este cese del sufrimiento se conoce como nirvana. Puede ser que eso fuese lo que sintiera Gell-Mann al finalizar sus trabajos, y, de ahí la adopción del nombre y todo lo que lleva consigo de simbología.

El noble camino es una de las enseñanzas budistas fundamentales; la cuarta parte de las Cutro Nobles Verdades. En la simbología budista, el noble camino es usualmente representado con la rueda del dharma, donde cada rayo representa un elemento del sendero. Este símbolo también se utiliza para el budismo en general.
Los elementos del noble camino óctuple se subdividen en tres categorías básicas: sabiduría, conducta ética y entrenamiento de la mente (o meditación); para rehabilitar y desacondicionar la mente. En todos los elementos del noble camino, la palabra «correcta» es una traducción de la palabra “sammā” (en pali), que significa ‘plenitud’, ‘coherencia’, ‘perfección’ o ‘ideal’. El noble camino es: Sabiduría.
Pero sigamos con el trabajo.
Las matemáticas SU(3) también admiten multipletes de diez miembros. Cuando se propuso este esquema se conocían nueve bariones con espín 3/2. Los esquemas SU(3) se obtienen al representar dos propiedades fundamentales de las partículas, la extrañeza S frente al isoespín I₃ , en una gráfica.
Imagen de trazas en la cámara de burbujas del primer evento observado incluyendo bariones Ω, en el Laboratorio Nacional Brookhaven. Dependiendo de su masa y tamaño las partículas producen distintos remolinos en la cámara de burbujas.
De esta manera, Gell-Mann predijo un décimo barión, el omega-menos (Ω¯), y pudo estimar con bastante precisión su masa porque las masas de los otros nueve bariones variaban de una forma sistemática en el gráfico (también consiguió entender que las variaciones de la masa eran una consecuencia de una interacción simple). Sin embargo, estaba claro que la Ω¯, con una extrañeza S = -3, no tenía ninguna partícula en la que desintegrarse que no estuviera prohibida por las leyes de conservación de la interacción fuerte. De modo que, la Ω¯ sólo podía ser de tan sólo 10¯²³ segundos como los demás miembros del multiplete, sino que tenía que ser del orden de 10¯¹⁰ segundos. Consecuentemente, esta partícula debería viajar varios centímetros antes de desintegrarse y esto la haría fácilmente detectable. La Ω¯ fue encontrada en 1964 con exactamente las mismas propiedades que había predicho Gell-Mann.
Se identificaron estructuras multipletes para la mayoría de los demás bariones y mesones y Gell-Mann también consiguió explicarlas. Sugirió que los mesones, igual que los bariones, debían estar formados por elementos constitutivos “más fundamentales aún”. Gell-Mann trabajaba en el Instituto de Tecnología de California en Pasadena (CalTech), donde conversaba a menudo con Richard Feynman. Eran ambos físicos famosos pero con personalidades muy diferentes. Gell-Mann, por ejemplo, es conocido como un entusiasta observador de Pájaros, familiarizado con las artes y la literatura y orgulloso de su conocimiento de lenguas extranjeras.

A comienzos de los años sesenta, un profesor del Instituto de Tecnología de California (Caltech) imparte un curso completo de física ante una cada día más numerosa. Su nombre: Richard Feynman
Feynman fue un hombre hecho a sí mismo, un analista riguroso que se reía de cualquier cosa que le recordara la autoridad establecida. Hay una anécdota que parece no ser cierta de hecho, pero que me parece tan buena que no puedo evitar el contarla; podía haber sucedido de esta forma. Gell-Mann le dijo a Feynman que tenía un problema, que estaba sugiriendo un nuevo tipo de ladrillos constitutivos de la materia y que no sabía qué nombre darles. Indudablemente debía haber de haber pensado en utilizar terminología latina o griega, como ha sido costumbre siempre en la nomenclatura científica. “Absurdo”, le dijo Feynman; “tú estás hablando de cosas en las que nunc ase había pensado antes. Todas esas preciosas pero anticuadas palabras están fuera de lugar. ¿Por qué no los llamas simplemente “shrumpfs”, “quacks” o algo así?”.

Los pequeños componentes de la materia ordinaria
Cuando algún tiempo después le pregunté a Gell-Mann, éste negó que tal conversación hubiera tenido lugar. Pero la palabra elegida fue quark, y la explicación de Gell-Mann fue que la palabra venía de una frase de Fynnegan’s Wake de James Joyce; “¡Tres quarks para Muster Mark!”. Y, efectivamente así es. A esas partículas les gusta estar las tres juntas. Todos los bariones están formados por tres quarks, mientras que los mesones están formados por un quark y un antiquark.


Los propios quarks forman un grupo SU(3) aún más sencillo. Los llamaremos “arriba (u)”, “abajo” (d), y “extraño” (s). Las partículas “ordinarias” contienen solamente quarks u y d. Los hadrones “extraños” contienen uno o más quarks s (o antiquarks ŝ).
La composición de quarks de espín 3/2 se puede ver en cualquier tabla de física.. La razón por la que los bariones de espín ½ sólo forman un octete es más difícil de explicar. Está relacionada con el hecho de que en estos estados, al menos dos de los quarks tienen que ser diferentes unos de otros.

Junto con los descubrimientos de los Hadrones y de sus componentes, los Quarks, durante la primera mitad del sigo XX, se descubrieron otras partículas. Los Hadrones forman dos ramas, los mesones formados por dos qiuarks y los bariones por tres.

La Mecánica cuántica es muy extraña
Realmente, la idea de que los hadrones estuvieran formados por ladrillos fundamentales sencillos había sido también sugerida por otros. George Zweig, también en el Cal Tech, en Pasadena, había tenido la misma idea. Él había llamado a los bloques constitutivos “ases!, pero es la palabra “quark” la que ha prevalecido. La razón por la que algunos nombres científicos tienen más éxito que otros es a veces difícil de comprender.
Pero en esta teoría había algunos aspectos raros. Aparentemente, los quarks (o ases) siempre existen en parejas o tríos y nunca se han visto solos. Los experimentadores habían intentado numerosas veces detectar un quark aislado en aparatos especialmente diseñados para ello, pero ninguno había tenido éxito.

Loa quarks –si se pudieran aislar- tendrían propiedades incluso más extrañas. Por ejemplo, ¿cuáles serían sus cargas eléctricas? Es razonable suponer que tanto los quarks u como los quarks s y d deban tener siempre la misma carga. La comparación de la tabla 5 con la tabla 2 sugiere claramente que los quarks d y s tienen carga eléctrica -1/3 y el quark u tiene carga +2/3. Pero nunca se han observado partículas que no tengan carga múltiplo de la del electrón o de la del protón. Si tales partículas existieran, sería posible detectarlas experimentalmente. Que esto haya sido imposible debe significar que las fuerzas que las mantienen unidas dentro del hadrón son necesariamente increíblemente eficientes.

Todos sabemos que los Lepotines son: El elentrón, el Muón y la partícula Tau y, cada una de ellas tiene su tipo de neutrino: el electrónico, el muónico y el tauónico.
Aunque con la llegada de los quarks se ha clarificado algo más la flora y la fauna de las partículas subatómicas, todavía forman un conjunto muy raro, aún cuando solamente unas pocas aparezcan en grandes cantidades en el universo (protones, neutrones, electrones y fotones). Como dijo una vez Sybren S. de Groot cuando estudiaba neutrinos, uno realmente se enamora de ellos. Mis estudiantes y yo amábamos esas partículas cuyo comportamiento era un gran misterio. Los leptones, por ser casi puntuales, son los más sencillos, y por tener espín se ven afectados por la interacción que actúa sobre ellos de forma muy complicada, pero la interacción débil estaba bastante bien documentada por entonces.

Los hadrones son mucho más misteriosos. Los procesos de choque entre ellos eran demasiado complicados para una teoría respetable. Si uno se los imagina como pequeñas esferas hachas de alguna clase de material, aún quedaba el problema de entender los quarks y encontrar la razón por la que se siguen resistiendo a los intentos de los experimentadores para aislarlos.
emilio silvera
Si queréis saber más sobre el tema, os recomiendo leer el libro Partículas de Gerard ´t Hooft
Oct
15
Intrincada búsqueda: ¡La Gravedad cuántica!
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (0)
Comments (0)


Nunca han importado muchos los peligros que tengamos que correr para buscar las respuestas de lo profundamente escondido en la Naturaleza, ni tampoco ha importado hasta donde ha tenido que viajar la imaginación para configurar modelos y teorías que, más tarde, queremos verificar.
También una teoría cuántica de la gravedad debería ampliar nuestro conocimiento de efectos cuánticos predichos por enfoques tentativos de otras teorías cuánticas, como la existencia de radiación de Hawking.”
¡Y mucho más sobre este mismo tema!

Entre los teóricos, el casamiento de la relatividad general y la teoría cuántica es el problema central de la física moderna. A los esfuerzos teóricos que se realizan con ese propósito se les llama “supergravedad”, “súpersimetría”, “supercuerdas” “teoría M” o, en último caso, “teoría de todo o gran teoría unificada”.

“El concepto de una “teoría del todo” está arraigado en el principio de causalidad y su descubrimiento es la empresa de acercarnos a ver a través de los ojos del demonio de Laplace. Aunque dicha posibilidad puede considerarse como determinista, en una “simple fórmula” puede todavía sobrevivir la física fundamentalmente probabilista, como proponen algunas posturas actuales de la mecánica cuántica. Esto se debe a que aun si los mecanismos que gobiernan las partículas son intrínsecamente azarosos, podemos conocer las reglas que gobiernan dicho azar y calcular las probabilidades de ocurrencia para cada evento posible. Sin embargo, otras interpretaciones de la ecuación de Schrödinger conceden poca importancia al azar: este solo se tendría importancia dentro del átomo y se diluiría en el mundo macroscópico. Otras no obstante la niegan completamente y la consideran una interpretación equivocada de las leyes cuánticas. En consecuencia, la mayor dificultad de descubrir una teoría unificada ha sido armonizar correctamente leyes que gobiernan solo un reducido ámbito de la naturaleza y transformarlas en una única teoría que la explique en su totalidad, tanto en su mundo micro como macroscópico y explique la existencia de todas las interacciones fundamentales: las fuerzas gravitatoria, electromagnética, nuclear fuerte y nuclear débil.”
Ahí tenemos unas matemáticas exóticas que ponen de punta hasta los pelos de las cejas de algunos de los mejores matemáticos del mundo (¿y Perelman? ¿Por qué nos se ha implicado?). Hablan de 10, 11 y 26 dimensiones, siempre, todas ellas espaciales menos una que es la temporal. Vivimos en cuatro: tres de espacio (este-oeste, norte-sur y arriba-abajo) y una temporal. No podemos, ni sabemos o no es posible instruir, en nuestro cerebro (también tridimensional), ver más dimensiones. Pero llegaron Kaluza y Klein y compactaron, en la longitud de Planck las dimensiones que no podíamos ver. ¡Problema solucionado!
¿Quién puede ir a la longitud de Planck para poder contemplar esas cuerdas vibrantes si es que están allí?

Ni vemos la longitud de Planck ni las dimensiones extra y, nos dicen que para poder profundizar hasta esa distancia, necesitamos disponer de la Energía de Planck, es decir 1019 GeV, una energía que ni en las próximas generaciones estará a nuestro alcance. Pero mientras tanto, hablamos de que, en 2.015, el LHC buscará las partículas de la “materia oscura”. ¡Qué gente!
La puerta de las dimensiones más altas quedó abierta y, a los teóricos, se les regaló una herramienta maravillosa. En el Hiperespacio, todo es posible. Hasta el matrimonio de la relatividad general y la mecánica cuántica, allí si es posible encontrar esa soñada teoría de la Gravedad cuántica.
Así que, los teóricos, se han embarcado a la búsqueda de un objetivo audaz: buscan una teoría que describa la simplicidad primigenia que reinaba en el intenso calor del universo en sus primeros tiempos, una teoría carente de parámetros, donde estén presentes todas las respuestas. Todo debe ser contestado a partir de una ecuación básica.
¿Dónde radica el problema?

Nuestro universo ¿es tridimensional y no podemos esas dimensiones extra de las que tanto hablan en las teorías más avanzadas pero, no verificadas?
El problema está en que la única teoría candidata no tiene conexión directa con el mundo de la observación, o no lo tiene todavía si queremos expresarnos con propiedad. La energía necesaria para ello, no la tiene ni el nuevo acelerador de partículas LHC que con sus 14 TeV no llegaría ni siquiera a vislumbrar esas cuerdas vibrantes de las que antes os hablaba.
La verdad es que, la teoría que ahora tenemos, el Modelo Estándar, concuerda de manera exacta con todos los datos a bajas energías y contesta cosas sin sentido a altas energías. Ya sabéis lo que pasa cuando queremos juntar la relatividad con la cuántica: ¡Aparecen los infinitos que no son renormalizables!

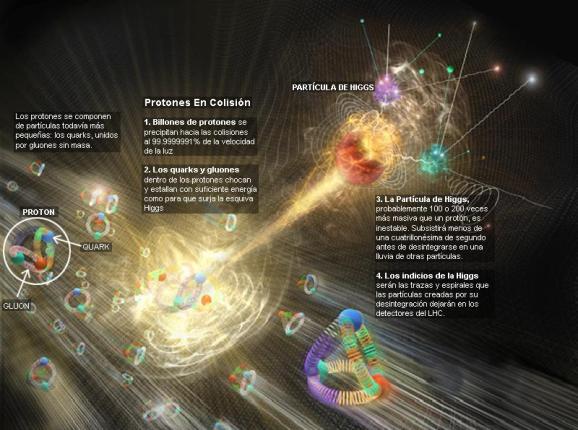
Con sus 20 parámetros aleatorios (parece que uno de ellos ha sido hallado -el bosón de Higgs-), el Modelo estándar de la física de partículas que incluye sólo tres de las interacicones fundamentales -las fuerzas nucleares débil y fuerte y el electromagnetismo-, ha dado un buen resultado y a permitido a los físicos trabajar ampliamente en el conocimiento del mundo, de la Naturaleza, del Universo. Sin embargo, deja muchas preguntas sin contestar y, lo cierto es que, se necesitan nuevas maneras, nuevas formas, nuevas teorías que nos lleven más allá.
¡Necesitamos algo más avanzado!
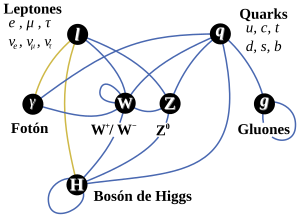
Se ha dicho que la función de la partícula de Higgs es la de dar masa a las partículas que conocemos y están incluidas en el Modelo estándar, se nos ha dicho que ha sido encontrada y el hallazgo ha merecido el Nobel de Física. Sin embargo… nada se ha dicho de cómo ésta partícula transmite la masa a las demás. Faltan algunas explicaciones.
El secreto de todo radica en conseguir la simplicidad: el átomo resulto ser complejo lleno de esas infinitesimales partículas electromagnéticas que bautizamos con el nombre de electrones, resultó que tenía un núcleo que contenía, a pesar de ser tan pequeño, casi toda la masa del átomo. El núcleo, tan pequeño, estaba compuesto de otros objetos más pequeños aún, los quarks que estaban instalados en nubes de otras partículas llamadas gluones y, ahora, queremos continuar profundizando, sospechamos, que después de los quarks puede haber algo más.
¿Es el efecto frenado que sufren las partículas que corren por el océano de Higgs, el que les da la masa?
Bueno, la idea nueva que surgió es que el espacio entero contiene un campo, el campo de Higgs, que impregna el vacío y es el mismo en todas partes. Es decir, que si miramos a las estrellas en una noche clara estamos mirando el campo de Higgs. Las partículas influidas por este campo, toman masa. Esto no es por sí mismo destacable, pues las partículas pueden tomar energía de los campos (gauge) de los que hemos comentado, del campo gravitatorio o del electromagnético. Si llevamos un bloque de plomo a lo alto de la Torre Eiffel, el bloque adquiriría energía potencial a causa de la alteración de su posición en el campo gravitatorio de la Tierra.

Como E=mc2, ese aumento de la energía potencial equivale a un aumento de la masa, en este caso la masa del Sistema Tierra-bloque de plomo. Aquí hemos de añadirle amablemente un poco de complejidad a la venerable ecuación de Einstein. La masa, m, tiene en realidad dos partes. Una es la masa en reposo, m0, la que se mide en el laboratorio cuando la partícula está en reposo. La partícula adquiere la otra parte de la masa en virtud de su movimiento (como los protones en el acelerador de partículas, o los muones, que aumentan varias veces su masa cuando son lanzados a velocidades cercanas a c) o en virtud de su energía potencial de campo. Vemos una dinámica similar en los núcleos atómicos. Por ejemplo, si separamos el protón y el neutrón que componen un núcleo de deuterio, la suma de las masas aumenta.
Peor la energía potencial tomada del campo de Higgs difiere en varios aspectos de la acción de los campos familiares. La masa tomada de Higgs es en realidad masa en reposo. De hecho, en la que quizá sea la versión más
apasionante de la teoría del campo de Higgs, éste genera toda la masa en reposo. Otra diferencia es que la cantidad de masa que se traga del campo es distinta para las distintas partículas.
Los teóricos dicen que las masas de las partículas de nuestro modelo estándar miden con qué intensidad se acoplan éstas al campo de Higgs.
La influencia de Higgs en las masas de los quarks y de los leptones, nos recuerda el descubrimiento por Pieter Zeeman, en 1.896, de la división de los niveles de energía de un electrón cuando se aplica un campo magnético al átomo. El campo (que representa metafóricamente el papel de Higgs) rompe la simetría del espacio de la que el electrón disfrutaba.
Hasta ahora no tenemos ni idea de que reglas controlan los incrementos de masa generados por el Higgs (de ahí la expectación creada por el acelerador de partículas LHC). Pero el problema es irritante: ¿por qué sólo esas masas –Las masas de los W+, W–, y Zº, y el up, el down, el encanto, el extraño, el top y el bottom, así como los leptones – que no forman ningún patrón obvio?

No dejamos de experimentar para saber ccómo es nuestro mundo, la Naturaleza, el Universo que nos acoge
Las masas van de la del electrón 0’0005 GeV, a la del top, que tiene que ser mayor que 91 GeV. Deberíamos recordar que esta extraña idea (el Higgs) se empleó con mucho éxito para formular la teoría electrodébil (Weinberg-Salam). Allí se propuso el campo de Higgs como una forma de ocultar la unidad de las fuerzas electromagnéticas y débiles. En la unidad hay cuatro partículas mensajeras sin masa –los W+, W–, Zº y fotón que llevan la fuerza electrodébil. Además está el campo de Higgs, y, rápidamente, los W y Z chupan la esencia de Higgs y se hacen pesados; el fotón permanece intacto. La fuerza electrodébil se fragmenta en la débil (débil porque los mensajeros son muy gordos) y la electromagnética, cuyas propiedades determina el fotón, carente de masa. La simetría se rompe espontáneamente, dicen los teóricos. Hay otra descripción según la cual el Higgs oculta la simetría con su poder dador de masa.
Las masas de los W y el Z se predijeron con éxito a partir de los parámetros de la teoría electrodébil. Y las relajadas sonrisas de los físicos teóricos nos recuerdan que Gerard ^t Hooft y Veltman dejaron sentado que la teoría entera esta libre de infinitos.


La teoría de supercuerdas tiene tantas sorpresas fantásticas que cualquiera que investigue en el tema reconoce que está llena de magia. Es algo que funciona con tanta belleza… Cuando cosas que no encajan juntas e incluso se repelen, si se acerca la una a la otra alguien es capaz de formular un camino mediante el cual, no sólo no se rechazan, sino que encajan a la perfección dentro de ese sistema, como ocurre ahora con la teoría M que acoge con naturalidad la teoría de la relatividad general y la teoría mecánico-cuántica; ahí, cuando eso se produce, está presente la belleza.

Lo que hace que la teoría de supercuerdas sea tan interesante es que el marco estándar mediante el cual conocemos la mayor parte de la física es la teoría cuántica y resulta que ella hace imposible la gravedad. La relatividad general de Einstein, que es el modelo de la gravedad, no funciona con la teoría cuántica. Sin embargo, las supercuerdas modifican la teoría cuántica estándar de tal manera que la gravedad no sólo se convierte en posible, sino que forma parte natural del sistema; es inevitable para que éste sea completo.
¿Por qué es tan importante encajar la gravedad y la teoría cuántica? Porque no podemos admitir una teoría que explique las fuerzas de la naturaleza y deje fuera a una de esas fuerzas. Así ocurre con el Modelo Estándar que deja aparte y no incluye a la fuerza gravitatoria que está ahí, en la Naturaleza.
La teoría de supercuerdas se perfila como la teoría que tiene implicaciones si tratamos con las cosas muy pequeñas, en el microcosmos; toda la teoría de partículas elementales cambia con las supercuerdas que penetra mucho más; llega mucho más allá de lo que ahora es posible.

La topología es, el estudio de aquellas propiedades de los cuerpos geométricos que permanecen inalteradas por transformaciones continuas. La topología es probablemente la más joven de las ramas clásicas de las matemáticas. En contraste con el álgebra, la geometría y la teoría de los números, cuyas genealogías datan de tiempos antiguos, la topología aparece en el siglo diecisiete, con el nombre de analysis situs, ésto es, análisis de la posición.
De manera informal, la topología se ocupa de aquellas propiedades de las figuras que permanecen invariantes, cuando dichas figuras son plegadas, dilatadas, contraídas o deformadas, de modo que no aparezcan nuevos puntos, o se hagan coincidir puntos diferentes. La transformación permitida presupone, en otras palabras, que hay una correspondencia biunívoca entre los puntos de la figura original y los de la transformada, y que la deformación hace corresponder puntos próximos a puntos próximos. Esta última propiedad se llama continuidad, y lo que se requiere es que la transformación y su inversa sean ambas continuas: así, trabajarnos con homeomorfismos.

En cuanto a nuestra comprensión del universo a gran escala (galaxias, el Big Bang…), creo que afectará a nuestra idea presente, al esquema que hoy rige y, como la nueva teoría, el horizonte se ampliará enormemente; el cosmos se presentará ante nosotros como un todo, con un comienzo muy bien definido y un final muy bien determinado.
Para cuando eso llegue, sabremos lo que es, como se genera y dónde están situados los orígenes de esa “fuerza”, “materia”, o, “energía” que ahora no sabemos ver para explicar el anómalo movimiento de las galaxias o la expansión del espacio que corre sin freno hacia… ¿Otro universo que tira del nuestro, como ocurren con las galaxias que terminan por fusionarse?
emilio silvera
Oct
8
El Micro Mundo de los Átomos
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (0)
Comments (0)
Cuando por primera vez se puso este trabajo, dio lugar a comentarios que nos llevan hasta la realidad de hasta donde, resulta para nosotros incomprensible ese micro mundo de la cuántica, ese “universo” infinitesimal donde ocurren cosas que, no llegamos a comprender.


Sí, existe otro mundo que no vemos pero, ¡está en éste!
La mecánica cuántica domina en el micromundo de los átomos y de las partículas “elementales”. Nos enseña que en la naturaleza cualquier masa, por sólida o puntual que pueda parecer, tiene un aspecto ondulatorio. Esta onda no es como una onda de agua. Es una onda de información. Nos indica la probabilidad de detectar una partícula. La longitud de onda de una partícula, la longitud cuántica, se hace menor cuanto mayor es la masa de esa partícula.
Por el contrario, la relatividad general era siempre necesaria cuando se trataba con situaciones donde algo viaja a la velocidad de la luz, o está muy cerca o donde la gravedad es muy intensa. Se utiliza para describir la expansión del universo o el comportamiento en situaciones extremas, como la formación de agujeros negros. Sin embargo, la gravedad es muy débil comparada con las fuerzas que unen átomos y moléculas y demasiado débil para tener cualquier efecto sobre la estructura del átomo o de partículas subatómicas, se trata con masas tan insignificantes que la incidencia gravitatoria es despreciable. Todo lo contrario que ocurre en presencia de masas considerables como planetas, estrellas y galaxias, donde la presencia de la gravitación curva el espacio y distorsiona el tiempo.

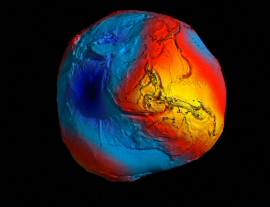
La Gravedad hace que la Tierra se vea como un mapa. Es una vista altamente exagerada, pero ilustra a las claras cómo la atracción gravitatoria que se manifiesta desde la masa de roca bajo nuestros pies no es la misma en todo lugar. La gravedad es más fuerte en áreas amarillas y más débil en las azules. (Imagen tomada por el satélite Goce)
Como resultado de estas propiedades antagónicas, la teoría cuántica y la teoría relativista gobiernan reinos diferentes, muy dispares, en el universo de lo muy pequeño o en el universo de lo muy grande. Nadie ha encontrado la manera de unir, sin fisuras, estas dos teorías en una sola y nueva de Gravedad-Cuántica.
¿Cuáles son los límites de la teoría cuántica y de la teoría de la relatividad general de Einstein? Afortunadamente, hay una respuesta simple y las unidades de Planck nos dicen cuales son.

Supongamos que tomamos toda la masa del universo visible y determinamos su longitud de onda cuántica. Podemos preguntarnos en qué momento esta longitud de onda cuántica del universo visible superará su tamaño. La respuesta es: cuando el universo sea más pequeño en tamaño que la longitud de Planck, es decir, 10-33 centímetros, más joven que el Tiempo de Planck, 10-43 segundos y supere la temperatura de Planck de 1032 grados. Las unidades de Planck marcan la frontera de aplicación de nuestras teorías actuales. Para comprender en que se parece el mundo a una escala menor que la longitud de Planck tenemos que comprender plenamente cómo se entrelaza la incertidumbre cuántica con la gravedad. Para entender lo que podría haber sucedido cerca del suceso que estamos tentados a llamar el principio del universo, o el comienzo del tiempo, tenemos que penetrar la barrera de Planck. Las constantes de la naturaleza marcan las fronteras de nuestro conocimiento existente y nos dejan al descubierto los límites de nuestras teorías.
En los intentos más recientes de crear una teoría nueva para describir la naturaleza cuántica de la gravedad ha emergido un nuevo significado para las unidades naturales de Planck. Parece que el concepto al que llamamos “información” tiene un profundo significado en el universo. Estamos habituados a vivir en lo que llamamos “la edad de la información”. La información puede ser empaquetada en formas electrónicas, enviadas rápidamente y recibidas con más facilidad que nunca antes.

Los tiempos cambian y la manera de informar también, lejos nos queda ya aquellos toscos aparatos impresores del pasado, ahora, en espacios muy reducidos, tenemos guardada más información que antes había en una colección de libros.
Nuestra evolución en el proceso rápido y barato de la información se suele mostrar en una forma que nos permite comprobar la predicción de Gordon Moore, el fundador de Intel, llamada ley de Moore, en la que, en 1.965, advirtió que el área de un transistor se dividía por dos aproximadamente cada 12 meses. En 1.975 revisó su tiempo de reducción a la mitad hasta situarlo en 24 meses. Esta es “la ley de Moore” cada 24 meses se obtiene una circuiteria de ordenador aproximadamente el doble, que corre a velocidad doble, por el mismo precio, ya que, el coste integrado del circuito viene a ser el mismo, constante.

Los límites últimos que podemos esperar para el almacenamiento y los ritmos de procesamiento de la información están impuestos por las constantes de la naturaleza. En 1.981, el físico israelí, Jacob Bekenstein, hizo una predicción inusual que estaba inspirada en su estudio de los agujeros negros. Calculó que hay una cantidad máxima de información que puede almacenarse dentro de cualquier volumen. Esto no debería sorprendernos. Lo que debería hacerlo es que el valor máximo está precisamente determinado por el área de la superficie que rodea al volumen, y no por el propio volumen. El número máximo de bits de información que puede almacenarse en un volumen viene dado precisamente por el cómputo de su área superficial en unidades de Planck. Supongamos que la región es esférica. Entonces su área superficial es precisamente proporcional al cuadrado de su radio, mientras que el área de Planck es proporcional a la longitud de Planck al cuadrado, 10-66 cm2. Esto es muchísimo mayor que cualquier capacidad de almacenamiento de información producida hasta ahora. Asimismo, hay un límite último sobre el ritmo de procesamiento de información que viene impuesto por las constantes de la naturaleza.

La información llega a todos los rincones del Mundo
No debemos descartar la posibilidad de que seamos capaces de utilizar las unidades de Planck-Stoney para clasificar todo el abanico de estructuras que vemos en el universo, desde el mundo de las partículas elementales hasta las más grandes estructuras astronómicas. Este fenómeno se puede representar en un gráfico que recree la escala logarítmica de tamaño desde el átomo a las galaxias.
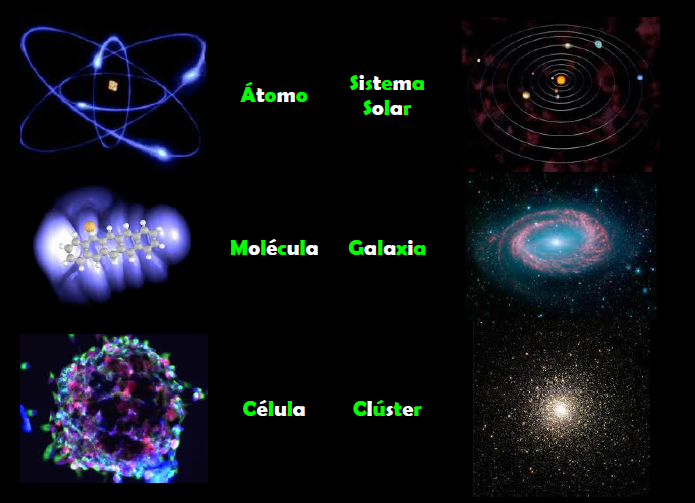
Todas las estructuras del universo existen porque son el equilibrio de fuerzas dispares y competidoras que se detienen o compensan las unas a las otras; la atracción y la repulsión. Ese es el equilibrio de las estrellas donde la repulsión termonuclear tiende a expandirla y la atracción (contracción) de su propia masa tiende a comprimirla; así, el resultado es la estabilidad de la estrella. En el caso del planeta Tierra, hay un equilibrio entre la fuerza atractiva de la gravedad y la repulsión atómica que aparece cuando los átomos se comprimen demasiado juntos. Todos estos equilibrios pueden expresarse aproximadamente en términos de dos números puros creados a partir de las constantes e, h, c, G y mprotón.
α = 2πe2 / hc ≈ 1/137
αG = (Gmp2)2 / hc ≈ 10-38
La identificación de constantes adimensionales de la naturaleza como a (alfa) y aG, junto con los números que desempeñan el mismo papel definitorio para las fuerzas débil y fuerte de la naturaleza, nos anima a pensar por un momento en mundos diferentes del nuestro.

Estos otros mundos pueden estar definidos por leyes de la naturaleza iguales a las que gobiernan el universo tal como lo conocemos, pero estarán caracterizados por diferentes valores de constantes adimensionales. Estos cambios numéricos alterarán toda la fábrica de los mundos imaginarios. Los átomos pueden tener propiedades diferentes. La gravedad puede tener un papel en el mundo a pequeña escala. La naturaleza cuántica de la realidad puede intervenir en lugares insospechados.
Lo único que cuenta en la definición del mundo son los valores de las constantes adimensionales de la naturaleza (así lo creían Einstein y Planck). Si se duplica el valor de todas las masas no se puede llegar a saber, porque todos los números puros definidos por las razones de cualquier par de masas son invariables.
Cuando surgen comentarios de números puros y adimensionales, de manera automática aparece en mi mente el número 137. Ese número encierra más de lo que estamos preparados para comprender; me hace pensar y mi imaginación se desboca en múltiples ideas y teorías. Einstein era un campeón en esta clase de ejercicios mentales que él llamaba “libre invención de la mente”. El gran físico creía que no podríamos llegar a las verdades de la naturaleza sólo por la observación y la experimentación. Necesitamos crear conceptos, teorías y postulados de nuestra propia imaginación que posteriormente deben ser explorados para averiguar si existe algo de verdad en ellos. Con los adelantos actuales, estudiando la luz lejana de cuásares muy antiguos, se estudia si la constante de estructura fina (α) ha variado con el paso del tiempo.
El Universo es muy grande, inmensamente grande y, probablemente, todo lo que nuestras mentes puedan imaginar podrá exisitr en alguna parte de esas regiones perdidas en las profundidades cósmicas, en los confines del Espacio- Tiempo, en lugares ignotos de extraña belleza en los que otros mundos y otras criaturas tendrán, su propio habitat que, siendo diferente al nuestro, también, sus criaturas, estarán buscando el significado de las leyes del Universo.
emilio silvera
Oct
2
Los Quarks invisibles
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (0)
Comments (0)

Una vez que se ha puesto orden entre las numerosas especies de partículas, se puede reconocer una pauta. Igual que Dimitri Ivanovich Mendeleev descubrió el sistema periódico de los elementos químicos en 1869, así también se hizo visible un sistema similar para las partículas. Esta pauta la encontraron independientemente el americano Murray Gell-Mann y el israelí Yuval Ne’eman. Ocho especies de mesones, todos con el mismo espín, u ocho especies de bariones, con el mismo espín, se podían reagrupar perfectamente en grupos que llamaremos multipletes. El esquema matemático correspondiente se llama SU(3). Grupletes de ocho elementos forman un octete “fundamental”. Por esta razón Gell-Mann llamó a esta teoría el “óctuplo camino”. Lo tomó prestado del budismo de acuerdo con el cual el camino hacia el nirvana es el camino óctuplo.
Pero las matemáticas SU(3) también admiten multipletes de diez miembros. Cuando se propuso este esquema se conocían nueve bariones con espín 3/2. Los esquemas SU(3) se obtienen al representar dos propiedades fundamentales de las partículas, la extrañeza S frente al isoespín I₃ , en una gráfica.
Imagen de trazas en la cámara de burbujas del primer evento observado incluyendo bariones Ω, en el Laboratorio Nacional Brookhaven. Dependiendo de su masa y tamaño las partículas producen distintos remolinos en la cámara de burbujas.
De esta manera, Gell-Mann predijo un décimo barión, el omega-menos (Ω¯), y pudo estimar con bastante precisión su masa porque las masas de los otros nueve bariones variaban de una forma sistemática en el gráfico (también consiguió entender que las variaciones de la masa eran una consecuencia de una interacción simple). Sin embargo, estaba claro que la Ω¯, con una extrañeza S = -3, no tenía ninguna partícula en la que desintegrarse que no estuviera prohibida por las leyes de conservación de la interacción fuerte. De modo que, la Ω¯ sólo podía ser de tan sólo 10¯²³ segundos como los demás miembros del multiplete, sino que tenía que ser del orden de 10¯¹⁰ segundos. Consecuentemente, esta partícula debería viajar varios centímetros antes de desintegrarse y esto la haría fácilmente detectable. La Ω¯ fue encontrada en 1964 con exactamente las mismas propiedades que había predicho Gell-Mann.
Se identificaron estructuras multipletes para la mayoría de los demás bariones y mesones y Gell-Mann también consiguió explicarlas. Sugirió que los mesones, igual que los bariones, debían estar formados por elementos constitutivos “más fundamentales aún”. Gell-Mann trabajaba en el Instituto de Tecnología de California en Pasadena (CalTech), donde conversaba a menudo con Richard Feynman. Eran ambos físicos famosos pero con personalidades muy diferentes. Gell-Mann, por ejemplo, es conocido como un entusiasta observador de Pájaros, familiarizado con las artes y la literatura y orgulloso de su conocimiento de lenguas extranjeras.

A comienzos de los años sesenta, un profesor del Instituto de Tecnología de California (Caltech) imparte un curso completo de física ante una cada día más numerosa. Su nombre: Richard Feynman
Feynman fue un hombre hecho a sí mismo, un analista riguroso que se reía de cualquier cosa que le recordara la autoridad establecida. Hay una anécdota que parece no ser cierta de hecho, pero que me parece tan buena que no puedo evitar el contarla; podía haber sucedido de esta forma. Gell-Mann le dijo a Feynman que tenía un problema, que estaba sugiriendo un nuevo tipo de ladrillos constitutivos de la materia y que no sabía qué nombre darles. Indudablemente debía haber de haber pensado en utilizar terminología latina o griega, como ha sido costumbre siempre en la nomenclatura científica. “Absurdo”, le dijo Feynman; “tú estás hablando de cosas en las que nunc ase había pensado antes. Todas esas preciosas pero anticuadas palabras están fuera de lugar. ¿Por qué no los llamas simplemente “shrumpfs”, “quacks” o algo así?”.

Los pequeños componentes de la materia ordinaria
Cuando algún tiempo después le pregunté a Gell-Mann, éste negó que tal conversación hubiera tenido lugar. Pero la palabra elegida fue quark, y la explicación de Gell-Mann fue que la palabra venía de una frase de Fynnegan’s Wake de James Joyce; “¡Tres quarks para Muster Mark!”. Y, efectivamente así es. A esas partículas les gusta estar las tres juntas. Todos los bariones están formados por tres quarks, mientras que los mesones están formados por un quark y un antiquark.

Los propios quarks forman un grupo SU(3) aún más sencillo. Los llamaremos “arriba (u)”, “abajo” (d), y “extraño” (s). Las partículas “ordinarias” contienen solamente quarks u y d. Los hadrones “extraños” contienen uno o más quarks s (o antiquarks ŝ).
La composición de quarks de espín 3/2 se puede ver en cualquier tabla de física.. La razón por la que los bariones de espín ½ sólo forman un octete es más difícil de explicar. Está relacionada con el hecho de que en estos estados, al menos dos de los quarks tienen que ser diferentes unos de otros.

Junto con los descubrimientos de los Hadrones y de sus componentes, los Quarks, durante la primera mitad del sigo XX, se descubrieron otras partículas. Los Hadrones forman dos ramas, los mesones formados por dos qiuarks y los bariones por tres.
Realmente, la idea de que los hadrones estuvieran formados por ladrillos fundamentales sencillos había sido también sugerida por otros. George Zweig, también en el Cal Tech, en Pasadena, había tenido la misma idea. Él había llamado a los bloques constitutivos “ases!, pero es la palabra “quark” la que ha prevalecido. La razón por la que algunos nombres científicos tienen más éxito que otros es a veces difícil de comprender.
Pero en esta teoría había algunos aspectos raros. Aparentemente, los quarks (o ases) siempre existen en parejas o tríos y nunca se han visto solos. Los experimentadores habían intentado numerosas veces detectar un quark aislado en aparatos especialmente diseñados para ello, pero ninguno había tenido éxito.

Loa quarks –si se pudieran aislar- tendrían propiedades incluso más extrañas. Por ejemplo, ¿cuáles serían sus cargas eléctricas? Es razonable suponer que tanto los quarks u como los quarks s y d deban tener siempre la misma carga. La comparación de la tabla 5 con la tabla 2 sugiere claramente que los quarks d y s tienen carga eléctrica -1/3 y el quark u tiene carga +2/3. Pero nunca se han observado partículas que no tengan carga múltiplo de la del electrón o de la del protón. Si tales partículas existieran, sería posible detectarlas experimentalmente. Que esto haya sido imposible debe significar que las fuerzas que las mantienen unidas dentro del hadrón son necesariamente increíblemente eficientes.

Todos sabemos que los Lepotines son: El elentrón, el Muón y la partícula Tau y, cada una de ellas tiene su tipo de neutrino: el electrónico, el muónico y el tauónico.
Aunque con la llegada de los quarks se ha clarificado algo más la flora y la fauna de las partículas subatómicas, todavía forman un conjunto muy raro, aún cuando solamente unas pocas aparezcan en grandes cantidades en el universo (protones, neutrones, electrones y fotones). Como dijo una vez Sybren S. de Groot cuando estudiaba neutrinos, uno realmente se enamora de ellos. Mis estudiantes y yo amábamos esas partículas cuyo comportamiento era un gran misterio. Los leptones, por ser casi puntuales, son los más sencillos, y por tener espín se ven afectados por la interacción que actúa sobre ellos de forma muy complicada, pero la interacción débil estaba bastante bien documentada por entonces.

Los hadrones son mucho más misteriosos. Los procesos de choque entre ellos eran demasiado complicados para una teoría respetable. Si uno se los imagina como pequeñas esferas hachas de alguna clase de material, aún quedaba el problema de entender los quarks y encontrar la razón por la que se siguen resistiendo a los intentos de los experimentadores para aislarlos.
emilio silvera
Si queréis saber más sobre el tema, os recomiendo leer el libro Partículas de Gerard ´t Hooft
Sep
17
Un gato vivo y muerto en dos sitios al mismo tiempo
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (0)
Comments (0)
Investigadores de EE UU logran entrelazar grupos de cuatro fotones y mantenerlños estables, un paso necesario para la creación de ordenadores cuánticos

A Erwin Schrödinger su ejemplo del gato en la caja le parecía ridículo
Erwin Schrödinger recibió un Nobel por sus aportaciones a la física, tiene un cráter a su nombre en la cara oculta de la Luna y realizó aportaciones filosóficas fundamentales para la genética. Sin embargo, su nombre es mundialmente conocido por un experimento mental que planteó en 1935 en el que un gato podía estar muerto y vivo al mismo tiempo. En aquel caso creado para ilustrar la extrañeza de la mecánica cuántica, que el físico austriaco calificaba de ridículo, se introducía un gato en una caja de acero junto a una pequeña cantidad de material radiactivo. La cantidad era tan pequeña que solo existía un 50% de posibilidades de que durante la hora siguiente uno de los átomos decayese. Si eso sucedía, se activaría un mecanismo que llenaría la caja de ácido hidrociánico, uno de los gases tóxicos utilizados en las trincheras de la Primera Guerra Mundial, y el gato moriría.

De acuerdo con los principios de la mecánica cuántica, durante el tiempo que durase el experimento, el gato estaría vivo y muerto al mismo tiempo, resultado de un fenómeno conocido como superposición. Sin embargo, esa circunstancia cambiaría cuando abriésemos la caja para acabar con la incertidumbre. En ese momento, de vuelta a la dura e incontrovertible realidad de la física clásica, el gato estaría o vivo o muerto.
Dos partículas entrelazadas lo seguirán estando aunque las separen un millón de kilómetros
Con el tiempo, los científicos han sido capaces de manipular los estados cuánticos de la materia y es posible que en el futuro este conocimiento sirva para construir potentes ordenadores cuánticos. Esta semana, en un artículo que se publica en la revista Science, un equipo de físicos de la Universidad de Yale (EE UU) muestra cómo ha logrado mantener un “gato de Schröedinger” cuántico vivo y muerto en dos lugares a la vez.

En realidad, estos gatos cuánticos son grupos de hasta cuatro fotones con estados entrelazados pese a estar en recipientes separados. El entrelazamiento es un fenómeno cuántico por el que las partículas subatómicas pueden alinear sus estados cuando están en contacto y mantenerlo después separadas, incluso a millones de kilómetros de distancia. El equipo de Yale, liderado por Chen Wang, fue capaz de introducir los fotones en receptáculos separados y modificar su estado, como el gato que está vivo o muerto, observando cómo cambiaban de forma coordinada.
El interés del trabajo, según explica Oriol Romero-Isart, investigador en el Instituto de Física Teórica de la Universidad de Innsbruck (Austria), es que “permite crear dos qbits (sistemas cuánticos que servirían para gestionar la información en ordenadores cuánticos) y aplicar correcciones para que duren más”. La inestabilidad de estos qbits hace que sean poco prácticos para construir máquinas cuánticas y es un reto para producir aplicaciones prácticas con este tipo de física. Normalmente, sin la aplicación de correcciones, un qbit se destruiría en menos de un segundo. Con las correcciones, comenzaría acercándose la posibilidad de emplear el potencial de un sistema en el que las partículas no solo sirven para codificar información a partir de unos y ceros, como en la computación convencional, sino que pueden aprovechar la posibilidad de que estén en varios estados al mismo tiempo.
La capacidad del grupo de Yale para crear “gatos de Schrödinger” de un gran número de fotones es importante porque para corregir los errores que hacen que el qbit se diluya en muy poco tiempo es mejor tener un sistema con muchas piezas. “Si nos imaginamos un sistema que pueda tener varios estados, en el que las partículas son canicas rojas y azules, si solo tienes una canica, cuando cambia el color, pierdes la información. Pero si tengo 100 canicas del mismo color, si solo cambia una de información, podría reparar el error y mantener la información gracias al resto”, explica Romero-Isart.

Los simuladores cuánticos serán una aplicación previa a los potentes ordenadores cuánticos
Las posibilidades que abren estudios como el publicado en Science son enormes, pero la extrañeza cuántica tiene sus límites. Aunque dos partículas entrelazadas seguirán estándolo aunque las mandemos a planetas separados por un millón de kilómetros, este sistema no serviría para transmitir información más rápido que la luz. La física no permite esa herejía y en este caso se conserva el dogma porque no es posible manipular a nuestro antojo el estado de esas partículas entrelazadas.
Entre las aplicaciones prácticas más cercanas de las máquinas cuánticas, Romero-Isart, que ha planteado la posibilidad de realizar un experimento en el que un objeto con millones de átomos esté en dos lugares a la vez, señala la simulación cuántica. “Se trataría de hacer un prototipo, de la misma manera que se hace con modelos de menor tamaño en aviación, para recrear un sistema cuántico muy complejo, como la física de los sólidos”, señala. “Saber cómo interaccionan los electrones en un sólido puede ayudarnos a entender cómo se puede crear un material en el que haya superconductividad a temperatura ambiente”, añade. Ahora, los materiales empleados para conducir la electricidad a temperatura ambiente, como el cobre, producen una enorme resistencia que limita su eficiencia. Este tipo de progresos llegarían antes que los ordenadores cuánticos, una tecnología posible, pero que aún requerirá mucho tiempo para hacerse realidad.
















 Totales: 71.791.842
Totales: 71.791.842 Conectados: 24
Conectados: 24


























