Abr
17
Aquella vida primigenia
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en El Origen de las cosas ~
Clasificado en El Origen de las cosas ~
 Comments (0)
Comments (0)
Hemos venido comentando sobre la vida en nuestro planeta, la evolución, nuestros orígenes y algunos dones que nos adornan como el del habla y, sin olvidar el crecimiento de nuestro cerebro que ha posibilitado que “naciera” la mente. Sin embargo, no nos hemos parado a pensar en algunos aspectos de la historia que nos llevarían a comprender cabalmente y que esa “historia de la vida” adquiera algún sentido, que la podamos comprender en todo su esplendor. Uno de esos aspectos, quizás el principal, sea la diversidad metabólica de los microorganismos procariotas, un aspecto clave para explorar la historia de “la vida primigenia”.
En la actualidad se acepta que los procariotas fueron los precursores de los organismos eucariotas. Sin embargo hay grandes diferencias entre esos dos grupos celulares. Una de esas diferencias reside en la organización génica y en los mecanismos de sintetizar el ARN mensajero. Un trabajo publicado esta semana en PLoS Biology afirma que los eucariotas podrían proceder de cianobacterias termófilas ya que su organización génica recuerda rudimentariamente a la de los eucariotas
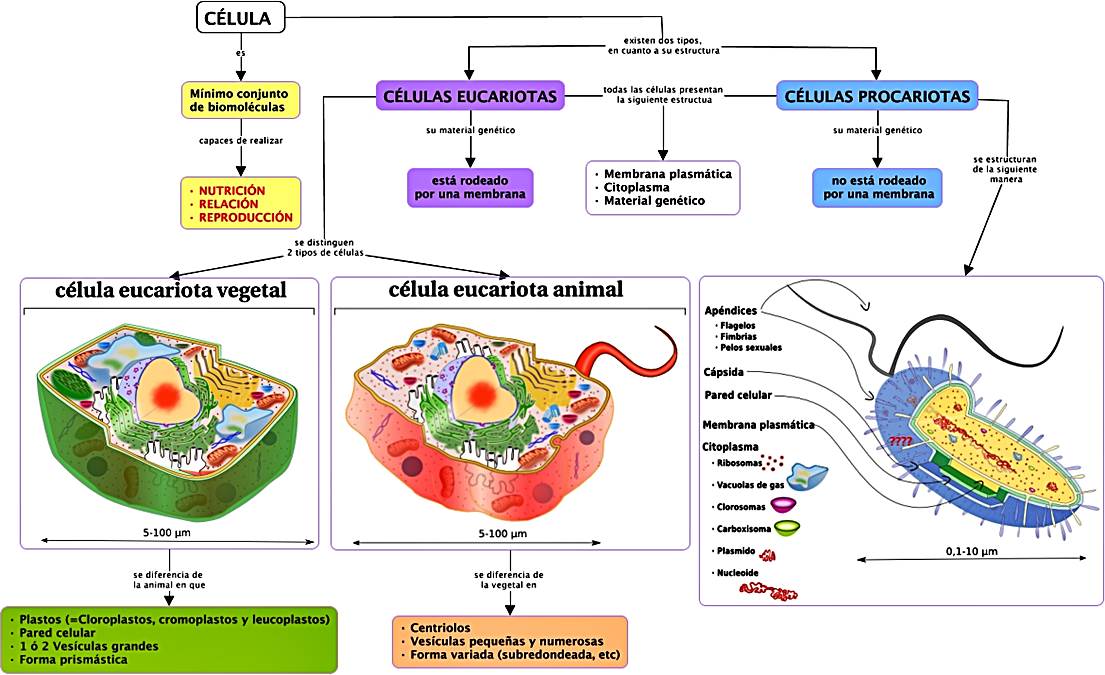
Los organismos procariotas (bacterias y arqueas) y eucariotas (protistas, hongos, animales y plantas) comparten una bioquímica común, sin embargo difieren en un elevados número de procesos y de estructuras. A pesar de eso se considera a los procariotas como los precursores de la célula eucariota. A lo largo de los años se han ido recogiendo datos experimentales que avalan esta teoría y en este artículo se mostrarán los resultados presentados en una publicación que va en esa vía.

Conviene que nos familiaricemos ( y, asombremos) con las numerosas formas de metabolismos que utilizan los procariotas para vivir y que averigüemos donde encajan estos minúsculos organismos del árbol de la via antes de que podamos seguir escuchando las historias que paleontólogos nos puedan contar de sus andanzas a la búsqueda de fósiles que nos hablen de aquella vida en el pasado.
Al igual que los eucariotas, muchas bacterias respiran oxígeno. Pero otras bacterias utilizan para la respiración nitrato disuelto (NO3–) en lugar de Oxígeno, y aún otras usan iones sulfato (SO42-) u óxidos metálicos de hierro o maganeso. Unos pocos procariotas pueden incluso utilizar CO2, que hacen reaccionar con ácido acético en un proceso que genera gas natural, que el el metano (CH4) -del que no hace mucho, la NASA a detectado un gran foco en Marte-. Los organismos procariotas han desarrollado además toda suerte de reacciones de fermentación.

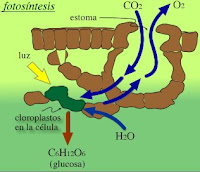
Las bacterias también exhiben variaciones sobre el tema de la fotosíntesis. Las cianobacterias, un grupo debacterias fotosintéticas teñidas de color verde-azulado por la clorofila y otros pigmentos, captan la luz del Sol y fijan CO2 de forma muy parecida a como lo hacen las algas y plantas terrestres eucariotas. Sin embargo, cuando en el medio hay sulfuro de hidrógeno (H2S, bien conocido por su característico olor a “huevos podridos”), muchas cianobacterias utilizan este gas en lugar del agua para obtener los electrones que requiere la fotosíntesis. Como productos secundarios se forman entonces azufre y sulfato, no oxígeno.
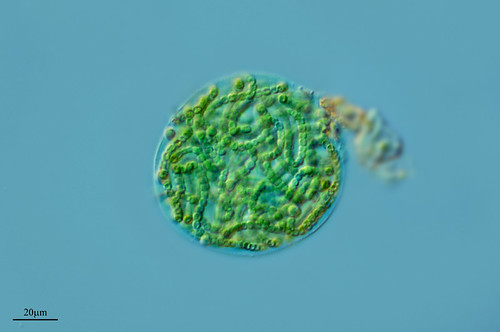
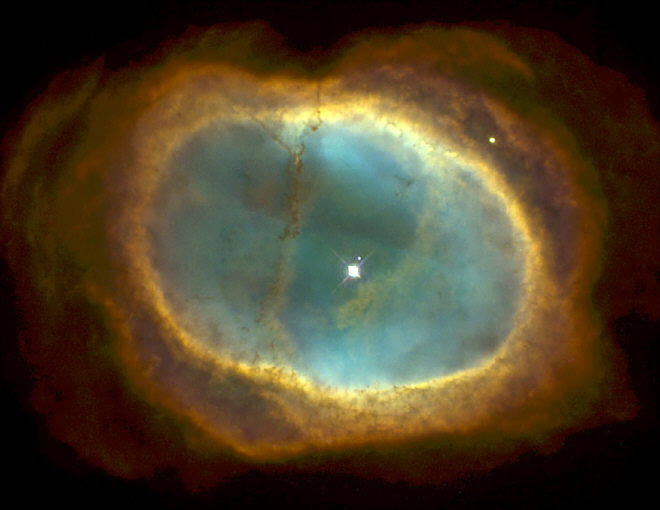
Cianobacterias
Las cianobacterias representan el grupo de células más primitivo. Son organismos extremadamente simples que pueden vivir como sencillas células, como finos filamentos, al igual que los que se muestran aquí, o como colonias simples. Las cianobacterias son capaces de resistir una amplia variedad de condiciones ambientales, desde hábitats de agua dulce o marina, hasta terrenos nevados y glaciares. Asimismo pueden sobrevivir y prosperar con temperaturas muy altas. Las cianobacterias actualmente están clasificadas dentro del reino Monera, no se consideran algas porque estructuralmente se parecen mas a las bacterias, pero es necesario colocarlas aquí ya que vendrían a ser el primer eslabón evolutivo en el reino vegetal.
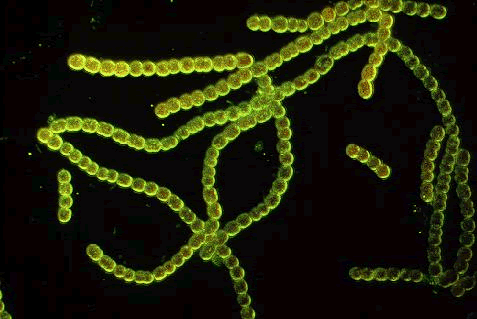
Las Cianobacterias constituyen sólo uno de los cinco grupos distintos de bacterias fotosintéticas. En los otros grupos, el aporte de electrones por H2S, gas hidrógeno (H2) o moléculas orgánicas es obligado, y nunca se produce oxígeno. Estas bacterias fotosintéticas captan la luz con bacterioclorofila en lusgar de la clrofila, más familiar,. Algunas utilizan los mismos procesos bioquímicos que las cianobacterias y las plantas verdes para fijae dióxido de carbono, pero otras usan vías metabólocas muy distintas, y un tercer grupo se sirve de una fuente de carbono orgánico en lugar de CO2.
Esta variedad de cianobacterias son componentes del plancton que realizan la fotosíntesis. Organismos unicelulares procariotas componentes del plancton de los ecosistemas acuáticos.
Las variaciones bacterianas sobre temas metabólicos de la respiración, la fermentación, la fotosíntesis son, pues, impresionantes, pero los organismos procarioticos han desarrollado todavía otro modo de crecer que es completamente desconocido en los eucariotas: la quimiosíntesis. Como los aorganismos fotosintéticos, los microbios quimiosintéticos toman el carbono del CO2, pero obtienen la energía de reacciones químicas y no de la radiación solar, lo que consiguen combinando oxígeno o nitrato (o, de forma menos frecuente, el sulfato, el hierro oxidizado o el maganeso) se combina con gas hidrógeno, metano o formas reducidas de hierro, sulfuro o nitrógeno de tal modo que la célula capta la energía desprendida por la reacción. Los procariotas metanogénicos resultan de particular interés para la ecología y la evolución; estas distintas células extraen energía de una reacción entre hidrógeno y dióxido de carbono en la que libera metano (estará ahí la procedencia del foco detectado en Marte).

Bueno, no estaría nada mal que, la fuente de Metano detectada en el Planeta Marte se debiera a la presencia allí de importantes colonias de cianobacterias que extraen energía de una reacción entre hidrógeno y dióxido de carbono en la que libera metano que pudiera ser el foco allí detectado.
No somos conscientes de que: “Las vías metabólicas de los Procariotas son las que sustentan los ciclos bioquímicos que hacen posible el mantener la Tierra en su condición de planeta habitable. Fijémonos, por ejemplo en el dióxido de carbono.

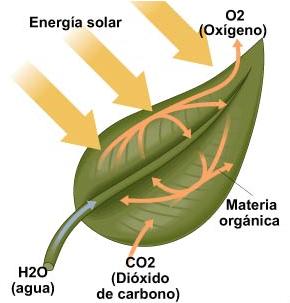
Los Volcanes aportan CO2 a los océanos y a la atmósfera, pero la fotosíntesis lo sustrae a un ritmo aún más rápido. Tan rápido, de hecho, que los organismos fotosintéticos podrían desproveer de CO2 a la atmósfera actual en poco menos de una década. Naturalmente no ocurre así, y ello se debe sobre todo a que esencialmente la respiración realiza la reacción fotosintética en sentido inverso. Mientras que los organismos fotosintéticos hacen reaccionar CO2 con agua para producir azícares y oxígeno, los seres vivos que respiran (entre los que nos incluímos todos nosotros) hacen reaccionar azúcar con oxígeno y en el proceso liberamos agua y dióxido de carbono. Conjuntamente, la fotosíntesis y la respiración reciclan el carbono en la biosfera y sostiene así la vida y su ambiente a lo largo del tiempo.
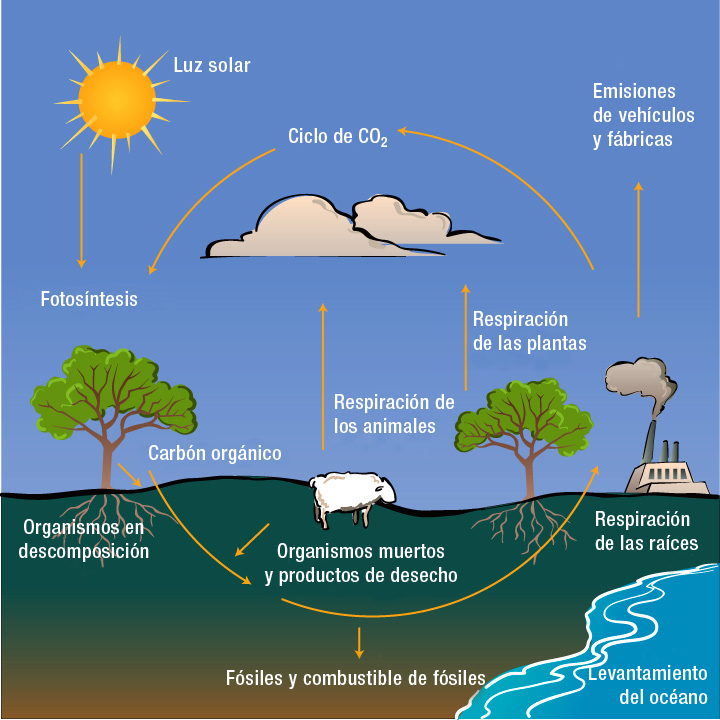
Ciclo del Carbón
El carbón es un elemento. Forma parte de los oceanos, aire, rocas, suelos y seres vivos. El carbón no permanece en un mismo lugar, ¡siempre está en movimiento!.
- El carbón va de la atmósfera a las plantas.
En la atmósfera, el carbón se combina con el oxígeno en un gas llamado bióxido de carbono (CO2). Con ayuda del Sol, mediante el proceso conocido como fotosíntesis, el bióxido de carbono es extraído del aire y se convierte en alimento. - El carbón va de las plantas a los animales.
Mediante las cadenas alimenticias, el carbón de las plantas va hacia los animales que se alimentan de ellas. Los animales que se alimentan de otros animales también obtienen el carbón a través de sus alimentos. - El carbón va de plantas y animales al suelo. .
Cuando plantas y animales mueren, sus cuerpos, madera y hojas se descomponen en el suelo. Parte de la materia descompuesta queda enterrada y tras millones y millones de años, se convierte en combustible fósil. - El carbón va de seres vivos a la atmósfera.
Cada vez que exhalas, estás liberando bióxido de carbono (CO2) hacia la atmósfera. Los animales y las plantas se deshacen del gas bióxido de carbono mediante el proceso conocido como respiración. - El carbón de los combustibles fósiles va a la atmósfera cuando el combustible es quemado.
Cuando los seres humanos queman combustibles fósiles para dar energía a sus fábricas, plantas eléctricas, automóviles y camiones, la mayoría del carbón penetra la atmósfera rapidamente en forma gas bióxido de carbono. Cada año, cinco mil quinientos millones de toneladas de carbón son liberadas en forma de combustibles fósiles quemados. ¡Esto equivale al peso de100 millones de elefantes africanos!. De la gran cantidad de carbón que liberan los combustibles, 3.3 mil millones de toneladas penetran la atmósfera, y la mayoría del resto queda disuelta en el agua de mar. - El carbón se mueve de la atmósfera a los océanos.
Los océanos y otros cuerpos de agua absorben algo del carbón de la atmósfera. El carbón se disuelve en el agua. Los animales marinos usan al carbón para crear el material de sus esqueletos y caparazones.
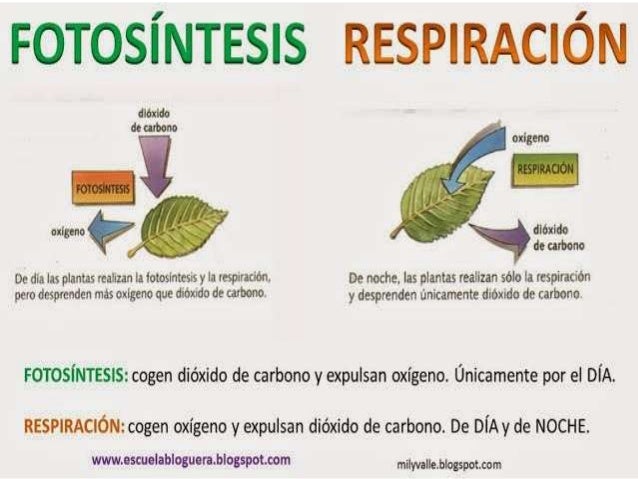
ANALISIS COMPARATIVO Y EVOLUTIVO DE LA RESPIRACIÓN Y FOTOSISTESIS
Creación de oxígeno. Las cianobacterias son las antecesoras de los cloroplastos celulares de los vegetales. En la fotosíntesis, gracias a la energía aportada por la luz solar, se unen el dióxido de carbono y el agua para formar azúcares. Como producto de desecho, se arroja oxígeno a la atmósfera. En la respiración, por el contrario, se queman azúcares en las mitocondrias celulares, aportando la energía necesaria para las funciones vitales. En esa combustión se consume oxígeno atmosférico y se arrojan, como productos de desecho, dióxido de carbono y agua.
No es difícil imaginar un ciclo del Carbono simple en el cual las cianobacterias fijen CO2 en forma de materia orgánica y suministren oxígeno al medio mientras que las bacterias no fotosintéticas hacen lo contrario, al respirar oxígeno y generar el CO2. Las plantas y las algas pueden realizar la misma función que las cianobacterias, y los protozoos, los hongos y los animales pueden sustituir a las bacterias respiradoras (en ese sentido los procariotas y los eucariotas son funcionalmente equivalentes). Pero dejemos que algunas células caigan hasta el fondo del océano y queden enterradas en sedimentos desprovistos de oxígeno. Aquí las limitaciones del metabolismo eucariota resultan evidentes, pues se necesitan reacciones que no consuman oxígeno (reacciones anaeróbicas) para poder completar el ciclo del carbono.
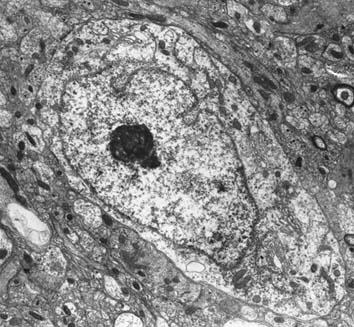
Célula Eucariota
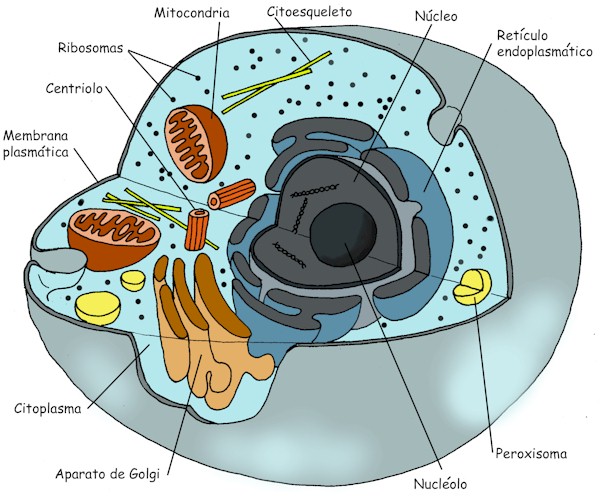
Arriba sus características más generales.
Son células más modernas, procedentes de procesos de simbiosis entre procariotas, con núcleo separado.Son más grandes, de entre 20 y 40 micras de media. Presentan, en su citoplasma, gran cantidad y variedad de orgánulos. Al agruparse forman tejidos. La célula eucariota presenta tres partes bien diferenciadas: Una Membrana celular que separa el medio externo del medio interno. Un Núcleo diferenciado separado por una doble membrana del Citoplasma, donde se encuentran los orgánulos celulares.
Está claro que hablar de todo esto, nos ecige mucho más tiempo y espacio, toda vez que, el “universo” de las cianobacterias y demás congéneres que, con nosotros ocupan el planeta Tierra, tiene tanta importancia en el devenir de la vida que, un pequeño resumen de algunas de sus características simplemente nos aclaran algún que otro extremo aislado pero que, al menos, trata de que seámos conscientes de que, sin ellas, nosotros difícilmente podríamos estar aquí, ya que, entre cosas cosas, son las responsables directas de que el planeta tenga el sistema ecológico necesario para sustentar la vida.
emilio silvera
Mar
18
Preguntamos pero… ¡No siempre nos saben contestar!
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en El Origen de las cosas ~
Clasificado en El Origen de las cosas ~
 Comments (0)
Comments (0)
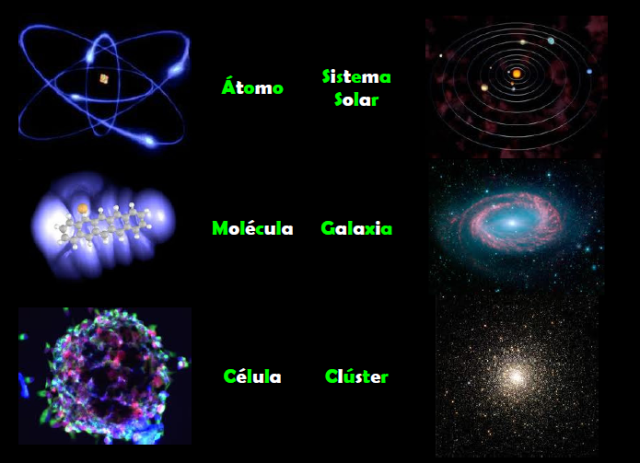
Todo es materia, es decir, está conformado por Quarks y Leptones
Los astrónomos han confirmado mediante observaciones espectroscópicas que los átomos son realmente los mismos en cualquier lugar del Cosmos, Un átomo de Carbono en la galaxia Andrómeda es exactamente igual que un átomo de Carbono de la Galaxia Vía Láctea, son idénticos y también, idénticos, a los átomos de Carbono de la Tierra. Cinco elementos químicos desempeñan un papel estelar en la Biología terrestre:
Carbono
Oxígeno
Hidrógeno
Nitrógeno, y
Fósforo
Estos elementos están entre los más abundantes del Universo. Sin embargo, no siempre fue así. Hubo un tiempo, antes de que nacieran las primeras estrellas, que en el Universo todo era Hidrógeno y Helio, los materiales primordiales a partir de los cuales, pudieron surgir todos los demás en los hornos nucleares de las estrellas y en las explosiones supernovas.
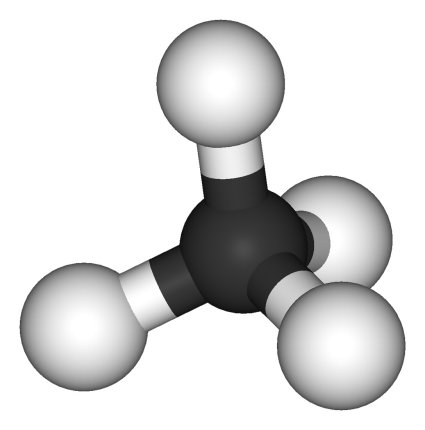

Arriba tenemos el oxígeno, el agua y un átomo de carbono, y, sin ellos la vida tal como la conocemos no sería posible en nuestro Universo.
Todas las leyes de la física nos muestran que la existencia y sostenimiento de la vida se asientan en equilibrios y medidas o cantidades específicas. La estructura general del universo, el lugar de la Tierra en el mismo, las características materiales de ésta –aire, luz, agua, etc.–, se basan en propiedades esenciales para nuestra supervivencia y, sobre todo eso… ¡El Carbono!
El Carbono es el elemento auténticamente vital. Merece un lugar de honor debido a una propiedad química única: los átomos de Carbono (como tantas veces expliqué aquí) pueden unirse para formar moléculas de cadena extendida, o polímeros, de variedad y complejidad ilimitadas. Las Proteínas y el ADN son dos ejemplos de dichas moléculas de cadena larga.
Si no fuera por el Carbono, la vida como la conocemos sería imposible. Probablemente sería imposible cualquier cualquier tipo de vida. Soy muy remiso (aunque no descarto nada), a que existan formas de vida que no estén basadas en el Carbono.
Cuando el Universo “empezó” con el “Big Bang”, el Carbono estaba completamente ausente. El intenso calor del nacimiento cósmico impedía cualquier núcleo atómico compuesto. En lugar de ello, el material cósmico consistía en una sopa de partículas elementales tales como protones y neutrones que pudieron conformar los núcleos de átomos de hidrógeno. Sin embargo, a medida que el universo se expandía y enfriaba durante los primeros minutos, las reacciones nucleares transmutaron parte del hidrógeno en helio.

Muchos millones de años más tarde, en las estrellas, por algo que se llama “proceso triple Alfa”, surgió el Carbono en el Universo. No siendo el tema aquí el de explicar como se llega en las estrellas al Carbono a partir del helio, seguiremos hablando de la química cósmica.
La Química es algo más que unos tubos de ensayo, y, está presente de manera natural por todo el espacio interestelar. Allá por los 70 me llamó poderosamente la atención el descubrimiento de moléculas de amoníaco y de agua en el espacio exterior. ¿Cómo llegaron a llí? Bueno, todos conocemos esas inmensas nubes estelares que llamamos Nebulosas y, en ellas, se producen, a partir de materiales sencillos, esos cambios que tan poderosamente llaman nuestra atención.
El timo de átomo más común en el universo, después del hidrógeno y el helio, es el oxígeno. El oxígeno puede combinarse con hidrógeno para formar grupos grupos oxhidrilos (HO) y moléculas de agua (H2O), que tiene una marcada tendencia a unirse a otros grupos y moléculas del mismo tipo que encuentren por el camino, de forma que poco a poco se van constituyendo pequenísimasm partículas compuestas por millones y millones de tales moléculas. Los grupos oxhidrilo y las moléculas de agua pueden llegar a constitur una parte importante del polvo cósmico. Allá por el año 1965 se detectó por primera vez grupos oxhidrilo en el espacio y se comenzó a estudiar su distribución. desde entonces, se han encontrado allí, moléculas más, complejas que contienen átomos de carbono, de hidrógeno y de oxígeno. También átomos de calcio, sodio, potasio y hierro han sido detectados al observar la luz que dichos átomos absorben.

En regiones como la que arriba podemos ver, están presentes elementos que no siempre sospechamos
Actualmente, la lista de las moléculas descubiertas en el espacio es larga y más de cien sustancias químicas la adornan, siendo muchas de esas moléculas interestelares orgánicas. La más abundante es el monóxido de carbono, pero también hay abundancia de acetileno, formaldehido y alcohol. También se han detectado moléculas orgánicas más complejas, tales como aminoácidos y HAP (hidrocarburos aromáticos policíclicos). Ahora está claro que no sólo abunda en todo el Universo elementos que favorecen la Vida, sino que también lo hacen muchas de las moléculas orgánicas realmente utilizadas por la vida. Con miles de millones de años disponibles para que la química cósmica pudiera generar dichas sustancias, ha habido tiempo más que suficiente para que estas se formen en las nubes moleculares gigantes de las que emergen las estrellas y los sistemas solares como el nuestro.

Nubes Moleculares Gigantes en este caso (NGC 7822 en Cefeo). Colapsos gravitacionales, estrellas nuevas, vientos estelares, abundante radiación ultravioleta, todas esas fuentes de energías que dan lugar al nacimiento de estrellas nuevas, hacen también posible que, los materiales se mezclen y sufran mutaciones de simples a complejos y, a partir de ellos, nacen los nuevos sistemas planetarios y…¡la Vida!
Que en un principio, sin temor a equivocarnos podemos decir que la génesis de la vida ha sido posible a partir de lo que en el espacio pasó, ¿qué duda nos puede caber? Incluso, no se descarta que los materiales que trajeron la vida al planeta Tierra, fuera deposita por cometas.

El cometa West, con sus colas de plasma y polvo
Los Cometas que a pesar de todo lo que sabemos de ellos, siguen siendo algo enigmáticos, incluso algunos que han sido minuciosamente observados durante siglos. Muchos son los que dicen que llevan la semilla de la Vida con ellos y, de vez en cuando, la siembran en algún planeta que, como la Tierra, recibe sus esporádicas visitas.
Mucho se podría hablar aquí de cómo llegaron a formarse los cometas a partir de aquella Nebulosa planetaria pero, no siendo el tema de hoy, lo dejaremos en lo que ya hemos explicado y que, de manera muy simple y general, os dará una idea de lo que en el Universo puede pasar y de cómo, todo se confabula para que la vida, sea posible.
En la parte primera hemos hablado de los supermicrobios y de otras cuestiones que nos acercan al saber, al menos, de cómo hemos tratado de conocer el origen de la Vida en nuestro mundo, uan pregunta que más o menos ha quedado contestada pero, a medias, toda vez que, contestar a la pregunta primera de… ¿qué es la vida? no he podido, me faltan conocimientos para ello.

Para documentarme, he leído sobre el misterioso origen de la vida, he tratado de saber qué es la vida, he buceado en la historia de las moléculas antiguas, he dado un largo paseo por el Edén de los microbios y sus dominios, he tratado de estudiar lo que es el principio de generación biológica y química, a todo ello, he añadido meros conocimientos del hueco de entropía y la Gravedad como fuente de Orden, He querido saber sobre el árbol de la vida y me he querido enterar de qué hallaron los expertos en las rocas antiguas, qué fósiles había allí como huella de la vida del pasado, también procuré saber si era posible la generación expontánea y sobre “la sopa primordial”. Me interesé sobre el Azar en relación con el Origen de la Vida.
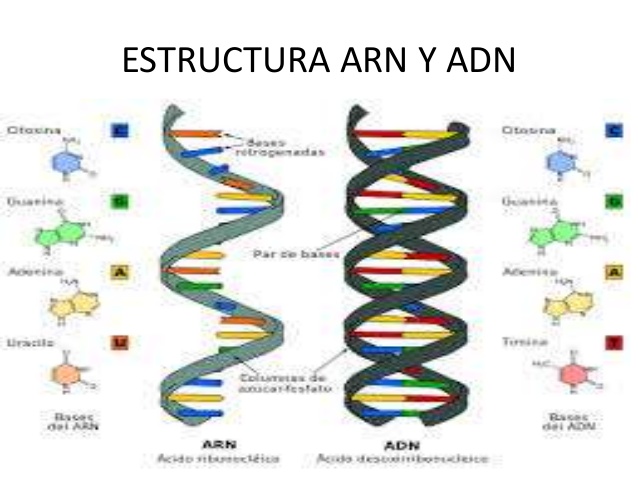
También sobre las células replicantes que nos trajeron la vida, el código genético de la reproducción, el ARN y el ADN. No me olvidé del Polvo de Estrellas y de la Química cósmica para hacer posible una génesis a partir del espacio exterior y, en fin, muchos espacios y muchas razones más que me han llevado a conocer, lo que creemos que la vida es. Sin embargo, a pesar de todo eso, con algunos conocimientos más de los que tenía hace veinte años sobre el tema pero, sigo sin saber contestar la pregunta:
¿Qué es la Vida?
emilio silvera
Sep
20
Teoría del proceso seguido por la Tierra en su evolución
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en El Origen de las cosas ~
Clasificado en El Origen de las cosas ~
 Comments (5)
Comments (5)
En este Blog, una de las premisas más importante, en realidad convertida en un Principio a seguir, es dar voz al visitante y, no sólo en comentarios, sino en los posibles trabajos que puedan querer exponer para divulgar sus ideas, y, en este caso,el visitante José C. Gómez, me envía un Correo que dejo aquí reproducido:

El origen del agua y su ciclo en la naturaleza, no es entendida por los europeos hasta finales del siglo XVII. Sin embargo, en al año 500 a.C los chinos ya conocían
Veámos que nos dice sobre el tema José C. Gómez
|
Amigo José C. Gómez, es bueno que sigas pensando y mejorando tus ideas que, como decía Eintein, lo mejor para la mente son los ejercicios mentales y, este que nos manda, es un buen ejercicio.
Saludos.
Oct
11
¡Las matemáticas! o, demostración de nuestro ingenio
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en El Origen de las cosas ~
Clasificado en El Origen de las cosas ~
 Comments (7)
Comments (7)
Alguien nacido en la India y que más tarde, se trasladó a Inglaterra donde se dedicó a la docencia, en cierta ocasión dijo: “Como la cola de un pavo real, como la gema en la cabeza de una serpiente, así están las matemáticas a la cabeza de todo el conocimiento”. Pocos científicios del mundo moderno estarían en desacuerdo con estas palabras. Las matemáticas están presentes (de una u otra manera) en todas las disciplinas del saber y, sin duda, es uno de los mayores logros de la Humanidad.

Nuestra historia tradicional (de Occidente), nos dice que fueron los griegos quienes crearon las matemáticas hacia el año 600 a. C. y que fue la cultura grecorromana la que las elaboró hasta el año 400 d. C., época en la cual esta disciplina cayó en profundo letargo que duraría unos mil años y no despertaría hasta la llegada de la Europa pos-renacentista. Sin embargo, hay pruebas abundantes de que las culturas no occidentales realizaron importantes contribuciones a las matemáticas europeas, o, al menos, desarrollaron técnicas matemáticas que precedieron a los descubrimientos europeos. Por ejemplo:

Lo principal de los trabajos de Ramanujan está en sus “Cuadernos Perdidos”, escritos por él en nomenclatura y notación particular, con ausencia de demostraciones, lo que ha provocado una hercúlea tarea de desciframiento y reconstrucción, aún no concluida. Fascinado por el número pi, desarrolló potentes algoritmos para calcularlo. Uno de ellos, reelaborado por los hermanos Jonathan y Peter Borwein (que fueron los matemáticos a los que encargaron traducir sus Cuadernos Perdidos, resultó así:

Los tres cuadernos que escribió y que son una de las hazañas más asombrosas de todo el pensamiento humano amarillean y se pudren víctimas del clima y los insectos en la universidad Tata de la India. Pero, de Ramanujan hemos hablado aquí en otras ocasiones, sigamos con el trabajo que nos ocupa sobre las matemáticas.
• Los Hindúes desarrollaron el uso del cero y los números negativos quizá unos mil años antes de que estos conceptos fueran aceptados en Europa. Los mayas inventaron su propio cero -de hecho, una gran cantidad de ellos- más o menos al mismo tiempo que los hindúes.
• Ciertas tablillas de barro escritas unos mil años antes de la civilización griega revelan indicios de la existencia de un álgebra bastante sofisticada entre los sumerios. Existen papiros del siglo XVIII a. C., y también anteriores a esa fecha, en los que se ve que los egipcios utilizaban ecuaciones simples para abordar problemas relativos a la distribución de alimentos y otros suministros.


Los egipcios sabían que, la trigonometría es una rama de las matemáticas que significa “medición de triángulos”.
Los antiguos egipcios y babilonios conocían los teoremas sobre los lados de los triángulos semejenates. Las sociedades pre-helénicas carecían de estos conocimientos, por lo que estudiaban los lados en su medida (trilaterometría). En el segundo milenio a.C, los egipcios utilizaban la trigonometría para la construcción de pirámides.
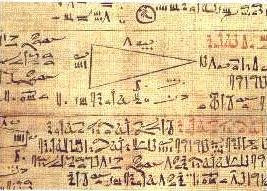
Su contenido se data del 2000 al 1800 a. C. Fue escrito por el escriba Ahmes aproximadamente en 1650 a. C., a partir de escritos de doscientos años de antigüedad.
Así, esta imagen nos muestra el conocido como Papiro de Ahmes que contiene el siguiente problema de trigonometría: ” Si una pirámide es de 250 codos de alto y al lado de su base de 360 codos de largo, ¿cúal es su Seked?” Solución: la cantidad para la Seked es la cotangente del ángulo que forman la base de la pirámide y su cara.
• En el tercer milenio a. C. los babilonios desarrollaron un sistema de numeración que contemplaba el principio del valor según la posición. (En nuestro sistema de base 10, por ejemplo, 348 significa 8 unidades, 4 decenas y 3 centenas.) El Sistema de numeración Sexagesimal (base 60) de los babilonios puede parecer incómodo en un principio, pero Copérnico utilizó fracciones sexagesimales para construir su modelo del sistema solar y nosotros utilizamos este sistema para medir el tiempo y los ángulos (la hora tiene 60 minutos y cada minuto se divide en 60 segundos).

Sistema Sexagesimal Babilónico
• Los escribas que trabajaban en los templos de Egipto conocían la fórmula que se usa para calcular el volumen del cilindro mucho antes de que existieran griegos que supiesen leer y escribir, por lo que conocieron la existencia del misterioso factor π mucho antes que los griegos. Los egipcios inventaron también el conceopto de mínimo comín denominador, así como una tabla de fracciones cuya preparación, según estimaciones de expertos modernos, requirió la realización de veintiocho mil tediosos cálculos.

Sí, el conocimiento de los números y las matemáticas se pierde en la noche de los tiempos y, desde hace milenios están alojados en la Mente de la Humanidad que, los tiene en sus manos para hacer el uso requerido en cada caso y lugar para hacernos más comprensible y fácil la vida. ¿Qué sería de nosotros sin las matemáticas?

• En el año 2000 a. C., los sacerdotes en Mesopotamia (una región de la que hemos hablado hace muy poco tiempo, y, donde la Civilización sumeria desarrolló todo su talento e inventiva para el progreso), desarrollaron unas extensas tablas de cuadrados. Sabemos esto por las tablillas de barro con textos en escritura cuneiforme que han sido halladas en las bibliotecas de los templos. Hay que recordar que los europeos en el siglo XIV ni siquiera tenían Tablas de multiplicar.
• Gottfried Leibniz, el coinventor del cálculo, afrimaba haber descubierto el secreto del modo de descifrar los diagramas del sabio chino de la antigüedad Fu Hsi. Leibniz sostenía que los diagramas de Fu Hsi se correspondían con su propio sistema binario moderno de aritmética.
• Los hindúes inventaron una incipiente forma de cálculo siglos antes de que Leibniz inventara el cálculo en Europa.


Mohammed Ibn Musa abu Djafar Al-Khwarizmi. Murió: hacia el 850 en Bagdad (hoy Irak)
Matemático, astrónomo y geógrafo musulmán, Mohammed Ibn Musa abu Djafar Al-Khwarizmi, nació probablemente en la ciudad persa de Khwarizm (actual Khiva, en Uzbekistan), situada al sudeste del mar de Aral, en la vieja ruta de la seda, que había sido conquistada 70 años antes por los árabes. Su nombre significa “Mohamed, hijo de Moisés, padre de Jafar, el de Khwarizm”.
Hacia el 820, Al’Khwarizmi fue llamado a Bagdad por el califa abasida Al Mamun, segundo hijo de Harun ar Rashid, conocido por todos gracias a las “Mil y una noches”. Al Mamun continuó el enriquecimiento de la ciencia árabe y de la Academia de Ciencias creada por su padre, llamada la Casa de la Sabiduría. Se tradujeron al árabe obras científicas y filosóficas griegas e hindúes, y contaba con observatorios astronómicos. En este ambiente científico y multicultural se educó y trabajó Al-Khwarizmi, el cual dedicó sus tratados de álgebra y astronomía al propio califa. Todo este florecimiento traería importantes consecuencias en el desarrollo de la ciencia en Europa, principalmente a través de España.
• Así, los árabes acuñaron el término álgebra e inventaron las fracciones decimales: 0,25 para ¼, etc. Los europeos, antes de sacar pecho cuando de matemáticas se habla, debemos mirar hacia atrás en el tiempo y hacia otros pueblos que, antes que nosotros, hicieron bien su trabajo.

Aristóteles supo reconocer el mérito de los egipcios a los que atorgó la autoría de haber desarrollado las matemáticas antes de que sus paisanos lo hicieran, aunque los expresó de una forma un poco ambigua: “Las ciencias matemáticas nacieron en el entorno de Egipto porque allí la clase sacerdotal disfrutaba de tiermpo de ocio”.
De todas las maneras, es de justicia reconocer las cosas y, el historiador de matemáticas Morris Kline, el más prominente de América, nos dice: “Comparar las matemáticas de los egipcios y los babilonios con los logros de sus sucesores inmediatos, los griegos, es como comparar los grabados de los niños que aprenden a escribir con la gran literatura”. Esto, sin dejar de reconocer que sumerios, babilonios y egipcios fueron los pioneros, junto a los hundues y chinos, de las matemáticas que más tarde, fueron desarrolladas por griegos.
La historia es más extensa pero, el tiempo se me acaba y el trabajo me espera, otro día seguiremos desarrollando este tema fascinante de las matemáticas que, junto con la escritura y el lengujae, viene a ser uno de los mayores logros de la Humanidad.
emilio silvera
Feb
2
¡Las Matemáticas! ¿Dónde radica su origen?
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en El Origen de las cosas ~
Clasificado en El Origen de las cosas ~
 Comments (0)
Comments (0)
Nuestro patrimonio matemático y nuestro orgullo occidentales depende irremediablemente de los logros de la antigua Grecia. Dichos logros se han exagerado tanto que a menudo resulta difícil distinguir qué parte de la matemática moderno procede de los griegos y cuál es la que tiene su origen en los babilonios, los egipcios, los hindúes, los chinos, los árabes, etc. Las matemáticas de los griegos eran muy imaginativas y es grande la deuda que tenemos con ellos.
Sin duda alguna la obra cumbre de la Matemática griega, que aún hoy levanta pasiones entre los matemáticos y científicos en general es sin duda Los Elementos de Euclides. Generalmente se cree, erróneamente, que los Los Elementos de Euclides contienen únicamente un resumen sumario y y exhaustivo de toda la Geometría griega.

En realidad los Los Elementos supusieron la gran síntesis no sólo de la producción geométrica griega hasta el siglo III a. C. sino también de un compendio, usando el lenguaje geométrico, de toda la Matemática elemental: Geometría plana y espacial, Aritmética y Álgebra.
A este respecto escribió Proclos: «Son singularmente admirales sus Elementos de Geometría (de Euclides) por el orden que reina en ellos, la selección de los teoremas y problemas tomados como elementos y también la variedad de los razonamientos desarrollados de todas las maneras y que conducen a la convicción» y más adelante expresa «Los Elementos son una guía segura y completa para la consideración científica de los objetos geométricos».
Sin embargo, si nuestras matemáticas actuales se basaran exclusivamente en Pitágoras, Euclides, Demócrito, Arquímes y otros griegos, sería una disciplina muy deficiente. Claro que, la realidad es que la historia de las matemáticas en occidente no se puede remontar a ninguna escuela y a ningún período que sean anteriores a la etapa de los griegos jónicos.

Euclides se le considera el gran sistematizador y maestro de la matemática griega, ésta alcanza su cenit con la figura de Arquímedes: uno de los más grandes matemáticos y científicos de todos los tiempos. A Arquímedes se le deben innumerables cálculos de áreas y volúmenes; algunos tan importantes y difíciles como el área de la superficie esférica o una vuelta de espiral. A partir del siglo XIII se recuperó su obra en Europa Occidental, pero no fue hasta el XVI cuando los matemáticos volvieron a adquirir la suficiente capacidad para entenderla.

Arquímedes era natural de Siracusa pero se formó en Alejandría bajo la correspondiente influencia de la ideología platónica de una matemática esencialmente teórica y abstracta. No obstante a ello, la actividad de este genio fue tremendamente original y diferente de la ciencia alejandrina ya que mezcló, enfrentándose contra todos los prejuicios platónicos, técnicas extraídas de la Mecánica, de lo infinitesimal, lo operativo. No obstante si bien ese era su modus operandi, lo escondía deliberadamente al escribir sus obras, ya que, todas ellas tienen la estructura euclidiana: comienza por las hipótesis para pasar a proposiciones impecablemente demostradas usando generalmente el método de exhaución de Eudoxo -para lo cual debía conocer de antemano la solución-. Esto último dio pie a las sospechas de muchos matemáticos -Wallis y Barrow entre ellos- de que Arquímedes tenía un método.
Teorema de Pitágoras
Busto de Pitágoras y su teorema
En 1952 Kline escribió: “Fue en el extraordinariamente propicio suelo de Grecia donde [las matemáticas] garantizaron finalmente una nueva forma de controlar la existencia humana y florecieron espectacularmente durante un breve período de tiempo…Con el declive de la civilización griega la planta quedó aletargada durante unos mil años…[hasta que] esa planta fue llevada de manera adecuada a Europa y plantada una vez más en terreno fértil”.
La Escuela de Atenas. Pintura de Rafael Sanzio
La escuela jónica, con Tales de Mileto (cuyo nombre lleva un importante teorema de geometría elemental, (el Teorema de Tales), fue la primera en comenzar la deducción matemática, hacia el año 600 a. C.
De un modo esquemático, se interpreta a menudo el significado de esta afirmación entendiendo que ha habido tres etapas en la historia de las matemáticas.
1. Hacia el año 6oo a. C., los antiguos griegos inventaron las matemáticas, que estuvieron desarrollándose hasta aproximadamente el año 400 d. C., momento en el cual desaparecieron de la faz de la Tierra.
2. A esto siguió un período oscuro para las matemáticas, que duró más de mil años. Algunos expertos admiten que los árabes mantuvieron vivas las matemáticas griegas durante la Edad Media.
3. En la Europa del siglo XVI se produce el redescubrimiento de las matemáticas griegas y esta disciplina vuelve a florecer de nuevo hasta el momento actual.

Pappus, es considerado como el último gran geómetra griego. A él debemos La Colección Matemática, obra de un inmenso valor histórico gracias a la cual conocemos hoy los trabajos de muchos matemáticos griegos -como por ejemplo Apolonio-. Incluimos aquí la primera impresión de esta importante obra editada por Federico Commandino en Venecia en 1589. Fue a partir de ella que resurge el interés a mediados del siglo XIX por la historia de la matemática griega y que daría como fruto impresionantes ediciones de las obras de Euclides, Arquímedes, Apolonio, Diofanto, Pappus, etc.

Tras Pappus ya sólo encontramos comentaristas como Teón, su hija Hipatia o Proclo. El final de la Matemática y, en general, de la ciencia griega lo simboliza la terrible muerte de Hipatia en Alejandría: fue brutalmente torturada y asesinada por un grupo de cristianos exaltados por Cirilo -después San Cirilo- en marzo del año 415 d. C. Cuenta un historiador de la época «la encerraron en una iglesia llamada Caesium; la desnudaron; le arrancaron la piel y le desgarraron la carne de su cuerpo utilizando conchas afiladas, hasta que su último aliento salió de su cuerpo; la descuartizaron; llevaron sus trozos hasa un lugar llamado Cinaron y los quemaron hasta reducirlos a cenizas». Fueron tiempos complicados para los científicos y, terribles, si además de científico se era mujer. Como colofón a esta sección de nuestra exposición incluimos un manuscrito griego del siglo XVI que contiene los comentarios de Teón, padre de Hipatia, a las Hármonicas.

Nuestros números modernos -del 0 al 9- se desarrollaron en la India durante la segunda etapa, el llamado período oscuro de las matemáticas. Las matemáticas existían ya mucho antes de que los griegos construyeran su primer ángulo recto. Otras veces hemos hablado aquí de las matemáticas hindúes contenidas en los Sulbasutras (las reglas de la cuerda). Escritos en alguna fecha comprendida entre los años 800 y 500 a. C., los Sulbasutras demuestran, entre otras cosas, que los indios de este período tenían su propia visión del teorema de Pitágoras así como un procedimiento para obtener la raíz cuadrada de 2 con una precisión de hasta cinco cifras decimales. Los Sulbasutras ponen de manifiesto la existencia de un rico conocimiento geométrico que fue anterior a los griegos.
 En el papiro Ahmes vemos que el cálculo de áreas tendía a emplear la conversión de la figura a analizar en “algo parecido a una figura conocida” que permita llegar al área buscada. Un sistema de cálculos parciales cuya suma permita obtener el área de la figura inicial. Veremos este método en el cálculo del área del círculo. Es quizá un primer paso hacia la demosción geométrica y un intento de encontrar las relaciones mutuas entre figuras geométricas, pero que se quedó ahí, en un primer paso, y al que nunca se le ha dado la importancia que tiene. Por este método se justifica el cálculo del área de un triángulo isósceles.
En el papiro Ahmes vemos que el cálculo de áreas tendía a emplear la conversión de la figura a analizar en “algo parecido a una figura conocida” que permita llegar al área buscada. Un sistema de cálculos parciales cuya suma permita obtener el área de la figura inicial. Veremos este método en el cálculo del área del círculo. Es quizá un primer paso hacia la demosción geométrica y un intento de encontrar las relaciones mutuas entre figuras geométricas, pero que se quedó ahí, en un primer paso, y al que nunca se le ha dado la importancia que tiene. Por este método se justifica el cálculo del área de un triángulo isósceles.
Existe un conjunto de matemáticas no europeas que fueron desenterradas hacia mediados del siglo XX, incluidas las matemáticas de Mesopotamia, Egipto, China, la India, el mundo árabe y la América precolombina. De todos es bien conocido que los propios griegos, entre ellos Demócrito, Aristóteles, Herodoto y otros, prodigaron alabanzas a los egipcios, reconociéndolos como sus gurús matemáticos (aunque no con estas palabras). El hecho es que fueron muchos antes que los griegos.
Merece la pena comenzar este artículo con la misma cita de Laplace que usamos en el artículo en el que dimos una primera revisión de las matemáticas indias.

Laplace escribió:
“El ingenioso método de expresar cada número posible utilizando un conjunto de diez símbolos (cada uno de ellos con un valor en su posición y un valor absoluto), surgió en la India. La idea parece hoy en día tan simple que su significado y profundidad no son apreciados en su justa medida. Su simplicidad subyace en el modo en el que facilitó el cálculo y colocó la aritmética en la primera posición entre las invenciones más útiles. La importancia del invento se aprecia con más facilidad cuando se considera que estaba mucho más allá que las ideas de dos de los mayores hombres de la antigüedad, Arquímedes y Apolonio.”

CIVILIZACIÓN SUMERIA Y BABILONICA.- Hacia el año 4000 a.C. en el sudeste de la mesopotámica se instalaron los sumerios y su capital fue Ur, posteriormente en el año 2500 a.C. este pueblo fue dominado por los acadios, un pueblo semita cuya capital era Acad, gobernados en esa época por Sargón, de esta forma la brillante cultura sumeria quedó fusionada con la acadia. Posteriormente este imperio cayó en poder de los babilonios hacia el año de 2270 a.C., gobernando el rey Hammurabi y haciendo de Babilonia su capital, durante su reinado floreció un período de alto nivel cultural.
Los babilonios fueron los primeros en contribuir al desarrollo de las matemáticas, la aritmética alcanzó su más alto nivel de desarrollo. En los restos arqueológicos de las Tablas de Senkreh, llamadas así por el lugar donde fueron descubiertas a orillas del Éufrates en 1854, se encontraron otras referencias literarias antiguas de esta civilización. En otros restos arqueológicos de Nuffar, existían tablas de multiplicar grabadas con caracteres cuneiformes, de números enteros dispuestos en columnas con valores superiores a 180 000.
Los primeros símbolos escritos de estas culturas, representaban los números con marcas en forma de cuña de acuerdo a su escritura cuneiforme. Los babilonios tenían un método de contar un poco complicado, su sistema numérico era en base sesenta (60), o sea, contaban de sesenta en sesenta, llamadas sesentenas babilónicas, Su aritmética se basaba en dos números ejes, el 10 y 60, teniendo en cuenta el posicionamiento de estos caracteres así mismo se leían e interpretaban, en la figura de arriba.
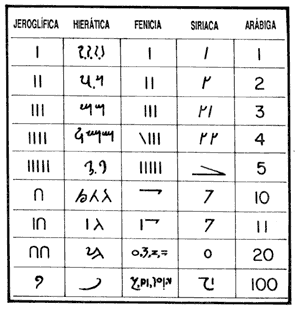
Resulta difícíl o imposible encontrar o hablar de una cultura que no tuviera alguna forma de contar, es decir, algún método para establecer la comparación entre un conjunto de objetos y una serie de números, marcadores u otros símbolos que sirvieran para registrar una cantidad estableciendo una correspondencia, ya fuera con símbolos escritos o en forma de cuentas, nudos o muescas realizadas en una madera, una piedra o en un hueso. Contar es hacer matemáticas y, en todas las cuturas existieron individuos capaces de hacerlo.
El sistema de numeración egipcio, era un sistema decimal de base 10.

La historia de las matemáticas en Egipto es larga, ya que comienza hacia el año 3200 a. C., cuando se inventó un sistema de escritura, y se alarga hasta el año 332 a. C., cuando Alejandro Magno conquistó y helenizó Egipto. Nuestras fuentes son escasas, porque el papiro se deteriora en un medio ambiente húmedo. Los únicos documentos legibles son los hallados en cementerios y templos de la franja desértica situada a lo largo del Nilo o en su delta. La mayoría data del Imperio Medio, entre 2000 y 1700 a. C. En total no hay más que cinco papiros, un par de tablillas de madera con ejercicios y una laja de piedra. Sin embargo, encontramos en estos documentos una rica tradición matemática. ¿Quién sabe lo que estaban haciendo con los números en las grandes ciudades?

Arriba Papiro de Rhind.
De los Babilonios: Los registros que se tienen son de naturaleza arqueológica, en arcilla, y, por supuesto, se encuentran limitados de muchas maneras. No nos permiten una visión exacta de las características en que se desarrollaron cultural y matemáticamente. En relación con Mesopotamia, los registros más antiguos datan del 3 500 a.C. y terminan en el 539 a.C, fecha en la que estos territorios fueron conquistados por Persia.
Hay alrededor de 500 000 tablillas de arcilla que constituyen las fuentes principales de la cultura babilónica, y entre ellas unas 500 son de interés para las matemáticas. La mayoría de los registros de que se dispone son del periodo llamado Antiguo, más o menos alrededor del 2 500 a.C.
El sistema cuneiforme de escritura fue descifrado a mediados del siglo XIX por George Frederick Grotefend y Henry Creswicke Rawlinson.
La aritmética más desarrollada en la civilización Mesopotámica fue la Acadiana. Dos de las características más importantes de su sistema numérico fueron la base 60 y la notación posicional. No obstante, debe señalarse que los babilonios no usaban solamente la base 60. En ocasiones, aparecía la base 10, pero otras bases también. Al igual que sucede con otras culturas y sistemas numéricos, con los babilonios se dio una forma combinada de sistemas numéricos determinados por circunstancias históricas o incluso regionales. En lo que sí parece haber consenso es que se dio el uso bastante sistemático de la base 60 para todos los cálculos relacionados con la astronomía. Esto debe subrayarse.

Tanto el sistema sexagesimal como el sistema del valor del lugar han permanecido en posesión permanente de la humanidad. Nuestra división presente de la hora en 60 minutos y 3 600 segundos data de los sumerios, al igual que nuestra división del círculo en 360 grados, cada grado en 60 minutos y cada minuto en 60 segundos. Hay razón para creer que esta opción de 60 en lugar de 10 como una unidad ocurrió en un esfuerzo por unificar sistemas de medida, aunque el hecho de que 60 tiene muchos divisores también puede haber jugado un papel. Acerca del sistema del valor posicional, su importancia permanente se ha comparado con el alfabeto (ambas invenciones reemplazaron un simbolismo complejo por un método fácilmente entendible por muchas personas). Es razonable suponer que hindúes y griegos obtuvieron las rutas de las caravanas hacia Babilonia; también sabemos que los académicos musulmanes lo describieron como una invención india. La tradición babilónica, sin embargo, puede haber influido en la aceptación tardía del sistema posicional.” (Struik, A Concise History of Mathematics, p. 26].
No poseían sin embargo el cero, ni tampoco algún símbolo para expresar la diferencia entre la parte entera y la fraccionaria de un número. Estos problemas implicaban cierto nivel de ambigüedad en el sistema numérico. De hecho, se afirma que -aunque lo usaban- no se trataba de un sistema posicional absoluto.
Para los babilonios, los símbolos fundamentales eran del 1 al 10 y los números del 1 al 59 se formaban combinando algunos de estos símbolos.
De las tablilas babilónicas, unas 300 son dedicadas a las matemáticas y hablan de cuentas y préstamos con interés, de multiplicaciones y otros problemas cotidianos. Otras, sin embargo, nos hablan de problemas mucho más avanzados con la superficie de la circunferencia, o, ¡el teorema de Pitágoras! y las propiedades de los triaángulos. Problemas de segundo, tercero y hasta de cuarto grado. También resolvían sistemas de ecuaciones. ¡Aspmbroso para aquellos tiempos!
Este problema de los Babilonios se basa en el Teorema de Pitágoras porque:
Bueno amigos, en un repaso tan superficial de lo que fueron las matemáticas, no puede extenderme tanto como para dejar una relación pormenorizada de todas las civilizaciones y personajes que merecen estar aquí reflejados. Sin embargo, el corto repaso, deja una muestra de lo que fueron aquellos primeros principios matemáticos y que dejan bien claro que, de ninguna manera, fuimos nosotros los que las inventamos en aquelos primeros principios.
emilio silvera















 Totales: 85.446.744
Totales: 85.446.744 Conectados: 95
Conectados: 95