« ¡Las leyes físicas! A veces sorprendentes,

[?]

Diversidad de ideas

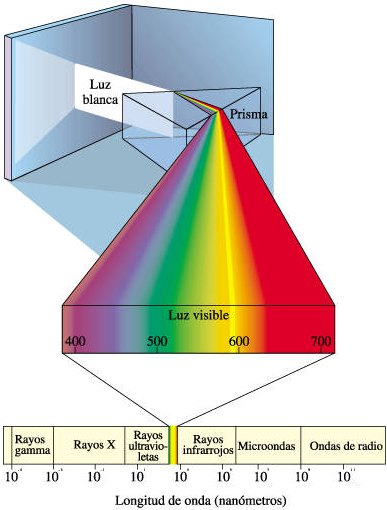
Me gusta escribir sin tener un objetivo predeterminado y hacer un vuelo rasante sobre la física para escribir todo lo que estoy “viendo” (lo que sin llamarlo, acude a mi mente en cada instante). Es un buen ejercicio de repaso de cosas diversas que recuerdas. Por ejemplo, ahora mismo me llega la idea de que, desde la más remota antigüedad nos viene fascinando los fenómenos ópticos. De hecho, los estudios encaminados a desvelar la naturaleza de la luz han sido uno de los motores más fructíferos de la física. A ello se dedica la óptica, hoy día una de las áreas más activas de la física.

algunos pudieron asombrarse ante esta imágen de esplendorosa belleza natural, ¿qué produjo tal fenómeno? Pero hablamos del auge en el campo de la óptica…¿dónde radica el impulso de esa disciplina?

Buena prueba de ello es la rápida sucesión de Premios Nobel en ese campo en años recientes: 1.997, 2.001 y 2.005. LRoy J. Glauber, de la Universidad de Harvard, “por sus contribuciones a la teoría cuántica de la coherencia óptica“. Estas contribuciones se recogen esencialmente en tres artículos publicados en 1.963 (sa mitad del último premio fue a manos de e lo reconocen en 2.005). Sobre ellas se ha desarrollado la óptica cuántica. En la luz se apreció por primera vez la naturaleza dual onda-partícula de los objetos cuánticos.

El comportamiento ondulatorio de la luz sirvió de prueba experimental para la teoría electromagnética de Maxwell. La idea de la luz como un haz de fotones reapareció con Einstein en 1.905 para explicar el efecto fotoeléctrico (que le valió el Nobel de física). El dualismo onda-partícula de la luz, que De Broglie extendió a las partículas materiales, es contradictorio en el marco de la física clásica. Para reconciliar ambas imágenes hubo que desarrollar la física cuántica. No obstante, como señalaba Glauber en uno de los artículos mencionados, “la teoría cuántica ha tenido una influencia sobre la óptica que es sólo una fracción de la que históricamente ha tenido la óptica sobre la teoría cuántica”.

Premio Nobel de Física de 2.005. Roy J. Glauber, de la Universidad de Harvard, Theodor W. Hänsch, del Instituto Max Plack y John L. Hall, de la Universidad de Colorado, comparten el premio Nobel de Física 2005. Glauber lo recibe por su contribución a la teoría cuántica de la coherencia óptica, mientras que Hänsch y Hall por sus contribuciones a la espectroscopía de precisión basada en láser, incluyendo la técnica de barrido de frecuencia óptica.

Motivado por los experimentos de Hanbury-Brown y Twiss en 1.954-56, y por la invención del láser en 1.960, Glauber realizó una aplicación de la electrodinámica cuántica a problemas ópticos. Mientras que los experimentos previos habían usado interferencia de amplitudes y registraban intensidades con un solo detector, Hanbury-Brown y Twiss estudiaron correlaciones en las intensidades recibidas de una estrella por dos detectores separados, observando que los fotones térmicos parecen emitirse agrupados (bunched). ¿También los de un haz de láser? Esta y otras cuestiones llevaron a Glauber a desarrollar la teoría cuántica de la coherencia, basada en los estados coherentes y en la teoría cuántica de la fotodetección. Estudiando coincidencias retardadas en la detección de fotones por varios detectores, Glauber introdujo una sucesión de funciones de correlación que mostraban las características cuánticas de la radiación y permitían diferenciar entre haces de luz con la misma distribución espectral, pero diferente estadística de fotones.

 En el universo temprano los fotones se convertían continuamente en pares

Particularmente relevantes han sido los estudios posteriores de “luz no clásica”, tales como resonancia-fluorescencia de un solo átomo, que muestra el llamado antibunching, luz cuyo ruido cuántico depende de la fase; y pares de fotones entrelazados.

El estado más común de la materia en el universo, no es ni líquido, ni sólido, ni gaseoso, sino que es el plasma; el estado de la materia que conforman las estrellas. Sin embargo, particularmente apuesto por una idea que no se va de mi cabeza, el estado último de la materia es la luz.

La otra mitad del Premio Nobel se otorgó a partes iguales a John L. Hall, de la Universidad de Colorado, JILA y NIST, Boulder y a Theodor W. Hänsch, del Max Planck Instit für Quantenoptik, Garching, y de la Ludwig-Maximilians-Universität, Munich, “por sus contribuciones al desarrollo de métodos de espectroscopia láser de precisión, incluyendo la técnica de peines de frecuencias ópticas“.

        espectroscopia de absorción atómica

 A lo largo de toda la historia la ingeniería se ha convertido en unas de las fuentes de solución a todos los problemas de la humanidad, de la mano de las ciencias y la tecnología, la cual ha aportado tantos métodos de mayor exactitud como lo es el utilizado por la espectrofotometría de absorción atómica; ya que es una técnica capaz de detectar  y determinar cuantitativamente la mayoría de los elementos del sistema periódico.

En espectroscopia se analiza la composición en frecuencias de la luz absorbida o emitida por la materia, lo cual proporciona información valiosa, por ejemplo, sobre la estructura cuántica de los átomos.

Los galardonados lideraron un proyecto espectacular en el desarrollo de métodos para producir y medir estas frecuencias ópticas, con una precisión actual de 15 cifras significativas y potencial de 18. De hecho, este tipo de medidas son de las de mayor precisión alcanzadas en física y permiten abordar cuestiones de gran interés básico, como la observación de la variación temporal de “constantes” fundamentales, como la estructura fina (α = 1/137, ó 2πe²/hc). Tienen también repercusión en el desarrollo de relojes atómicos ultraprecisos (con desajuste menor a una décima de segundo cada 100 años), útiles por ejemplo en sistemas GPS.

No dejamos de enviar ingenios al espacio para tratar de medir la Densidad Crítica y poder saber en qué clase de universo nos encontramos: Plano, cerrado o abierto. Pero, también mandamos satélirtes artificiales que, desde el cielo, dominan y controlan aspectos de la Tierra que nos son muy útiles en navegación, circulación víal, y otros muchos conceptos que, tanto en la vida cotidiana como en la investigación, nos sitúan en el más alto nivel de la tecnología…del futuro.

En espectroscopia óptica de precisión han de determinarse frecuencias de varios cientos de THz en términos de la definición del patrón de tiempo representado por desdoblamiento hiperfino del estado fundamental del cesio a 9’2 GHz. Hasta el año 2.000, esta tarea requería esfuerzos heroicos porque los detectores sólo permiten comparar directamente frecuencias separadas por algunas decenas de GHz. Se usaban por tanto complejas cadenas de generación de sucesivos armónicos de la frecuencia del cesio.

Esas cadenas eran costosas, delicadas, y de hecho, sólo algunos laboratorios las desarrollaron. El problema se ha simplificado enormemente con la introducción por Hall y Hänsch del llamado peine de frecuencias ópticas, formado por del orden de un millón de frecuencias equiespaciadas unos 100 MHz y cubriendo varios cientos de THz. De estas frecuencias pueden realizarse una medida absoluta con el patrón de cesio. Por tanto el peine sirve como una “regla” para determinar cualquier frecuencia óptica desconocida. Estos peines o sintetizadores de frecuencias, que ya se comercializan, usan láseres de femtosegundos y un nuevo tipo de fibra óptica microestructurada o de cristal fotónico…

¿Dónde estará el límite?

emilio silvera

[?]

Nuestro patrimonio matemático y nuestro orgullo occidentales depende irremediablemente de los logros de la antigua Grecia. Dichos logros se han exagerado tanto que a menudo resulta difícil distinguir qué parte de la matemática moderno procede de los griegos y cuál es la que tiene su origen en los babilonios, los egipcios, los hindúes, los chinos, los árabes, etc. Las matemáticas de los griegos eran muy imaginativas y es grande la deuda que tenemos con ellos.

Sin duda alguna la obra cumbre de la Matemática griega, que aún hoy levanta pasiones entre los matemáticos y científicos en general es sin duda Los Elementos de Euclides. Generalmente se cree, erróneamente, que los Los Elementos de Euclides contienen únicamente un resumen sumario y exhaustivo de toda la Geometríia griega. En realidad los Los Elementos  supusieron la gran síntesis no sólo de la producción geométrica griega hasta el siglo III a. C. sino también de un compendio, usando el lenguaje geométrico, de toda la Matemática elemental: Geometría plana y espacial, Aritmética y Álgebra.

A este respecto escribió Proclos: «Son singularmente admirales sus Elementos de Geometría (de Euclides) por el orden que reina en ellos, la selección de los  teoremas y problemas tomados como elementos y también la variedad de los razonamientos desarrollados de todas las maneras y que conducen a la convicción» y más adelante expresa «Los Elementos son una guía segura y completa para la consideración científica de los objetos geométricos».

Sin embargo, si nuestras matemáticas actuales se basaran exclusivamente en Pitágoras, Euclides, Demócrito, Arquímes y otros griegos, sería una disciplina muy deficiente. Claro que, la realidad es que la historia de las matemáticas en occidente no se puede remontar a ninguna escuela y a ningún período que sean anteriores a la etapa de los griegos jónicos.

[?]

“En Cosmología, las condiciones “iniciales” raramente son absolutamente iniciales, pues nadie sabe como calcular el estado de la materia y el espacio-tiempo antes del Tiempo de Planck, que culminó alrededor de 10^-43 de segundo Después del Comienzo del Tiempo.”

Es verdaderamente encomiable la pertinaz insistencia del ser humano por saber, y, en el ámbito de la Astronomía, desde los más remotos “tiempos” que podamos recordar o de los que tenemos alguna razón, nuestra especie ha estado interesada en saber, el origen de los objetos celestes, los mecanismos que rigen sus movimientos y las fuerzas que están presentes.

Claro que, nosotros, los Humanos, llevamos aquí el tiempo de un parpadeo del ojo si lo comparamos con el Tiempo del Universo. Sin embargo, nos hemos valido de todos los medios posibles para llegar al entendimiento de las cosas, incluso sabemos del pasado a través del descubrimiento de la vida media de los elementos y mediante algo que denominamos datación, como la del Carbono 14, podemos saber de la edad de muchos objetos que, de otra manera, sería imposible averiguar. La vida de los elementos es muy útil y, al mismo tiempo, nos habla de que todo en el Universo tiene un Tiempo Marcado. Por ejemplo, la vida media del Uranio 238 sabemos que es de 4.000 millones de años, y, la del Rubidio tiene la matusalénica vida media de 47.000 millones de años, varias veces la edad que ahora tiene el Universo.

Lepidolita, una de las mayores fuentes del raro rubidio y del cesio. El rubidio también fue descubierto, como el cesio, por los físicos alemanes Robert Wilhem Bunsen y Gustav Robert Kirchhoff en 1861; en este caso por el método espectroscópico. Su nombre proviene del latín “rubidus” (rubio), debido al color de sus líneas en el espectro.

[?]

¡Maldito Capital!

Hay cuestiones de las que no debemos quedar en la sombra de la ignorancia. El conocimiento de lo que pasa en el mundo es muy conveniente para poder saber, dónde estamos y qué maquinaciones se han venido y se vienen realizando para que, las criaturas del mundo “libre”, no sean tan libres y estén supeditadas a unas minorias sin escrúpulos que que lo quieren dirigir… ¡Hasta el destino Humano! está en sus manos.

A la derecha de la página del Blog, en el lugar que se denomina Enlaces, aparece: ¡Maldito Capital! – Se describe lo que es la realidad del mundo. Merece la pena que le dediquéis un rato para saber, de qué van las cosas.

emilio silvera

[?]