Nov
11
Siempre haremos preguntas
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en El saber del mundo ~
Clasificado en El saber del mundo ~
 Comments (0)
Comments (0)
El libre Albedrío? ¿Dónde está?

El cerebro es capaz de inventar recuerdos de hechos que nunca ocurrieron. La capacidad humana para aprender, inventar, buscar recursos, … ¡Es casi ilimitada! siempre ha encontrado una respuesta a los problemas planteados y, a medida que avanzamos y nuestro cerebro evoluciona, más caminos se abren ante nosotros
Lo cierto es que, cada día que pasa, nuevos descubrimientos astronómicos nos llevan hacia el asombro y la maravilla… ¿Cómo puede la Naturaleza hacer las cosas que hace?
¡Sabemos tanto de las estrellas!¡Nos queda tanto por saber!

En el núcleo se alcanzan los 15.000.000 de grados y se producen las transisiciones de fase de la transmutación de elementos. La nucleosíntesis estelar es el conjunto de reacciones nucleares que tienen lugar en las estrellas durante el proceso de evoluciòn estelar anterior al colapso gravitatorio. Estos procesos empezaron a entenderse a principios del siglo XX cuando quedó claro que solo las reacciones nucleares podían explicar la gran longevidad de la fuente de calor y luz del Sol. Aproximadamente el 90% de la energía producida por las estrellas vendrá de las reacciones de fusión del hidrógeno para convertirlo en helio. Más del 6% de la energía generada vendrá de la fusión del helio en carbono. El proceso sigue hasta el Hierro, donde no puede continuar y se produce la “muerte de la estrella como tal en la secuencia principal.
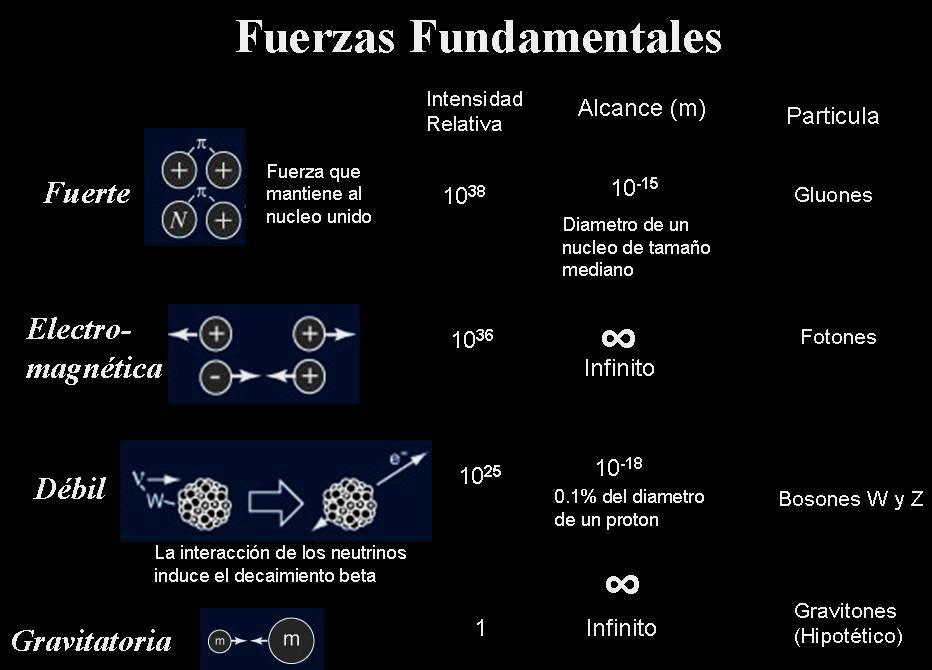
El modelo estándar de la física de partículas es una teoría relativista de campos cuánticos desarrollada entre 1970 y 1973 basada en las ideas de la unificación y simetrías que describe la estructura fundamental de la materia y el vacío considerando las partículas elementales como entes irreducibles cuya cinemática está regida por las cuatro interacciones fundamentales conocidas. Aunque tenemos que decir que, la Gravedad, esa fuerza que mantiene unidos los planetas en las sistemas planetarios y nuestros pies al suelo de la Tierra, no se quiere juntar con las otras tres fuerzas, campa solitaria por el Cosmos.


Aunque es cierto que “sobre gustos no hay nada escrito”, los humanos nos sentimos más a gusto con las caras más simétricas. En la cultura popular, y salvo alguna rara excepción, las caras asimétricas están relacionadas con la maldad. Los biólogos encontraron rápidamente una explicación evolutiva: los individuos más evolucionados pueden mantener sus formas simétricas inclusive cuando están expuestos al estrés y las enfermedades. Es decir, cuando las partes del cuerpo que tienden a la simetría no lo son, costará más pasar esos genes porque será rechazado por potenciales parejas. De esta manera la evolución distingue a la simetría como una característica valiosa.

David (1501-1504), de Miguel Ángel, Galería de la Academia de Florencia.
El desnudo de una figura presenta una simetría bilateral casi perfecta. Ciertamente, parte del atractivo del mismo, tanto en la realidad como en el arte, reside en la identificación de los lados derecho e izquierdo del cuerpo mediante mediante una simetría especular. La figura femenina raramente presenta asimetrías. La asimetría de un varón se rompe solamente por la curiosa circunstancia de que su testículo izquierdo cuelga más bajo que el derecho.

(1532), de Lucas Cranach el Viejo, Städelsches Kunstinstitut, Fráncfort del Meno, censurada por el Metro de Londres en 2008.
Evidentemente, cada cuerpo, considerado de forma individual, puede otras desviaciones menores de su simetría: un hombro más alto que otro, un pecho mayor que su pareja, una ligera desviación de la columna, una peca o un antojo en un costado…, pero tales anomalías, en su mayor parte, pueden encontrarse tanto a un lado como al otro.

La simetría bilateral se mantiene en el interior del cuerpo, en en los músculos y en el esqueleto, pero queda rota por la disposición fuertemente asimétrica de algunos órganos. El corazón, el estómago y el páncreas están desviados hacia la izquierda; el hígado y el apéndice, hacia la derecha. El pulmón derecho es mayor que el izquierdo. Los retorcimientos y vueltas de los intestinos son completamente asimétricos. El cordón umbilical humano, una magnifica hélice triple formada por dos arterias y una vena, puede enrollarse en cualquiera de los dos sentidos.

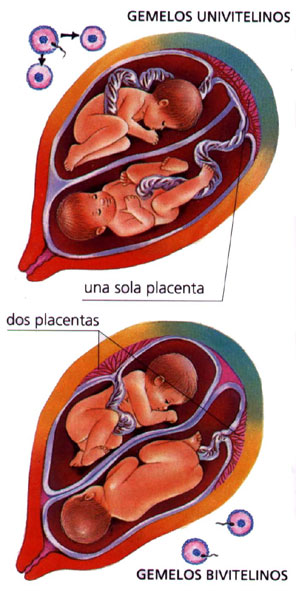
Los mellizos que se desarrollan por la fecundación simultánea de dos óvulos separados, pueden tener detalles asimétricos en un sentido en uno de ellos, y en el contrario en el otro, pero esto no ocurre con mayor frecuencia que la que cabría esperar como fruto del azar. Es una creencia generalizada que los gemelos (formados a partir de un único óvulo, que se divide inmediatamente después de la fecundación) tiene una marcada tendencia a aparentar especulares recíprocas. Por desgracia, las estadísticas al respecto son confusas y muchos expertos creen que los gemelos idénticos no se presentan como imágenes especulares uno de otro en mayor medida que cualquier otro tipo de hermanos.

En el caso de gemelos siameses (gemelos idénticos, unidos uno a otro a causa de un a partición tardía e incompleta del óvulo), el tema no ofrece duda alguna. Son exactamente enantiomorfos en casi todos los detalles: si uno es diestro, el otro es zurdo; si uno tiene el remolino del pelo que va en el sentido de las agujas del reloj, el de su hermano/hermana irá en el sentido contrario. Diferencias en los oídos, los dientes…, aparecen en ambos como especulares unas respecto de otras (hasta en eso es perfecta la Naturaleza). Las huellas dactilares o de la palma de la mano derecha de uno serán muy parecidas a las correspondientes a la mano izquierda del otro.
Todavía más: un gemelo siamés tendrá “vísceras transpuestas”; sus órganos internos estarán colocados de manera inversa, el corazón a la derecha, el hígado a la izquierda. Esta transposición de órganos, o inverse situs, como se denomina a veces, se da siempre en cualquier par de gemelos siameses, pero puede aparecer también en no incluidas en estas circunstancias.

Merece la pena hacer notar que Lewis Carroll, en A través del espejo (Alianza Editorial, 1990), pretende tomar los gemelos idénticos Tararí y Tarará como imágenes especulares uno de otro. Cuando los hermanos Tara ofrecen enlazar sus manos con Alicia, uno de ellos alarga su derecha; el otro la izquierda. Si observamos detenidamente las ilustraciones de Tenniel, especialmente la que muestra los dos gemelos uno frente a otro, para la batalla, veremos que los ha dibujado como si fueran enantiomorfos.

Claro que, algunos son completos
En el comportamiento y los hábitos de los seres humanos hay muchos ejemplos de marcada asimetría; los más evidentes son consecuencia de que la mayoría de las personas son diestras. La mano derecha está controlada por la parte izquierda del cerebro, y la parte derecha de éste controla la mano izquierda, por lo que la condición de diestro es, en realidad, un fenómeno de lateralidad izquierda del cerebro. Hubo un tiempo en el que se creía que los bebés nacían sin tendencia alguna de tipo genético que favoreciera el uso de una mano concreta, que la lateralidad de un niño era exclusivamente el resultado de las enseñanzas de sus padres. Platón era un notable defensor de esta opinión.
“En el uso de las manos estamos, y estábamos, viciados por las manías de nuestras intitutrices y madres -escribe Platón en sus Leyes-, pues aunque nuestros miembros están compensados por naturaleza, creamos una diferencia entre ellos como consecuencia de un mal hábito.”
Sabemos hoy en día que Platón estaba equivocado. Como hace notar Aristóteles con buen criterio. De todas las maneras, la tendencia innata para muchas personas de usar preferentemente la mano derecha es común desde que la puede constatarlo de manera evidente.

Losantropólogs culturales no han encontrado todavía ni una sola sociedad, o incluso una tribu , en la que la norma sea la lateralidad izquierda: los esquimos, los indios americanos, los maoríes y los africanos son todos diestros. Los antiguos egipcios, griegos y romanos eran diestros. Naturalmente, si retrocemos todavía más en la Historia, la evidencia de la lateralidad diestra es ya escasa e indirecta y hay que dilucidarla a partir del estudio de la forma de sus utensilios y armas, así como de las pinturas que muestran los hombres trabajando o en la batalla.
Las propias palabras que se usan en muchas lenguas para designar la izquierda y la derecha dan testimonio de un sesgo universal hacia el lado derecho. En , ir a derechas es hacer las cosas correctamente, mientras que no dar una a derechas, es sinónimo de hacerlo todo mal.

Ser diestro en algo es lo mismo que poseer una habilidad especial para ello, mientras que una cosa siniestra (del latín sinester, izquierda) es una cosa hecha con mala intención. En otras lenguas el significado viene a ser más o menos el mismo. Los italianos, tan suyos ellos, llaman a la mano izquierda stanca, fatigada, o manca, la que no se tiene. Lo cierto es que, por lo , los zurdos son ambidiestros.
Para tener una buena visión histórica de mlos prejuicios virulentos contra los zurdos en cualquier parte del mundo, veáse el séptimo capítulo de The Dragons of Eden, de Carl Sagan (Random House, 1977), y el delicioso de Jack Fincher, Sinister People (Putnam, 1977). Este último da una lista de más de cien personajes famosos que fueron zurdos.

Por lo que hemos observado , y hasta donde sabemos, la especie humana tiene la tendencia a utilizar la mano derecha. Claro que no sabemos. La mayoría de los mamíferos subhumanos son ambidiestros y, ¿cómo serán las especies que viven en otros mundos? El personaje de arriba, al menos, parece que es zurdo.
Lo cierto es que, poco importa si somos zurdos o no, la igualdad en lo esencial es casi idéntica. La verdadera diferencia está en el cerebro, en la manera de ver las cosas, en cómo cada cual enfoca los problemas y qué soluciones aplica a cada situación, en que perspectiva podamos tener de nuestra Sociedad, de nuestras leyes, de nuestros derechos, de la moral y la ética… Todo lo demás, son circunstancias anecdóticas que poco influyen en el devenir del mundo.
emilio silvera
Oct
8
¡El Universo y Nosotros! ¿Sabremos algún día la verdadera relación?
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en El saber del mundo ~
Clasificado en El saber del mundo ~
 Comments (0)
Comments (0)

Max Planck nos decía:
“La ciencia no puede resolver el misterio final de la Naturaleza. Y esto se debe a que, en el último análisis, nosotros somos parte del misterio que estamos tratando de resolver”.
Y, desde luego, no parece que fuese muy desencaminado, nuestra complejidad es tan grande que, llegar a comprendernos, no será nada fácil.


Las respuestas está en nuestras Mentes, sólo hay que saber buscar
¿Quién no ha tenido alguna vez, la sensación de que sabe la respuesta ? ¿De que todo está ahí, en su mente, escondido y a punto de salir a la superficie? Esas sensaciones que parecen querer hablarnos, contarnos ese secreto tan largamente perseguido por muchos y no desvelado por ninguno. Sin embargo, ese momento es efímero y, lo mismo que llegó, se fue. La frustración que deja en nostros esa sensación de tener ese algo a mano y de que se nos esfume y desaparezca sin más, es verdaderamente…dolorosa.
Bueno, a mí me pasa continuamente, siento que de un momento a otro, mi mente, me daría respuestas a preguntas que no han sido contestadas. El tiempo inexorable pasa y, las respuestas no llegan. ¡Qué impotencia! Parece como si una gran Nebulosa ocupara nuestra mente y todo lo tuviera envuelto en una espesa niebla que no nos deja ver lo que buscamos.

Imagino que, de vez en cuando, la niebla se ve despejada por alguna especie de “viento solar” dejando ver lo que allí está presente. En algunas mentes, entonces, saltan esas respuestas (Newton, Planck, Einstein y otros) y son ofrecidas al mundo para que puedan continuar avanzando.
Los aspectos inconscientes de la actividad mental, como las rutinas motoras y cognitivas, así como los recuerdos, intenciones y expectativas inconscientes, las preocupaciones y los estados de ánimos, desempeñan un papel fundamental a la hora de conformar y dirigir nuestras experiencias conscientes. Todo está siempre estrechamente relacionado, nada ocurre en nosotros que no esté unido a lo que pasa en nuestro entorno, somos una parte de un todo que se llama Universo, y, aún cuando somos autónomos en el pensamiento y en la manera de obrar, existen condicionantes exteriores que inciden, de una u otra manera en nosotros, en lo que somos.

Sin la fuerza de Gravedad, nuestras mentes serían diferentes (o no serían), estamos estrechamente conectados a las fuerzas que rigen el Cosmos y, precisamente, somos como somos, porque las fuerzas fundamentales de la Naturaleza, son como son y hacen posible la vida y la existencia de seres pensantes y evolucionados que son capaces de tener conciencia de SER, de hacer preguntas tales como: ¿de donde venimos? ¿Hacia donde vamos?

La qualia y la discriminación, correlatos neuronales de la percepción del color, ¿ un grupo neuronal, un quale ¿, los gualia y el núcleo dinámico, los qualia en el tiempo neuronal, el desarrollo de los qualia: referencia al propio yo, lo consciente y lo inconsciente, los puertos de entrada y de salida, los bucles largos y rutinas cognitivas, aprendizaje por el estudio y la experiencia, rupturas talamocorticales: posibilidades de núcleos escindidos, la observación, el lenguaje, el pensamiento, los mensajes exteriores, la unificación de datos y la selección lógica de respuestas, y, por fin: el significado último de las cosas (las preguntas de la filosofía), la metafísica.
Sí, por todas estas fases del estudio y del pensamiento he tenido que pasar para llegar a una simple conclusión:

No pocas veces, la imagen de nuestra imaginación nos juega malas trastadas y nos hace ver… ¡Lo que ya no somos!
“No somos la imagen de nadie” y, simplemente, como seres que evolucionamos, sin que nos demos cuenta, mutamos y nos adaptamos al medio cambiante y, mientras eso ocurre, llegan mensajes que no comprendemos a la primera. No, no exagero, dentro de esa imagen de frágil físico y de escasa capacidad para poder dar respuesta a ciertas preguntas, en realidad, se esconden cualidades y potenciales que, no sabemos ni podemos medir. En realidad, somos una compleja estructura de pensamientos que puede llegar…muy lejos.
Dentro de nuestro ser están todas las respuestas y solo necesitamos tiempo para encontrarlas. Nuestra mente, es la energía del Universo, aún no sabemos utilizarla y pasaran, posiblemente, millones de años hasta que estemos preparados para saber lo que en realidad, es la conciencia.

Mientras eso llega, algunos curiosos como yo, con más voluntad que conocimientos, tratan de especular con ideas y conceptos que nos puedan dar alguna luz sobre tan complicado problema.
Nuestra mente es una maravilla de la Naturaleza, algo tan grande que, a pesar de los muchos avances y conocimientos alcanzados, no podemos explicar… aún.
Está claro que, como me ha comentado un amigo, la materia tiene memoria y, es precisamente esa memoria, la que hace posible el avance de nuestros conocimientos a través de la mente que, sin duda, está directamente conectada con el resto del Universo y las fuerzas que lo gobiernan que son las que hacen posible su funcionamiento tal como acontece.

La curiosidad y la sabiduría, esas gotas del transcurrir del tiempo que salpican el río de la vida a través de la experiencia y nos hace saber… ¡Algunas cosas!
Pero nada es tan sencillo ni podemos hablar de lo sensorial sin tener en cuenta el plano más simple y cotidiano que está referido a la materia, a nuestro cuerpo, las sensaciones, las experiencias vivídas, lo que aprendemos, el estudio y la profundqa observación que nos lleva de la mano de la curiosidad hasta la fuente de la que mana el agua de la sabiduría.
Entender las claves que explican el devenir de la vida sobre este planeta, con la idea en el horizonte de aspiraciones intelectuales a que nos aboca la conciencia del SER, no resulta fácil, la complejidad de la empresa exige tener en cuenta múltiples factores que no siempre estamos preparados para comprender, y, sobre todo, debemos ser muy conscientes de que formamos parte de un Universo inmenso, y, estamos supeditamos a las fuerzas que lo rigen. Lo mejor para hacer nuestras vidas más fáciles, es tratar de comprender la Naturaleza de ese Universo nuestro.
Sí, el Universo podría ser considerado como la mayor Obra de Arte que, a su vez, es capaz de generar otras Obras de Arte que, en alguna ocasión, dan mucho que pensar, ya que, el surgir de la vida partierndo del simple hidrógeno que evoluciona en las estrellas del cielo…es ¡Increíble! pero, sin embargo, nada más cierto hay.
¡La Vida! Siempre me llamó la atención y elevó el grado de curiosidad ese gran misterio que llamamos ¡vida!, y, cada vez que he tenido la oportunidad, no me he perdido el poder aprender alguna cosa sobre ella. Ya os he contado en otras ocasiones mi experiencia con la eminente y privilegiada mente de…
Lynn Margulis comenzó a explorar los caminos de la genética a partir de un libro escrito en el siglo XIX por Edmund B.Webs. En ese texto encontró reflexiones sobre la herencia citoplasmática y datos sobre las bacterias, entonces no muy consideradas en el estudio del origen de la vida.

Lynn Margulis fue una importante e influyente bióloga estadounidense. Además de ser una de las madres del evolucionismo, aportó notables conocimientos a la ciencia, como por ejemplo, su teoría de la aparición de las células eucariotas, o la de la simbiogénesis, por nombrar solo algunas.
La doctora Margulis fue profesora del Departamento de Geociencias de la Universidad de Massachusselts (Estados Unidos) relacionó el papel de las bacterias con la microbiología, una ciencia surgida de la medicina, de la salud pública y del procedimiento seguido para procesar los alimentos. De ahí saltó al estudio del tema que ocupa su curso magistral: Contribución de los microbios a la evolución.

El pequeño Monasterio franciscano de La Rábida en Huelva, dónde Colón fue acogido por los frailes y se fraguó el viaje a Las Américas.La zona está enclavada en un margen del Río Odiel y los terrenos de de Bosques y Pinares con senderos para pasear.


Junto al Monasterio se levanta un enorme obelisco que fue construido en conmemoración del cuarto centenario del nuevo continente y, en su interior, como podeis ver arriba, existen obras pictóricas conmemorativas de la gesta que pintó Daniel Vazquez Díaz. El monasterio tipológicamente pertenece al Gótico-Mudéjar incorporado a la Rábida desde el período Almohade.

La iglesia-Santuario es de dimensiones pequeñas y estructura compacta posee una sola nave y un hermoso artesonado de influencia mudéjar que cubre la bóveda primitiva. El ábside posee arcos apuntados. En las paredes conserva pinturas de Juan de Dios realizadas en el Siglo XVIII que tratan temas de la vida de San Francisco.

El claustro del Monasterio de la Rábida es pequeño y sigue el modelo de San Isidoro y Guadalupe: estilo mudéjar. Se amplió en el siglo XVII con un cuerpo superior y se le incorporaron almenas como protección de invasiones.
Tiene en sus paredes frescos del siglo XV que han sido restauradas. El claustro estuvo punto de desaparecer en 1855 por la desamortización, y salvado el conjunto por el Gobernador Alonso. Es uno de los monumentos mas importantes y significativos en la historia de España y de América, fue declarado primer monumento histórico de los pueblos Hispanos y en 1856 fue declarado el tercer monumento nacional y patrimonio de la humanidad.

Me desvío del tema. Muy cerca del entorno, junto al Monasterio, está la Sede de la Universidad Internacional Iberoamericana de La Rábida, en la que, se imparten Cursos de verano y se acogen a grandes personalidades en los distintos campos del saber que dan conferencias muy apreciadas. Aquí, en el pasado no muy lejano, tuve la suerte de asistir a una de Lynn Margulis y pude hablar con ella que respondío a mis preguntas con amabilidad y sabiduría.
Ella centraba el curso en la enorme importancia que tenían los microbios para nosotros, no siempre bien valorados. Los microbios pueden ser definidos como organismos que no podemos ver a simple vista y, la cultura popular dice que tan sólo sirven de agentes para canalizar enfermedades, pero esa apreciación conlleva un error muy serio. Por ejemplo: el 10% del peso del cuerpo humano en seco está compuesto por microbios, sin los cuales no podemos vivir ni siquiera un día. Ellos asumen tareas tan importantes como la de generar el oxígeno del aire que precisamos para respirar. Además, tienen un papel fundamental en la evolución de la vida: todos los seres vivos considerados simples –animales, plantas, hongos, etc.- están hechos de microbios en combinación simbiótica con otros organismos. Se trata de una historia que se aleja en el pasado hasta 3.500 millones de años en el curso de la vida sobre la superficie de nuestro planeta: La Tierra.

Los conceptos que maneja y esgrime la doctora en genética, están encuadrados en una visión totalmente contradictoria con la religión y otros muchos conceptos culturales.
Pregunté a la doctora Margulis si la mala imagen de los microbios nacía de un estudio deficiente de la microbiología, o si simplemente surgía a partir de tópicos sin fundamentos. Su contestación fue:
“La asociación de esos pequeños organismos con aspectos negativos se explica por el origen de su estudio científico, que siempre estuvo relacionado con descubrimientos ligados a la investigación en torno a enfermedades. Junto a esta idea, lo cierto es que pensamos en formas ideales que corresponden al esquema platónico de hace casi 30 siglos, cuando en realidad no existen tales ideas sino organismos que interaccionan con el medio ambiente en el que se encuentran. Esta colaboración recibe el nombre de ecología. De hecho, el concepto de independencia no tiene sentido en este campo: al margen de los microbios moriríamos inmediatamente”.
Nos creemos lo contrario pero, siempre seremos aprendices, no tenemos tiempo para más
Aquel día, como casi todos los días de mi vida, aprendí cosas nuevas y muy interesantes que me confirmaron que nuestras vidas, podrían ser cualquier cosa, menos simples. Es tal el nivel de complejidad implicado que, precisamente por eso, no somos capaces de explicarla al completo, solo vamos dominando parcelas limitadas que, algún día, al ser unidas, nos darán las respuesta.

En fin amigos, que como habreis podido deducir, aunque nuestras limitaciones nos impongan barreras, no debemos rendirnos ante ninguna de ellas y, si persistimos, finalmente encontraremos el camino de pasarlas para poder ir un poco más allá. Era Jhon Wheeler el que nos decía: “Vivímos en una isla rodeada por un mar de ignorancia. Mientras nuestra isla de conocimiento crece, también crece la costa de nuestra ignorancia.” Pero, cada nuevo conocimiento que adquirimos, hace la isla mayor, y, la ignorancia decrece en esa pequeña proporción”
Claro que, si los conocimientos que vamos adquiriendo son continuados… Finalmente, ¿podríamos secar ese mar de ignorancia?
Pero, ¿que tiene todo esto que ver con el título del trabajo? Bueno, lo único que puedo decir es que, nosotros… ¡También somos universo!
emilio silvera
Jun
5
Siempre haremos preguntas
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en El saber del mundo ~
Clasificado en El saber del mundo ~
 Comments (0)
Comments (0)
El libre Albedrío? ¿Dónde está?


Aunque es cierto que “sobre gustos no hay nada escrito”, los humanos nos sentimos más a gusto con las caras más simétricas. En la cultura popular, y salvo alguna rara excepción, las caras asimétricas están relacionadas con la maldad. Los biólogos encontraron rápidamente una explicación evolutiva: los individuos más evolucionados pueden mantener sus formas simétricas inclusive cuando están expuestos al estrés y las enfermedades. Es decir, cuando las partes del cuerpo que tienden a la simetría no lo son, costará más pasar esos genes porque será rechazado por potenciales parejas. De esta manera la evolución distingue a la simetría como una característica valiosa.

David (1501-1504), de Miguel Ángel, Galería de la Academia de Florencia.
El desnudo de una figura presenta una simetría bilateral casi perfecta. Ciertamente, parte del atractivo del mismo, tanto en la realidad como en el arte, reside en la identificación de los lados derecho e izquierdo del cuerpo mediante mediante una simetría especular. La figura femenina raramente presenta asimetrías. La asimetría de un varón se rompe solamente por la curiosa circunstancia de que su testículo izquierdo cuelga más bajo que el derecho.

(1532), de Lucas Cranach el Viejo, Städelsches Kunstinstitut, Fráncfort del Meno, censurada por el Metro de Londres en 2008.
Evidentemente, cada cuerpo, considerado de forma individual, puede tener otras desviaciones menores de su simetría: un hombro más alto que otro, un pecho mayor que su pareja, una ligera desviación de la columna, una peca o “un antojo” en un costado…, pero tales anomalías, en su mayor parte, pueden encontrarse tanto a un lado como al otro.

La simetría bilateral se mantiene en el interior del cuerpo, en en los músculos y en el esqueleto, pero queda rota por la disposición fuertemente asimétrica de algunos órganos. El corazón, el estómago y el páncreas están desviados hacia la izquierda; el hígado y el apéndice, hacia la derecha. El pulmón derecho es mayor que el izquierdo. Los retorcimientos y vueltas de los intestinos son completamente asimétricos. El cordón umbilical humano, una magnifica hélice triple formada por dos arterias y una vena, puede enrollarse en cualquiera de los dos sentidos.


Los mellizos que se desarrollan por la fecundación simultánea de dos óvulos separados, pueden tener detalles asimétricos en un sentido en uno de ellos, y en el contrario en el otro, pero esto no ocurre con mayor frecuencia que la que cabría esperar como fruto del azar. Es una creencia generalizada que los gemelos (formados a partir de un único óvulo, que se divide inmediatamente después de la fecundación) tiene una marcada tendencia a aparentar especulares recíprocas. Por desgracia, las estadísticas al respecto son confusas y muchos expertos creen que los gemelos idénticos no se presentan como imágenes especulares uno de otro en mayor medida que cualquier otro tipo de hermanos.

En el caso de gemelos siameses (gemelos idénticos, unidos uno a otro a causa de un a partición tardía e incompleta del óvulo), el tema no ofrece duda alguna. Son exactamente enantiomorfos en casi todos los detalles: si uno es diestro, el otro es zurdo; si uno tiene el remolino del pelo que va en el sentido de las agujas del reloj, el de su hermano/hermana irá en el sentido contrario. Diferencias en los oídos, los dientes…, aparecen en ambos como especulares unas respecto de otras (hasta en eso es perfecta la Naturaleza). Las huellas dactilares o de la palma de la mano derecha de uno serán muy parecidas a las correspondientes a la mano izquierda del otro.
Todavía más: un gemelo siamés tendrá “vísceras transpuestas”; sus órganos internos estarán colocados de manera inversa, el corazón a la derecha, el hígado a la izquierda. Esta transposición de órganos, o inverse situs, como se denomina a veces, se da siempre en cualquier par de gemelos siameses, pero puede aparecer también en no incluidas en estas circunstancias.

Merece la pena hacer notar que Lewis Carroll, en A través del espejo (Alianza Editorial, 1990), pretende tomar los gemelos idénticos Tararí y Tarará como imágenes especulares uno de otro. Cuando los hermanos Tara ofrecen enlazar sus manos con Alicia, uno de ellos alarga su derecha; el otro la izquierda. Si observamos detenidamente las ilustraciones de Tenniel, especialmente la que muestra los dos gemelos uno frente a otro, para la batalla, veremos que los ha dibujado como si fueran enantiomorfos.

Claro que, algunos son completos
En el comportamiento y los hábitos de los seres humanos hay muchos ejemplos de marcada asimetría; los más evidentes son consecuencia de que la mayoría de las personas son diestras. La mano derecha está controlada por la parte izquierda del cerebro, y la parte derecha de éste controla la mano izquierda, por lo que la condición de diestro es, en realidad, un fenómeno de lateralidad izquierda del cerebro. Hubo un tiempo en el que se creía que los bebés nacían sin tendencia alguna de tipo genético que favoreciera el uso de una mano concreta, que la lateralidad de un niño era exclusivamente el resultado de las enseñanzas de sus padres. Platón era un notable defensor de esta opinión.
“En el uso de las manos estamos, y estábamos, viciados por las manías de nuestras intitutrices y madres -escribe Platón en sus Leyes-, pues aunque nuestros miembros están compensados por naturaleza, creamos una diferencia entre ellos como consecuencia de un mal hábito.”
Sabemos hoy en día que Platón estaba equivocado. Como hace notar Aristóteles con buen criterio. De todas las maneras, la tendencia innata para muchas personas de usar preferentemente la mano derecha es común desde que la puede constatarlo de manera evidente.

Losantropólogos culturales no han encontrado todavía ni una sola sociedad, o incluso una tribu , en la que la norma sea la lateralidad izquierda: los esquimos, los indios americanos, los maoríes y los africanos son todos diestros. Los antiguos egipcios, griegos y romanos eran diestros. Naturalmente, si retrocemos todavía más en la Historia, la evidencia de la lateralidad diestra es ya escasa e indirecta y hay que dilucidarla a partir del estudio de la forma de sus utensilios y armas, así como de las pinturas que muestran los hombres trabajando o en la batalla.
Las propias palabras que se usan en muchas lenguas para designar la izquierda y la derecha dan testimonio de un sesgo universal hacia el lado derecho. En , ir a derechas es hacer las cosas correctamente, mientras que no dar una a derechas, es sinónimo de hacerlo todo mal.

Ser diestro en algo es lo mismo que poseer una habilidad especial para ello, mientras que una cosa siniestra (del latín sinester, izquierda) es una cosa hecha con mala intención. En otras lenguas el significado viene a ser más o menos el mismo. Los italianos, tan suyos ellos, llaman a la mano izquierda stanca, fatigada, o manca, la que no se tiene. Lo cierto es que, por lo , los zurdos son ambidiestros.
Para tener una buena visión histórica de mlos prejuicios virulentos contra los zurdos en cualquier parte del mundo, veáse el séptimo capítulo de The Dragons of Eden, de Carl Sagan (Random House, 1977), y el delicioso de Jack Fincher, Sinister People (Putnam, 1977). Este último da una lista de más de cien personajes famosos que fueron zurdos.

Por lo que hemos observado , y hasta donde sabemos, la especie humana tiene la tendencia a utilizar la mano derecha. Claro que no sabemos. La mayoría de los mamíferos subhumanos son ambidiestros y, ¿cómo serán las especies que viven en otros mundos? El personaje de arriba, al menos, parece que es zurdo.
Lo cierto es que, poco importa si somos zurdos o no, la igualdad en lo esencial es casi idéntica. La verdadera diferencia está en el cerebro, en la manera de ver las cosas, en cómo cada cual enfoca los problemas y qué soluciones aplica a cada situación, en que perspectiva podamos tener de nuestra Sociedad, de nuestras leyes, de nuestros derechos, de la moral y la ética… Todo lo demás, son circunstancias anecdóticas que poco influyen en el devenir del mundo.
emilio silvera
Oct
3
Nuestra percepción y la realidad: Dos cosas distintas
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en El saber del mundo ~
Clasificado en El saber del mundo ~
 Comments (2)
Comments (2)

Nuestra realidad es que cada uno de nosotros percibimos, entendemos y actuamos de manera diferente en la vida. Cada uno posee su propia realidad del mundo y de él mismo. Estamos construidos a base de creencias, y esas creencias son las que influyen de manera decisiva en nuestra realidad y en nuestra conducta, por lo tanto, son las “culpables” de que consigamos o no nuestros objetivos. Básicamente nuestra realidad está formada por nuestra educación, nuestro entorno, nuesstra preparación, nuestra capacidad intelectual…

“Nuestra tarea más urgente es dejar de identificarnos con el pensamiento, dejar de estar poseídos por él”
Eso nos aconseja Eckhart Tolle, y, no siempre resulta ser de esa manera, Hay ocasiones en la que, nuestros pensamientos son la guía que nos pueden llevar al buen destino, y, si lo que dice (que no lo aclara) está referido a los pensamientos de los otros, simplemente se trata de discernir dónde radica la verdad, en lo que nos dicen o en lo que nosotros creemos. Claro que, no todos creen siempre en lo correcto.
Nosotros los humanos, nunca estamos seguros de nada y, buscando esa seguridad, creamos modelos con los que tratamos de acercarnos más y más a esa realidad que presentimos, y de esa manera encontramos la forma de aproximarnos a esa realidad intuida. En la vida cotidiana, en el hombre de la calle, se halla muy extendido el Practicismo o Realismo ingenuo, se admite, sin más reflexión, que la realidad existe y no se plantean el problema de cuestionar tal existencia. Sin embargo, para los filósofos, el problema de la existencia o no de la Realidad Metafísica y la certeza sobre el conocimiento que sobre ella extraen nuestros sentidos (Epistemología) ha sido, desde los primeros filósofos griegos (pre-socráticos), y continua siendo, uno de los grandes problemas filosóficos que todavía no ha sido resuelto. Es decir, una cuestión sobre la que no tenemos respuesta unánimemente aceptada por todos los pensadores.

Los humanos, desde que fuimos conscientes de nuestro Ser, hemos estado desarrollando diferentes corrientes de pensamientos filosóficos (o doctrinas) que han tratado de responder al problema de si existe o no la realidad fuera de nuestra mente. Películas actuales como “Matrix” es una buena muestra de que el problema de la realidad todavía nos tiene intrigados a los seres humanos de hoy.
La epistemología es una rama de la filosofía que se ocupa de la validez y fiabilidad de los conocimientos que obtenemos los humanos. Viene a ser como una teoría crítica del conocimiento. Desde el punto de vista epistemológico se han planteado cuestiones tales como:
- ¿Se corresponde la realidad con larepresentación mental que el hombre tiene? ¿O el mundo psíquico es un producto inventado por la mente humana?
- ¿Es fiable y válida la información que los órganos sensoriales captan? ¿O nos engañan nuestros sentidos?
- ¿Cómo llegamos a tener conciencia de la existencia de un espacio poblado de objetos y sujetos (mundo)?
- ¿Es realmente el Universo, como nosotros lo percibimos, o, siendo nuestros sentidos imperfectos nos muestra un universo diferente al que es?

No todos perciben “el mundo” de la misma manera. Tampoco resuelven sus problemas de igual forma

Pero vayamos a algo concreto y pensemos, por ejemplo, en la técnica reiterativa que se utiliza para obtener “soluciones” en casos como el problema de los tres cuerpos (por ejemplo) tiene un inconveniente. A veces no funciona, no siempre podemos decir a priori si va a funcionar o no. La técnica que se aplica para “resolver” las ecuaciones diferenciales pertinentes (recordemos que no se pueden resolver analíticamente) implica realizar aproximaciones sucesivas, en las cuales, como es sabido, el primer paso del proceso de cálculo sólo da una solución aproximada; el segundo paso añade (con un poco de suerte) una correccción para obtener una aproximación más precisa de la realidad; el tercer paso nos da una aproximación aún mejor, y así sucesivamente hasta que nos parezca que la aproximación es lo suficientemente buena para el objetivo que nos hayamos propuesto. Pero nunca podremos conseguir con exactitud la “respuesta” que encaja a la perfección con el comportamiento de los objetos del mundo real en lo que se centra nuestro interés en ese determinado y sobre ese objetivo en particular.
Ninguna idea nos ha llegado de manera instantánea y depurada en todos sus conceptos, sino que, han sido ideas que han tenido que ir siendo depuradas más y más a conseguir esa realidad que buscábamos haciendo que, el esquema encontrado, se parezca lo más posible al mundo que nos rodea y que podemos observar. Esa es, en pocas palabras la historia de la Relatividad de Einstein que ajunto muchas ideas y conceptos conseguir sus teorías que están muy cercas de lo que el mundo es.
Lo que hacemos es sumar una serie de números -en principio, una serie de números infinitamente larga- A los matemáticos les interesa estas series infinitas para sus propios objetivos, independientemente de la importancia quer puedan tener para los estudios del comportamiento de las cosas tales como los planetas que orbitan alrededor del Sol, y conocen una gran cantidad de series infinitas cuyas sumas se comportan lo suficientemente bien como para ofrecer una aproximación cada vez mejor de un concreto.
El eterno e irracional número Pi
Un buen ejemplo lo constituye uno de los procedimientos que se utilizan habitualmente para calcular el valor aproximado de π, el cociente la circunferencia de un círculo y su diámetro. Se puede calcular realmente el valor de π/4, con tanta precisión como se desee, sumando la serie numérica:
1 – 1/3 + 1/5 – 1/7 ….
Esto nos da una primera aproximación del valor de π que sería (4 x 1), que no es muy brillante; una segunda aproximación cuyo valor sería 2,6666… (4 x 2/3), que es algo mejor, y que, curiosamente, se encuentra al otro lado de la respuesta «correcta»; una tercera aproximación que sería 3,46666…, y así sucesivamente. Estas aproximaciones van siendo cada vez mejores y convergen en el verdadero valor de π, en este caso concreto ambos lados. Pero el proceso es tedioso -la suma del primer millón de términos de la serie nos da para pi (π) un valor de 3,1415937, que sólo es correcto en sus cinco primeras cinco cifras decimales, No obstante, se puede calcular π de este modo hasta el grado de precisión que se desee (hasta alguna cifra de los decimales), si tienes la paciencia necesaria.

Hacemos una parada aquí para dejar una nota que nos dice que independiente de cualquier otra consdideración, lo cierto es que, en matemáticas y la teoría del caos y entre otros temas. Si hablamos de “Pi” nos topamos con múltiples sorpresas y él está representado en el diseño de la doble espiral de ADN, el Efecto mariposa y la Torah, entre otras muchísimas cosas que se escriben con Pi. Es un número tan misterioso que lo podemos ver por todas partes representado de una u otra manera. Desde la más remota antigüedad, fascinó a los más grandes pensadores.
No pocos están convencisos de la existencia de patrones que se repiten en los distintos órdenes de la vida. Descubrirlos implicaría, nada más y nada , que deducir el mundo. Yo no dejaría de lado, en todo esto la teoría del Caos que podría definirse (¡en forma muy simplona!) como el estudio de sistemas complejos siempre cambiantes. Los resultados que consideramos ´impredecibles´ ocurrirán en sistemas que son sensibles a los cambios pequeños en sus inicios. El ejemplo más común es conocido como “Efecto mariposa”. La teoría supone que el batir de alas de una mariposa en la China en un determinado período de tiempo podría causar cambios atmosféricos imperceptibles en el clima de New York.
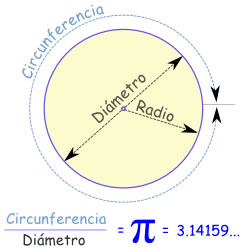
Pi (π) es la decimosexta letra del alfabeto griego y el símbolo que representa el misterio matemático más viejo del mundo: la proporción de la circunferencia de un círculo a su diámetro.
El escrito conocido más temprano de la proporción viene del año 1650 antes de Cristo en Egipto, donde un escriba calculó el valor como 3.16 (con un pequeñísimo error). Aunque ahora, nosotros tenemos métodos para calcular los dígitos de pi (3.1415…) sus restos de valor exacto todavía son un misterio.
Desde 1794, cuando se estableció que Pi era irracional e infinita, las personas han buscando un patrón en el cordón interminable de números.
Cosa curiosa, Pi puede encontrarse por todas partes, en la astronomía, en la física, en la luz, en el sonido, en el suelo, etc. Algunos cálculos advierten que tendría más de 51 mil millones de dígitos, pero hasta el momento no se ha detectado un patrón discernible que surja de sus números. De hecho, la primera sucesión 123456789 aparece muy cerca de los 500 millones de dígitos en la proporción.

En la actualidad hay algunas computadoras superpoderosas tratando de resolver la cuestión. En el film, la computadora bautizada por Max Euclid literalmente “estalla” al acercarse a la verdad del cálculo. ¿Y entonces?… Azar, fe, creencias, ciencia, métodos…y siempre un misterio último sin resolver.
¿El hallazgo de patrones será la respuesta? Tal vez por eso los pitagóricos amaban la /patrón espiral… porque ella está por todas partes en la naturaleza: en los caracoles, en los cuernos del carnero, en las volutas de humo, en la leche sobre el café, en la cara de un girasol, en las huellas digitales, en el ADN y en la Vía Láctea.
3.1415926535897932384626433832795028841971693993…

Sí, son muchas las mentes más claras que se han interesado por este fascinante π. En su libro de 1989 “La nueva mente del emperador”, Roger Penrose comentó sobre las limitaciones en el conocimiento humano con un sorprendente ejemplo: Él conjeturó que nunca más probable es saber si una cadena de 10 7s consecutivo aparece en la expansión digital del número pi . A tan sólo 8 años más tarde, Yasumasa Kanada utiliza una computadora para encontrar exactamente esa cadena, empezando por el dígito de pi …. 17387594880th
Muchos son los números mágicos que, como Phi, al que llaman ¡El Mágico Número del Oro! Están relacionados con las cosas del mundo, del universo y de nosotros mismos. Como decían enm la Escuela pitagórica: ¡Todo es número!
1, 2, 2+1= 3, 3+2= 5, 5+3= 8, 5+8= 13 , etc.


¿Por qué los huracanes, remolinos, galaxias y agujeros negros desarrollan su dinámica en base a la proporción aúrea?

¿Saben que las dimensiones físicas del cuerpo humano cumplen también las relaciones de aspecto dadas por 1,6180…?
¿Cómo es posible que el vuelo de una rapaz al acecho también describa la elipse marcada por esta serie?

¿Por qué la ciudad de La Meca está ubicada en la posición geográfica cuya distancia a los Polos y a los solsticios cumple la relación PHI?
Podemos incluso encontrar esta asombrosa serie en la relación de aspecto de la espiral de adn y en los latidos del corazón.


Sin embargo, al final, algunos creen que, como todo esta relacionado, sabremos reconocer el mensaje que trata de enviarnos π y que, hasta el momento no hemos sabido comprender. Y, por otra , existen otras cuestiones que también estamos tratandode dilucidar para aproximarnos a esa realidad incomprendida que, estándo aquí, no podemos ver. Por ejmplo:
Roger Penrose dedicó bastante más tinta en defender los argumentos de Shadows of Mind que en escribir dicha obra. En una de sus contrarréplicas, publicada en la revista Psyche (Enero, 1996), nos ofrece una de las versiones más claras de su famoso argumento.
Supongamos que todos los métodos de razonamiento matemático humanamente asequibles válidos la demostración de cualquier tesis están contenidos en el conjunto F. Es más, en F no sólo introducimos lo que entenderíamos por lógica matemática (axiomas y reglas de inferencia) sino todo lo matemáticamente posible para tener un modelo matemático del cerebro que utiliza esa lógica (todos los algoritmos necesarios para simular un cerebro). F es, entonces, el modelo soñado por cualquier ingeniero de AI: un modelo del cerebro y su capacidad para realizar todo cálculo lógico imaginable para el hombre. Y, precisamente, ese es el modelo soñado porque la AI Fuerte piensa que eso es un ser humano inteligente. Así, cabe preguntarse: ¿Soy F? Y parece que todos contestaríamos, a priori, que sí.

¿Es la verdad inalcanzable?
Sin embargo, Roger Penrose, piensa que no, y demostrarlo utiliza el celebérrimo teorema de Gödel, que venimos a recordar a muy grosso modo: un sistema axiomático es incompleto si contiene enunciados que el sistema no puede demostrar ni refutar (en lógica se llaman enunciados indecidibles). Según el teorema de incompletitud, todo sistema axiomático consistente y recursivo para la aritmética tiene enunciados indecidibles. Concretamente, si los axiomas del sistema son verdaderos, puede exhibirse un enunciado verdadero y no decidible dentro del sistema.
Si yo soy F, como soy un conjunto de algoritmos (basados en sistemas axiomáticos consistentes y recursivos), contendré algún teorema (proposiciones que se infieren de los axiomas de mi sistema) que es indecidible. Los seres humanos nos damos , somos conscientes de que ese teorema es indecidible. De repente nos encontraríamos con algo dentro de nosotros mismos con lo que no sabríamos qué hacer. Pero en esto hay una contradicción con ser F, porque F, al ser un conjunto de algoritmos, no sería capaz de demostrar la indecibilidad de ninguno de sus teoremas por lo dicho por Gödel… Una máquina nunca podría darse cuenta de que está ante un teorema indecidible. Ergo, si nosotros somos capaces de descubrir teoremas indecidibles es porque, algunas veces, actuamos mediante algo diferente a un algoritmo: no sólo somos lógica matemática.

Claro que, cómo podría un robot imitar nuestros múltiples, locos y dispares pensamientos:
- Los Computadores nunca podrán reemplazar la estupidez humana.
- El hombre nace ignorante, la educación lo idiotiza.
- Una persona inteligente resuelve problemas, el genio los evita.
- Las consideran que guardar un secreto, es no revelar la fuente.
- Todas las mujeres tienen algo bonito… así sea una prima lejana.
- La felicidad es una lata de atún, con el abrelatas un poco distante.
- El único animal que no resiste aplausos es el mosquito.
- El amor está en el cerebro, no en el corazón.
- Definición de nostalgia “es la alegría de estar triste”.
- “Mi segundo órgano favorito es el cerebro”.

En qué se parecen los hombres a una computadora: En que cuando más lo necesitas, se les cae el sistema.
Vale, ¿y qué consecuencias tiene eso? la AI muy graves. Penrose piensa no sólo que no somos computadores sino que ni siquiera podemos tener un computador que pueda simular matemáticamente nuestros procesos mentales. Con esto Penrose no está diciendo que en múltiples ocasiones no utilicemos algoritmos (o no seamos algoritmos) cuando pensemos, sólo dice (lo cual es más que suficiente) que, habrá al menos algunas ocasiones, en las que no utilizamos algoritmos o, dicho de otro modo, hay algún componente en nuestra mente del cual no podemos construir un modelo matemático, qué menos que intentar replicarlo computacionalmente en un ordenador.

Además el asunto se hace más curioso cuanto más te adentras en él. ¿Cuáles podrían ser esos elementos no computables de nuestra mente? La respuesta ha de ser un rotundo no tenemos ni idea, porque no hay alguna de crear un método matemático para saber qué elementos de un sistema serán los indecidibles. Esto lo explicaba muy bien Turing con el famoso problema de la parada: si tenemos un ordenador que está procesando un problema matemático y vemos que no se para, es decir, que tarda un tiempo en resolverlo, no hay manera de saber si llegará un en el que se parará o si seguirá eternamente funcionando (y tendremos que darle al reset que termine). Si programamos una máquina para que vaya sacando decimales a pi, no hay forma de saber si pi tiene una cantidad de decimales tal que nuestra máquina tardará una semana, seis meses o millones de años en sacarlos todos o si los decimales de pi son infinitos.
De misma forma, no podemos saber, por definición, qué elementos de nuestra mente son no computables. A pesar de ello, Penrose insiste en que lo no computable en nuestra mente es, nada más y nada menos, que la conciencia, ya que, explica él, mediante ella percibimos la indecibilidad de los teoremas. Es posible, ya que, aunque a priori no pudiéramos saber qué elementos no son decidibles, podríamos encontrarnos casualmente con alguno de ellos y podría ser que fuera la conciencia. Pero, ¿cómo es posible que nuestro cerebro genere conciencia siendo el cerebro algo aparentemente sujeto a computación? Penrose tiene que irse al mundo cuántico, en el que casi todo lo extraño sucede, para encontrar fenómenos no modelizables por las matemáticas y, de paso, resolver el problema del origen físico de la conciencia.
Las neuronas no nos valen. Son demasiado grandes y pueden ser modelizadas por la mecánica clásica. Hace falta algo más pequeño, algo que, por su naturaleza, exprese la incomputabilidad de la conciencia. Penrose se fija en el citoesqueleto de las neuronas formado por unas estructuras llamadas microtúbulos. micronivel está empapado de fenómenos cuánticos no computables, siendo el funcionamiento a nivel neuronal, si acaso, una sombra amplificadora suya, un reflejo de la auténtica actividad generadora de conciencia. ¡Qué emocionante! Pero, ¿cómo generan estos microtúbulos empapados de efectos cuánticos la conciencia? Penrose dice que no lo sabe, que ya bastante ha dicho…
O sea señor Penrose, que después de todo el camino hecho, al final, estamos cómo al principio: no tenemos ni idea de qué es lo que genera la conciencia. Sólo hemos cambiado el problema de lugar. Si antes nos preguntábamos cómo cien mil millones de neuronas generaban conciencia, nos preguntamos cómo los efectos cuánticos no computables generan conciencia. Penrose dice que habrá que esperar a que la mecánica cuántica se desarrolle más. Crick o Searle nos dicen que habrá que esperar a ver lo que nos dice la neurología… ¡Pero yo no puedo esperar!
Además, ¿no parece extraño que la conciencia tenga algo que ver con el citoesqueleto de las neuronas? La función del citoesqueleto celular suele ser sustentar la célula, hacerla estable en su locomoción… ¿qué tendrá que ver eso con ser consciente? Claro que en el actual de la ciencia igual podría decirse: ¿qué tendrá que ver la actividad eléctrica de cien mil millones de neuronas con que yo sienta que me duele una muela?
Todo eso está bien pero, ¿Qué es PI?

“Corta 1/9 del diámetro y construye un cuadrado sobre la longitud restante. cuadrado tiene el mismo área que el circulo”.

Ago
16
Siempre haremos preguntas
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en El saber del mundo ~
Clasificado en El saber del mundo ~
 Comments (0)
Comments (0)
El libre Albedrío? ¿Dónde está?


Aunque es cierto que “sobre gustos no hay nada escrito”, los humanos nos sentimos más a gusto con las caras más simétricas. En la cultura popular, y salvo alguna rara excepción, las caras asimétricas están relacionadas con la maldad. Los biólogos encontraron rápidamente una explicación evolutiva: los individuos más evolucionados pueden mantener sus formas simétricas inclusive cuando están expuestos al estrés y las enfermedades. Es decir, cuando las partes del cuerpo que tienden a la simetría no lo son, costará más pasar esos genes porque será rechazado por potenciales parejas. De esta manera la evolución distingue a la simetría como una característica valiosa.

David (1501-1504), de Miguel Ángel, Galería de la Academia de Florencia.
El desnudo de una figura presenta una simetría bilateral casi perfecta. Ciertamente, parte del atractivo del mismo, tanto en la realidad como en el arte, reside en la identificación de los lados derecho e izquierdo del cuerpo mediante mediante una simetría especular. La figura femenina raramente presenta asimetrías. La asimetría de un varón se rompe solamente por la curiosa circunstancia de que su testículo izquierdo cuelga más bajo que el derecho.

(1532), de Lucas Cranach el Viejo, Städelsches Kunstinstitut, Fráncfort del Meno, censurada por el Metro de Londres en 2008.
Evidentemente, cada cuerpo, considerado de forma individual, puede otras desviaciones menores de su simetría: un hombro más alto que otro, un pecho mayor que su pareja, una ligera desviación de la columna, una peca o un antojo en un costado…, pero tales anomalías, en su mayor parte, pueden encontrarse tanto a un lado como al otro.

La simetría bilateral se mantiene en el interior del cuerpo, en en los músculos y en el esqueleto, pero queda rota por la disposición fuertemente asimétrica de algunos órganos. El corazón, el estómago y el páncreas están desviados hacia la izquierda; el hígado y el apéndice, hacia la derecha. El pulmón derecho es mayor que el izquierdo. Los retorcimientos y vueltas de los intestinos son completamente asimétricos. El cordón umbilical humano, una magnifica hélice triple formada por dos arterias y una vena, puede enrollarse en cualquiera de los dos sentidos.


Los mellizos que se desarrollan por la fecundación simultánea de dos óvulos separados, pueden tener detalles asimétricos en un sentido en uno de ellos, y en el contrario en el otro, pero esto no ocurre con mayor frecuencia que la que cabría esperar como fruto del azar. Es una creencia generalizada que los gemelos (formados a partir de un único óvulo, que se divide inmediatamente después de la fecundación) tiene una marcada tendencia a aparentar especulares recíprocas. Por desgracia, las estadísticas al respecto son confusas y muchos expertos creen que los gemelos idénticos no se presentan como imágenes especulares uno de otro en mayor medida que cualquier otro tipo de hermanos.

En el caso de gemelos siameses (gemelos idénticos, unidos uno a otro a causa de un a partición tardía e incompleta del óvulo), el tema no ofrece duda alguna. Son exactamente enantiomorfos en casi todos los detalles: si uno es diestro, el otro es zurdo; si uno tiene el remolino del pelo que va en el sentido de las agujas del reloj, el de su hermano/hermana irá en el sentido contrario. Diferencias en los oídos, los dientes…, aparecen en ambos como especulares unas respecto de otras (hasta en eso es perfecta la Naturaleza). Las huellas dactilares o de la palma de la mano derecha de uno serán muy parecidas a las correspondientes a la mano izquierda del otro.
Todavía más: un gemelo siamés tendrá “vísceras transpuestas”; sus órganos internos estarán colocados de manera inversa, el corazón a la derecha, el hígado a la izquierda. Esta transposición de órganos, o inverse situs, como se denomina a veces, se da siempre en cualquier par de gemelos siameses, pero puede aparecer también en no incluidas en estas circunstancias.

Merece la pena hacer notar que Lewis Carroll, en A través del espejo (Alianza Editorial, 1990), pretende tomar los gemelos idénticos Tararí y Tarará como imágenes especulares uno de otro. Cuando los hermanos Tara ofrecen enlazar sus manos con Alicia, uno de ellos alarga su derecha; el otro la izquierda. Si observamos detenidamente las ilustraciones de Tenniel, especialmente la que muestra los dos gemelos uno frente a otro, para la batalla, veremos que los ha dibujado como si fueran enantiomorfos.

Claro que, algunos son completos
En el comportamiento y los hábitos de los seres humanos hay muchos ejemplos de marcada asimetría; los más evidentes son consecuencia de que la mayoría de las personas son diestras. La mano derecha está controlada por la parte izquierda del cerebro, y la parte derecha de éste controla la mano izquierda, por lo que la condición de diestro es, en realidad, un fenómeno de lateralidad izquierda del cerebro. Hubo un tiempo en el que se creía que los bebés nacían sin tendencia alguna de tipo genético que favoreciera el uso de una mano concreta, que la lateralidad de un niño era exclusivamente el resultado de las enseñanzas de sus padres. Platón era un notable defensor de esta opinión.
“En el uso de las manos estamos, y estábamos, viciados por las manías de nuestras intitutrices y madres -escribe Platón en sus Leyes-, pues aunque nuestros miembros están compensados por naturaleza, creamos una diferencia entre ellos como consecuencia de un mal hábito.”
Sabemos hoy en día que Platón estaba equivocado. Como hace notar Aristóteles con buen criterio. De todas las maneras, la tendencia innata para muchas personas de usar preferentemente la mano derecha es común desde que la puede constatarlo de manera evidente.

Losantropólogs culturales no han encontrado todavía ni una sola sociedad, o incluso una tribu , en la que la norma sea la lateralidad izquierda: los esquimos, los indios americanos, los maoríes y los africanos son todos diestros. Los antiguos egipcios, griegos y romanos eran diestros. Naturalmente, si retrocemos todavía más en la Historia, la evidencia de la lateralidad diestra es ya escasa e indirecta y hay que dilucidarla a partir del estudio de la forma de sus utensilios y armas, así como de las pinturas que muestran los hombres trabajando o en la batalla.
Las propias palabras que se usan en muchas lenguas para designar la izquierda y la derecha dan testimonio de un sesgo universal hacia el lado derecho. En , ir a derechas es hacer las cosas correctamente, mientras que no dar una a derechas, es sinónimo de hacerlo todo mal.
Ser diestro en algo es lo mismo que poseer una habilidad especial para ello, mientras que una cosa siniestra (del latín sinester, izquierda) es una cosa hecha con mala intención. En otras lenguas el significado viene a ser más o menos el mismo. Los italianos, tan suyos ellos, llaman a la mano izquierda stanca, fatigada, o manca, la que no se tiene. Lo cierto es que, por lo , los zurdos son ambidiestros.
Para tener una buena visión histórica de mlos prejuicios virulentos contra los zurdos en cualquier parte del mundo, veáse el séptimo capítulo de The Dragons of Eden, de Carl Sagan (Random House, 1977), y el delicioso de Jack Fincher, Sinister People (Putnam, 1977). Este último da una lista de más de cien personajes famosos que fueron zurdos.

Por lo que hemos observado , y hasta donde sabemos, la especie humana tiene la tendencia a utilizar la mano derecha. Claro que no sabemos. La mayoría de los mamíferos subhumanos son ambidiestros y, ¿cómo serán las especies que viven en otros mundos? El personaje de arriba, al menos, parece que es zurdo.
Lo cierto es que, poco importa si somos zurdos o no, la igualdad en lo esencial es casi idéntica. La verdadera diferencia está en el cerebro, en la manera de ver las cosas, en cómo cada cual enfoca los problemas y qué soluciones aplica a cada situación, en que perspectiva podamos tener de nuestra Sociedad, de nuestras leyes, de nuestros derechos, de la moral y la ética… Todo lo demás, son circunstancias anecdóticas que poco influyen en el devenir del mundo.
emilio silvera
















 Totales: 75.002.108
Totales: 75.002.108 Conectados: 84
Conectados: 84