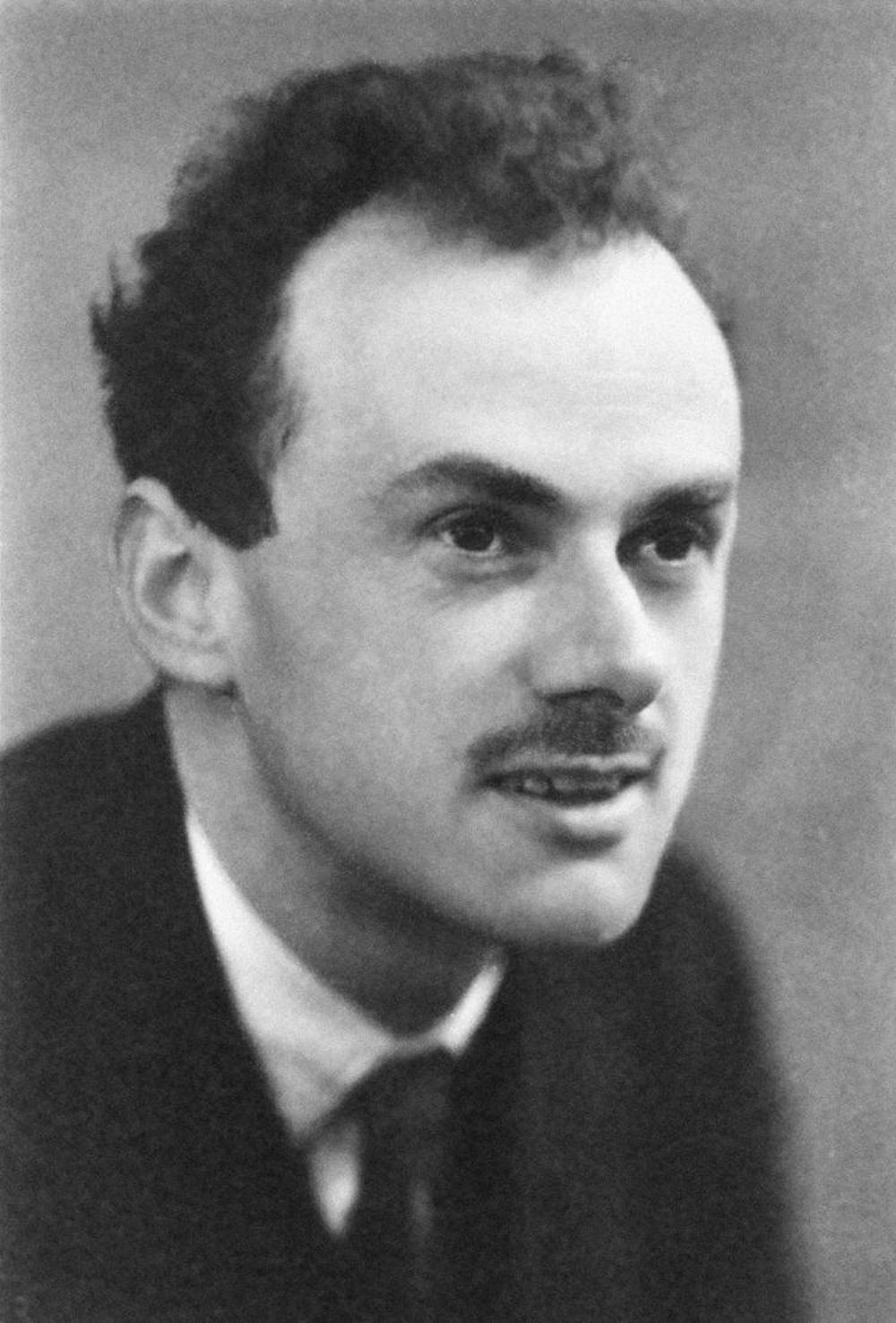Dic
19
Teorías, masas, partículas, dimensiones…
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (0)
Comments (0)

Una nos habla del Cosmos y de como el espacio se curva ante la presencia de masas, la otra, nos habla de funciones de ondas, entrelazamientos cuánticos, de diminutos objetos que conforman la materia y hacen posibles los átomos y la vida.



Entre los teóricos, el casamiento de la relatividad general y la teoría cuántica es el problema central de la física moderna. A los esfuerzos teóricos que se realizan con ese propósito se les llama “super-gravedad“, “súper-simetría“, “super-cuerdas” “teoría M” o, en último caso, “teoría de todo o gran teoría unificada“.
Ahí tenemos unas matemáticas exóticas que ponen de punta hasta los pelos de las cejas de algunos de los mejores matemáticos del mundo (¿y Perelman? ¿Por qué nos se ha implicado?). Hablan de 10, 11 y 26 dimensiones, siempre, todas ellas espaciales menos una que es la temporal. Vivimos en cuatro: tres de espacio (este-oeste, norte-sur y arriba-abajo) y una temporal. No podemos, ni sabemos o no es posible instruir, en nuestro cerebro (también tridimensional), ver más dimensiones. Pero llegaron Kaluza y Klein y compactaron, en la longitud de Planck las dimensiones que no podíamos ver.
¡Problema solucionado!
Unidades de Planck

La longitud de Planck (ℓP) u hodón (término acuñado en 1926 por Robert Lévi) es la distancia o escala de longitud por debajo de la cual se espera que el espacio deje de tener una geometría clásica. Una medida inferior previsiblemente no puede ser tratada adecuadamente en los modelos de física actuales debido a la aparición de efectos de Gravedad Cuántica.
¿Quién puede ir a la longitud de Planck para verla? A distancias comparables con la longitud de Planck, se cree que están sucediendo cosas muy curiosas que rebasan ampliamente los límites de nuestra imaginación. A diferencia de la filosofía reduccionista que propone que lo más complejo está elaborado -axiomáticamente- a partir de lo más elemental, lo que está sucediendo en la escala de Planck no parece tener nada de elemental o sencillo. Se cree que a esta escala la continuidad del espacio-tiempo en vez de ir marchando sincronizadamente al parejo con lo que vemos en el macrocosmos de hecho stá variando a grado tal que a nivel ultra-microscópico el tiempo no sólo avanza o se detiene aleatoriamente sino inclusive marcha hacia atrás, una especie de verdadera máquina del tiempo. Las limitaciones de nuestros conocimientos sobre las rarezas que puedan estar ocurriendo en esta escala en el orden de los 10-35 metros, la longitud de Planck, ha llevado a la proposición de modelos tan imaginativos y tan exóticos como la teoría de la espuma cuántica que supuestamente veríamos aún en la ausencia de materia-energía si fuésemos ampliando sucesivamente una porción del espacio-tiempo plano.
No pocos han tratado de encontrar la puerta para acceder a esas dimensiones extras que pregonan algunas teorías. Sin embargo, hasta el momento, nadie ha dado con el camino para poder llegar a ellas y traspasarlas para ver, lo que pueda existir más allá de las dimensiones que rigen en nuestro propio mundo.
La puerta de las dimensiones más altas quedó abierta y, a los teóricos, se les regaló una herramienta maravillosa. En el Hiperespacio, todo es posible. Hasta el matrimonio de la relatividad general y la mecánica cuántica, allí si es posible encontrar esa soñada teoría de la Gravedad cuántica.
Así que, los teóricos, se han embarcado a la búsqueda de un objetivo audaz: buscan una teoría que describa la simplicidad primigenia que reinaba en el intenso calor del universo en sus primeros tiempos, una teoría carente de parámetros, donde estén presentes todas las respuestas. Todo debe ser contestado a partir de una ecuación básica.
¿Dónde radica el problema?
El problema está en que la única teoría candidata no tiene conexión directa con el mundo de la observación, o no lo tiene todavía si queremos expresarnos con propiedad. La energía necesaria para ello, no la tiene ni el LHC que ha trabajado a 14 TeV, y, necesitaria disponer de la energía de Planck, es decir 1019 GeV, y dicha energía, queda lejos, muy lejos de nuestro alcance en el presente y, si alguna vez podemos disponer de ella esrtaría situada muy lejos en el futuro.
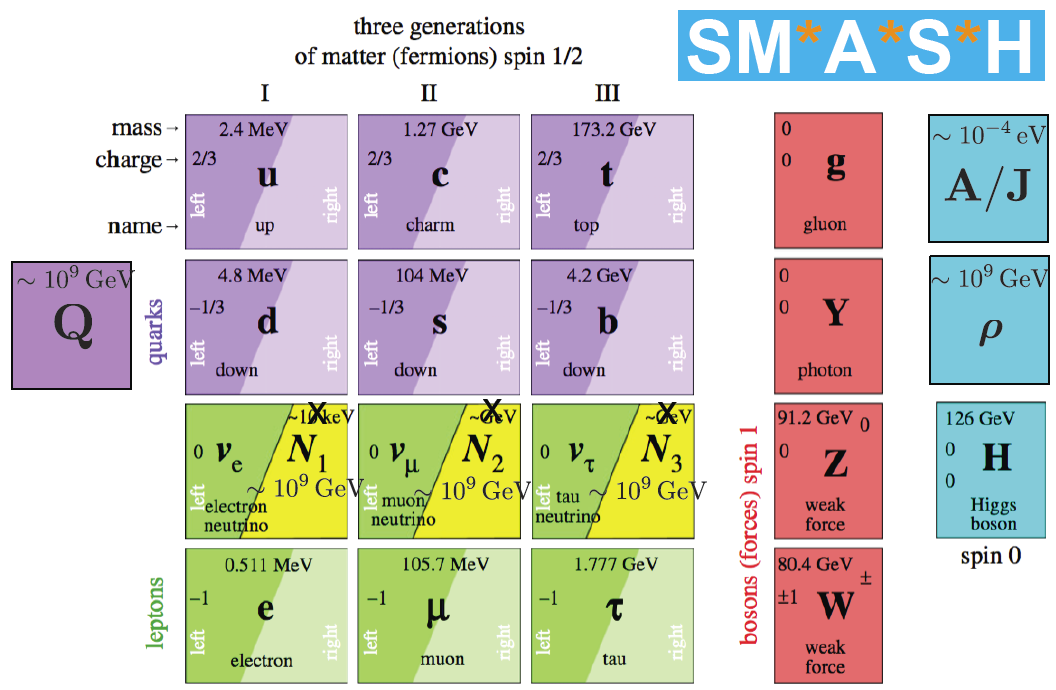
La verdad es que, la teoría que ahora tenemos, el Modelo Estándar, concuerda de manera exacta con todos los datos a bajas energías y contesta cosas sin sentido a altas energías.
¡Necesitamos algo más avanzado!
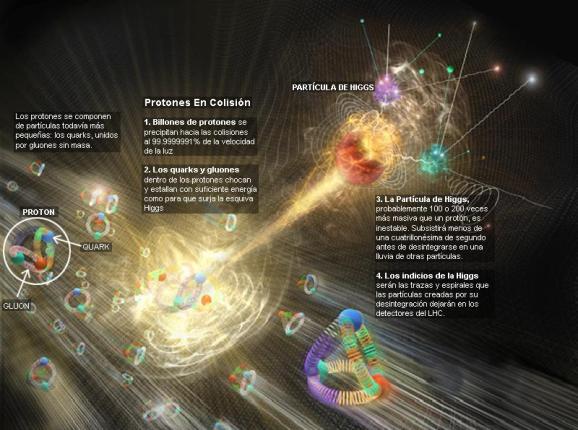
Cada partícula tiene encomendada una misión, la de Higgs, ya sabemos lo que dicen por ahí.es la dadora de masa a las demás partículas (cosa que -particularmente- no tengo nada claro).
Se ha dicho que la función de la partícula de Higgs es la de dar masa a las Cuando su autor lanzó la idea al mundo, resultó además de nueva muy extraña. El secreto de todo radica en conseguir la simplicidad: el átomo resulto ser complejo lleno de esas infinitesimales partículas electromagnéticas que bautizamos con el nombre de electrones, resultó que tenía un núcleo que contenía, a pesar de ser tan pequeño, casi toda la masa del átomo. El núcleo, tan pequeño, estaba compuesto de otros objetos más pequeños aún, los quarks que estaban instalados en nubes de otras partículas llamadas gluones y, ahora, queremos continuar profundizando, sospechamos, que después de los quarks puede haber algo más.
Bueno, la idea nueva que surgió es que el espacio entero contiene un campo, el campo de Higgs, que impregna el vacío y es el mismo en todas partes. Es decir, que si miramos a las estrellas en una noche clara estamos mirando el campo de Higgs. Las partículas influidas por este campo, toman masa. Esto no es por sí mismo destacable, pues las partículas pueden tomar energía de los campos (gauge) de los que hemos comentado, del campo gravitatorio o del electromagnético. Si llevamos un bloque de plomo a lo alto de la Torre Eiffel, el bloque adquiriría energía potencial a causa de la alteración de su posición en el campo gravitatorio de la Tierra.
Masa y energía son dos aspectos de la misma cosa
Cuando los físicos hablan de la belleza de algunas ecuaciones, se refieren a las que, como ésta, dicen mucho con muy pocos caracteres. De hecho, puede que ésta sea la ecuación más famosa conocida en nuestro mundo.
Como E=mc2, ese aumento de la energía potencial equivale a un aumento de la masa, en este caso la masa del Sistema Tierra-bloque de plomo. Aquí hemos de añadirle amablemente un poco de complejidad a la venerable ecuación de Einstein. La masa, m, tiene en realidad dos partes. Una es la masa en reposo, m0, la que se mide en el laboratorio cuando la partícula está en reposo. La partícula adquiere la otra parte de la masa en virtud de su movimiento (como los protones en el acelerador de partículas, o los muones, que aumentan varias veces su masa cuando son lanzados a velocidades cercanas a c) o en virtud de su energía potencial de campo. Vemos una dinámica similar en los núcleos atómicos. Por ejemplo, si separamos el protón y el neutrón que componen un núcleo de deuterio, la suma de las masas aumenta.
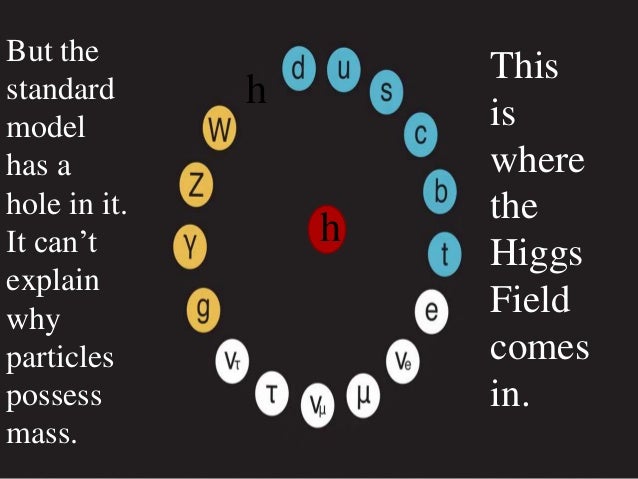
Pero la energía potencial tomada del campo de Higgs difiere en varios aspectos de la acción de los campos familiares. La masa tomada de Higgs es en realidad masa en reposo. De hecho, en la que quizá sea la versión más apasionante de la teoría del campo de Higgs, éste genera toda la masa en reposo. Otra diferencia es que la cantidad de masa que se traga del campo es distinta para las distintas partículas.
Los teóricos dicen que las masas de las partículas de nuestro modelo estándar miden con qué intensidad se acoplan éstas al campo de Higgs.
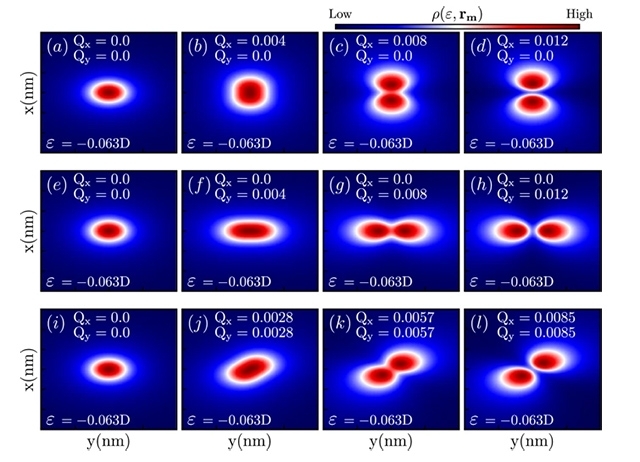
La influencia de Higgs en las masas de los quarks y de los leptones, nos recuerda el descubrimiento por Pieter Zeeman, en 1.896, de la división de los niveles de energía de un electrón cuando se aplica un campo magnético al átomo. El campo (que representa metafóricamente el papel de Higgs) rompe la simetría del espacio de la que el electrón disfrutaba.
Hasta hace bien poco no teniamos ni idea de que reglas controlan los incrementos de masa generados por el Higgs (de ahí la expectación creada por el nuevo acelerador de partículas LHC cuando la buscaba). Pero el problema es irritante: ¿por qué sólo esas masas -Las masas de los W+, W–, y Zº, y el up, el down, el encanto, el extraño, el top y el bottom, así como los leptones – que no forman ningún patrón obvio?

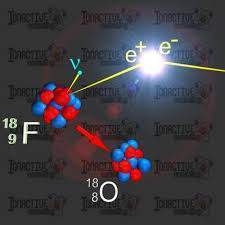
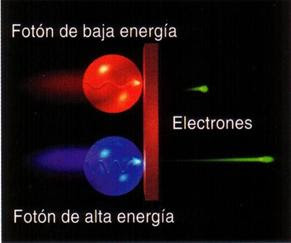
Positrón. Electrón con carga positiva. La interacción con el electrón puede resultar en la aniquilación de ambos, con lo que se produce un par de fotones cuya energía equivale a la masa del par electrón-positrón. Esta propiedad define al positrón como la antipartícula asociada al electrón.
Las masas van de la del electrón 0’0005 GeV, a la del top, que tiene que ser mayor que 91 GeV. Deberíamos recordar que esta extraña idea (el Higgs) se empleó con mucho éxito para formular la teoría electrodébil (Weinberg-salam). Allí se propuso el campo de Higgs como una forma de ocultar la unidad de las fuerzas electromagnéticas y débiles. En la unidad hay cuatro partículas mensajeras sin masa -los W+, W–, Zº y fotón que llevan la fuerza electrodébil. Además está el campo de Higgs, y, rápidamente, los W y Z chupan la esencia de Higgs y se hacen pesados; el fotón permanece intacto. La fuerza electrodébil se fragmenta en la débil (débil porque los mensajeros son muy gordos) y la electromagnética, cuyas propiedades determina el fotón, carente de masa. La simetría se rompe espontáneamente, dicen los teóricos. Prefiero la descripción según la cual el Higgs oculta la simetría con su poder dador de masa.
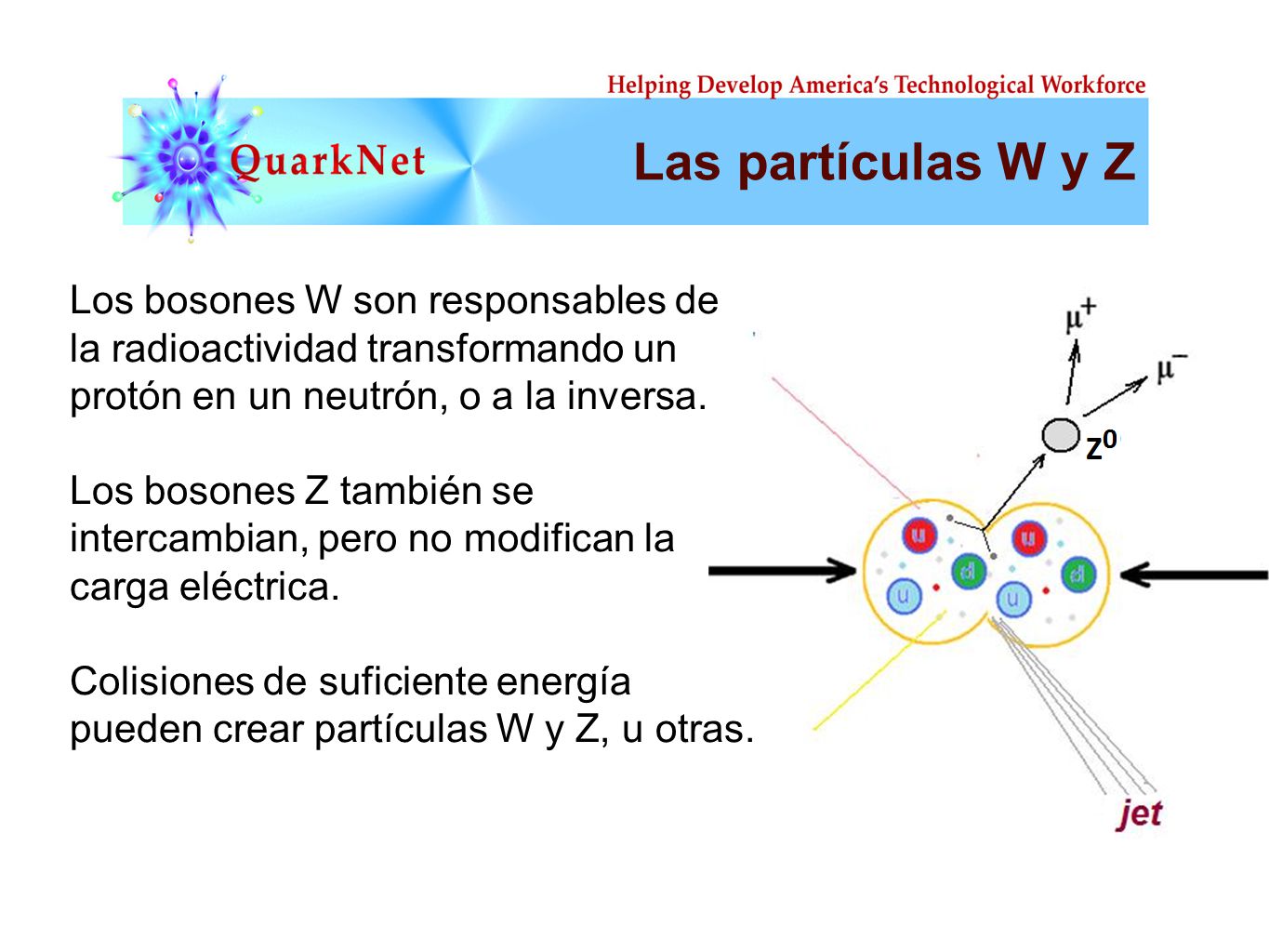
Las masas de los W y el Z se predijeron con éxito a partir de los parámetros de la teoría electrodébil. Y las relajadas sonrisas de los físicos teóricos nos recuerdan que Gerard ^t Hooft y Veltman dejaron sentado que la teoría entera esta libre de infinitos.
Pero, encierra tantos misterios la materia que, a veces me hace pensar en que la podríamos denominar de cualuquier manera menos de inerte ¡Parece que la materia está viva!
Son muchas las cosas que desconocemos y, nuestra curiosidad nos empuja continuamente a buscar esas respuestas.


La Teoría de las masas de las partículas
El electrón y el positrón son notables por sus pequeñas masas (sólo 1/1.836 de la del protón, el neutrón, el antiprotón o antineutrón), y, por lo tanto, han sido denominados leptones (de la voz griega lentos, que significa “delgado”).
Aunque el electrón fue descubierto en 1.897 por el físico británico Josepth John Thomson (1856-1940), el problema de su estructura, si la hay, no está resuelto. Conocemos su masa y su carga negativa que responden a 9,1093897 (54) x 10-31 Kg la primera y, 1,602 177 33 (49) x 10-19 culombios, la segunda, y también su radio clásico: r0 = e2/mc2 = 2’82 x 10-13 m. No se ha descubierto aún ninguna partícula que sea menos cursiva que el electrón (o positrón) y que lleve una carga eléctrica, sea lo que fuese (sabemos como actúa y cómo medir sus propiedades, pero aun no sabemos qué es), tenga asociada un mínimo de masa, y que esta es la que se muestra en el electrón.
Lo cierto es que, el electrón, es una maravilla en sí mismo. El Universo no sería como lo conocemos si el electrón (esa cosita “insignificante”), fuese distinto a como es, bastaría un cambio infinitesimal para que, por ejemplo, nosotros no pudiéramos estar aquí ahora.

¡No por pequeño, se es insignificante! Para sus padres lo más grande del mundo
Recordémoslo, todo lo grande está hecho de cosas pequeñas.
En realidad, existen partículas que no tienen en absoluto asociada en ellas ninguna masa (es decir, ninguna masa en reposo). Por ejemplo, las ondas de luz y otras formas de radiación electromagnéticas se comportan como partículas (Einstein en su efecto fotoeléctrico y De Broglie en la difracción de electrones*.
Esta manifestación en forma de partículas de lo que, de ordinario, concebimos como una onda se denomina fotón, de la palabra griega que significa “luz”.

El fotón tiene una masa de 1, una carga eléctrica de o, pero posee un espín de 1, por lo que es un bosón. ¿Cómo se puede definir lo que es el espín? Los fotones toman parte en las reacciones nucleares, pero el espín total de las partículas implicadas antes y después de la reacción deben permanecer inmutadas (conservación del espín). La única forma que esto suceda en las reacciones nucleares que implican a los fotones radica en suponer que el fotón tiene un espín de 1. El fotón no se considera un leptón, puesto que este termino se reserva para la familia formada por el electrón, el muón y la partícula Tau con sus correspondientes neutrinos: Ve, Vu y VT.
Existen razones teóricas para suponer que, cuando las masas se aceleran (como cuando se mueven en órbitas elípticas en torno a otra masa o llevan a cabo un colapso gravitacional), emiten energía en forma de ondas gravitacionales. Esas ondas pueden así mismo poseer aspecto de partícula, por lo que toda partícula gravitacional recibe el nombre de gravitón.

Aunque sea la más débil de las cuatro fuerzas elementales… ¡Es inmensamente importante para nuestro Universo!
La fuerza gravitatoria es mucho, mucho más débil que la fuerza electromagnética. Un protón y un electrón se atraen gravitacionalmente con sólo 1/1039 de la fuerza en que se atraen electromagnéticamente. El gravitón (aún sin descubrir) debe poseer, correspondientemente, menos energía que el fotón y, por tanto, ha de ser inimaginablemente difícil de detectar.
De todos modos, el físico norteamericano Joseph Weber emprendió en 1.957 la formidable tarea de detectar el gravitón. Llegó a emplear un par de cilindros de aluminio de 153 cm. De longitud y 66 de anchura, suspendidos de un cable en una cámara de vacío. Los gravitones (que serían detectados en forma de ondas), desplazarían levemente esos cilindros, y se empleó un sistema para detectar el desplazamiento que llegare a captar la cienmillonésima parte de un centímetro.

Han llevado años captarlas, las ondas gravitatorias llevadas por el gravitón son débiles
Las débiles ondas de los gravitones, que producen del espacio profundo, deberían chocar contra todo el planeta, y los cilindros separados por grandes distancias se verán afectados de forma simultánea. En 1.969, Weber anunció haber detectado los efectos de las ondas gravitatorias. Aquello produjo una enorme excitación, puesto que apoyaba una teoría particularmente importante (la teoría de Einstein de la relatividad general). Desgraciadamente, nunca se pudo comprobar mediante las pruebas realizadas por otros equipos de científicos que duplicaran el hallazgo de Weber.
De todas formas, no creo que, a estas alturas, nadie pueda dudar de la existencia de los gravitones, el bosón mediador de la fuerza gravitatoria. La masa del gravitón es o, su carga es o, y su espín de 2. Como el fotón, no tiene antipartícula, ellos mismos hacen las dos versiones.

Tenemos que volver a los que posiblemente son los objetos más misteriosos de nuestro Universo: Los agujeros negros. Si estos objetos son lo que se dice (no parece que se pueda objetar nada en contrario), seguramente serán ellos los que, finalmente, nos faciliten las respuestas sobre las ondas gravitacionales y el esquivo gravitón.
La onda gravitacional emitida por el agujero negro produce una ondulación en la curvatura del espacio-temporal que viaja a la velocidad de la luz transportada por los gravitones.
Hay aspectos de la física que me dejan totalmente sin habla, me obligan a pensar y me transporta de este mundo material nuestro a otro fascinante donde residen las maravillas del Universo. Hay magnitudes asociadas con las leyes de la gravedad cuántica. La longitud de Planck-Wheeler, ![]() es la escala de longitud por debajo de la cual el espacio tal como lo conocemos deja de existir y se convierte en espuma cuántica. El tiempo de Planck-Wheeler (1/c veces la longitud de Planck-Wheeler o aproximadamente 10-43 segundos), es el intervalo de tiempo más corto que puede existir; si dos sucesos están separados por menos que esto, no se puede decir cuál sucede antes y cuál después. El área de Planck-Wheeler (el cuadrado de la longitud de Planck-Wheeler, es decir, 2,61×10-66cm2) juega un papel clave en la entropía de un agujero negro.
es la escala de longitud por debajo de la cual el espacio tal como lo conocemos deja de existir y se convierte en espuma cuántica. El tiempo de Planck-Wheeler (1/c veces la longitud de Planck-Wheeler o aproximadamente 10-43 segundos), es el intervalo de tiempo más corto que puede existir; si dos sucesos están separados por menos que esto, no se puede decir cuál sucede antes y cuál después. El área de Planck-Wheeler (el cuadrado de la longitud de Planck-Wheeler, es decir, 2,61×10-66cm2) juega un papel clave en la entropía de un agujero negro.
Me llama poderosamente la atención lo que conocemos como las fluctuaciones de vacío, esas oscilaciones aleatorias, impredecibles e in-eliminables de un campo (electromagnético o gravitatorio), que son debidas a un tira y afloja en el que pequeñas regiones del espacio toman prestada momentáneamente energía de regiones adyacentes y luego la devuelven.

El vacío no existe… ¡Siempre hay!
Ordinariamente, definimos el vacío como el espacio en el que hay una baja presión de un gas, es decir, relativamente pocos átomos o moléculas. En ese sentido, un vacío perfecto no contendría ningún átomo o molécula, pero no se puede obtener, ya que todos los materiales que rodean ese espacio tienen una presión de vapor finita. En un bajo vacío, la presión se reduce hasta 10-2 pascales, mientras que un alto vacío tiene una presión de 10-2-10-7 pascales. Por debajo de 10-7 pascales se conoce como un vacío ultraalto.
No puedo dejar de referirme al vaciotheta (vació θ) que, es el estado de vacío de un campo gauge no abeliano (en ausencia de campos fermiónicos y campos de Higgs).

El vacío theta es el punto de partida para comprender el estado de vacío de las teoría gauge fuertemente interaccionantes, como la cromodinámica cuántica. En el vacío theta hay un número infinito de estados degenerados con efecto túnel entre estos estados. Esto significa que el vacío theta es análogo a una fundón de Bloch* en un cristal.
Se puede derivar tanto como un resultado general o bien usando técnicas de instantón. Cuando hay un fermión sin masa, el efecto túnel entre estados queda completamente suprimido.
Cuando hay campos fermiónicos con masa pequeña, el efecto túnel es mucho menor que para campos gauge puros, pero no está completamente suprimido.
Nos podríamos preguntar miles de cosas que no sabríamos contestar. Nos maravillan y asombran fenómenos naturales que ocurren ante nuestros ojos pero que tampoco sabemos, en realidad, a que son debidos. Si, sabemos ponerles etiquetas como, por ejemplo, la fuerza nuclear débil, la fisión espontánea que tiene lugar en algunos elementos como el protactinio o el torio y, con mayor frecuencia, en los elementos que conocemos como transuránicos.

“Los elementos transuránicos o elementos transuránicos son elementos químicos con número atómico mayor que 92, el número atómico del elemento Uranio. El nombre de trans-uránidos significa «más allá del uranio».”
93. Neptunio
94. Plutonio
95. Americio
96. Curio
97. Berkelio
98. Californio
99. Einstenio
100. Fermio
101. Mendelevio
102. Nobelio
103. Lawrencio
104. Rutherfordio
105. hahnium
06. Seaborgio
107. Bohrio
108. hassio
109. meitnerio
110. darmstadtio
111. roentgenio
112 copernicio
113 nihonio
114 flerovio
115 moscovio
116 livermorio
117 teneso
118 oganesón
La mayoría de los elementos generados de forma artificial se pueden obtener como elemento sintético vía reacciones nucleares o acelerador de partículas. La vida media de estos elementos suele decrecer con el número atómico. Existen, no obstante excepciones, que incluyen el dubnio y algunos isótopos del curio. El químico Glenn T. Seaborg (Premio Nobel de Química) llegó a crear leyes empíricas capaces de predecir estas anomalías. Todas ellas se categorizan en lo que viene a denominarse como “isla de estabilidad”. Los elementos transuránicos no descubiertos todavía, o que no han sido denominados de forma oficial, emplearán la nomenclatura indicada por la ITUPAC. A pesar de ello la denominación de algunos elementos transuránicos en el pasado y hoy en día son fuentes de controversia.
A medida que los núcleos se hacen más grandes, la probabilidad de una fisión espontánea aumenta. En los elementos más pesados de todos (einstenio, fermio y mendelevio), esto se convierte en el método más importante de ruptura, sobre pasando a la emisión de partículas alfa.
Emilio Silvera Vázquez
Dic
19
El fascinante “universo” cuántico
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (1)
Comments (1)


Las leyes que gobiernan el mundo físico tienen dos características importantes: muchas leyes de la naturaleza permanecen inalterables, no se alteran cuando cambia la escala, pero hay otros fenómenos, tales como una vela encendida o las gotas de agua, que no cambian del mismo modo. La implicación final es que el mundo de los objetos muy pequeños será completamente diferente del mundo ordinario.
El producto de la incertidumbre en la posición de una partícula y la incertidumbre en su momento nunca puede ser inferior a la mitad de la constante de Planck reducida: Δ x Δ p ≥ ℏ / 2 . Δ x Δ p ≥ ℏ / 2 . Esta relación expresa el principio de incertidumbre de Heisenberg.
En 1928 Dirac se propuso encontrar la ecuación del electrón libre relativista, porque la ecuación de Schrödinger no cumplía con los requisitos de la teoría de Einstein¹, es decir, no trataba por igual espacio y tiempo, y no incorporaba la energía en reposo (el famoso E=mc²). Además de eso no explicaba el espín, una propiedad fundamental de las partículas sin equivalencia clásica, pero que separa la naturaleza en dos familias totalmente distintas: bosones (como el fotón, de espín entero) y fermiones (como el electrón, de espín semientero). Para los que no sois físicos el espín os resultará una tontería pero debéis saber que es tan importante que las fuerzas de la naturaleza se transmiten sólo por bosones, mientras que las partículas más elementales están formadas sólo por fermiones.
La Ecuación
siendo m la masa en reposo del electrón, c la velocidad de la luz p el operador de momento, ℏ la constante reducida de Planck, x y t las coordenadas del Espacio y el Tiempo, respectivamente; y ψ (x, t) una función de onda de cuatro componentes. La función de onda ha de ser formulada como un espinor (objeto matemático similar a un vector que cambia de signo con una rotación de 2π descubierto por Pauli y Dirac) de cuatro componentes, y no como un simple escalar, debido a los requerimientos de la relatividad especial. Los α son operadores lineales que gobiernan la función de onda, escritos como una matriz y son matrices de 4×4 conocidas como matrices de Dirac. Hay más de una forma de escoger un conjunto de matrices de Dirac; un criterio práctico es:
La ecuación de Dirac es una ecuación de ondas relativista de la mecánica cuántica formulada por Paul Dirac en 1928. Da una descripción de las partículas elementales con masa de espín 1/2 como el electrón, y es consistente con los principios de la mecánica cuántica y de la teoría de la relatividad especial, explicando de forma natural la existencia del espín y de las antipartículas. Sin embargo, es sólo una aproximación a la electro dinámica cuántica que describe la interacción de partículas cargadas mediante interacciones eléctricas.
La ecuación de Schrödinger independiente del tiempo predice que las funciones de onda pueden tener la forma de ondas estacionarias, denominados estados estacionarios (también llamados “orbitales”, como en los orbitales atómicos o los orbitales moleculares).
La función de onda de Schrödinger es un constructo matemático, que no representa una realidad física, asociada a una partícula libre, de energía y momento , que se mueve con velocidad , el cual, multiplicada con su conjugada, nos da la función de probabilidad de encontrar una partícula en determinado punto del espacio tiempo.
Schrödinger sugirió que el movimiento de los electrones en el átomo correspondía a la dualidad onda-partícula y, en consecuencia, los electrones podían moverse alrededor del núcleo como ondas estacionarias.
La función de onda en la mecánica cuántica se puede considerar como una representación del estado de movimiento discontinuo aleatorio de las partículas, y en un nivel más profundo, puede representar la propiedad disposicional de las partículas que determina su movimiento discontinuo aleatorio.
Ahora tendríamos que hablar algo de la mecánica cuántica y, en ese ámbito, las reglas de la mecánica cuántica funcionan tan bien que resultaría realmente difícil refutarlas. Acordaos de los trucos ingeniosos descubiertos por Werner Heisenberg, Paul Dirac, o, Schrödinger que vinieron a mejorar y completar las reglas generales. Sin embargo, algunos de aquellos pioneros (Einstein y el mismo Schrödinger), sin embargo, presentaron serias objeciones a dicha interpretación de la naturaleza de lo muy pequeño.
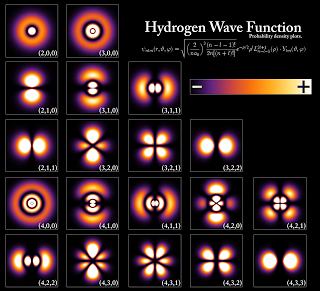
Resuelta la ecuación, con ayuda de Weyl, Schrödinger obtuvo el espectro del átomo de hidrógeno, partes discreta y continua, para lo que añadió la condición
a largas distancias.
Esta cosita tan pequeñita, el electrón, es inversamente proporcional en importancia para que el mundo, la Naturaleza, y, nuestro Universo sea como es. Se ha conseguido fotografiar a un electrón. Poder filmar y fotografiar un electrón no es fácil por dos razones: primero, gira alrededor del núcleo atómico cada 0,000000000000000140 segundos , y, porque para fotografiar un electrón es necesario bombardearlo con partículas de luz (y cualquier que haya intentado sacarle una foto a un electrón sabe que hay que hacerlo sin flash). La imagen de la izquierda es el resultado.
El electrón fue descubierto en 1.897 por el físico británico Joseph John Thomson (1.856 – 1940). El problema de la estructura (si la hay) del electrón no está resuelto. Si el electrón se considera como una carga puntual, su autoenergía es infinita y surgen dificultades en la ecuación conocida como de Lorentz–Dirac.
Muchas veces hemos hablado del electrón que rodea el núcleo, de su carga eléctrica negativa que complementa la positiva de los protones y hace estable al átomo; tiene una masa de solamente 1/1.836 de la del núcleo más ligero, el del hidrógeno que está formado por un solo protón. La importancia del electrón es vital en el universo.



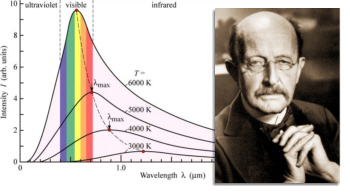
Pero busquemos los “cuantos”. La física del siglo XX empezó exactamente en el año 1900, cuando el físico alemán Max Planck propuso una posible solución a un problema que había estado intrigando a los físicos durante años. Es el problema de la luz que emiten los cuerpos calentados a una cierta temperatura, y también la radiación infrarroja emitida, con menor intensidad, por los objetos más fríos (radiación de cuerpo negro).
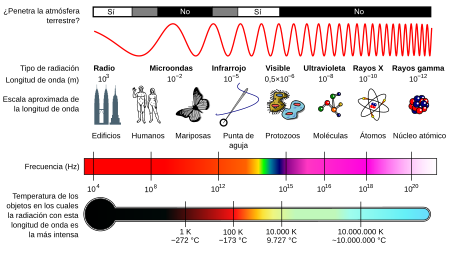
Estaba bien aceptado entonces que esta radiación tenía un origen electromagnético y que se conocían las leyes de la naturaleza que regían estas ondas electromagnéticas. También se conocían las leyes para el frío y el calor, la así llamada “termodinámica”, o al menos eso parecía. Pero si utilizamos las leyes de la termodinámica para calcular la intensidad de una radiación, el resultado no tiene ningún sentido. Los cálculos nos dicen que se emitiría una cantidad infinita de radiación en el ultravioleta más lejano y, desde luego, esto no es lo que sucede. Lo que se observa es que la intensidad de la radiación muestra un pico a una cierta longitud de onda característica, y que la intensidad disminuye tanto para longitudes mayores como para menores. Esta longitud de onda característica es inversamente proporcional a la temperatura absoluta de objeto radiante (la temperatura absoluta se define por una escala de temperatura que empieza a 273º bajo cero). Cuando a 1.000 ºC un objeto se pone al “rojo vivo”, el objeto está radiando en la zona de luz visible.

Lo que Planck propuso fue simplemente que la radiación sólo podía ser emitida en paquetes de un tamaño dado. La cantidad de energía de uno de esos paquetes, o cuantos, es inversamente proporcional a la longitud de onda, y por tanto, proporcional a la frecuencia de radiación emitida. La fórmula es E = hν, donde E es la energía del paquete, ν es la frecuencia y h es una nueva constante fundamental de la naturaleza, la constante de Planck. Cuando Planck calculó la intensidad de la radiación térmica imponiendo esta nueva condición, el resultado coincidió perfectamente con las observaciones.



Poco tiempo después, en 1905, Einstein formuló esta teoría de una manera mucho más tajante: él sugirió que los objetos calientes no son los únicos que emiten radiación en paquetes de energía, sino que toda la radiación consiste en múltiplos del paquete de energía de Planck. El príncipe francés Louis-Victor de Broglie, dándole otra vuelta a la teoría, propuso que no sólo cualquier cosa que oscila tiene energía, sino que cualquier cosa con energía se debe comportar como una “onda” que se extiende en una cierta región del espacio, y que la frecuencia ν de la oscilación verifica la ecuación de Planck. Por lo tanto, los cuantos asociados con los rayos de luz deberían verse como una clase de partículas elementales: el fotón. Todas las demás clases de partículas llevan asociadas diferentes ondas oscilantes de campos de fuerza, pero esto lo veremos más adelante.

El Electrón como Onda y partícula
El curioso comportamiento de los electrones en el interior del átomo, descubierto y explicado por el famoso físico danés Niels Bohr, se pudo atribuir a las ondas de de Broglie. Poco después, en 1926, Edwin Schrödinger descubrió cómo escribir la teoría ondulatoria de de Broglie con ecuaciones matemáticas exactas. La precisión con la cual se podían realizar cálculos era asombrosa, y pronto quedó claro que el comportamiento de todos los objetos pequeños quedaba exactamente determinado por las recién descubiertas “ecuaciones de ondas cuánticas”.
Está bien comprobado que la mecánica cuántica funciona de maravilla…, pero, sin embargo, surge una pregunta muy formal: ¿qué significan realmente estas ecuaciones?, ¿qué es lo que están describiendo? Cuando Isaac Newton, allá en 1867 formuló cómo debían moverse los planetas alrededor del Sol, estaba claro para todo el mundo qué significaban sus ecuaciones: que los planetas estaban siempre en una posición bien definida des espacio y que sus posiciones y sus velocidades en un momento concreto determinan inequívocamente cómo evolucionarán las posiciones y las velocidades en el tiempo.
Pero para los electrones todo es diferente. Su comportamiento parece estar envuelto en misterio. Es como si pudieran “existir” en diferentes lugares simultáneamente, como si fueran una nube o una onda, y esto no es un efecto pequeño. Si se realizan experimentos con suficiente precisión, se puede determinar que el electrón parece capaz de moverse simultáneamente a lo largo de trayectorias muy separadas unas de otras.
¿Qué puede significar todo esto?

Superposición cuántica

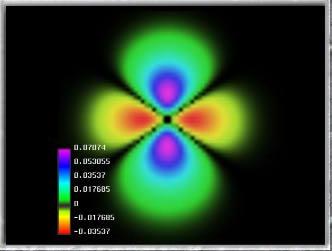
La notable capacidad de un electrón de existir en dos lugares al mismo tiempo ha sido controlada en el material electrónico más comun el – silicio – por primera vez, siendo este un gran avance para la electrónica moderna y tiene un potencial enorme para el futuro y para la creación de la computadora cuántica.
Imagen: El movimiento de los electrones en el silicio. El electrón gira alrededor de una átomo de fósforo embebido en la estructura cristalina del silicio, que se muestra en plata. La distribución de densidad electrónica no perturbado, a partir de la ecuaciones de la mecánica cuántica del movimiento se muestra en amarillo. Un pulso de láser de electrones puede modificar el estado de manera que tiene la distribución de la densidad se muestra en verde. Nuestro pulso láser en primer lugar, que llegan desde la izquierda, pone el electrón en una superposición de ambos estados, que podemos controlar con un segundo impulso, también desde la izquierda, para dar un pulso que se detecte que, saliendo a la derecha. Las características de este “eco” del pulso nos hablan de la superposición que hemos hecho.
Cuando podamos dominar el “universo” de lo muy pequeño… ¡Nuestro Universo será otro para nosotros!

Las leyes de la mecánica cuántica han sido establecidas con mucha precisión; permite cómo calcular cualquier cosa que queramos saber. Pero si queremos “interpretar” el resultado, nos encontramos con una curiosa incertidumbre fundamental: que varias propiedades de las partículas pequeñas no pueden estar bien definidas de manera simultánea. Por ejemplo, podemos determinar la velocidad de una partícula con mucha precisión, pero entonces no sabremos exactamente dónde se encuentra; o a la inversa, podemos determinar la posición con precisión, pero entonces su velocidad queda mal definida. Si una partícula tiene espín (rotación alrededor de su eje), la dirección alrededor de la cual está rotando (la orientación del eje) no puede ser definida con gran precisión.
No es fácil explicar de forma sencilla de dónde viene esta incertidumbre, pero existen ejemplos en la vida cotidiana que tienen algo parecido. La altura de un tono y la duración en el tiempo durante el cual oímos el tono tienen una incertidumbre mutua similar. Para afinar un instrumento musical se debe escuchar una nota durante un cierto intervalo de tiempo y compararla, por ejemplo, con un diapasón que debe vibrar también durante un tiempo. Notas muy breves no tienen bien definido el tono.
Sí, la música influye en el cerebro
Para que las reglas de la mecánica cuántica funcionen, es necesario que todos los fenómenos naturales en el mundo de las cosas pequeñas estén regidos por las mismas reglas. Esto incluye a los virus, bacterias e incluso a las personas. Sin embargo, cuando más grande y más pesado es un objeto, más difícil es observar las desviaciones de las leyes del movimiento “clásicas” debidas a la mecánica cuántica. Me gustaría referirme a esta exigencia tan importante y tan peculiar de la teoría con la palabra “holismo”. Esto no es exactamente lo mismo que entienden algunos filósofos por holismo, y que podría definir como “el todo es más que la suma de sus partes”. Si la física nos ha enseñado algo es justo lo contrario. Un objeto compuesto de un gran número de partículas puede ser entendido exactamente si se conocen las propiedades de sus partes (partículas); basta que sepamos sumar correctamente (¡y esto no es nada fácil en mecánica cuántica!). Lo que entiendo por holismo es que, efectivamente, el todo es la suma de las partes, pero sólo se puede hacer la suma si todas las partes obedecen a las mismas leyes. Por ejemplo, la constante de Planck, h, que es igual a 6’626075… × 10-34 Julios segundo, debe ser exactamente la misma para cualquier objeto en cualquier sitio, es decir, debe ser una constante universal.
Aunque la semilla la puso Planck en 1900, fue a partir de 1930 cuando la mecánica cuántica se aplicó con mucho éxito a problemas relacionados con núcleos atómicos, moléculas y materia en estado sólido. La mecánica cuántica hizo posible comprender un extenso conjunto de datos, de otra manera enigmáticos. Sus predicciones han sido de una exactitud notable. Ejemplo de esto último es la increíble precisión de diecisiete cifras significativas del momento magnético del electrón calculadas por la EDC (Electrodinámica Cuántica) comparadas con el experimento.
Si viajamos hacia lo muy pequeño tendremos que ir más allá de los átomos, que son objetos voluminosos y frágiles comparados con lo que nos ocupará a continuación: el núcleo atómico y lo que allí se encuentra. Los electrones, que ahora vemos “a gran distancia” dando vueltas alrededor del núcleo, son muy pequeños y extremadamente robustos. El núcleo está constituido por dos especies de bloques: protones y neutrones. El protón (del griego πρώτος, primero) debe su nombre al hecho de que el núcleo atómico más sencillo, que es el hidrógeno, está formado por un solo protón. Tiene una unidad de carga positiva. El neutrón recuerda al protón como si fuera su hermano gemelo: su masa es prácticamente la misma, su espín es el mismo, pero en el neutrón, como su propio nombre da a entender, no hay carga eléctrica; es neutro.
La masa de estas partículas se expresa en una unidad llamada mega-electrón-voltio o MeV, para abreviar. Un MeV, que equivale a 106 electrón-voltios, es la cantidad de energía de movimiento que adquiere una partícula con una unidad de carga (tal como un electrón o un protón) cuando atraviesa una diferencia de potencial de 106 (1.000.000) voltios. Como esta energía se transforma en masa, el MeV es una unidad útil de masa para las partículas elementales.
Sí, las reglas de la mecánica cuántica son extrañas y misteriosas, pero… ¿Las vamos entendiendo?
Las reglas de la mecánica cuántica funcionan tan bien que refutarlas resulta realmente difícil. Los trucos ingeniosos descubiertos por Werner Heisemberg, Paul Dirac y muchos otros mejoraron y completaron las reglas generales. Pero Einstein y otros pioneros como Erwin Schrödinger siempre presentaron serias objeciones a esta interpretación. Quizá funcione bien, pero ¿dónde está exactamente el electrón?, ¿en el punto x o en el punto y? En pocas palabras, ¿dónde está en realidad?, y ¿cuál es la realidad que hay detrás de nuestras fórmulas? Si tenemos que creer a Bohr, no tiene sentido buscar tal realidad. Las reglas de la mecánica cuántica, por sí mismas, y las observaciones realizadas con detectores son las únicas realidades de las que podemos hablar.

Hablar de Mecánica Cuántica es como hacerlo de la Quinta (la Cuarta es el Tiempo) Dimensión
La mecánica cuántica puede ser definida o resumida así: en principio, con las leyes de la naturaleza que conocemos ahora se puede predecir el resultado de cualquier experimento, en el sentido que la predicción consiste en dos factores: el primer factor es un cálculo definido con exactitud del efecto de las fuerzas y estructuras, tan riguroso como las leyes de Isaac Newton para el movimiento de los planetas en el Sistema Solar; el segundo factor es una arbitrariedad estadística e incontrolable definida matemáticamente de forma estricta. Las partículas seguirán una distribución de probabilidades dadas, primero de una forma y luego de otra. Las probabilidades se pueden calcular utilizando la ecuación de Schrödinger de función de onda (Ψ) que, con muchas probabilidades nos indicará el lugar probable donde se encuentra una partícula en un momento dado.

¿Ganaré algún día esa lotería que me quite de trabajar por necesidad?
Muchos estiman que esta teoría de las probabilidades desaparecerá cuando se consiga la teoría que explique, de forma completa, todas las fuerzas; la buscada teoría del todo, lo que implica que nuestra descripción actual incluye variables y fuerzas que (aún) no conocemos o no entendemos. Esta interpretación se conoce como hipótesis de las variables ocultas.
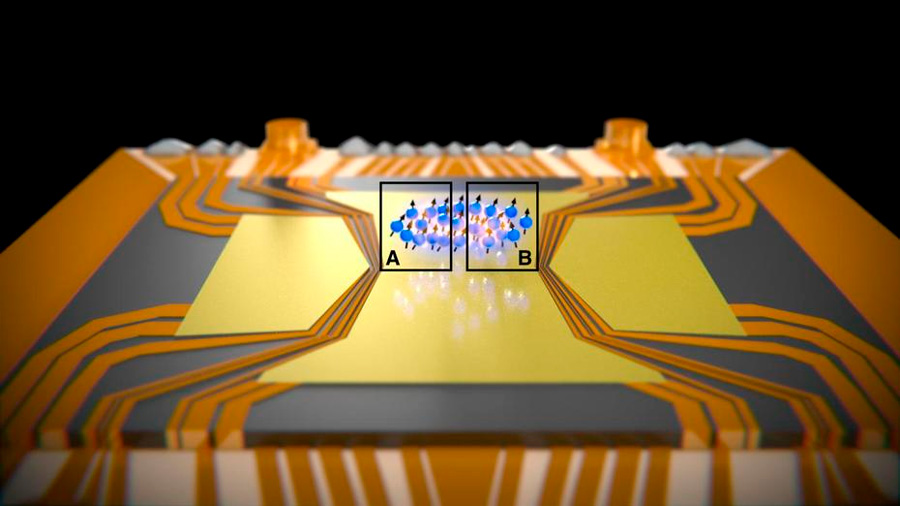
Por primera vez, se observa la paradoja de Einstein-Podolsky-Rosen en un sistema de muchas partículas
Albert Einstein, Nathan Rosen y Boris Podolski idearon un “Gedankenexperiment”, un experimento hipotético, realizado sobre el papel, para el cual la mecánica cuántica predecía como resultado algo que es imposible de reproducir en ninguna teoría razonable de variables ocultas. Más tarde, el físico irlandés John Stewar Bell consiguió convertir este resultado en un teorema matemático; el teorema de imposibilidad.

Bueno, a todo esto, una cosa sí que nos queda clara, como la posibilidad asombrosa de nuestras Mentes a germinar ideas que salen bulliciosas al mundo. No todas llegan a su destino. Sin embargo, las que lo hacen, marcan un hito y nos señalan el camino a seguir en ese largo viaje (en realidad interminable -nunca podremos saberlo todo sobre todas las cosas-), a la búsqueda del saber del Mundo y del Universo en fin.
Emilio Silvera Vázquez
Dic
13
La Masa y la Energía ¿Qué son en realidad?
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (0)
Comments (0)


Todos los intentos y los esfuerzos por hallar una pista del cuál era el origen de la masa fallaron. Feynman escribió su famosa pregunta: “¿Por qué pesa el muón?”. Ahora, por lo menos, tenemos una respuesta parcial, en absoluto completa. Una voz potente y ¿segura? nos dice: “!Higgs¡” Durante más de 60 años los físicos experimentadores se rompieron la cabeza con el origen de la masa, y ahora el campo Higgs presenta el problema en un contexto nuevo; no se trata sólo del muón. Proporciona, por lo menos, una fuente común para todas las masas. La nueva pregunta feynmaniana podría ser: ¿Cómo determina el campo de Higgs la secuencia de masas, aparentemente sin patrón, que da a las partículas de la materia?
La variación de la masa con el estado de movimiento, el cambio de masa con la configuración del sistema y el que algunas partículas (el fotón seguramente y los neutrinos posiblemente) tengan masa en reposo nula son tres hechos que ponen entre dicho que el concepto de masa sea un atributo fundamental de la materia. Habrá que recordar aquel cálculo de la masa que daba infinito y nunca pudimos resolver; los físicos sólo se deshicieron de él “re-normalizándolo”, ese truco matemático que emplean cuando no saben encontrar la respuesta al problema planteado.
Ese es el problema de trasfondo con el que tenemos que encarar el problema de los quarks, los leptones y los vehículos de las fuerzas, que se diferencian por sus masas. Hace que la historia de Higgs se tenga en pie: la masa no es una propiedad intrínseca de las partículas, sino una propiedad adquirida por la interacción de las partículas y su entorno.
La idea de que la masa no es intrínseca como la carga o el espín resulta aún más plausible por la idílica idea de que todos los quarks y fotones tendrían masa cero. En ese caso, obedecerían a una simetría satisfactoria, la quiral, en laque los espines estarían asociados para siempre con su dirección de movimiento. Pero ese idilio queda oculto por el fenómeno de Higgs.


¡Ah, una cosa más! Hemos hablado de los bosones gauge y de su espín de una unidad; hemos comentado también las partículas fermiónicas de la materia (espin de media unidad). ¿Cuál es el pelaje de Higgs? Es un bosón de espin cero. El espín supone una direccionalidad en el espacio, pero el campo de Higgs da masa a los objetos dondequiera que estén y sin direccionalidad. Al Higgs se le llama a veces “bosón escalar” [sin dirección] por esa razón.
La interacción débil, recordareis, fue inventada por E. Fermi para describir la desintegración radiactiva de los núcleos, que era básicamente un fenómeno de poca energía, y a medida que la teoría de Fermi se desarrolló, llegó a ser muy precisa a la hora de predecir un enorme número de procesos en el dominio de energía de los 100 MeV. Así que ahora, con las nuevas tecnologías y energías del LHC, las esperanzas son enormes para, por fin, encontrar el bosón Higgs origen de la masa… y algunas cosas más.

Fabiola Gianotti, portavoz del experimento ATLAS, hablando con Peter Higgs y le dice:
“En nuestros datos observamos claros signos de una nueva partícula compatible con la teoría de Higgs, con un nivel aproximado de 5 sigma [99,977% de eficiencia], en la región de masa alrededor de los 126 GeV. El increíble rendimiento del LHC y el ATLAS y los enormes esfuerzos de mucha gente nos han traído a este excitante punto, pero hace falta un poco más de tiempo para preparar estos resultados cara a su publicación.”
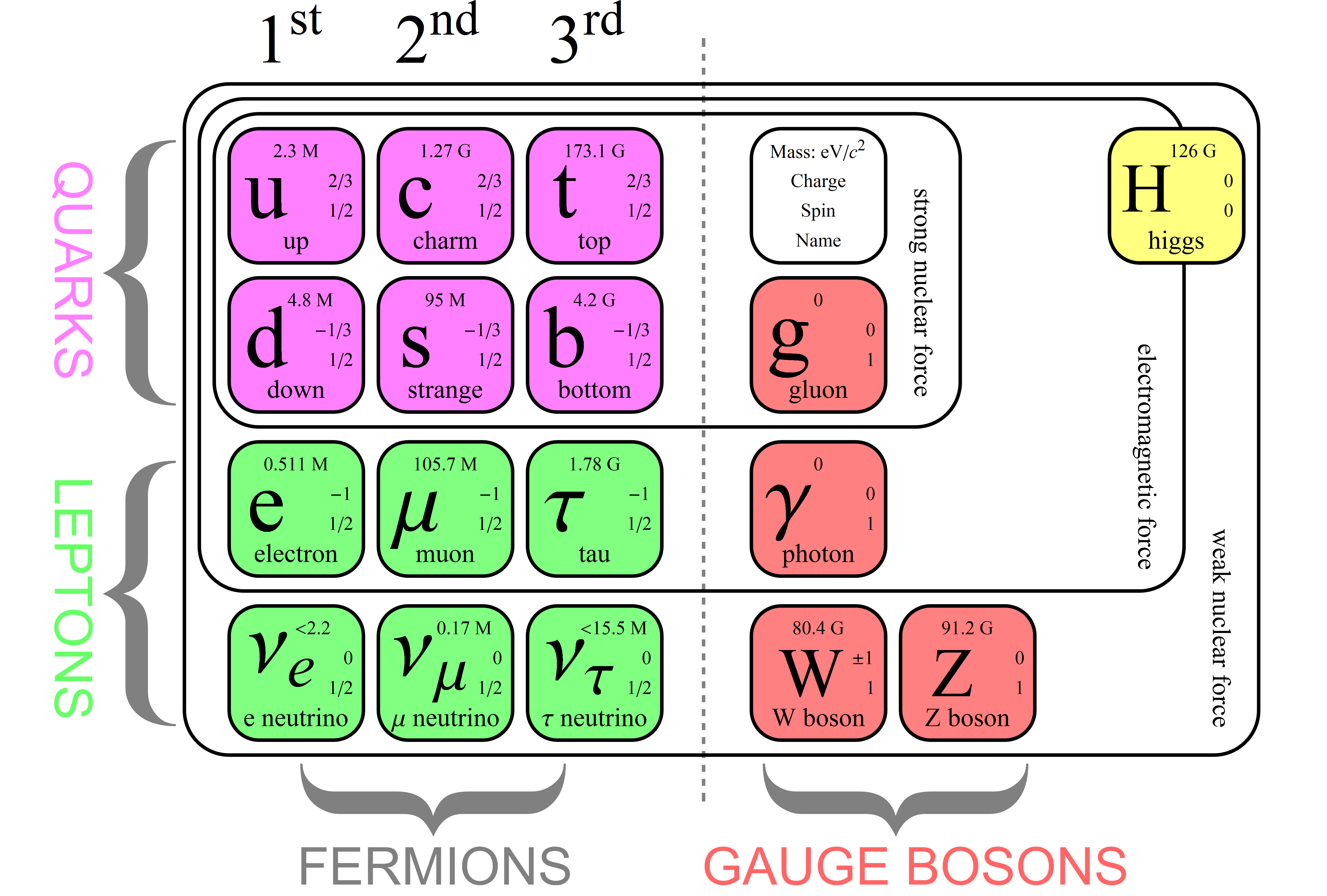
El Modelo Estándar describe las partículas de todo cuanto nos rodea, incluso de nosotros mismos. Toda la materia que podemos observar, sin embargo, no parece significar más que el 4% del total. Higgs podría ser el puente para comprender el 96% del universo que permanece oculto.
El 4 de julio de 2012 se anunció el descubrimiento de un nuevo bosón. Punto. En diciembre de 2012 se empezó a hablar de “un” Higgs (en lugar de “el” Higgs), pero oficialmente seguía siendo un nuevo bosón. ¿Importa el nombre? El Premio Nobel de Física para el bosón de Higgs sólo será concedido cuando el CERN afirme con claridad y rotundidad que se ha descubierto “el” Higgs, si el CERN es conservador, la Academia Sueca lo es aún más. Sin embargo, el rumor es que quizás baste con que el CERN diga que se ha descubierto “un” Higgs.

¿Por qué, a pesar de todas las noticias surgidas desde el CERN, creo que no ha llegado el momento de celebrarlo? ¿Es acaso el Higgs lo encontrado?
Hay que responder montones de preguntas. ¿Cuáles son las propiedades de las partículas de Higgs y, lo que es más importante, cuál es su masa? ¿Cómo reconoceremos una si nos la encontramos en una colisión de LHC? ¿Cuántos tipos hay? ¿Genera el Higgs todas las masas, o solo las hace incrementarse? ¿Y, cómo podemos saber más al respecto? También a los cosmólogos les fascina la idea de Higgs, pues casi se dieron de bruces con la necesidad de tener campos escalares que participasen en el complejo proceso de la expansión del Universo, añadiendo, pues, un peso más a la carga que ha de soportar el Higgs.
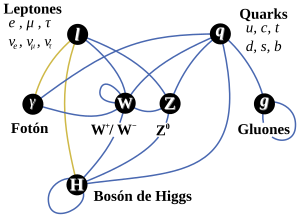
El campo de Higgs, tal y como se lo concibe ahora, se puede destruir con una energía grande, o temperaturas altas. Estas generan fluctuaciones cuánticas que neutralizan el campo de Higgs. Por lo tanto, el cuadro que las partículas y la cosmología pintan juntas de un universo primitivo puso y de resplandeciente simetría es demasiado caliente para Higgs. Pero cuando la temperatura cae bajo los 10’5 grados kelvin o 100 GeV, el Higgs empieza a actuar y hace su generación de masas. Así por ejemplo, antes de Higgs teníamos unos W, Z y fotones sin masa y la fuerza electro-débil unificada.
El Universo se expande y se enfría, y entonces viene el Higgs (que engorda los W y Z, y por alguna razón ignora el fotón) y de ello resulta que la simetría electrodébil se rompe. Tenemos entonces una interacción débil, transportada por los vehículos de la fuerza W+, W–, Z0, y por otra parte una interacción electromagnética, llevada por los fotones. Es como si para algunas partículas del campo de Higgs fuera una especie de aceite pesado a través del que se moviera con dificultad y que las hiciera parecer que tienen mucha masa. Para otras partículas, el Higgs es como el agua, y para otras, los fotones y quizá los neutrinos, es invisible.

Para cada suceso, la línea del haz es el eje común de los cilindros de malla de alambre ECAL y HCAL. ¿Cuál es el mejor candidato W? el mejor candidato Z? En cada evento, ¿dónde ocurrió la colisión y el decaimiento de las partículas producidas? Lo cierto es que, en LHC se hacen toda clase de pruebas para saber del mundo de las partículas, de dónde vienen y hacia dónde se dirigen y, el Bosón de Higgs, es una asignatura pendiente a pesar de las noticias y de los premios
De todas las maneras, es tanta la ignorancia que tenemos sobre el origen de la masa que, nos agarramos como a un clavo ardiendo el que se ahoga, en este caso, a la partícula de Higgs que viene a ser una de las soluciones que le falta al Modelo Estándar para que todo encaje con la teoría.
¡Ya veremos en que termina todo esto! Dicen que descubrieron el famoso Bosón pero… Y, aunque el que suena siempre es Higgs, lo cierto es que los autores de la teoría del “Bosón de Higgs”, son tres a los que se ha concedido, junto al CERN, el Premio Principe de Asturias. Peter Ware Higgs —el primero en predecir la existencia del bosón— junto a los físicos François Englert, y el belga Robert Brout—fallecido en el año 2011— y que no ha podido disfrutar del Nóbel.

Peter Higgs, de la Universidad de Edimburgo, introdujo la idea en la física de partículas. La utilizaron los teóricos Steven Weinberg y V. Salam, que trabajaban por separado, para comprender como se convertía la unificada y simétrica fuerza electrodébil, transmitida por una feliz familia de cuatro partículas mensajeras de masa nula, en dos fuerzas muy diferentes: la QED con un fotón carente de masa y la interacción débil con sus W+, W– y Z0de masa grande. Weinberg y Salam se apoyaron en los trabajos previos de Sheldon Glasgow, quien tras los pasos de Julian Schwinger, sabía sólo que había una teoría electrodébil unificada, coherente, pero no unió todos los detalles. Y estaban Jeffrey Goldstone y Martines Veltman y Gerard’t Hooft. También hay otras a los que había que mencionar, pero lo que siempre pasa, quedan en el olvido de manera muy injusta. Además, ¿Cuántos teóricos hacen falta para encender una bombilla?
La verdad es que, casi siempre, han hecho falta muchos. Recordemos el largo recorrido de los múltiples detalle sueltos y físicos que prepararon el terreno para que, llegara Einstein y pudiera, uniéndolo todo, exponer su teoría relativista.
Sobre la idea de Peter Higgs, Veltman, uno de sus arquitectos, dice que es una alfombra bajo la que barremos nuestra ignorancia. Glasgow es menos amable y lo llamó retrete donde echamos las incoherencias de nuestras teorías actuales. La objeción principal: que no teníamos la menor prueba experimental que ahora parece que va asomando la cabeza en el LHC.

![]()
Esperemos que la partícula encontrada, el bosón hallado, sea en realidad el Higgs dador de masa a las demás partículas pero… ¡Cabe la posibilidad de que sólo sea el hermano menor! de la familia. El modelo estándar es lo bastante fuerte para decirnos que la partícula de Higgs de menor masa (podría haber muchas) debe “pesar” menos de 1 TeV. ¿Por qué? Si tiene más de 1 TeV, el modelo estándar se vuelve incoherente y tenemos la crisis de la unitariedad.
Después de todo esto, tal como lo están planteando los del CERN, se puede llegar a la conclusión de que, el campo de Higgs, el modelo estándar y nuestra idea de cómo se hizo el Universo dependen de que se encuentre el Bosón de Higgs. Y ahora, por fin, el mayor Acelerador del mundo, el LHC, nos dice que el Bosón ha sido encontrado y las pruebas tienen una fiabilidad enorme.
¡La confianza en nosotros mismos, no tiene límites! Pero el camino no ha sido recorrido por completo y quedan algunos tramos que tendremos que andar para poder, al fín, dar una explicación más completa, menos oscura y neblinosa que lo que hasta el momento tenemos, toda vez que, del Bosón de Higgs y de su presencia veráz, dependen algunos detalles de cierta importancia para que sean confirmados nuestros conceptos de lo que es la masa y, de paso, la materia.
¿Pasará igual con las cuerdas?
Emilio Silvera Vázquez
Agradecido le quedo a León Lederman que con sus ideas ha nutrido el presente trabajo.
Dic
13
La maravilla de… ¡Los cuantos!
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (0)
Comments (0)
La Física del siglo XX empezó exactamente en el año 1900, cuando el físico alemán Max Planck propuso una posible solución a un problema que había estado intrigando a los físicos durante años. Es el problema de la luz que emiten los cuerpos calentados a una cierta temperatura, y también la radiación infrarroja emitida, con menos intensidad, por los objetos más fríos. Planck escribió un artículo de ocho páginas y el resultado fue que cambió el mundo de la física y aquella páginas fueron la semilla de la futura ¡mecánica cuántica! que, algunos años más tardes, desarrollarían físicos como Einstein (Efecto fotoeléctrico), Heisenberg (Principio de Incertidumbre), Feynman, Bhor, Schrödinger, Dirac…

Lo que Planck propuso fue simplemente que la radiación sólo podía ser emitida en paquetes de un tamaño dado: E = hv
Donde E es la energía del paquete, v es la frecuencia y h es una nueva constante fundamental de la naturaleza, la constante de Planck. Cuando Planck calculó la intensidad de la radiación térmica imponiendo esta nueva condición, el resultado coincidió perfectamente con las observaciones.
La expresión radiación se refiere a la emisión continua de energía de la superficie de todos los cuerpos. Los portadores de esta energía son las ondas electromagnéticas producidas por las vibraciones de las partículas cargadas que forman parte de los átomos y moléculas de la materia. La radiación electromagnética que se produce a causa del movimiento térmico de los átomos y moléculas de la sustancia se denomina radiación térmica o de temperatura.

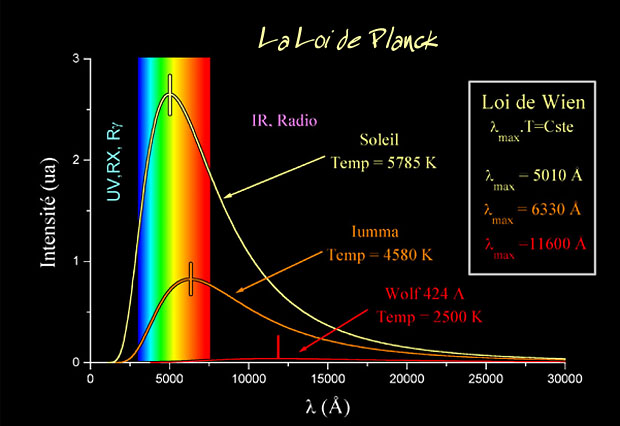
Ley de Planck para cuerpos a diferentes temperaturas.
Estaba bien aceptado entonces que esta radiación tenía un origen electromagnético y que se conocían las leyes de la naturaleza que regían estas ondas electromagnéticas. También se conocían las leyes para el frío y el calor, la así llamada “termodinámica”, o al menos eso parecía.

Pero si usamos las leyes de la termodinámica para calcular la intensidad de la radiación, el resultado no tiene ningún sentido. Los cálculos nos dicen que se emitiría una cantidad infinita de radiación en el ultravioleta más lejano, y, desde luego, esto no es lo que sucede. Lo que se observa es que la intensidad de la radiación muestra un pico o una cierta longitud de onda característica, y que la intensidad disminuye tanto para longitudes mayores como para longitudes menores. Esta longitud característica es inversamente proporcional a la temperatura absoluta del objeto radiante (la temperatura absoluta se define por una escala de temperatura que empieza a 273 ºC bajo cero). Cuando a 1.000 ºC un objeto se pone al “rojo vivo”, el objeto está radiando en la zona de la luz visible.

Acero al “rojo vivo”, el objeto está radiando en la zona de la luz visible
Lo que Planck propuso fue simplemente que la radiación sólo podía ser emitida en paquetes de un tamaño dado. La cantidad de energía de uno de esos paquetes, o cuantos, es inversamente proporcional a la longitud de onda y, por lo tanto, proporcional a la frecuencia de la radiación emitida. La sencilla fórmula es:
E = hv
Donde E es la energía del paquete, v es la frecuencia y h es una nueva constante fundamental de la naturaleza, la constante de Planck. Cuando Planck calculó la intensidad de la radiación térmica imponiendo esta nueva condición, el resultado coincidió perfectamente con las observaciones.

Poco tiempo después, en 1905, Einstein formuló esta teoría de una manera mucho más tajante: el sugirió que los objetos calientes no son los únicos que emiten radiación en paquetes de energía, sino que toda la radiación consiste en múltiplos del paquete de energía de Planck.
El príncipe francés Louis Victor de Broglie, dándole otra vuelta a la teoría, que no sólo cualquier cosa que oscila tiene una energía, sino que cualquier cosa con energía se debe comportar como una “onda” que se extiende en una cierta dirección del espacio, y que la frecuencia, v, de la oscilación verifica la ecuación de Planck. Por lo tanto, los cuantos asociados con los rayos de luz deberían verse como una clase de partículas elementales: el fotón. Todas las demás clases de partículas llevan asociadas diferentes ondas oscilatorias de campos de fuerza.

Es curioso el comportamiento de los electrones en el interior del átomo, descubierto y explicado por el famoso físico danés Niels Bohr, se pudo atribuir a las ondas de De Broglie. Poco después, en 1926, Edwin Schrödinger descubrió como escribir la teoría ondulatoria de De Broglie con ecuaciones matemáticas exactas. La precisión con la cual se podían realizar los cálculos era asombrosa, y pronto quedó claro que el comportamiento de todos los objetos pequeños quedaba exactamente determinado por las recién descubiertas “ecuaciones de onda cuántica”.

No hay duda de que la Mecánica Cuántica funciona maravillosamente bien. Sin embargo, surge una pregunta muy formal: ¿Qué significan realmente esas ecuaciones?, ¿Qué es lo que están describiendo? Cuando Isaac Newton, allá por el año 1687, formuló cómo debían moverse los planetas alrededor del Sol, estaba claro para todo el mundo lo que significaban sus ecuaciones: que los planetas están siempre en una posición bien definida en el espacio y que sus posiciones y sus velocidades en un momento concreto determinan inequívocamente cómo evolucionarán las posiciones y las velocidades con el tiempo.
Pero para los electrones todo esto es muy diferente. Su comportamiento parece estar envuelto en la bruma. Es como si pudieran “existir” en diferentes lugares simultáneamente, como si fueran una nube o una onda, y esto no es un efecto pequeño. Si se realizan experimentos con suficiente precisión, se puede determinar que el electrón parece capaz de moverse simultáneamente a lo largo de trayectorias muy separadas unas de otras. ¿Qué puede significar todo esto?
Niels Bohr consiguió responder a esta pregunta de forma tal que con su explicación se pudo seguir trabajando y muchos físicos siguen considerando su respuesta satisfactoria. Se conoce como la “interpretación de Copenhague” de la Mecánica Cuántica. En vez de decir que el electrón se encuentra en el punto x o en el punto y, nosotros hablamos del estado del electrón. Ahora no tenemos el estado “x” o el estado “y”, sino estados “parcialmente x” o “parcialmente y. Un único electrónpuede encontrarse, por lo tanto, en varios lugares simultáneamente. Precisamente lo que nos dice la Mecánica Cuántica es como cambia el estado del electrón según transcurre el tiempo.
Un “detector” es un aparato con el cual se puede determinar si una partícula está o no presente en algún lugar pero, si una partícula se encuentra con el detector su estado se verá perturbado, de manera que sólo podemos utilizarlo si no queremos estudiar la evolución posterior del estado de la partícula. Si conocemos cuál es el estado, podemos calcular la probabilidad de que el detector registre la partícula en el punto x.

Las leyes de la Mecánica Cuántica se han formulado con mucha precisión. Sabemos exactamente como calcular cualquier cosa que queramos saber. Pero si queremos “interpretar” el resultado, nos encontramos con una curiosa incertidumbre fundamental: que varias propiedades de las partículas pequeñas no pueden estar bien definidas simultáneamente. Por ejemplo, podemos determinar la velocidad de una partícula con mucha exactitud, pero entonces no sabremos exactamente dónde se encuentra; o, a la inversa. Si una partícula tiene “espín” (rotación alrededor de su eje), la dirección alrededor de la cual está rotando (la orientación del eje) no puede ser definida con gran precisión.
No es fácil explicar con sencillez de dónde viene esta incertidumbre, pero hay ejemplos en la vida cotidiana que tienen algo parecido. La altura de un tono y la duración en el tiempo durante el cual oímos el tono tienen una incertidumbre mutua similar.

¿Onda o partícula? ¡Ambas a la vez! ¿Cómo es eso?
Para que las reglas de la Mecánica Cuántica funcionen, es necesario que todos los fenómenos naturales en el mundo de las cosas pequeñas estén regidos por las mismas reglas. Esto incluye a los virus, bacterias e incluso a las personas. Sin embargo, cuanto más grande y más pesado es un objeto más difícil es observar las desviaciones de las leyes del movimiento “clásicas” debidas a la mecánica cuántica.
Me gustaría referirme a esta exigencia tan importante y tan peculiar de la teoría con la palabra “holismo”. Esto no es exactamente lo mismo que entienden algunos filósofos por “holismo”, y que se podría definir como “el todo es más que la suma de las partes”.
Bien, si la Física nos ha enseñado algo, es justamente lo contrario: un objeto compuesto de un gran número de partículas puede ser entendido exactamente si se conocen las propiedades de sus partes (las partículas): basta que uno sepa sumar correctamente (¡y esto no es nada fácil en mecánica cuántica!). Lo que yo entiendo por holismo es que, efectivamente, el todo es la suma de las partes, pero sólo se puede hacer la suma si todas las partes obedecen a las mismas leyes.
Por ejemplo, la constante de Planck, h = 6,626075…x 10 exp. -34 julios segundo, debe ser exactamente la misma para cualquier objeto en cualquier sitio, es decir, debe ser una constante universal.
Las reglas de la mecánica cuántica funcionan tan bien que refutarlas resulta realmente difícil. Los trucos ingeniosos descubiertos por Werner Heisenberg, Paul Dirac y muchos otros mejoraron y completaron las reglas generales. Pero Einstein y otros pioneros tales como Edwin Schrödinger, siempre presentaron serias objeciones a esta interpretación.
Quizá funcione bien, pero ¿Dónde está exactamente el electrón, en el punto x o en el punto y? Em pocas palabras, ¿dónde está en realidad?, ¿Cuál es la realidad que hay detrás de nuestras fórmulas? Si tenemos que creer a Bohr, no tiene sentido buscar tal realidad. Las reglas de la mecánica cuántica, por sí mismas, y las observaciones realizadas con detectores son las únicas realidades de las que podemos hablar.

Hasta hoy, muchos investigadores coinciden con la actitud pragmática de Bohr. Los libros de historia dicen que Bohr demostró que Einstein estaba equivocado. Pero no son pocos, incluyéndome a mí, los que sospechamos que a largo plazo el punto de vista de Einstein volverá: que falta algo en la interpretación de Copenhague. Las objeciones originales de Einstein pueden superarse, pero aún surgen problemas cuando uno trata de formular la mecánica cuántica para todo el Universo (donde las medidas no se pueden repetir) y cuando se trata de reconciliar las leyes de la mecánica cuántica con las de la Gravitación… ¡Infinitos!
La mecánica cuántica y sus secretos han dado lugar a grandes controversias, y la cantidad de disparates que ha sugerido es tan grande que los físicos serios ni siquiera sabrían por donde empezar a refutarlos. Algunos dicen que “la vida sobre la Tierra comenzó con un salto cuántico”, que el “libre albedrío” y la “conciencia” se deben a la mecánica cuántica: incluso fenómenos paranormales han sido descritos como efectos mecano-cuánticos.

Yo sospecho que todo esto es un intento de atribuir fenómenos “ininteligibles” a causas también “ininteligibles” (como la mecánica cuántica) dónde el resultado de cualquier cálculo es siempre una probabilidad, nunca una certeza.
Claro que, ahí están esas teorías más avanzadas y modernas que vienen abriendo los nuevos caminos de la Física y que, a mi no me cabe la menor duda, más tarde o más temprano, podrá explicar con claridad esas zonas de oscuridad que ahora tienen algunas teorías y que Einstein señalaba con acierto.
¿No es curioso que, cuando se formula la moderna Teoría M, surjan, como por encanto, las ecuaciones de Einstein de la Relatividad General? ¿Por qué están ahí? ¿Quiere eso decir que la Teoría de Einstein y la Mecánica Cuántica podrán al fin unirse en pacifico matrimonio sin que aparezcan los dichosos infinitos?
Bueno, eso será el origen de otro comentario que también, cualquier día de estos, dejaré aquí para todos ustedes.
Emilio Silvera Vázquez
Dic
12
Relatividad Especial: Luz, velodidad, tiempo, masa-energía
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (6)
Comments (6)
La radiación electromagnética es el producto de la variación periódica de los campos eléctrico y magnético. Un campo es una región del espacio en la que la materia está sometida a algún tipo de fuerza. En el caso de la radiación electromagnética, los campos son producidos por las partículas cargadas en movimiento. La luz visible es un tipo de radiación electromagnética. A veces se comporta como una onda que se propaga en el espacio, y otras veces se comporta como un conjunto de fotones. A este fenómeno se le denomina dualidad de la radiación.
Los distintos tipos de radiación electromagnética dependen directamente de las características de la onda, que son: frecuencia, longitud de onda y amplitud o intensidad. En realidad, como veremos a continuación, la frecuencia y la longitud de onda están directamente relacionadas, por lo que para describir completamente una onda, (la radiación electromagnética en nuestro caso) basta con dar información acerca de su amplitud y frecuencia (o longitud de onda). Las ondas electromagnéticas transportan energía siempre a la misma velocidad en el vacío: 299792 kilómetros por segundo, lo que se conoce como velocidad de la luz (c).


No todas las formas de radiación electromagnética pueden ser captadas por el ojo humano que sólo puede ver la que se nos aparece en forma de luz visible y de la cual depende nuestra consciencia visual del universo y sus contenidos. La Relatividad Especial nos dice que es precisamente la luz la que marca el límite de la velocidad que en el Universo se puede alcanzar. No vamos a meternos ahora en la polémica de si son ondas o partículas, o, las dos cosas según los casos. Sin embargo, una cosa sí que tenemos que dejar clara: Es una constante universal, aunque algunos se empeñen en querer quitarle esa primacía.

“El empuje warp, empuje por curvatura impulso de deformación o impulso de distorsión es una forma teórica de propulsión superlumínica. Este empuje permitiría propulsar una nave espacial a una velocidad equivalente a varios múltiplos de la velocidad de la luz, mientras se evitan los problemas asociados con la dilatación relativista del tiempo.”

La velocidad de la luz en el vacío es un límite que impone el Universo, nunca lo podremos superar. Sin embargo, es posible que con el paso del tiempo y el avance de los conocimientos tecnológicos, se pueda inventar la manera de “burlar” ese límite, no superarlo.
¿Será científicamente posible superar la velocidad de la Luz? ¿Los motores de curvatura que impulsaban a la nave Enterprise en sus escarceos por el espacio pueden convertirse en una realidad y permitirnos superar la velocidad de la luz?. Bueno, unos “científicos” de los que no recuerdo sus nombres, así lo han declarado. Sin embargo, si la velocidad de la luz puede ser superada, antes de que dicha proeza la puedan conseguir los hombres, creo que, si tal cambio de una constante natural llegara a producirse, sólo podría venir de cambios producidos en la misma Naturaleza, y, por nuestra parte, no podremos nunca superar la velocidad de la luz pero, sí podremos burlarla encontrando otros caminos hacia mundos y estrellas lejanos en remotas regiones del Universo.
Aunque muchas veces comentado, trataré de nuevo el tema de la velocidad de la luz y sus implicaciones reales en el transcurso del tiempo. La relatividad del movimiento es, por una parte, la clave para comprender la teoría de Einstein, y al mismo tiempo una fuente potencial de confusión.

¡El Tiempo transcurre inexorable, nada puede evitar que, como luciérnagas o gotas de agua, se escurra entre los “dedos” de nuestras efímeras vidas.
No es nada fácil dar una definición del tiempo, los intentos de hacerlo terminan a menudo dando vueltas y vueltas hasta llegar al punto de partida. Sin ir más lejos, en un trabajo mío de título “Pasado, Presente y Futuro. Una ilusión llamada Tiempo“, intenté explicar lo que es el tiempo y hablé de él desde distintos ángulos y bajo distintos puntos de vista. Durante muchas páginas trate el tiempo y me remonte hasta el Big Bang como fuente de su nacimiento, allí, junto a su hermano, el espacio, nació el tiempo. Sin embargo y pese a mi esfuerzo por esbozar una imagen escenificando lo que el Tiempo es… ¡No lo conseguí! Al igual que los mejores filósofos, fracasé en el intento y, la explicación es fácil: Nadie puede dar razón de algo que no conoce.
La precisión alcanzada con este tipo de reloj atómico es tan elevada que admite únicamente un error de un segundo en 30 000 000 años. El reloj más preciso del mundo se diseña en el Observatorio de París, donde los actuales relojes atómicos tardarían 52 millones de años para desfasarse un segundo. El nuevo objetivo de la investigación francesa es aumentar ese plazo a 32 000 millones de años. El estándar actual de los relojes atómicos en activo permite el atraso de un segundo cada 3700 millones de años (NIST).
En aquella ocasión, entre otras muchas cosas, hablé del reloj atómico de cesio-33, de la velocidad de la luz, de la fórmula matemática que explicaba la dilatación del tiempo a través de la velocidad, del tiempo de Planck, de las transformaciones de Lorentz, tiempo terrestre, tiempo dinámico, tiempo bariónico, tiempo estándar, tiempo universal, ¿Cuántos conceptos de tiempo podemos tener? Y, sin embargo, seguimos sin saber lo que el tiempo es, si es que, realmente, es algo más que una abstracción de nuestras mentes.
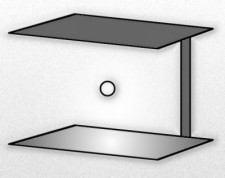
Podemos medir el tiempo en un reloj de luz pero nuestro objetivo es comprender cómo afecta el movimiento al transcurso del tiempo. Se conoce como “reloj de luz” al más sencillo del mundo y que consiste en dos pequeños espejos montados el uno frente al otro sobre un soporte, y entre ellos hay un único fotón de luz que salta del uno al otro. Si los espejos están separados unos 15 cm, el fotón tardará alrededor de una milmillonésima de segundo en realizar un viaje de ida y vuelta. Se puede considerar que el “tictac” de un reloj de luz se produce cada vez que un fotón hace un viaje de ida y vuelta completo. Mil millones de tictac indicarían que ha transcurrido un segundo. El fotón de uno a otro espejo realizando el viaje de ida y vuelta mil millones de veces en un segundo. El fotón no tiene masa y su velocidad es la de la luz, 299.792.458 m/s.
Tenemos que mencionar el carácter constante de la velocidad de la luz, y que el mismo implica que un reloj pueda marcar su tictac más lentamente. O dicho de otra manera, viajar a velocidades cercanas a la de la luz ralentiza el tiempo, así lo determina la teoría de la relatividad especial de Einstein. El tiempo transcurre más lentamente para un individuo en movimiento que para otro individuo que se encuentre en reposo. Si el razonamiento absolutamente sencillo que nos ha llevado a esta conclusión es correcto, entonces, ¿no tendríamos, por ejemplo, que poder vivir más tiempo estando en movimiento que permaneciendo inmóviles? Después de todo, si el tiempo transcurre más lentamente para un individuo en movimiento que para uno que está quieto, esta disparidad se podrá aplicar también, además de al tictac de un reloj, al latido de un corazón y al deterioro de algunas partes del cuerpo. Esto es así, y se ha confirmado directamente, no para la esperanza de vida de los humanos, sino para ciertas partículas del microespacio: los muones. No obstante, existe una pega importante que nos impide proclamar el hallazgo de la fuente de la juventud.
La ilusión de la fuente de la juventud que muchos han querido encontrar. NO existen los espejos mágicos

La fuente de la juventud, símbolo de la inmortalidad, es una legendaria fuente que supuestamente cura y devuelve la juventud a quienquiera que beba de sus aguas o se bañe en ellas.
Durante milenios, el sueño de hechiceros, magos y alquimistas ha sido el de encontrar el elixir de la eterna juventud. Y leyendas llegadas de los rincones de la tierra hablan de ríos, fuentes, árboles, frutos y pócimas con poderes para rejuvenecernos.
Pensar en la existencia de la fuente de la Juventud, no es nada nuevo. Muchos han sido los que la han buscado sin encontrarla, y, sin embargo, yo he tenido esa suerte pero, a pesar de ello, no es eterna como tantos esperaban. La “eternidad” no existe. Si acaso, en alguna circunstancia el paso del Tiempo se podría retrasar.
Cuando se encuentran en reposo en el laboratorio, los muones se desintegran mediante un proceso muy semejante a la desintegración de la radiactividad, en un promedio de tiempo de alrededor de dos millonésimas de segundo. Esta desintegración es un hecho experimental apoyado en una cantidad enorme de pruebas. El muón tiene una vida de 2 millonésimas de segundo, llegado a ese tiempo, se desintegra, explota para descomponerse en electrones y neutrinos.
Solenoide Compacto de Muones (CMS)
Estos experimentos con iones de plomo abren ´una nueva avenida en la investigación del programa del acelerador para sondear la materia tal como era en los primeros instantes del Universo´, justo después del Big Bang, según el CERN.
Muones lanzados a la velocidad de la luz que aumentan su masa

Fotografía facilitada por el Centro Europeo de Investigación Nuclear (CERN) de la reconstrucción de las primeras colisiones de iones de plomo, vistas por el detector de partículas llamado Solenoide Compacto de Muones (CMS) en la sede del CERN en Ginebra, Suiza.

Cadena de aceleradores
del Gran Colisionador de Hadrones (LHC)
Fotografía facilitada por el Centro Europeo de Investigación Nuclear (CERN) de la reconstrucción en línea del sistema High Level Trigger (HLT) que muestra pistas del Inner Tracking System (ITS) y la Cámara de Proyección de Tiempo (TPC) del ALICE de las primeras colisiones de iones de plomo, vistas por el detector de partículas llamado Solenoide Compacto de Muones (CMS) en la sede del CERN en Ginebra, Suiza. Estos experimentos con iones de plomo abren ´una nueva avenida en la investigación del programa del acelerador para sondear la materia tal como era en los primeros instantes del Universo, justo después del Big Bang, según el CERN.

La velocidad de la luz en el vacío (c), será siempre un muro infranqueable


Pero si los muones no están en reposo en el laboratorio, sino que viajan a través de un aparato denominado acelerador de partículas que los impulsa hasta alcanzar la velocidad de la luz, el promedio de su esperanza de vida medido por los científicos en el laboratorio aumenta drásticamente. Esto sucede realmente. A una velocidad de 298.168 kilómetros por segundo (alrededor del 99’5% de la velocidad de la luz), el tiempo de vida del muón se multiplica aproximadamente por diez. La explicación de esto, de acuerdo con la relatividad especial, es que los “relojes de pulsera” que llevan los muones hacen tictac mucho más lentamente que los relojes del laboratorio que están en reposo y su tictac es más rápido, o sea al ritmo normal cotidiano del transcurso del tiempo. Esta es una demostración muy directa y expresiva del efecto que produce el movimiento en el paso del tiempo. Si las personas pudieran moverse tan rápido como estos muones, su esperanza de vida subiría hasta los 800 años, al multiplicarse por el mismo factor 10 de los muónes.
¿Qué dónde está el truco?

Este movimiento no implica cambio alguno al no ser relativista, es un simple desplazamiento de lugar, la masa de la persona sigue siendo la misma.
Bueno, el que los muones en movimiento vivan 10 veces más tiempo que los muones en reposo se debe precisamente a que el movimiento “muy rápido” detiene el tiempo, no por completo, sino que lo ralentiza y lo hace ir más despacio. Claro que no todos los movimientos pueden conseguir este milagro.En nuestras vidas cotidianas en las que nos movemos con velocidades muy pequeñas comparadas con la de la luz, el tiempo transcurre de manera normal que, será rápido o lento en función de las circunstancias personales de cada uno de nosotros.

El Tiempo vuela
:format(jpg)/f.elconfidencial.com%2Foriginal%2F5ff%2Fdd3%2F211%2F5ffdd3211d8c300645b495a7571a2dd5.jpg)
El Tiempo se hace eterno si hay dolor mientras que, en la felicidad es efímero


¡La que formó el buen hombre! Entró en la Física como elefante en cacharrería
Este ejemplo es cotidiano y se coge la velocidad como protagonista de la demostración de lo que es la teoría de la relatividad especial. En el ejemplo del muón (que se podría extrapolar a una persona que viajara en una nave espacial a velocidades cercanas a la de la luz), el protagonista es el Tiempo, que como consecuencia de una alta velocidad se detiene para transcurrir más lento en función de la velocidad a la que se esté viajando, es el efecto predicho por la teoría de Einstein y demostrados experimentalmente. Los tiempos son relativos al movimiento de los observadores. El reloj viajero es más lento en un factor de
.
En otras ocasiones, comentando esto mismo, hice referencia al conocido, o más bien conocida paradoja de los gemelos. Uno, astronauta que parte para Alfa Centauro, y el otro, profesor que le despide. Ambos tienen 38 años. La nave parte hacia la estrella vecina y hace el viaje de ida y vuelta a la velocidad de la luz, descansando un día para tomar datos de la estrella. Al regreso, el hermano gemelo del astronauta va a recibirlo y cuando éste desciende de la nave, tiene la edad de 46’6 años, es decir, 8,6 años más que cuando salió que es el tiempo que ha tardado la nave en hacer el viaje de ida y vuelta, mientras que él ya está jubilado, tiene mucha más edad.
Resulta exactamente lo mismo que en el experimento del múón, el tiempo del gemelo astronauta que viajó muy rápido, pasó mucho más lento que el tiempo del gemelo profesor que siguió en la Tierra a un ritmo muchísimo más lento. Así la ecuación es inversa:
Movimiento rápido = Tiempo más lento y Movimiento más lento = Tiempo más rápido.
Por muy rápidos que podamos ir, aunque consigamos estirar el tiempo, todo sería una falsa ilusión, ya que, en ese exceso de tiempo sólo podríamos realizar las mismas cosas que en el tiempo normal, sólo que más lentamente.
Pero la ecuación no debe equivocarnos; el gemelo de la Tierra, el que ahora es más viejo, en realidad ha vivido mucho más que el otro, ha vivido toda una vida con todo lo que eso conlleva, mientras que el otro hermano, el viajero, sólo ha vivido un viaje; sí, algo largo (8’6 años luz), pero en dicho espacio de tiempo, al ser muy lento, sólo cabían las incidencias de un viaje en una nave espacial, mientras que el otro hermano ha comprimido el tiempo en cuanto a los muchos hechos que ha podido meter dentro, así que para él pasó mucho más rápido.

Nos tendríamos que preguntar ¿Por qué el Tiempo transcurre más rápido en el Espacio que en la Tierra
En realidad no es que el astronauta viviera más tiempo, sino que su tiempo pasaba mucho más lentamente porque él estaba corriendo más que su hermano, y corriendo tanto no da tiempo para hacer muchas cosas, sin embargo corriendo menos nos dará tiempo para todo. Ya sabes…Si tienes prisa…visteté despacio.
¡Qué locura!
Sí, es algo complicado, más de lo que pueda parecer, y sin embargo muy real. El astronauta vivió ese periodo de tiempo a cámara lenta, por eso “su tiempo” fue más largo o se tardó más tiempo para medirlo por el hecho cierto de que transcurría más lento. El fenómeno desapareció en el momento de tomar tierra, donde el tiempo era de nuevo el mismo para los dos hermanos. Así que durante la vida de 800 años al que antes aludíamos, en realidad podríamos hacer exactamente las mismas cosas que en la vida de 80 años, sólo que más lentamente.

Tenía buenas intenciones cuando propuso sus teorías pero, ¡la que ha formado!
La Relatividad Especial también dice que ocurre algo interesante al movernos a través del tiempo espacial, especialmente cuando tu velocidad relativa a otros objetos es cercana a la velocidad de la luz. El tiempo pasa más lentamente para ti que para las personas que has dejado atrás. No observarás este efecto hasta que regreses a esas personas estacionarias.
Así que después de todo esto llegamos a la conclusión del principio, la relatividad del movimiento es, por una parte, la clave para comprender la teoría de Einstein, y al mismo tiempo (repito) una fuente de confusión; hay que centrarse muy profundamente en el problema para llegar a verlo, de manera clara, en tu cabeza. A mí, al principio, no me entraba la idea. Después de un tiempo de ahondar en la relatividad especial, por fin se hizo la luz, y efectivamente el tiempo va más despacio para quien se mueva muy rápido.
En la vida cotidiana, donde las velocidades son pequeñas, las diferencias entre alguien que corre y otro que está parado, puede ser tan insignificante que, en realidad, es despreciable. Se podría viajar más rápido que la luz por un puente de Einstein-Rosen pero, ¿Dónde están esos puentes? Que sepamos, nadie ha visto ninguno.
Otra curiosidad de la relatividad especial es que el objeto que se mueva a la velocidad de la luz se acorta a lo largo de la dirección del movimiento. Por ejemplo, las ecuaciones de la relatividad especial demuestran que un objeto que se mueva aproximadamente al 98 por ciento de la velocidad de la luz, será medido por un observador inmóvil como un 80% más corto que cuando estaba parado, es lo que se conoce como la “Contracción de Lorentz”, que también es totalmente cierta. Pero además, a estas velocidades ocurre otra curiosidad: la masa del objeto aumenta considerablemente, ya que como el universo limita la velocidad que podemos alcanzar a la de la luz, cuando nos estamos acercando a ella, la energía que se traducía antes en velocidad, a partir de cierto punto se convierte en masa. No podemos olvidar que E = mc2, nos dice que la masa es energía y la energía es masa, son dos aspectos de la misma cosa.

Esquema sobre la contracción de Lorentz. (X′,cT′) representan las coordenadas de un observador en reposo a una barra, mientras que (X,cT) son las coordenadas de otro observador con respecto a dicha barra, por la naturaleza pseudoeuclídea del espacio-tiempo aun cuando el primer observador mide una longitud l, el segundo mide una longitud menor l/γ < l.
Einstein, en un principio, denominó a su teoría no como de la relatividad, la llamó teoría de la invariabilidad, para reflejar el carácter invariable de la velocidad de la luz. La obra de Einstein demostró que conceptos tales como espacio y tiempo, que anteriormente parecían estar separados y ser absolutos e inamovibles, en realidad están entrelazados y son relativos. Einstein demostró además que otras propiedades físicas del universo, sorprendentemente también están interrelacionadas. Arriba de esta misma página se reseña su famosa fórmula como uno de los ejemplos más importantes que afirma (y quedó más que demostrado) que E (energía) de un objeto y m (su masa) no están separados y se puede determinar la energía a través de la masa del objeto (multiplicando esta dos veces por la velocidad de la luz, o sea por c2).

Efímeros momentos… ¡La Eternidad no existe!
Sí, hemos podido comprobar millones de veces que masa y energía son la misma cosa. Sin embargo, en la actualidad desconocemos la naturaleza de la “materia y de la energía oscuras” que constituyen la mayor porción de aquello que compone el Universo (imagen abajo: MACS J0717.
Volvamos a un muón que se desplaza a un 99’999 por ciento de la velocidad de la luz, y su masa se multiplica por 224; a un 99’999 por ciento de la velocidad de la luz se multiplica por un factor que es más de 70.000. Como la masa del muón aumenta sin límite a medida que su velocidad se aproxima a la de la luz, sería necesario un impulso dado con una cantidad infinita de energía para alcanzar o superar la barrera de la velocidad de la luz. Como una cantidad infinita de energía no existe, de nuevo aparece el límite que el universo impone a la velocidad, nada podrá superar la velocidad de la luz. Al menos en este universo que conocemos donde las constantes universales, como la masa del electrón, la constante de estructura fina, o la velocidad de la luz, son como son para que el universo sea como lo conocemos y para que nosotros podamos estar aquí.
La constante de estructura fina de Sommerfeld (símbolo α) es la constante física fundamental que caracteriza la fuerza de la interacción electromagnética. Es una cantidad sin dimensiones, por lo que su valor numérico es independiente del sistema de unidades usado
Una mínima variación en alguna de estas constantes universales, seguramente habría impedido que nosotros surgiéramos a la vida en el planeta Tierra. Sin embargo, algunos no se paran a pensar y, de buenas a primeras, nos dicen que la velocidad de la luz no es el límite de la velocidad que se puede alcanzar en nuestro Universo. ¿Será posible? ¿Cómo algunos no piensan antes de hablar?
Emilio Silvera Vázquez
















 Totales: 75.670.067
Totales: 75.670.067 Conectados: 51
Conectados: 51