
Dic
11
Los Quarks invisibles
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (1)
Comments (1)
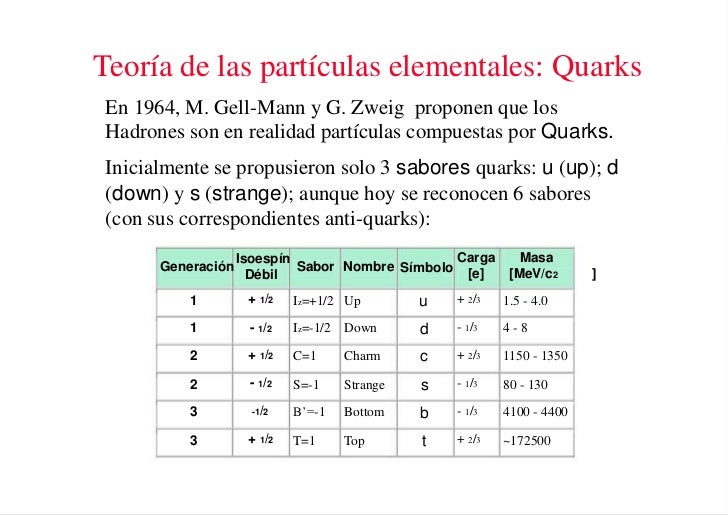
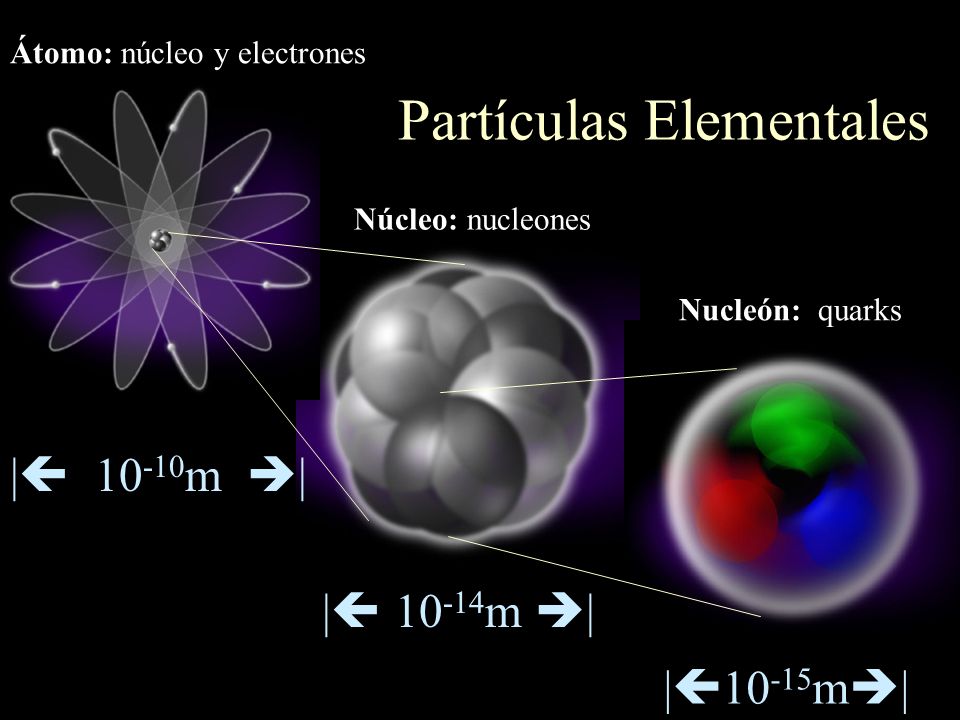
Una vez que se ha puesto orden entre las numerosas especies de partículas, se puede reconocer una pauta. Igual que Dimitri Ivanovich Mendeleev descubrió el sistema periódico de los elementos químicos en 1869, así también se hizo visible un sistema similar para las partículas. Esta pauta la encontraron independientemente el americano Murray Gell-Mann y el israelí Yuval Ne’eman. Ocho especies de mesones, todos con el mismo espín, u ocho especies de bariones, con el mismo espín, se podían reagrupar perfectamente en grupos que llamaremos multipletes. El esquema matemático correspondiente se llama SU(3). Grupletes de ocho elementos forman un octete “fundamental”. Por esta razón Gell-Mann llamó a esta teoría el “óctuplo camino”. Lo tomó prestado del budismo de acuerdo con el cual el camino hacia el nirvana es el camino óctuplo.

Rueda del dharma
El dharma chakra (o “rueda del darma”, “rueda de la ley”) es un símbolo que representa al dharma (‘ley’ o ‘religión’), en el hinduismo, el budismo y el jainismo. Ocasionalmente se traduce como ‘rueda de doctrina’. El dharmachakra o rueda del dharma.
El Noble Camino Óctuple es considerado, según el budismo, como la vía que lleva al cese del sufrimiento. Este cese del sufrimiento se conoce como nirvana. Puede ser que eso fuese lo que sintiera Gell-Mann al finalizar sus trabajos, y, de ahí la adopción del nombre y todo lo que lleva consigo de simbología.

El noble camino es una de las enseñanzas budistas fundamentales; la cuarta parte de las Cutro Nobles Verdades. En la simbología budista, el noble camino es usualmente representado con la rueda del dharma, donde cada rayo representa un elemento del sendero. Este símbolo también se utiliza para el budismo en general.
Los elementos del noble camino óctuple se subdividen en tres categorías básicas: sabiduría, conducta ética y entrenamiento de la mente (o meditación); para rehabilitar y desacondicionar la mente. En todos los elementos del noble camino, la palabra «correcta» es una traducción de la palabra “sammā” (en pali), que significa ‘plenitud’, ‘coherencia’, ‘perfección’ o ‘ideal’. El noble camino es: Sabiduría.
Pero sigamos con el trabajo.
Las matemáticas SU(3) también admiten multipletes de diez miembros. Cuando se propuso este esquema se conocían nueve bariones con espín 3/2. Los esquemas SU(3) se obtienen al representar dos propiedades fundamentales de las partículas, la extrañeza S frente al iso-espín I₃ , en una gráfica.
Primera observación de un neutrino en una cámara de burbujas, noviembre de 1970. El neutrino incidente golpea un protón (a la derecha en la foto). El neutrino se transforma en un leptón mu (la larga traza en medio de la foto). La traza corta es el protón. La tercera traza es de un mesón pi.
Arriba dos imágenes de trazas en la cámara de burbujas del primer evento observado incluyendo bariones Ω, en el Laboratorio Nacional Brookhaven. Dependiendo de su masa y tamaño las partículas producen distintos remolinos en la cámara de burbujas.
De esta manera, Gell-Mann predijo un décimo barión, el omega-menos (Ω¯), y pudo estimar con bastante precisión su masa porque las masas de los otros nueve bariones variaban de una forma sistemática en el gráfico (también consiguió entender que las variaciones de la masa eran una consecuencia de una interacción simple). Sin embargo, estaba claro que la Ω¯, con una extrañeza S = -3, no tenía ninguna partícula en la que desintegrarse que no estuviera prohibida por las leyes de conservación de la interacción fuerte. De modo que, la Ω¯ sólo podía ser de tan sólo 10¯²³ segundos como los demás miembros del multiplete, sino que tenía que ser del orden de 10¯¹⁰ segundos. Consecuentemente, esta partícula debería viajar varios centímetros antes de desintegrarse y esto la haría fácilmente detectable. La Ω¯ fue encontrada en 1964 con exactamente las mismas propiedades que había predicho Gell-Mann.
Se identificaron estructuras multipletes para la mayoría de los demás bariones y mesones y Gell-Mann también consiguió explicarlas. Sugirió que los mesones, igual que los bariones, debían estar formados por elementos constitutivos “más fundamentales aún”. Gell-Mann trabajaba en el Instituto de Tecnología de California en Pasadena (CalTech), donde conversaba a menudo con Richard Feynman. Eran ambos físicos famosos pero con personalidades muy diferentes. Gell-Mann, por ejemplo, es conocido como un entusiasta observador de Pájaros, familiarizado con las artes y la literatura y orgulloso de su conocimiento de lenguas extranjeras.

A comienzos de los años sesenta, un profesor del Instituto de Tecnología de California (Caltech) imparte un curso completo de física ante una cada día más numerosa. Su nombre: Richard Feynman
Feynman fue un hombre hecho a sí mismo, un analista riguroso que se reía de cualquier cosa que le recordara la autoridad establecida. Hay una anécdota que parece no ser cierta de hecho, pero que me parece tan buena que no puedo evitar el contarla; podía haber sucedido de esta forma. Gell-Mann le dijo a Feynman que tenía un problema, que estaba sugiriendo un nuevo tipo de ladrillos constitutivos de la materia y que no sabía qué nombre darles. Indudablemente debía haber de haber pensado en utilizar terminología latina o griega, como ha sido costumbre siempre en la nomenclatura científica. “Absurdo”, le dijo Feynman; “tú estás hablando de cosas en las que nunc ase había pensado antes. Todas esas preciosas pero anticuadas palabras están fuera de lugar. ¿Por qué no los llamas simplemente “shrumpfs”, “quacks” o algo así?”.


Los pequeños componentes de la materia ordinaria
Cuando algún tiempo después le pregunté a Gell-Mann, éste negó que tal conversación hubiera tenido lugar. Pero la palabra elegida fue quark, y la explicación de Gell-Mann fue que la palabra venía de una frase de Fynnegan’s Wake de James Joyce; “¡Tres quarks para Muster Mark!”. Y, efectivamente así es. A esas partículas les gusta estar las tres juntas. Todos los bariones están formados por tres quarks, mientras que los mesones están formados por un quark y un anti-quark.


Los propios quarks forman un grupo SU(3) aún más sencillo. Los llamaremos “arriba (u)”, “abajo” (d), y “extraño” (s). Las partículas “ordinarias” contienen solamente quarks u y d. Los hadrones “extraños” contienen uno o más quarks s (o antiquarks ŝ).
La composición de quarks de espín 3/2 se puede ver en cualquier tabla de física.. La razón por la que los bariones de espín ½ sólo forman un octete es más difícil de explicar. Está relacionada con el hecho de que en estos estados, al menos dos de los quarks tienen que ser diferentes unos de otros.

Junto con los descubrimientos de los Hadrones y de sus componentes, los Quarks, durante la primera mitad del sigo XX, se descubrieron otras partículas. Los Hadrones forman dos ramas, los mesones formados por dos quarks y los bariones por tres.
 .
.
:format(jpg)/f.elconfidencial.com%2Foriginal%2Fdd9%2F7af%2F724%2Fdd97af724d3beb0d79794af2f42d5d52.jpg)
La Mecánica cuántica es muy extraña
Realmente, la idea de que los hadrones estuvieran formados por ladrillos fundamentales sencillos había sido también sugerida por otros. George Zweig, también en el Cal Tech, en Pasadena, había tenido la misma idea. Él había llamado a los bloques constitutivos “ases!, pero es la palabra “quark” la que ha prevalecido. La razón por la que algunos nombres científicos tienen más éxito que otros es a veces difícil de comprender.
Pero en esta teoría había algunos aspectos raros. Aparentemente, los quarks (o ases) siempre existen en parejas o tríos y nunca se han visto solos. Los experimentadores habían intentado numerosas veces detectar un quark aislado en aparatos especialmente diseñados para ello, pero ninguno había tenido éxito.

Loa quarks –si se pudieran aislar- tendrían propiedades incluso más extrañas. Por ejemplo, ¿Cuáles serían sus cargas eléctricas? Es razonable suponer que tanto los quarks u como los quarks s y d deban tener siempre la misma carga. La comparación de la tabla 5 con la tabla 2 sugiere claramente que los quarks d y s tienen carga eléctrica -1/3 y el quark u tiene carga +2/3. Pero nunca se han observado partículas que no tengan carga múltiplo de la del electrón o de la del protón. Si tales partículas existieran, sería posible detectarlas experimentalmente. Que esto haya sido imposible debe significar que las fuerzas que las mantienen unidas dentro del hadrón son necesariamente increíblemente eficientes.

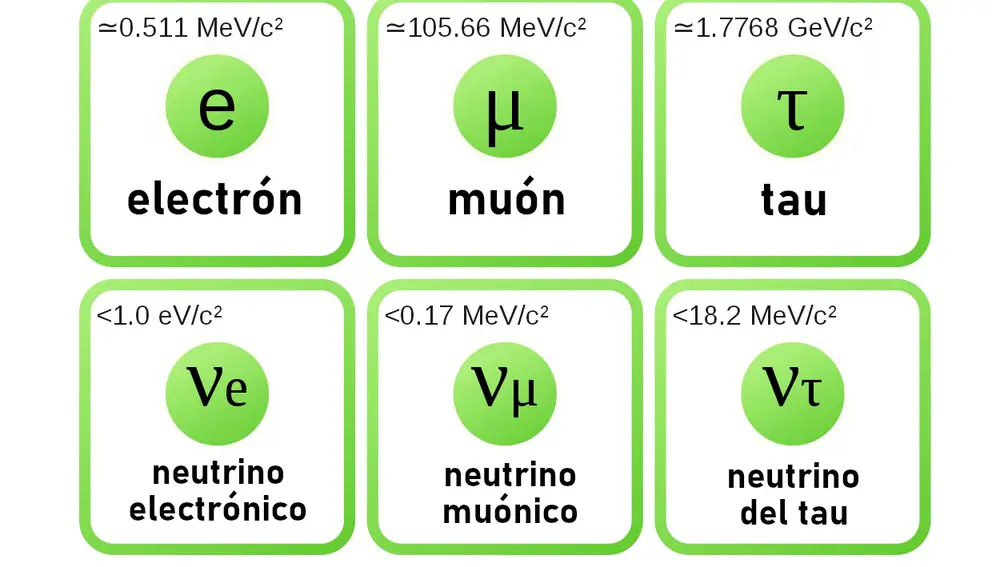
Todos sabemos que los Leptones son: El electrón, el muón y la partícula Tau y, cada una de ellas tiene su tipo de neutrino: el electrónico, el muónico y el tauónico.
Aunque con la llegada de los quarks se ha clarificado algo más la flora y la fauna de las partículas subatómicas, todavía forman un conjunto muy raro, aún cuando solamente unas pocas aparezcan en grandes cantidades en el universo (protones, neutrones, electrones y fotones). Como dijo una vez Sybren S. de Groot cuando estudiaba neutrinos, uno realmente se enamora de ellos. Mis estudiantes y yo amábamos esas partículas cuyo comportamiento era un gran misterio. Los leptones, por ser casi puntuales, son los más sencillos, y por tener espín se ven afectados por la interacción que actúa sobre ellos de forma muy complicada, pero la interacción débil estaba bastante bien documentada por entonces.

Los hadrones son mucho más misteriosos. Los procesos de choque entre ellos eran demasiado complicados para una teoría respetable. Si uno se los imagina como pequeñas esferas hachas de alguna clase de material, aún quedaba el problema de entender los quarks y encontrar la razón por la que se siguen resistiendo a los intentos de los experimentadores para aislarlos.
Emilio Silvera Vázquez
Si queréis saber más sobre el tema, os recomiendo leer el libro Partículas de Gerard ´t Hooft
Dic
6
Observando el movimiento combinado de núcleos y electrones
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (0)
Comments (0)

… IMDEA Nanociencia y el Instituto Politécnico de Zurich han logrado observar por primera vez el movimiento correlacionado de electrones y núcleos …
Gracias a los espectaculares avances que la tecnología láser ha experimentado en la última década, hoy es posible visualizar el movimiento de los electrones en el interior de átomos y moléculas. Para esto se utilizan pulsos de luz ultravioleta o de rayos X con una duración de tan sólo unos pocos cientos de atto-segundos (10 -18 segundos), que es la escala de tiempo en la que se mueven los electrones de forma natural.
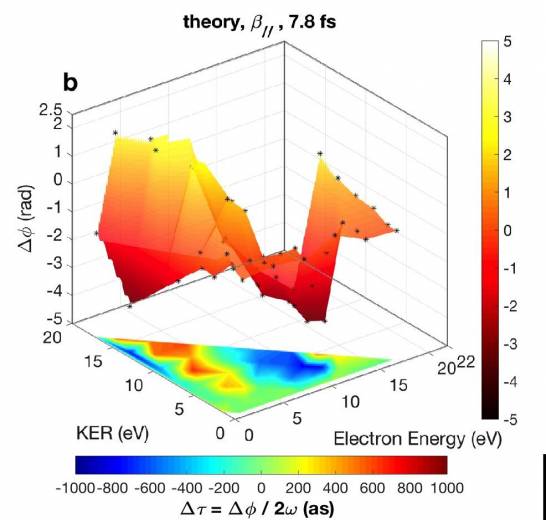
Para esto se utilizan pulsos de luz ultravioleta o de rayos X con una duración de tan sólo unos pocos cientos de attosegundos, que es la escala de tiempo en la que se mueven los electrones de forma natural. En una molécula, además de los electrones, también se mueven los núcleos atómicos que la componen.
En una molécula, además de los electrones, también se mueven los núcleos atómicos que la componen. En un reciente trabajo publicado en la revista Nature Physics, investigadores de la Universidad Autónoma de Madrid (UAM) (España), IMDEA Nanociencia e Instituto Politécnico de Zurich observaron por primera vez el movimiento combinado de electrones y núcleos en la molécula de hidrógeno (H2), demostrando explícitamente que existe una enorme interdependencia entre ellos.

Como electrones y núcleos son los responsables de la formación de enlaces químicos en las moléculas (desde el H2 al ADN), estos resultados abren la puerta a manipular las propiedades de estos enlaces actuando indistintamente sobre electrones o núcleos en intervalos de tiempos del orden de los atto-segundos.
Observando el movimiento combinado de núcleos y electrones
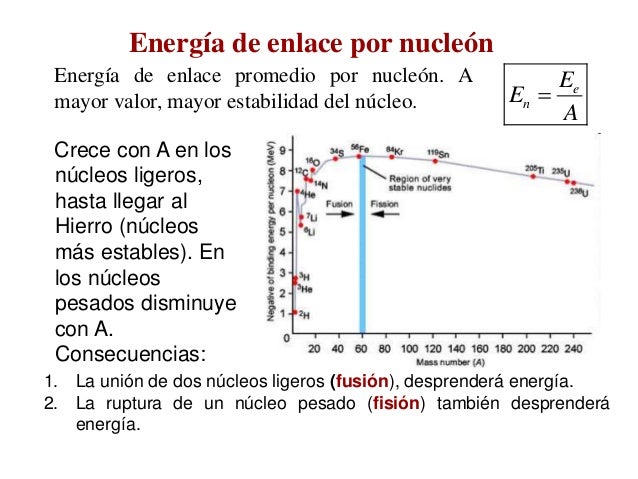
Las reacciones químicas son consecuencia de la rotura y formación de enlaces entre núcleos atómicos en una molécula, lo que conduce a la formación de otras moléculas distintas. El que los enlaces se formen o se rompan se debe principalmente al movimiento de los electrones, que con su carga eléctrica negativa apantallan la repulsión entre los núcleos de carga eléctrica positiva.
Sin embargo, estos últimos también se mueven, con lo que la reactividad química es en realidad un proceso dinámico que resulta del movimiento combinado de electrones y núcleos. En general, el movimiento de los núcleos es mucho más lento que el de los electrones, porque los primeros son mucho más pesados que los segundos.
![OC] Nubes de electrones de hidrógeno en 2D : r/dataisbeautiful](https://preview.redd.it/p41rvqbfyka51.jpg?auto=webp&s=23a4bf4ae359b5c2bc5b38a78937799da1cc60e0)

La figura muestra que el tiempo que tarda el electrón en abandonar la molécula de hidrógeno depende fuertemente de la energía del protón y viceversa, demostrando el alto grado de correlación que existe entre ambos tipos de movimiento. (Foto: UAM)
Por ejemplo, el núcleo más ligero que existe, el del átomo de hidrógeno (protón, p+), es aproximadamente 1.800 veces más pesado que un electrón (e-). Sin embargo, cuando una molécula absorbe energía de una fuente externa, por ejemplo la luz, los núcleos pueden llegar a moverse casi tan rápido como los electrones (dependiendo de cómo se repartan la energía entre ellos).

La mecánica cuántica nos mostró un “mundo” asombroso
En estos casos, cabe esperar que el movimiento de núcleos y electrones esté correlacionado, es decir, que el movimiento de unos condicione el movimiento de los otros. Como muchas de las reacciones químicas se inician irradiando las moléculas con luz externa, visualizar este movimiento correlacionado en tiempo real es de enorme importancia para entender cómo se producen tales reacciones.
“En nuestro grupo ya habíamos demostrado anteriormente que la combinación de pulsos de luz de attosegundos y femtosegundos con el denominado esquema bombeo-sonda, donde uno de los pulsos induce una cierta dinámica en un átomo o molécula y el otro toma ‘fotografías’ de la misma en distintos instantes, permitiendo visualizar el movimiento de uno o varios electrones, incluso cuando estos últimos se mueven de forma concertada”, afirma Fernando Martín, investigador de la UAM y director del trabajo.
Observación en tiempo real del movimiento correlacionado de núcleos y electrones
Por su parte, la coautora Alicia Palacios, también investigadora de la UAM, añade: “En este trabajo hemos demostrado que, utilizando un esquema bombeo-sonda en combinación con técnicas de detección de multi-coincidencia en las que se mide simultáneamente la energía y el momento de electrones y núcleos, es posible visualizar a la vez el movimiento de ambos tipos de partículas. Además, este movimiento está en efecto correlacionado”.

Para llegar a esta conclusión, los científicos realizaron un experimento en el que la molécula de hidrógeno se bombardeó con un tren de pulsos ultravioletas de atto-segundos, sincronizado con un pulso infrarrojo de femtosegundos, y variaron el retardo entre ambos tipos de pulsos con una precisión de tan solo unas decenas de atto-segundos.
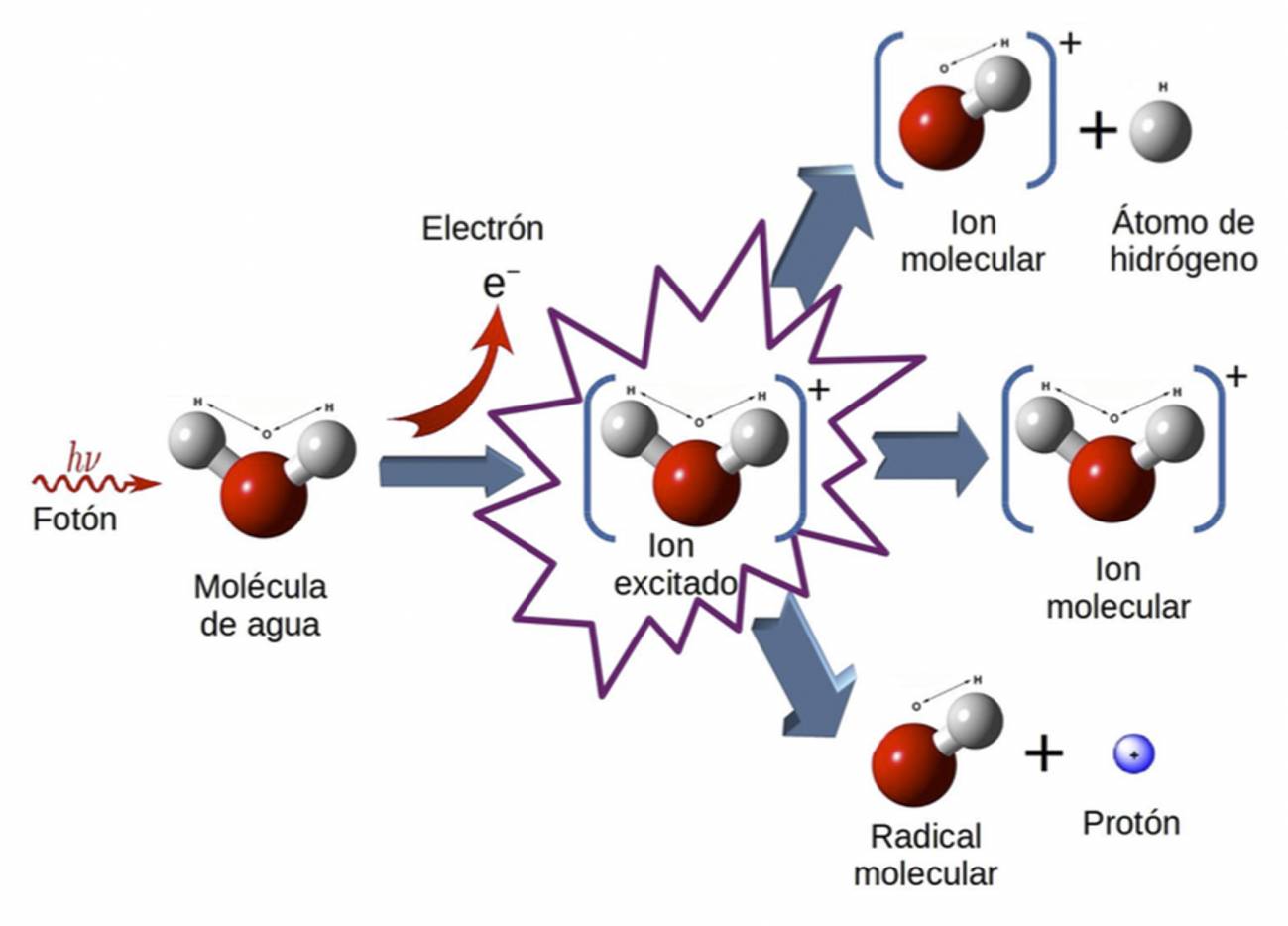
Esta secuencia de pulsos produce inevitablemente la ionización y la disociación de la molécula, dando lugar a la emisión de un electrón, un protón y un átomo de hidrógeno. La detección del electrón (e-) y del protón (p+) en coincidencia para todos los retrasos temporales, en combinación con elaborados cálculos mecano-cuánticos, permitió visualizar el movimiento concertado de estas dos partículas en la molécula.
Las gráficas muestran que el tiempo que tarda el electrón en abandonar la molécula de hidrógeno depende fuertemente de la energía del protón y viceversa, demostrando el alto grado de correlación que existe entre ambos tipos de movimiento. (Fuente: UAM)

Dic
5
El “mundo” de lo muy pequeño… ¡Es tan extraño!
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (1)
Comments (1)

Nube de electrones que rodea al núcleo
Sabemos que los electrones son partículas de la familia de los Leptones, tienen carga negativa, que existen en una nube alrededor del núcleo atómico. Son inimaginablemente pequeños, tan pequeños que se necesita de la mecánica cuántica para explicar su comportamiento peculiar. Sin embargo y a pesar de su pequeñez, son partículas fundamentales del Universo.
Algunas propiedades:

El valor del radio del electrón el SI es 2.817 940 322 7 (19) × 10−15 m.
Muchas veces hemos hablado del electrón que rodea el núcleo, de su carga eléctrica negativa que complementa la positiva de los protones y hace estable al átomo; tiene una masa de solamente 1/1.836 de la del núcleo más ligero (el del hidrógeno). La importancia del electrón es vital en el universo. Simplemente con que su carga fuera distinta en una pequeña fracción… ¡El mundo que nos rodea sería muy diferente! Y, ni la vida estaría presente en el Universo.
La Ciencia busca, teoriza y experimenta tratando de saber cómo funciona el universo
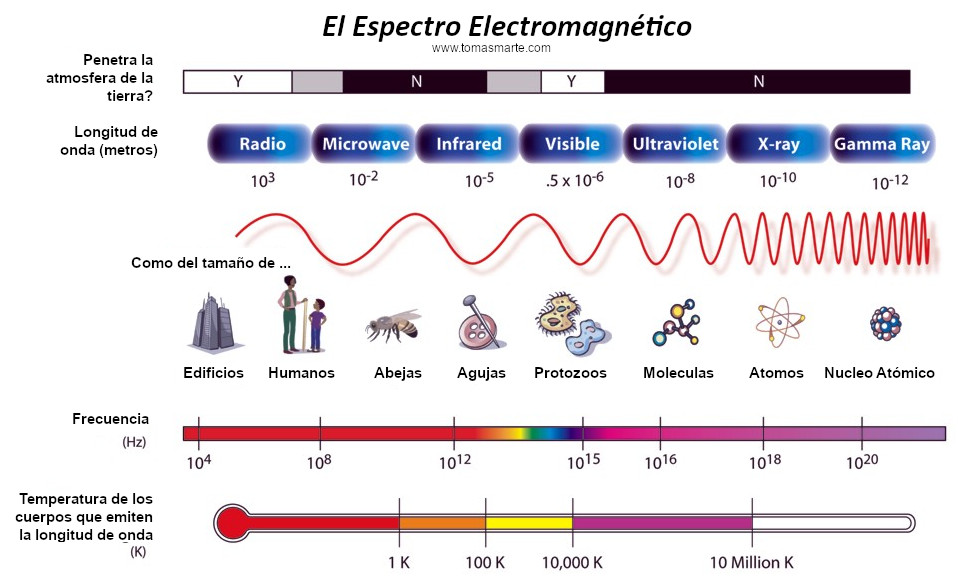
Pero busquemos los “cuantos”. La física del siglo XX empezó exactamente en el año 1900, cuando el físico alemán Max Planck propuso una posible solución a un problema que había estado intrigando a los físicos durante años. Es el problema de la luz que emiten los cuerpos calentados a una cierta temperatura, y también la radiación infrarroja emitida, con menor intensidad, por los objetos más fríos (radiación de cuerpo negro).

Hipótesis cuántica de Planck donde c es la velocidad de la luz en el vacío y k B k B es la constante de Boltzmann, k B = 1,380 × 10 −23 J/K . k B = 1,380 × 10 −23 J/K . La fórmula teórica expresada en la Ecuación 6.11 se denomina ley de radiación de cuerpo negro de Planck.
Estaba bien aceptado entonces que esta radiación tenía un origen electromagnético y que se conocían las leyes de la naturaleza que regían estas ondas electromagnéticas. También se conocían las leyes para el frío y el calor, la así llamada “termodinámica”, o al menos eso parecía. Pero si utilizamos las leyes de la termodinámica para calcular la intensidad de una radiación, el resultado no tiene ningún sentido. Los cálculos nos dicen que se emitiría una cantidad infinita de radiación en el ultravioleta más lejano y, desde luego, esto no es lo que sucede. Lo que se observa es que la intensidad de la radiación muestra un pico a una cierta longitud de onda característica, y que la intensidad disminuye tanto para longitudes mayores como para menores. Esta longitud de onda característica es inversamente proporcional a la temperatura absoluta de objeto radiante (la temperatura absoluta se define por una escala de temperatura que empieza a 273º bajo cero). Cuando a 1.000º C un objeto se pone al “rojo vivo”, el objeto está radiando en la zona de luz visible.

Lo que Planck propuso fue simplemente que la radiación sólo podía ser emitida en paquetes de un tamaño dado. La cantidad de energía de uno de esos paquetes, o cuantos, es inversamente proporcional a la longitud de onda, y por tanto, proporcional a la frecuencia de radiación emitida. La fórmula es E = hν, donde E es la energía del paquete, ν es la frecuencia y h es una nueva constante fundamental de la naturaleza, la constante de Planck. Cuando Planck calculó la intensidad de la radiación térmica imponiendo esta nueva condición, el resultado coincidió perfectamente con las observaciones.

Einstein realizó importantes descubrimientos en el campo fotoeléctrico. Éstos le hicieron merecedor del Premio Nobel de Física en 1922. El efecto fotoeléctrico afirma que un material es capaz de liberar o hacer circular electrones por un material conductor gracias a la energía recibida por un haz de luz.
Poco tiempo después, en 1905, Einstein formuló esta teoría de una manera mucho más tajante: él sugirió que los objetos calientes no son los únicos que emiten radiación en paquetes de energía, sino que toda la radiación consiste en múltiplos del paquete de energía de Planck. El príncipe francés Louis-Victor de Broglie, dándole otra vuelta a la teoría, propuso que no sólo cualquier cosa que oscila tiene energía, sino que cualquier cosa con energía se debe comportar como una “onda” que se extiende en una cierta región del espacio, y que la frecuencia ν de la oscilación verifica la ecuación de Planck. Por lo tanto, los cuantos asociados con los rayos de luz deberían verse como una clase de partículas elementales: el fotón. Todas las demás clases de partículas llevan asociadas diferentes ondas oscilantes de campos de fuerza, pero esto lo veremos más adelante.

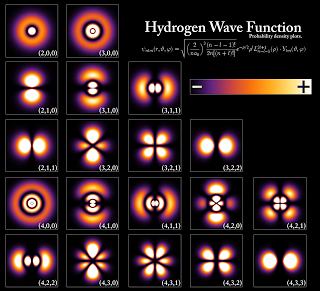
La función de onda de Schrödinger nos acercó a ese mundo infinitesimal
La primera es la imagen obtenida por los físicos en el laboratorio y, la segunda es la Imagen ilustrativa de la dualidad onda-partícula, con la cual se quiere significar cómo un mismo fenómeno puede tener dos percepciones distintas. Lo cierto es que, el mundo de lo muy pequeño es extraño y no siempre lo podemos comprender.
El curioso comportamiento de los electrones en el interior del átomo, descubierto y explicado por el famoso físico danés Niels Bohr, se pudo atribuir a las ondas de de Broglie. Poco después, en 1926, Edwin Schrödinger descubrió cómo escribir la teoría ondulatoria de de Broglie con ecuaciones matemáticas exactas. La precisión con la cual se podían realizar cálculos era asombrosa, y pronto quedó claro que el comportamiento de todos los objetos pequeños quedaba exactamente determinado por las recién descubiertas “ecuaciones de ondas cuánticas”.

Está bien comprobado que la mecánica cuántica funciona de maravilla…, pero, sin embargo, surge una pregunta muy formal: ¿Qué significan realmente estas ecuaciones?, ¿Qué es lo que están describiendo? Cuando Isaac Newton, allá en 1867 formuló cómo debían moverse los planetas alrededor del Sol, estaba claro para todo el mundo qué significaban sus ecuaciones: que los planetas estaban siempre en una posición bien definida des espacio y que sus posiciones y sus velocidades en un momento concreto determinan inequívocamente cómo evolucionarán las posiciones y las velocidades en el tiempo.

Teletransporte y efecto túnel
El electrón está situado en una órbita exterior, llega un fotón energético que choca contra él, el electrón desaparece, y, de inmediato aparece en otra órbita más energética cerca del núcleo. ¿Por dónde hizo el viaje?, ¿Cómo se desplazó de una órbita a otra sin recorrer las distancias que les separan?
Pero para los electrones todo es diferente. Su comportamiento parece estar envuelto en misterio. Es como si pudieran “existir” en diferentes lugares simultáneamente, como si fueran una nube o una onda, y esto no es un efecto pequeño. Si se realizan experimentos con suficiente precisión, se puede determinar que el electrón parece capaz de moverse simultáneamente a lo largo de trayectorias muy separadas unas de otras. ¿Qué puede significar todo esto?

El “universo de las partículas nunca ha sido fácil de comprender y su rica diversidad, nos habla de un vasto “mundo” que se rige por su propias reglas que hemos tenido que ir conociendo y seguimos tratando de saber, el por qué de esos comportamientos extraños y a veces misteriosos. Así, la pregunta anterior, de ¿qué puede significar todo eso?…

La pudo contestar Niels Bohr, de forma tal que, con su explicación se pudo seguir trabajando, y muchos físicos siguen considerando su respuesta satisfactoria. Se conoce como la interpretación de Copenhague de la mecánica cuántica.
¿Qué es cuantizar?


Así se estudia y experimenta en los aceleradores de partículas de qué está hecha la materia. El encontronazo y estallido final, nos descubre nuevas partículas. Estamos tratando de saber que puede existir más allá de los Quarks
Las leyes de la mecánica cuántica han sido establecidas con mucha precisión; permite cómo calcular cualquier cosa que queramos saber. Pero si queremos “interpretar” el resultado, nos encontramos con una curiosa incertidumbre fundamental: que varias propiedades de las partículas pequeñas no pueden estar bien definidas de manera simultánea. Por ejemplo, podemos determinar la velocidad de una partícula con mucha precisión, pero entonces no sabremos exactamente dónde se encuentra; o a la inversa, podemos determinar la posición con precisión, pero entonces su velocidad queda mal definida. Si una partícula tiene espín (rotación alrededor de su eje), la dirección alrededor de la cual está rotando (la orientación del eje) no puede ser definida con gran precisión.

No es fácil explicar de forma sencilla de dónde viene esta incertidumbre, pero existen ejemplos en la vida cotidiana que tienen algo parecido. La altura de un tono y la duración en el tiempo durante el cual oímos el tono tienen una incertidumbre mutua similar. Para afinar un instrumento musical se debe escuchar una nota durante un cierto intervalo de tiempo y compararla, por ejemplo, con un diapasón que debe vibrar también durante un tiempo. Notas muy breves no tienen bien definido el tono.


Para que las reglas de la mecánica cuántica funcionen, es necesario que todos los fenómenos naturales en el mundo de las cosas pequeñas estén regidos por las mismas reglas. Esto incluye a los virus, bacterias e incluso a las personas. Sin embargo, cuando más grande y más pesado es un objeto, más difícil es observar las desviaciones de las leyes del movimiento “clásicas” debidas a la mecánica cuántica. Me gustaría referirme a esta exigencia tan importante y tan peculiar de la teoría con la palabra “holismo”. Esto no es exactamente lo mismo que entienden algunos filósofos por holismo, y que podría definir como “el todo es más que la suma de sus partes”. Si la física nos ha enseñado algo es justo lo contrario. Un objeto compuesto de un gran número de partículas puede ser entendido exactamente si se conocen las propiedades de sus partes (partículas); basta que sepamos sumar correctamente (¡y esto no es nada fácil en mecánica cuántica!). Lo que entiendo por holismo es que, efectivamente, el todo es la suma de las partes, pero sólo se puede hacer la suma si todas las partes obedecen a las mismas leyes. Por ejemplo, la constante de Planck, h, que es igual a 6’626075… × 10-34 Julios segundo, debe ser exactamente la misma para cualquier objeto en cualquier sitio, es decir, debe ser una constante universal.
Mucho ha sido el camino andado hasta nuestros tratando de conocer los secretos de la naturaleza que, poco a poco, nos van siendo familiares. Sin embargo, es más el camino que nos queda por recorrer. Es mucho lo que no sabemos y, tanto el micro-mundo como en el vasto mundo de muy grande, hay que cosas que aún, no hemos llegado a comprender.

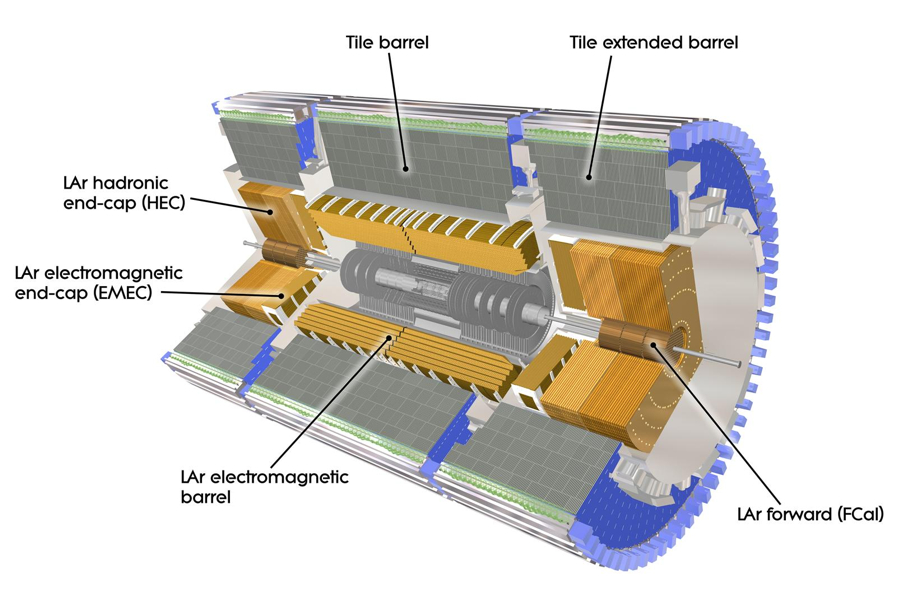

El detector ATLAS funcionó, y rastrearon las partículas subatómicas…
Las reglas de la mecánica cuántica funcionan tan bien que refutarlas resulta realmente difícil. Los “trucos” ingeniosos descubiertos por Werner Heisenberg, Paul Dirac y muchos otros mejoraron y completaron las reglas generales. Pero Einstein y otros pioneros como Erwin Schrödinger siempre presentaron serias objeciones a esta interpretación. Quizá funcione bien, pero ¿Dónde está exactamente el electrón?, ¿en el punto x o en el punto y? En pocas palabras, ¿Dónde está en realidad?, y ¿Cuál es la realidad que hay detrás de nuestras fórmulas? Si tenemos que creer a Bohr, no tiene sentido buscar tal realidad. Las reglas de la mecánica cuántica, por sí mismas, y las observaciones realizadas con detectores son las únicas realidades de las que podemos hablar.
Es cierto que, localizar y saber en qué punto exacto están esas pequeñas partículas… no es fácil
La mecánica cuántica puede ser definida o resumida así: en principio, con las leyes de la naturaleza que conocemos ahora se puede predecir el resultado de cualquier experimento, en el sentido que la predicción consiste en dos factores: el primer factor es un cálculo definido con exactitud del efecto de las fuerzas y estructuras, tan riguroso como las leyes de Isaac Newton para el movimiento de los planetas en el Sistema Solar; el segundo factor es una arbitrariedad estadística e incontrolable definida matemáticamente de forma estricta. Las partículas seguirán una distribución de probabilidades dadas, primero de una forma y luego de otra. Las probabilidades se pueden calcular utilizando la ecuación de Schrödinger de función de onda (Ψ) que, con muchas probabilidades nos indicará el lugar probable donde se encuentra una partícula en un momento dado.

La teoría de probabilidades se ocupa de asignar un cierto número a cada posible resultado que pueda ocurrir en un experimento aleatorio, con el fin de cuantificar dichos resultados y saber si un suceso es más probable que otro.
Muchos estiman que esta teoría de las probabilidades desaparecerá cuando se consiga la teoría que explique, de forma completa, todas las fuerzas; la buscada teoría del todo, lo que implica que nuestra descripción actual incluye variables y fuerzas que (aún) no conocemos o no entendemos. Esta interpretación se conoce como hipótesis de las variables ocultas.

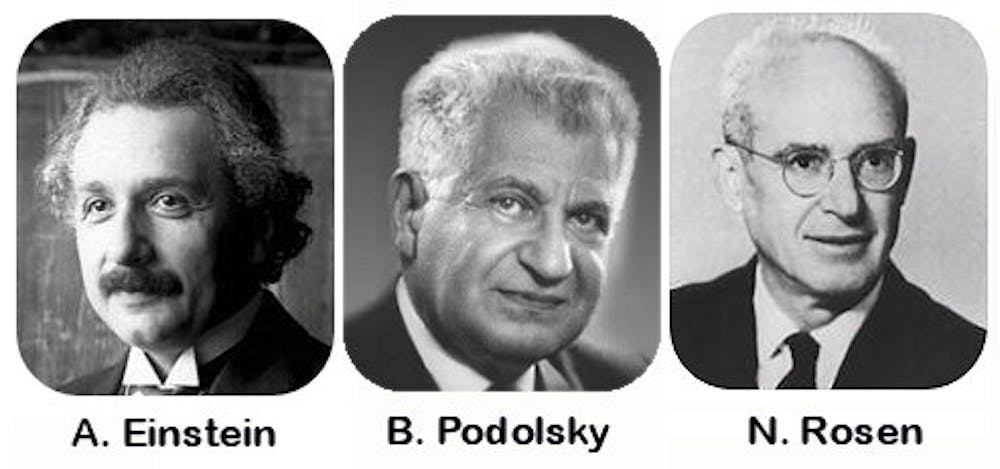
Albert Einstein, Nathan Rosen y Boris Podolski idearon un “Gedankenexperiment”, un experimento hipotético, realizado sobre el papel, para el cual la mecánica cuántica predecía como resultado algo que es imposible de reproducir en ninguna teoría razonable de variables ocultas. Más tarde, el físico irlandés John Stewar Bell consiguió convertir este resultado en un teorema matemático; el teorema de imposibilidad.
(“El teorema de Bell o desigualdades de Bell se aplica en mecánica cuántica para cuantificar matemáticamente las implicaciones planteadas teóricamente en la paradoja de Einstein-Podolsky-Rosen y permitir así su demostración experimental. Debe su nombre al científico norirlandés John S. Bell, que la presentó en 1964.

Ilustración del test de Bell para partículas de espín 1/2. La fuente produce un par de espín singlete, una partícula se envía a Alicia y otra a Bob. Cada una mide uno de los dos espines posibles.
El teorema de Bell es un meta-teorema que muestra que las predicciones de la mecánica cuántica (MC) no son intuitivas, y afecta a temas filosóficos fundamentales de la física moderna. Es el legado más famoso del físico John S. Bell. El teorema de Bell es un teorema de imposibilidad, que afirma que:
Ninguna teoría física de variables ocultas locales puede reproducir todas las predicciones de la mecánica cuántica.”)

¿Cómo saber el número que saldrá cuando lanzamos los dados?
¡¡La mecánica cuántica!!, o, la perplejidad de nuestros sentidos ante lo que ese “universo cuántico” nos ofrece que, generalmente, se sale de lo que entendemos por sentido común. Ahí, en el “mundo” de los objetos infinitesimales, suceden cosas que no siempre podemos comprender. Y, como todo tiene una razón, no dejamos de buscarla en cada uno de aquellos sorprendentes sucesos que en ese lugar se producen. Podríamos llegar a la conclusión de que, la razón está en todo y solo la encontramos una vez que llegamos a comprender, mientras tanto, todo nos resulta extraño, irrazonable, extramundano y, algunas veces…imposible. Sin embargo, ahí está. Dos elementos actúan de común acuerdo para garantizar que no podamos descorrer el velo del futuro, de lo que será después (podemos predecir aproximaciones, nunca certezas), el principal de esos elementos es la ignorancia nunca podremos saber el resultado final de éste o aquél suceso sin tener la certeza de las condiciones iniciales. En la mayoría de los sistemas físicos son, en mayor o menor medida dada su complejidad, del tipo caótico es tal que, el resultado de las interacciones entre elementos es sumamente sensibles a pequeñísimas variaciones de los estados iniciales que, al ser perturbados mínimamente, hacen que el suceso final sea y esté muy alejado del que se creía al comienzo.
Lo que nos lleva a confirmar que el futuro es siempre incierto. ¿Es bueno desconocer lo que nos pasará mañana? Bueno, el Universo cree que sí, y, así lo dispuso.
Emilio Silvera Vázquez
Nov
27
Todo lo grande está hecho… ¡De cosas pequeñas!
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (1)
Comments (1)
El tiempo de Planck o cronón (término acuñado en 1926 por Robert Lévi) es una unidad de tiempo, considerada como el intervalo temporal más pequeño que puede ser medido. Se denota mediante el símbolo tP. En cosmología, el tiempo de Planck representa el instante de tiempo más pequeño en el que las leyes de la física pueden ser utilizadas para estudiar la naturaleza y evolución del Universo. Se determina como combinación de otras constantes físicas en la forma siguiente:
 segundos
segundos
donde:
 es la constante de Planck reducida (conocida también como la constante de Dirac).
es la constante de Planck reducida (conocida también como la constante de Dirac). - G es la constante de Gravitación Universal;
- c es la velocidad de la luz en el vacío.
Los números entre paréntesis muestran la desviación estándar.
En este ámbito hablamos de las cosas muy pequeñas, las que no se ven.
Es el tiempo que necesita el fotón (viajando a la velocidad de la luz, c, para moverse a través de una distancia igual a la longitud de Planck. Está dado por , donde G es la constante gravitacional (6, 672 59 (85) x 10-11 N m2 kg-2), ħ es la constante de Planck racionalizada (ħ = h/2л = 1,054589 x 10-34 Julios segundo), c, es la velocidad de la luz (299.792.458 m/s).
El valor del tiempo del Planck es del orden de 10-44 segundos. En la cosmología del Big Bang, hasta un tiempo Tp después del instante inicial, es necesaria usar una teoría cuántica de la gravedad para describir la evolución del Universo. Todo, desde Einstein, es relativo. Depende de la pregunta que se formule y de quién nos de la respuesta.

¿El Tiempo? Muchos Filósofos lo quisieron explicar pero… ¡No pudieron!
Si preguntamos ¿Qué es el tiempo?, tendríamos que ser precisos y especificar si estamos preguntando por esa dimensión temporal que no deja de fluir desde el Big Bang y que nos acompaña a lo largo de nuestras vidas, o nos referimos al tiempo atómico, ese adoptado por el SI, cuya unidad es el segundo y se basa en las frecuencias atómicas, definida a partir de una línea espectral particular de átomo de cesio 133, o nos referimos a lo que se conoce como tiempo civil, tiempo coordinado, tiempo de crecimiento, tiempo de cruce, tiempo de integración, tiempo de relajación, tiempo dinámico o dinámico de Baricéntrico, dinámico terrestre, tiempo terrestre, tiempo de Efemérides, de huso horario, tiempo estándar, tiempo local, tiempo luz, tiempo medio, etc. etc. Cada una de estas versiones del tiempo, tiene una respuesta diferente, ya que, no es lo mismo el tiempo propio que el tiempo sidéreo o el tiempo solar, o solar aparente, o solar medio, o tiempo terrestre, o tiempo Universal. Como se puede ver, la respuesta dependerá de cómo hagamos la pregunta.

… Y, que el mismo tiempo suele borrar
En realidad, para todos nosotros el único tiempo que rige es el que tenemos a lo largo de nuestras vidas, los otros tiempos, son inventos del hombre para facilitar sus tareas de medida, de convivencia o de otras cuestiones técnicas o astronómicas pero, sin embargo, el tiempo es solo uno; ese que comenzó cuando nació el Universo y que finalizará cuando este llegue a su final.
Lo cierto es que, para las estrellas supermasivas, cuando llegan al final de su ciclo y deja de brillar por agotamiento de su combustible nuclear, en ese preciso instante, el tiempo se agota para ella. Cuando una estrella pierde el equilibrio existente entre la energía termonuclear (que tiende a expandir la estrella), y, la fuerza de gravedad (que tiende a comprimirla), al quedar sin oposición esta última, la estrella supermasiva se contrae aplastada bajo su propia masa. Queda comprimida hasta tal nivel que llega un momento que desaparece, para convertirse en un Agujero Negro, una singularidad, donde dejan de existir el “tiempo” y el espacio. A su alrededor nace un horizonte de sucesos que, si se traspasa, se es engullido por la enorme gravedad del Agujero Negro.

En la singularidad no se distorsiona, se para
El tiempo, de ésta manera, deja de existir en estas regiones del Universo que conocemos como singularidad. El mismo Big Bang -dicen- surgió de una singularidad de energía y densidad infinitas que, al explotar, se expandió y creó el tiempo, el espacio y la materia.
Como contraposición a estas enormes densidades de las enanas blancas, estrellas de neutrones y Agujeros Negros, existen regiones del espacio que contienen menos galaxias que el promedio o incluso ninguna galaxia; a estas regiones las conocemos como vacío cósmico. Han sido detectados vacíos con menos de una décima de la densidad promedio del Universo en escalas de hasta 200 millones de años luz en exploraciones a gran escala. Estas regiones son a menudo esféricas. El primer gran vacío en ser detectado fue el de Boötes en 1.981; tiene un radio de unos 180 millones de años luz y su centro se encuentra aproximadamente a 500 millones de años luz de la Vía Láctea. La existencia de grandes vacíos no es sorprendente, dada la existencia de cúmulos de galaxias y supercúmulos a escalas muy grandes.
Mientras que en estas regiones la materia es muy escasa, en una sola estrella de neutrones, si pudiéramos retirar 1 cm3 de su masa, obtendríamos una cantidad de materia increíble. Su densidad es de 1017 kg/m3, los electrones y los protones están tan juntos que se combinan y forman neutrones que se degeneran haciendo estable la estrella de ese nombre que, después del agujero negro, es el objeto estelar más denso del Universo.
Es interesante ver cómo a través de las matemáticas y la geometría, han sabido los humanos encontrar la forma de medir el mundo y encontrar las formas del Universo. Pasando por Arquímedes, Pitágoras, Newton, Gauss o Riemann (entre otros), siempre hemos tratado de buscar las respuestas de las cosas por medio de las matemáticas.
“Magia es cualquier tecnología suficientemente avanzada”
Arthur C. Clarke
Pero también es magia el hecho de que, en cualquier tiempo y lugar, de manera inesperada, aparezca una persona dotada de condiciones especiales que le permiten ver, estructuras complejas matemáticas que hacen posible que la Humanidad avance considerablemente a través de esos nuevos conceptos que nos permiten entrar en espacios antes cerrados, ampliando el horizonte de nuestro saber.

Recuerdo aquí uno de esos extraños casos que surgió el día 10 de Junio de 1.854 con el nacimiento de una nueva geometría: La teoría de dimensiones más altas que fue introducida cuando Georg Friedrich Bernhard Riemann dio su célebre conferencia en la facultad de la Universidad de Gotinga en Alemania. Aquello fue como abrir de golpe, todas las ventanas cerradas durante 2.000 años, de una lóbrega habitación que, de pronto, se ve inundada por la luz cegadora de un Sol radiante. Riemann regaló al mundo las sorprendentes propiedades del espacio multidimensional.
Su ensayo de profunda importancia y elegancia excepcional, “sobre las hipótesis que subyacen en los fundamentos de la geometría” derribó pilares de la geometría clásica griega, que habían resistido con éxito todos los asaltos de los escépticos durante dos milenios. La vieja geometría de Euclides, en la cual todas las figuras geométricas son de dos o tres dimensiones, se venía abajo, mientras una nueva geometría riemanniana surgía de sus ruinas. La revolución riemanniana iba a tener grandes consecuencias para el futuro de las artes y las ciencias. En menos de tres decenios, la “misteriosa cuarta dimensión” influiría en la evolución del arte, la filosofía y la Literatura en toda Europa. Antes de que hubieran pasado seis decenios a partir de la conferencia de Riemann, Einstein utilizaría la geometría riemanniana tetradimensional para explicar la creación del Universo y su evolución mediante su asombrosa teoría de la relatividad general Ciento treinta años después de su conferencia, los físicos utilizarían la geometría deca-dimensional para intentar unir todas las leyes del Universo. El núcleo de la obra de Riemann era la comprensión de las leyes físicas mediante su simplificación al contemplarlas en espacios de más dimensiones.

¿Cuántas dimensiones existen en el Universo?
Contradictoriamente, Riemann era la persona menos indicada para anunciar tan profunda y completa evolución en el pensamiento matemático y físico. Era huraño, solitario y sufría crisis nerviosas. De salud muy precaria que arruinó su vida en la miseria abyecta y la tuberculosis.
Riemann nació en 1.826 en Hannover, Alemania, segundo de los seis hijos de un pobre pastor luterano que trabajó y se esforzó como humilde predicador para alimentar a su numerosa familia que, mal alimentada, tendrían una delicada salud que les llevaría a una temprana muerte. La madre de Riemann también murió antes de que sus hijos hubieran crecido.
A edad muy temprana, Riemann mostraba ya los rasgos que le hicieron famoso: increíble capacidad de cálculo que era el contrapunto a su gran timidez y temor a expresarse en público. Terriblemente apocado era objeto de bromas de otros niños, lo que le hizo recogerse aún más en un mundo matemático intensamente privado que le salvaba del mundo hostil exterior.
Para complacer a su padre, Riemann se propuso hacerse estudiante de teología, obtener un puesto remunerado como pastor y ayudar a su familia. En la escuela secundaria estudió la Biblia con intensidad, pero sus pensamientos volvían siempre a las matemáticas. Aprendía tan rápidamente que siempre estaba por delante de los conocimientos de sus instructores, que encontraron imposible mantenerse a su altura. Finalmente, el director de la escuela dio a Riemann un pesado libro para mantenerle ocupado. El libro era la Teoría de números de Adrien-Marie Legendre, una voluminosa obra maestra de 859 páginas, el tratado más avanzado del mundo sobre el difícil tema de la teoría de números. Riemann devoró el libro en seis días.

Cuando el director le preguntó: “¿Hasta dónde has leído?”, el joven Riemann respondió: “Este es un libro maravilloso. Ya me lo sé todo”.
Sin creerse realmente la afirmación de su pupilo, el director le planteó varios meses después cuestiones complejas sobre el contenido del libro, que Riemann respondió correctamente.
Con mil sacrificios, el padre de Riemann consiguió reunir los fondos necesarios para que, a los 19 años pudiera acudir a la Universidad de Gotinga, donde encontró a Carl Friedrich Gauss, el aclamado por todos “Príncipe de las Matemáticas”, uno de los mayores matemáticos de todos los tiempos. Incluso hoy, si hacemos una selección por expertos para distinguir a los matemáticos más grandes de la Historia, aparecerá indudablemente Euclides, Arquímedes, Newton y Gauss.

Hannover, Alemania
Los estudios de Riemann no fueron un camino de rosas precisamente. Alemania sacudida por disturbios, manifestaciones y levantamientos, fue reclutado en el cuerpo de estudiantes para proteger al rey en el palacio real de Berlín y sus estudios quedaron interrumpidos.
En aquel ambiente el problema que captó el interés de Riemann, fue el colapso que, según el pensaba, suponía la geometría euclidiana, que mantiene que el espacio es tridimensional y “plano” (en el espacio plano, la distancia más corta entre dos puntos es la línea recta; lo que descarta la posibilidad de que el espacio pueda estar curvado, como en una esfera).
Para Riemann, la geometría de Euclides era particularmente estéril cuando se la comparaba con la rica diversidad del mundo. En ninguna parte vería Riemann las figuras geométricas planas idealizadas por Euclides. Las montañas, las olas del mar, las nubes y los torbellinos no son círculos, triángulos o cuadrados perfectos, sino objetos curvos que se doblan y retuercen en una diversidad infinita. Riemann, ante aquella realidad se rebeló contra la aparente precisión matemática de la geometría griega, cuyos fundamentos., descubrió el, estaban basados en definitiva sobre las arenas movedizas del sentido común y la intuición, no sobre el terreno firme de la lógica y la realidad del mundo.
Euclides nos habló de la obviedad de que un punto no tiene dimensión. Una línea tiene una dimensión: longitud. Un plano tiene dos dimensiones: longitud y anchura. Un sólido tiene tres dimensiones: longitud, anchura y altura. Y allí se detiene. Nada tiene cuatro dimensiones, incluso Aristóteles afirmó que la cuarta dimensión era imposible. En Sobre el cielo, escribió: “La línea tiene magnitud en una dirección, el plano en dos direcciones, y el sólido en tres direcciones, y más allá de éstas no hay otra magnitud porque los tres son todas.” Además, en el año 150 d. C. el astrónomo Ptolomeo de Alejandría fue más allá de Aristóteles y ofreció, en su libro sobre la distancia, la primera “demostración” ingeniosa de que la cuarta dimensión es imposible.
En realidad, lo único que Ptolomeo demostraba era que, era imposible visualizar la cuarta dimensión con nuestros cerebros tridimensionales (de hecho, hoy sabemos que muchos objetos matemáticos no pueden ser visualizados, aunque puede demostrarse que en realidad, existen). Ptolomeo puede pasar a la Historia como el hombre que se opuso a dos grandes ideas en la ciencia: el sistema solar heliocéntrico y la cuarta dimensión.
La ruptura decisiva con la geometría euclidiana llegó cuando Gauss pidió a su discípulo Riemann que preparara una presentación oral sobre los “fundamentos de la geometría”. Gauss estaba muy interesado en ver si su discípulo podía desarrollar una alternativa a la geometría de Euclides.
Riemann desarrolló su teoría de dimensiones más altas.
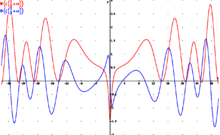
Parte real (rojo) y parte imaginaria (azul) de la línea crítica Re(s) = 1/2 de la función zeta de Riemann. Pueden verse los primeros ceros no triviales en Im(s) = ±14,135, ±21,022 y ±25,011. La hipótesis de Riemann, por su relación con la distribución de los números primos en el conjunto de los naturales, es uno de los problemas abiertos más importantes en la matemática contemporánea.
Finalmente, cuando hizo su presentación oral en 1.854, la recepción fue entusiasta. Visto en retrospectiva, esta fue, sin discusión, una de las conferencias públicas más importantes en la historia de las matemáticas. Rápidamente se entendió por toda Europa la noticia de que Riemann había roto definitivamente los límites de la geometría de Euclides que había regido las matemáticas durante los milenios.
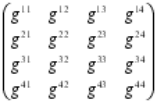
Riemann creó el tensor métrico para que, a partir de ese momento, otros dispusieran de una poderosa herramienta que les hacía posible expresar a partir del famoso teorema de Pitágoras (uno de los grandes descubrimientos de los griegos en matemáticas que establece la relación entre las longitudes de los tres lados de un triángulo rectángulo: afirma que la suma de los cuadrados de los lados menores es igual al cuadrado del lado mayor, la hipotenusa; es decir, si a y b son los longitudes de los dos catetos, y c es la longitud de la hipotenusa, entonces a2 + b2 = c2. El teorema de Pitágoras, por supuesto, es la base de toda la arquitectura; toda estructura construida en este planeta está basada en él. Claro que, es una herramienta para utilizar en un mundo tridimensional.)
![16 - Curso de Relatividad General [Tensor de Riemann]](https://i.ytimg.com/vi/SxFczZoSx_0/maxresdefault.jpg)
El tensor métrico de Riemann, o N dimensiones, fue mucho más allá y podemos decir que es el teorema para dimensiones más altas con el que podemos describir fenómenos espaciales que no son planos, tales como un remolino causado en el agua o en la atmósfera, como por ejemplo también la curvatura del espacio en presencia de grandes masas. Precisamente, el tensor de Riemann, permitió a Einstein formular su teoría de la gravedad y, posteriormente lo utilizo Kaluza y Klein para su teoría en la quinta dimensión de la que años más tarde se derivaron las teorías de super-gravedad, supersimetría y, finalmente las supercuerdas.

Para asombro de Einstein, cuando tuvo ante sus ojos la conferencia de Riemann de 1.854, que le había enviado su amigo Marcel Grossman, rápidamente se dio cuenta de que allí estaba la clave para resolver su problema. Descubrió que podía incorporar todo el cuerpo del trabajo de Riemann en la reformulación de su principio. Casi línea por línea, el gran trabajo de Riemann encontraba su verdadero lugar en el principio de Einstein de a relatividad general. Esta fue la obra más soberbia de Einstein, incluso más que su celebrada ecuación E=mc2. La reinterpretación física de la famosa conferencia de Riemann se denomina ahora relatividad general, y las ecuaciones de campo de Einstein se sitúan entre las ideas más profundas de la historia de la ciencia.
Supo aunar las ideas de muchos para construir algo asombroso
Emilio Silvera Vázquez
Nov
25
¿Será igual el Universo en todas partes?
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (0)
Comments (0)
En todo el Universo suceden las mismas cosas. La evolución de una estrella como el Sol, siempre será la misma, no importa en qué lugar esté. Cuando agote su combustible nuclear de fusión, viajará hasta la Gigante Roja, formará una Nebulosa planetaria y, finalmente, quedará como enana blanca.

La vieron caer y corrieron hasta el lugar. La escena era la que se podía esperar después de la caída de una nave en plena montaña. Los pocos testigos que por el lugar estaban, llamaron a las autoridades que enviaron, de inmediato, a personal especializado en este tipo de investigaciones.¡
“Mira, un trazo de la nave caída, ¿de qué materiales estará hecha? Nunca he visto algo así! ¿De dónde vendrán estos seres, de qué estará conformado su mundo? Esto preguntaba uno de los investigadores al otro que con él recogía muestras de aquella extraña nave accidentada y que, según el seguimiento hecho en su acercamiento a la Tierra, venía de más allá de los confines del Sistema Solar y, quién sabe de dónde pudieron partir. Sin embargo, el material que recogían, debería ser el mismo que está repartido por todo el Universo.
Lo único que puede diferir, es la forma en que se utilice, el tratamiento que se le pueda dar, y, sobre todo el poseer el conocimiento y la tecnología necesarios para poder obtener, el máximo resultado de las propiedades que dicha materia encierra. Porque, en última instancia ¿es en verdad inerte la materia?
¿Cómo pudo la materia “inerte” evolucionar hasta los pensamientos
Tiene y encierra tantos misterios la materia que estamos aún y años-luz de saber y conocer sobre su verdadera naturaleza. Nos podríamos preguntar miles de cosas que no sabríamos contestar. Nos maravillan y asombran fenómenos naturales que ocurren ante nuestros ojos pero que tampoco sabemos, en realidad, a que son debidos. Si, sabemos ponerles etiquetas como, por ejemplo, la fuerza nuclear débil, la fisión espontánea que tiene lugar en algunos elementos como el protactinio o el torio y, con mayor frecuencia, en los elementos que conocemos como transuránicos.
![⚗️ ¿Qué son los Elementos Transuránicos? ⚗️ [Fácil y Rápido] | QUÍMICA |](https://i.ytimg.com/vi/Gmb96-zqhyM/maxresdefault.jpg)

A medida que los núcleos se hacen más grandes, la probabilidad de una fisión espontánea aumenta. En los elementos más pesados de todos (einstenio, fermio y mendelevio), esto se convierte en el método más importante de ruptura, sobre pasando a la emisión de partículas alfa.

¡Parece que la materia está viva! ¿Cómo se pudo organizar como lo hizo?
Son muchas las cosas que desconocemos y, nuestra curiosidad nos empuja continuamente a buscar esas respuestas. El electrón y el positrón son notables por sus pequeñas masas (sólo 1/1.836 de la del protón, el neutrón, el antiprotón o antineutrón), y, por lo tanto, han sido denominados leptones (de la voz griega lentos, que significa “delgado”).
Aunque el electrón fue descubierto en 1.897 por el físico británico Josepth John Thomson (1856-1940), el problema de su estructura, si la hay, no está resuelto. Conocemos su masa y su carga negativa que responden a 9,1093897 (54)x10-31kg la primera y, 1,602 177 33 (49)x10-19 culombios, la segunda, y también su radio clásico: no se ha descubierto aún ninguna partícula que sea menos cursiva que el electrón (o positrón) y que lleve una carga eléctrica, sea lo que fuese (sabemos como actúa y cómo medir sus propiedades, pero aun no sabemos qué es), tenga asociada un mínimo de masa, y que esta es la que se muestra en el electrón.
Lo cierto es que, el electrón, es una maravilla en sí mismo. El Universo no sería como lo conocemos si el electrón (esa cosita “insignificante”), fuese distinto a como es, bastaría un cambio infinitesimal para que, por ejemplo, nosotros no pudiéramos estar aquí ahora para poder construir conjuntos tan bellos como el que abajo podemos admirar.

Pensemos en lo infinitesimal que son los electrones… ¡Sin ellos no habría átomos, moléculas, células ni materia!
¡No por pequeño, se es insignificante! De todas las maneras, las medidas dependen del contexto en el que se estén midiendo. El conjunto de la imagen de arriba nos parecerá grande pero, ¿Cómo de grande es si lo comparamos con la Galaxia?
Recordémoslo, todo lo grande está hecho de cosas pequeñas. En realidad, existen partículas que no tienen en absoluto asociada en ellas ninguna masa (es decir, ninguna masa en reposo). Por ejemplo, las ondas de luz y otras formas de radiación electromagnéticas se comportan como partículas (Einstein en su efecto fotoeléctrico y De Broglie en la difracción de electrones. Esta manifestación en forma de partículas de lo que, de ordinario, concebimos como una onda se denomina fotón, de la palabra griega que significa “luz”.

No pocas veces nos hemos preguntado: “¿Cómo puede tener energía los fotones si no tienen masa?
h = 6.626 × 10 -34 julios·s
c = 2.998 × 108 m/s
Al multiplicar estos dos se obtiene una expresión única, hc = 1.99 × 10-25 julios-m
La relación inversa anterior significa que la luz con fotones de alta energía (como la luz “azul”) tiene una longitud de onda corta. La luz que consta de fotones de baja energía (como la luz “roja”) tiene una longitud de onda larga.
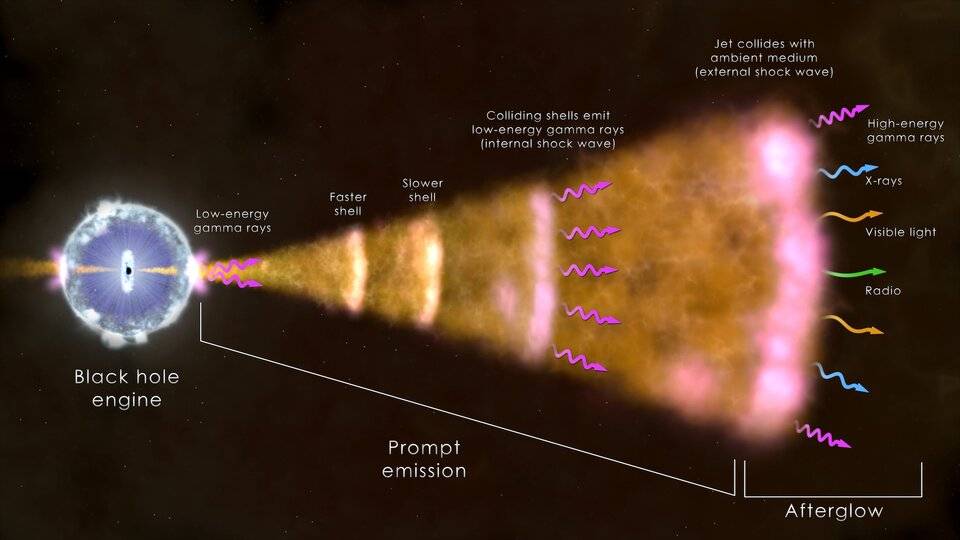
“Es la partícula portadora de todas las formas de radiación electromagnética, incluyendo a los rayos gamma, los rayos X, la luz ultravioleta, la luz visible, la luz infrarroja, las microondas, y las ondas de radio. El fotón tiene masa cero y viaja en el vacío con una velocidad constante c.”
“El fotón tiene una masa cero, una carga eléctrica de o, pero posee un espín de 1, por lo que es un bosón. ¿Cómo se puede definir lo que es el espín? Los fotones toman parte en las reacciones nucleares, pero el espín total de las partículas implicadas antes y después de la reacción deben permanecer inmutadas (conservación del espín). La única forma que esto suceda en las reacciones nucleares que implican a los fotones radica en suponer que el fotón tiene un espín de 1. El fotón no se considera un leptón, puesto que este termino se reserva para la familia formada por el electrón, el muón y la partícula Tau con sus correspondientes neutrinos: Ve, Vu y VT.”

Existen razones teóricas para suponer que, cuando las masas se aceleran (como cuando se mueven en órbitas elípticas en torno a otra masa o llevan a cabo un colapso gravitacional), emiten energía en forma de ondas gravitacionales. Esas ondas pueden así mismo poseer aspecto de partícula, por lo que toda partícula gravitacional recibe el nombre de gravitón.
La fuerza gravitatoria es mucho, mucho más débil que la fuerza electromagnética. Un protón y un electrón se atraen gravitacionalmente con sólo 1/1039 de la fuerza en que se atraen electromagnéticamente. El gravitón (aún sin descubrir) debe poseer, correspondientemente, menos energía que el fotón y, por tanto, ha de ser inimaginablemente difícil de detectar.
De todos modos, el físico norteamericano Joseph Weber emprendió en 1.957 la formidable tarea de detectar el gravitón. Llegó a emplear un par de cilindros de aluminio de 153 cm. De longitud y 66 de anchura, suspendidos de un cable en una cámara de vacío. Los gravitones (que serían detectados en forma de ondas), desplazarían levemente esos cilindros, y se empleó un sistema para detectar el desplazamiento que llegare a captar la cienmillonésima parte de un centímetro.

Las débiles ondas de los gravitones, que producen del espacio profundo, deberían chocar contra todo el planeta, y los cilindros separados por grandes distancias se verán afectados de forma simultánea. En 1.969, Weber anunció haber detectado los efectos de las ondas gravitatorias. Aquello produjo una enorme excitación, puesto que apoyaba una teoría particularmente importante (la teoría de Einstein de la relatividad general). Desgraciadamente, nunca se pudo comprobar mediante las pruebas realizadas por otros equipos de científicos que duplicaran el hallazgo de Weber.
De todas formas, no creo que, a estas alturas, nadie pueda dudar de la existencia de los gravitones, el bosón mediador de la fuerza gravitatoria. La masa del gravitón es o, su carga es o, y su espín de 2. Como el fotón, no tiene antipartícula, ellos mismos hacen las dos versiones.
Tenemos que volver a los que posiblemente son los objetos más misteriosos de nuestro Universo: Los agujeros negros. Si estos objetos son lo que se dice (no parece que se pueda objetar nada en contrario), seguramente serán ellos los que, finalmente, nos faciliten las respuestas sobre las ondas gravitacionales y el esquivo gravitón.
La onda gravitacional emitida por el agujero negro produce una ondulación en la curvatura del espacio-temporal que viaja a la velocidad de la luz transportada por los gravitones.

Hay aspectos de la física que me dejan totalmente sin habla, me obligan a pensar y me transporta de este mundo material nuestro a otro fascinante donde residen las maravillas del Universo. Hay magnitudes asociadas con las leyes de la gravedad cuántica. La longitud de Planck-Wheeler, es la escala de longitud por debajo de la cual el espacio tal como lo conocemos deja de existir y se convierte en espuma cuántica. El tiempo de Planck-Wheeler (1/c veces la longitud de Planck-Wheeler o aproximadamente 10-43segundos), es el intervalo de tiempo más corto que puede existir; si dos sucesos están separados por menos que esto, no se puede decir cuál sucede antes y cuál después. El área de Planck-Wheeler (el cuadrado de la longitud de Planck-Wheeler, es decir, 2,61×10-66cm2) juega un papel clave en la entropíade un agujero negro.
Me llama poderosamente la atención lo que conocemos como las fluctuaciones de vacío, esas oscilaciones aleatorias, impredecibles e ineliminables de un campo (electromagnético o gravitatorio), que son debidas a un tira y afloja en el que pequeñas regiones del espacio toman prestada momentáneamente energía de regiones adyacentes y luego la devuelven.
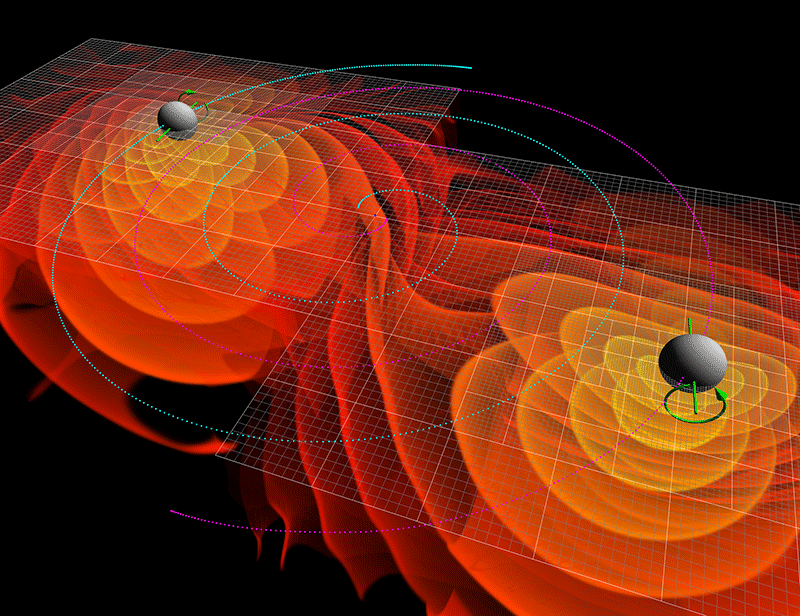
Andamos a la caza del vacío, del gravitón, de las ondas gravitatorias…
Ordinariamente, definimos el vacío como el espacio en el que hay una baja presión de un gas, es decir, relativamente pocos átomos o moléculas. En ese sentido, un vacío perfecto no contendría ningún átomo o molécula, pero no se puede obtener, ya que todos los materiales que rodean ese espacio tienen una presión de vapor finita. En un bajo vacío, la presión se reduce hasta 10-2 pascales, mientras que un alto vacío tiene una presión de 10-2-10-7 pascales. Por debajo de 10-7 pascales se conoce como un vacío ultraalto.
De ese “vacío” nos queda muchísimo por aprender. Al parecer, todos los indicios nos dicen que está abarrotado de cosas, y, si es así, no es lo que podemos llamar con propiedad vacío, ese extraño lugar es otra cosa, pero, ¿qué cosa es?
Antes se denominaba éter fluminígero (creo) a toda esa inmensa región. Más tarde, nuevas teorías vinieron a desechar su existencia. Pasó el tiempo y llegaron nuevas ideas y nuevos modelos, y, se llegó a la conclusión de que el Universo entero estaba permeado por “algo” que algunos llamaron los océanos de Higgs. Ahí, se tiene la esperanza de encontrar al esquivo Bosón (que dicen haber hallado pero que yo, no estoy muy seguro de que así sea) que le da la masa a las demás partículas, y, el LHC del CERN, es el encargado de la búsqueda para que el Modelo Estándar de la Física de Partículas se afiance más.

Andamos un poco a ciega, la niebla de nuestra ignorancia nos hace caminar alargando la mano para evitar darnos un mamporro. Pero a pesar de todo, seguimos adelante y, es más la fuerza que nos empuja, la curiosidad que nos aliente que, los posibles peligros que tales aventuras puedan conllevar.
Está claro que, dentro del Universo, existen “rincones” en los que no podemos sospechar las maravillas que esconden, ni nuestra avezada imaginación, puede hacerse una idea firme de lo que allí pueda existir. Incansables seguimos la búsqueda, a cada nuevo descubrimiento nuestro corazón se acelera, nuestra curiosidad aumenta, nuestras ganas de seguir avanzando van creciendo y, no pocas veces, el físico que, apasionado está inmerso en uno de esos trabajos de búsqueda e investigación, pasa las horas sin sentir el paso del tiempo, ni como ni duerme y su mente, sólo tiene puesto los sentidos en ese final soñado en el que, al fín, aparece el tesoro perseguido que, en la mayor parte de las veces, es una nueva partícula, un parámetro hasta ahora desconocido en los comportamientos de la materia, un nuevo principio, o, en definitiva, un nuevo descubrimiento que nos llevará un poco más lejos.
Encontrar nuevas respuestas no dará la opción de plantear nuevas preguntas.
Emilio Silvera Vázquez
















 Totales: 75.655.723
Totales: 75.655.723 Conectados: 47
Conectados: 47
























