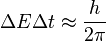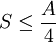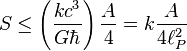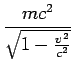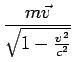Abr
5
¡Fluctuaciones de Vacío! ¿Que son?
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Cuántica ~
Clasificado en Física Cuántica ~
 Comments (0)
Comments (0)
Un fuerte campo gravitatorio puede inducir un efecto desbocado en las fluctuaciones cuánticas que se producen en el espacio, aparentemente vacío, …
En física cuántica, la fluctuación cuántica es un cambio temporal en la cantidad de energía en un punto en el espacio como resultado del Principio de Incertidumbre que imaginó Werner Heisenberg. De acuerdo a una formulación de este principio energía y tiempo se relacionan de la siguiente forma:
Esto significa que la conservación de la energía puede parecer violada, pero sólo por breves lapsos. Esto permite la creación de pares partícula-antipartícula de partículas virtuales. El efecto de esas partículas es medible, por ejemplo, en la carga efectiva del electrón, diferente de su carga “desnuda”. En una formulación actual, la energía siempre se conserva, pero los estados propios del Hamiltoniano no son los mismos que los del operador del número de partículas, esto es, si está bien definida la energía del sistema no está bien definido el número de partículas del mismo, y viceversa, ya que estos dos operadores no conmutan.
Las fluctuaciones del vacío entre una esfera y una superficie plana
En un estudio realizado por un equipo de físicos con avanzados aparatos, han hallado un resultado del que nos dicen:
“La materia se construye sobre fundamentos frágiles. Los físicos acaban de confirmar que la materia, aparentemente sustancial, es en realidad nada más que fluctuaciones en el vació cuántico. Los investigadores simularon la frenética actividad que sucede en el interior de los protones y neutrones, que como sabéis son las partículas que aportan casi la totalidad de la masa a la materia común.
Cada protón (o neutrón) se compone de tres quarks – véase ilustración – pero las masas individuales de estos quarks apenas comprenden el 1% del total de la masa del protón¿Entonces de dónde sale el resto? La teoría sostiene que esta masa es creada por la fuerza que mantiene pegados a los quarks, y que se conoce como fuerza nuclear fuerte. En términos cuánticos, la fuerza fuerte es contenida por un campo de partículas virtuales llamadas gluones, las cuales irrumpen aleatoriamente en la existencia para desaparecer de nuevo. La energía de estas fluctuaciones del vacío debe sumarse a la masa total del neutróny del protón.”

De ella se conforman galaxias y también, seres vivos
Tiene y encierra tantos misterios la materia que estamos aún y años-luz de y conocer sobre su verdadera naturaleza. Es algo que vemos en sus distintas formas materiales que configuran y conforman todo lo material desde las partículas elementales hasta las montañas y los océanos. Unas veces está en estado “inerte” y otras, se eleva hasta la vida que incluso, en ocasiones, alcanza la consciencia de SER. Sin embargo, no acabamos de dilucidar de dónde viene su verdadero origen, su esencia, lo que era antes de “ser” materia. ¿Existe acaso una especie de sustancia cósmica anterior a la materia? Y, si realmente existe esa sustancia… ¿Dónde está?
Claro que hemos llegado a saber que las llamadas fluctuaciones del vacío son oscilaciones aleatorias, impredecibles e ineliminables de un campo de fuerza (electromagnético o gravitatorio) que son debidas a un “tira y afloja” en el que pequeñas regiones del espacio toman prestada, momentáneamente, energía de regiones adyacentes y luego las devuelven. Pero…
– ¿Qué regiones adyacentes?
Acaso universos paralelos, acaso deformaciones del espacio-tiempo a escalas microscópicas, micros agujeros negros que pasan a ser agujeros blancos salidos de estas regiones o campos de fuerza que no podemos ver pero sí sentir, y, en última instancia, ¿por qué se forman esas partículas virtuales que de inmediato se aniquilan y desaparecen antes de que puedan ser capturadas? ¿Qué sentido tiene todo eso?

Las consecuencias de la existencia del cuanto mínimo de acción fueron revolucionarios para la comprensión del vacío. Mientras la continuidad de la acción clásica suponía un vacío plano, estable y “realmente” vacío, la discontinuidad que supone el cuanto nos dibuja un vacío inestable, en continuo cambio y muy lejos de poder ser considerado plano en las distancias atómicas y menores. El vacío cuántico es de todo menos vacío, en él la energía nunca puede quedar estabilizada en valor cero, está fluctuando sobre ese valor, continuamente se están creando y aniquilando todo tipo de partículas, llamadas por eso virtuales, en las que el producto de su energía por el tiempo de su existencia efímera es menor que el cuanto de acción. Se llaman fluctuaciones cuánticas del vacío y son las responsables de que exista un que lo inunda todo llamado campo de punto cero.
Pero volvamos de nuevo a las fluctuaciones de vacío, que al igual que las ondas “reales” de energía positiva, están sujetas a las leyes de la dualidad onda/partícula; es decir, tienen tanto aspectos de onda como aspectos de partícula.
Las ondas fluctúan de forma aleatoria e impredecible, con energía positiva momentáneamente aquí, energía negativa momentáneamente allí, y energía cero en promedio. El aspecto de partícula está incorporado en el concepto de partículas virtuales, es decir, partículas que pueden nacer en pares (dos partículas a un tiempo), viviendo temporalmente de la energía fluctuacional tomada prestada de regiones “vecinas” del , y que luego se aniquilan y desaparecen, devolviendo la energía a esas regiones “vecinas”. Si hablamos de fluctuaciones electromagnéticas del vacío, las partículas virtuales son fotonesvirtuales; en el caso de fluctuaciones de la gravedad en el vacío, son gravitones virtuales.
De las llamadas fluctuaciones de vacío pueden surgir, partículas virtuales y quién sabe que cosas más… Hasta un nuevo Universo.

Son muchas las preguntas que no tienen respuestas
Parece que las fluctuaciones ocurren en cualquier lugar, pero que, son tan minúsculas que ningún observador o experimentador las ha detectado de una manera franca hasta la fecha y, se sabe que están ahí por experimentos que lo han confirmado. Estas fluctuaciones son más poderosas cuanto menos escala se considera en el espacio y, por debajo de la longitud de Planck-Wheeler las fluctuaciones de vacío son tan enormes que el espacio tal como lo conocemos “pareciera estar hirviendo” para convertirse en una especie de espuma cuántica que parece que en realidad, cubre todo el espacio “vacío cuántico” que sabemos que está ahí y es el campo del que surgen esas partículas virtuales que antes mencionaba.

¿Espuma cuántica? Si profundizamos mucho en la materia… Podríamos ver otro universo distinto al nuestro. Las cosas miles de millones de veces más pequeñas que en nuestro mundo cotidiano, no parecen las mismas cosas.
Hay magnitudes asociadas con las leyes de la gravedad cuántica. La longitud de Planck-Wheeler, ![]() es la escala de longitud por debajo de la cual el tal como lo conocemos deja de existir y se convierte en espuma cuántica. El tiempo de Planck-Wheeler (1/c veces la longitud de Planck-Wheeler o aproximadamente 10-43 segundos), es el intervalo de tiempo más corto que puede existir; si dos sucesos están separados por menos que esto, no se puede decir cuál sucede antes y cuál después. El área de Planck-Wheeler (el cuadrado de la longitud de Planck-Wheeler, es decir, 2,61×10-66cm2) juega un papel clave en la entropía de un agujero negro. ¡Qué locura!
es la escala de longitud por debajo de la cual el tal como lo conocemos deja de existir y se convierte en espuma cuántica. El tiempo de Planck-Wheeler (1/c veces la longitud de Planck-Wheeler o aproximadamente 10-43 segundos), es el intervalo de tiempo más corto que puede existir; si dos sucesos están separados por menos que esto, no se puede decir cuál sucede antes y cuál después. El área de Planck-Wheeler (el cuadrado de la longitud de Planck-Wheeler, es decir, 2,61×10-66cm2) juega un papel clave en la entropía de un agujero negro. ¡Qué locura!

La teoría que junte lo grande y lo pequeño. Las que ahora tenemos no dejan que la Gravedad se junte con la cuántica. Parece que en la teoría de cuerdas subyace esa teoría pero… no se puede verificar.
Como tantas veces hemos comentado, los trabajos que se han realizado sobre poder construir una teoría cuántica de la gravedad nos llevan a un sorprendente de implicaciones. Por un lado, sólo se ha podido conceptuar a la gravedad cuántica, siempre y cuando, el universo tenga más de cuatro dimensiones. Además, se llega a considerar que en la era de Planck, tanto el universo como la gravedad pudieron ser una sola cosa compacta estructurada por objetos cuánticos infinitamente diminutos, como los que suponemos que conforman las supercuerdas. A esta escala, el mismísimo espaciotiempo estaría sometido a imprescindibles fluctuaciones muy semejantes a las que causan las partículas al nacer y desaparecer de la existencia en el espaciotiempo ordinario. Esta noción ha conducido a los teóricos a describir el universo de la era cuántica como una especie de extremadamente densa y agitada espuma que pudo haber contenido las vibrantes cuerdecillas que propugnan los cosmólogos cuerdistas.
Los físicos especulan que el cosmos ha crecido a desde una «nada» primigenia que al nacer comenzó el principio del tiempo y que, en ese parto, contenía toda la materia y toda la energía.

En física como en todas las demás disciplinas científicas, los conocimientos avanzan y las teorías que sostuvieron los cimientos de nuestros conocimientos se van haciendo viejas y van teniendo que ser reforzadas con las nuevas y más poderosas “vigas” de las nuevas ideas y los nuevos hallazgos científicos que hacen posible ir perfeccionando lo que ya teníamos.
Recientemente se han alzado algunas voces contra el Principio de Incertidumbre de Heisenberg. He podido leer en un artíoculo de la prestigiosa Revista Nature, un artículo del premio Nobel de Física Gerald ´t Hoofft, en el que propone que la naturaleza probabilistica de la mecánica cuántica, desaparecería a la escala de Planck, en la que el comportamiento de la materia sería determinista; a longitudes mayores, energías más pequeñas.
El mundo de lo muy pequeño (el micro espacio), a nivel atómico y subatómico, es el dominio de la física cuántica, así nunca podríamos saber, de acuerdo m con el principio de incertidumbre, y, en un momento determinado, la posición y el estado de una partícula. Este estado podría ser una función de la escala espacio-temporal. A esta escala tamaños todo sucede demasiado deprisa para nosotros.

El “universo cuántico” nada es lo que parece a primera vista, allí entramos en otro mundo que en nada, se parece al nuestro
Cuando hablamos de la mecánica cuántica, tenemos mirar un poco hacia atrás en el tiempo y podremos darnos del gran impacto que tuvo en el devenir del mundo desde que, en nuestras vidas, apareció el átomo y, más tarde, sus contenidos. Los nombres de Planck, Einstein, Bohr, Heisenberg, Schrödinger, Pauli, Bardeen, Roentgen, Dirac y muchos otros, se pudieron a la cabeza de la lista de las personas más famosas. Aquel primer premio Nobel de Física otorgado en 1900 a Roentgen por descubrir los rayos X, en el mismo año llegaría el ¡cuanto! De Planck que inspiró a Einstein para su trabajo sobre el Efecto fotoeléctrico que también, le valdría el Nobel, y, a partir de ese momento, se desencadenó una especie de alucinante por saber sobre el átomo, sus contenidos, y, de qué estaba hecha la materia.
La conocida como Paradoja EPR y los conceptos de Tiempo y , presente, pasado y futuro.
“Nadie ha resuelto la paradoja del gato de Schröedinger, ni la paradoja de Einstein-Podolsky-Rosen. El principio de incertidumbre no se ha explicado y se asume como un dogma, lo mismo pasa con el spin. El spin no es un giro pero es un giro. Aquí hay un desafío al pensamiento humano. ¡Aquí hay una aventura del pensamiento!”
Fueron muchas las polémicas desatadas a cuenta de las aparentes incongruencias de la moderna Mecánica Cuántica. La paradoja de Einstein-Podolsky-Rosen, denominada “Paradoja EPR”, trata de un experimento mental propuesto por Albert Einstein, Boris Podolsky y Nathan Rosen en 1935. Es relevante, pues pone de manifiesto un problema aparente de la mecánica cuántica, y en las décadas siguientes se dedicaron múltiples esfuerzos a desarrollarla y resolverla.
A Einstein (y a muchos otros científicos), la idea del entrelazamiento cuántico le resultaba extremadamente perturbadora. Esta particular característica de la mecánica cuántica permite preparar estados de dos o más partículas en los cuales es imposible obtener útil sobre el estado total del sistema haciendo sólo mediciones sobre una de las partículas.

Por otro lado, en un entrelazado, manipulando una de las partículas, se puede modificar el estado total. Es decir, operando sobre una de las partículas se puede modificar el estado de la otra a distancia de manera instantánea. Esto habla de una correlación entre las dos partículas que no tiene paralaje en el mundo de nuestras experiencias cotidianas. Cabe enfatizar pues que cuando se mide el estado de una partícula, enseguida sabemos el estado de la otra, lo cual aparentemente es instantáneo, es decir, sin importar las distancias a las que se encuentren las partículas, una de la otra, ambas saben instantáneamente el estado de la otra.
El experimento planteado por EPR consiste en dos partículas que interactuaron en el pasado y que quedan en un estado entrelazado. Dos observadores reciben cada una de las partículas. Si un observador mide el momento de una de ellas, sabe cuál es el momento de la otra. Si mide la posición, gracias al entrelazamiento cuántico y al principio de incertidumbre, puede la posición de la otra partícula de forma instantánea, lo que contradice el sentido común.

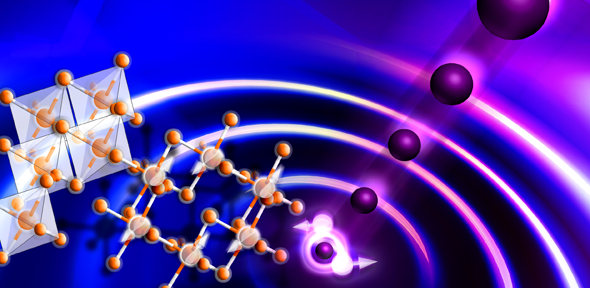
Animación que muestra dos átomos de oxígeno fusionándose para formar una molécula de O2 en su estado cuántico fundamental. Las nubes de color representan los orbitales atómicos. Los orbitales 2s y 2p de cada átomo se combinan para formar los orbitales σ y π de la molécula, que la mantienen unida. Los orbitales 1s, más interiores, no se combinan y permiten distinguir a cada núcleo. Lo que ocurre a escalas tan pequeñas es fascinante.
Si nos pudiéramos convertir en electrones, por ejemplo, sabríamos dónde y cómo estamos en cada momento y podríamos ver asombrados, todo lo que estaba ocurriendo a nuestro alrededor que, entonces sí, veríamos transcurrir a un ritmo más lento del que podemos detectar en los electrones desde nuestro macroestado espacio temporal. El electrón, bajo nuestro punto de vista se mueve alrededor del núcleo atómico a una velocidad de 7 millones de km/h.
A medida que se asciende en la escala de tamaños, hasta el tiempo se va ajustando a esta escala, los objetos, a medida que se hacen mayores se mueven más despacio y, además, tienen más duración que los pequeños objetos infinitesimales del micro mundo cuántico. La vida media de un neutron es de unos 15 minutos, por ejemplo, mientras que la vida media de una estrellas se puede contar en miles de millones de años.
En nuestra macroescala, los acontecimientos y ,los objetos se mueven a velocidades que a nosotros nos parecen normales. Si se mueven con demasiada lentitud nos parece que no se mueven. Así hablamos de escala de tiempo geológico, para referirnos al tiempo y velocidad de la mayor parte de los acontecimientos geológicos que afectan a la Tierra, el tiempo transcurre aquí en millones de años y nosotros ni lo apreciamos; nos parece que todo está inmóvil. Nosotros, los humanos, funcionamos en la escala de años (tiempo biológico).

El Tiempo Cosmológico es aún mucho más dilatado y los objetos cósmicos (mundos, estrellas y galaxias), tienen una mayor duración aunque su movimiento puede ser muy rápido debido a la inmensidad del espacio universal en el que se mueven. La Tierra, por ejemplo, orbita alrededor del Sol a una velocidad media de 30 Km/s., y, el Sol, se desplaza por la Galaxia a una velocidad de 270 km/s. Y, además, se puede incrementar el tiempo y el espacio en su andadura al estar inmersos y ligados en una misma maya elástica.
Así, el espacio dentro de un átomo, es muy pequeño; dentro de una célula, es algo mayor; dentro de un animal, mayor aún y así sucesivamente… hasta llegar a los enormes espaciosa que separan las estrellas y las galaxias en el Universo.

Distancias astronómicas separan a las estrellas entre sí, a las galaxias dentro del cúmulo, y a los cúmulos en los supercúmulos.
Las distancias que separan a los objetos del Cosmos se tienen que medir con unidades espaciales, tal es su inmensa magnitud que, nuestras mentes, aunque podamos hablar de ellas de manera cotidiana, en realidad, no han llegado a asimilarlas. Y, a todo ésto, los físicos han intentado con denuedo elaborar una teoría completa de la gravedad que incluya la mecánica cuántica. Los cálculos de la mayoría de las teorías propuesta de la «gravedad cuántica» arrojan numerosos infinitos. Los físicos no están seguros si el problema es técnico o conceptual. No obstante, incluso prescindiendo de una teoría completa de gravedad cuántica, se puede deducir que los efectos de la teoría cuántica, habrían cruciales durante los primeros 10-43 segundos del inicio del universo, cuando éste tenía una densidad de 1093 gramos por centímetro cúbico y mayor. (El plomo sólido tiene una densidad de aproximadamente diez gramos por centímetro cúbico.) Este período, que es el que corresponde a la era de Planck, y a su estudio se le llama cosmología cuántica. Como el universo en su totalidad habría estado sujeto a grandes incertidumbres y fluctuaciones durante la era de Planck o era cuántica, con la materia y la energía apareciendo y desapareciendo de un vacío en grandes cantidades, el concepto de un principio del universo podría no tener un significado bien definido. En todo caso, la densidad del universo durante este período es de tal magnitud que escapa a nuestra comprensión. Para propósitos prácticos, la era cuántica podría considerarse el estado inicial, o principio, del universo. En consecuencia, los procesos cuánticos ocurridos durante este período, cualquiera sea su naturaleza, determinaron las iniciales del universo.

Una cosa nos ha podido quedar clara: Los científicos para lograr conocer la estructura del universo a su escala más grande, deben retroceder en el tiempo, centrando sus teorías en el momento en que todo comenzó. Para ello, como todos sabéis, se han formulado distintas teorías unificadoras de las cuatro fuerzas de la naturaleza, con las cuales se han modelado acontecimiento y en el universo primitivo casi a todo lo largo del camino hasta el principio. Pero cómo se supone que debió haber habido un «antes», aparece una barrera que impide ir más allá de una frontera que se halla fijada a los 10-43 [s] después del Big Bang, un instante conocido como «momento de Planck», en homenaje al físico alemán Max Planck.

Esta barrera existe debido a que antes del momento de Planck, durante el período llamado la «era de Planck o cuántica», se supone que las cuatro fuerza fundamentales conocidas de la naturaleza eran indistinguibles o se hallaban unificadas , que era una sola fuerza. Aunque los físicos han diseñado teorías cuánticas que unen tres de las fuerzas, una por una, a través de eras que se remontan al momento de Planck, hasta ahora les ha prácticamente imposible armonizar las leyes de la teoría cuántica con la gravedad de la relatividad de Einstein, en un sólo modelo teórico ampliamente convincente y con posibilidades claras de ser contrastado en experimentos de laboratorio y, mucho menos, con observaciones.
Y después de todo esto, sólo una caso me queda clara: ¡Lo poco que sabemos! A pesar de la mucha imaginación que ponemos en las cosas que creemos conocer.
Emilio Silvera
Abr
2
La necesidad agudiza la imaginación
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (0)
Comments (0)
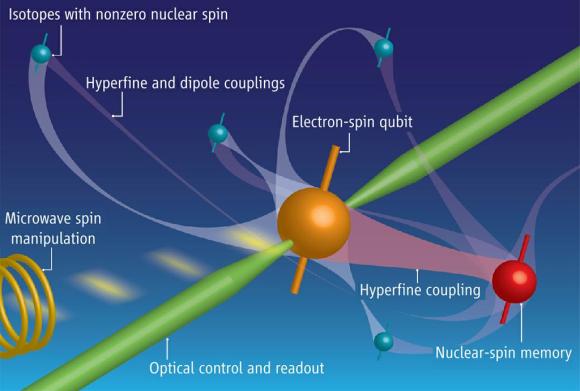
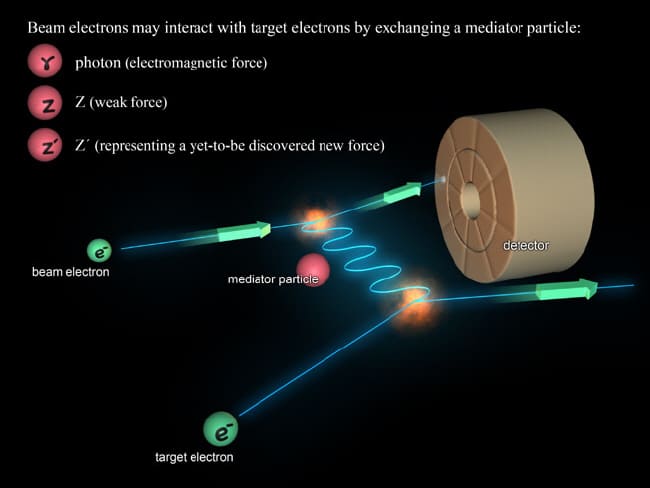
La fuerza nuclear débil nos habla de materiales que, de manera natural, emiten radiación y se desintegran. Al pensar en la desintegración me ha traído a la memoria aquellos libros de Asimov que nos explicaba cuestiones de ciencia y nos decía existen materiales que se desintegran de manera natural y que son materiales fértiles, o que sin serlo, se pueden transformar en otros que sí lo son.
Al hablar de material fértil me estoy refiriendo a núclidos que pueden absorber neutrones formar material fisible. El uranio-238, por ejemplo, absorbe un neutrón para formar uranio-239, que se desintegra en plutonio-239. Este es el de conversión que la imaginación del hombre hace que ocurra en un reactor reproductor.

Lo explicaré con más detalles: El Reactor Reproductor Rápido es un reactor de neutrones rápidos diseñado producir combustible generando más material fisible del que consume. El FBR es uno de los tipos posibles de reactores reproductores.
Veámos: El uranio-235 es un combustible práctico, es decir, los neutrones lentos son capaces de que el uranio-235 se fisione, o lo que es lo mismo, se rompan sus átomos en dos, produciendo neutrones lentos, que a su vez inducen otras fisiones atómicas. El uranio-233 y el plutonio-239 son también combustibles nucleares prácticos por las mismas razones.
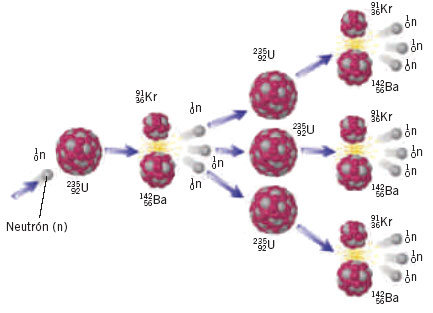
Desgraciadamente, el uranio-233 y el plutonio-239 no existen en natural sino en trazas mínimas, y el uranio-235, aunque existe en cantidades apreciables, no deja de ser raro. En cualquier muestra de uranio natural, sólo siete de cada mil átomos son de uranio-235, el resto es uranio-238.

Uranio
El uranio natural extraído de las minas contiene un 99´3 % de U-238 y apenas el 0´7 % de U-235.
El uranio-238, la variedad común de uranio, no es un combustible nuclear práctico. Así que, el uranio que más abunda en la naturaleza no sirve combustible nuclear. Podemos conseguir que se fisione, pero sólo con neutrones rápidos. Los átomos de uranio-238 que se rompen en dos, producen neutrones lentos, que no bastan para producir o inducir nuevas fisiones. El uranio-238 cabría compararlo a la madera húmeda: es posible que arda, pero acabará por apagarse.

El uranio es un elemento químico metálico de color plateado-grisáceo de la serie de los actínidos, su símbolo químico es U y su número atómico es 92. Por ello posee 92 protones y 92 electrones, con una valencia de 6. Su núcleo puede contener entre 142 y 146 neutrones, sus isótopos más abundantes son el 238U que posee 146 neutrones y el 235U con 143 neutrones. El uranio tiene el mayor peso atómico de entre todos los elementos que se encuentran en la naturaleza. El uranio es aproximadamente un 70% más denso que el plomo, aunque menos denso que el oro o el wolframio. Es levemente radioactivo. Fue descubierto como óxido en 1789 por M. H. Klaproth que lo llamó así en el honor del planeta Urano que acababa de ser descubierto en 1781.
Supongamos, sin embargo, que se separa el uranio-235 del uranio-238 ( más bien difícil) y que se utiliza aquel para hacer funcionar un reactor nuclear. Los átomos de uranio-235 que forman el combustible del reactor se fisionan y esparcen miríadas de neutrones lentos en todas direcciones. Si el reactor está rodeado por una capa de uranio ordinario (que en su mayor es uranio-238), los neutrones que van a parar allí son absorbidos por el uranio-238 y, aunque no pueden hacer que el uranio-238 se fisione, sí pueden provocar otros cambios que finalmente, producirán plutonio-239. Separando este plutonio-239 del uranio (tarea muy fácil), puede ser utilizado como combustible nuclear practico para la fisión.
De esta manera, el reactor nuclear genera combustible a partir de un material (uranio-238) que no lo es. Este es el motivo de que al reactor nuclear que hace posible la transformación se le llame “reactor generador”.
Un reactor generador bien diseñado puede producir más plutonio-239 que el uranio-234 consumido para ello. De este modo, las reservas totales de uranio de la Tierra (y no sólo las de uranio-235) se convierten en potenciales de combustible nuclear.

Torio
Carlo Rubbia, exdirector del CERN (los mismos que hicieron el Colisionador de Hadrones) y ganador del premio Nobel de física en 1984, ha trabajado buena de su carrera en el desarrollo de tecnologías para la producción de energía a partir de torio y calcula que con un reactor adecuado, este proceso de fisión podría generar a partir de 1 tonelada del elemento la misma cantidad de energía que 200 toneladas de uranio y 3.500.000 toneladas de carbón.
El torio, tal se da en la naturaleza, consiste todo él en torio-232, que al igual que el uranio-238, no es un combustible nuclear práctico, porque requiere neutrones rápidos para fisionarse. Pero si se coloca torio-232 alrededor de un reactor nuclear, sus átomos absorberán los neutrones y, sin experimentar fisión alguna, se convertirán en átomos de uranio-233. el uranio-233 es un combustible práctico que se puede separar fácilmente del torio, el resultado es otra variedad del reactor generador, que convierte las reservas de torio en un combustible nuclear en potencia.


Mientras que no se descubra otra manera de producir energía, el Uranio seguirá.
La cantidad total de uranio y de torio que hay en la Tierra es unas 800 veces mayor que las reservas de uranio-235, lo que significa que el buen uso de los reactores generadores podría multiplicar por 800 la oferta potencial de energía extraída de plantas de fisión nuclear.
En este punto, sin dejar de elogiar la inteligencia del hombre que ha sabido encontrar la manera de transformar una materia inservible en otra practica, hay que decir que la energía de fisión nuclear genera también muchos problemas.
Como estará comprobando al lector de este , el autor ha querido esta vez diversificar los temas y plasmar una variedad múltiple que facilite el conocimiento de distintas cosas que ocurren en la naturaleza, o que la mano del hombre hace que ocurran, y todas estas cuestiones tratadas aquí van encaminadas a resolver preguntas que en alguna ocasión nos hemos podido , tales como:
¿Por qué al calentar un metal se pone primero rojo, luego naranja, después amarillo, pero a continuación blanco en lugar de seguir el espectro y ponerse verde?
¿Y el color en las estrellas?
Cuando un herrero está trabajando, el metal adquiere diferentes colores según recibe el calor de la fragua. Primero se mostrará de un rojo intenso, ir progresivamente adoptando tonos más claros, pasando del anaranjado al amarillo, y por fin al blanco. Con las estrellas pasa igual, Con el diagrama de arriba se demuestra una progresión entre estrellas enanas, amarillas y frías, subiendo hasta llegar a las supergigantes rojas y azules más calientes, y más grandes.
Si se pudiera seguir calentando el hierro, éste adquiriría tonos azulados. Estos cambios en la coloración son una consecuencia directa del aumento de la temperatura, que permitirá mayor maleabilidad. El Cúmulo del Joyero (en la constelación de la Cruz del Sur), fotografiado arriba, muestra cómo ocurre lo mismo con las estrellas, de manera que encontraremos estrellas azules, las más calientes, blancas, amarillas, anaranjadas y rojas, las más “frías”. A veces, estos colores pueden percibirse a simple vista, Antares (Alpha Scorpii) que es de color rojo, o Rigel (Beta Orionis) blanco-azulada.
En la Naturaleza rigen las mismas leyes todos y, en todas partes se producen los mismos fenómenos debidos a las mismas causas, en este caso: ¡La Temperatura!
Cualquier objeto, a cualquier energía superior al cero absoluto, radia ondas electromagnéticas. Si su temperatura es muy baja, emite sólo ondas de radio largas, muy pobres en energías. Al aumentar la temperatura, radia una cantidad mayor de ondas, pero empieza a radiar ondas de radio más cortas (y más energéticas). Si la temperatura sigue subiendo, empiezan a radiarse microondas aún más energéticas y después radiaciones infrarrojas.

Esto no quiere decir que a una temperatura dada sólo se emitan ondas de radio largas, un poco más arriba sólo ondas de radio cortas, luego sólo microondas y después sólo infrarrojos. En realidad, se emite toda la gama de radiaciones, pero siempre hay una radiación máxima, es decir, una gama de longitudes de onda que son las más radiadas, flanqueadas por cantidades menores en el lado de las energías bajas y por cantidades todavía más pequeñas en el de las altas.
Un objeto alcanza la temperatura del cuerpo humano (37°C), el máximo de radiación se encuentra en los infrarrojos largos. El cuerpo humano también radia ondas de radio, pero las longitudes de ondas más cortas y más energéticas son siempre las más fáciles de detectar por ser los más potentes.

Cuando la temperatura alcanza aproximadamente los 600°C, el máximo de radiación se halla en el infrarrojo corto. Pero a estas alturas la pequeña cantidad de radiación que se halla en el lado de las energías altas adquiere una importancia especial, porque entra ya en la región de la luz visible roja. El objeto reluce entonces con un rojo intenso.
Este rojo constituye sólo un pequeño porcentaje de la radiación total, pero da la casualidad de que nuestro ojo lo percibe, le otorgamos toda nuestra atención y decimos que el objeto está al “rojo vivo”.
Si la temperatura sigue subiendo, el máximo de radiación continúa desplazándose las longitudes de ondas cortas y cada vez se emite más luz visible de longitudes cada vez menores. Aunque el objeto radia más luz roja, se van agregando poco a poco luz anaranjada y luz amarilla en cantidades menores pero significativas. Al llegar a los 1.000°C la mezcla de colores la percibimos como naranja, y a los 2.000°C como amarilla. Lo cual no significa que a los 1.000°C sólo se radie luz naranja y a los 2.000°C sólo se radie luz amarilla, porque si fuese así, habría efectivamente que esperar que lo siguiente fuese “color verde”. Lo que en realidad vemos son mezclas de colores.

Al llegar a los 6.000°C (la temperatura superficial del Sol), el máximo de radiación está en el amarillo visible y lo que llega a nuestros ojos son grandes cantidades de luz visible, el violeta hasta el rojo. La incidencia simultánea de toda la gama de luz visible sobre nuestra retina nos da la sensación de blanco, y de ahí el color del Sol.
Los objetos más calientes aún que el Sol radian todas las longitudes de ondas de luz visible y en cantidades todavía mayores, el máximo de radiación se desplaza al azul, de modo que la mezcla se desequilibra y el blanco adquiere un tinte azulado.
Toda esta travesía se produce para objetos calientes que emiten “espectros continuos”, es decir, que radian luz en la forma de una ancha banda de longitudes de ondas. Ciertas sustancias en adecuadas, radian sólo luz de determinadas longitudes de onda. El nitrato de bario radia luz verde cuando se calienta, y con ese fin se lo utiliza en los fuegos de artificio, “calor verde”, podríamos decir.


Nitrato de Bario que produce el color verde en los bonitos fuegos artificiales
¡Qué bonito es saber!
Los gases “Nobles”
En alguna ocasión todos hemos oído mencionar la palabra “gases nobles”, y sin embargo no siempre sabemos lo que son y el por qué le llaman así. Los elementos que reaccionan difícilmente o que no reaccionan en absoluto con otros elementos se denominan “inertes”. El nitrógeno y el platino son ejemplos de elementos inertes.
En la última década del siglo pasado se descubrieron en la atmósfera una serie de gases que no parecían intervenir en ninguna reacción química. Estos nuevos gases (helio, neón, argón, kripton, xenón y radón) son más inertes que cualquier otro elemento y se agrupan bajo el de gases inertes.
Los elementos inertes reciben a veces el calificativo de “nobles” porque esa resistencia a reaccionar con otros elementos recordaba un poco a la altanería de la aristocracia. El oro y el platino son ejemplos de “metales nobles”, y por la misma razón se llaman a veces “gases nobles” a los gases inertes. Hasta 1.962, el más común era el de gases inertes, quizá porque lo de nobles parecía poco apropiados en sociedades democráticas.
Es apropiado incluir una descripción de este grupo de elementos conocido en un capítulo dedicado a los halógenos, porque el flúor es el único elemento conocido que entra en combinación química directa con los dos gases nobles más pesados, el xenón y el criptón, resultando en compuestos estables.
Los gases nobles surgen en la naturaleza como constituyentes menos abundantes de la atmósfera. La primera indicación de la existencia de los gases nobles fue divulgada por el químico ingles Cavendish, en 1784.
La razón de que los gases inertes sean inertes es que el conjunto de electrones de cada uno de sus átomos está distribuido en capas especialmente estables. La más exterior, en concreto, tiene 8 electrones. Así la distribución electrónica del neón es (2,8) y la del argón (2,8,8). Como la adición o sustracción de electrones rompe distribución estable, no pueden producirse cambios electrónicos. Lo cual significa que no pueden producirse reacciones químicas y que estos elementos son inertes.
bien, el grado de inercia depende de la fuerza con que el núcleo, cargado positivamente y situado en el centro del átomo sujeta a los 8 electrones de la capa exterior. Cuantas más capas electrónicas haya entre la exterior y el centro, más débil será la atracción del núcleo central sobre los electrones de esa última capa de electrones.

El Radón es un gas radiactivo de origen natural procedente de la desintegración radiactiva de pequeñas cantidades de uranio presentes en rocas y suelo, es el responsable de miles de muertes por cáncer de pulmón en Europa cada año. El gas se filtra en los edificios a través del suelo y de los sótanos, puede acumularse llegando a niveles elevados, especialmente en espacios cerrados y poco ventilados.
Quiere esto decir que el gas inerte más complejo es también el menos inerte. El gas inerte de estructura atómica más complicada es el radón. Sus átomos tienen una distribución electrónica de (2,8,18,32,18,8). El radón, sin embargo está sólo constituido por isótopos radiactivos y es un elemento con el que difícilmente se pueden experimentos químicos. El siguiente en orden de complejidad es el xenón, que es estable. Sus átomos tienen una distribución electrónica de (2,8,18,18,8).

Se sabe desde hace décadas que la abundancia en la Tierra del xenón es menor de lo que debería ser según las proporciones observadas del resto de gases nobles. Las abundancias de estos gases se usan por los geoquímicos para evaluar y datar los principales procesos terrestres, incluyendo la formación de la atmósfera. Para poder hacerlo parten de una hipótesis básica: que los gases nobles son inertes en toda circunstancia. Un realizado por Gary Schrobilgen y David Brock, de la Universidad McMaster (Canadá), cuyos resultados se publican en el Journal of the American Chemical Society explica la baja abundancia del xenón y pone en evidencia que el xenón no es tan noble se suponía.
Los electrones más exteriores de los átomos de xenón y radón están bastante alejados del núcleo y, por consiguiente, muy sueltos. En presencia de átomos que tienen una gran apetencia de electrones, son cedidos rápidamente. El átomo con mayor apetencia de electrones es el flúor, y así fue como en 1.962 el químico canadiense Neil Bartlett consiguió formar compuestos de xenón y flúor.
Desde entonces se han conseguido formar también compuestos de radón y kriptón. Por eso los químicos rehúyen el de gases inertes, porque a fin de cuentas, esos gases no son completamente inertes. Hoy día se ha impuesto la denominación de “gases nobles”, y existe toda una rama de la química que se ocupa de los “compuestos de gases nobles”.

Naturalmente, cuanto más pequeño es el átomo de un gas noble, más inerte es, y no se ha encontrado nada que sea capaz de arrancarles algún electrón. El argón, cuya distribución electrónica es de 2,8,8 y el neón, con 2,8 electrones respectivamente, sigue siendo completamente inerte. Y el más inerte de todos es el helio, cuyos átomos contienen una sola capa electrónica con dos electrones (que es lo máximo que alojar esta primera capa) que al estar en la primera linea cerca del núcleo positivo, están fuertemente atraídos al tener su carga eléctrica el signo negativo.
finalizar diré que los gases nobles (gases inertes, gases raros) están clasificados en el grupo 18 (antiguamente 0) de la Tabla periódica de los elementos y se definen por símbolos que responden a: helio (He), neón (Ne), argón (Ar), kriptón (Kr), xenón (Xe) y radón (Rn).
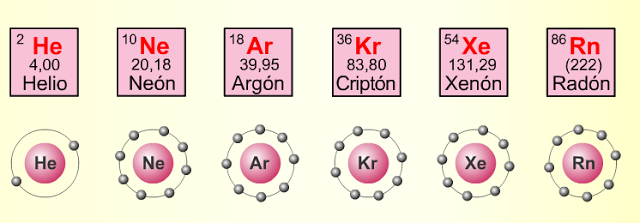
Ya se dijo antes la configuración electrónica de cada uno de ellos y todas las capas internas están completamente ocupadas, lo que hace que estos elementos, por tanto, constituyan la terminación de un periodo y posean configuración de capa completa, por lo que sus energías de ionización son muy elevadas y su reactividad química escasa.
Como son monoatómicos, las moléculas de los gases nobles poseen simetría esférica, y las fuerzas intermoleculares son muy débiles, por lo que sus entalpías de vaporización son muy bajas.
Con todo lo anteriormente expuesto sobre los gases nobles, espero que el lector del aquí reflejado pueda tener una idea más amplia y un conocimiento más certero sobre lo que en realidad son los denominados como “gases nobles”.
En comparación con la inmensidad del universo, nos queda aún muchísimo que aprender. Si nos limitamos a nuestro entorno más cercano, la Tierra, ¿cómo hemos podido llegar tan lejos?
¡La curiosidad! y ¡La necesidad! ¡El Instinto! y ¡La Evolución! Todo ello, amigos míos, nos lleva a querer saber y, para ello, debemos desvelar los secretos de la Naturaleza, que por cierto, no resulta nada fácil. Llevamos miles de años intentando comprender y, de momento, sólo sabemos… ¡Algunas cosas!
Emilio Silvera
Fuente: Variada y destacando, Cien preguntas básicas sobre ciencia de Asimov.
Mar
30
Si existe la perfección, estará en la Naturaleza
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (5)
Comments (5)
El Universo está construido según un plan cuya profunda simetría está presente de algún modo en la estructura interna de nuestro intelecto. Y, desde luego, si lo pensamos profundamente, tendremos que dar la razón a Paul Valery por tales pensamientos, ya que, la Mente Humana, alcanzó cotas inimaginables. Sin embargo, si realmente existe la perfección, ésta está, en la Naturaleza. Nosotros siempre seremos imperfectos y nos dejaremos llevar por los sentimientos.

¡Agua! El Universo está lleno de agua por todas partes y, si eso es así ¿qué pasa con la vida?
Hubo un tiempo, el el Universo muy temprano, en el que la temperatura estaba encima de algunos cientos de veces la masa del protón, cuando la simetría aún no se había roto, y la fuerza débil y electromagnética no sólo eran la misma matemáticamente, sino realmente la misma. Un físico que hubiera podido estar allí presente, en aquellos primeros momento, no habría podido observar ninguna diferencia real entre las fuerzas producidas por el intercambio de estas cuatro partículas: la W+, la W– , la Z y el Fotón.

Al llegar a escalas cada vez menores, también hemos entrado en ámbitos de energías de unión cada vez mayores. Un átomo puede ser despojado de su electrón aplicando sólo unos miles de electrón-voltios de energía, más para dispersar los nucleones que conforman un núcleo atómico se requieren varios millones de electrón-voltios, y para librar los quarks que constituyen cada nucleón se necesitaría cientos de veces más energía. Así, hemos llegado a comprender que, las estructuras más pequeñas y más fundamentales están ligadas por niveles de energía mayores porque sus estructuras mismas fueron forjadas en el calor del big bang.
También hemos llegado a comprender que, las fuerzas de la naturaleza que gobiernan la electricidad, el magnetismo, la radiactividad y las reacciones nucleares están confinadas a un “mundobrana” tridimensional, mientras que la gravedad actúa en todas las dimensiones y es consecuentemente más débil. Seguramente ese será el motivo por el cual, encontrar al Bosón mediador de la fuerza, el Gravitón, resulta tan difícil.
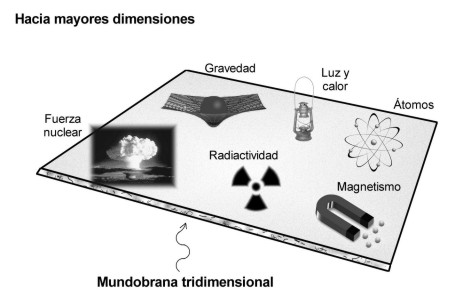
De manera similar, aunque menos clara, las teorías de supersimetrías conjeturaban que las cuatro fuerzas tal vez estaban ligadas por una simitría que se manifestaba en los niveles de energía aún mayores que caracterizaban al universo ya antes del big bang. La intodución de un eje histórico en la cosmologia y la física de particulas (como decía ayer en uno de los trabajos), beneficio a ambos campos. Los físicos proporcionaron a los cosmólogos una amplia gama de herramientas útiles para saber cómo se desarrolló el universo primitivo. Evidentemente, el Big Bang no fue una muralla de fuego de la que se burló Hoyle, sino un ámbito de suscesos de altas energías que muy posiblemente pueden ser comprensibles en términos de teoría de campo relativista y cuántica.

La cosmología, por su parte, dio un tinte de realidad histórica a las teorías unificadas. Aunque ningún acelerador concebible podrían alcanzar las titánicas energías supuestas por las grandes teorías unificadas y de la supersimetría, esas exóticas ideas aún pueden ser puestas a prueba, investigando si las partículas constituyentes del universo actual son compatibles con el tipo de historia primitiva que implican las teorías. Las partículas elementales aparentemente proporcionan las claves de algunos de los misterios fundamentales de la Cosmología temprana… y resulta que la Cosmología brinda una especia de terreno de prueba para alguna de las ideas de la física de partículas elementales. Esto implica que los aceleradores de partículas, como los telescopios, funcionen como máquinas del tiempo. Un telescopio penetra en el pasado en virtud del tiempo que tarda la luz en desplazarse entre las estrellas; un acelerador recrea, aunque sea fugazmente, las condiciones que prevalecían en el Universo primitivo.

Moléculas, átomos y conexiones para formar pensamientos que nos llevaron hacia los conocimientos que hoy, tras muchos miles de millones de años de evolución del Universo, hizo posible la aparición de especies que, tras miles de años de experiencia, de observación, y, de imaginar…, llegó a conseguir la intuición necesaria para presentir que, formamos parte de un todo inmenso del que sólo somos una parte, la que piensa. También la que tiene que descubrir, los secretos de la Naturaleza, en ello, le va la existencia en el futuro.

Hemos aprendido que cuanto más íntimamente examinemos la Naturaleza, tanto más lejos hacia atrás vamos en el tiempo. Alguna vez he puesto el ejemplo de mirar algo que no es familiar, el dorso de la mano, por ejemplo, e imaginemos que podemos observarlo con cualquier aumento deseado.
Con un aumento relativamente pequeño, podemos ver las células de la piel, cada una con un aspecto tan grande y complejo como una ciudad, y con sus límites delineados por la pared celular. Si elevamos el aumento, veremos dentro de la célula una maraña de ribosomas serpenteando y mitocondrias ondulantes, lisosomas esféricos y centríolos, cuyos alrededores están llenos de complejos órganos dedicados a las funciones respiratorias, sanitarias y de producción de energía que mantienen a la célula.
Ya ahí tenemos pruebas de historia. Aunque esta célula particular solo tiene unos pocos años de antigüedad, su arquitectura se remonta a más de mil millones de años, a la época en que aparecieron en la Tierra las células eucariota o eucarióticas como la que hemos examinado.
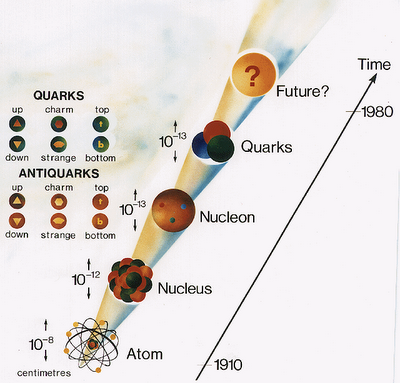
Hemos llegado a poder discernir la relación directa que vincula el tamaño, la energía de unión y la edad de las estructuras fundamentales de la Naturaleza. Ahora, hemos llegado a comprender muchas de las cosas que, hasta bien poco tiempo, eran auténticos secretos que, el Universo, celosamente se guardaba, y, esa comprensión, nos llevará más lejos y nos permitirá realizar un largo camino hacia el corazón mismo de la materia, donde según parece, pueden residir objetos infinitesimales, más pequeños que los Quarks, en esa distancia inalcanzable ahora que hemos llamado, el Límite de Planck.
Aún estamos en el camino, no hemos podido llegar más lejos y, con la ayuda de los aceleradores hemos podido llegar hasta una diez billonésima de segundo después del big bang que es menos que un pestañeo con los párpados en toda la historia humana registrada. A pesar de ello, extrañamente, la investigación de la evolución del Universo recién nacido indica que ocurrieron muchas cosas aún antes, durante la primera ínfima fracción de un segundo. Todos los teóricos han tratado de elaborar una explicación coherente de los primeros momentos de la historia cósmica. Por supuesto, sus ideas fueron esquemáticas e incompletas, muchas de sus conjeturas, sin duda, se juzgaran deformadas o sencillamente erróneas, pero constituyeron una crónica mucho más aclaradora del Universo primitivo que la que teníamos antes.
Recreación del Universo primitivo al que no hemos podido llegar en el momento mismo de su creación, nos ha sido imposible recrear ese momento que llamamos big bang, las matemáticas no funcionan al tratar de formular la ecuación precisa que nos muestre aquel momento.

Los neutrinos dejaron al descubierto la simetría rota del universo
Al principio, cuando el universo era simétrico, sólo existía una sola fuerza que unificaba a todas las que ahora conocemos, la gravedad, las fuerzas electromagnéticas y las nucleares débil y fuerte, todas emergían de aquel plasma opaco de alta energía que lo inundaba todo. Más tarde, cuando el universo comenzó a enfriarse, se hizo transparente y apareció la luz, las fuerzas se separaron en las cuatro conocidas, emergieron los primeros quarks para unirse y formar protones y neutrones, los primeros núcleos aparecieron para atraer a los electrones que formaron aquellos primeros átomos. Doscientos millones de años más tarde, se formaron las primeras estrellas y galaxias. Con el paso del tiempo, las estrellas sintetizaron los elementos pesados de nuestros cuerpos, fabricados en supernovas que estallaron, incluso antes de que se formase el Sol. Podemos decir, sin temor a equivocarnos, que una supernova anónima explotó hace miles de millones de años y sembró la nube de gas que dio lugar a nuestro sistema solar, poniendo allí los materiales complejos y necesarios para que algunos miles de millones de años más tarde, tras la evolución, apareciéramos nosotros.
¡Qué cosas! El asombro se junta con la maravilla y nos lleva a comprender que, la ignorancia, quizá sea nuestro mayor patrimonio, ya que, el saber es escaso y comprender, comprendemos con cierta lentitud, la que impone el ritmo del Universo. Todo tiene su tiempo marcado y nuestra comprensión…también.
Emilio Silvera
Mar
29
¿La Física? ¡Una maravilla! Nos dice cómo funciona la Naturaleza
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (5)
Comments (5)

“En el mundo de los seres vivos, la escala o tamaño crea importantes diferencias. En muchos aspectos, la anatomía de un ratón es una copia de la de un elefante, pero mientras que un ratón trepar por una pared prácticamente vertical sin mucha dificultad (y se puede caer desde una altura varias veces mayor que su propio tamaño sin hacerse daño), un elefante no sería capaz de realizar tal hazaña. Con bastante generalidad se puede afirmar que los efectos de la gravedad son menos importantes cuanto menores sean los objetos que consideremos (sean vivos o inanimados).”


Cuando llegamos a los seres unicelulares, se ve que ellos no hay distinción entre arriba y abajo. Para ellos, la tensión superficial del agua es mucho más importante que la fuerza de la gravedad a esa escala. Tranquilamente se pueden mover y desplazar por encima de una superficie acuática. Los pluricelulares no pueden hacer tal cosa.

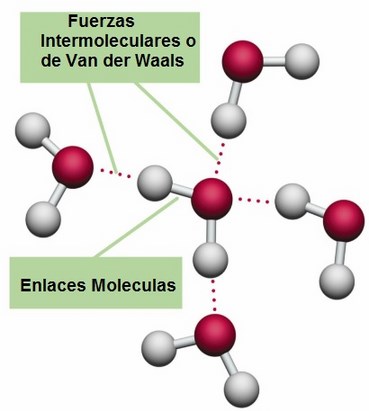
La tensión superficial es una consecuencia de que todas las moléculas y los átomos se atraen unos a otros con una fuerza que nosotros llamamos de Van der Waals. fuerza tiene un alcance muy corto; para ser precisos, diremos que la intensidad de esta fuerza a una distancia r es aproximadamente 1/r7. Esto significa que si se reduce la distancia dos átomos a la mitad de la fuerza de Van der Waals con la que se atraen uno a otro se hace 2 × 2 × 2 × 2 × 2 × 2 × 2 = 128 veces más intensa. Cuando los átomos y las moléculas se acercan mucho unos a otros quedan unidos muy fuertemente a través de esta fuerza. El conocimiento de esta fuerza se debe a Johannes Diderik Van der Waals (1837 – 1923) con su tesis sobre la continuidad del líquido y gaseoso que le haría famoso, ya que en esa época (1873), la existencia de las moléculas y los átomos no estaba completamente aceptado.
La tensión superficial del agua, es el efecto físico (energía de atracción entre las moléculas) que “endurece” la capa superficial del agua en reposo y permite a algunos insectos, como el mosquito y otros desplazarse por la superficie del agua sin hundirse.

El famoso físico inglés James Clerk Maxwell, que formuló la teoría del electromagnetismo de Faraday, quedó muy impresionado por este de Van der Waals.
Los tamaños de los seres uniceculares, animales y vegetales, se miden en micrómetros o “micras”, donde 1 micra es 1/1.000 de milímetro, aproximadamente el tamaño de los detalles más pequeños que se pueden observar con un microscopio ordinario. El mundo de los microbios es fascinante, pero no es el objeto de este trabajo, y continuaremos el viaje emprendido las partículas elementales que forman núcleos, átomos, células y materia, así como las fuerzas que intervienen en las interacciones fundamentales del universo y que afecta a todo lo que existe.

Hemos hablado del electrón que rodea el núcleo, de su carga eléctrica negativa que complementa la positiva de los protones y hace estable al átomo; una masa de solamente 1/1.836 de la del núcleo más ligero (el del hidrógeno). La importancia del electrón es vital en el universo.
Pero busquemos los “cuantos”. La física del siglo XX empezó exactamente en el año 1900, cuando el físico alemán Max Planck propuso una posible solución a un problema que había intrigando a los físicos durante años. Es el problema de la luz que emiten los cuerpos calentados a una cierta temperatura, y también la radiación infrarroja emitida, con menor intensidad, por los objetos más fríos (radiación de cuerpo negro).

Estaba bien aceptado entonces que esta radiación tenía un origen electromagnético y que se conocían las leyes de la naturaleza que regían estas ondas electromagnéticas. También se conocían las leyes para el frío y el calor, la así llamada “termodinámica”, o al menos eso parecía. Pero si utilizamos las leyes de la termodinámica para calcular la intensidad de una radiación, el resultado no tiene ningún sentido. Los cálculos nos dicen que se emitiría una cantidad infinita de radiación en el ultravioleta más lejano y, luego, esto no es lo que sucede. Lo que se observa es que la intensidad de la radiación muestra un pico a una cierta longitud de onda característica, y que la intensidad disminuye tanto para longitudes mayores como para menores. Esta longitud de onda característica es inversamente proporcional a la temperatura absoluta de objeto radiante (la temperatura absoluta se define por una escala de temperatura que empieza a 273º bajo cero). Cuando a 1.000º C un objeto se pone al “rojo vivo”, el objeto está radiando en la zona de luz visible.
Radiación de Cuerpo Negro
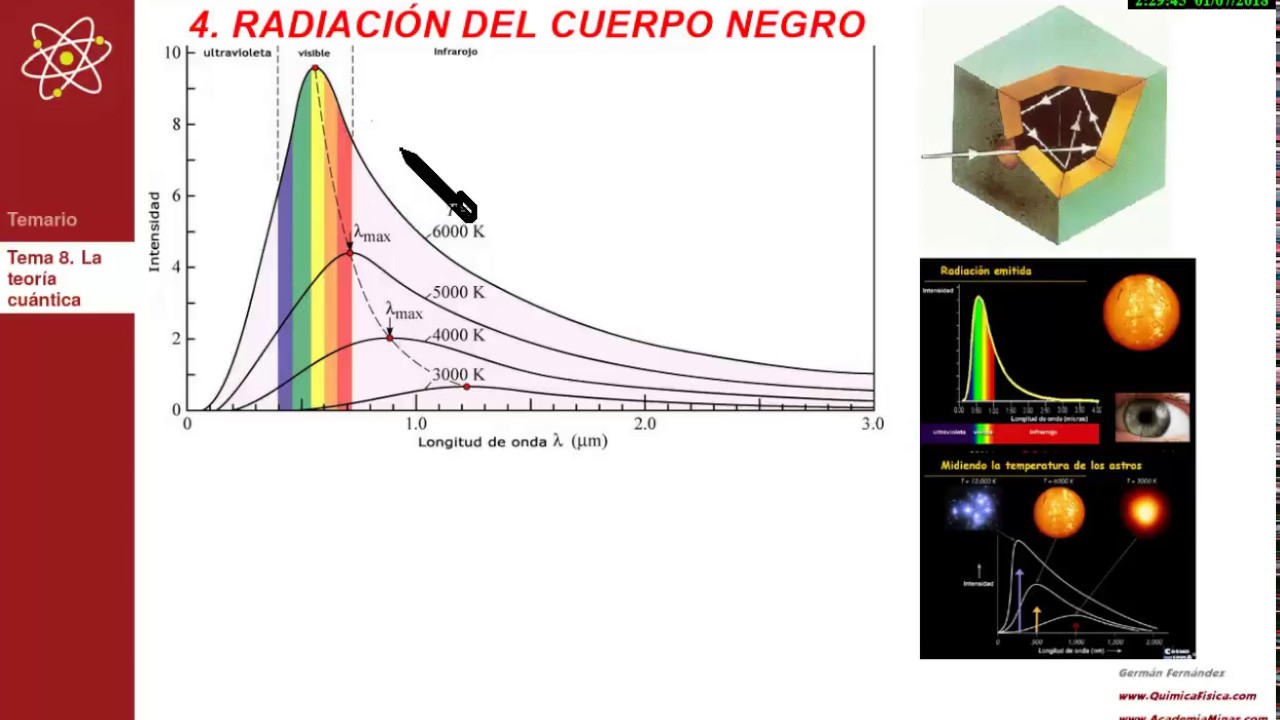
Un cuerpo negro es un objeto teórico o ideal que absorbe toda la luz y toda la energía radiante que incide sobre él. Nada de la radiación incidente se refleja o pasa a través del cuerpo negro. A pesar de su , el cuerpo negro emite luz y constituye un modelo ideal físico para el estudio de la emisión de radiación electromagnética. El nombre Cuerpo negro fue introducido por Gustav Kirchhoff en 1862.

La luz emitida por un cuerpo negro se denomina radiación de cuerpo negro. Todo cuerpo emite energía en de ondas electromagnéticas, siendo esta radiación, que se emite incluso en el vacío, tanto más intensa cuando más elevada es la temperatura del emisor. La energía radiante emitida por un cuerpo a temperatura ambiente es escasa y corresponde a longitudes de onda superiores a las de la luz visible (es decir, de menor frecuencia). Al elevar la temperatura no sólo aumenta la energía emitida sino que lo hace a longitudes de onda más cortas; a esto se debe el cambio de color de un cuerpo cuando se calienta. Los cuerpos no emiten con igual intensidad a todas las frecuencias o longitudes de onda, sino que siguen la ley de Planck.
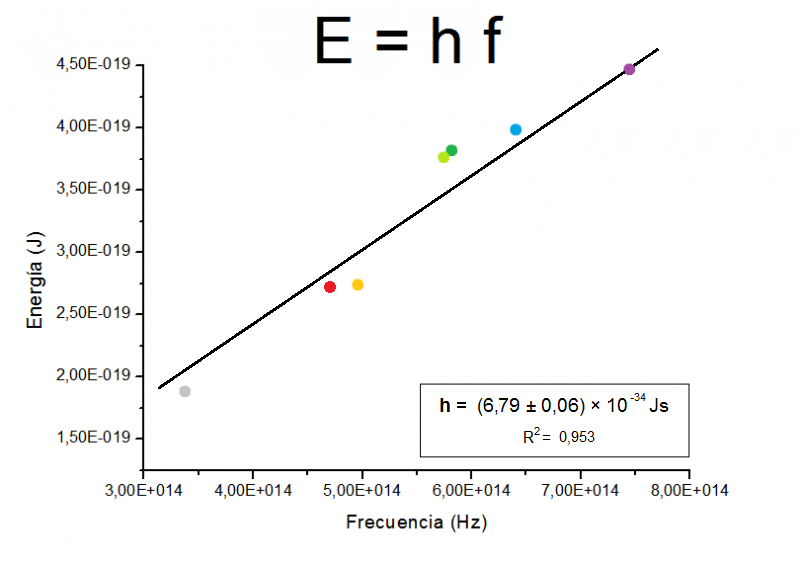
Lo que Planck propuso fue simplemente que la radiación sólo podía ser emitida en paquetes de un tamaño dado. La cantidad de energía de uno de esos paquetes, o cuantos, es inversamente proporcional a la longitud de onda, y por tanto, proporcional a la frecuencia de radiación emitida. La fórmula es E = hν, donde E es la energía del paquete, ν es la frecuencia y h es una nueva constante fundamental de la naturaleza, la constante de Planck. Cuando Planck calculó la intensidad de la radiación térmica imponiendo nueva condición, el resultado coincidió perfectamente con las observaciones.
Poco tiempo después, en 1905, Einstein formuló esta teoría de una manera mucho más tajante: él sugirió que los objetos calientes no son los únicos que emiten radiación en paquetes de energía, sino que toda la radiación consiste en múltiplos del paquete de energía de Planck. El príncipe francés Louis-Victor de Broglie, dándole otra vuelta a la teoría, propuso que no sólo cualquier cosa que oscila tiene energía, sino que cualquier cosa con energía se debe comportar una “onda” que se extiende en una cierta región del espacio, y que la frecuencia ν de la oscilación verifica la ecuación de Planck. Por lo tanto, los cuantos asociados con los rayos de luz deberían verse una clase de partículas elementales: el fotón. Todas las demás clases de partículas llevan asociadas diferentes ondas oscilantes de campos de fuerza, esto lo veremos más adelante.
El curioso comportamiento de los electrones en el interior del átomo, descubierto y explicado por el famoso físico danés Niels Bohr, se pudo atribuir a las ondas de de Broglie. Poco después, en 1926, Edwin Schrödinger descubrió cómo escribir la teoría ondulatoria de de Broglie con ecuaciones matemáticas exactas. La precisión con la cual se podían realizar cálculos era asombrosa, y pronto quedó claro que el comportamiento de todos los objetos pequeños quedaba exactamente determinado por las recién descubiertas “ecuaciones de ondas cuánticas”.
Está bien comprobado que la mecánica cuántica funciona de maravilla…, pero, sin embargo, surge una pregunta muy formal: ¿qué significan realmente estas ecuaciones?, ¿qué es lo que están describiendo? Isaac Newton, allá en 1867 formuló cómo debían moverse los planetas alrededor del Sol, estaba claro todo el mundo qué significaban sus ecuaciones: que los planetas estaban siempre en una posición bien definida des espacio y que sus posiciones y sus velocidades en un momento concreto determinan inequívocamente cómo evolucionarán las posiciones y las velocidades en el tiempo.
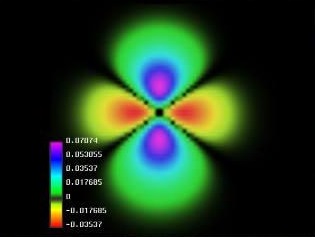
Pero los electrones todo es diferente. Su comportamiento parece estar envuelto en misterio. Es como si pudieran “existir” en diferentes lugares simultáneamente, como si fueran una nube o una onda, y esto no es un efecto pequeño. Si se realizan experimentos con suficiente precisión, se puede determinar que el electrón parece capaz de moverse simultáneamente a lo largo de trayectorias muy separadas unas de otras. ¿Qué puede significar todo esto?
Niels Bohr consiguió responder a esta pregunta de tal que con su explicación se pudo seguir trabajando, y muchos físicos siguen considerando su respuesta satisfactoria. Se conoce como la interpretación de Copenhague de la mecánica cuántica.

Si la mecánica cuántica tiene cosas extrañas y el espín es una de ellas. Y si uno piensa que la intuición le ayudará a comprender todo esto, pues no lo hará, o es poco probable que lo haga. Las partículas tienen un espín fundamental. Al igual que la carga eléctrica o la masa, el espín ayuda a definir que de partícula es cada una.
Las leyes de la mecánica cuántica han sido establecidas con mucha precisión; permite cómo calcular cualquier cosa que queramos saber. Pero si queremos “interpretar” el resultado, nos encontramos con una curiosa incertidumbre fundamental: que varias propiedades de las partículas pequeñas no pueden estar bien definidas de manera simultánea. Por ejemplo, podemos determinar la velocidad de una partícula con mucha precisión, pero entonces no sabremos exactamente dónde se encuentra; o a la inversa, podemos determinar la posición con precisión, pero entonces su velocidad queda mal definida. Si una partícula tiene espín (rotación alrededor de su eje), la dirección alrededor de la cual está rotando (la orientación del eje) no puede ser definida con gran precisión.

La posición y el momento de una partícula nunca lo podremos saber con precisión ilimitada.
No es fácil explicar de forma sencilla de dónde viene esta incertidumbre, pero existen ejemplos en la vida cotidiana que tienen algo parecido. La altura de un tono y la duración en el tiempo durante el cual oímos el tono tienen una incertidumbre mutua similar. Para afinar un instrumento se debe escuchar una nota durante un cierto intervalo de tiempo y compararla, por ejemplo, con un diapasón que debe vibrar también durante un tiempo. Notas muy breves no tienen bien definido el tono.
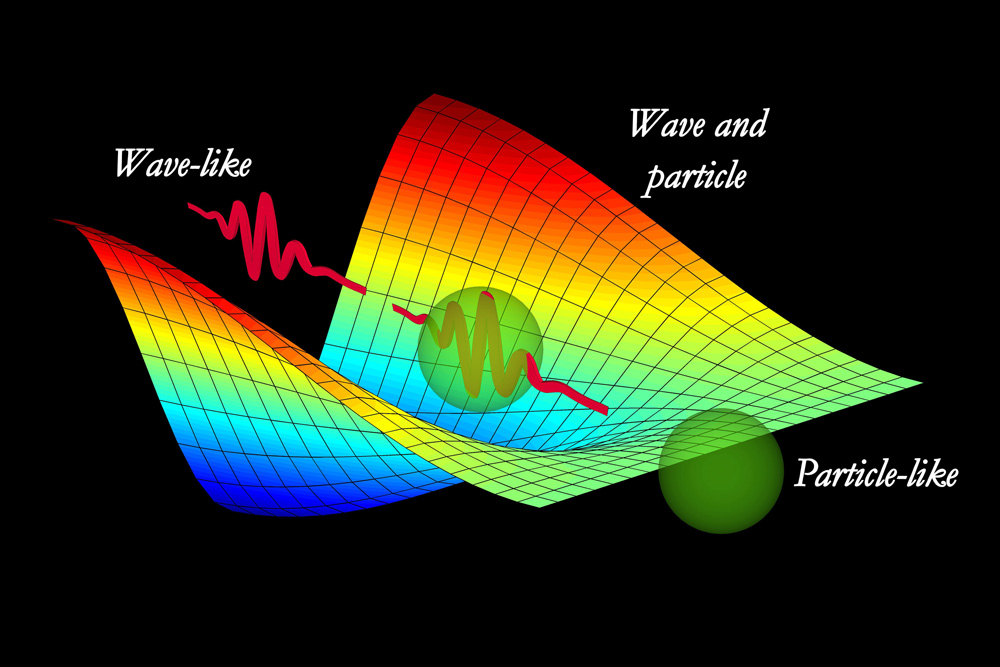
Para que las reglas de la mecánica cuántica funcionen, es necesario que todos los fenómenos naturales en el mundo de las cosas pequeñas estén regidos por las mismas reglas. Esto incluye a los virus, bacterias e incluso a las personas. Sin embargo, cuando más grande y más pesado es un objeto, más difícil es observar las desviaciones de las leyes del movimiento “clásicas” debidas a la mecánica cuántica. Me gustaría referirme a exigencia tan importante y tan peculiar de la teoría con la palabra “holismo”. Esto no es exactamente lo mismo que entienden algunos filósofos por holismo, y que podría definir como “el todo es más que la suma de sus partes”. Si la física nos ha enseñado algo es justo lo contrario. Un objeto compuesto de un gran de partículas puede ser entendido exactamente si se conocen las propiedades de sus partes (partículas); basta que sepamos sumar correctamente (¡y esto no es nada fácil en mecánica cuántica!). Lo que entiendo por holismo es que, efectivamente, el todo es la suma de las partes, pero sólo se puede hacer la suma si todas las partes obedecen a las mismas leyes. Por ejemplo, la constante de Planck, h, que es igual a 6’626075… × 10-34 Julios segundo, debe ser exactamente la misma para cualquier objeto en cualquier sitio, es decir, debe ser una constante universal.
La mecánica cuántica es muy extraña a nuestro “sentido común”, sabemos que se desenvuelve en ese “universo” de lo muy pequeño, alejado de nuestra vida cotidiana en el macrocosmos tetradimensional que, no siempre coincide con lo que, en aquel otro infinitesimal acontece.
Las reglas de la mecánica cuántica funcionan tan bien que refutarlas resulta realmente difícil. Los trucos ingeniosos descubiertos por Werner Heisenberg, Paul Dirac y muchos otros mejoraron y completaron las reglas generales. Pero Einstein y otros pioneros como Erwin Schrödinger siempre presentaron serias objeciones a interpretación. Quizá funcione bien, pero ¿dónde está exactamente el electrón?, ¿en el punto x o en el punto y? En pocas palabras, ¿dónde está en realidad?, y ¿cuál es la realidad que hay detrás de nuestras fórmulas? Si tenemos que creer a Bohr, no tiene sentido buscar tal realidad. Las reglas de la mecánica cuántica, por sí mismas, y las observaciones realizadas con detectores son las únicas realidades de las que podemos hablar.
Es cierto que, existe otro universo dentro de nuestro del que, aún, nos queda mucho por aprender.

La mecánica cuántica puede ser definida o resumida así: en principio, con las leyes de la naturaleza que conocemos se puede predecir el resultado de cualquier experimento, en el sentido que la predicción consiste en dos factores: el primer factor es un cálculo definido con exactitud del efecto de las fuerzas y estructuras, tan riguroso como las leyes de Isaac Newton para el movimiento de los planetas en el Sistema Solar; el segundo factor es una arbitrariedad estadística e incontrolable definida matemáticamente de estricta. Las partículas seguirán una distribución de probabilidades dadas, primero de una forma y luego de otra. Las probabilidades se pueden calcular utilizando la ecuación de Schrödinger de función de onda (Ψ) que, con muchas probabilidades nos indicará el lugar probable donde se encuentra una partícula en un dado.
Muchos estiman que esta teoría de las probabilidades desaparecerá cuando se consiga la teoría que explique, de forma completa, todas las fuerzas; la buscada teoría del todo, lo que implica que nuestra descripción actual incluye variables y fuerzas que (aún) no conocemos o no entendemos. Esta interpretación se conoce como hipótesis de las variables ocultas.”

¿Podría ser el Universo un Holograma?
También Gerard ‘t Hooft es el autor de lo que han dado en llamar l principio holográfico es una conjetura especulativa acerca de las teorías de la Gravedad Cuántica propuesta en 1993 por este autor, y mejorada y promovida por Leonard Susskin en 1995. Postula que toda la información contenida en cierto volumen de un espacio concreto se puede conocer a partir de la información codificable sobre la frontera de dicha región. Una importante consecuencia es que la cantidad máxima de información que puede contener una determinada región de espacio rodeada por una superficie diferenciable está limitada por el área total de dicha superficie.
Por ejemplo, se pueden modelar todos los eventos que ocurran en un cuarto o una habitación creando una teoría en la que sólo tome en cuenta lo que suceda en sus paredes. En el principio holográfico también se afirma que por cada cuatro Unidades de Planck existe al menos un grado de libertad (o una unidad constante de Bolttzmann k de máxima entropía). Esto se conoce como frontera de Bekenstein:
donde S es la entropía y A es la unidad de mensura considerada. En unidades convencionales la fórmula anterior se escribe:
donde:
 , es la constante de Boltzmann.
, es la constante de Boltzmann.
 , es la vecolcidad de la luz.
, es la vecolcidad de la luz.
 , es la constante gravitacional universal.
, es la constante gravitacional universal.
 , es la constante de Planck racionalizada.
, es la constante de Planck racionalizada. , es la longitud de Planck.
, es la longitud de Planck.
Claro que esta… ¡Es otra Historia!
Emilio Silvera
Mar
19
Misterios de la Naturaleza
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Relativista ~
Clasificado en Física Relativista ~
 Comments (4)
Comments (4)
¿Por qué la materia no puede moverse más deprisa que la velocidad de la luz? Porque cuando se acerca a las velocidades relativistas, es decir, la velocidad de la luz en el vacío, c, la energía inercial se convierte en masa y, al llegar a c (299.792,458 m/s), sería infinita.
Si un enjambre de fotones pasaran por delante de nosotros, estando en el vacío Espacial, sólo veríamos una ráfaga luminosa pasar tan rauda que sería vista y no vista.
“Las propiedades de los fotones pueden estudiarse en experimentos donde se los hace incidir sobre la materia. Se observa así que, aunque los fotones no tienen masa, tienen un momento lineal
, cuyo módulo es proporcional a su energía
(11) Esto es un resultado de la relatividad especial, según la cual la energía y el momento de una partícula con velocidad
son
(12) (13) La energía y el momento de una partícula a la velocidad de la luz serían infinitos, lo cual no es físicamente aceptable, a no ser que su masa sea cero, en cuyo caso se obtendría una indeterminación
, que podría tener un límite finito. Como los fotones se propagan a la velocidad de la luz, deben tener masa nula.”
Fotones que salen disparados a la velocidad de c. ¿Qué podría seguirlos?
Para contestar esta pregunta hay que advertir al lector que la energía suministrada a un cuerpo puede influir sobre él de distintas maneras. Si un martillo golpea a un clavo en medio del aire, el clavo sale despedido y gana energía cinética o, dicho de otra manera, energía de movimiento. Si el martillo golpea sobre un clavo, cuya punta está apoyada en una madera dura e incapaz de moverse, el clavo seguirá ganando energía, pero esta vez en forma de calor por rozamiento al ser introducido a la fuerza dentro de la madera.
Albert Einstein demostró en su teoría de la relatividad especial que la masa cabía contemplarla como una forma de energía (E = mc2.) Al añadir energía a un cuerpo, esa energía puede aparecer en la forma de masa o bien en otra serie de formas.
En condiciones ordinarias, la ganancia de energía en forma de masa es tan increíblemente pequeña que sería imposible medirla. Fue en el siglo XX (al observar partículas subatómicas que, en los grandes aceleradores de partículas, se movían a velocidades de decenas de miles de kilómetros por segundo) cuando se empezaron a encontrar aumentos de masa que eran suficientemente grandes para poder detectarlos. Un cuerpo que se moviera a unos 260.000 Km por segundo respecto a nosotros mostraría una masa dos veces mayor que cuando estaba en reposo (siempre respecto a nosotros).

No, un púlsar tampoco puede ser más rápido que la luz
La energía que se comunica a un cuerpo libre puede integrarse en él de dos maneras distintas:
- En forma de velocidad, con lo cual aumenta la rapidez del movimiento.
- En forma de masa, con lo cual se hace “más pesado”.
La división entre estas dos formas de ganancia de energía, tal como la medimos nosotros, depende en primer lugar de la velocidad del cuerpo (medida, una vez más, por nosotros).
Si el cuerpo se mueve a velocidades normales, prácticamente toda la energía se incorpora a él en forma de velocidad: se moverá más aprisa sin cambiar su masa.
A medida que aumenta la velocidad del cuerpo (suponiendo que se le suministra energía de manera constante) es cada vez menor la energía que se convierte en velocidad y más la que se transforma en masa. Observamos que, aunque el cuerpo siga moviéndose cada vez más rápido, el ritmo de aumento de velocidad decrece. Como contrapartida, notamos que gana más masa a un ritmo ligeramente mayor.

En gracia quizás podamos superarla pero, en velocidad…no creo, c es el tope que impone el Universo para la velocidad.
Al aumentar aún más la velocidad y acercarse a los 299.792’458 Km/s, que es la velocidad de la luz en el vacío, casi toda la energía añadida entra en forma de masa. Es decir, la velocidad del cuerpo aumenta muy lentamente, pero la masa es la que sube a pasos agigantados. En el momento en que se alcanza la velocidad de la luz, toda la energía añadida se traduce en masa que, llegado a cierto límite, podría ser infinita y, como infinito no hay nada, nos quedamos con que nunca, nada, podrá sobrepasar esa velocidad.
En esta ecuación, el término pc representa el momento del objeto (o, lo que es lo mismo, el producto de su masa por la velocidad a la que se desplaza), multiplicado por la velocidad de la luz. De hecho, la versión de esta ecuación que todos conocemos (E = mc2) representa la energía que posee un objeto cuando está quieto (cuando v = 0 y, por tanto, pc = 0, así que E = mc2 + 0).
la masa (la resistencia al movimiento) es una propiedad que refleja la cantidad de energía que compone un objeto y se manifiesta a través de su inercia. Nos podemos preguntas: ¿Por qué la masa de un objeto aumenta a medida que incrementa su velocidad y de dónde sale esa masa que se suma?

“El caso es que la ecuación completa de Einstein nos dice que la energía total de un objeto equivale a la energía que tiene cuando está quieto (mc), más la energía cinética que gana cuando empieza a moverse (pc). Por tanto, un objeto que se mueva muy rápido tendrá más energía que otro objeto idéntico, pero que está en reposo.”
De todo esto podemos deducir que siendo la velocidad de la luz en el vacío un límite que impone el Universo, cuando se va acercando a c, la velocidad se verá frenada y, la energía de inercia se convierte en masa (E = mc2 ).

El cuerpo no puede sobrepasar la velocidad de la luz porque para conseguirlo hay que comunicarle energía adicional, y a la velocidad de la luz toda esa energía, por mucha que sea, se convertirá en nueva masa, con lo cual la velocidad no aumentaría ni un ápice.
Todo esto no es pura teoría, sino que tal como ha sido comprobado, es la realidad de los hechos.
¿Qué velocidad podría ser la de la luz en otros mundos paralelos que pudieran existir fuera de nuestro universo?

Ninguna nave, por los medios convencionales, podrá nunca superar la velocidad de la luz
La velocidad de la luz es la velocidad límite en el universo. Cualquier cosa que intente sobrepasarla adquiriría una masa infinita, y, siendo así (que lo es), nuestra especie tendrá que ingeniarse otra manera de viajar para poder llegar a las estrellas, ya que, la velocidad de la luz nos exige mucho tiempo para alcanzar objetivos lejanos, con lo cual, el sueño de llegar a las estrellas físicamente hablando, está lejos, muy lejos. Es necesario encontrar otros caminos alejados de naves que, por muy rápida que pudieran moverse, nunca podrían superar la velocidad de la luz, el principio que impone la relatividad especial lo impide, y, siendo así, ¿cómo iremos? La única manera sería burlar a c, si podemos, al fin, abrir una ventana al hiperespacio.
La velocidad de la luz, por tanto, es un límite en nuestro universo; no se puede superar. Siendo esto así, el hombre tiene planteado un gran reto, no será posible el viaje a las estrellas si no buscamos la manera de esquivar este límite de la naturaleza, ya que las distancias que nos separan de otros sistemas solares son tan enormes que, viajando a velocidades por debajo de la velocidad de la luz, sería casi imposible alcanzar el destino deseado.

De momento sólo con los Telescopios podemos llegar tan lejos. Ahí han captado la galaxia más lejana del Universo
Los científicos, físicos experimentales, tanto en el CERN como en el FERMILAB, aceleradores de partículas donde se estudian y los componentes de la materia haciendo que haces de protones o de muones, por ejemplo, a velocidades cercanas a la de la luz choquen entre sí para que se desintegren y dejen al descubierto sus contenidos de partículas aún más elementales. Pues bien, a estas velocidades relativistas cercanas a c (la velocidad de la luz), las partículas aumentan sus masas; sin embargo, nunca han logrado sobrepasar el límite de c, la velocidad máxima permitida en nuestro universo.

Se han observado haces de muones lanzados a la velocidad de C, y el resultado fue que aumentaron su masa 10 veces.
Es preciso ampliar un poco más las explicaciones anteriores que no dejan sentadas todas las cuestiones que el asunto plantea, y quedan algunas dudas que incitan a formular nuevas preguntas, como por ejemplo: ¿por qué se convierte la energía en masa y no en velocidad?, o ¿por qué se propaga la luz a 299.793 Km/s y no a otra velocidad?


Sí, la Naturaleza nos habla, simplemente nos tenemos que parar para poder oír lo que trata de decirnos y, entre las muchas cosas que nos dice, estarán esos mensajes que nos indican el camino por el que debemos coger para burlar a la velocidad de la luz, conseguir los objetivos y no vulnerar ningún principio físico impuesto por la Naturaleza.
La única respuesta que podemos dar hoy es que así, es el universo que nos acoge y las leyes naturales que lo rigen, donde estamos sometidos a unas fuerzas y unas constantes universales de las que la velocidad de la luz en el vacío es una muestra.

Habiando lanzado un haz de muones que alcanzó velocidades relativistas, y, se dieron cuenta que su peso, había crecido diez veces. Como la velocidad de la luz es un límite del Universo, los muones se fueron frenando a medida que se acercaban a c, y la energía de inercia se convirtió en masa.
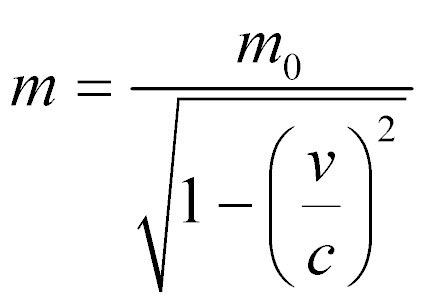
La relatividad de la masa
La teoría de la invariancia predice que la masa observada de un objeto aumentará a medida que aumente la velocidad relativa del objeto. Curiosamente, este efecto se había observado incluso antes de la teoría de Einstein, cuando los científicos se sorprendieron al notar un aumento en la masa de los electrones de alta velocidad en los tubos de vacío. Este efecto se observa fácilmente hoy en día en los aceleradores de partículas, donde las partículas elementales cargadas, como los electrones o los protones, se aceleran mediante campos electromagnéticos a velocidades tan altas como 0,9999999 de la velocidad de la luz. Las masas de estas partículas aumentan exactamente la cantidad predicha por la fórmula de Einstein. A esa velocidad, el aumento de su masa mm es aproximadamente 2236 veces la masa en reposo. De hecho, los aceleradores circulares deben diseñarse para tener en cuenta este aumento de masa.

Ingenios que inventó el hombre y que nos revelan secretos profundamente escondido
A velocidades grandes cercanas a la de la luz (velocidades relativistas) no sólo aumenta la masa del objeto que viaja, sino que disminuye también su longitud en la misma dirección del movimiento (contracción de Lorentz) y en dicho objeto y sus ocupantes – si es una nave – se retrasa al paso del tiempo, o dicho de otra manera, el tiempo allí transcurre más despacio.
A menudo se oye decir que las partículas no pueden moverse “más deprisa que la luz” y que la “velocidad de la luz” es el límite último de velocidad. Pero decir esto es decir las cosas a medias, porque la luz viaja a velocidades diferentes dependiendo del medio en el que se mueve. Donde más deprisa se mueve la luz es en el vacío: allí lo hace a 299.792’458 Km/s. Este sí es el límite último de velocidades que podemos encontrar en nuestro universo.

Fotones emitidos por un rayo coherente conformado por un láser
Tenemos el ejemplo del fotón, la partícula mediadora de la fuerza electromagnética, un bosón sin masa que recorre el espacio a esa velocidad antes citada. Hace no muchos días se habló de la posibilidad de que unos neutrinos hubieran alcanzado una velocidad superior que la de la luz en el vacío y, si tal cosa fuera posible, o, hubiera pasado, habríamos de relegar parte de la Teoría de la Relatividad de Einstein que nos dice lo contrario y, claro, finalmente se descubrió que todo fue una falsa alarma generada por malas mediciones. Así que, la teoría del genio, queda intacta.
¡La Naturaleza! Observémosla.
Emilio silvera V.
















 Totales: 75.405.021
Totales: 75.405.021 Conectados: 67
Conectados: 67