Mar
16
El Universo complejo y… ¿Nosotros?
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (1)
Comments (1)
También nosotros somos cuantos de luz
¡El Universo! Gracias a la Astronomía, la Astrofísica y otras disciplinas y estudios relacionados, estamos conociendo cada día lo que en realidad es nuestro Universo que, nos tiene deparadas muchas, muchas sorpresas y maravillas que ni podemos imaginar. ¡Son tantas las cosas que aún tenemos que aprender de éste Universo Inmenso!
El hombre se ha preguntado durante largo tiempo, “¿de qué está hecho el mundo?” Demócrito de Abdera nos hablaba del “átomo” y Empédocles de “elementos”, otros, se referían a la sustancia cósmica a la que llamaban Ylem, aquella “semilla” primera que daría lugar a la venida de la materia. ¿No será el Ylem, lo que hoy llaman materia oscura?

El Modelo Estándar aunque ha sido una gran máquina de trabajo para los físicos, no es un Modelo completo: ¿Por qué no están ahí los neutrinos? ¿Qué pasa con la fuerza de la Gravedad que se resiste a juntarse con la Mecánica cuántica? Y, que decir de los casi 20 parámetros aleatorios (metidos con calzador para completar el Modelo), sólo uno, el Bosón de Higgs se ha verificado.
El Universo complejo y… ¿Nosotros?
En la imagen se indican las regiones donde tuvieron lugar sucesos de gran importancia y que fueron capturadas en el ultravioleta extremo. Las líneas blancas trazan el campo magnético solar (Crédito: K. Schrijver & A. Title). Ni los 150 millones de kilómetros que nos separan de la estrella más importante para nosotros, nos impiden hurgar y desvelar sus secretos, y, desde luego, hacemos muy bien, es mucho lo que nos va en ello. Saber y conocer lo que allí ocurra es, nuestra garantía de vida. Bueno, si no tanto como eso sí al menos tener la posibilidad de información por si, llegado el caso, podemos prevenir algún desastre.

Einstein tenía razón
Satélite Gravity Probe B. Dedicado a medir la curvatura del campo gravitatorio terrestre debido a la teoría de la relatividad de Einstein. La gravedad ha sido medida y comprobada de muchas maneras pero… ¡Gravedad cuántica! ¿qué es eso? La imaginación anda más rápida que los conocimientos. Sin embargo, así hemos ido avanzando en el transcurrir del Tiempo. Ahora andamos a vueltas con la “materia oscura” que nadie sabe (a ciencia cierta) lo que es, yo la llamo materia cósmica y me parece más apropiado.

¿Os acordáis? ¿Cuántos niños no habrán soñado con escenas como estas?
Cuando hablo de lo muy pequeño, puedo llegar a entender muy bien lo que es, lo que son, “licencias literarias” el papel de nada se queja y el lápiz puede escribir lo que quiera y piense el que lo sostiene, según le dicte su imaginación. Claro que, cuando comparamos ese mundo de ilusiones e imaginación con el mundo real, todo el edificio se viene abajo. ¡Lástima!
Todos los niños pequeños juegan con pequeños muñecos que son soldados, guerreros o seres de otras galaxias con poderes mágicos y, ellos, en su inocente mundo sin maldad, los dirigen con sus manitas gordezuelas al desarrollo de luchas y aventuras sin fin. Jonathan Swift, nos deleitó con aquellas aventuras de Gulliver, un aventurero que llegó a las tierras de Lilliput: Allí, todo era muy pequeño, la naturaleza, las plantas, los habitantes del lugar y sus casas y palacios, embarcaciones y todos los animales.
Gulliver era allí un gigante de proporciones inmensas: Incluso llegó a extinguir un fuego con una simple chorrada (es decir, hizo pipí) y acabó de inmediato con el (para ellos) enorme fuego.

Hemos demostrado tener mucha imaginación y las historias y leyendas que nos llegan desde el pasado está mezclada con la Mitología de los pueblos que, en todos los rincones del mundo crearon sus propios mitos que nos dibujan escenarios que hablan de la inmensa diversidad. Siempre hemos buscado algo pero nunca logramos encontrarlo todo. ¡La búsqueda continúa!

Su algún día muy lejos en el futuro, nos convertimos en seres de luz, de manera que podamos desplazarnos de manera instantánea solo con el pensamiento, de una a otra galaxia, atravesar Nebulosas ponzoñosas sin sufrir daño alguno, No pertenecer al Universo, sino ser parte integrante de el… Así y solo así, podríamos saber lo que está pasando al otro lado del universo, y, no tener necesidad de plantear preguntas cuyas respuestas ya conocemos.
BUeno, soñar es tan barato.
Al menos de momento, tenemos que admitir que es así. No creo que alguna vez podamos adquirir un conocimiento pleno de todas las cosas. Siempre nos quedarán secretos que desvelar y misterios por descubrir, y, la inmensa variedad y la vastedad compleja de la Naturaleza, tendrá siempre para nosotros, algunos rincones oscuros en los que moran respuestas que deseamos , y que sin embargo, es posible, que nunca las podamos atisbar.





¿Oiremos alguna vez que han encontrado los restos de la Atlántida?
“De todos los misterios que andan por el mundo, ninguno puede competir con las historias de tierras pérdidas y civilizaciones que ya no existen, y entre todas ellas, destaca sobremanera una: la desaparición de la Atlántida, un continente entero, que existió más allá de las Columnas de Hércules (Gibraltar) o quién sabe dónde. A la Atlántida, se la tragó la tierra, en día y una noche, sin dejar rastro ni de ella ni de la floreciente civilización que poseía. “… ¡Según nos cuentan!

Lo cierto es que cuando miramos hacia atrás en el tiempo, sí que tenemos motivos para el asombro
Los orígenes del conocimiento quedan lejos y se pierde en la noche de los tiempos: Sumeria, Babilonia, Egipto, China, La India, Persia y más tarde Grecia y el Islam, Toda América y sus Civilizaciones y Europa. Nos tenemos que guiar por los vestigios dejados por aquellos pueblos que, desgraciadamente, el tiempo se ha encargado de borrar en la mayor parte de los casos y sólo hemos podido recuperar pequeñas obras y destruidas construcciones. De las más importantes en volumen, se ha conservado una gran colección por todo el mundo que nos habla de lo que fueron aquellos pueblos.

Con bastante amplitud hemos hablado aquí del Universo, de su “nacimiento” y de su posible “muerte”. De manera individual hemos hablado de los objetos que lo pueblan y de las fuerzan que lo rigen. Por ejemplo, el Cúmulo Copo de Nieve en la Nebulosa del Cono, es como tántas otras Nebulosas, el resultado de la explosión de una estrella al final de sus días. Las estrellas nunca quieren morir del todo y, cuando lo hacen al finalizar sus ciclos de fusión, se convierten en otros objetos distintos y, sus materiales sobrantes son dejados esparcidos por grandes regiones del espacio interestelar, en forma de bellas nebulosas de las que surgen nuevas estrellas, nuevos mundos y… -seguramente- nuevas formas de vida.

Es el Cúmulo de Galaxias llamado Pandora
Ahora sabemos que el Universo está constituido de innumerables galaxias que forman cúmulos que, a su vez, se juntan en supercúmulos. Estas galaxias están abarrotadas de estrellas y las estrellas, no pocas veces, están acompañadas de planetas que forman sistemas planetarios. Nosotros, los humanos, hemos realizado profundas observaciones que, con nuestros modernos ingenios, nos han podido llevar hasta el espacio profundo, allí donde habitan galaxias que nacieron hace ahora doce mil millones de años.

Los vientos estelares emitidos por las estrellas jóvenes, distorsionan el material presente en las Nebulosas, y, de la maisma manera, en presencia de masa … ¡se crean nuevas estrellas y nuevos mundos en los que, si el Azar los sitúa en el lugar adecuado, la Zona Habitable, podrían surgir formas de vida como ocurrió aquí en la Tierra.



Hemos estado divagando sobre lo que nos espera en el futuro
Podemos imaginar muchas cosas y dibujar en nuestras mentes miles de escenarios diferentes de lo que será el futuro de la Humanidad: Alcanzaremos los conocimientos para poder vivir 200 años, la tecnología robótica avanzará tanto que, nuestra especie terminará fundiéndose con ella, de tal manera que podremos llegar a ser auténticos cyborgs, medio humanos y medio robots. También es posible que podamos conseguir durar algunos millones de años más y, de esa manera, tendremos tiempo para dominar las energías que se producen en las estrellas y en los agujeros negros. Tendremos tiempo para salir de nuestro confinamiento terrestre y crear bellas ciudades en mundos lejanos, la Humanidad se esparcirá por toda la Galaxia. También es posible que, dentro de unos días, unos meses o unos años, llegue ese meteorito inesperado y acabe con todos nuestros sueños. Otra posiblidad, es la de que podamos ser invadidos por seres de otros mundos que, con mentalidades muy diferentes, no traigan buenas intenciones. También entra dentro de lo posible que…
“Ningún hombre puede cruzar el mismo río dos veces, porque ni el hombre ni el agua serán los mismos.”

Como nunca nadie pudo estar en otro Universo, tenemos que imaginarlos y basados en la realidad del nuestro, realizamos conjeturas y comparaciones con otros … ¡Que podrían ser! En nuestro Universo existen cientos de miles de estrellas y mundos, más de cien mil millones de galaxias y, todo objeto se repite una y otra vez, y, siendo así (que lo es) ¿por qué no habrían de existir otros universos?

Hablar de una Naturaleza simétrica sería condenar a nuestro Universo a la monotonía de la igualdad, y, todos sabemos que en él se encuentra todo lo que existe, la Materia, el Tiempo y el Espacio, todo ello acompañado por fuerzas que hacen de nuestro universo el que conocemos y, dentro de toda esa inmensidad, también se encuentran la simetría y la asimetría, en nuestro mundo el día y la noche. La riqueza de la diversidad que conforma ese todo que el Universo es.

La exploración de la simetría y la asimetría en la Naturaleza comenzaba con el mayor de los objetos naturales: ¡El propio Universo! Y, hemos ido reduciendo gradualmente la escala de tamaños con estructuras cada vez más pequeñas. En otras ocasiones hemos tenido aquí mismo la oportunidad de hablar de la simetría que encontramos en la Naturaleza de las plantas y de los animales. , desviamos nuestra atención hacia estructuras todavía menores, las diversas sub-unidades que constituyen todas las sustancias materiales, vivas o inertes.
de continuar y para aquellos que lo puedan desconocer, será conveniente que tengan una conciencia clara de qué son exactamente estas unidades inferiores. Comenzando con las más pequeñas y yendo después en sentido ascendente, la escala sería:

Las partículas elementales que están descritas en el Modelo estándar actual de la física de partículas que conforman la materia y las fuerzas con las que interaccionan y que, donde hemos podido saber, están divididas en familias:
Leptones: partículas puntuales con una dimensión espacial inapreciable. Los seis leptonesconocidos son el electrón, el muón y el tauón, y el neutrino asociado a uno de ellos, el neutrino electrónico, muónico y tauónico.
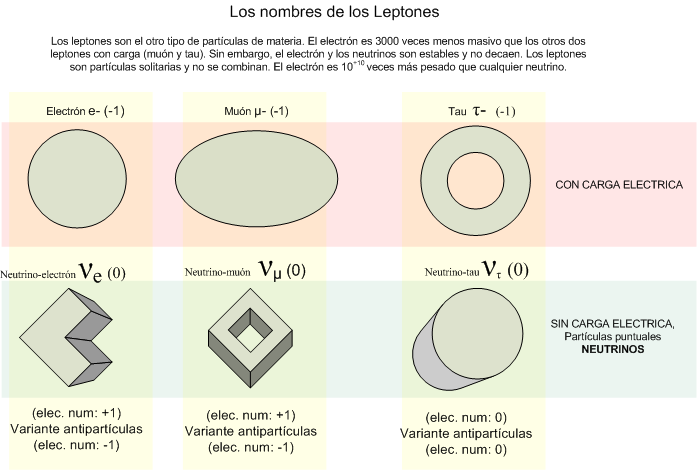
Hadrones: Son aquellas partículas que se cree que están compuestas de pequeñas partículas puntuales llamadas quarks. Se han identificado cientos de hadrones, de los cuales los más importantes son el protón y el neutrón, ya que junto con el electrón forman la materia ordinaria.

Bosones: Partículas de “cambio”, partículas “soporte”, partículas “mensajeras” o partículas “indicadoras”. Contienen o son intermediarias de las cuatro fuerzas: electromagnetismo (conducido por el fotón), la fuerza débil (conducida por los vectores bosones intermedios), la gran fuerza nuclear (por los gluones) y la gravedad (por el gravitón aún no detectado). A finales de lños años setenta, las fuerzas elecdtromagnética y débil se unificaron en lo que llamamos la fuerza electrodébil. La teoría electrodébil predice un bosón masivo denominado partícula de Higgs que,según los del CERN, se cazó en el año 2.012. Sin embargo, faltan muchas explicaciones sobre dicho hallazgo.
Representación de los tres bosones intermediarios en la fuerza electrodébil
Una vez descritas, muy someramente, las partículas de la materia y las fuerzas que rigen el universo conocido, tendríamos que pasar, de inmediato, al paso próximo que estaría representado por el átomo que, hasta donde conocemos, es la menor unidad estructural en la que dividirse la materia sin que pierda sus propiedades. En el centro de todo átomo está el núcleo, que debe contener al menos un protón, pero habitualmente está formado por una mezcla de protones y neutrones. Alrededor del núcleo, agrupados en “capas”, están los electrones. El átomo más sencillo, el de Hidrógeno, un núcleo con un protón, alrededor del cual se mueve un único electrón. El átomo más complejo que se ha encontrado en la Naturaleza es el del Uranio, con 92 electrones. En el laboratorio se han encontrado algunos elementos más complejos a los que se llaman transuránicos, es decir, que van más allá del uranio y que no se encuentran en la Naturaleza, son artificiales.

A merced del Universo, sobre el frágil puente de nuestra ignorancia y ante la luz cegadora de nuestras propias mentes que no nos deja “ver” el infinito mundo del conocimiento de las cosas, de la Naturaleza y de nosotros mismos. presentó “El Origen de las Especies”, allá por el año 1887, Thomas Henry Huxley dijo:
“Lo conocido es finito, lo desconocido infinito; intelectualmente nos hallamos en un islote en medio del océano ilimitado de lo inexplicable. La tarea de generación es reclamar un poco más de terreno, añadir algo de extensión y solidez de nuestras posesiones”

Como es algo que me despierta la curiosidad, con bastante asiduidad, hemos hablado aquí del Tiempo, y nos hemos preguntado qué puede ser. He dicho que pasado, presente y Futuro es sólo una Ilusión que llamamos Tiempo. Sin embargo, nosotros, los humanos, estamos condenados a vivir en un perpetuo presente, nunca podremos conocer eso que llamamos futuro y que será el Tiempo de los que vendrán detrás de nosotros y, la paradoja es, que para ellos, también será un Tiempo presente. Nadie nunca podrá conocer el futuro. Bueno… ¡Imaginarlo Sí!

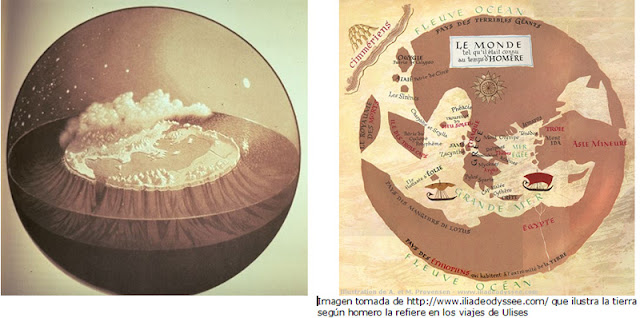
Esta misma entrada ha sido vista aquí en varias ocasiones pero, lo que representa, tiene el derecho a que sea divulgada una y otra vez. Se trata de la historia de intrépidos viajeros-aventureros que con su valor, hicieron posible el conocimiento de nuevas tierras y nuevas gentes. Algunos tenían en la mente la existencia de lugares maravillosos y no se paraban a pensar en los peligros que tratar de descubrirlos conlleva. Otros, buscaban tesoros y no pocos salían en busca de las aventuras que esperaban vivir en asombrosas situaciones, lugares y gente que ni podían imaginar.
Parecida era la concepción de la tierra representada en el primer mapamundi griego del que se tienen referencias. Hablan de él y lo describen Heródoto y Estrabón. Lo dibujó Anaximandro (ca. 611-545 a.C.) y sabemos que el mapa abarcaba todo el ámbito de la tierra habitable con todos los mares y ríos conocidos. La tierra, según la representó Anaximandro, era un cilindro oblongo, dos veces más ancho (de Este a Oeste) que alto (de norte a sur). Se distribuía alrededor del mar Mediterráneo y estaba a su vez rodeada por un río-océano. Esta tierra cilíndrica y oblonga estaba habitada únicamente en su disco superior -al que los griegos llamaban ecúmenos, diferenciando la tierra habitada y habitable de la tierra-planeta-, y permanecía libremente suspendida en el centro de una esfera completa que era el cielo. No se caía, porque al ser equidistante de todo, no podía caer hacia ningún lado.

La concepción del mundo ha sido siempre muy variada para los distintos pueblos
Pasamos a comentar hechos y sobre personajes que, en distintas épocas y partes del mundo, hicieron posible el avance de nuestros conocimientos, todos y todo contribuyó a ello, cada cosa y cada personaje en su medida, y, unificados lo hicieron posible. Hoy nosotros, podemos aprender de todo aquello, y podemos saber como llegaron a conseguir los conocimientos que tenemos en muchos aspectos de nuestras experiencias transmitidas por estudiosos de hace muchos siglos.
Pitágoras fundo su escuela después de viajar a Egipto para aprender matemáticas
Aquellos hombres arriesgaban sus vidas por saber, fueron muchos de los clásicos griegos los pertenecientes a este grupo viajero, y, a pesar del riesgo que ello conllevaba, viajaban a lugares lejanos buscando saber de matemáticas o de astronomía.
Todos hemos oído hablar, con más o menos frecuencia, de “Sistemas Complejos”, aquí mismo en estas páginas, la palabra sale a relucir con cierta frecuencia y, no me extraña que “la palabreja” cree una barrera, dado que, para muchas personas, “complejo” significa “complicado” y suponen automáticamente que, si un sistema es complicado, será difícil de comprender. La naturaleza posee una fuerte tendencia a estructurarse en forma de entes discretos excitables que interactúan y que se organizan en niveles jerárquicos de creciente complejidad, por ello, los sistemas complejos no son de ninguna manera casos raros ni curiosidades sino que dominan la estructura y función del universo.
Claro que, no siempre ese temor a lo difícil y complicado, está justificado y, tal suposición no es, necesariamente correcta. En realidad, un sistema complejo es tan solo un sistema que está formado por varios componentes más sencillos que ejercen entre sí una interacción mutua que, naturalmente, tiene sus consecuencias. Si miramos la imagen de arriba, vemos una inmensa y hermosa Nebulosa que está formada por una serie de “cosas” sencillas como lo son el gas hidrógeno y el polvo interestelar entre otros y, en presencia de energías, la gravedad y otros parámetros, ahí ocurren cosas tales como, el nacimiento de estrellas y la aparición de mundos…entre otras.
Los grandes triunfos de la Ciencia se han logrado, en gran medida, descomponiendo los sistemas complejos en sus componentes simples, es decir, estudiar por partes lo que allí está presente (en caso necesario, como primera aproximación, dando el paso suplementario de pretender que todos los componentes son más sencillos de lo que son en realidad) para llegar a comprender el todo.
No siempre vemos lo que es. El auto engaño de la Mente… ¡Qué poderoso es!
Nuestra realidad es que uno de nosotros percibimos, entendemos y actuamos de manera diferente en la vida. Cada uno poseemos nuestra propia realidad del mundo y de nosotros mismos. Estamos construidos a base de creencias, y esas creencias son las que influyen de manera decisiva en nuestra realidad y en nuestra conducta, por lo tanto, son las culpables de que consigamos o no nuestros objetivos. Básicamente nuestra realidad está formada por nuestras creencias.
Ninguna idea nos ha llegado de manera instantánea y depurada en todos sus conceptos, sino que, han sido ideas que han tenido que ir siendo depuradas más y más a conseguir esa realidad que buscábamos haciendo que, el esquema encontrado, se parezca lo más posible al mundo que nos rodea y que podemos observar. Esa es, en pocas palabras la historia de la Relatividad de Einstein que juntó muchas ideas y conceptos conseguir sus teorías que están muy cercas de lo que el mundo es.
El Cañón natural más grande del sistema solar
El Valle Marineris es, de hecho, el más complejo entramado de cañones fluviales de todo el Sistema Solar con una longitud de 4 100 kilómetros, una anchura próxima a los 500 y zonas en las que la profundidad alcanza algo más de los cuatro kilómetros. Aunque la primera impresión pueda ser la de que la conformación se debe a movimientos de la corteza marciana, lo cierto es que, después de muchos estudios se puede dar por hecho que fue el agua el verdadero agente que modeló lo que podríamos considerar como uno de los más bellos y extensos “Parques Nacionales” de todo el Sistema Solar.
Vía Láctea (como otras galaxias espirales) es una zona de reducción de entropía…, así se deduce de varios estudios realizados y se puede argumentar que, … Efectivamente, existe un parámetro oculto universal que crea la Entropía negativa que, como por ejemplo hacemos nosotros al reproducirnos, estamos luchando contra la Entropía destructiva y creamos nuevas vidas.

Si existe, la Conciencia Cósmica estará mezclada con esas Nebulosas, con las estrellas, e, incluso en un agujero negro, nada la podría destruir.
“Una inteligencia que conociese, en un momento determinado, todas las fuerzas que operan en la Naturaleza, así como las posiciones momentáneas de todas las cosas que constituyen el universo, sería capaz de condensar en una sola fórmula los movimientos de los cuerpos más grandes del mundo y los de los átomos más ligeros, siempre que su intelecto sea bastante poderoso para someter a análisis todos los datos; para él nada sería incierto, el pasado y el futuro estarían presentes ante sus ojos.”
Inmensas galaxias cuajadas de estrellas, nebulosas y mundos. Espacios interestelares en los que se producen transmutaciones de materia que realizan el asombroso “milagro” de convertir unas cosas en otras distintas. Un Caos que lleva hacia la normalidad. Estrellas que explosionan y riegan el espacio de gas y polvo constituyentes de materiales en el que se forjarán nuevas estrellas, nuevos mundos y nuevas formas de vida. Así es como ocurren las cosas en este universo nuestro que no hemos llegado a conocer. De hecho, ni sabemos a ciencia cierta si su “nacimiento” fue debido, realmente, al Big Bang.
Me gustaría continuar con el resumen de lo que hemos tratado durante todo el año pero… ¡Es dificil! “El Tiempo” me lo impide y, ya seguiremos hablando de todos estos temas interesantes en el año venidero que, nos dará muchas sorpresas con nuevos descubrimientos e inventos que nos llevan a ese futuro que nunca podremos conocer.
¡Bonito paseo!
Emilio Silvera Vázquez
Mar
16
El Tiempo de Planck y otros
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (0)
Comments (0)
Nuestra estrella gira en torno al centro de la galaxia. Lo hace a una velocidad de 828 000 km/h. Tarda unos 230 millones de años en completar una vuelta a la galaxia (si bien se suele utilizar una franja que va de los 225 a los 250 millones de años). Este concepto es conocido como un año galáctico.
Sí, estamos en…
¡Un Universo dinámico!
El viaje el Sol por la de la Galaxia

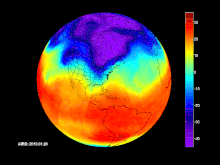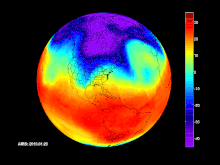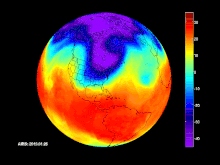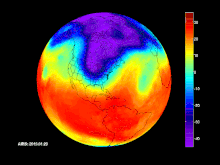

Los átomos, las estrellas, las galaxias, el Sol, los seres vivos… Todo está en un movimiento permanente, también el Tiempo es dinámico y no deja de viajar hacia ese Futuro que nunca podremos conocer. Lo dinámico de nuestras vidas lo podemos ver en los cambios que padecemos dese que venimos al mundo, como las estrellas, también nosotros, como sistemas cerrados que somos (a nivel individual), somos afectado por la Entropía que, nunca deja de aumentar, hasta dejarnos sin fuerzas para crear trabajo.
Hemos podido llegar a unas alturas en el mundo de la exploración científica que, nos posibilita reconocer los impactos de los cambios que se producen con el devenir del Tiempo en la Naturaleza y, hemos llegado a comprender que, el Universo, es dinámico. Hacia finales del siglo XIX se había llegado a saber que hubo un tiempo en el que la Tierra, y nuestro Sistema solar, no existían; que la especie humana debía haber cambiado en apariencia y en el promedio de su capacidad mental a lo largo de enormes períodos de tiempo; y que en cierto sentido, amplio y general, el Universo debería estar degradándose, haciéndose un lugar menos hospitalario y ordenado. Durante el siglo XX pudimos ampliar esa imagen de un Universo cambiante y seguimos haciéndolo en el XXI.
Cosas que no todos conocéis
Mileva Marić Ruzić y Einstein
Del familiar Einstein, tan conocidos por todos los aficionados a la Física y también por algunos que no lo son, existen aspectos de su vida que no siempre han sido aireados y, por lo general, son desconocidos para el gran público que sólo sabe de su gran obra y de su esplendor pero, como todos en esta vida, él también pasó por sus momentos bajos y tuvo que sufrir situaciones adversas.
Como alumno, la verdad, no era muy apreciado por sus profesores, el mismo Minkowski, cuando publicó la teoría de la relatividad especial, le recordaba como un alumno poco disciplinado, algo vago y que faltaba a clases para irse a navegar con Mileva Maric, en las clases se aburría. Incluso se cuenta aquella anécdota de su profesor de griego que, viendo lo desaliñado que era y el poco interés que ponía en las clases, llegó a decirle: “muchacho, en esto de la ciencia no llegarás a ninguna parte, es mejor que te dediques a otra cosa”. El hombre pasó a la Historia por sus “proféticas” palabras.
El símbolo del taijitu, la forma más conocida de representar juntos el yin y el yang

La dinámica de la Fusión nuclear hade que las estrellas se expanda y la Fuerza de Gravedad hace que se contraiga, así, las dos fuerzsas iguales se equilibran y la estrella vive miles de millones de años
Todos los objetos del Universo son el resulta de fuerzas antagónicas que, al ser iguales, se equilibran y consiguen la estabilidad. Las estrellas son el mejor ejemplo: La Gravedad trata de comprimir a la estrella que, mediante la fusión tiende a expandirse y, la lucha de esas dos fuerzas crea la estabilidad.

Estas estructuras, podemos decir que son entidades estables que existen en el Universo. Existen porque son malabarismos estables entre fuerzas competidoras de atracción y repulsión. Por ejemplo, en el caso de un planeta, como la Tierra, hay un equilibrio entre la fuerza atractiva de la Gravedad y la repulsión atómica que aparece cuando los átomos se comprimen demasiado juntos. Todos estos equilibrios pueden expresarse aproximadamente en términos de dos números puros creados a partir de las constantes e (electrón), h (constante de Planck), G (constante de gravitación) y mp (masa del protón), c (la velocidad de la luz en el vacío). Pero, ¿que es el Tiempo de Planck.
Tiempo de Planck
![]() 10-43 s. = 5.391247(60)×10−43 s
10-43 s. = 5.391247(60)×10−43 s
Es el tiempo que necesita el fotón (viajando a la velocidad de la luz, c, para moverse a través de una distancia igual a la longitud de Planck. Está dado por segundos, donde G es la constante gravitacional (6’672 59 (85) ×10-11 N m2 kg-2), ħ es la constante de Planck racionalizada (ħ = h/2π = 1’054589 × 10-34 Julios segundo) y c es la velocidad de la luz (299.792.458 m/s).
El tiempo de Planck, nombrado en honor al físico alemán Max Planck, es una unidad de tiempo extremadamente breve, es decir aproximadamente:
0.0000000000000000000000000000000000000000001 segundos, una fracción tan diminuta que resulta difícil de imaginar.
Es curioso que hemos podido llegar por diversos medios y experimentos hasta unos momentos después del Big Bang. Sin embargo, nunca pudimos ir más allá del Tiempo de Planck, parece existir una línea invisible que nos impide entrar en aquella fracción de segundo para poder saber lo que pasó. Ningún telescopio por muy potente que sea, ningún acelerador de partículas, nada, ha podido nunca traspasar ese límite.
El valor del tiempo del Planck es del orden de 10-43 segundos. En la cosmología del Big Bang, hasta un tiempo (Tp) después del instante inicial, es necesaria usar una teoría cuántica de la gravedad para describir la evolución del universo.
Como decía antes:
Expresado en números corrientes que todos podamos entender, su valor es 0’000.000.000.000.000.000.000.000.000.000.000.000.000.000.1 de 1 segundo, que es el tiempo que necesita el fotón para recorrer la longitud de Planck, de 10-35 m (veinte órdenes de magnitud menor que el tamaño de del protón de 10-15 metros). el límite de Planck es Lp = √(Għ/c3 ≈ 1’61624 x 10-35 m.
Todo, desde Einstein, es relativo. Depende de la pregunta que se formule y de quién nos de la respuesta.
El tiempo es la escalera con peldaños infinitos que nos llevan hasta el fin de la eternidad…
Si preguntamos ¿Qué es el tiempo?, tendríamos que ser precisos y especificar si estamos preguntando por esa dimensión temporal que no deja de fluir desde el Big Bang y que nos acompaña a lo largo de nuestras vidas, o nos referimos al tiempo:
- Atómico, ese adoptado por el SI, cuya unidad es el segundo y se basa en las frecuencias atómicas, definida a partir de una línea espectral particular de átomo de cesio-133.
- O nos referimos a lo que se conoce como tiempo civil, tiempo coordinado, tiempo de crecimiento, tiempo de cruce.
- Tiempo de integración.
- Tiempo de relajación.
- tiempo dinámico o dinámico de Baricéntrico.
- Dinámico terrestre, tiempo terrestre.
- Tiempo de Efemérides.
- Tiempo de huso horario.
- Tempo estándar.
- tiempo local, tiempo luz.
- Tiempo medio.
- Tiempo de vida media de las cosas y de los seres vivos.
Cada una de estas versiones del tiempo tiene una respuesta diferente, ya que no es lo mismo el tiempo propio que el tiempo sidéreo o el tiempo solar, o solar aparente, o solar medio, o tiempo terrestre, o tiempo universal. Como se puede ver, la respuesta dependerá de cómo hagamos la pregunta.
Al hablar de un reloj atómico de cesio (RAC), nos referimos a un dispositivo que usa como referencia a la frecuencia de emisión del isótopo de cesio 133Cs, donde dicha emisión está medida en la línea espectral de microondas, la cual, se encuentra aproximadamente entre 300 MHz y 30 GHz.
Reloj de Cesio cuyo funcionamiento se basa en la diferencia de energía entre dos estados del núcleo de Cesio-133 cuando se sitúa en un campo magnético. En un tipo, los átomos de cesio-133 son irradiados con radiación de radiofrecuencia, cuya frecuencia es elegida para corresponder a la diferencia de energía entre los dos estados. Es decir, nos valemos de un sistema complejo para determinar lo que el tiempo es basado en lo que de él nos indica la Naturaleza.
En realidad, para todos nosotros el único tiempo que rige es el que tenemos a lo largo de nuestras vidas; los otros tiempos, son inventos del hombre para facilitar sus tareas de medida, de convivencia o de otras cuestiones técnicas o astronómicas pero, sin embargo, el tiempo es sólo uno; ese que comenzó cuando nació el universo y que finalizará cuando éste llegue a su final.
Lo cierto es que para las estrellas supermasivas, cuando llegan al final de su ciclo y dejan de brillar por agotamiento de su combustible nuclear, en ese preciso instante, el tiempo se agota para ella. Cuando una estrella pierde el equilibrio existente entre la energía termonuclear (que tiende a expandir la estrella) y la fuerza de gravedad (que tiende a comprimirla), al quedar sin oposición esta última, la estrella supermasiva se contrae aplastada bajo su propia masa. Queda comprimida hasta tal nivel que llega un momento que desaparece, para convertirse en un agujero negro, una singularidad, donde dejan de existir el “tiempo” y el espacio. A su alrededor nace un horizonte de sucesos, que si se traspasa se es engullido por la enorme gravedad del agujero negro.

Según todos los indicios, la Física nos dice que, al llegar a la singularidad de un agujero negro, no podremos encontrar ni tiempo ni espacio. Es una región que, estando en este mundo, es como si estuviera en otro al que sólo se podrá llegar a través de la teoría tan esperada de la gravedad cuántica. Aquí, en la Singularidad, la Relatividad de Einstein llega y hace mutis por el foro.
El tiempo, de esta manera, deja de existir en estas regiones del universo que conocemos como singularidad. El mismo Big Bang surgió de una singularidad de energía y densidad infinitas que, al explotar, se expandió y creó el tiempo, el espacio y la materia.
Como contraposición a estas enormes densidades de las enanas blancas, estrellas de neutrones y agujeros negros, existen regiones del espacio que contienen menos galaxias que el promedio o incluso ninguna galaxia; a estas regiones las conocemos como vacío cósmico. Han sido detectados vacíos con menos de una décima de la densidad promedio del universo en escalas de hasta 200 millones de años luz en exploraciones a gran escala. Estas regiones son a menudo esféricas. El primer gran vacío en ser detectado fue el de Boötes en 1.981; tiene un radio de unos 180 millones de años luz y su centro se encuentra aproximadamente a 500 millones de años luz de la Vía Láctea. La existencia de grandes vacíos no es sorprendente, dada la existencia de cúmulos de galaxias y supercúmulos a escalas muy grandes.
Muchos son los misterios que nos quedan por resolver y muchos también los objetos que, estando ahí, aún no han sido localizados. La vastedad del inmenso Universo, hace difícil saber la realidad de todo su contenido y, necesitaremos siglos de estudio y observación para poder acernos, aunque sea mínimamente, a sus secretos.
Mientras que en estas regiones la materia es muy escasa, en una sola estrella de neutrones, si pudiéramos retirar 1 cm3 de su masa, obtendríamos una cantidad de materia increíble. Su densidad es de 1017 Kg/m3; los electrones y los protones están tan juntos que se combinan y forman neutrones que se degeneran haciendo estable la estrella de ese nombre que, después del agujero negro, es el objeto estelar más denso del universo.
Es interesante ver cómo a través de las matemáticas y la geometría, han sabido los humanos encontrar la forma de medir el mundo y encontrar las formas del universo. Pasando por Arquímedes, Pitágoras, Newton, Gauss o Riemann (entre otros), siempre hemos tratado de buscar las respuestas de las cosas por medio de las matemáticas.

Arthur C. Clarke nos decía:
“Magia es cualquier tecnología suficientemente avanzada”

Pero también es magia el hecho de que en cualquier tiempo y lugar, de manera inesperada, aparezca una persona dotada de condiciones especiales que le permiten ver estructuras complejas matemáticas que hacen posible que la humanidad avance considerablemente a través de esos nuevos conceptos que nos permiten entrar en espacios antes cerrados, ampliando el horizonte de nuestro saber.
Recuerdo aquí uno de esos extraños casos que surgió el día 10 de Junio de 1.854 con el nacimiento de una nueva geometría: la teoría de dimensiones más altas que fue introducida cuando Georg Friedrich Bernhard Riemann dio su célebre conferencia en la facultad de la Universidad de Göttingen en Alemania. Aquello fue como abrir de golpe todas las ventanas cerradas durante 2.000 años de una lóbrega habitación que, de pronto, se ve inundada por la luz cegadora de un Sol radiante. Riemann regaló al mundo las sorprendentes propiedades del espacio multidimensional.


La nueva geometría de Riemann nos dijo como era la realidad del espacio, del Universo
Su ensayo, de profunda importancia y elegancia excepcional, “sobre las hipótesis que subyacen en los fundamentos de la geometría” derribó pilares de la geometría clásica griega, que habían resistido con éxito todos los asaltos de los escépticos durante dos milenios. La vieja geometría de Euclides, en la cual todas las figuras geométricas son de dos o tres dimensiones, se venía abajo, mientras una nueva geometría riemanniana surgía de sus ruinas. La revolución riemanniana iba a tener grandes consecuencias para el futuro de las artes y las ciencias. En menos de tres decenios, la “misteriosa cuarta dimensión” influiría en la evolución del arte, la filosofía y la literatura en toda Europa. Antes de que hubieran pasado seis decenios a partir de la conferencia de Riemann, Einstein utilizaría la geometría riemanniana tetradimensional para explicar la creación del universo y su evolución mediante su asombrosa teoría de la relatividad general. Ciento treinta años después de su conferencia, los físicos utilizarían la geometría decadimensional para intentar unir todas las leyes del universo. El núcleo de la obra de Riemann era la comprensión de las leyes físicas mediante su simplificación al contemplarlas en espacios de más dimensiones.
Contradictoriamente, Riemann era la persona menos indicada para anunciar tan profunda y completa evolución en el pensamiento matemático y físico. Era huraño, solitario y sufría crisis nerviosas. De salud muy precaria que arruinó su vida en la miseria abyecta y la tuberculosis. Al igual que aquel otro genio, Ramanujan, murió muy joven.
Emilio Silvera Vázsquez
Mar
14
Revoluciones científicas ¡La Relatividad!
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Relativista ~
Clasificado en Física Relativista ~
 Comments (2)
Comments (2)
Dentro de 150 años podríamos publicar una foto similar y decir:
Es la primera persona que alcanza los 158 años de edad y aparenta 50, se logró ralentizar el envejecimiento gracias a descubrimientos en genética, ya han quedado atrás aquellos factores que ahora, en el año 2.175 han desaparecido, tales como:
Aquellas afecciones más comunes de la vejez cabe citar la pérdida de audición, las cataratas y los errores de refracción, los dolores de espalda y cuello, la osteoartritis, las neumopatías obstructivas crónicas, la diabetes, la depresión y la demencia y otras ya desterradas casi por completo.
El Nuevo Acelerador de Partículas Albert Einstein, utilizando energías de 1019 GeV, ha logrado llegar hasta las cuerdas vibrantes de la Teoría, verificando así, cerca de 200 años más ta5rde, la dichosa teoría de Ed. Witten y otros antes y después que el. Ya sabemos realmente cuales son los componentes primigenios de la materia.
La Nave Aurora (que partió de la Tierra hace 9 días), llega al planeta Próxima b utilizando el Hiperespacio (una manera de doblar el Espacio acortando las distancias entre regiones muy lejanas), de tal manera que se logra burlar esa imposibilidad de alcanzar la velocidad de la luz (no de vencerla), y, por fin se podrá explorar esas regiones antes fuera de nuestro alcance.
Hoy, día 11 de enero de 2.175, se celebra el 40 aniversario de la publicación de la nueva Teoría de la Gravedad Cuántica que, las nuevas máquinas de computación cuántica pudieron confirmar que dicha teoría estaba subyacente en la Teoría de cuerdas.
El Modelo Estándar de la Física de Partículas está completo, ya operan en el las cuatro fuerzas fundamentales, y, cuando se juntan las Teorías de Planck y de Einstein… ¡No apareen los dichosos infinitos!
Hace ahora un años que se logró perforar la superficie de Europa, y, para el asombro de todos, se captaron imágenes con un robot sumergido, de asombrosos animales, algunos de inmensas proporciones. Todavía quedan muchos secretos por descubrir en aquel pequeño “mundo”.
Finalmente ese primer contacto se producirá

Hace ya más de 50 años que se pudo descartas la existencia de la “materia oscura”, confundida con la sustancia primigenia original en el Universo, gracias a la cual se pudieron formar las galaxias. Se pudo verificar que el movimiento anómalo de las galaxias era debido a la atracción gravitatoria que un universo vecino ejerce sobre el nuestro, al igual que el nuestro la ejerce sobre aquel.
Llegan a su fin las reuniones de los Presidentes de todos los Gobiernos del Mundo, las señales recibidas desde un mundo lejano (por fin verificadas que provienen de seres inteligentes por sus mensajes matemáticos (no importa los signos que puedan utilizar “ellos”, finalmente el resultado de sumar 2 + 2 = 4.
No sabemos como serán y qué intenciones tendrán, lo mejor es prevenir mejor que curar. La votación para elegir a un Presidente mundial dará comienzo el próximo día 7 de enero de 2.175. Se impone la necesidad de unificar criterios para poder hacer frente a lo que se avecina.
Así podríamos continuar formulando cientos de preguntas como: ¿Qué maravillas tendremos dentro de 150 años? ¿Qué adelantos científicos se habrán alcanzado? ¿Qué planetas habremos colonizado? ¿Habrá sucedido ya ese primer contacto del que tanto hablamos? ¿Cuántas “Tierras” habrán sido encontradas? ¿Qué ordenadores utilizaremos? ¿Será un hecho cotidiano el viaje espacial tripulado? ¿Estaremos explotando las reservas energéticas de Titán? ¿Qué habrá pasado con la Teoría de Cuerdas? Y, ¿Habrá, por fin aparecido la dichosa materia oscura? Haciendo todas estas preguntas de lo que será o podrá ser, nos viene a la memoria todo lo que fue y que nos posibilita hacer estas preguntas.

Una cosa nos debe quedar bien clara, nada dentro de 150 años será lo mismo que ahora. Todo habrá cambiado en los distintos ámbitos de nuestras vidas y, a excepción del Amor y los sentimientos que sentiremos de la misma manera (creo), todo lo demás, habrá dado lugar a nuevas situaciones, nuevas formas de vida, nuevas sociedades, nuevas maneras y, podríamos decir que una Humanidad nueva, con otra visión y otras perspectivas.

Nuevas maneras de sondear la Naturaleza y desvelar los secretos. Son muchas las cosas que no sabemos
Pero echemos una mirada al pasado. Dejando a un lado a los primeros pensadores y filósofos, como Tales, Demócrito, Empédocles, Ptolomeo, Copérnico, Galileo, Kepler y otros muchos de tiempos pasados, tenemos que atender a lo siguiente:
Nuestra Física actual está regida y dominada por dos explosiones cegadoras ocurridas en el pasado: Una fue aquel artículo de 8 páginas que escribiera Max Planck, en ese corto trabajo dejó sentados los parámetros que rigen la Ley de la distribución de la energía radiada por un cuerpo negro. Introdujo en física el concepto novedoso de que la energía es una cantidad que es radiada por un cuerpo en pequeños paquetes discretos, en vez de en una emisión continua. Estos pequeños paquetes se conocieron como cuantos y la ley formulada es la base de la teoría cuántica.
En amigo físico me decía: cuando escribo un libro, procuro no poner ecuaciones, cada una de ellas me quita diez lectores. Siguiendo el ejemplo, procuro hacer lo mismo (aunque no siempre es posible) pero, en esta ocasión dejaremos el desarrollo de la energía de Planck del que tantas veces se habló aquí, y, ponernos ahora a dilucidar ecuaciones no parece lo más entretenido, aunque el lenguaje de la ciencia, no pocas veces es el de los números. Mira abajo sino es así.

![59 - Curso de Relatividad General [Ecuaciones de Campo & Constante Cosmológica]](https://i.ytimg.com/vi/HI3m80zLo24/maxresdefault.jpg)

¿Son tantas!
En cualquier evento de Ciencia, ahí aparecen esos galimatías de los números y letras que pocos pueden comprender, dicen que es el lenguaje que se debe utilizar cuando las palabras no pueden expresar lo que se quiere decir. Y, lo cierto es que, así resulta ser.
Después de lo de Planck y su radiación de cuerpo negro, cinco años más tarde, irrumpió en escena otra revolución de la Física se produjo en 1.905, cuando Albert Einstein con su relatividad especial nos dio un golpecito en nuestras cabezas para despertar en ellas nuestra comprensión de las leyes que gobiernan el Universo.
Nos dijo que la velocidad de la luz es la máxima alcanzable en nuestro universo, que la masa y la energía son la misma cosa, que si se viaja a velocidades cercanas a la de la luz, el tiempo se ralentiza pero, el cuerpo aumentará su masa y se contraerá en el sentido de la misma…Y, todo eso, ha sido una y mil veces comprobado. Sin embargo, muchas son las pruebas que se realizan para descubrir los fallos de la teoría, veamos una:
Los científicos que estudian la radiación gamma de una explosión de rayos lejanos han encontrado que la velocidad de la luz no varía con la longitud de onda hasta escalas de distancia por debajo de la longitud de Planck. Ellos dicen que esto desfavorece a algunas teorías de la gravedad cuántica que postulan la violación de la invariancia de Lorentz.
La invariancia de Lorentz se estipula que las leyes de la física son las mismas para todos los observadores, independientemente de dónde se encuentren en el universo. Einstein utilizó este principio como un postulado de la relatividad especial, en el supuesto de que la velocidad de la luz en el vacío, no depende de que se esté midiendo, siempre y cuando la persona esté en un sistema inercial de referencia. En más de 100 años la invariancia de Lorentz nunca ha sido insuficiente.
Interferómetro de Michelson
Sin embargo, los físicos siguen sometiendo a pruebas cada vez más rigurosas, incluyendo versiones modernas del famoso experimento con el interferómetro de Michelson y Morley. Esta dedicación a la precisión se explica principalmente por el deseo de los físicos para unir la mecánica cuántica con la relatividad general, dado que algunas teorías de la gravedad cuántica (incluyendo la teoría de cuerdas y la gravedad cuántica de bucles) implica que la invariancia Lorentz podría romperse. Granot y sus colegas estudiaron la radiación de una explosión de rayos gamma (asociada con una explosión de gran energía en una galaxia distante) que fue descubierto por la NASA Fermi Gamma-Ray Space Telescope, el 10 de mayo de este año. Se analizó la radiación en diferentes longitudes de onda para ver si había indicios de que los fotones con energías diferentes llegaron a los detectores de Fermi en diferentes momentos.

En múltiples trabajos publicados se habían considerado problemas en los que dos acontecimientos (eventos) que no ocurrían simultáneamente (al mismo tiempo) para un observador eran simultáneos para otro, o problemas en los que dos acontecimientos diferentes tenían lugar en la misma posición para uno de los observadores, lo cual nos permitía hacer una simplificación del tipo t = t’ o una simplificación del tipo x = x’. Pero hay acontecimientos que no ocurren al mismo tiempo para dos observadores distintos y que tampoco se repiten en el mismo lugar en ninguna de las coordenadas espaciales. Sobre este tipo de acontecimientos aún podemos llevar a cabo un análisis definiendo matemáticamente una “distancia” entre dichos acontecimientos que incluya en una sola definición las diferencias de tiempo (temporales) y las diferencias de posición (espaciales). Las transformaciones de Lorentz se utilizan como herramienta poderosa para 5resolver problemas.

Tal difusión de los tiempos de llegada parece indicar que la invariancia Lorentz efectivamente había sido violada, es decir que la velocidad de la luz en el vacío depende de la energía de la luz y no es una constante universal. Cualquier dependencia de la energía sería mínima, pero aún podría resultar en una diferencia mensurable en los tiempos de llegada de fotones debido a los miles de millones de años luz de a la que se encuentran las explosiones de rayos gamma.
De la calidad de Einstein como persona nos habla un detalle: Cuando el Presidente Chaim Weizmann de Israel murió en 1952, a Einstein se le ofreció la presidencia, pero se negó, diciendo que no tenía “ni la habilidad natural ni la experiancia para tratar con seres humanos.” Luego escribió que se sentía muy honrado por el ofrecimiento del estado de Israel, pero a la vez triste y avergonzado de no poder aceptarla.
Pero sigamos con la segunda revolución de su teoría que se dio en dos pasos: 1905 la teoría de la relatividad especial y en 1.915, diez años después, la teoría de la relatividad general que varió por completo el concepto del Cosmos y nos llevó a conocer de manera más profunda y exacta la Gravedad de Newton.
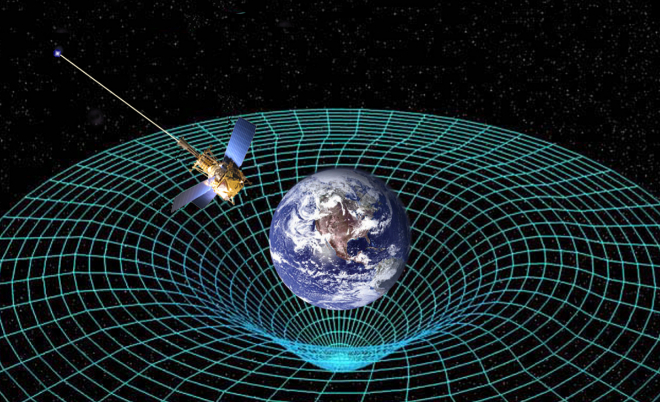
Einstein nos decía que el espacio se curva en presencia de grandes masas
En la Teoría Especial de la Relatividad, Einstein se refirió a sistemas de referencias inerciales (no acelerados). Asume que las leyes de la física son idénticas en todos los sistemas de referencia y que la velocidad de la luz en el vacío, c, es constante en el todo el Universo y es independiente de la velocidad del observador.
La teoría desarrolla un sistema de matemáticas con el fin de reconciliar estas afirmaciones en aparente conflicto. Una de las conclusiones de la teoría es que la masa de un cuerpo, aumenta con la velocidad (hay una ecuación que así lo demuestra), y, tal hecho, ha sido sobradamente comprobado en los aceleradores de partículas donde un muón, ha aumentado más de diez veces su masa al circular a velocidades cercanas a la de la luz. Y el muón que tiene una vida de dos millonésimas de segundo, además, al desplazarse a velocidades relativistas, también ven incrementado el tiempo de sus vidas.
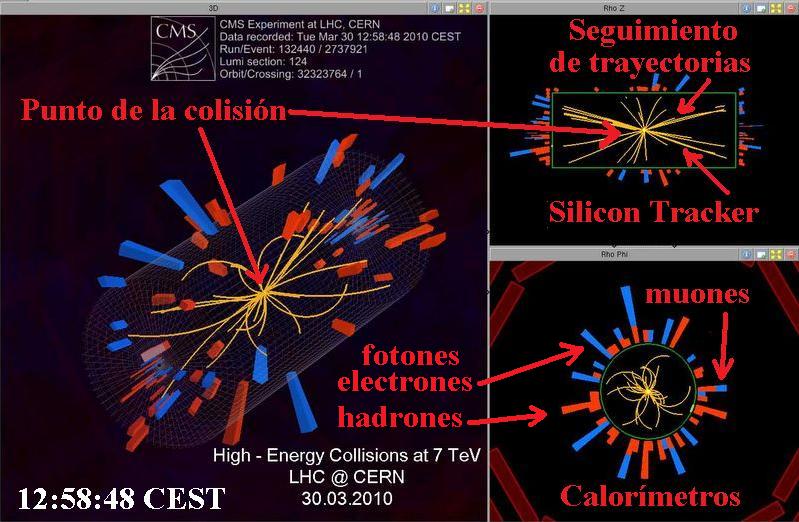
El LHC es un esfuerzo internacional, donde participan alrededor de siete mil físicos de 80 países. Consta de un túnel en forma de anillo, con dimensiones interiores parecidas a las del metro subterráneo de la Ciudad de México, y una circunferencia de 27 kilómetros. Está ubicado entre las fronteras de Francia y Suiza, cerca de la ciudad de Ginebra, a profundidades que van entre los 60 y los 120 metros debido a que una parte se encuentra bajo las montañas del Jura
Einstein también concluyó que si un cuerpo pierde una energía L, su masa disminuye en L/c2. Einstein generalizó esta conclusión al importante postulado de que la masa de un cuerpo es una medida de su contenido en energía, de acuerdo con la ecuación m=E/c2 ( o la más popular E=mc2).
Otras de las conclusiones de la teoría de Einstein en su modelo especial, está en el hecho de que para quien viaje a velocidades cercanas a c (la velocidad de la luz en el vacío), el tiempo transcurrirá más lento. Dicha afirmación también ha sido experimentalmente comprobada.
Todos estos conceptos, por nuevos y revolucionarios, no fueron aceptados por las buenas y en un primer momento, algunos físicos no estaban preparados para comprender cambios tan radicales que barrían de un plumazo, conceptos largamente arraigados.
Todo lo grande está hecho de cosas pequeñas
Fue Max Planck, el Editor de la Revista que publicó el artículo de Albert Einstein, quien al leerlo se dió cuenta de la enorme importancia de lo que allí se decía. A partir de aquel momento, se convirtió en su valedor, y, en verdad, Einstein, reconoció públicamente tal ayuda.
En la segunda parte de su teoría, la Relatividad General, Einstein concluyó que el espacio y el tiempo están distorsionados por la materia y la energía, y que esta distorsión es la responsable de la gravedad que nos mantiene en la superficie de la Tierra, la misma que mantiene unidos los planetas del Sistema Solar girando alrededor del Sol y, también la que hace posible la existencia de las Galaxias.

¡La Gravedad! Siempre está presente e incide en los comportamientos de la materia
Nos dio un conjunto de ecuaciones a partir de los cuales se puede deducir la distorsión del tiempo y del espacio alrededor de objetos cósmicos que pueblan el Universo y que crear esta distorsión en función de su masa. Se han cumplido 100 años desde entonces y miles de físicos han tratado de extraer las predicciones encerradas en las ecuaciones de Einstein (sin olvidar a Riemann ) sobre la distorsión del espacio-tiempo.
Un agujero negro es lo definitivo en distorsión espaciotemporal, según las ecuaciones de Einstein: está hecho única y exclusivamente a partir de dicha distorsión. Su enorme distorsión está causada por una inmensa cantidad de energía compactada: energía que reside no en la materia, sino en la propia distorsión. La distorsión genera más distorsión sin la ayuda de la materia. Esta es la esencia del agujero negro.

No deja de crecer al engullir la materia circundante, su diámetro se hice mucho más grande
Si tuviéramos un agujero negro del tamaño de la calabaza más grande del mundo, de unos 10 metros de circunferencia, entonces conociendo las leyes de la geometría de Euclides se podría esperar que su diámetro fuera de 10 m.: л = 3,14159…, o aproximadamente 3 metros. Pero el diámetro del agujero es mucho mayor que 3 metros, quizá algo más próximo a 300 metros. ¿ Cómo puede ser esto ? Muy simple: las leyes de Euclides fallan en espacios muy distorsionados.

Con esta teoría de la Relatividad General, entre otros pasos importantes, está el hecho de que dió lugar al nacimiento de la Cosmología que, de alguna manera, era como mirar con nueva visión a lo que l Universo podía significar, Después de Einstein, el Universo no fue el mismo.
El análisis de la Gravitación que aquí quedó plasmado interpreta el Universo como un continuo espacio-tiempo de cuatro dimensiones en el el que la presencia de una masa (como decía antes) curva el espacio para crear un campo gravitacional.
De la veracidad y comprobación de las predicciones de ésta segunda parte de la Teoría Relativista, tampoco, a estas alturas cabe duda alguna, y, lo más curioso del caso es que, después de casi un siglo (1.915), aún los físicos están sacando partido de las ecuaciones de campo de la teoría relativista en su versión general o de la Gravedad.
Tan importante es el trabajo de Einstein que, en las nuevas teorías, en las más avanzadas, como la Teoría M (que engloba las cinco versiones de la Teoría de Cuerdas), cuando la están desarrollando, como por arte de magía y sin que nadie las llame, surgen, emergen, las ecuaciones de Einstein de la Relatividad General.
Emilio Silvera Vázquez
Mar
9
No lo sabemos explicar pero, es tan importante en nuestras vidas. Me...
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (2)
Comments (2)
¿Fue el Tiempo el único testigo de…
Si miramos hacia atrás en el Tiempo, podremos comprobar que, desde siempre, hemos estado a merced de los agentes naturales que llegaron para causar grandes estragos en la población que según los casos se vio mermada por miles y millones de muertos. El que nos asedió en 2019, tengo la sensación de que no es tan natural, y, si algún día se llega a saber que fue provocado… Y si los humanos seguimos comportándonos así ¡Traerá malas consecuencias para el Mundo!
Nosotros, los Humanos, somos bastante prepotentes y, a estas alturas nos podemos creer que lo sabemos todo y que nada puede hacernos mella, nuestros conocimientos nos pueden librar de todo… ¡Cuan equivocado estamos! Pero vayamos a repasar algunos detalles y hechos en los que, el actor principal es el Tiempo. Durante su transcurrir crecemos y nos educan para estar preparados cada cual en el ámbito elegido para servir al colectivo, no importa si se es mecánico, doctor o físico, todo es necesario para el bien común
“La didáctica es la rama de la pedagogía que se ocupa de orientar la acción educadora sistemática, y en sentido más amplio, es el conjunto de conocimientos aplicables a todo sujeto, plantea las cuestiones generales de toda enseñanza comunes a todas las materias.
La didáctica es la disciplina pedagógica del carácter practico y normativo que tiene por objeto especifico la técnica de la enseñanza, esto es, la técnica de incentivar y de orientar eficazmente a los alumnos y alumnas en el aprendizaje”Agricultor o panadero, cirujano o científico investigador, astrónomo o historiador, Físico de partículas o Asesor Fiscal, Empresario o Filósofo… ¡Ah! También la Política es necesaria cuando se desarrolla de manera adecuada, Todos desarrollan una misión en la Sociedad que, con otras muchas, conforman el entramado de conocimientos que hacen posible la convivencia y que sigamos avanzando hacia el futuro.
Colectivamente, el tiempo es muy importante, cada uno de nosotros hacemos un trabajo y desarrollamos una actividad que se va sumando a la de los demás, con el tiempo, el trabajo, ese conocimiento adquirido, continúa aumentando y, ese tiempo “infinito” es el que necesitamos, nosotros y los que vendrán detrás para resolver problemas muy graves que se presentarán en el futuro y que, de poder o no poder resolverlos, dependerá que la Humanidad perdure.
El tiempo será la mejor herramienta con la que podemos contar para resolver todos los problemas. Así lo dijo Hilbert:
“Por muy inabordables que parezcan estos problemas, y por muy desamparados que nos encontremos frente a ellos hoy, tenemos la íntima convicción de que debe ser posible resolverlos mediante un número finito de deducciones lógicas. Y, para ello, la mejor herramienta es el tiempo, él nos dará todas las respuestas a preguntas que hoy no podemos ni sabemos contestar”.
En la tumba de David Hilbert (1862-1943), en el cementerio de Gotinga (Alemania), dice:
“Debemos saber. Sabremos”.
Mar
8
Equilibrio, estabilidad: el resultado de dos fuerzas contrapuestas
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (3)
Comments (3)

Curvas de potencial en un sistema de dos cuerpos (aquí el Sol y la Tierra), mostrando los cinco puntos de Lagrange. Las flechas indican pendientes alrededor de los puntos L –acercándose o alejándose de ellos. Contra la intuición, los puntos L4 y L5son máximos.
Los puntos de Lagrange, también denominados puntos L o puntos de libración, son las cinco posiciones en un sistema orbital donde un objeto pequeño, sólo afectado por la gravedad, puede estar teóricamente estacionario respecto a dos objetos más grandes, como es el caso de un satélite artificial con respecto a la Tierra y la Luna. Los puntos de Lagrange marcan las posiciones donde la atracción gravitatoria combinada de las dos masas grandes proporciona la fuerza centrípeta necesaria para rotar sincrónicamente con la menor de ellas. Son análogos a las órbitas geosincrónicas que permiten a un objeto estar en una posición «fija» en el espacio en lugar de en una órbita en que su posición relativa cambia continuamente. Una definición más precisa pero técnica es que los puntos de Lagrange son las soluciones estacionarias del problema de los tres cuerpos.

Diagrama del sistema Sol-Tierra, que muestra el punto L2, más alejado que la órbita lunar.
El telescopio que suplió al viejo Hubble. Un dato curioso sobre este telescopio es que no estará situado en la órbita terrestre, se situará en el punto de Lagrange L2. Los puntos de Lagrange son las posiciones donde la gravedad del Sol y la Tierra se equilibran, de manera que un objeto puede permanecer estable, sin salir despedido hacia el espacio profundo. El James West se ha situado en esta posición es para aislarlo de la contaminación que existe en la órbita terrestre.

El James West Space Telescope o JWST durante mucho tiempo ha sido promocionado como el reemplazo para el telescopio espacial Hubble. El telescopio está considerado como uno de los proyectos más ambiciosos de la ciencia espacial emprendido. A pesar del enorme desafío, el telescopio se está acercando a la terminación. El telescopio ha servido como un aula técnico sobre las complejidades involucrada con un proyecto tan complejo. También ha servido para desarrollar nuevas tecnologías que son utilizadas por los ciudadanos promedio en sus vidas cotidianas.
En nuestro Universo todo resulta ser el equilibrio de dos fuerzas contrapuestas que se igualan y se equilibran para alcanzar la estabilidad que es requerida para que todo exista en ese nivel de normalidad que hace de nuestro universo el que podemos observar y, los fenómenos que se producen, los cambios, siempre van encaminados a eso, a conseguir ese equilibrio que observamos.
Fuerzas positivas y negativas hacen que el núcleo de los átomos sea estable y las galaxias están sujetas por la Gravedad que mantiene las estrellas juntas y que no dejan que la expansión las pueda deshacer. El el núcleo de los átomos están los protones cargados con fuerzas positivas que atraen el mismo número de electrones que orbitan a su alrededor, y, al estar cargados con fuerzas negativas que se equilibran con las de los protones, el átomo es muy estable.
El núcleo se expande y la fuerza de Gravedad la reduce, lo que hace el equilibrio de la estrella
Cuando hablamos de equilibrio lo estamos haciendo del estado en el que un sistema tiene su energía distribuida de la manera estadísticamente más probable, un estado del sistema en el que las fuerzas, influencia, reacciones, etc., se compensan las unas a las otras de manera que no se permiten cambios y prevalece la estabilidad.
Equilibrio estático en tres dimensiones
Un cuerpo se encuentra en equilibrio estático si las resultantes de todas las fuerzas y todos los pares que actúan en él son ambas cero; se si halla en reposo, estará ciertamente no acelerado. Un cuerpo de ese tipo en el reposo se encuentra en equilibrio estable si después de un ligero desplazamiento vuelve a su posición original. Existen diversas variantes que no merece la pena mencionar aquí para no hacer aburrido el trabajo.
También existe el equilibrio térmico y se dice que un cuerpo está en equilibrio térmico si no hay ningún intercambio de calor dentro de él o entre el y sus alrededores. Un sistema se encuentra en equilibrio térmico cuando cuando una reacción y su inversa está teniendo lugar a la misma velocidad. Estos son ejemplos de equilibrios dinámicos, en los que la actividad en un sentido está compensada por la actividad en el sentido inverso. De nuevo el equilibrio o estabilidad creado por fuerzas contrapuestas.
La energía se equipara según una teoría de propuesta por Ludwig Boltzmann y fundamentada teóricamente por James Clerk Maxwell, en virtud de la cual la energía de las moléculas de un gas en una muestra grande en equilibrio térmico está dividida por igual entre todos los grados de libertad disponibles, siendo la energía media de cada grado de libertad kT/2, donde k es la constante de Boltzmann y T es la temperatura termodinámica. La proposición no es en general cierta si los efectos cuánticos son importantes, pero frecuentemente es una buena aproximación.

El cuadro nos muestra una Ilustración de los distintos tipos de simetría en las formas orgánicas (Field Museum, Chicago).
Claro que si hablamos de simetrías, nos podríamos perder un un laberinto de clases y formas: esférica, cilíndrica, reflectiva, traslacional, helicoidal, de rotación, de ampliación, bilateral, radial… (muchas otras). Pero si nos referimos de manera simple a lo que es o entendemos por una simetría, nos estaremos refiriendo al conjunto de invariancias de un sistema.

Al aplicar una transformación de simetría sobre un sistema, el sistema queda inalterado. La simetría es estudiada matemáticamente usando teoría de grupos. Algunas de las simetrías son directamente físicas. Algunos ejemplos son las reflexiones y rotaciones de las moléculas y las transformaciones de las redes cristalinas.

Las dos fuerzas contrapuestas en los seres vivos inteligentes de nuestro mundo, está precisamente en nosotros mismos: El hombre y la Mujer, juntos, forman un sólo ente de equilibrio perfecto que nos lleva al más alto nivel de simetría y belleza, y, tal equilibrio y conjunción, hace posible el milagro de la replicación.
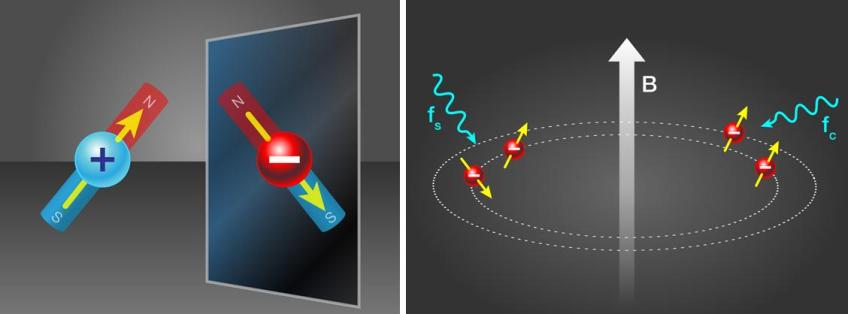
“La Trampa de Antihidrógeno (ATRAP) es un pequeño experimento en el CERN cuyo objetivo es comparar la antimateria con la materia, en concreto, átomos de anti-hidrógeno (formados por un antiprotón y un positrón, o antielectrón) con átomos de hidrógeno (formados por un protón y un electrón). Acaban de publicar la medida más precisa del momento magnético del antiprotón, 2,792847356(23) veces el magnetón nuclear, que coincide con el del protón en al menos cinco partes por millón (0,0005%), una nueva medida (directa) de la invarianza CPT”
(Francis (th)E mule Science’s News).
Existen simetrías más generales y abstractas como la invariancia CPT y las simetrías asociadas a las teorías gauge (tendríamos que mirar en simetrías rotas y supersimetría para ampliar el concepto en su más amplio espectro y concepción de lo que la simetría es. En el Universo, las simetrías están por todas partes: Estrellas, mundos, galaxias…
Me encantó leer:

“Resulta gratificante descubrir que en nuestro país, en el Instituto de Física Corpuscular de la Universidad de València, un grupo de científicos ha liderado una importante investigación internacional para descubrir directamente la ruptura de la simetría del tiempo en las leyes físicas”
La ruptura de simetría del tiempo en las leyes físicas. ¿Por qué?
El Físico J. Bernabeu decía:

“Hay una razón que se entiende inmediatamente. Aquellas partículas elementales con que se descubrió, y después confirmó, la asimetría de materia/antimateria, y que son precisamente en las que esperamos la ruptura de simetría temporal, son partículas inestables que se desintegran en el tiempo. Si una partícula se desintegra es imposible poder utilizarla para poder hacer el sentido opuesto del movimiento. Esta razón, que parece tan clara, es efectivamente el impedimento básico por el que un test de la simetría por inversión temporal en partículas que se desintegran no había podido hacerse.”
Por mi parte (Mente inquieta e inconforme con cualquier explicación a la primera), deja llevar y piensa que, la ruptura de simetría temporal del Tiempo es debida a que, se interrumpe su discurrir en presencia de escenarios distintos, ya que, se ha sabido que cerca de un agujero negro se ralentiza o incluso podría llegar a pararse por completo. ¿No es eso una asimetría temporal? ¿ero… ¡Qué sabré Yo!?
Emilio Silvera Vázquez















 Totales: 74.919.799
Totales: 74.919.799 Conectados: 67
Conectados: 67







































:format(jpg):quality(99):watermark(f.elconfidencial.com/file/bae/eea/fde/baeeeafde1b3229287b0c008f7602058.png,0,275,1)/f.elconfidencial.com/original/a4c/1e2/2c9/a4c1e22c9fb3d32b5254c2e451f5a207.jpg)