Ene
23
¿Viajes en el Tiempo? ¡Otro sueño de la Humanidad!
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (1)
Comments (1)
En cromodinámica cuántica, la propiedad de libertad asintótica hace que la interacción entre quarks sea más débil cuanto más cerca están unos de otros (confinación de los quarks) y la fuerza crece cuando los quarks tratan de separarse, es la única fuerza que crece con la distancia. Los quarks y los gluones están confinados en una región cuyo valor se define por:
R » ћc /L » 10-13 cm

Poder contemplar Quarks libres sólo podría haber sido posible en aquellos primeros momentos, antes de la formación de los hadrónes. En realidad, la única manera de que pudiéramos observar quarks libres, sería en un ambiente con la temperatura del universo primitivo, es la temperatura de desconfinamiento.
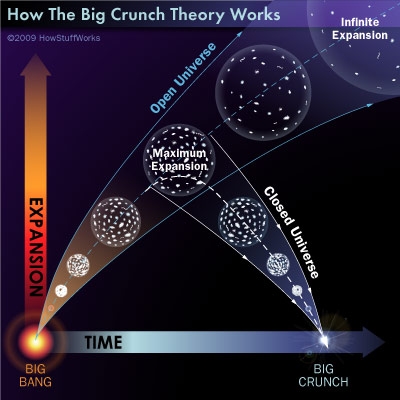
Ahora se cree que el Big Crunch nunca se producirá y que la muerte del Universo será térmica, es decir, una temperatura del cero absoluto que lo paralizará todo, ni los átomos se moverán en ese frío de muerte que dejará un universo congelado donde ni brillaran las estrellas ni estará presente ninguna clase de vida.
En la parte anterior de este mismo trabajo, estaba hablando del Big Crunch y me pasé a otro (los quarks), así que cerremos este capítulo del Big Crunch que está referido a un estado final de un universo cerrado de Friedmann (es decir, uno en el que la densidad excede a la densidad crítica). Dicho universo se expande desde el Big Bang inicial, alcanza un radio máximo, y luego colapsa hacia un Big Crunch, donde la densidad de la materia se vuelve infinita después de que la gravedad haga parar la expansión de las galaxias que, lentamente al principio, y muy rápidamente después, comenzarán a desplazarse en sentido contrario, desandarán el camino para que toda la materia del universo se junte en un punto, formado una singularidad en la que dejaría de existir el espacio-tiempo. Después del Big Crunch debería haber otra fase de expansión y colapso, dando lugar a un universo oscilante. universo que se va y universo que viene.

Pero, ¿y nosotros?, ¿Qué pintamos aquí?
¡Mirado así no parece que seamos gran cosa!
Antes de pasar a otros temas, retomemos el de los viajes en el tiempo y las paradojas que pueden originar.

Una versión de la máquina del tiempo de Thorne consiste en dos cabinas, cada una de las cuales contiene dos placas de metal paralelas. Los intensos cambios eléctricos creados entre cada par de placas de metal paralelas (mayores que cualquier cosa posible con la tecnología actual) rizan el tejido del espacio-tiempo, creando un agujero en el espacio que une las dos cabinas. Una cabina se coloca entonces en una nave espacial y es acelerada a velocidades próximas a la de la luz, mientras que la otra cabina permanece en la Tierra. Puesto que un agujero de gusano puede conectar dos regiones des espacio con tiempos diferentes, un reloj en la cabina de la nave marcha más despacio que un reloj en la cabina de la Tierra. Debido a que el tiempo transcurriría a diferentes velocidades en los dos extremos del agujero de gusano, cualquiera que entrase en un extremo del agujero de gusano sería instantáneamente lanzado al pasado o al futuro.

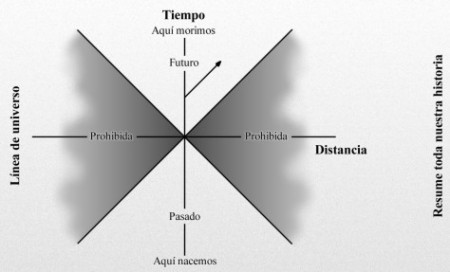
Viajar al pasado y conocer a personajes famosos a los que contar las novedades científicas. Algunos dicen que el viaje en el Tiempo está prohibido, aunque es posible. Siempre hemos tenido una gran imaginación y, cuando se sabíamos contestar a una cuestión compleja… ¡Inventamos la respuesta!
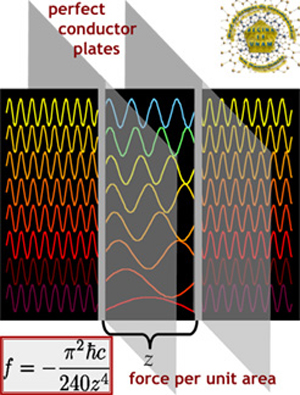
Normalmente, una de las ideas básicas de la física elemental es que todos los objetos tienen energía positiva. Las moléculas vibrantes, los vehículos que corren, los pájaros que vuelan, los niños jugando tienen todos energía positiva. Por definición, el espacio vacío tiene energía nula. Sin embargo, si podemos producir objetos con “energías negativas” (es decir, algo que tiene un contenido de energía menor que el vacío), entonces podríamos ser capaces de generar configuraciones exóticas de espacio y tiempo en las que el tiempo se curve en un circulo.

Parece que la función de las placas metálicas paralelas consiste en generar la materia o energía exótica necesaria para que las bocas de entrada y salida del agujero de gusano permanezcan abiertas y, como la materia exótica genera energía negativa, los viajeros del tiempo no experimentarían fuerzas gravitatorias superiores a 1g, viajando así al otro extremo de la galaxia e incluso del universo o de otro universo paralelo de los que promulga Stephen Hawking. En apariencia, el razonamiento matemático de Thorne es impecable conforme a las ecuaciones de Einstein.
Normalmente, una de las ideas básicas de la física elemental es que todos los objetos tienen energía positiva. Las moléculas vibrantes, los vehículos que corren, los pájaros que vuelan, los niños jugando tienen todos energía positiva. Por definición, el espacio vacío tiene energía nula. Sin embargo, si podemos producir objetos con “energías negativas” (es decir, algo que tiene un contenido de energía menor que el vacío), entonces podríamos ser capaces de generar configuraciones exóticas de espacio y tiempo en las que el tiempo se curve en un circulo.

Muchas son las máquinas del tiempo que hemos desarrollado en nuestra imaginación
Por el momento, al no ser una propuesta formal, no hay veredicto sobre la máquina del tiempo de Thorne. Su amigo, Stephen Hawking, dice que la radiación emitida en la entrada del agujero sería suficientemente grande como contribuir al contenido de materia y energía de las ecuaciones de Einstein. Esta realimentación de las ecuaciones de Einstein distorsionaría la entrada del agujero de gusano, incluso cerrándolo para siempre. Thorne, sin embargo, discrepa en que la radiación sea suficiente para cerrar la entrada.
Aquí es donde interviene la teoría de supercuerdas. Puesto que la teoría de supercuerdas es una teoría completamente mecano-cuántica que incluye la teoría de la relatividad general de Einstein como un subconjunto, puede ser utilizada para calcular correcciones a la teoría del agujero de gusano original.
En principio nos permitiría determinar si la condición AWEC es físicamente realizable, y si la entrada del agujero de gusano permanece abierta para que los viajeros del tiempo puedan disfrutar de un viaje al pasado.
Nuestra línea de universo resume toda nuestra historia, que nacemos hasta que morimos. Cuanto más rápido nos movemos más se inclina la línea de universo. Sin embargo, la velocidad más rápida a la que podemos viajar es la velocidad de la luz. Por consiguiente, una de este diagrama espacio-temporal está “prohibida”; es decir, tendríamos que ir a mayor velocidad que la luz para entrar en esta zona prohibida por la relatividad especial de Einstein, que nos dice que nada en nuestro universo puede viajar a velocidades superiores a c.

Agujero de Gusano, ese sueño que hemos inventado para engañar a la velocidad de la luz
“Amos Ori describe una máquina para viajar en el tiempo que podría ser construida por una civilización más avanzada que la nuestra dentro de 100 o 200 años. Esa máquina tendría la capacidad teórica de provocar una curvatura del espacio con un campo de gravedad local en su interior suficientemente poderoso que sería en la práctica una máquina para viajar en el tiempo. “
Sí, ¿pero dónde está esa energía negativa para viajar en el Tiempo?

Este concepto más bien simple se conoce con un nombre que suena complicado: la condición de energía media débil (average weak energy condition, o AWEC). Como Thorne tiene cuidado en señalar, la AWEC debe ser violada; la energía debe hacerse temporalmente negativa para que el viaje en el tiempo tenga éxito. Sin embargo, la energía negativa ha sido históricamente anatema para los relativistas, que advierten que la energía negativa haría posible la antigravedad y un montón de otros fenómenos que nunca se han visto experimentalmente.
Pero Thorne señala al momento que existe una forma de obtener energía negativa, y esto es a través de la teoría cuántica.
Estamos inmersos en una gran sopa cuántica de la que no somos conscientes pues la mayor parte de la energía que circula a nuestro alrededor, es imperceptible para nuestros sentidos físicos….
En 1.948, el físico holandés Hendrik Casimir demostró que la teoría cuántica puede crear energía negativa: tomemos simplemente dos placas de metal paralelas y descargadas ordinariamente, el sentido común nos dice que estas dos placas, puesto que son eléctricamente neutras, no ejercen ninguna fuerza entre sí. Pero Casimir demostró que, debido al principio de incertidumbre de Werner Heisenberg, en el vacío que separa estas dos placas existe realmente una agitada actividad, con billones de partículas y antipartículas apareciendo y desapareciendo constantemente. Aparecen a partir de la “nada” y vuelven a desaparecer en el “vacío”. Puesto que son tan fugaces, son, en su mayoría, inobservables, y no violan ninguna de las leyes de la física. Estas “partículas virtuales” crean una fuerza neutra atractiva entre estas dos placas que Casimir predijo que era medible.

Cuando Casimir publicó el artículo, se encontró con un fuerte escepticismo. Después de todo, ¿Cómo pueden atraerse dos objetos eléctricamente neutros, violando así las leyes normales de la electricidad clásica? Esto era inaudito. Sin embargo, en 1.985 el físico M. J. Sparnaay observó este efecto en el laboratorio, exactamente como había predicho Casimir. Desde entonces (después de un sin fin de comprobaciones), ha sido bautizado como el efecto Casimir.
Una manera de aprovechar el efecto Casimir mediante grandes placas metálicas paralelas descargadas, sería el descrito para la puerta de entrada y salida del agujero de gusano de Thorne para poder viajar en el tiempo.

Por el momento, al no ser una propuesta formal, no hay veredicto sobre la máquina del tiempo de Thorne. Su amigo, Stephen Hawking, dice que la radiación emitida en la entrada del agujero sería suficientemente grande como para contribuir al contenido de materia y energía de las ecuaciones de Einstein. Esta realimentación de las ecuaciones de Einstein distorsionaría la entrada del agujero de gusano, incluso cerrándolo para siempre. Thorne, sin embargo, discrepa en que la radiación sea suficiente para cerrar la entrada.
Aquí es donde interviene la teoría de supercuerdas. Puesto que la teoría de supercuerdas es una teoría completamente mecano-cuántica que incluye la teoría de la relatividad general de Einstein como un subconjunto, puede ser utilizada para calcular correcciones a la teoría del agujero de gusano original.
En principio nos permitiría determinar si la condición AWEC es físicamente realizable, y si la entrada del agujero de gusano permanece abierta para que los viajeros del tiempo puedan disfrutar de un viaje al pasado.
Podríamos ver como se forman las nebulosas y nacen y mueren las estrellas
Antes comentaba algo sobre disfrutar de un viaje al pasado pero, pensándolo bien, no estaría yo tan seguro. Rápidamente acuden a mi mente múltiple paradojas que, de una u otra especie han sido narradas, principalmente por escritores de ciencia-ficción que, por lo general, son los precursores del futuro.
Si viajar en el tiempo finalmente pudiera ser posible, cosas parecidas a esta locura ¡”podrían ocurrir”! I. B. S. Haldane, nos decía:
“La naturaleza no sólo es más extraña de lo que suponemos; es más extraña de lo que podamos suponer”.
Claro que, llamamos extrañeza a todo aquello que no entendemos, nos resulta desconocido y a veces asombroso, y, cuando desvelamos esos secretos profundamente escondido en las entrañas de la Naturaleza, nos familiarizamos con ellos y nos resultan familiares y cotidianos. El saber como nacen, viven y mueren las estrellas es un ejemplo.
Emilio Silvera Vázquez
Ene
23
La Relatividad Especial sigue gozando de buena Salud
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (3)
Comments (3)
Hace algunos años, en la prensa de todo el mundo salían noticias como esta:

¿Neutrinos más rápidos que la luz?
“Un equipo científico que trabajaba con el detector subterráneo Opera, en el laboratorio de Gran Sasso (Italia), ha obtenido unos resultados que pueden ser muy satisfactorios o muy incómodos. La presentación de los mismos está prevista para hoy, en el Laboratorio europeo de Física de Partículas (CERN, junto a Ginebra) como un seminario científico altamente especializado. Pero los rumores corren ya hace unos días porque lo que estos científicos plantean es que han medido neutrinos (partículas elementales de escasa masa y que apenas interaccionan con la materia) que, aparentemente, se desplazan más rápido que la luz. De confirmarse, sería un bombazo en la física, puesto que es un pilar de la teoría de Einstein que nada puede superar la velocidad de la luz.”


The OPERA detector at the Gran Sasso laboratory. The picture shows both supermodules (SM1 and SM2), and the target and muon spectrometers in each SM.
Después de eso, ya sabemos todos lo que pasó y, los dos responsables principales han tenido que dimitir, la Luz sigue siendo la primera en llegar a cualquier sitio.
Ene
13
¡Partículas! Sus particularidades
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (3)
Comments (3)
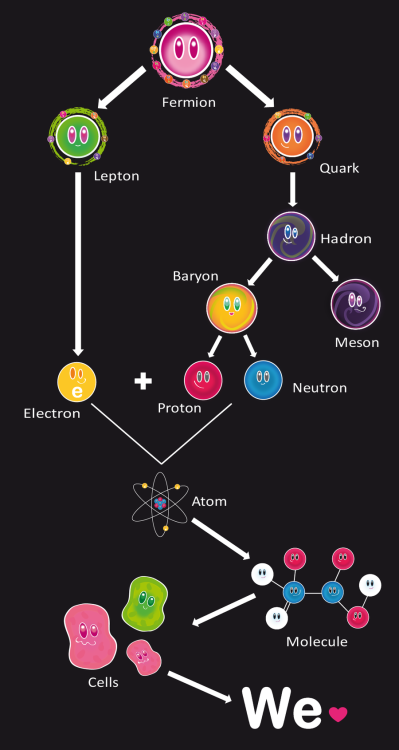
Adentrarse en el universo de las partículas que componen los elementos de la Tabla Periódica, y en definitiva, la materia conocida, es verdaderamente fantástico”. Esos pequeños objetos que no podemos ver, de dimensiones infinitesimales, son, en definitiva, los componentes de todo lo que contemplamos a nuestro alrededor: Las montañas, ríos, Bosques, océanos, los más exoticos animales y, hasta
nosotros mismos, estamos hechos de Quarks y Leptones que, en nuestro caso, han podido evolucionar hasta llegar…¡A los pensamientos!

Desde los Quarks hasta los pensamientos ¿Qué no discurrirá la Mente Humana?
los Quarks hasta los pensamientos ¿Qué no discurrirá la Mente Humana?
Estas dos familias de partículas conforman todo lo que podemos ver a nuestro alrededor, la materia del Universo y, si la “materia oscura” en realidad existe, no sabemos de qué pueda estar hecha y las clases de partículas que la puedan conformar. Habrá que esperar y, de momento , hablaremos de lo que conocemos.
, hablaremos de lo que conocemos.


El matrimonio Joliot-Curie en el Laboratorio
Tan pronto como los Joliot-Curie crearon el primer isótopo radiactivo artificial, los físicos se lanzaron en tropel a producir tribus enteras de ellas. En realidad, las variedades radiactivas de cada elemento en la tabla periódica son producto de laboratorio. En la moderna tabla periódica, cada elemento es una familia con miembros estables e inestables, algunos procedentes de la naturaleza, otros sólo del laboratorio. Por ejemplo, el hidrógeno presenta tres variedades: en primer lugar, el corriente, que tienen un solo protón.
elemento en la tabla periódica son producto de laboratorio. En la moderna tabla periódica, cada elemento es una familia con miembros estables e inestables, algunos procedentes de la naturaleza, otros sólo del laboratorio. Por ejemplo, el hidrógeno presenta tres variedades: en primer lugar, el corriente, que tienen un solo protón.
Harold Urey
En 1.932, el químico Harold Urey logró aislar el segundo. Lo consiguió sometiendo a lenta evaporación una gran cantidad de agua, de acuerdo con la teoría de que los residuos representarían una concentración de la forma más pesada del hidrógeno que se conocía, y, en efecto, cuando se examinaron al espectroscopio las últimas gotas de agua no evaporadas, se descubrió en el espectro una leve línea cuya posición matemática revelaba la presencia de hidrógeno pesado.
más pesada del hidrógeno que se conocía, y, en efecto, cuando se examinaron al espectroscopio las últimas gotas de agua no evaporadas, se descubrió en el espectro una leve línea cuya posición matemática revelaba la presencia de hidrógeno pesado.
No todo ha sido bueno desde entonces pero, teníamos que avanzar en el saber y, la clave está en saber utilizar adecuadamente esos conocimientos.
entonces pero, teníamos que avanzar en el saber y, la clave está en saber utilizar adecuadamente esos conocimientos.

Sabemos que los elementos naturales son 92 y que hemos encontrado otros artificiales que hemos llamado transuránicos, es decir, más allá del Uranio que es el número 92 de la T. P.
“El núcleo de hidrógeno pesado está constituido por un protón y un neutrón. Como tiene un número
másico de 2, el isótopo es hidrógeno. Urey llamó a este átomo deuterio (de la voz griega deuteros, “segundo”), y el núcleo deuterón. Una molécula de agua que contenga deuterio se denomina agua pesada, que tiene puntos de ebullición y congelación superiores al agua ordinaria, ya que la masa del deuterio es dos veces mayor que la del hidrógeno corriente. Mientras que ésta hierve a 100º C y se congela a 0º C, el agua pesada hierve a 101’42º C y se congela a 3’79º C. El punto de ebullición del deuterio es de -23’7º K, frente a los 20’4º K del hidrógeno corriente. El deuterio se presenta en la naturaleza en la proporción de una parte
por cada 6.000 partes de hidrógeno corriente. En 1.934 se otorgó a Urey el premio Nobel de Química por su descubrimiento del deuterio.”

El deuterio resultó ser una partícula muy valiosa para bombardear los núcleos. En 1.934, el físico australiano Marcus Lawrence Edwin Oliphant y el austriaco P. Harteck atacaron el deuterio con deuterones y produjeron una tercera forma de hidrógeno, constituido por un protón y dos neutrones. La reacción se planteó así:
de hidrógeno, constituido por un protón y dos neutrones. La reacción se planteó así:
hidrógeno 2 + hidrógeno 2 = hidrógeno 3 + hidrógeno 1
Este nuevo
hidrógeno superpesado se denominó tritio (del griego tritos, “tercero”); su ebullición a 25º K y su fusión a 20’5º K.
Como es mi costumbre, me desvío del tema y sin poderlo evitar, mis ideas (que parecen tener vida propia), cogen los caminos más diversos. Basta con que se cruce en el camino del trabajo que realizo un fugaz recuerdo; lo sigo y me lleva a destinos distintos de los que me propuse al comenzar. Así, en este caso, me pasé a la química, que también me gusta mucho y está directamente relacionada con la física; de hecho son hermanas: la madre, las matemáticas, ese lenguaje especial que hablamos cuando las palabras no pueden explicar las cosas, y, la única, que finalmente lo podrá explicar todo lo complejo que existe en la Naturaleza.
que realizo un fugaz recuerdo; lo sigo y me lleva a destinos distintos de los que me propuse al comenzar. Así, en este caso, me pasé a la química, que también me gusta mucho y está directamente relacionada con la física; de hecho son hermanas: la madre, las matemáticas, ese lenguaje especial que hablamos cuando las palabras no pueden explicar las cosas, y, la única, que finalmente lo podrá explicar todo lo complejo que existe en la Naturaleza.

En Ginebra.- Físicos en el centro de investigación CERN están logrando colisiones de alta carga energética de partículas subatómicas en su intento por recrear las condiciones inmediatamente posteriores al Big Bang, el cual llevó al inicio del universo 13.700 millones de años atrás. Mucho se ha criticado al LHC y, sin embargo, es un gran paso adelante que nos posibilitará saber, como
inmediatamente posteriores al Big Bang, el cual llevó al inicio del universo 13.700 millones de años atrás. Mucho se ha criticado al LHC y, sin embargo, es un gran paso adelante que nos posibilitará saber, como es el Universo y, nos descubrirá algunos de sus secretos. Hará posible que avancemos en el conocimiento sobre de dónde venimos, cómo el universo temprano evolucionó, cómo tienen y adquieren su masa las partículas y, algunas cosas más.
es el Universo y, nos descubrirá algunos de sus secretos. Hará posible que avancemos en el conocimiento sobre de dónde venimos, cómo el universo temprano evolucionó, cómo tienen y adquieren su masa las partículas y, algunas cosas más.
Los haces dentro del LHC colisionan en cuatro lugares alrededor del anillo acelerador, los cuales corresponden a las posiciones de cuatro detectores de partículas: ATLAS, CMS, ALICE y LHCb. Adicionalmente, hay otros detectores más pequeños que forman parte de este acelerador:
TOTEM, LHCf, MoEDAL-MAPP, FASER y SND@LHC.
Todo eso se logra mediante las colisiones de haces partículas que son lanzadas a velocidades relativistas y que, al chocar con otro lanzado en el sentido contrario, producen el efecto que arriba en la imagen podéis ver, es como recrear el momento de la creación, es decir, el big bang en miniatura. La materia se descompone en otras partículas más simples, se llega hasta las entrañas más profundas para poder estudiarla y saber.
de la creación, es decir, el big bang en miniatura. La materia se descompone en otras partículas más simples, se llega hasta las entrañas más profundas para poder estudiarla y saber.

Los Bosones son las partículas mediadoras de las cuatro fuerzas
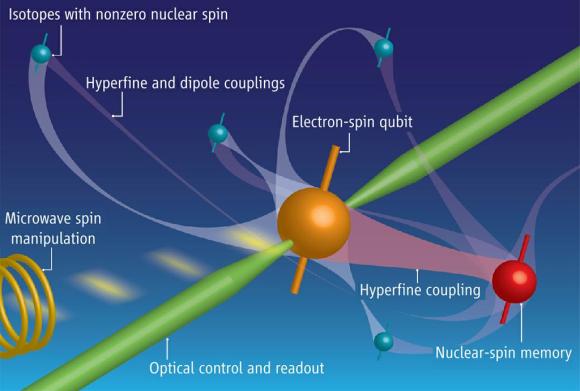
La colisión de un quark (la esfera roja) desde un protón (la esfera naranja) con un gluon (la esfera verde) desde
un protón (la esfera naranja) con un gluon (la esfera verde) desde otro protón con espín opuesto. El espín está representado por las flechas azules alrededor de los protones y del quark. Los signos de interrogación azules alrededor del gluon representan la pregunta: ¿Están los gluones polarizados? Las partículas expulsadas de la colisión son una lluvia de quarks y un fotón (la esfera púrpura).
otro protón con espín opuesto. El espín está representado por las flechas azules alrededor de los protones y del quark. Los signos de interrogación azules alrededor del gluon representan la pregunta: ¿Están los gluones polarizados? Las partículas expulsadas de la colisión son una lluvia de quarks y un fotón (la esfera púrpura).
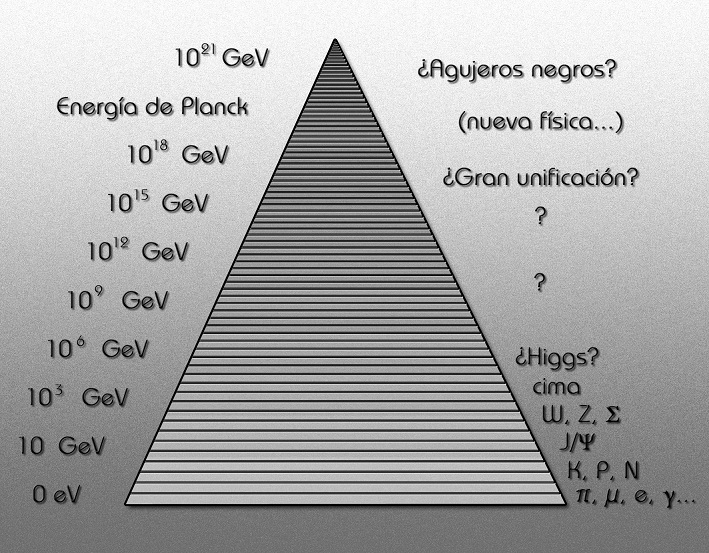
La escala de energía es la que marcará nuestro nivel de conocimiento del Universo
El Gran Colisionador de Hadrones (LHC), la mayor máquina del mundo en su tipo , colisionó rayos de partículas a un récord de energía de 7 teraelectron voltios (TeV), tres veces y medio más rápido de lo conseguido anteriormente en un acelerador de partículas. Sin embargo, hasta que podamos llegar a la energía de Planck, para poder atisbar las cuerdas, falta mucho, muchísimo camino que recorrer…si finalmente, lo podemos lograr.
, colisionó rayos de partículas a un récord de energía de 7 teraelectron voltios (TeV), tres veces y medio más rápido de lo conseguido anteriormente en un acelerador de partículas. Sin embargo, hasta que podamos llegar a la energía de Planck, para poder atisbar las cuerdas, falta mucho, muchísimo camino que recorrer…si finalmente, lo podemos lograr.
Una manera de ver la Naturaleza “por dentro” es hacer que haces de partículas choquen de manera violenta entre sí y nos enseñen de qué están hechas.
sí y nos enseñen de qué están hechas.
Los científicos quieren creer que la naturaleza prefiere la economía en sus creaciones y que siempre parece evitar redundancias innecesarias al crear estructuras físicas, biológicas y químicas. La Naturaleza, siempre lleva su dinámica al ritmo más económico posible, no se produce absolutamente nada que sea superfluo, sino que, con lo estrictamente necesario, todo transcurre como debe.
debe.
Estamos hablando de las partículas y no podemos dejar a un lado el tema del movimiento rotatorio de las mismas. Usualmente se ve cómo la partícula gira sobre su eje, a semejanza de un trompo, o como la Tierra o el Sol, o nuestra galaxia o, si se me permite decirlo, como el propio universo. En 1.925, los físicos holandeses George Eugene Uhlenbeck y Samuel Abraham Goudsmit aludieron por primera vez a esa rotación de las partículas. Éstas, al girar, generan un minúsculo campo electromagnético; tales campos han sido objeto de medidas y exploraciones, principalmente por parte del físico alemán Otto Stern y el físico norteamericano Isaac Rabi, quienes recibieron los premios Nobel de Física en 1.943 y 1.944 respectivamente, por sus trabajos sobre dicho fenómeno.
del físico alemán Otto Stern y el físico norteamericano Isaac Rabi, quienes recibieron los premios Nobel de Física en 1.943 y 1.944 respectivamente, por sus trabajos sobre dicho fenómeno.
Esas partículas (al igual que el protón, el neutrón y el electrón), que poseen espines que pueden medirse en números mitad, se consideran según un sistema de reglas elaboradas independientemente, en 1.926, por Fermi y Dirac; por ello, se las llama y conoce como estadísticas Fermi-dirac. Las partículas que obedecen a las mismas se denominan fermiones, por lo cual el protón, el electrón y el neutrón son todos fermiones.

Estadística Fermi-Dirac para las Fermiones. La estadística de Fermi-Dirac es la forma de contar estados de ocupación de forma estadística en un sistema de fermiones. Forma parte de la Mecánica Estadística. Y tiene aplicaciones sobre todo en la Física del estado
de contar estados de ocupación de forma estadística en un sistema de fermiones. Forma parte de la Mecánica Estadística. Y tiene aplicaciones sobre todo en la Física del estado sólido.
sólido.
Hay también partículas cuya rotación, al duplicarse, resulta igual a un número par. Para manipular sus energías hay otra serie de reglas, ideadas por Einstein y el físico indio S. N. Bose. Las partículas que se adaptan a la estadística Bose-Einstein son bosones, como por ejemplo la partícula alfa.
par. Para manipular sus energías hay otra serie de reglas, ideadas por Einstein y el físico indio S. N. Bose. Las partículas que se adaptan a la estadística Bose-Einstein son bosones, como por ejemplo la partícula alfa.
Estadística Bose-Einstein para los Bosones
Las reglas de la mecánica cuántica tienen que ser aplicadas si queremos describir estadísticamente un sistema de partículas que obedece a reglas de esta teoría en vez de los de la mecánica clásica. En estadística cuántica, los estados de energía se considera que están cuantizados. La estadística de Bose-Einstein se aplica si cualquier número
teoría en vez de los de la mecánica clásica. En estadística cuántica, los estados de energía se considera que están cuantizados. La estadística de Bose-Einstein se aplica si cualquier número de partículas puede ocupar un estado cuántico dado. Dichas partículas son bosones, que tienden a juntarse.
de partículas puede ocupar un estado cuántico dado. Dichas partículas son bosones, que tienden a juntarse.
Los bosones tienen un momento angular nh/2π, donde n es 0 o un entero, y h es la constante de Planck. Para bosones idénticos, la función de ondas es siempre simétrica. Si sólo una partícula puede ocupar un estado cuántico, tenemos que aplicar la estadística Fermi-Dirac y las partículas (como también antes dije) son los fermiones que tienen momento angular (n + ½)h / 2π y cualquier función de ondas de fermiones idénticos es siempre antisimétrica. La relación entre el espín y la estadística de las partículas está demostrada por el teorema espín-estadística. El teorema de la estadística del espín de la mecánica cuántica establece la relación directa entre el espín de una especie de partícula con la estadística que obedece. Fue demostrado por Fierz y Pauli en 1940, y requiere el formalismo de teoría cuántica de campos.
cuántico, tenemos que aplicar la estadística Fermi-Dirac y las partículas (como también antes dije) son los fermiones que tienen momento angular (n + ½)h / 2π y cualquier función de ondas de fermiones idénticos es siempre antisimétrica. La relación entre el espín y la estadística de las partículas está demostrada por el teorema espín-estadística. El teorema de la estadística del espín de la mecánica cuántica establece la relación directa entre el espín de una especie de partícula con la estadística que obedece. Fue demostrado por Fierz y Pauli en 1940, y requiere el formalismo de teoría cuántica de campos.
En un espacio de dos dimensiones es posible que haya partículas (o cuasipartículas) con estadística intermedia entre bosones y fermiones. Estas partículas se conocen con el nombre de aniones; para aniones idénticos, la función de ondas no es simétrica (un cambio de fase de +1) o antisimétrica (un cambio de fase de -1), sino que interpola continuamente entre +1 y -1. Los aniones pueden ser importantes en el análisis del efecto Hall cuántico fraccional y han sido sugeridos como un mecanismo para la superconductividad de alta temperatura.
de aniones; para aniones idénticos, la función de ondas no es simétrica (un cambio de fase de +1) o antisimétrica (un cambio de fase de -1), sino que interpola continuamente entre +1 y -1. Los aniones pueden ser importantes en el análisis del efecto Hall cuántico fraccional y han sido sugeridos como un mecanismo para la superconductividad de alta temperatura.
Debido al principio de exclusión de Pauli, es imposible que dos fermiones ocupen el mismo estado cuántico (al contrario de lo que ocurre con los bosones). La condensación Bose-Einstein es de importancia fundamental para explicar el fenómeno de la superfluidez. A temperaturas muy bajas (del orden de 2×10-7 K) se puede formar un condensado de Bose-Einstein, en el que varios miles de átomos dorman una única entidad (un superátomo). Este efecto ha sido observado con átomos de rubidio y litio. Como ha habréis podido suponer, la condensación Bose-Einstein es llamada así en honor al físico Satyendra Nath Bose (1.894 – 1.974) y a Albert Einstein. Así que, el principio de exclusión de Pauli tiene aplicación no sólo a los electrones, sino también a los fermiones; pero no a los bosones.
cuántico (al contrario de lo que ocurre con los bosones). La condensación Bose-Einstein es de importancia fundamental para explicar el fenómeno de la superfluidez. A temperaturas muy bajas (del orden de 2×10-7 K) se puede formar un condensado de Bose-Einstein, en el que varios miles de átomos dorman una única entidad (un superátomo). Este efecto ha sido observado con átomos de rubidio y litio. Como ha habréis podido suponer, la condensación Bose-Einstein es llamada así en honor al físico Satyendra Nath Bose (1.894 – 1.974) y a Albert Einstein. Así que, el principio de exclusión de Pauli tiene aplicación no sólo a los electrones, sino también a los fermiones; pero no a los bosones.

El principio de exclusión de Pauli, formulado por el físico austriaco Wolfgang Pauli en 1925 , es un concepto fundamental en la física cuántica y la química, especialmente en lo que respecta a la estructura de los átomos y las moléculas. También es importante para comprender la formación final (en la evolución de las estrellas -en relación a sus masas-, de las estrellas enanas blancas y de neutrones.
Si nos fijamos en todo lo que estamos hablando aquí, es fácil comprender cómo forma un campo magnético la partícula cargada que gira, pero ya no resulta tan fácil saber por qué ha de hacer lo mismo un neutrón descargado. Lo cierto es que cuando un rayo de neutrones incide sobre un hierro magnetizado, no se comporta de la misma forma
un campo magnético la partícula cargada que gira, pero ya no resulta tan fácil saber por qué ha de hacer lo mismo un neutrón descargado. Lo cierto es que cuando un rayo de neutrones incide sobre un hierro magnetizado, no se comporta de la misma forma que lo haría si el hierro no estuviese magnetizado. El magnetismo del neutrón sigue siendo un misterio; los físicos sospechan que contiene cargas positivas y negativas equivalente a cero, aunque por alguna razón desconocida, logran crear un campo magnético cuando gira la partícula. Es de especial interés ya que los momentos magnéticos aparecen por el movimiento de cargas eléctricas, y puesto que el neutrón es una partícula neutra, ese momento
que lo haría si el hierro no estuviese magnetizado. El magnetismo del neutrón sigue siendo un misterio; los físicos sospechan que contiene cargas positivas y negativas equivalente a cero, aunque por alguna razón desconocida, logran crear un campo magnético cuando gira la partícula. Es de especial interés ya que los momentos magnéticos aparecen por el movimiento de cargas eléctricas, y puesto que el neutrón es una partícula neutra, ese momento magnético da indicios de la existencia de una substructura, es decir, que el neutrón está constituido por otras partículas, eléctricamente cargadas (¿Quarks?)
magnético da indicios de la existencia de una substructura, es decir, que el neutrón está constituido por otras partículas, eléctricamente cargadas (¿Quarks?)

También en las estrellas de neutrones está presente el campo magnético
en las estrellas de neutrones está presente el campo magnético
Particularmente creo que, si el neutrón tiene masa, si la masa es energía (E = mc2), y si la energía es electricidad y magnetismo (según Maxwell), el magnetismo del neutrón no es tan extraño, sino que es un aspecto de lo que en realidad es: materia. La materia es la luz, la energía, el magnetismo, en definitiva, la fuerza que reina en el universo y que está presente de una u otra forma en todas partes (aunque no podamos verla).Y, la explicación más sencilla es que, el Neutrón tenga carga positiva y negativa que se anulan mutuamente, y, de esa manera, adquiere su propiedad neutra.
en todas partes (aunque no podamos verla).Y, la explicación más sencilla es que, el Neutrón tenga carga positiva y negativa que se anulan mutuamente, y, de esa manera, adquiere su propiedad neutra.
Emilio Silvera Vázquez
Ene
9
Desde la materia “inerte”… ¡Hasta los pensamientos!
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física Relativista ~
Clasificado en Física Relativista ~
 Comments (1)
Comments (1)
El ojo humano, uno de los transmisores de los sentidos que nutren al cerebro de información
Lo mismo que desconocemos la auténtica naturaleza de la Luz, que según creo encierra muchos secretos que tenemos que desvelar para conocer la realidad de la Naturaleza y del Universo, de la misma manera, tenemos que llegar a desvelar los secretos que se encierra en esa esencial y sencilla sustancia que llamamos agua, ya Tales de Mileto nos hablaba de la importancia que esa sustancia tenía para la vida.
Un equipo de investigadores suecos descubre dos estados líquidos del agua con grandes diferencias en su estructura y densidad. La Ciencia nos vuelve a demostrar que no conocemos básicamente muchos de los secretos que encierra la Naturaleza, y, en el agua han hallado uno de ellos. De la misma manera existen en otros muchos lugares insospechados.
¿Cómo es posible que, a partir de la materia “inerte”, hayan podido surgir seres vivos e incluso, algunos que, como nosotros puedan pensar? Que cosa mágica se pudo producir en el corazón de las estrellas para que, materiales sencillos como el Hidrógeno se convirtieran a miles de millones de grados de calor en otros que, como el Carbono, Oxigeno y Nitrógeno…, muchos miles de millones de años más tardes, en mundos perdidos en sistemas planetarios como el nuestro, dieran lugar a la formación de Protoplasma vivo del que surgieron aquellos infinitesimales seres que llamamos bacterias y que, posibilitaron la evolución hacia
que, materiales sencillos como el Hidrógeno se convirtieran a miles de millones de grados de calor en otros que, como el Carbono, Oxigeno y Nitrógeno…, muchos miles de millones de años más tardes, en mundos perdidos en sistemas planetarios como el nuestro, dieran lugar a la formación de Protoplasma vivo del que surgieron aquellos infinitesimales seres que llamamos bacterias y que, posibilitaron la evolución hacia formas de vida superiores?
formas de vida superiores?

Los sentidos: las herramientas que utiliza el cerebro para estar comunicado con el exterior
estar comunicado con el exterior
La percepción, los sentidos y los pensamientos… Para poder entender la conciencia como proceso es preciso que entendamos cómo funciona nuestro cerebro, su arquitectura y desarrollo con sus funciones dinámicas. Lo que no está claro es que la conciencia se encuentre causalmente asociada a ciertos procesos cerebrales pero no a otros.
proceso es preciso que entendamos cómo funciona nuestro cerebro, su arquitectura y desarrollo con sus funciones dinámicas. Lo que no está claro es que la conciencia se encuentre causalmente asociada a ciertos procesos cerebrales pero no a otros.
El cerebro humano ¿es especial?, su conectividad, su dinámica, su forma de funcionamiento, su relación con el cuerpo y con el mundo exterior, no se parece a nada que la ciencia conozca. Tiene un carácter único y ofrecer una imagen fidedigna del cerebro no resulta nada fácil; es un reto tan extraordinario que no estamos preparados para cumplir en este momento. Estamos lejos de ofrecer esa imagen completa, y sólo podemos dar resultados parciales de esta enorme maravilla de la Naturaleza.
de funcionamiento, su relación con el cuerpo y con el mundo exterior, no se parece a nada que la ciencia conozca. Tiene un carácter único y ofrecer una imagen fidedigna del cerebro no resulta nada fácil; es un reto tan extraordinario que no estamos preparados para cumplir en este momento. Estamos lejos de ofrecer esa imagen completa, y sólo podemos dar resultados parciales de esta enorme maravilla de la Naturaleza.
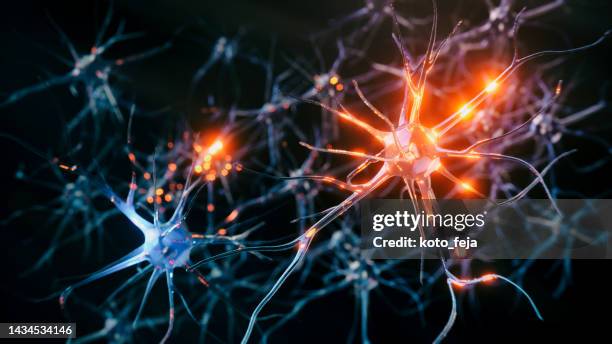
Aquí se fraguan los pensamientos como en las galaxias lo hacen las estrellas
Nuestro cerebro adulto, con poco más de 1 Kg de peso, contiene unos cien mil millones de células nerviosas o neuronas. La parte o capa ondulada más exterior o corteza cerebral, que es la parte del cerebro de evolución más reciente, contiene alrededor de treinta millones de neuronas y un billón de conexiones o sinapsis. Si contáramos una sinapsis cada segundo, tardaríamos 32 millones de años en acabar el recuento. Si consideramos el número
o capa ondulada más exterior o corteza cerebral, que es la parte del cerebro de evolución más reciente, contiene alrededor de treinta millones de neuronas y un billón de conexiones o sinapsis. Si contáramos una sinapsis cada segundo, tardaríamos 32 millones de años en acabar el recuento. Si consideramos el número posible de circuitos neuronales, tendremos que habérnoslas con cifras hiper-astronómicas. Un 10 seguido de, al menos, un millón de ceros (en comparación, el número de partículas del universo conocido asciende a “tan sólo” un 10 seguido de 79 ceros). ¡A que va a resultar que no somos tan insignificantes!
posible de circuitos neuronales, tendremos que habérnoslas con cifras hiper-astronómicas. Un 10 seguido de, al menos, un millón de ceros (en comparación, el número de partículas del universo conocido asciende a “tan sólo” un 10 seguido de 79 ceros). ¡A que va a resultar que no somos tan insignificantes!


Si pudiéramos ver la actividad cerebral, sería como una máquina incandescente
El suministro de datos que llega en forma de multitud de mensajes procede de los sentidos, que detectan el entorno interno y externo, y luego envía el resultado a los músculos para dirigir lo que hacemos y decimos. Así pues, el cerebro es como un enorme ordenador que realiza una serie de tareas basadas en la información que le llega de los sentidos. Pero, a diferencia de un ordenador, la cantidad de material que entra y sale parece poca cosa en comparación con la actividad interna. Seguimos pensando, sintiendo y procesando información incluso cuando cerramos los ojos y descansamos.
que llega en forma de multitud de mensajes procede de los sentidos, que detectan el entorno interno y externo, y luego envía el resultado a los músculos para dirigir lo que hacemos y decimos. Así pues, el cerebro es como un enorme ordenador que realiza una serie de tareas basadas en la información que le llega de los sentidos. Pero, a diferencia de un ordenador, la cantidad de material que entra y sale parece poca cosa en comparación con la actividad interna. Seguimos pensando, sintiendo y procesando información incluso cuando cerramos los ojos y descansamos.
Con tan enorme cantidad de circuitos neuronales, ¿Cómo no vamos a ser capaces de descifrar todos los secretos de nuestro universo? ¿De qué seremos capaces cuando podamos disponer de un rendimiento cerebral del 80 ó 90 por ciento? Algunas veces hemos oído comentar: “Sólo utilizamos un diez por ciento del cerebro…” En realidad, la frase no indica la realidad, se refiere al hecho de que, aunque utilizamos el cerebro en su totalidad, se estima que está al diez por ciento de su capacidad real que, será una realidad a medida que evolucione y, en el futuro, esa capacidad de hoy será un 90 por ciento mayor.
podamos disponer de un rendimiento cerebral del 80 ó 90 por ciento? Algunas veces hemos oído comentar: “Sólo utilizamos un diez por ciento del cerebro…” En realidad, la frase no indica la realidad, se refiere al hecho de que, aunque utilizamos el cerebro en su totalidad, se estima que está al diez por ciento de su capacidad real que, será una realidad a medida que evolucione y, en el futuro, esa capacidad de hoy será un 90 por ciento mayor.

Aún no conocemos bien la direccionalidad de los circuitos neuronales
la direccionalidad de los circuitos neuronales
El límite de lo que podremos conseguir tiene un horizonte muy lejano. Y, llega un momento en el cual, se puede llegar a pensar que no existen limites en lo que podemos conseguir: Desde hablar sin palabras sonoras a la auto-transportación. Si -como pienso- somos pura energía pensante, no habrá límite alguno; el cuerpo que ahora nos lleva de un lugar a otro, ya no será necesario, y como los fotones que no tienen masa, podremos desplazarnos a velocidades lumínicas.
nos lleva de un lugar a otro, ya no será necesario, y como los fotones que no tienen masa, podremos desplazarnos a velocidades lumínicas.
Creo que estoy corriendo demasiado en el tiempo, volvamos a la realidad. A veces mi mente se dispara. Lo mismo visito mundos extraordinarios con mares luminosos de neón líquido poblados por seres transparentes, que viajo a galaxias muy lejanas pobladas de estrellas de fusión fría circundadas por nubes doradas compuestas de antimateria en la que, los positrones medio congelados, se mueven lentamente formando un calidoscopio de figuras alucinantes de mil colores. ¡La mente, qué tesoro!


¿Quién podría decir, si no se les explicara, que son “mundos” diferentes”. “Nuestras nueronas son estrellas; nuestra sinapsis es una galaxia; nuestro cerebro es el universo” A diferentes escalas, tal vez a diferentes niveles …
La unidad a partir de la cual se configuran todas las fabulosas actividades del cerebro es una célula del mismo, la neurona. Las neuronas son unas células fantásticamente ramificadas y extendidas, pero diminutas que, sin embargo y en sentido figurado, podríamos decir que son tan grandes como el universo mismo.
el universo mismo.
Cuando seamos capaces de convertir en realidad todo aquello en lo que podamos pensar, entonces, habremos alcanzado la meta. Para que eso pueda llegar a ocurrir, aún falta mucho tiempo. Sin embargo, si el Universo no lo impide y nuestro transcurrir continúa, todo lo que podamos imaginar… podrá ser posible. Incluso imposibilidades físicas de hoy, dejarán de existir mañana y, ¡la Mente! posiblemente (al igual que hoy ordena a las distintas partes del cuerpo que realice esta o aquella función), se encargará de que todo funcione bien, erradicará cualquier enfermedad que nos pueda atacar y, tendrá el conjunto del “sistema” en perfectas condiciones de salud, lo cual me lleva a pensar que, para cuando eso llegue, los médicos serán un recuerdo del pasado.
de salud, lo cual me lleva a pensar que, para cuando eso llegue, los médicos serán un recuerdo del pasado.
En una increíble maraña de nervios y conexiones sin fin…. ¡surgen los pensamientos!
Es curioso y sorprendente la evolución alcanzada por la Mente Humana. El mundo físico se representa gobernado de acuerdo a leyes matemáticas. Desde este punto de vista, todo lo que hay en el universo físico está realmente gobernado en todos sus detalles por principios matemáticos, quizá por ecuaciones tales que aún no hemos podido llegar a comprender y, ni que sabemos que puedan existir.
este punto de vista, todo lo que hay en el universo físico está realmente gobernado en todos sus detalles por principios matemáticos, quizá por ecuaciones tales que aún no hemos podido llegar a comprender y, ni que sabemos que puedan existir.
Lo más seguro es que la descripción real del mundo físico esté pendiente de matemáticas futuras, aún por descubrir , fundamentalmente distintas de las que ahora tenemos. Llegarán nuevos Gauss, Riemann, Euler, o, Ramanujans… que, con sus nuevas ideas transformarán el pensamiento matemático para hacer posible que podamos, al fin, comprender lo que realmente somos.
, fundamentalmente distintas de las que ahora tenemos. Llegarán nuevos Gauss, Riemann, Euler, o, Ramanujans… que, con sus nuevas ideas transformarán el pensamiento matemático para hacer posible que podamos, al fin, comprender lo que realmente somos.

Son nuestras Mentes, productos de la evolución del Universo que, a partir de la materia inerte, ha podido alcanzar el estadio bio-químico de la consciencia y, al ser conscientes, hemos podido descubrir que existen “números misteriosos” dentro de los cuales subyacen mensajes que tenemos que desvelar.
que existen “números misteriosos” dentro de los cuales subyacen mensajes que tenemos que desvelar.
Antes tendremos que haber descifrado las funciones modulares de los cuadernos perdidos de Ramanujan, o por ejemplo, el verdadero significado del número 137, ése número puro adimensional que encierra los misterios del electrón (e) – electromagnetismo -, de la constante de Planck (h) – el cuando
137, ése número puro adimensional que encierra los misterios del electrón (e) – electromagnetismo -, de la constante de Planck (h) – el cuando de acción –y de la luz (c), la relatividad -.
de acción –y de la luz (c), la relatividad -.
El complejo sistema nervioso
Los resultados son lentos, no se avanza con la rapidez que todos deseamos. Sin embargo, eso ocurre por algo, el ritmo del Universo considerado como Naturaleza, podríamos decir que está determinado por una Naturaleza “sabia” y, si actúa de esa manera… ¡Por algo será! Deja que de vez en cuando, sobresalgan algunas mentes y se eleven por encima del común, de ejemplos tenemos la historia llena. Esos “saltos” de la conciencia son los tiempos que marca el Universo para que, poco a poco, se produzca nuestra evolución, es la única forma de que todo se haga de manera correcta y de que, los nuevos pensamientos se vayan asentando debidamente en las Mentes futuras. Pongamos un ejemplo:
de que todo se haga de manera correcta y de que, los nuevos pensamientos se vayan asentando debidamente en las Mentes futuras. Pongamos un ejemplo:
Conjetura de Poincaré:
“En matemáticas, y más precisamente en topología, la conjetura de Poincaré (también llamada hipótesis de Poincaré) es un resultado sobre la esfera tridimensional (la 3-esfera); la hipótesis dejó de ser una conjetura para convertirse en un teorema tras su comprobación en 2003 por el matemático Grigori Perelman. El teorema sostiene que la esfera tridimensional, también llamada 3-esfera o hiperesfera, es la única variedad compacta tridimensional en la que todo lazo o círculo cerrado (1-esfera) se puede deformar (transformar) en un punto. Este último enunciado es equivalente a decir que sólo hay una variedad cerrada y simplemente conexa de dimensión 3: la esfera tridimensional.”
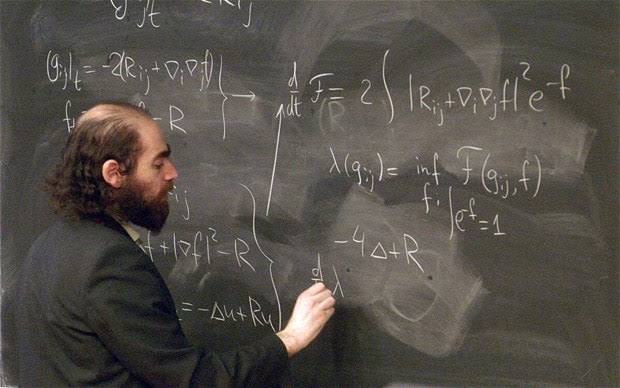
“En matemáticas, y con más exactitud en topología, el teorema de Poincaré (anteriormente llamado conjetura de Poincaré o hipótesis de Poincaré) es un … Grigori Perelmán.”
Poincaré expuso su conjetura y, más de un siglo después, Perelmán la resolvió. Riemann expuso su geometría del espacio curvo, y hasta 60 años más tarde no fue descubierta por Einstein para hacer posible su formulación de la relatividad general, donde describe cómo las grandes masas distorsionan el espacio y el tiempo por medio de la fuerza de gravedad que generan. El conocimiento humano avanza al ritmo que le impone la Naturaleza.
posible su formulación de la relatividad general, donde describe cómo las grandes masas distorsionan el espacio y el tiempo por medio de la fuerza de gravedad que generan. El conocimiento humano avanza al ritmo que le impone la Naturaleza.
![[dark-matter-625x450.jpg]](http://3.bp.blogspot.com/_gLo7v9af5Sg/SWXgCyeo8cI/AAAAAAAABTE/p3tYMUr7GAc/s1600/dark-matter-625x450.jpg)
¡Son tantos los secretos que nos quedan por desvelar! la Naturaleza es la portadora de todas las respuestas…Observémosla con atención y, aprendamos de ella y, de ser posible, procuremos no molestarla, “Ella” nos permite estar aquí para que evolucionemos y, algún día, cuando seamos mayores…quizás nos deje formar parte de algo más…¿mental?
de algo más…¿mental?
No, no será nada fácil imitar a la Naturaleza…¡Esa perfección! Sin embargo, llegados a ese punto, debemos pensar que nosotros también formamos parte de ella, la parte que piensa y, si es así, ¿qué cometido tendremos asignado en este Universo? Esa es la pregunta que ninguno de los grandes pensadores de la Historia, han podido contestar.
Pensar, por ejemplo, en las complejas matemáticas topológicas requeridas por la teoría de supercuerdas puede producir incomodidad en muchas personas que, aún siendo físicos, no están tan capacitados como para entender tan profundas ideas (me incluyo).
producir incomodidad en muchas personas que, aún siendo físicos, no están tan capacitados como para entender tan profundas ideas (me incluyo).
Bernhard Riemann introdujo muchas nuevas ideas y fue uno de los más grandes matemáticos. En su corta vida (1.826 – 1.866) propuso innumerables propuestas matemáticas que cambiaron profundamente el curso del pensamiento de los números en el planeta Tierra, como el que subyace en la teoría relativista en su versión general de la gravedad, entre otras muchas (superficie de Riemann, etc.). Riemann les enseñó a todos a considerar las cosas de un modo diferente.
otras muchas (superficie de Riemann, etc.). Riemann les enseñó a todos a considerar las cosas de un modo diferente.
La superficie de Riemann asociada a la función holomorfa “tiene su propia opinión” y decide por sí misma cuál debería ser el, o mejor, su dominio, con independencia de la región del plano complejo que nosotros podamos haberle asignado inicialmente.
su propia opinión” y decide por sí misma cuál debería ser el, o mejor, su dominio, con independencia de la región del plano complejo que nosotros podamos haberle asignado inicialmente.
Podríamos encontrar otros muchos tipos de superficies de Riemann.

Superficie de Riemann que aparece al extender el dominio de la función 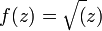
Este bello concepto desempeña un papel importante en algunos de los intentos modernos de encontrar una nueva base para la física matemática (muy especialmente en la teoría de cuerdas), y al final, seguramente se descubrirá el mensaje que encierra.
bello concepto desempeña un papel importante en algunos de los intentos modernos de encontrar una nueva base para la física matemática (muy especialmente en la teoría de cuerdas), y al final, seguramente se descubrirá el mensaje que encierra.
El caso de las superficies de Riemann es fascinante, aunque desgraciadamente sólo es para iniciados. Proporcionaron los primeros ejemplos de la noción general de variedad, que es un espacio que puede pensarse “curvado” de diversas maneras, pero que localmente (por ejemplo, en un entorno pequeño de cualquiera de sus puntos), parece un fragmento de espacio euclídeo ordinario.
pensarse “curvado” de diversas maneras, pero que localmente (por ejemplo, en un entorno pequeño de cualquiera de sus puntos), parece un fragmento de espacio euclídeo ordinario.
En matemática, la esfera de Riemann (o plano complejo extendido), llamado en honor al matemático del siglo XIX del mismo nombre , es una esfera obtenida del plano complejo mediante la adición de un punto del infinito. La esfera es la representación geométrica de los números complejos extendidos
, es una esfera obtenida del plano complejo mediante la adición de un punto del infinito. La esfera es la representación geométrica de los números complejos extendidos  , (véase fig.1 y fig.2), la cual consiste en los números complejos ordinarios en conjunción con el símbolo
, (véase fig.1 y fig.2), la cual consiste en los números complejos ordinarios en conjunción con el símbolo  para
para representar el infinito.
representar el infinito.
La esfera de Riemann, superficie de Riemann compacta, el teorema de la aplicación de Riemann, las superficies de Riemann y aplicaciones complejas… He tratado de exponer en unas líneas la enorme importancia de este personaje para las matemáticas en general y la geometría y para la física en particular. Es uno de esos casos a los que antes me refería. Después de él, la Humanidad ha tenido un parón en el desarrollo de las ideas hasta que asimilaron las suyas y, después, llegó Einstein y otros.
personaje para las matemáticas en general y la geometría y para la física en particular. Es uno de esos casos a los que antes me refería. Después de él, la Humanidad ha tenido un parón en el desarrollo de las ideas hasta que asimilaron las suyas y, después, llegó Einstein y otros.

La Geometría de Riemann de los espacios curvos
Tenemos que convenir que todo, sin excepción, es relativo y resulta ya evidente la gran crisis de la noción de realidad “veritas” que el mundo padece, la ciencia BASE, la matemática, sufrió el varapalo a partir de la matemática topológica de Poincaré, y el desarrollo sorpresivo de la matemática del caos; de pronto el idealismo de la ecuación diferencial queda derribado : el mundo que funciona como un reloj de Tolomeo queda finiquitado; ¿Donde puñetas está la materia perdida?; de pronto nuestras consciencias “comprenden” que la “verdad” no existe, es decir, que no existe nuestra realidad del mundo.
un reloj de Tolomeo queda finiquitado; ¿Donde puñetas está la materia perdida?; de pronto nuestras consciencias “comprenden” que la “verdad” no existe, es decir, que no existe nuestra realidad del mundo.
Y, mientras tanto, nuestras mentes siguen su camino, siempre queriendo ir más allá y siempre profundizando en los secretos de la Naturaleza de lo que tenemos muchos ejemplos, tales como nuestras consideraciones sobre los dos aspectos de la relatividad general de Einstein, a saber, el principio de la relatividad, que nos dice que las leyes de la física son ciegas a la distinción entre reposo y movimiento uniforme; y el principio de equivalencia, que nos dice de qué forma sutil deben modificarse estas ideas para englobar el campo gravitatorio.
sutil deben modificarse estas ideas para englobar el campo gravitatorio.

Mediante la combinación de diversas observaciones de telescopios, y la ayuda del trabajo de modelación avanzada, el equipo de Emanuele Farina, de la Universidad de Insubria en la provincia de Como, Italia, y Michele Fumagalli del Instituto Carnegie de Ciencia, en Washington, D.C., Estados Unidos, fue capaz de captar como tal el trío de quásares, llamado QQQ J1519+0627. La luz de esos quásares ha viajado 9.000 millones de años-luz para
llegar hasta nosotros, lo que significa que dicha luz fue emitida cuando el universo tenía sólo un tercio de su edad actual.

Todo es finito, es decir, que tiene
un fin, y la velocidad de la luz no podía ser una excepción. No existe el infinito ni la eternidad. Tampoco existe la Nada, siempre hay.
Ahora hay que hablar del tercer ingrediente fundamental de la teoría de Einstein, que está relacionada con la finitud de la velocidad de la luz. Es un hecho notable que estos tres ingredientes básicos puedan remontarse a Galileo; en efecto, parece que fue también Galileo el primero que tuvo una expectativa clara de que la luz debería viajar con velocidad finita, hasta el punto de que intentó medir dicha velocidad. El método que propuso (1.638), que implica la sincronización de destellos de linternas entre colinas distantes, era, como sabemos hoy, demasiado tosco (otro ejemplo de la evolución que, con el tiempo, se produce en nuestras mentes). Él no tenía forma
hay que hablar del tercer ingrediente fundamental de la teoría de Einstein, que está relacionada con la finitud de la velocidad de la luz. Es un hecho notable que estos tres ingredientes básicos puedan remontarse a Galileo; en efecto, parece que fue también Galileo el primero que tuvo una expectativa clara de que la luz debería viajar con velocidad finita, hasta el punto de que intentó medir dicha velocidad. El método que propuso (1.638), que implica la sincronización de destellos de linternas entre colinas distantes, era, como sabemos hoy, demasiado tosco (otro ejemplo de la evolución que, con el tiempo, se produce en nuestras mentes). Él no tenía forma alguna de anticipar la extraordinaria velocidad de la luz.
alguna de anticipar la extraordinaria velocidad de la luz.
Parece que tanto Galileo como Newton tenían poderosas sospechas respecto a un profundo papel que conecta la naturaleza de la luz con las fuerzas que mantienen la materia unida y, si consideramos que esa fuerza que hace posible la unión de la materia reside en el corazón de los átomos (en sus núcleos), podemos hacernos una clara idea de lo ilimitado que puede
Newton tenían poderosas sospechas respecto a un profundo papel que conecta la naturaleza de la luz con las fuerzas que mantienen la materia unida y, si consideramos que esa fuerza que hace posible la unión de la materia reside en el corazón de los átomos (en sus núcleos), podemos hacernos una clara idea de lo ilimitado que puede ser el pensamiento humano que, ya en aquellos tiempos -en realidad mucho anters- pudo llegar a intuir las fuerzas que están presentes en nuestro Universo.
ser el pensamiento humano que, ya en aquellos tiempos -en realidad mucho anters- pudo llegar a intuir las fuerzas que están presentes en nuestro Universo.
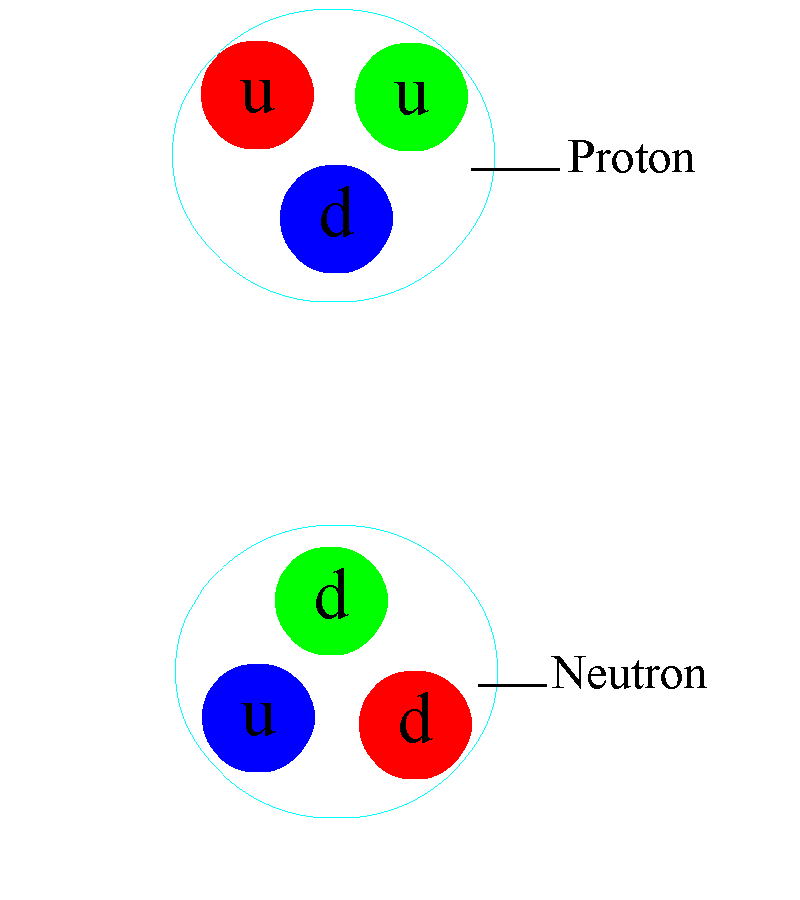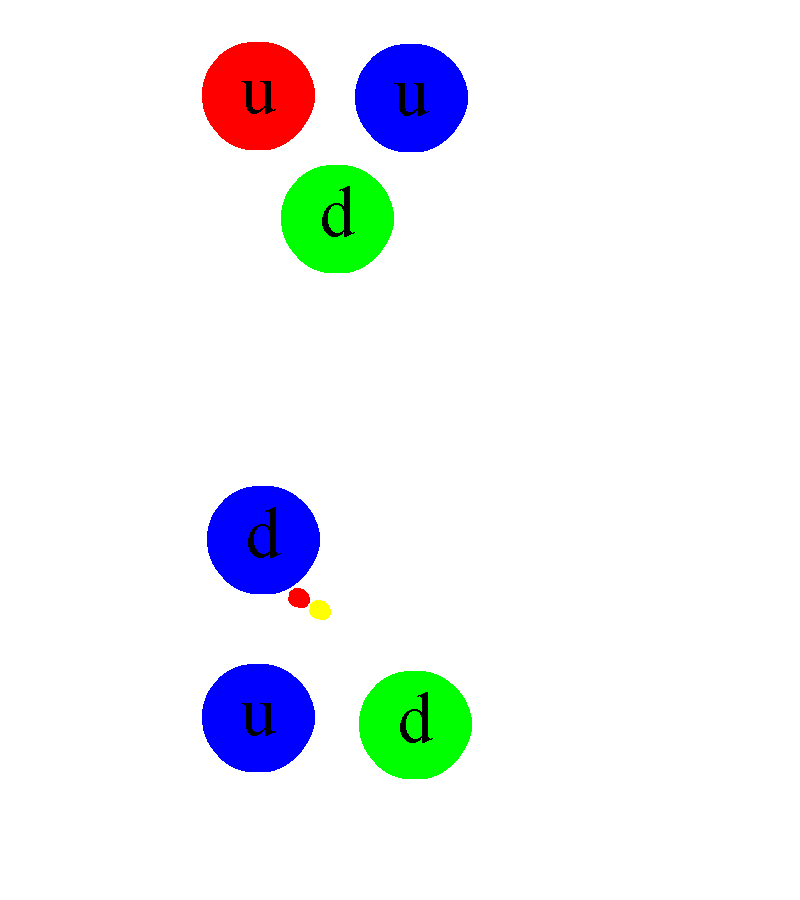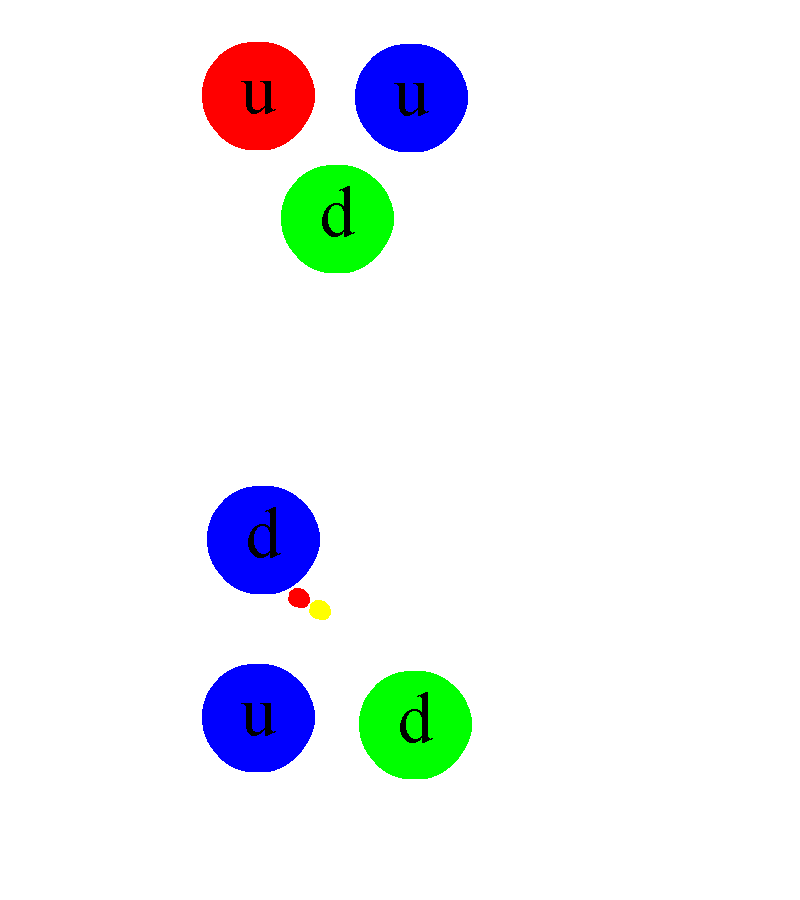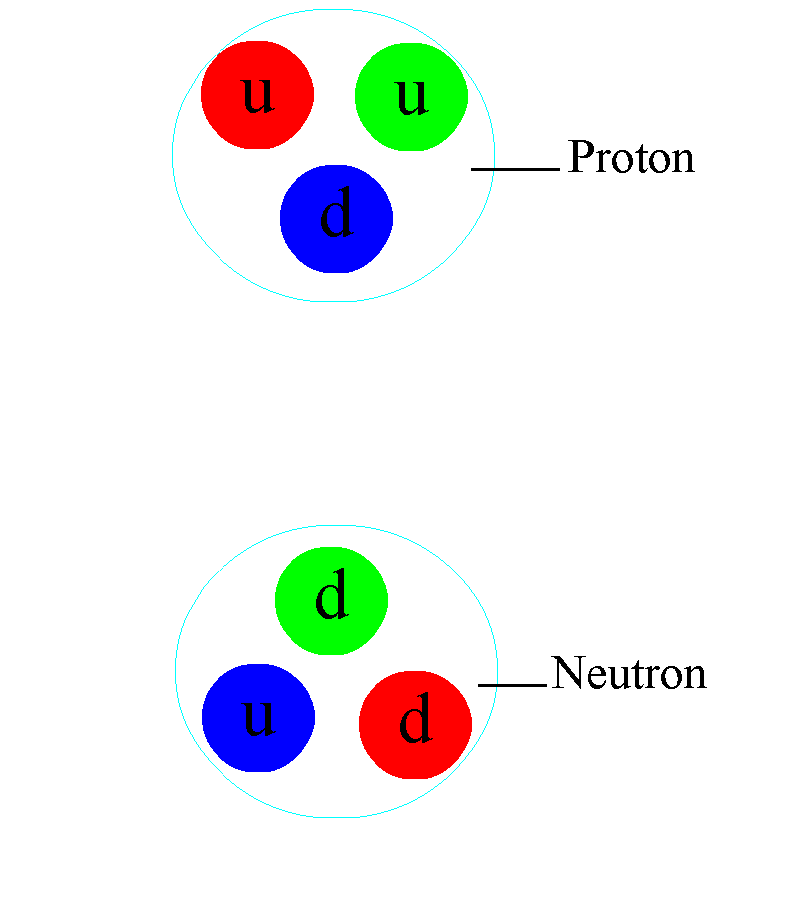
En los núcleos atómicos reside la fuerza (nuclear fuerte) que hace posible la existencia de la materia que comienza por los átomos que, al juntarse y formar células, hace posible que éstas se junten y formen moléculas que a su vez, se reúnen para formar sustancias y cuerpos.
formar sustancias y cuerpos.
Pero la comprensión adecuada de estas ideas tuvo que esperar hasta el siglo XX, cuando se reveló la verdadera naturaleza de las fuerzas químicas y de las fuerzas que mantienen unidos los átomos individuales. Ahora sabemos que tales fuerzas tienen un origen fundamentalmente electromagnético (que vincula y concierne a la implicación del campo electromagnético con partículas cargadas) y que la teoría del electromagnetismo es también la teoría de la luz.
Para entender los átomos y la química se necesitan otros ingredientes procedentes de la teoría cuántica, pero las ecuaciones básicas que describen el electromagnetismo y la luz fueron propuestas en 1.865 por el físico escocés James Clark Maxwell, que había sido inspirado por los magníficos descubrimientos experimentales de Michael Faraday unos treinta años antes y que él plasmó en una maravillosa teoría.
entender los átomos y la química se necesitan otros ingredientes procedentes de la teoría cuántica, pero las ecuaciones básicas que describen el electromagnetismo y la luz fueron propuestas en 1.865 por el físico escocés James Clark Maxwell, que había sido inspirado por los magníficos descubrimientos experimentales de Michael Faraday unos treinta años antes y que él plasmó en una maravillosa teoría.

El electromagnetismo es una rama de la Física que estudia y unifica los fenómenos eléctricos y magnéticos en una sola teoría. El electromagnetismo es una teoría de campos; es decir, las explicaciones y predicciones que provee se basan en magnitudes físicas vectoriales dependientes de la posición en el espacio y del tiempo.
Esta teoría del electromagnetismo de Maxwell tenía la particularidad de que requería que la velocidad de la luz tuviera un valor fijo y definido, que normalmente se conoce como c, y que en unidades ordinarias es aproximadamente 3 × 108 metros por segundo. Maxwell, guiado por los experimentos de Faraday, hizo posible un hecho que cambió la historia de la humanidad para siempre. Un hecho de la misma importancia que el descubrimiento del fuego, la rueda o los metales. El matemático y poeta escocés unificó los campos eléctrico y magnético a través de unas pocas ecuaciones que describen como
teoría del electromagnetismo de Maxwell tenía la particularidad de que requería que la velocidad de la luz tuviera un valor fijo y definido, que normalmente se conoce como c, y que en unidades ordinarias es aproximadamente 3 × 108 metros por segundo. Maxwell, guiado por los experimentos de Faraday, hizo posible un hecho que cambió la historia de la humanidad para siempre. Un hecho de la misma importancia que el descubrimiento del fuego, la rueda o los metales. El matemático y poeta escocés unificó los campos eléctrico y magnético a través de unas pocas ecuaciones que describen como estos campos se entretejen y actúan sobre la materia.
estos campos se entretejen y actúan sobre la materia.


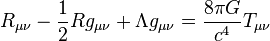
Claro que, estos importantísimos avances han sido simples escalones de la “infinita” escalera que tenemos que subir y, la misma relatividad General de Einstein no ha sido (después de un siglo) aún comprendida en su plenitud y muchos de sus mensajes están escondidos en sus ecuaciones de campo (arriba) en lo más profundo de nuestras mentes que, ha sabido parcialmente descubrir parte del mensaje de Einstein pero
parte del mensaje de Einstein pero , seguimos buscando, ahora hemos dado con las Ondas gravitacionales pero… ¿Qué más puede haber ahí? ¿Cómo se puede decir tanto con unos pocos signos?
, seguimos buscando, ahora hemos dado con las Ondas gravitacionales pero… ¿Qué más puede haber ahí? ¿Cómo se puede decir tanto con unos pocos signos?
Sin embargo, esto nos presenta un enigma si queremos conservar el principio de relatividad. El sentido común nos diría que si se mide que la velocidad de la luz toma el valor concreto c en el sistema de referencia del observador, entonces un segundo observador que se mueva a una velocidad muy alta con respecto al primero medirá que la luz viaja a una velocidad diferente, aumentada o disminuida, según sea el movimiento del segundo observador.

Estaría bueno que, al final se descubriera que alfa (α) tuviera un papel importante en la compleja teoría de cuerdas, ¿Por qué no? En realidad alfa, la constante de estructura fina, nos habla del magnetismo, de la constante de Planck y de la relatividad especial, es decir, la velocidad de la luz y, todo eso, según parece, emergen en las ecuaciones topológicas de la moderna teoría de cuerdas. ¡Ya veremos!
Pero el principio de relatividad exigiría que las leyes físicas del segundo observador (que definen en particular la velocidad de la luz que percibe el segundo observador) deberían ser idénticas a las del primer observador. Esta aparente contradicción entre la constancia de la velocidad de la luz y el principio de relatividad condujo a Einstein (como
la constancia de la velocidad de la luz y el principio de relatividad condujo a Einstein (como de hecho, había llevado previamente al físico holandés Hendrick Antón Lorentz y muy en especial al matemático francés Henri Poincaré) a un punto de vista notable por el que el principio de relatividad del movimiento puede
de hecho, había llevado previamente al físico holandés Hendrick Antón Lorentz y muy en especial al matemático francés Henri Poincaré) a un punto de vista notable por el que el principio de relatividad del movimiento puede hacerse compatible con la constancia de una velocidad finita de la luz.
hacerse compatible con la constancia de una velocidad finita de la luz.

¿Cómo funciona esto? Sería normal que cualquier persona creyera en la existencia de un conflicto irresoluble entre los requisitos de una teoría como la de Maxwell, en la que existe una velocidad absoluta de la luz, y un principio de relatividad según el cual las leyes físicas parecen las mismas con independencia de la velocidad del sistema de referencia utilizado para su descripción.
su descripción.
¿No podría hacerse que el sistema de referencia se moviera con una velocidad que se acercara o incluso superara a la de la luz? Y según este sistema, ¿no es cierto que la velocidad aparente de la luz no podría seguir siendo la misma que era antes? Esta indudable paradoja no aparece en una teoría, tal como la originalmente preferida por Newton (y parece que también
indudable paradoja no aparece en una teoría, tal como la originalmente preferida por Newton (y parece que también por Galileo), en la que la luz se comporta como partículas cuya velocidad depende de la velocidad de la fuente. En consecuencia, Galileo y Newton podían seguir viviendo cómodamente con un principio de relatividad.
por Galileo), en la que la luz se comporta como partículas cuya velocidad depende de la velocidad de la fuente. En consecuencia, Galileo y Newton podían seguir viviendo cómodamente con un principio de relatividad.

La velocidad de la luz en el vacío es una constante de la Naturaleza y, cuando cientos de miles de millones de millones salen disparados de esta galaxia hacia el vacío espacial, su velocidad de 299.792.450 metros por segundo, es constante independientemente de la fuente que pueda emitir los fotones y de si ésta está en reposo o en movimiento.
el vacío espacial, su velocidad de 299.792.450 metros por segundo, es constante independientemente de la fuente que pueda emitir los fotones y de si ésta está en reposo o en movimiento.
Así que, la antigua imagen de la naturaleza de la luz entró en conflicto a lo largo de los años , como era el caso de observaciones de estrellas dobles lejanas que mostraban que la velocidad de la luz era independiente de la de su fuente. Por el contrario, la teoría de Maxwell había ganado fuerza, no sólo por el poderoso apoyo que obtuvo de la observación (muy especialmente en los experimentos de Heinrich Hertz en 1.888), sino también por la naturaleza convincente y unificadora de la propia teoría, por la que las leyes que gobiernan los campos eléctricos, los campos magnéticos y la luz están todos subsumidos en un esquema matemático de notable elegancia y simplicidad.
, como era el caso de observaciones de estrellas dobles lejanas que mostraban que la velocidad de la luz era independiente de la de su fuente. Por el contrario, la teoría de Maxwell había ganado fuerza, no sólo por el poderoso apoyo que obtuvo de la observación (muy especialmente en los experimentos de Heinrich Hertz en 1.888), sino también por la naturaleza convincente y unificadora de la propia teoría, por la que las leyes que gobiernan los campos eléctricos, los campos magnéticos y la luz están todos subsumidos en un esquema matemático de notable elegancia y simplicidad.

Las ondas luminosas como las sonoras, actúan de una u otra manera dependiendo del medio en el que se propagan.
las sonoras, actúan de una u otra manera dependiendo del medio en el que se propagan.
En la teoría de Maxwell, la luz toma forma de ondas, no de partículas, y debemos enfrentarnos al hecho de que en esta teoría hay realmente una velocidad fija a la que deben viajar las ondas luminosas.
de ondas, no de partículas, y debemos enfrentarnos al hecho de que en esta teoría hay realmente una velocidad fija a la que deben viajar las ondas luminosas.
El punto de vista geométrico-espaciotemporal nos proporciona una ruta particularmente clara hacia la solución de la paradoja que presenta el conflicto entre la teoría de Maxwell y el principio de relatividad.
la teoría de Maxwell y el principio de relatividad.
Este punto de vista espaciotemporal no fue el que Einstein adoptó originalmente (ni fue el punto de vista de Lorentz, ni siquiera, al parecer, de Poincaré), pero, mirando en retrospectiva, podemos ver la potencia de este enfoque. Por el momento
punto de vista espaciotemporal no fue el que Einstein adoptó originalmente (ni fue el punto de vista de Lorentz, ni siquiera, al parecer, de Poincaré), pero, mirando en retrospectiva, podemos ver la potencia de este enfoque. Por el momento , ignoremos la gravedad y las sutilezas y complicaciones asociadas que proporciona el principio de equivalencia y otras complejas cuestiones, que estimo aburrirían al lector no especialista, hablando de que en el espacio-tiempo se pueden concebir grupos de todos los diferentes rayos de luz que pasan a ser familias de íneas de universo.
, ignoremos la gravedad y las sutilezas y complicaciones asociadas que proporciona el principio de equivalencia y otras complejas cuestiones, que estimo aburrirían al lector no especialista, hablando de que en el espacio-tiempo se pueden concebir grupos de todos los diferentes rayos de luz que pasan a ser familias de íneas de universo.
Baste saber que, como quedó demostrado por Einstein, la luz, independientemente de su fuente y de la velocidad con que ésta se pueda mover, tendrá siempre la misma velocidad en el vacío, c, o 299.792.458 metros por segundo. Cuando la luz atraviesa un medio material, su velocidad se reduce. Precisamente, es la velocidad c el límite alcanzable de la velocidad más alta del universo. Es una constante universal y, como hemos dicho, es independiente de la velocidad del observador y de la fuente emisora.
y, como hemos dicho, es independiente de la velocidad del observador y de la fuente emisora.

El Universo está dentro de nuestras Mentes
¡La Mente! Qué caminos puede recorrer y, sobre todo ¿Quién la guía? Comencé este trabajo con la imagen del ojo humano y hablando de los sentidos y de la consciencia y mira donde he finalizado…Sí, nos falta mucho camino por recorrer para llegar a desvelar los misterios de la Mente que, en realidad, es la muestra más alta que el Universo nos puede mostrar de lo que puede surgir a partir de la sencillez de los átomos de hidrógeno que, evolucionados, primero en las entrañas de las estrellas y después en los circuitos de nuestras mentes, llega hasta los pensamientos y la imaginación que…son palabras mayores de cuyo alcance, aún no tenemos una idea que realmente refleje su realidad.
con la imagen del ojo humano y hablando de los sentidos y de la consciencia y mira donde he finalizado…Sí, nos falta mucho camino por recorrer para llegar a desvelar los misterios de la Mente que, en realidad, es la muestra más alta que el Universo nos puede mostrar de lo que puede surgir a partir de la sencillez de los átomos de hidrógeno que, evolucionados, primero en las entrañas de las estrellas y después en los circuitos de nuestras mentes, llega hasta los pensamientos y la imaginación que…son palabras mayores de cuyo alcance, aún no tenemos una idea que realmente refleje su realidad.
Pero, ¿existe alguna realidad?, o, por el contrario todo es siempre cambiante y lo que hoy es mañana no existirá, si “realmente” es así, ocurre igual que con el tiempo. La evolución es algo que camina siempre hacia adelante, es inexorable, nunca se para y, aunque como el tiempo pueda ralentizarse, finalmente sigue su camino hacia esos lugares que ahora , sólo podemos imaginar y que, seguramente, nuestros pensamientos no puedan (por falta de conocimientos) plasmar en lo que será esa realidad futura.
, sólo podemos imaginar y que, seguramente, nuestros pensamientos no puedan (por falta de conocimientos) plasmar en lo que será esa realidad futura.
Emilio Silvera Vázquez
Dic
22
Nuevas ideas, ideas viejas
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Física ~
Clasificado en Física ~
 Comments (0)
Comments (0)
¿Empezó todo con una singularidad? ¿Salió el Universo del interior de un A.N.?

El Tiempo, el Universo, el Inicio de todo.
Se han llevado a cabo muchos modelos y las distintas teorías que circulan por ahí nos hablan de muchas cuestiones. Sin embargo, la relatividad general predice que tiene que haber una singularidad en el pasado, y cerca de esa singularidad la curvatura (del espacio) debe de ser muy alta; la relatividad clásica se anula, y habrá que tomar en cuenta los efectos cuánticos. A fin de comprender las condiciones iniciales del universo, debemos dirigirnos a la mecánica cuántica, y el estado cuántico del universo determinará las condiciones del universo clásico.

– Una de las principales finalidades de la Geoquímica es establecer las leyes que rigen el comportamiento, distribución, proporciones relativas y relaciones entre los distintos elementos químicos.
– Los datos de abundancias de elementos e isótopos en los distintos tipos de estrellas nos van a servir para establecer hipótesis del origen de los elementos.
– Los datos de composición del Sol y las estrellas nos permiten establecer hipótesis sobre el origen y evolución de las estrellas. Cualquier hipótesis que explique el origen del Sistema Solar debe explicar también el origen de la Tierra, como planeta de dicho Sistema Solar.

Cuando Einstein irrumpió en la Física, nadie le conocía y sólo era un oscuro empleado de la Oficina de Patentes de Berna en Suiza. Él, sin embargo, no había dejado de estar al día y seguí todo aquello que se pudiera mover en relñación a su pasión: La Física. Los escritos de Mach, de Lorentz, de Maxwell, de Planck… Todo ello le llevó a elaborar su famosa teoría relativista que convulsionó el mundo de la ciencia y, si me apuras mucho, hasta el ámbito filosófico cambió a partir de la relatividad. Una teoría que venía a decir cosas increibles como que la masa era energía congelada, que la luz marcaba el límite de la velocidad del universo, o, que el tiempo se ralentizaba si se marcha a velocidades cercanas a c. Esos extraños postulados no fueron, en un principio, bien entendidos por la física del momento.

Manuscrito de Einstein con la fórmula de la Teoría de la Relatividad. Cuando esto se dio a conocer al mundo, muchos miraron escépticos la fórmula y las implicaciones que de ella se podrían derivar, aquello podría cambiar lo firmemente establecido: ¡sacrilegio! ¿qué será de la Física si hacemos caso a lo que diga cualquiera?
Siempre ha sido así, el Status Institucional establecido, bien acomodado en los sillones de las academias y corporaciones, hacen la señal de la cruz, como para espantar al diablo, cada vez que aparecen nuevas ideas que, en realidad, les aterra, toda vez que les puede remover de sus asientos y prebendas, ya que, generalmente, dejan al descubierto que todo lo que predomina, está asentado en una falsa base de criterios y teorías que no siempre, son las correctas ni pueden ser demostradas y, mientras tanto eso ocurre, ellos, ¡a vivir que son dos días!

En el trabajo “No siempre la física se puede explicar con palabras”, el amigo Tom Vood nos deja el siguiente comentario que, siendo de interés aquí os lo inserto para que todos, podáis pensar en lo que aquí expone: Creo que sus ideas deben ser divulgadas.
!”Te dejo una entre muchas “revelaciones” reciente, calentitas solo para ti; que no quisiera que se divulgaran. Pero le dejo a su responsabilidad, si borrarlas, si usted cree que debo seguir como guerrillero de la ciencia o debe ser conocidas estas ideas por toda la comunidad científica. Disculpa, pero no logro discernir eso. Pero como admiras tanto a Einstein y yo soy tan tonto, te la insinúo por arribita: (Según el modelo de la interacción Luz-Luz).
¿Sabes por que las energíasmasas (partículas, o electromagnéticos confinados) no pueden superar la velocidad de la luz?
Bueno Einstein se moriría por explicárselo; a pesar de que para los modernos físicos esas preguntas ilegales no se le hacen a la física; recuerda el famoso: ¡no preguntes y calcula! Como diciendo, no eres físico, sino físico-matemático. O lo que no se, o no me puedo explicar, no lo puedes preguntar, es de mal gusto hacerlo, o de ignorantes. ¡Que daño Dios!
Bueno, pues una partícula según mi modelo es energíacampo confinada o electromagnético confinado en forma de energíamasa y por lo tanto cuando alcanza la velocidad de la luz, ocurre la ruptura de simetría que lo regresa a ser de nuevo energíacampo.
Más riguroso: Si una energíamasa alcanza la velocidad de la luz, se convierte en energíacampo.
De aquí se extraen miles de corolarios:
-Las energíasmasas (partículas) si alcanzan la velocidad de la luz, solo que una vez que la alcanzan, se rompe su topología de confinación, de energíasmasas y se liberan de nuevo como energíascampos. Algo que nunca dejaron de ser. Es que eso nunca las cinco física anteriores lo prohibían; por algo era. Mi modelo no mutila, incorpora,… Son los físicos, los que al no tener un buen modelo, medio que lo veían implícito así en la teoría; que eso no podía suceder. Pero si sucede, solo que nunca pueden sostenerse así.

Tom parece tener en sus manos las respuestas pero… se les escapa entre los dedos
-Nunca una energíamasa (partícula con masa) podrá superar la velocidad de la luz. La conclusión Eisteniana que nadie se ha podido explicar. Vez que fácil es todo, una vez que se va ha la física.
-La velocidad de la luz no es una barrera, la barrera es la ley que confina la energíacampo, en forma de energíamasa. Esa topología, geometría; o relaciona geometrías/energía.
-Toda aniquilación, desintegración y explosión tipo Big Bang (odio, o no creo lo del Big Bang) de los cuerpos del macrocosmo, es por la misma causa.
-De esto se extrae (del modelo también) la ley universal permitibilidad máxima de energía por unidad de espaciotiempo… El VICEVERSA; porque si no todo fuera energíascampos y la naturaleza no ocurre así: Toda energíacampo (luz,…) se confina como energíamasa, cuando su velocidad se hace cero.
-O lo que es lo mismo, ninguna partícula sin masa puede llegar a alcanzar el estado de reposo. Otra cosa que ningún modelo ha explicado, aunque es evidente que es un principio natural. Como todo lo que les explico. ¡Total, si eso es ilegal para el establishment!
De aquí se infieren muchas preguntas, conclusiones, paradojas, o explicaciones más racionales, a muchas cosas que decimos explicadas o que no hemos explicado todavía.

También nosotros estamos inmersos en un campo de energía-masa
La energíascampos (ustedes siempre piensen en la luz como yo al principio, para que no se pierdan) nunca puede estar en reposo (que la energía no puede estar en reposo es conocido, por eso es energía), pero como si existen circunstancias físicas muy especiales, donde esta puede ir disminuyendo su velocidad hasta que sea cero; la naturaleza resuelve esta paradoja, confinando las energíascampos, en diferentes topologías que donde se conserva como energíascampos (mas fácil verlo si piensan en luz); pero exteriormente se manifiesta como un ente, que puede estar en reposo o moverse como un todo; como lo que llamamos partículas con masa ( para mi energíasmasas).
Otra idea que puede ayudarlos a digerir esto: la energíacampo oscila, están acotadas entre la velocidad cero y la velocidad “c”. Esa oscilación, tipo superficie de agua hirviente, es lo que ocurre en la superficie de un agujero negro. Otra revelación de la riqueza física que despliega el modelo.

Te explico mejor: Cuando una energíacampo (luz) cae en un campo tan intenso como el de un agujero negro, su velocidad comienza a disminuir, llegado al “horizonte” (concepto que hay que ampliar) donde su velocidad seria cero; según mi modelo se confina como una energíamasa y trataría de moverse como un todo. Y aquí pueden ocurrir varias cosas que no te he explicado. Según la geometría que adopte la confinación, podrá ser un fermión izquierdo o derecho (una partícula o una antipartícula); así que puede ocurrir aniquilación…
También podría ocurrir que esa partícula (o energíamasa) alcance la velocidad de la luz; es decir regrese ha ser energíacampo, ya te explique por que. Ahora, la gravitación es energíacampo también, y aquí ocurre que ella penetra a la partícula (el mismo proceso de la aniquilación, todo es lo mismo, hay una regularidad natural entre el micromundo y el macromundo, que nadie ve), satura la estabilidad de su topología, y esta se desintegra (aquí tienes la explicación de todos los procesos de desintegración y con el, los tiempos de vida). Pero desintegración en mi razonamientos, en el modelo; es decaer en otra topología de menor energía y cuando esas topologías estables, quedan agotadas por las leyes naturales, que los físicos llamamos de conservación (carga, spin, Isoespin, CP, CPT,…); no le queda otro remedio a la energíamasa; que volver ha ser una energíacampo.

Estaría bien que Tom pudiera, por fín, atrapar con los dedos de la Mente, su teoría Luz-Luz (débil-fuerte) para asombrar al mundo.
Bueno espero haberte complacido en algo, “tuvisteis la exclusividad”, lo dejo ahí porque para que lo digieran y porque tengo muchos problemas que resolver. Tampoco tengo tiempo de leer lo que escribí (como ya es costumbre); pero ustedes son inteligentes como para no crucificarme, así que corrígeme ha tus Dones. Pueden divulgar a su antojo, como siempre les digo, “mi física de café con leche”. Tómense su tiempo para digerirlo, para acostumbrarse a estas nuevas concepciones físicas, esto párese merecerlo, parece novedoso.
Gracias amigo, te agradecemos las revelaciones que, si al fin se abren camino, nos podrían llevar a terrenos más cercanos a la realidad física del mundo. Daríamos un paso adelante en la comprensión del Universo y, como pasa siempre que obtenemos alguna nueva respuesta…¡Podríamos seguir planteando nuevas preguntas! que por cierto, ahora no podemos hacer por no tener ese conocimiento que tú tratas de entregar al mundo.

Sigamos con la Gravedad Cuántica
La física será incompleta y conceptualmente insatisfactoria en tanto no se disponga de una teoría adecuada de la gravedad cuántica. Todos hemos oido hablar de la incompatibilidad de las dos teorías que sustentan hoy por hoy toda la Física y que, todosm también sabemos que, son teorías incompletas que necesitan de una reunificación en un todo poderoso que todo lo puesda explicar.
Durante el siglo XX, la física se fundamentó, en general, sobre dos grandes pilares: la mecánica cuántica y la teoría de relatividad. Sin embargo, a pesar de los enormes éxitos logrados por cada una de ellas, las dos aparecen ser incompatibles. Esta embarazosa contradicción, en el corazón mismo de física teórica, se ha transformado en uno de los grandes desafíos permanentes en la ciencia.
La teoría de la relatividad general da cuenta a la perfección de la gravitación. Por su parte, la aplicación a la gravedad de la mecánica cuántica requiere de un modelo específico de gravedad cuántica. A primera vista, parecería que la construcción de una teoría de gravedad cuántica no sería más problemático que lo que resultó la teoría de la electrodinámica cuántica (EDC), que ya lleva más de medio siglo con aplicaciones más que satisfactorias.
En lo medular, la EDC describe la fuerza electromagnética en términos de los cambios que experimentan las llamadas partículas virtuales, que son emitidas y rápidamente absorbidas de nuevo; el principio de incertidumbre de Heisenberg nos dice que ellas no tienen que conservar la energía y el movimiento. Así la repulsión electrostática entre dos electrones puede ser considerada como la emisión, por parte de un electrón, de fotones virtuales y que luego son absorbidos por el otro.

La misma mecánica, pero a través de los cambios de la partícula virtual de la gravedad el «gravitón» (el quantum del campo gravitacional), podría considerarse para estimar la atracción gravitacional entre dos cuerpos. Pero gravitones nunca se han visto. La gravedad es tan débil que puede obviarse a escala molecular, donde los efectos cuánticos son importantes. Ahora, si los cambios que podrían realizarse en los gravitones sólo se producen en la interacción entre dos puntos de masa, es posible, entonces, que en los cuerpos masivos se ignore los efectos cuánticos. El principio de incertidumbre de Heisenberg nos señala que no podemos medir simultáneamente la posición y la velocidad de una partícula subatómica, pero esta indeterminación es imperceptible para los planetas, las estrellas o las galaxias.

Sí, pero, ¿qué me dices del gravitón?
Pero el principal obstáculo, sin embargo, es la cantidad de complicados procesos que implica examinar un gran número de gravitones. La gravedad se diferencia crucialmente del electromagnetismo al no ser lineal. Esta inlinealidad surge porque la gravedad posee la energía, y ésta tiene la masa, que gravita. En el lenguaje cuántico, esto implica que gravitones interactúan recíprocamente con otro gravitones, a diferencia de los fotones, que interactúan sólo con cargas y corrientes eléctricas y no con otros fotones. Ahora, como los gravitones interactúan el uno con el otro, las partículas de materia son rodeadas por complejas redes de gravitones virtuales que forman «lazos cerrados», muy semejante a «árboles bifurcados».
En la teoría de campo cuántica, los lazos cerrados son un signo de problema; ellos normalmente producen respuestas infinitas en los cálculos de procesos físicos. En EDC, tales lazos ocurren cuando un electrón emite y absorbe de nuevo su propio fotón. En ese caso, los infinitos son soslayados a través de un procedimiento matemático conocido como renormalización. Si éste es hecho correctamente, se obtienen razonables respuestas. La QED es lo que se llama una teoría renormalizable porque todos los infinitos pueden ser soslayados sistemáticamente; en efecto, solo un conjunto de operaciones matemáticas es suficiente para eliminar los infinitos.

Parece que aquí puede estar la solución
Lamentablemente, tal procedimiento sistemático no es operativo cuando la mecánica cuántica es aplicada a la relatividad general; la teoría es, por lo tanto, «no-renormalizable». Cada proceso que implique progresivamente más lazos cerrados de gravitones introduce nuevas variantes de términos infinitos. Lo anterior, coarta la investigación para muchísimos fenómenos de interés, y sugiere que puede que haya básicamente algo que esté errado en la relatividad general, en la mecánica cuántica, o en ambas.
Pero miremos más allá del problema de renormalización, ¿qué pasaría si nos remontáramos a un momento en que todo lo que podemos ver, y hasta lo que hay más allá de nuestro «horizonte» de 13.000 millones de años luz, estaba comprimido hasta un volumen menor que el de un núcleo atómico? A estas densidades descomunales, que se dieron durante los primeros 10-43 segundos del universo (lo que se conoce como «tiempo de Planck»), tanto los efectos cuánticos como la gravedad habrían sido importantes. ¿Qué pasa cuando los efectos cuánticos convulsionan todo un universo?

Por ello, la física será incompleta y conceptualmente insatisfactoria en tanto no se disponga de una teoría adecuada de la gravedad cuántica. Algunos teóricos creen que ya es tiempo de explorar las leyes físicas que prevalecían en el tiempo de Planck, y han propuesto algunas hipótesis interesantes. Sin embargo, no hay consenso sobre qué ideas hay que descartar. Lo que es seguro es que debemos rechazar nuestras queridas concepciones del espacio y el tiempo basadas en el sentido común: el espaciotiempo a muy pequeña escala podría tener una estructura caótica, espumosa, sin ninguna flecha temporal bien definida; puede que haya una generación y fusión continua de agujeros negros primores y minúsculos. La actividad podría ser lo bastante violenta para generar nuevos dominios espaciotemporales que evolucionarían como universos independientes. Eventos más tardíos (en particular la fase inflacionaria que se describe en el capítulo XVI) podrían haber borrado cualquier rastro de la era cuántica inicial. El único lugar donde podrían observarse efectos cuántico-gravitatorios sería cerca de las singularidades centrales de los agujeros negros (de donde ninguna señal puede escapar). Una teoría sin consecuencias evidentes fuera de estos dominios tan exóticos e inaccesibles no es verificable. Para que se la tome en serio debe estar íntimamente insertada o, en su efecto, articulada en alguna teoría con fundamento empírico, o bien debe percibirse como una conclusión inevitable y convincente.
Durante las últimas décadas, varias tentativas han sido hechas para buscarle una solución al problema de la no-renormalización de la gravedad cuántica y caminar hacia la unificación de todas las fuerzas. La aproximación más esperanzadora para alcanzar ese viejo anhelo de los físicos es la teoría de las «supercuerdas», que ya anteriormente vimos.

Sin embargo, recordemos aquí que en la teoría de las supercuerdas se presume una escala natural energética determinada por la energía de Planck, alrededor de unos 1019 GeV. Esto es 1017 veces más alto que los tipos de energías que pueden ser producidos en los aceleradores de partículas más grandes, lo que imposibilita contrastar con la teoría la existencia misma de las supercuerdas. No obstante, los teóricos esperan que a escala de energía accesible tanto la física, la relatividad general, el electromagnetismo, las fuerzas nucleares débiles y fuertes, las partículas subatómicas surjan de la teoría de las supercuerdas como una aproximación. Así, se espera conseguir con ese modelo de cuerdas no sólo una ajustada descripción de la gravedad cuántica, sino que también intentar con ella la anhelada unificación de las fuerzas.
La teoría defiende la existencia de diez dimensiones espaciales y una temporal. Esas dimensiones estarían en las propias cuerdas, y por eso no las vemos. Con esto de las dimensiones me pasa lo mismo que con la “materia oscura”, son buenos artilugios para pasar página y dar por bueno lo que aún no se ha podido verificar.
Lamentablemente, no hay un único límite de baja energía para la teoría de las supercuerdas como tampoco un sólo modelo de la teoría. Por un tiempo, lo anterior pareció como una barrera infranqueable, pero en años recientes, y a través de una mayor abstractación matemática, se ha construido un nuevo modelo de supercuerdas conocido como «la teoría M» que amalgama dentro de ella otras teorías de supercuerdas.
Por ahora, es demasiado pronto para pronunciarse si la teoría M es finalmente el medio que reconciliará la gravitación y la mecánica cuántica, pero sí debería poder cumplir con algunas expectativas, como ser las de explicar algunos hechos básicos sobre el mundo físico. Por ejemplo, el espaciotiempo de cuatro dimensional tendría que surgir de la teoría, más bien que ser insertado en ella. Las fuerzas y las partículas de naturaleza también deberían ser descritas, preferentemente incluyendo sus propiedades claves, como fuerzas de interacción y masas. Sin embargo, a no ser que la teoría M, o una variante futura, pueda ser proyectada a la baja energía de los laboratorio de física para poder ser contrastada, corre el riesgo de empezar a ser olvidada y finalmente archivada como uno más de los muchos y elegantes ejercicios matemáticos que se han elaborado para la física en los últimos tiempos.
Cuerdas o filamentos vibrantes en el corazón de la materia
Si la teoría de supercuerda es una pérdida de tiempo o no, ello está por verse. Por ahora, el desafío más duro a superar por la teoría es entender por qué el espacio de 9 dimensiones más el tiempo se «comprime» bajo el aspecto de nuestro espacio habitual tetradimensional (el tiempo más las tres dimensiones espaciales), en vez de hacerlo en tres o cinco dimensiones, y ver cómo sucede esto. Aún hay un espacio infranqueable entre la teoría de supercuerdas y los fenómenos observables. La teoría de supercuerdas plantea problemas demasiado difíciles ahora mismo para los matemáticos. En este aspecto, es muy diferente de la mayor parte de teorías físicas: normalmente, el aparato matemático de las teorías se desarrolla antes que éstas. Por ejemplo, Einstein utilizó conceptos geométricos desarrollados en el siglo XIX, no tuvo que partir de cero para construir las matemáticas que necesitaba.
Por su parte, los físicos cuerdistas se acorralan en lo que es fácil de comprobar, es difícil de calcular y lo que es fácil de calcular, es difícil comprobar. En consecuencia, pareciera que el camino que se está siguiendo es pretender desarrollar la teoría más y más, y hacer cálculos cada vez más difíciles de manera de poder predecir cosas que sean fáciles de observar. ¿El camino tendrá tiempo y final? Nadie tiene por ahora la respuesta.

Aquella charla … 23-28 Julio, MPI, Múnich, Alemania, a cargo de John H. Schwarz (Caltech), uno de los padres de la teoría de cuerdas, no tuvo desperdicio.
El físico Eugene Wigner escribió un célebre artículo sobre este particular que llevaba por título «La irrazonable efectividad de la matemática en las ciencias físicas». También es un hecho notable que el mundo exterior muestre tantas estructuras susceptibles de descripción en «lenguaje» matemático (sobre todo cuando tales estructuras se alejan mucho de las experiencias cotidianas que moldearon la evolución de nuestros cerebros). Edward Witten, el principal experto en supercuerdas, describe dicha teoría como «una física del siglo XXI que cayó en el siglo XX». Sin embargo, sería más extraordinario que seres humanos de cualquier siglo llegaran a desarrollar una teoría tan «final» y general como pretenden ser las supercuerdas.
Salvo mejor parecer.
Emilio Silvera
















 Totales: 74.966.620
Totales: 74.966.620 Conectados: 15
Conectados: 15