Feb
7
El Universo cercano
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en General ~
Clasificado en General ~
 Comments (0)
Comments (0)
Repasar nuestra vecindad y los objetos que la pueblan, saber algo más de nuestro entorno cercano



¿La Vida? Lo único que se me ocurre para contestar es decir que la Vida es el nivel más alto de la evolución de la Materia. Entendiendo, eso sí, que ese “nivel más alto” es aquel en el que se ha llegado hasta la consciencia de Ser. Cuando nos hemos percatado de que “somos”, entonces y sólo entonces hemos sido conscientes de que formamos parte del inmenso Universo.
Es verdaderamente admirable constatar cómo ha ido evolucionando nuestro entendimiento del Mundo que nos rodea, de la Naturaleza, del Universo. Hubo un tiempo en el que, los individuos de nuestra especie deambulaban por este planeta pero, no sabían comprender el “mundo”, ni podían pensar siquiera en el misterio que representaban los fenómenos naturales que a su alrededor se sucedían.

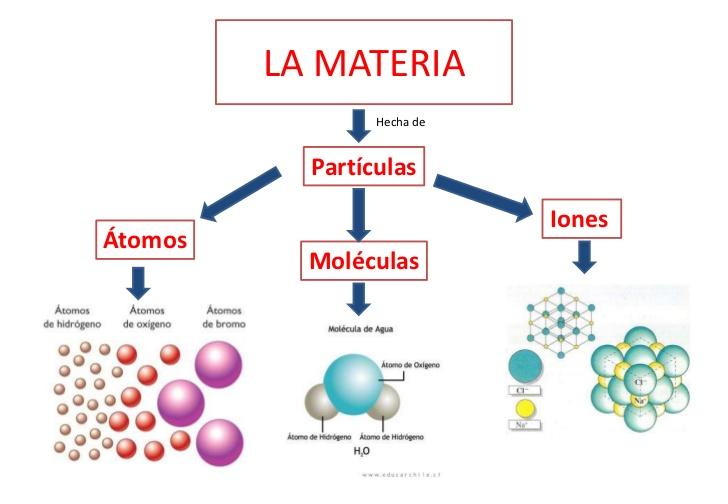
Pasado el tiempo, pudieron mirar hacia arriba y, la presencia de aquellos puntitos brillantes en la oscura y misteriosa penumbra de la noche, despertó su curiosidad consciente y se pudieron hacer algunas preguntas. Muchas decenas de miles de años más tarde, nuestro deambular por el planeta, las experiencias y la observación de la Naturaleza, nos llevó a comprender, algunas de las cosas que antes no tenían explicación. Pensadores del pasado dejaron la huella de sus inquietudes y los llamados filósofos naturales, hicieron el ejercicio de dibujar el “mundo” según ellos lo veían. Nos hablaron de “elementos” de “átomos” y, aunque no era el concepto que ahora de esas palabras podamos tener, ya denotaba una gran intuición en el pensamiento humano que trataba de entender la Naturaleza y cómo estaban hechas las cosas que nos rodeaban. Ellos, a la materia primigenia la llamaron “Ylem” la sustancia cósmica.
de esas palabras podamos tener, ya denotaba una gran intuición en el pensamiento humano que trataba de entender la Naturaleza y cómo estaban hechas las cosas que nos rodeaban. Ellos, a la materia primigenia la llamaron “Ylem” la sustancia cósmica.

Es cierto que siempre hemos querido abarcar más de lo que nuestra “sabiduría” nos podía permitir. Ahora , en el presente, las cosas no han cambiado y tratamos de explicar lo que no sabemos, y, para ello, si hay que inventarse la “materia oscura”, las “fluctuaciones de vacío”, los “universos paralelos”, los “agujeros de gusano”, o, cualesquiera otros conceptos o fenómenos inexistentes en el mundo material o experimental… ¡qué más da! Lo importante es exponer las ideas que nos pasen por la cabeza que, de alguna manera, pasando el tiempo, se harán realidad. Nuestras mentes, como digo, siempre fueron por delante de nosotros mismos y ha dejado al descubierto esa intuición que nos caracteriza y que, de alguna manera, nos habla de esos hilos invisibles que, de alguna manera, nos conecta con el resto del Universo del que, al fin y al cabo, formamos parte
, en el presente, las cosas no han cambiado y tratamos de explicar lo que no sabemos, y, para ello, si hay que inventarse la “materia oscura”, las “fluctuaciones de vacío”, los “universos paralelos”, los “agujeros de gusano”, o, cualesquiera otros conceptos o fenómenos inexistentes en el mundo material o experimental… ¡qué más da! Lo importante es exponer las ideas que nos pasen por la cabeza que, de alguna manera, pasando el tiempo, se harán realidad. Nuestras mentes, como digo, siempre fueron por delante de nosotros mismos y ha dejado al descubierto esa intuición que nos caracteriza y que, de alguna manera, nos habla de esos hilos invisibles que, de alguna manera, nos conecta con el resto del Universo del que, al fin y al cabo, formamos parte .
.
El agua representa el 80% de la composición de la mayoría de los organismos e interviene masiva y decisivamente en la realización de sus procesos metabólicos; asimismo, desempeña un importante papel en la fotosíntesis de las plantas y sirve de hábitat a una gran parte de los seres vivos.

Tales de Mileto fue el primero en expresar la importancia que tenía el agua para la Vida
Ahora , que hemos podido realizar un cierto avance en el “conocimiento del mundo que nos rodea”, no le damos la verdadera importancia que tienen algunos pensamientos del pasado que, en realidad, son los responsables de que ahora, nos encontremos en el nivel de conocimiento que hemos podido conquistar. Tales de Mileto, uno de los siete sabios de Grecia, fue el primero que dejó a un lado la mitología para utilizar la lógica y, entre otras muchas cosas, indicó la importancia que tenía el agua para la existencia de la vida. Empédocles nos habló de los elementos y Demócrito del a-tomo o átomo., Arquitas de Tarento (filósofo, soldado y músico), el amigo de Platón y seguidor de Pitágoras, ya se preguntaba: ¿Es el Universo infinito?rquitas de Trento
, que hemos podido realizar un cierto avance en el “conocimiento del mundo que nos rodea”, no le damos la verdadera importancia que tienen algunos pensamientos del pasado que, en realidad, son los responsables de que ahora, nos encontremos en el nivel de conocimiento que hemos podido conquistar. Tales de Mileto, uno de los siete sabios de Grecia, fue el primero que dejó a un lado la mitología para utilizar la lógica y, entre otras muchas cosas, indicó la importancia que tenía el agua para la existencia de la vida. Empédocles nos habló de los elementos y Demócrito del a-tomo o átomo., Arquitas de Tarento (filósofo, soldado y músico), el amigo de Platón y seguidor de Pitágoras, ya se preguntaba: ¿Es el Universo infinito?rquitas de Trento
Él mismo se contestaba diciendo que todo tenía un límite y, pensaba en el final que lindaba con el “vacío”, allí donde nada impedía que su espada, lanzada con fuerza en el borde del universo, siguiera su camino sin fin, ninguna fuerza podría pararla y con ninguna clase de materia podría chocar. Así, con esos pensamientos surgidos de la mente humana, podemos constatar que, desde siempre, hemos tratado de saber de qué están hechas las cosas, cómo funciona la Naturaleza y de qué manera se comporta el universo y por qué lo hace de esa manera y no de otra.
siempre, hemos tratado de saber de qué están hechas las cosas, cómo funciona la Naturaleza y de qué manera se comporta el universo y por qué lo hace de esa manera y no de otra.

El Universo se expande y nuestras mentes también. Eso que llamamos Tiempo siguió su transcurrir inexorable, los pensamientos de los grandes pensadores se fueron acumulando en un sin fin de conjeturas y teorías que, poco a poco, pudimos ir comprobando mediante la observación, el estudio y la experimentación hasta que, pudimos llegar a saber de qué estaban hechas las estrellas y cómo la materia se transmutaba en sus hornos nucleares para crear elementos que hicieron posible el surgir de la vida en los mundos (no creo que la vida esté supeditada a este mundo nuestro).
crear elementos que hicieron posible el surgir de la vida en los mundos (no creo que la vida esté supeditada a este mundo nuestro).
 poder solidificar los elementos de la vida para crear, en algunos de los muchos mundos presentes en las galaxias, el protoplasma vivo que diera lugar a esa primera célula replicante que comenzara la fascinante aventura de la vida hasta llegar a los pensamientos.
poder solidificar los elementos de la vida para crear, en algunos de los muchos mundos presentes en las galaxias, el protoplasma vivo que diera lugar a esa primera célula replicante que comenzara la fascinante aventura de la vida hasta llegar a los pensamientos.Aveces me pregunto si realmente existe una Conciencia Cósmica, todo lo que ha pasado no puede ser fruto del Azar
Es difícil asimilar todo lo que sucede en la Naturaleza, desde la fusión nuclear en las estrellas para formar elementos, pasando por la complejidad del núcleo atómico y todo lo que dentro de él está contenido a pesar de su ínfima pequeñez, o, ¿Qué mejor ejemplo? el surgir de la Vida a partir de la “materia inerte” por la evolución permitida por el transcurrir inexorable del Tiempo.

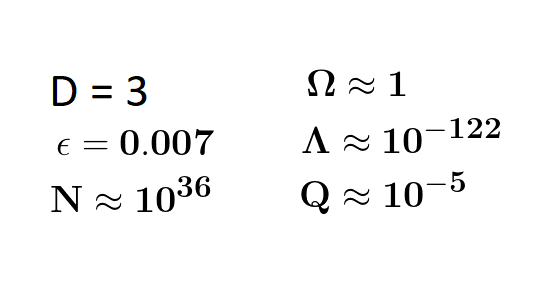
En física, la noción de ajuste fino se refiere a la situación en la que un cierto número de parámetros deben tener un valor muy preciso para poder explicar tal o cual fenómeno observado, y, la presencia de la Vida.
Si el Universo no es consciente… ¿Cómo explicar el ajuste fino para hacer posible nuestra presencia?
Si nos preguntaran: ¿Es consciente el Universo? Tendríamos que contestar de manera afirmativa, toda vez que, al menos una sección importante de él, ¡la que piensa!, representada por seres vivos y que forman parte de ese inmenso universo, Sí que lo es. La vida es la consecuencia de la materia evolucionada hasta su más alto nivel y, a partir de ella, ha podido surgir eso que llamamos cerebro, un lugar de tal complejidad que es capaz de generar ideas y de él emana también ese algo inmaterial que llamamos mente, un ente inmaterial y superior que trasciende y va más allá, lo que los filósofos llamaron Ser y quisieron explicar mediante la metafísica, toda vez que, al estar fuera de la materia, nada podía la Física decir. Todavía, no sabemos lo que la vida es y tampoco, podemos explicar lo que es la energía, o, por exponer algún concepto de los muchos que denota nuestra ignorancia, tampoco podemos contestar a una simple pregunta: ¿Qué es el Tiempo? ¿Existe en realidad o simplemente es una abstracción de la mente? Ya hablamos aquí de eso hace unos días.
de ese inmenso universo, Sí que lo es. La vida es la consecuencia de la materia evolucionada hasta su más alto nivel y, a partir de ella, ha podido surgir eso que llamamos cerebro, un lugar de tal complejidad que es capaz de generar ideas y de él emana también ese algo inmaterial que llamamos mente, un ente inmaterial y superior que trasciende y va más allá, lo que los filósofos llamaron Ser y quisieron explicar mediante la metafísica, toda vez que, al estar fuera de la materia, nada podía la Física decir. Todavía, no sabemos lo que la vida es y tampoco, podemos explicar lo que es la energía, o, por exponer algún concepto de los muchos que denota nuestra ignorancia, tampoco podemos contestar a una simple pregunta: ¿Qué es el Tiempo? ¿Existe en realidad o simplemente es una abstracción de la mente? Ya hablamos aquí de eso hace unos días.

Lo cierto es que nuestra especie ha dejado profundas huellas de su deambular por el mundo. Muchos de sus “tesoros y obras” quedaron enterrados en las profundidades del tiempo o inundados por los diluvios que las distintas civilizaciones que fueron nos contaron con sus maravillosas leyendas que, en realidad, trataban de explicar algo que sucedió y que no llegaban a comprender y, para ello, inventaban bonitas historias en las que, narraban hechos que quedaron difuminados por la fantasía hasta el punto de no saber, en el presente, hasta que punto eran ciertas o no las bonitas “historias” que nos contaron.
ello, inventaban bonitas historias en las que, narraban hechos que quedaron difuminados por la fantasía hasta el punto de no saber, en el presente, hasta que punto eran ciertas o no las bonitas “historias” que nos contaron.

Sí, puede tardar pero, al final, todo llega, todo cambia, nada permanece, y, todo tiene “su” Tiempo
Lo que sucede es que, con frecuencia, cuando surgen ideas nuevas que tienden a querer explicar científicamente lo que es la Naturaleza, aparecen viejos datos que relacionan esas nuevas ideas con aquellos viejos problemas. Tenemos que admitir que todavía “no sabemos” cómo es la realidad del mundo y que, nuestra realidad, no tiene que coincidir con la verdadera realidad que incansables buscamos.
que relacionan esas nuevas ideas con aquellos viejos problemas. Tenemos que admitir que todavía “no sabemos” cómo es la realidad del mundo y que, nuestra realidad, no tiene que coincidir con la verdadera realidad que incansables buscamos.
De hecho, no sabemos explicar ni cómo se pudieron formar las galaxias, y, a pesar de ello, no tenemos empacho de hablar de singularidades y agujeros de gusano o de universos paralelos. ¡La imaginación!, creo que sin ella, no habríamos podido llegar hasta aquí. La imaginación unida a la curiosidad ha sido desde siempre, el motor que nos llevó hacia el futuro.
siempre, el motor que nos llevó hacia el futuro.

Si en realidad existe “el infinito”, seguro que está en nuestras mentes, o, posiblemente en otras que, como las nuestras, han imaginado cómo ensanchar el mundo y universo de los pensamientos sin límite alguno, el único límite que existe, amigos míos, es el de nuestra ignorancia para llegar a comprender lo que la Naturaleza es. En la Naturaleza están todas las respuestas a las preguntas que planteamos y que nadie sabe contestar. En ella, en la Naturaleza, buscan nuestros ingenios esas respuestas y, para poder encontrarlas hemos inventado los aceleradores de partículas, los microscopios y telescopios y aparatos que, como los espectrómetros de masa y otros nos llevan a ese “otro universo” que el ojo desnudo no puede ver pero que, no deja de ser y estar en nuestro propio mundo, y, al ser conscientes de ello, también lo somos de nuestras limitaciones. En realidad, la única manera de avanzar es ser consciente de que no sabemos, toda vez que, si creyéramos que ya lo sabíamos todo… ¿para qué seguir buscando?
llegar a comprender lo que la Naturaleza es. En la Naturaleza están todas las respuestas a las preguntas que planteamos y que nadie sabe contestar. En ella, en la Naturaleza, buscan nuestros ingenios esas respuestas y, para poder encontrarlas hemos inventado los aceleradores de partículas, los microscopios y telescopios y aparatos que, como los espectrómetros de masa y otros nos llevan a ese “otro universo” que el ojo desnudo no puede ver pero que, no deja de ser y estar en nuestro propio mundo, y, al ser conscientes de ello, también lo somos de nuestras limitaciones. En realidad, la única manera de avanzar es ser consciente de que no sabemos, toda vez que, si creyéramos que ya lo sabíamos todo… ¿para qué seguir buscando?
Todo está hecho
 una Galaxia hasta el fiero león que habita en la selva
una Galaxia hasta el fiero león que habita en la selva
/arc-anglerfish-arc2-prod-gruponacion.s3.amazonaws.com/public/OBGSXVBBAVARTN4M6K3M3IRSB4.jpg)
La importancia de las cosas no está, ni en lo grande o lo pequeñas que puedan ser. La importancia reside en la función que cada cosa puede desempeñar.

Todas las cosas son
Con esas sencillas palabras, el sabio, elevó a todas las cosas a la categoría de SER. ¿Tendrá memoria la materia? ¿Será posible que eso que llamamos materia “inerte”, no sea en realidad tan inocua ni tan insensible como imaginamos? Es posible que cada estado de la materia sea un paso necesario para poder llegar hasta su estado de consciencia que, en este mundo, se ha revelado en nosotros.
de la materia sea un paso necesario para poder llegar hasta su estado de consciencia que, en este mundo, se ha revelado en nosotros.
Emilio Silvera V.
Feb
7
Números y dimensiones en el Universo
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en General ~
Clasificado en General ~
 Comments (0)
Comments (0)
Con las matemáticas podemos construir muchos escenarios
- 4 Dimensiones Espaciotemporales: Tres dimensiones espaciales y una dimensión temporal. Es la base para ubicar eventos y objetos.
- Teoría de Cuerdas (10D): Propone 9 dimensiones espaciales y 1 temporal. Las dimensiones extras son muy pequeñas y compactificadas, impidiendo su interacción directa.
- Teoría M (11D): Una unificación de las teorías de cuerdas que sugiere 10 dimensiones espaciales y 1 temporal, donde las partículas son vibraciones de cuerdas.
- El Modelo de Randall-Sundrum (5D): Describe un universo de 5 dimensiones, donde la gravedad se propaga libremente mientras la materia está atrapada en una “brana” de 4 dimensiones.
- Dimensiones Conocidas: 4 (3 espaciales + 1 temporal).
- Dimensiones en Teoría de Cuerdas: 10 (9 espaciales + 1 temporal).
- Dimensiones en Teoría M: 11 (10 espaciales + 1 temporal).
Feb
7
¡El Universo y la vida!
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en General ~
Clasificado en General ~
 Comments (0)
Comments (0)
Se ha investigado mucho sobre el tema. Sin embargo, el verdadero origen de la Vida…¡No se sabe!
La vida (a partir de su primer paso, y, un largo camino para llegar al primer individuo de cada especie) surgió en el Universo de manera espontánea por la evolución de la materia y (no sabemos si debido al Azar), bajo ciertas circunstancias muy especiales que estaban presentes en ciertos lugares del Universo, lo que dio lugar al surgir de la vida tal como la conocemos y, posiblemente, de muchas más formas desconocidas para nosotros. Y, todo eso amigos, es Entropía Negativa. Ahora, Las características de un ser vivo son siempre una recombinación de la información genética heredada. De todas las maneras, hay que aclarar que la vida existe porque el Universo es como lo observamos, sus características permiten su presencia. Hay vida en nuestro universo debido a que las cuatro fuerzas fundamentales y las constantes universales lo permiten.
CONSECUENCIA LOGICA: Las variaciones dentro de una misma especie son el resultado de una gran cantidad de información genética presente ya en sus antepasados y, como consecuencia de la lógica evolución, de la aparición espontánea de nueva información genética…

Aquí, en todo su esplendor, tenemos un trozo de Universo que, nos está hablando de la creación. Esas estrellas brillantes, azuladas y supermasivas que radian en el ultravioleta ionizando toda la región circundante, es un signo, inequívoco de que la vida está cerca. Elementos sencillos se transformaran en otros más complejos y, aparecerán aminoácidos y la química-biológica que hacer, mucho más tarde, que sea posible la aparición de la vida en algún mundo perdido en las profundidades de una Galaxia que, como la nuestra, tendrá otras “Tierras” y otros “Seres”.
Cuántas veces se preguntó la Humanidad: ¿Hay vida en el Universo, además de la que existe en la Tierra? Las leyes de la Física, aplicables a toda la materia y la energía, tienen sin duda un papel fundamental en la comprensión del Universo y por ello la Astrofísica ha tenido un desarrollo espectacular en los últimos tiempos a pesar de la escasez de materia como la que conocemos.
La pregunta sobre si existe vida más allá de la Tierra ha sido formulada a lo largo de la historia, constituyendo uno de los interrogantes filosóficos y científicos más persistentes de la humanidad. Aunque la búsqueda científica moderna es relativamente reciente, el debate sobre la pluralidad de mundos habitados se remonta a la antigua Grecia, evolucionando desde la especulación filosófica hasta la astrobiología actual.
Por otro lado, como el Universo es muy grande, las densidades medias son muy bajas y la materia se encuentra normalmente en estructuras muy simples, en forma de átomos y partículas individuales. La composición química del Universo y sus procesos son por ello también importantes para comprender su evolución, dando pie al uso más o menos extendido de astroquímica. Sin embargo, las moléculas complejas son relativamente raras y los organismos vivos muchísimo más. La parte Biológica del Universo que conocemos se reduce a nuestro propio planeta por lo que parece excesivo poder hablar de Astrobiología. Por qué tenemos que preocuparnos por una parte tan ínfima del Universo. Ciertamente porque los seres humanos pertenecemos a esta extraña componente y, ya que no podemos reproducir en el laboratorio el paso de la química a la biología, es en el contexto del Universo (el gran Laboratorio) y su evolución en el que podemos analizar los límites y las condiciones necesarias para que emerja la vida en cualquier sitio.

En las Nebulosas nacen las estrellas, en sus hornos nucleares se producen las transiciones de fases necesarias para crear los elementos complejos necesarios para la vida. Si alrededor de las nuevas estrellas surgen nuevos mundos, ¿por qué tras miles de millones de años de evolución no puede surgir la vida en ellos, si como existe la posibilidad, están situados en la zona habitable? Las leyes del Universo son las mismas en todas partes y, todas las regiones del Cosmos, por muy alejadas que estén, están sometidas a ellas. Si en el planeta Tierra está presente el agua corriente, una atmósfera y la vida, ¿Por qué sería diferente en otros planetas similares que a millones pululan por nuestro Universo?
La Astrobiología es una ciencia que ha surgido en la frontera entre varias disciplinas clásicas: la Astronomía, la Biología, la Física, la Química o la Geología. Su objetivo final es comprender cómo surgió la vida en nuestro Universo, cómo se distribuye y cuál es su evolución primitiva, es decir, cómo pudo establecerse en su entorno.

En otras palabras, trata de comprender el papel de la componente biológica del Universo, conectando la astrofísica y la astroquímica con la biología. Intenta para ello comprende el origen de la vida. : El paso de los procesos químicos prebióticos a los mecanismos bioquímicos y a la biología propiamente dicha.
Naturalmente, en Astrobiología nos planteamos preguntas fundamentales, como la propia definición de lo que entendemos como Vida, cómo y cuándo pudo surgir en la Tierra, su existencia actual o en el pasado en otros lugares o si es un hecho fortuito o una consecuencia de las leyes de la Física. Algunas de estas cuestiones se las viene formulando la humanidad desde el principio de los tiempos, pero ahora por primera vez en la historia, los avances de las ciencias biológicas y de la exploración mediante tecnología espacial, es posible atacarlas desde un punto de vista puramente científico. Para ello, la Astrobiología centra su atención en estudiar cuáles son los procesos físicos, químicos y biológicos involucrados en la aparición de la vida y su adaptabilidad, todo ello en el contexto de la evolución y estructuración, o auto-organización, del Universo.
NGC 3031
Muchos son los que postulan que, las galaxias espirales son auto-generadoras a través de las explosiones supernovas y, siembran el espacio interestelar de la semilla creadora de la vida, además, este proceso regenerativo crea entropía negativa tratando de luchar contra el deterioro de la galaxia como sistema cerrado que de esta forma se mantiene y perdura. Nuevas y energéticas estrellas azuladas pueblan las regiones galácticas que se llenan de promesas futuras de nuevos mundos y nuevas formas de vida.
Como cualquier otra ciencia, la Astrobiología está sujeta a la utilización del método científico y por tanto a la observación y experimentación junto con la discusión y confrontación abierta de las ideas, el intercambio de datos y el sometimiento de los resultados al arbitraje científico. La clave de la metodología de esta nueva ciencia está en la explotación de las sinergias que se encuentran en las fronteras entre las disciplinas básicas mencionadas anteriormente, una región poco definida, cuyos límites se fijan más por la terminología que por criterios epistemológicos.

Un aspecto importante de la investigación en el campo de la Astrobiología es la herramienta fundamental que representa el concepto de complejidad. La vida es un proceso de emergencia del orden a partir del caos que puede entenderse en medios no aislados y, por tanto libres de la restricción de la segunda ley de la termodinámica, como un proceso complejo. En este sentido, la emergencia de patrones y regularidades en el Universo, ligados a procesos no lineales, y el papel de la auto-organización representan aspectos esenciales para comprender el fenómeno de la vida. Transiciones de estado, intercambios de información, comportamientos fuera de equilibrio, cambios de fase, eventos puntuales, estructuras autorreplicantes, o el propio crecimiento de la complejidad, cobran así pleno sentido en Astrobiología.

El Universo es… ¡Demasiado grande para que estemos solos! Las distancias que no separan de otros mundos, la inmensa extensión de un universo para nosotros “infinito”. El Proyecto SETI ha explorado el Espacio exterior en busca de vida sin éxito hasta la fecha. Claro que, el resultado es comprensible si tenemos en cuenta que, el espacio explorado sería como comparar una piscina olímpica con el océano Pacífico.
Muchos han sido, a lo largo de la historia de la Humanidad, los que visionaron el futuro que nos espera: “Yo puedo imaginar un infinito número de mundos parecidos a la Tierra, con un jardín del Edén en cada uno”. Lo afirmaba Giordano Bruno finales del siglo XVI, antes de ser quemado por orden de la Inquisición Romana. Y, sí, muchas veces nos hicimos esa pregunta…
¿Habrá vida en otros mundos?

Planetas inimaginables ¿Qué formas de vida acogerán? La pregunta que se plantea encima de la imagen de arriba tiene una fácil contestación: SÍ, hay otras formas de vida en el Universo, en planetas parecidos o iguales que la Tierra. Si no fuese así, la lógica y la estadística dejarían de tener sentido.
Un problema básico de esta ciencia, ya mencionado al principio, es la cantidad de datos disponibles, de sujetos de estudio. No conocemos más vida que la existente en la Tierra y ésta nos sirve de referencia para cualquier paso en la búsqueda de otras posibilidades. La astrobiología trata por ello de analizar la vida más primitiva que conocemos en nuestro planeta así como su comportamiento en los ambientes más extremos que encontremos para estudiar los límites de su supervivencia y adaptabilidad. Por otro lado, busca y analiza las condiciones necesarias para la aparición de entornos favorables a la vida, o habitables, en el Universo mediante la aplicación de métodos astrofísicos y de astronomía planetaria. Naturalmente, si identificáramos sitios en nuestro sistema solar con condiciones de habitabilidad sería crucial la búsqueda de marcadores biológicos que nos indiquen la posible existencia de vida presente o pasada más allá de la distribución de la vida en el Universo o, en caso negativo, acotaríamos aún más los límites de la vida en él.
Titán tiene una atmósfera parecida a la Tierra de hace algunos millones de años
Titán, más allá de los anillos. Ahí podríamos encontrar lo que con tanto afán buscamos: otras formas de vida que, de una vez por todas, nos ofrezca la certeza de que no estamos solos en tan vasto Universo y, dada la conformación y características de ese pequeño mundo, no podríamos extrañarnos de que, la vida, incluso pudiera estar basada en otro elemento distinto del Carbono.
Diferentes condiciones ambientales pueden haber dado lugar a la vida e incluso permitido la supervivencia de algunos organismos vivos generados de forma casual, como experimento de la naturaleza. La Astrobiología trata de elucidar el papel de la evolución del Universo, y especialmente de cuerpos planetarios, en la aparición de la vida. En esta búsqueda de ambientes favorables para la vida, y su caracterización, en el sistema solar, la exploración espacial se muestra como una componente esencial de la Astrobiología. La experimentación en el laboratorio y la simulación mediante ordenadores o en cámaras para reproducir ambientes distintos son una herramienta que ha de ser complementada por la exploración directa a través de la observación astronómica, ligada al estudio de planetas extrasolares, o mediante la investigación in situ de mundos similares en cierta forma al nuestro, como el planeta Marte o algunos satélites de los planetas gigantes Júpiter y Saturno, como Europa, Encelado o el de arriba, Titán.

Después de un viaje de siete años a través del sistema solar abordo de la nave Cassini, la sonda Huygens de la ESA, pudo con éxito, pasar a través de la atmósfera de Titán (la mayor luna de Saturno) tomar tierra a salvo en su superficie para poder enviarnos datos e imagines que nos dejaron con la boca abierta por el asombro de lo que allí existe y , de lo que pueda estar presente… ¿Vida microbiana?
La componente instrumental y espacial convierte a la Astrobiología en un ejemplo excelente de la conexión entre ciencia y tecnología. Los objetivos científicos de la Astrobiología, hemos visto, que requieren un tratamiento trans-disciplinar, conectando áreas como la física y la astronomía con la química y la biología. Esta metodología permite explotar sinergias y transferir conocimiento de unos campos a otros para beneficio del avance científico. Pero además, la Astrobiología está íntimamente ligada a la exploración espacial que requiere el desarrollo de instrumentación avanzada. Se necesitan tecnologías específicas como la robótica o los biosensores habilitadas para su empleo en condiciones espaciales y entornos hostiles muy diferentes al del laboratorio. Naturalmente la Astrobiología emplea estos desarrollos también para transferir conocimiento y tecnologías a otros campos de investigación científica y en particular, cuando es posible, incluso al sector productivo.
Pero repasemos, para avanzar, cuáles son las áreas científicas propias de la Astrobiología. Como se ha dicho, es una ciencia interdisciplinar para el estudio del origen, evolución y distribución de la vida en el Universo. Para ello requiere una comprensión completa e integrada de fenómenos cósmicos, planetarios y biológicos. La astrobiología incluye la búsqueda y la caracterización de ambientes habitables en nuestro sistema solar y otros planetas alrededor de estrellas más alejadas, la búsqueda y análisis de evidencias de química prebiótica o trazas de vida larvada o extinguida en cuerpos del sistema solar como Marte o en lunas de planetas gigantes como Júpiter y Saturno. Asimismo se ocupa de investigaciones sobre los orígenes y evolución de la vida primitiva en la Tierra analizando el comportamiento de micro organismos en ambientes extremos.

Hidratación durante 3 h. ¿Qué no habrá por ahí fuera? Otros como los Acidófilos: Se desarrollan en ambientes de alta acidez, como el Picrophilus, los organismos de la cuenca del Río Tinto, en Huelva o la arquea que habita en una mina californiana llamada Iron Mountain, que crece en PH negativo. Los Organismos radiófilo o radio-resistente es aquél capaz de sobrevivir y prosperar en ecosistemas con niveles muy altos de radiaciones ionizantes. Los Halófilos que se Se desarrollan en ambientes hipersalinos, como las del género Halobacterium, que viven en entornos como el Mar Muerto.
Bacterias termófilas
Los Termófilos: Se desarrollan en ambientes a temperaturas superiores a 45 °C, algunos de ellos, los Hipertermófilos tienen su temperatura optima de crecimiento por encima de los 80 °C., como el Pyrococcos furiosus, donde las chimeneas termales submarinas son testigos de ese asombroso hecho. Otros, como los Psicrófilos, que se desarrollan en ambientes de temperatura muy fría, como la Polaromanas vacuaolata. También tenemos los tardígrados, que se deshidratan para quedar como muertos durante cientos de años en condiciones de criptobiosis y pueden resistir en el espacio. Otros viven sin oxígeno, los hay que habitan a muchos metros bajo la superficie, o, algunos que existen con un bajo índice de humedad. En fin, la gama es amplia y nos muestra una enorme lista de protagonistas que, em medios imposible pueden vivir sin el menor problema. Y, si eso es así (que lo es), ?qué problema puede existir para que exista vida en otros planetas?
Los seres vivos surgen por todo el Universo y en las más extremas condiciones. Simplemente con observar lo que aquí tenemos, en nuestro planeta, nos podemos hacer una idea de lo que encontraremos por ahí fuera. Creo (aunque pudiera haber otras) que la vida en el Universo estará basada, como la nuestra, en el Carbono. El Carbono es el material más idóneo para ello por sus características especiales.
Desde el punto de vista más astronómico, la Astrobiología estudia la evolución química del Universo, su contenido molecular en regiones de formación estelar, la formación y evolución de discos proto-planetarios y estrellas, incluyendo la formación de sistemas planetarios y la caracterización de planetas extrasolares. En este campo en particular se han producido avances recientes muy importantes con la obtención de imágenes directas de planetas extrasolares y la identificación de algunos de ellos como puntos aislados de su estrella central gracias a técnicas de interferometría.
Inmensas Nubes moleculares habitan en las galaxias y, dentro de ellas, al calor de las estrellas se producen transiciones de fase que nos traen la química-biológica para que la vida sea posible.

La caracterización de atmósferas de planetas extrasolares con tránsitos han permitido detectar CO₂ en la atmósfera de otros mundos y se ha descubierto el planeta más parecido a la Tierra por su tamaño y suelo rocoso aunque con un período demasiado corto para ser habitable. El lanzamiento de la misión Kepler de la NASA nos permite abrigar esperanzas de encontrar finalmente un planeta “hermano” del nuestro en la zona de habitabilidad de otra estrella.
El campo de la Astronomía planetaria, la Astrobiología estudia la evolución y caracterización de ambientes habitables en el sistema solar con el fin de elucidar los procesos planetarios fundamentales para producir cuerpos habitables.

A la izquierda Marte a la derecha Riotinto, sólo están separados por las Temperaturas reinantes y la atmósfera. Parece que un día lejano fueron iguales en muchas cosas.
Esto incluye el análisis de ambientes extremos y análogos al de Marte en nuestro planeta, como resulta ser la cuenca del Río Tinto en Huelva, así como la exploración de otros cuerpos del sistema solar, Marte en particular. Y, a propósito de Marte, recuerdo la emoción que sentí cuando la NASA detectó un foco de CH4 en el planeta. Al igual que los eucariotas, muchas bacterias respiran oxígeno. Pero otras bacterias utilizan para la respiración nitrato disuelto (NO3) en lugar de Oxígeno, y aún otras usan iones sulfato (SO42-) u óxidos metálicos de hierro o manganeso. Unos pocos procariotas pueden incluso utilizar CO2, que hacen reaccionar con ácido acético en un proceso que genera gas natural, que es el gas metano CH4 detectado en Marte. Dado que el planeta no muestra actividad volcánica, la fuente de dicho metano, ¿por qué no? podría ser bacteriana.
Estructura celular de una bacteria, típica célula procariota. El metabolismo de los procariotas es enormemente variado y resisten condiciones ambientales sorprendentes por lo extremas en parámetros como la temperatura y la acidez, entre otros,
El descubrimiento en Marte de agua en forma de hielo así como las claras evidencias de la existencia de agua líquida en su superficie en el pasado, proporcionadas por la observación de modificaciones de la componente mineralógica atribuidas al agua líquida en el subsuelo. Hoy por hoy, se considera que la presencia de agua líquida es una condición necesaria, aunque no suficiente, para la aparición de la vida ya que proporciona el caldo de cultivo para que las moléculas prebióticas se transformen en microorganismos biológicos.
En estas investigaciones el estudio del satélite Titán de Saturno mediante la sonda europea Huygens ha marcado un hito importante al acercarnos a un entorno prebiótico donde el metano ejerce un papel dominante.
En este sentido la posibilidad de explorar el satélite Europa, alrededor de Júpiter, es un claro objetivo de la Astrobiología dado que la espesa corteza de hielo que lo cubre puede esconder una gran masa de agua líquida.

Finalmente, la Astrobiología también contempla una serie de actividades más próximas al laboratorio en el que se analiza la evolución molecular, desde la química prebiótica, pasando por la adaptación molecular, hasta los mecanismos bioquímicos de interacción y adaptación al entorno. En este campo son muy importantes los estudios centrados en los límites de la biología, como la virología, y herramientas para la comprensión de los mecanismos de transmisión de información, de supervivencia y adaptabilidad, como las cuasi-especies. Entre los últimos avances de la química prebiótica de interés para la Astrobiología se encuentra el análisis de la quiralidad, una preferencia de la química de los organismos vivos por una simetría específica que nos puede acercar al proceso de su formación durante el crecimiento de la complejidad y la jerarquización de los procesos. Naturalmente, los mecanismos de transferencia de información genética resultan críticos para comprender la adaptabilidad molecular y son otro objetivo prioritario de la Astrobiología.
Está claro que la historia científica de la creación de la vida puede resultar una narración apasionante que, correctamente explicada en unión de los conocimientos que hoy poseemos del Universo, puede conseguir que comprendamos la inevitabilidad de la vida, no sólo ya en el planeta Tierra (único lugar -de momento-) en el que sabemos que está presente, sino por todos los confines del inmenso Universo. La diversidad biológica que podríamos contemplar de poder observar lo que por ahí fuera existe, nos llevaría más allá de un simple asombro.


Son formas de vida complejas Extrañas medusas
Si pudiéramos conocer todas las formas de vida que existen la Tierra…. En realidad solo viven el 1% de las especies que poblaron nuestro planeta.
Pero, ¿es realmente cierto que la ignorancia supera al conocimiento como camino más directo hacia el asombro? Bueno, lo que sí sabemos que es cierto es el hecho de que, cuanto más sabemos de las cosas, menos propensos somos al asombro. Y, siendo mucho lo que desconocemos de la historia de la vida y también de la del Universo, podemos decir que sabemos lo suficiente para “saber” que no estamos solos.
Algún día (espero que no demasiado lejano en el tiempo), encontraremos la prueba irrefutable de la existencia de la vida fuera de la Tierra. Espero que lo que hallemos no difiera exageradamente de lo que aquí existe y de lo que existió, seguramente, en esos otros lugares, el recorrido de la vida habrá sido muy similar al nuestro, y, la mayor diversidad de la vida será microbiana, esas formas primarias de vida que reconocemos como los verdaderos diminutos arquitectos de los ecosistemas terrestres. Aquí en la Tierra, la historia completa de la vida abarca unos 4.000 millones de años, desde los extraños mundos de los océanos sulfurosos que se extendían bajo una atmósfera asfixiante, pasando por bacterias que respiraban hierro, hasta llegar por fin a nuestro familiar mundo de oxígeno y ozono, de valles boscosos, de animales que nadan, corren o vuelan. Ni Sheherazade podría haber imaginado un cuento más fascinante.
Hace poco NASA publicó esta foto de una de las lunas de Júpiter. Es volcánica, y genera océanos de lava y azufre. ¿Quién sabe lo que ahí pueda estar presente? Desde luego yo no puedo afirmar ni negar nada. Sin embargo, según lo descubierto aquí en la Tierra, mejor dejar la respuesta para más adelante.
Somos ególatras y nos creemos más de lo que somos. En realidad, simples peones
Hemos alcanzado un nivel de desarrollo intelectual muy aceptable y, puesto que somos grandes animales, se nos puede perdonar que tengamos una visión del mundo que tiende a celebrar lo nuestro, pero la realidad es que nuestra perspectiva es errónea. Tenemos un concepto de nosotros mismos que, habiendo sido elaborado en nuestro cerebro tiende a ser tan irreal que, incluso llegamos a creernos especiales, y, la verdad es que, lo que tenemos de especial queda reducido al ámbito familiar, social y poco más. En el contexto del Universo, ¿Qué somos?

La última teoría de Stephen Hawking, desarrollada con Thomas Hertog antes de morir, sugiere que el universo no es infinito y que es más simple de lo pensado,. Utilizando la teoría de cuerdas, el modelo propone que el universo tiene límites, domesticando el concepto de multiverso para hacerlo comprobable mediante ondas gravitacionales.
Creer que en un Universo “infinito” sólo existen unos seres que habitan un minúsculo objeto redondo, un grano de tierra de una simple Galaxia de entre cien millones…Parece, al menos, pretencioso. Dejemos que la Astrobiología nos indique el camino a seguir, que nuestros ingenios espaciales nos abran el camino y, cuando llegue el momento, partamos a conocer a nuestros hermanos.
La Fuente:
Volumen 23, número 3 de 2009 de la Revista Española de Física, donde se publicó un magnifico trabajo de D. Álvaro Giménez, del Centro de Astrobiología INTA-CSIC. También tiene su parte aquí Andrew H. Knoll, reconocido paleontólogo que, en su libro La vida en un planeta joven, nos ofrece una apasionante narración sobre la vida, y, finalmente, lo poco que por mi parte he podido aportar.
Publica: Emilio Silvera V.
Feb
5
¿El Origen del Universo? ¿Quién puede saber eso?
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en General ~
Clasificado en General ~
 Comments (3)
Comments (3)
“¿Dónde estabas tú cuando yo puse los cimientos de la Tierra? Dilo si tienes entendimiento?”
Claro que a esta pregunta, lo único que podríamos contestar sería:
¿Quién tiene entendimiento pleno?
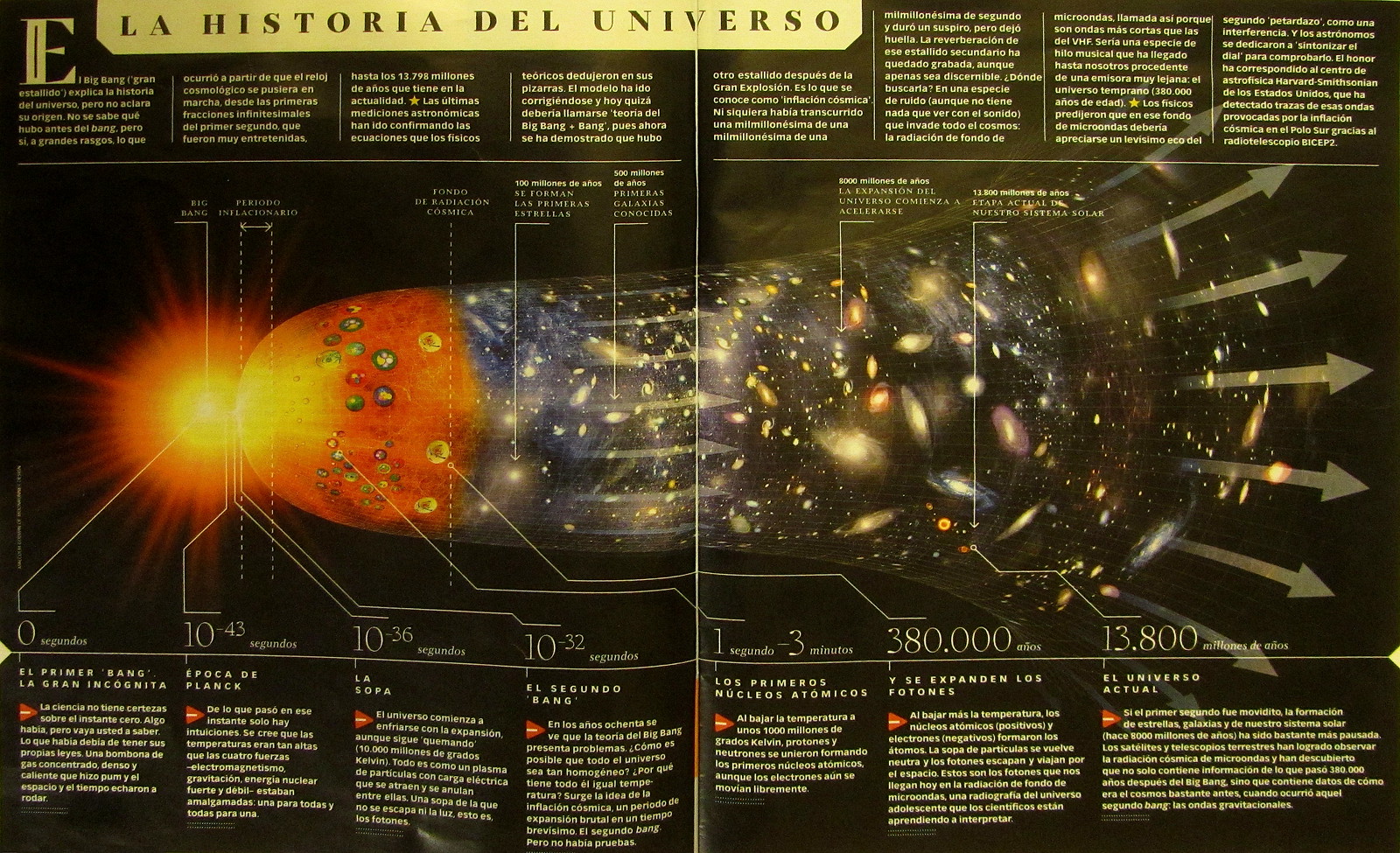
La especulación sobre el origen del universo es una vieja actividad humana que está sin resolver, ya que, pretendemos saber algo que no sabemos si llegó a ocurrir, toda vez que incluso, podría ser, que el universo esté aquí desde siempre. Y, si llegó como algo nuevo, tampoco sabemos, a ciencia cierta, cómo y de dónde lo hizo. Pero, nosotros, los humanos, no dejamos de especular con esta cuestión de compleja resolución y dejamos volar nuestra imaginación en forma de conjeturas y teorías que, no siempre son el fiel reflejo de lo que pudo pasar que, de momento, permanece en el más profundo anonimato.

Claro que la Humanidad y el Universo están tan juntos (nosotros también somos universo), tan conectados que, sería imposible que no hablaran de él, y, sobre todo, que no trataran de saber su comienzo (si es que lo hubo) y, hurgar en su dinámica para poder entender nuestra presencia aquí junto con las estrellas de las que procedemos y de las galaxias que son las “villas” del Universo que alojan a cientos de millones de mundos ¿habitados? que, como la Tierra, tienen otras criaturas que también, ellas se preguntan por el principio y el final para poder conocer sus destinos.
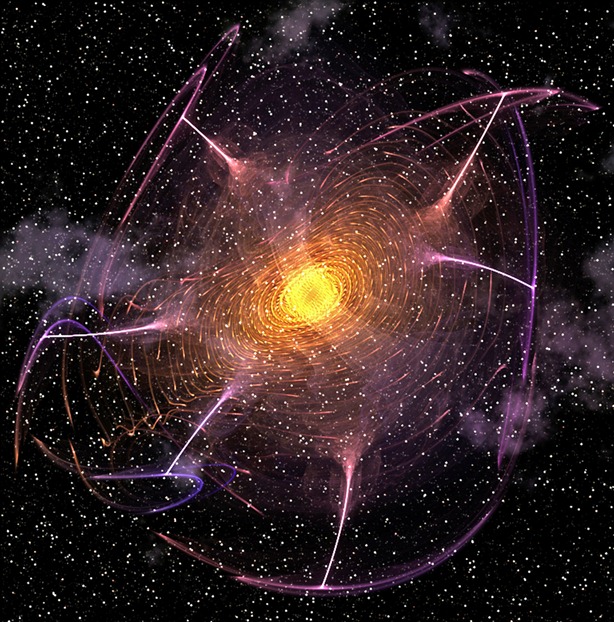
Si surgió es porque había, nada puede aparecer a partir de la “Nada” que, en realidad, no existe
Algunos nos dicen que el Universo surgió de la “Nada” y, está claro que la Nada no puede existir y, si surgió es porque había, con lo cual, la Nada queda invalidada. Pero, si hubo un suceso de creación, ¿Qué duda nos puede caber de que tuvo que haber una causa? Lo cierto es que, en las distintas teorías de la “creación” del universo, existen muchas reservas. No puedo quitarme del pensamiento ¡Una Fluctuación de Vacío!

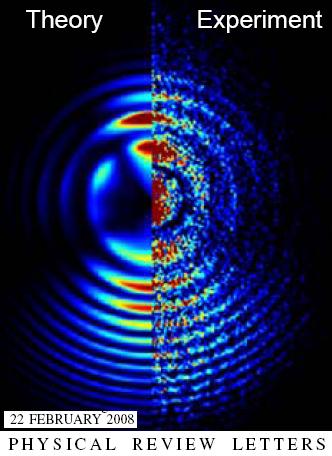
En experimentos científicos se han medido las Fluctuaciones del Vacío
Resulta que el “vacío” está lleno a rebozar.
No obstante tales reservas, unos pocos científicos trataron de investigar la cuestión de cómo pudo haberse originado el universo, aunque admitiendo que sus esfuerzos quizás eran “prematuros”, como dijo Weinberg con suavidad. En el mejor de los casos, contemplado con una mirada alentadora, el trabajo realizado hasta el momento, parece haber encendido una lámpara en la antesala de la génesis. Lo que allí quedó iluminado era muy extraño, pero era, en todo caso, estimulante. No cabía descubrir algo familiar en las mismas fuentes de la creación.

Hemos podido contemplar como en la Nebulosa del Águila nacen nuevas estrellas masivas. Sin embargo, no hemos llegado a poder saber, con certeza como surgió el Universo entero y de dónde y porqué lo hizo para conformar un vasto espacio-tiempo lleno de materia que evolucionaría hasta poder conformar las estrellas y los mundos en enormes galaxias, y, en esos mundos, pudieron surgir criaturas que, conscientes de SER, llegaron desde un nivel animal rudimentario, hasta los más sofisticados pensamientos que les hicieron preguntarse: ¿Quiénes somos, de dónde venimos, hacia dónde vamos? Y, esas preguntas, realizadas 14.000 millones de años después del comienzo del tiempo, y junto a la pregunta del origen del Universo, todavía, no han podido ser contestadas. Nuestro intelecto evoluciona pero, sus límites son patentes.

Una estrella que se forma en la Nebulosa comienza siendo proto-estrellas y, cuando entra en la secuencia principal, brilla durante miles de millones de años durante los cuales crea nuevos elementos a partir del más sencillo, el Hidrógeno. Los cambios de fase que se producen por fusión en el horno nuclear de las estrellas, son los que han permitido que existieran los materiales necesarios para la química de la vida que, al menos hasta donde sabemos, no apareció en nuestro planeta Tierra, hasta hace unos 4.o0o millones de años, y, desde entonces, ha estado evolucionando para que ahora, nosotros, podamos preguntas, por el origen del universo.
Nada puede surgir de la nada (que en realidad no existe, siempre hay).
Los científicos han imaginado y han puesto sobre la mesa para su estudio, dos hipótesis, la llamada génesis del vacío, y la otra, génesis cuántica y ambas, parecían indicar mejor lo que el futuro cercano podía deparar al conocimiento humano sobre el origen del Universo.
La Génesis de vacío: El problema central de la cosmología es explicar como algo surge de la nada. Por “algo” entendemos la totalidad de la materia y la energía, el espacio y el tiempo: el universo que habitamos. Pero la cuestión de lo que significa NADA es más sutil. En la ciencia clásica, “nada” era un vacío, el espacio vacío que hay entre dos partículas de materia. Pero esta concesión siempre planteaba problemas, como lo atestigua la prolongada indagación sobre si el espacio estaba lleno de éter, y en todo caso no sobrevivió al advenimiento de la física cuántica.
El vacío cuántico nunca es realmente vacío, sino que resoba de partículas “virtuales”. Las partículas virtuales pueden ser concebidas como la posibilidad esbozada por el principio de indeterminación de Heisenberg de que una partícula “real” llegue en un tiempo determinado a un lugar determinado. Como las siluetas que salen de pronto en un campo de tiro policial, representan no sólo lo que es sino también lo que podría ser. Desde el punto de vista de la física cuántica, toda partícula “real” está rodeada por una corona de partículas y antipartículas virtuales que borbotean del vacío, interaccionan unas con otras y luego desaparecen.
Las ondas fluctúan de forma aleatoria e impredecible, con energía positiva momentáneamente aquí, energía negativa momentáneamente allí, y energía cero en promedio. El aspecto de partícula está incorporado en el concepto de partículas virtuales, es decir, partículas que pueden nacer en pares (dos partículas a un tiempo), viviendo temporalmente de la energía que se producen en las fluctuaciones tomada prestada de regiones “vecinas” del espacio, y que luego se aniquilan y desaparecen, devolviendo la energía a esas regiones “vecinas”. Si hablamos de fluctuaciones electromagnéticas del vacío, las partículas virtuales son fotones virtuales; en el caso de fluctuaciones de la gravedad en el vacío, son gravitones virtuales.
Fluctuaciones en el Vacío Cuántico
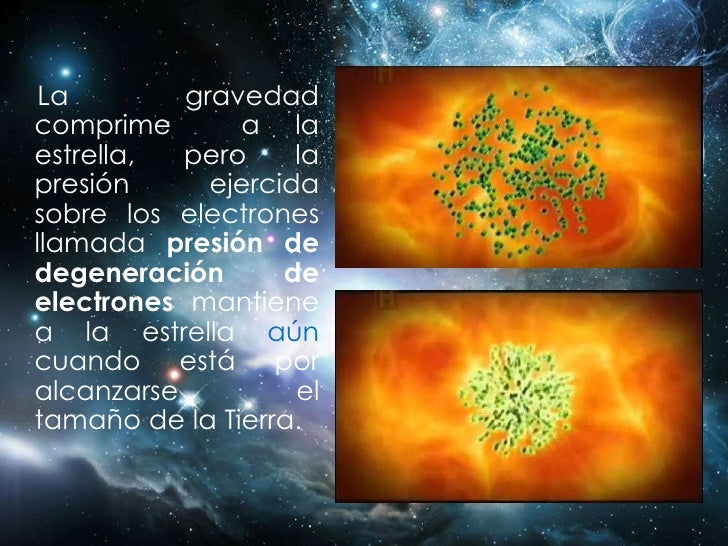
Claro que, en realidad, sabemos poco de esas regiones vecinas de las que tales fluctuaciones toman la energía. ¿Qué es lo que hay allí? ¿Está en esa región la tan buscada partícula de Higgs? Sabemos que las fluctuaciones de vacío son, para las ondas electromagnéticas y gravitatorias, lo que los movimientos de degeneración claustrofóbicos son para los electrones. Si confinamos un electrón a una pequeña región del espacio, entonces, por mucho que uno trate de frenarlo y detenerlo, el electrón está obligado por las leyes de la mecánica cuántica a continuar moviéndose aleatoriamente, de forma impredecible. Este movimiento de degeneración claustrofóbico que produce la presión mediante la que una estrella enana blanca se mantiene contra su propia compresión gravitatoria o, en el mismo caso, la degeneración de neutrones mantiene estable a la estrella de neutrones, que obligada por la fuerza que se genera de la degeneración de los neutrones, es posible frenar la enorme fuerza de gravedad que está comprimiendo la estrella.
Una cosa sí sabemos, las reglas que gobiernan la existencia de las partículas virtuales se hallan establecidas por el principio de incertidumbre y la ley de conservación de la materia y de la energía.

En un nuevo estudio, un grupo de físicos ha propuesto que la gravedad podría disparar un efecto desbocado en las fluctuaciones cuánticas, provocando que crezcan tanto que la densidad de energía del vacío del campo cuántico podría predominar sobre la densidad de energía clásica. Este efecto de predominancia del vacío, el cual surge bajo ciertas condiciones específicas pero razonables, contrasta con la ampliamente sostenida creencia de que la influencia de la gravedad sobre los fenómenos cuánticos debería ser pequeña y subdominante.
Claro que, hablar aquí del vacío en relación al surgir del universo, está directamente asentado en la creencia de algunos postulados que dicen ser posible que, el universo, surgiera de una Fluctuación de vacío producida en otro universo paralelo y, desde entonces, funciona de manera autónoma como un nuevo universo de los muchos que son en el más complejo Meta-verso.

Inmediatamente después de que la llamada espuma cuántica del espacio-tiempo permitiera la creación de nuestro Universo, apareció una inmensa fuerza de repulsión gravitatoria que fue la responsable de la explosiva expansión del Universo primigenio (inflación(*)).Las fluctuaciones cuánticas del vacío, que normalmente se manifiestan sólo a escalas microscópicas, en el Universo inflacionario en expansión exponencial aumentaron rápidamente su longitud y amplitud para convertirse en fluctuaciones significativas a nivel cosmológico.
En el Modelo corriente del Big Bang que actualmente prevalece y que, de momento, todos hemos aceptado al ser el que más se acerca a las observaciones realizadas, el universo surgió a partir de una singularidad, es decir, un punto de infinita densidad y de inmensa energía que, explosionó y se expansionó para crear la materia, el espacio y el tiempo que, estarían gobernados por las cuatro leyes fundamentales de la naturaleza:
Fuerzas nucleares débil y fuerte, el electromagnetismo y la Gravedad. Todas ellas, estarían apoyadas por una serie de números que llamamos las constantes universales y que hacen posible que nuestro universo, sea tal como lo podemos contemplar. Sin embargo, existen algunas dudas de que, realmente, fuera esa la causa del nacimiento del Universo y, algunos postulan otras causas como transiciones de fase en un universo anterior y otras, que siendo más peregrinas, no podemos descartar.
Nosotros, estamos confinados en el planeta Tierra que es un mundo suficientemente preparado para acoger nuestras necesidades físicas, pero, de ninguna manera podrá nunca satisfacer nuestras otras necesidades de la Mente y del intelecto que produce imaginación y pensamientos y que, sin que nada la pueda frenar, cual rayo de luz eyectado desde una estrella masiva refulgente, nuestros pensamientos vuelan también, hacia el espacio infinito y con ellos, damos rienda suelta a nuestra más firme creencia de que, nuestros orígenes están en las estrellas y hacia las estrellas queremos ir, allí, amigos míos, está nuestro destino.
Nuestro destino y nuestro origen están en las estrellas
El Universo es grande, inmenso, casi infinito pero, ¿y nosotros? Bueno, al ser una parte de él, al ser una creación de la Naturaleza, estamos formando parte de esta inmensidad y, precisamente, nos ha tocado desempeñar el papel de la parte que piensa, ¿tendrá eso algún significado?
Yo, no lo sé… Pero… ¿¡Quién sabe realmente!?
Emilio Silvera V.
Feb
5
Un paseo por el Universo
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en General ~
Clasificado en General ~
 Comments (0)
Comments (0)
Cygnus Loop (W78 fuente de radio, o Sharpless 103) es un remanente grande supernova (SNR) en la constelación de Cygnus, una nebulosa de emisión que mide casi 3 ° de ancho. Algunos arcos del bucle, conocidos colectivamente como la Nebulosa del Velo o Nebulosa Cirrus, emite luz visible.
La parte visual del Cygnus Loop es conocida como la Nebulosa del Velo, también llamada la Nebulosa Cirrus o la Nebulosa filamentosa. Varios componentes tienen nombres e identificadores separados, incluyendo el “Velo occidental” o “Escoba de bruja“, “Velo del Este“, y Triángulo de Pickering.
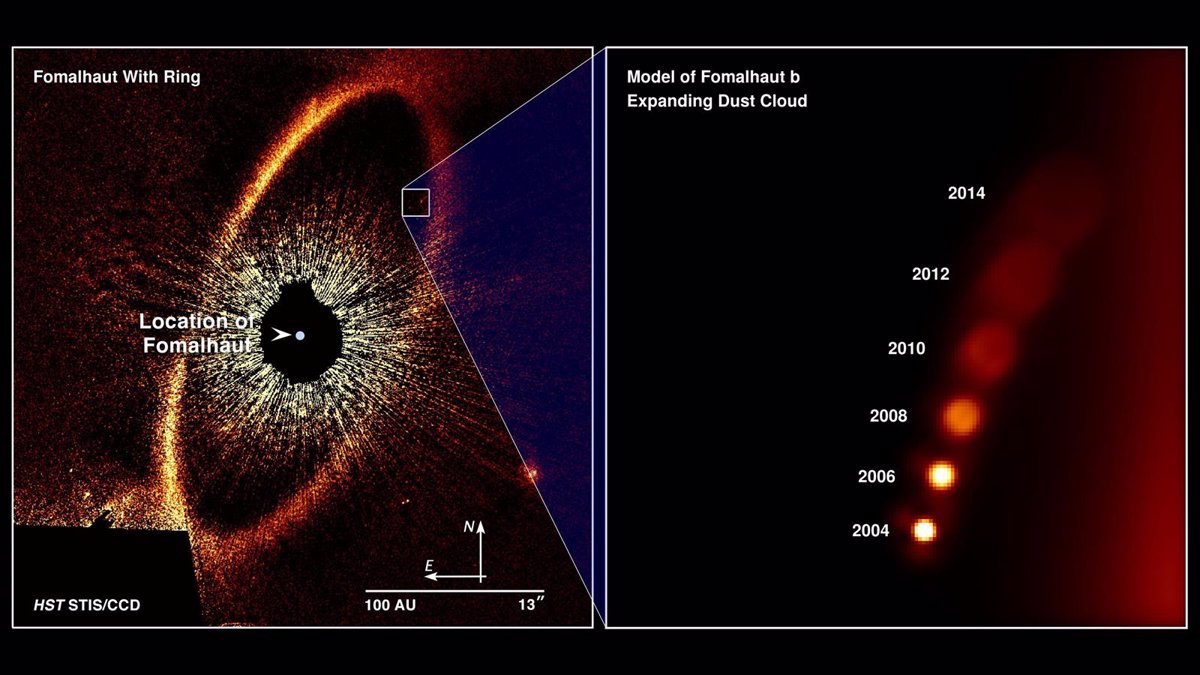
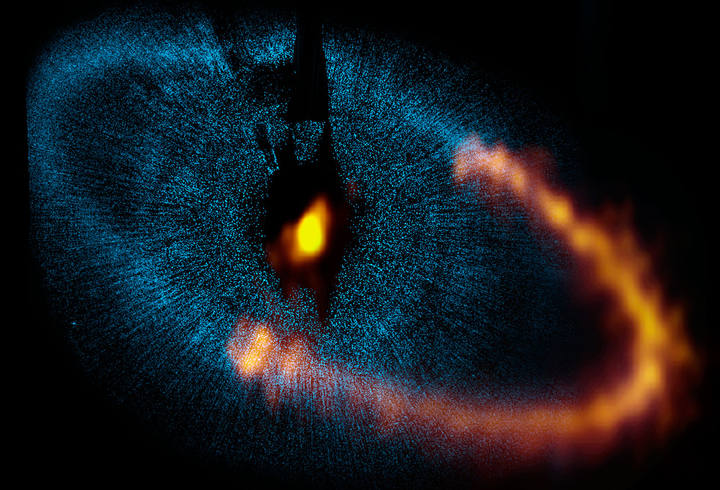
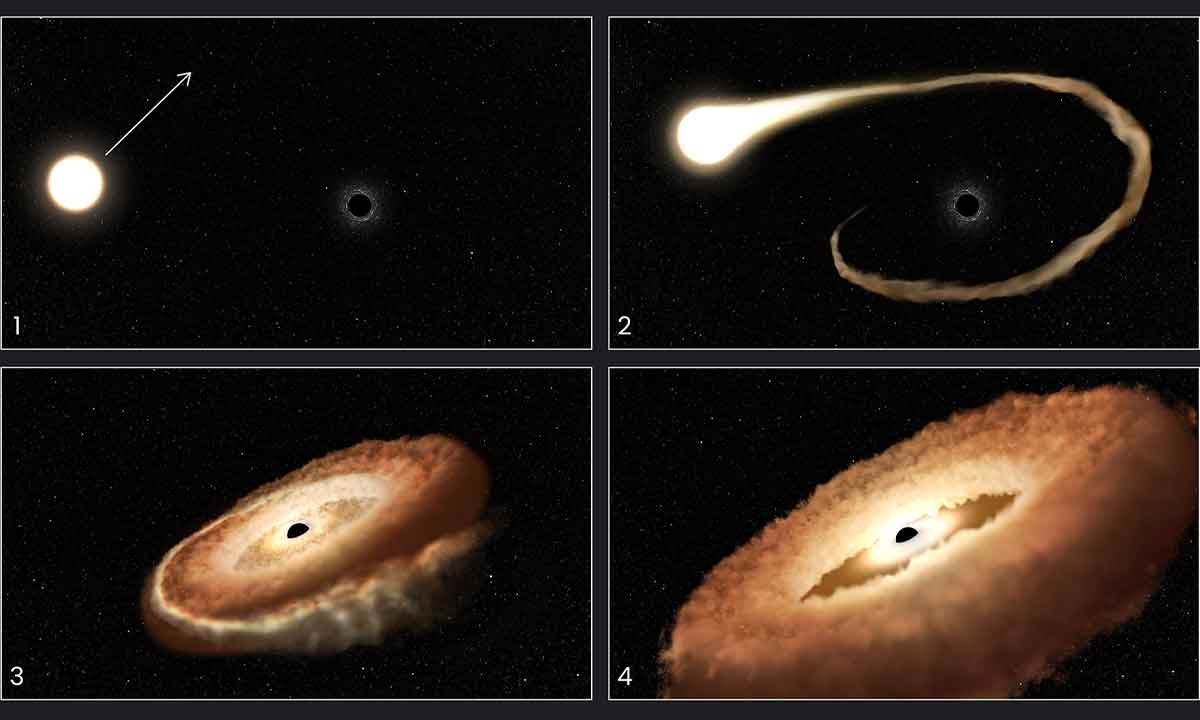
Fomalhaut b, el planeta que nunca existió
La ESO ha obtenido la imagen infrarroja más precisa de la Nebulosa Carina captada por el Telescopio de Largo Alcance del Observatorio Austral Europeo. La Nebulosa de la Quilla, también llamada Nebulosa de Carina, Nebulosa de Eta Carinae o NGC 3372, es una gran nebulosa de emisión (cuatro veces más grande que Orión) que rodea varios cúmulos abiertos de estrellas. Entre estas estrellas se encuentran Eta Carinae y HD 93129A, dos de las estrellas más masivas y más luminosas en la Vía Láctea. La nebulosa se encuentra a una distancia estimada de entre 6 500 a 10 000 años-luz de la Tierra. Se encuentra localizada en la constelación de la Quilla (Carina). Esta nebulosa contiene diversas estrellas tipo O.

Constelación dela Popa
Carina (la quilla), es una constelación austral austral que forma parte de la antigua constelación de Argo Navis (el navío Argo). La Unión Astronómica Internacional la dividió en cuatro componentes: Carina (la Quilla), Vela (la Vela), Puppis (la Popa) y Pyxis (el compás o la Brújula).


Argo Navis Nebulosa Carina

Los restos de la supernova Vela, a ojos del telescopio VLT y Puppis
“Argo Navis. Extensa constelación en el hemisferio sur celeste, que representaba el navío en que viajaron Jasón y los Argonautas en la mitología griega. Esta es la única constelación descrita por Claudio Ptolomeo que no se reconoce en la actualidad, debido a que fue dividida en varias constelaciones.”
Las fuerzas de marea de la galaxia compañera más pequeña y su tirón gravitacional han causado que la pareja simule un conjunto en forma de rosa, la llamada “rosa del espacio”.

Aquí la joven estrella S106 IR expulsa material a gran velocidad y perturba el gas y el polvo que la rodean, rebelándose contra su ’nube madre’. La postal captada por el Hubble tiene forma de ángel con las alas extendidas. El 16 diciembre de 2011, una de las cámaras de gran campo del telescopio espacial Hubble ha captado esta imagen de una nube de hidrógeno gigante iluminada por una brillante estrella joven. La imagen revela cuán violentas pueden llegar a ser las etapas finales del proceso de formación estelar.
“Sharpless 2-106 (Sh2-106 or S106 for short) is a bipolar emission nebula and HII region. It measures about 2 light-years long by 0.5 light-year across and is located about 2,000 light-years away in the constellation Cygnus, in a relatively isolated region of the Milky Way.”
Pese a los colores celestiales de esta imagen, nada ocurre tranquilamente en la región de formación estelar Sh 2-106, o S106. En ella se aloja la joven estrella S106 IR, que expulsa a gran velocidad material que altera el gas y el polvo circundantes. Esta estrella tiene una masa 15 veces superior a la del sol y está en las etapas finales de su formación; pronto, cuando entre en la fase de su evolución llamada ‘de secuencia principal’ –el equivalente a la etapa adulta de su vida estelar-, se calmará y brillará durante algunos millones de años. Vivirá menos que el Sol, ya que, su voracidad en consumir el material estelar será mucho mayor.






Todos esos materiales lucen los colores que corresponden a los distintos elementos ionizados por la radiación estelar
Emilio Silvera V.
















 Totales: 86.227.982
Totales: 86.227.982 Conectados: 93
Conectados: 93