Ya sabemos que, nuestros ancestros, ante los fenómenos naturales que no podían comprender, echaban manos de lo divino, una fuerza superior estaba avisándoles de que, podían ser castigados. En todos las Civilizaciones (como hemos podido comprobar), algunos avispados se dieron cuenta del poder que tenía ese “Ente Divino”, y, lo utilizaron para montar un oráculo que les permitiera vivir cómodamente y estar bien alimentados, dormir bajo buenos techos, y, acercarse al núcleo del poder y la riqueza para impartir parabienes (no ayuda real), a los fieles crédulos que los seguían escuchando sus amenazas del infierno y el poder que ellos tenían de salvar sus Almas a cambio de buenas dádivas.

El invento del Alma ¡qué gran negocio!

¿Las ideas? ¡Qué peligro!

No siempre tener ideas y, sobre todo, expresarlas en alta voz, ha resultado conveniente.

Es la única libertad que nos podemos permitir.  El pensar libremente y para nosotros mismos, otra cosa es el exponer nuestros pensamientos a los demás.  Unas veces por inconveniente, otras por pudor, otras por temor a las críticas, y otras por parecernos a nosotros mismos indignas de ser conocidas…,  así se pierden grandes ideas.

La promesa de salvar al Alma

En otros ámbitos, y, a lo largo de los tiempos, se aposentaron otros senderos que idearon las clases dominantes para manejar las mentes del pueblo llano y confundir, la ya de por sí endeble preparación que poseían.

Si pudiera iría en busca del Alma etérea, y, hablaría con ella, le haría esas grandes preguntas que nadie ha sabido nunca contestar. Claro que, la primera pregunta que habría que contestar sería: ¿Existe en realidad el Alma, o, por el contrario, es un invento interesado del hombre?

Es verdad que, nosotros, los Humanos, nos aferramos a las vivencias de nuestra niñez, las enseñanzas que recibimos en la infancia en el Colegio y, a lo que nos decían nuestros educadores, y, siendo así, no pocas veces he podido “sentir” el Alma en los ojos brillantes de mis hijos, en cuyos profundos e infinitos senderos, he podido vislumbrar el Universo entero.

 

Es verdad que, nosotros, los Humanos, nos aferramos a las vivencias de nuestra niñez, las enseñanzas que recibimos en la infancia en el Colegio y, a lo que nos decían nuestros educadores, y, siendo así, no pocas veces he podido “sentir” el Alma en los ojos brillantes de mis hijos, en cuyos profundos e infinitos senderos, he podido vislumbrar el Universo entero.

También, en una mirada de mi amada esposa, he podido sentir el Alma. En un bello paisaje, en una hermosa y brillante Galaxia, en las nubes que forman figuras arabescas y siempre cambiantes, en la hermosa fronda de un verde bosque, en el trinar de las aves y en su hermosos plumajes, en las Nebulosas cargadas de estrellas brillantes, en el pulso de una estrella de Neutrones, en…en…en…¿puede estar el Alma en tantos lugares?

Mientras crecemos se producen cambios en nuestros cuerpos y en los órganos vitales, nuevas células crecen y suplantan a las que ya dieron su rendimiento. Sin embargo, llegado el momento del final de nuestro ciclo, nada puede evitar que nos vayamos para siempre, y, ahí radica el origen de la gran idea de las religiones, al prometer, esa salvación más allá de la muerte del cuerpo que no del Alma que es inmortal.

También, en una mirada de mi amada esposa, he podido sentir el Alma. En un bello paisaje, en una hermosa y brillante Galaxia, en las nubes que forman figuras arabescas y siempre cambiantes, en la hermosa fronda de un verde bosque, en el trinar de las aves y en su hermosos plumajes, en las Nebulosas cargadas de estrellas brillantes, en el pulso de una estrella de Neutrones, en…en…en…¿puede estar el Alma en tantos lugares?

¿Será el Alma, si acaso, una ráfaga de luz que habita dentro de nosotros y nos deja cuando nos llega el final? Bueno, esa fue la idea original, y, desde luego, dejó pingües beneficios a muchos que la explotaron. ¡El Alma! Posiblemente sea la idea más luminosa desde que el hombre existe.

 

 

Un pensamiento difuso y confuso que nos inculcaron y subyace dentro de nuestras mentes…vagando por algún rincón del cerebro alguna vocecilla nos dice…”Alma” Alma” para que no olvidemos las palabras de aquellos “santones” que, a nuestros ancestros le inculcaban la idea para obtener sus rentas a cambio de la salvación en el más allá.

Es verdaderamente meritoria la idea del Alma, una idea poderosa que hace posible la esperanza en el “más allá” (posibilitando que otros vivieran mejor en el más acá), la vida después de la muerte.  Todos podemos ver como el cuerpo se destruye cuando se muere, sin embargo, el Alma invisible, puede dejar el cuerpo y etérea flotar hasta los cielos (si hemos sido buenos) o a los infiernos (si hemos sido malos).

Mirando la Historia y lo que ahora mismo nos rodea, si eso es así ¿Cómo tendría que ser de grande el Infierno? ¡Si todos vivieran acorde a lo que predican! Sin embargo no es así, y, tal verdad, nos lleva a desconfiar cuando se dice una cosa y se hace la contraria.

Si no haces lo que predicas…

 

 

La rentabilidad obtenida por la Idea del Alma ha sido grande. En el tema de las religiones, aparte de lo que particularmente pueda creer o no creer, siempre he sido respetuoso con la elección que los demás hayan podido hacer. Todos, sin excepción, debemos tener la libertad de escoger el camino que estimemos más adecuado para todos los ámbitos de nuestras vidas, y, la religión, para muchos, es importante en sus vidas y eso, hay que respetarlo. Pero, también quiero que se respete lo que yo pienso de ciertas cuestiones.

Verdaderamente, la noción de “Alma” podría ser considerada como una de las ideas más grandes de la Humanidad, ha sido muy bien manejada por las religiones para poder dirigir y atemorizar a los pueblos que, ignorantes, estaban a merced de la amenaza divina que en boca de los sacerdotes del momento, fustigaban sin piedad sus conciencias llevadas, a un callejón sin salida de una culpabilidad inexistente que las hacía vulnerables.

Sí, algunos dirán que es más poderosa la idea de Dios que también es más universal, y,  algunos se preguntarán si ambas ideas no se sobreponen.  Y así es, la idea de Dios ha sido una idea poderosísima  a lo largo de la Historia, y continúa siéndolo en gran parte del planeta.  Al mismo tiempo, sin embargo, hay dos buenas razones para pensar que el Alma ha sido (y sigue siendo) una idea más influyente y fecunda que la idea misma de la divinidad.

Gandhi decía que si no existe otra vida, ésta es un timo al que todos queremos aferrarnos.

Una razón es que, con la invención de la otra vida (una idea que no todas las religiones comparten, pero sin la cual una entidad como el Alma tendría mucho menos sentido), se abrió el camino – como antes comentaba- para que las religiones organizadas controlaran las mentes de los hombres para su propio beneficio, hay que tener presente que, por ejemplo la Iglesia, sólo nos da bendiciones, sin embargo, siempre está dispuesta a coger todo lo que pueda.  Si el  pueblo llano conociera las posesiones y riquezas de la Iglesia, el boato y suntuosidad de sus grandes representantes que, impasibles, ven morir a miles y decenas de miles de criaturas en los distintos lugares de la Tierra, sin mover ni un dedo para remediarlo, sin conocieran esto digo, muchos de ellos no pisarían más una iglesia. Y, por otra parte, esa misma Iglesia despiadada y fría, tiene representantes que vagan por los lugares más inhóspitos y necesitamos del mundo y, no pocas veces, han dado su vida por los demás. ¿Cómo entendemos eso?

Ese túnel que finaliza en un luz blanca cegadora que muchos que han estado cercanos a la muerte dicen haber podido ver…¿qué será? Seguramente una ilusión de la Mente que, en un estado traumático, puede, representar escenas apacibles que vengan a relajar el momento y el dolor.

Durante la antigüedad tardía y la Edad Media, la tecnología del Alma, dio un juego excelente para sacerdotes y religiones. Su relación con la “otra vida”, con la divinidad y, en especial, con el clero, permitió a las autoridades religiosas ejercer un poder extraordinario.

No se puede negar que, la idea del Alma, enriqueció inmensamente la mente de los seres humanos a lo largo de los siglos, pero tampoco se puede negar que también es cierto que durante ese mismo tiempo mantuvo a raya el pensamiento y la libertad. ¿Os acordáis de Galileo, o, de Giordano Bruno? Aquellos hechos fueron los detonantes del retrasó el progreso y contribuyó a mantener al pueblo (en su mayor parte) ignorante y sometido al clero educado y culto.

Otro invento que se las trae, ¿de cuántas maneras se puede representar el mal del mundo?

Sólo tenemos que pensar en la desfachatez con que el fraile Johan Tetzel afirmaba que era posible comprar indulgencias para las “aAlmas” del purgatorio, y que estas saldrían volando al cielo tan pronto como las monedas golpearan el plato.  Los abusos como estos, aún persisten hoy en día, nada más claro como ejemplo el ver la cantidad de ancianos y viudas que solos en la vida y enfermos, dejan sus fortunas a la Iglesia que, por cierto, tienen situadas sus propiedades en los mejores enclaves de las ciudades.

Los abusos a que se prestaba lo que algunos llaman “tecnologías del alma” fueron uno de los principales factores que condujeron a la Reforma, la cual, a pesar de lo ocurrido con Juan Calvino en Ginebra, fundamentalmente despojó al clero del control de la fe e impulsó la duda y el descreimiento.

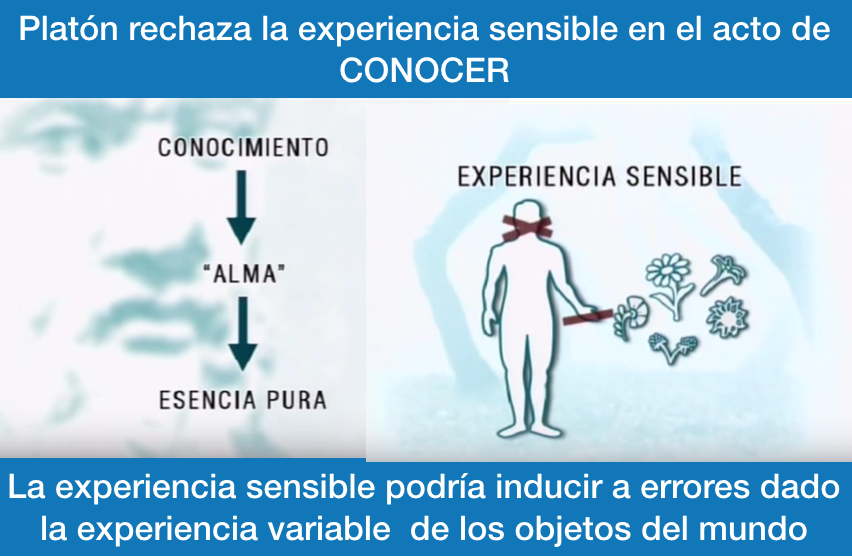
Las diversa transformaciones del alma (la idea de que estaba contenida en el semen en la Grecia de Aristóteles,  el alma tripartita del Timen platónico, la concepción medieval y renacentista del Homo duplex, la idea del alma como mujer, o como ave, el diálogo entre el alma y el cuerpo de Marvell, “las monadas” de Leibniz) pueden resultar hoy bastante pintorescas, pero en su época fueron cuestiones muy serias, y constituyeron importantes etapas en la ruta hacia la idea moderna del ser.

En un anterior trabajo os hablé de manera bastante extensa sobre estas cuestiones del ser, el alma, la conciencia y, en definitiva, del cerebro que es habitad natural de todas estas cuestiones.  La filosofía y la metafísica están presentes haciendo compañía a lo que entendemos por ser conscientes. Las profundidades del ser (nuestro complejo de interioridad) se manifestó en la llamada Era Axial, en términos aproximados, entre los siglos VII y IV a. de C.

Por aquella época, más o menos de manera simultánea, ocurrió algo similar en Palestina, la India,  China, Grecia y muy posiblemente también en Persia.  En cada uno de estos casos, la religión establecida se había vuelto en extremo ritualista y exhibicionista.  En particular, en todas partes habían surgido sacerdotes que se habían adjudicado una posición de altísimos privilegios, con lo cual, Vivian de manera totalmente opuesta a lo que predicaban.

Vivían y siguen viviendo en los mejores Edificios, mientras sus semejantes mueren de frío teniendo por único techo las estrellas. Aquella casta privilegiada, controlaba el acceso a Dios o a los dioses (según los casos), y se beneficiaba de su elevado estatus que, sobre todo, ponían al servicio de los poderosos de turno. Pero en todas estas culturas, surgieron profetas molestos que, al pregonar la salvación del Alma desde otro prisma distinto, dejaban al descubierto las mentiras interesadas de estos sacerdotes y falsas religiones.

   Los Upanishads

Surgieron profetas (en Israel) u hombres sabios (Buda y los autores de los Upanishads en la India, Confucio en China,  etc.)  Que denunciaron al clero y recomendaron la introspección, a sostener que la ruta hacia la auténtica santidad implicaba algún tipo de abnegación y de estudio íntimo.  Platón sentó las bases de la supremacía de la mente sobre la materia.

Todos estos hombres mostraron el camino a través del ejemplo personal, y su mensaje es muy similar al que más tarde predicaron Jesús y,  más tarde, San Agustín y algún otro. No siempre los representantes de las religiones resultaban ser “falsos profetas”, muchos de ellos fueron un ejemplo de honestidad y vivieron haciendo honor a sus palabras.

Por mi parte, ni pretendo que nadie adopte mis ideas personales, ni trato de que renieguen de las suyas, cada cual tendrá una idea de lo que pueda y no pueda ser. Desde pequeño nos inculcaron unas ideas que son difíciles de desterrar en nuestras mentes. Sin embargo, el haber vivido cerca de esas lugares (misas diarias antes de comenzar las clases), y, observar los comportamientos, lo que pregonaban los representantes de esa religión y lo que en realidad hacían… También es un buen acicate para tener las ideas claras sobre lo que es y lo que no es.

El que crea en ese salvador  al final de sus vidas… ¡Morirá con esa esperanza!

El que tenga asumido que la muerte es su último escenario… ¡Morirá en Paz!

Ya sabéis: Cuando nos vayamos de este mundo de problemas y de dolor (con algunas pequeñas alegrías), una cosa es segura: ¡Ninguna estrella dejará de brillar por el!

Y, como decía aquel gran pensador: ” Con el paso de los Eones, hasta la muerte morirá.”

Emilio Silvera Vázquez

[?]

              CERN y ESA: una década de colaboración

Los grandes aceleradores de partículas y las misiones espaciales comparten un entorno de trabajo sometido a intensas radiaciones, extremas (bajas) temperaturas y alto vacío. En ambos casos se ha de procesar una ingente cantidad de información de manera rápida y autónoma.

Mucho se puede ganar mediante la cooperación entre científicos e ingenieros de los dos campos. Por ello, hace diez años, la ESA y el CERN firmaron un acuerdo bilateral de cooperación para compartir conocimientos e información, y desarrollar instrumentación de uso común. Un ejemplo es el telescopio espacial Euclides, lanzado en julio de 2023, cuyo objetivo es explorar el lado oscuro (materia y energía oscuras) del universo, trazando un mapa de su estructura a gran escala, correspondiente a miles de millones de estrellas, cubriendo en la primera fase 132 grados cuadrados del cielo (indicado en la figura mediante el área segmentada coloreada). Se espera abarcar un tercio de la esfera celeste a lo largo del tiempo nominal (seis años) de la misión.

Primeros test en el espacio del telescopio Euclid

El IAC ha contribuido al desarrollo instrumental del proyecto, específicamente en la unidad de control del espectrógrafo y el fotómetro de infrarrojo cercano. Además, el IAC participa activamente en la explotación científica de los datos.

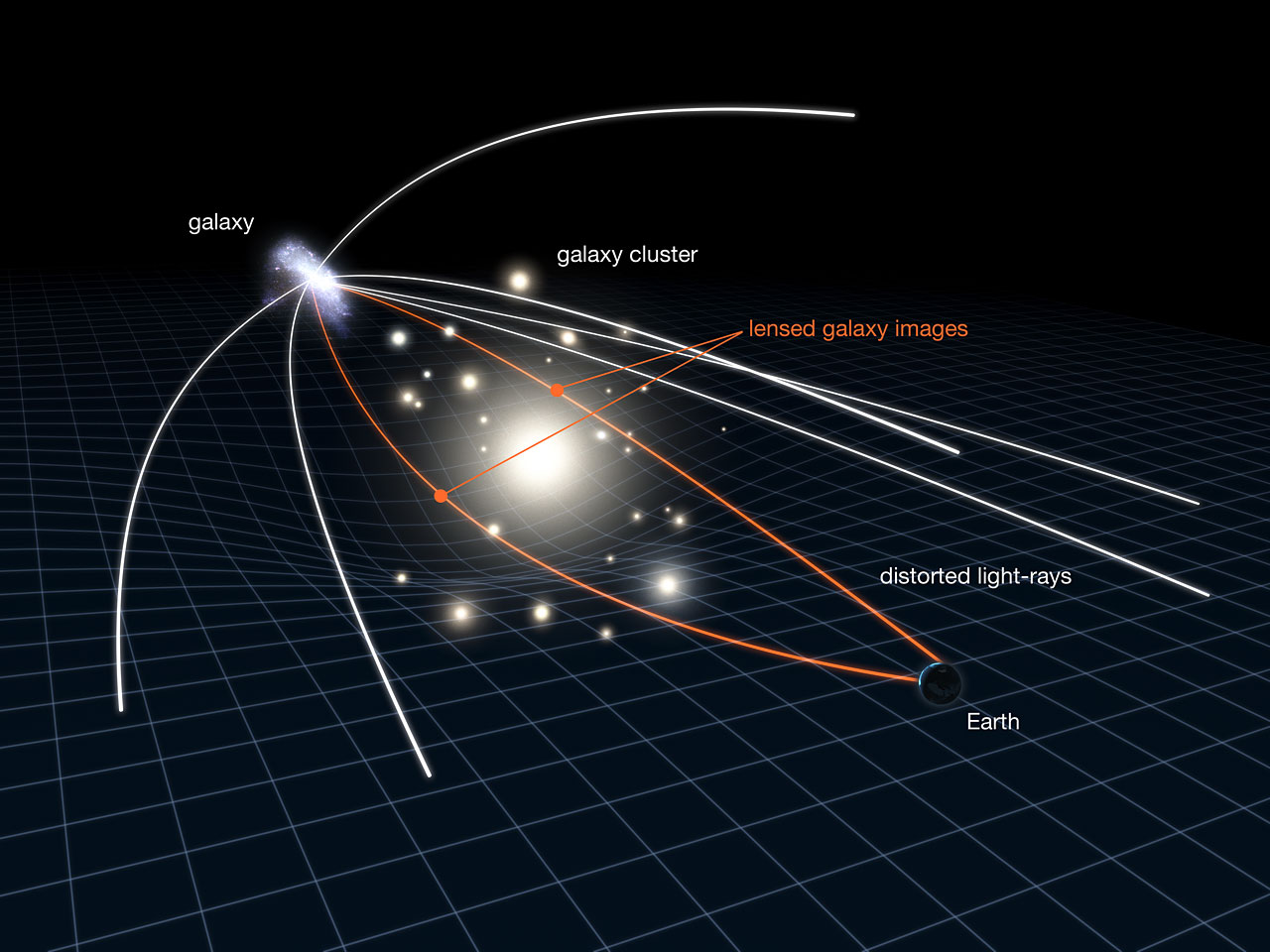
Por su parte, el IFCA ha trabajado en el análisis de datos relacionados con el fenómeno conocido como lente gravitacional y la formación de estructuras cósmicas, una de las herramientas más potentes para investigar la materia oscura. Asimismo, el IFCA ha participado en estudios sobre la morfología y evolución de galaxias, analizando cómo su estructura y propiedades cambian a lo largo de miles de millones de años. Además, en Euclides participan alrededor de 80 empresas europeas, de las cuales 9 son españolas, entre ellas Airbus, Alter Technology, Crisa, Deimos Space, GTD, Navair, Sener y Thales Alenia Space España. Futuras colaboraciones CERN-ESA en cosmología, astrofísica y astronomía de multi-mensajeros incluirán el Laser Interferometer Space Antenna (LISA) y el New Athena X-ray Observatory.

‘Next-Level’ Chaos Traces the True Limit of Predictability

Otras noticias y novedades en el Boletín de Marzo de la R.S.E.F.

[?]

Es la caldera volcánica más grande del mundo, si por fin sale a la superficie… Las consecuencias serán muy serias.

[?]

Lo que no podemos dudar es que la Mente, es un Universo en sí misma

El poder de la Mente es… ¿Infinito! Bueno, de alguna manera sí que lo es. ¿Quién no ha viajado a lugares lejanos y fantásticos, solo con cerrar los ojos e imaginarlos?

Claro que no solo construye fantasías, la Mente es la autora de grandes verdades descubiertas por la Ciencia, la intuición, la imaginación, la curiosidad… Todos “ingredientes” que habitan en la poderosa Mente, y, no pocas veces nos llevaron a desvelar misterios del Universo celosamente guardados.

La Mente que puede inhibir el miedo de un peligro inminente, dentro de ella reina la idea de que, si ocurre lo peor, le espera un paraíso. Ideas religiosas, verdades científicas, imaginaciones de lo que podría ser, todo ello contribuye a la existencia de ese poder mental que nos lleva más allá de lo que cabría esperar que podemos llegar.

La Mente es la creadora de ideas y pensamientos, es la cuna en la que nacen los sentimientos, como en las Nebulosas nacen las brillantes estrellas. ¿Cómo poder explicar lo que sentimos al pensar en el Ser Amado?

Ningún filósofo ha podido dar una explicación creíble del por qué, el enamorado, inmerso en ese sentimiento que llamamos Amor, lo pueden dar todo a cambio de nada,. Un poeta llegó a decir:

“Sufrir por algo que vale la pena… ¡Es una Alegría”

¿Cómo no darlo todo por los seres queridos?

Todo eso y mucho más es la Mente, algo que no hemos llegado a comprender, algo que no es material, algo que surge de una maraña de células eléctricas que llamamos neuronas. ¿No será la Mente ese gran poder que intuimos y que llamamos Conciencia Cósmica?

¿Sabría el Universo que íbamos a venir?

¡Sabemos tan poco!

¡Tenemos tantas dudas!

Si alguna vez llegamos a saber lo que la Mente es… ¡Tendremos todas las respuestas!

Emilio Silvera Vázquez

[?]