Feb
4
¡La Ciencia! ¿Cómo podríamos definirla?
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en La Ciencia ~
Clasificado en La Ciencia ~
 Comments (0)
Comments (0)
No existe una buena definición de la Ciencia. Algunas Sociedades Científicas se decidieron a dejar la suya propia pero, nunca quedaron satisfechos, ya que, si la definición era muy amplia, podría colarse en ella pseudociencias tales como ; si la hacían demasiado restrictiva, podrían quedar excluidos temas como la teoría de cuerdas, la biología evolutiva e incluso la Astronomía.
lo que este simple comentario trata de reflejar, bastaría decir que la Ciencia es un estudio lógico y sistemático de la Naturaleza y del mundo físico que abarca todo el Universo y todo lo que dentro de él está presente. Generalmente incluye tanto experimento como teorías que son verificadas por aquellos.

’El túnel de la ciencia’, en el Museo de Artes e Historia del Forum Cultural de Guanajuato. México
La ciencia (del Latín scientia “conocimiento”) es el conjunto de conocimientos sistemáticamente estructurados, y susceptibles de ser articulados unos con otros formar un todo en un entendimiento “general” de la Naturaleza del Universo.
Aunque la definición pueda resultar algo floja, es, sin embargo un compendio general de lo que entendemos por ciencia. Más arriba escribo “generalmente” en cursiva, porque si planteáramos una exigencia absoluta de experimentos, tendríamos que excluir la Astronomía, la más antigua de todas las ciencias, ya que no es posible recrear nuevas estrellas o galaxias en Laboratorio, ni escenificar la creación del sistema solar. Sin embargo, en Astronomía las observaciones son a menudo tan valiosas los mismos experimentos. El Cometa Halley regresa con una regularidad sorprendente; el Sol sale cada mañana.
El filósofo Karl Popper añadió el requisito de la “refutación” La Ciencia es refutable; la Religión no lo es. Una Teoría o una Ley científica nunca pueden ser demostradas de manera absoluta; de ahí que sea posible refutarlas. Por ejemplo, Newton dijo que la fuerza es igual al producto de la masa por la aceleración (D = ma). No podemos demostrar que todos los objetos de todas las galaxias obedecen ley o que todos los objetos obedecerán siempre esta Ley. Sin embargo, para demostrar la falsedad de esta Ley bastaría un solo experimento. (Albert Einstein y varios expertos en física cuántica han demostrado que algunos de los conceptos de Newton son erróneos.) Por lo tanto, los científicos deben proponer sólo teorías que puedan ser refutadas, tal como afirmó Popper. Estas Teorías han de ser comprobables. No existe tal requisito en el caso de la Religión, en la que prevalece la fe a ciegas.

La Mente Humana está en conexión con el Universo
Dicho esto, sigue habiendo problemas con la definición. , por ejemplo, es refutable. Si nuestros astrólogos nos dicen que nos encontraremos con una guapa extranjera el martes, esto puede comprobarse. Por otra parte, la teoría de las supercuerdas, planteada por algunos físicos como la “teoría del todo”, requeriría un acelerador de partículas con un diámetro de diez años-luz para poder refutarla. La mayor parte de la Biología evolutiva tampoco puede comprobarse experimentalmente. No se puede reproducir la evolución de una especie, ni recrear los dinosaurios comenzando con un animal unicelular. Si aplicamos la regla de la refutación demasiado estrictamente, tendremos que incluir la astrología en el campo de la ciencia y excluir la biología evolutiva, la teoría de cuerdas e incluso quizá la Astronomía.
En consecuencia, es mejor que no nos tomemos demasiado en serio lo de la “refutación” del filósofo de la Ciencia, ya que, de otro modo, podríamos vernos obligados a excluir toda la Ciencia de los antiguos griegos. Estos no sólo eludían el experimento, sino que abominaban de ellos, confiando en que la razón estaba por encima de la evidencia empírica.
Yo, sí he llegado a tener mi propia definición de la Ciencia: “Es el estudio que nos lleva, a través de la observación y el experimento, a la verdadera realidad de la Naturaleza, y, ello, utilizamos nuestra imaginación para construir modelos y teorías que nos acerquen a esa verdad que presentimos y tratamos de desvelar”.
Los que bebemos de la Ciencia, sentimos que Dios se aleja más y más. Sin embargo, no podemos dejar de sentir que, de alguna manera, algo superior nos vigila, yo lo achaco a ese miedo ancestral que, siempre, hemos tenido por lo desconocido y que, inmerso en una profunda ignorancia, no pocas veces hemos querido explicar mediante causas “divinas”, y, sin embargo, cuando, finalmente, hemos dado con las respuestas, estas eran de este mundo y, siempre, eran respuestas lógicas que la Naturaleza nos ofrecía y que no sabíamos compreneder.“ ¿El Creador? Es el Universo con sus complejos sistemas de ritmos y energías el que nos lleva hacia ese futuro que deseamos alcanzar. No existe ningún creador.
Bueno, la definición que de la Ciencia que hago y reseño encima de la imagen de arriba, no será perfecta pero, cumplir los objetivos propuestos es válida y suficiente aunque (como es el caso) le falten algunos matices.
Aquí, en página, siempre nos hemos limitado a aquellas disciplinas más estrictas: La Física, La Astronomía, La Cosmología, La Geología, La Química y La Tecnología, Sin olvidar las matemáticas, ya que son indispensables para la Ciencia y están ineludiblemente conexionada con todas ellas que, de una u otra manera, las necesita para poder expresar, en su más alto grado, lo más profundo que esa Ciencia nos quiere decir. Es decir, las matemáticas son el lenguaje del que se vale la Ciencia para decir al mundo lo que realmente son en cada una de sus vertientes. He dejado aparte y sin querer tratar de ellas, las disciplinas más ligeras –La Antropología, La Agronomía, La Psicología, La Medicina y otras del mismo estilo o parecidas- para otros momentos.
Algo que nunca he tomado en consideración ha sido el pragmatismo de la Ciencia o la motivación de los científicos. Estas cuestiones se han utilizado a menudo para desacreditar las Ciencias no occidentales: sí es un bien hecho, pero no es “puro”, o, a la inversa, no resulta práctico. En cuanto a la motivación, muchos descubrimientos científicos fueron impulsados por la religión: los matemáticos árabes perfeccionaron el álgebra en parte para facilitar las leyes islámicas de la herencia, del mismo modo que los védicos de la India resolvieron raíces cuadradas para construir los altares de los sacrificios con unas dimensiones adecuadas. En estos casos la Ciencia estuvo al servicio de la religión, pero no obstante era Ciencia.
La ley de los epónimos de Stigler, formulada por el experto en estadística Stephen Stigler, afirma que ningún descubrimiento científico lleva el de su descubridor original. El periodista Jim Holt indica que la propia Ley Stigler confirma lo que dice, ya que Stigler admite que la Ley que lleva su nombre fue descubierta por otra persona, concretamente por Robert K. Merton, un especialista en Sociología de la Ciencia.
El área del cuadrado construido sobre la hipotenusa de un triángulo rectángulo, es igual a la suma de las áreas de los cuadrados construidos sobre los catetos.
todos los casos en que se cumple la Ley de Stigler, el más famoso es el del Teorema de Pitágoras (a²+ b² = c², donde a y b son los lados perpendiculares y c es la hipotenusa). Jakob Bronowski escribe lo siguiente:
“Hasta la , el Teorema de Pitágoras sigue siendo el teorema más importante de todas las matemáticas. Esta afirmación puede parecer atrevida y extraordinaria, pero no es extravagante, ya que lo que el teorema de Pitágoras establece es una caracterización fundamental del espacio en que nos movemos y es en este teorema donde dicha caracterización se expresa por primera vez traducida a números. Además, el encaje exacto de los números describe las leyes exactas que rigen el universo. De hecho, se ha propuesto que los números correspondientes a las dimensiones de los triángulos rectángulos sean mensajes que podrían enviarse (de hecho se ha hecho) a planetas de otros sistemas estelares a modo de test, para comprobar si estos planetas tienen ocupación debida a seres dotados de vida racional.
Claro que el problema está en que, no fue Pitágoras el primero que propuso “su” teorema. Los hindúes, los egipcios y los babilonios utilizaban “tríos de números pitagóricos” para determinar ángulos rectos en la construcción de edificios. Un trío de números pitagóricos es un conjunto de tres números que representan las dimensiones de los lados de un triángulo rectángulo. El trío más habitual es 3 : 4 : 5 (3² + 4² = 5² o 9 + 16 = 25). Pitágoras “inventó” este teorema el año 550 a. C. Los Babilonios, según todos los indicios, ya habían catalogado quizá cientos de tríos antes del año 2000 a. C., en una época muy anterior a la de Pitágoras. Uno de los tríos que hallaron los babilonios tienen unos números tan enormes como: 3.367 : 3.456 : 4.825.”

El ojo humano tiene sus limitaciones para ver, sin embargo, la imaginación no tiene barreras y, a lo largo de la historia de la Humanidad se han dado pruebas de lo lejos que pueden llegar nuestros pensamientos.Los Babilonios, egipcios e Hindúes le dejaron un campo sembrado a Pitágoras que, en realidad, sólo tuvo que recoger la abundante cosecha. Él sí supo “ver”.
Ahí están y existen indicios de que los babilonios utilizaron diversas técnicas algebraicas derivadas de la fórmula a² + b² = c². Lo que reconocerse como un logro de Pitágoras, que impresionó a muchos, fue la elaboración de una demostración geométrica del teorema… El área del cuadrado construido sobre la hipotenusa de un triángulo rectángulo, es igual a la suma de las áreas de los cuadrados construidos sobre los catetos.
Fue Euclides quien proclamó dos siglos más tardes la idea de que la demostración podía ser algo más importante que el propio teorema. Por consiguiente, las matemáticas no occidentales han quedado consideradas como unas matemáticas de segunda categoría debido a que se apoyan sobre una base empírica y no sobre demostraciones.

Ambos métodos son útiles. La Geometría euclidiana que aprendimos la mayoría de nosotros es axiomática. Parte4 de un axioma, es decir, una ley que se supone cierta, y los teoremas se deducen razonando de manera descendente a partir de ahí. Es deductiva y axiomática. Siglos más tarde, al-Hazin en Oriente y Galileo en Occidente contribuyeron a popularizar un método inductivo y empírico para la Ciencia, algo más parecido a lo que los babilonios, los egipcios y los hindúes habían utilizado. No se parte de suposiciones sino de y mediciones, para luego razonar de forma ascendente hacia verdades que recubren los datos conocidos. Lo que actualmente llamamos Ciencia es una materia que en su mayor parte es empírica. Cuando Isaac Newton recopiló relativos al paso de los cometas, a las lunas de Júpiter y de Saturno y a las mareas que se producían en el estudio del río Támesis para elaborar una gran síntesis en los Principia, estaba trabajando de una manera empírica e inductiva.
Las matemáticas son ligeramente diferentes, pero muchos matemáticos ven la necesidad de realizar tanto trabajos basados en las demostraciones como trabajos basados en las observaciones empíricas. Un caso puntero que podemos mencionar es el del gran matemático indio Srinivasa Ramanujan, cuyos “cuadernos perdidos” de anotaciones contienen el germen de la teoría de las supercuerdas y cuyos trabajos han sido utilizados para calcular el π hasta millones de dígitos en su parte decimal.

Uno de los secretos más profundos de la teoría de cuerdas, que aún no es bien comprendido, es por qué está definida sólo en diez, once y veintiséis dimensiones. Es ahí, donde la Teoría se hace fuerte y nos facilita la posibilidad de su desarrollo.
Si calculamos cómo se rompen y se vuelven a juntar las cuerdas en el espacio N-dimensional, constantemente descubrimos que pululan términos absurdos que destruyen las maravillosas propiedades de la teoría. Afortunadamente, estos términos indeseados aparecen multiplicados por (N-10). Por consiguiente, para hacer que desaparezcan estas anomalías, no tenemos otra elección cuántica que fijar N = 10. La teoría de cuerdas, de hecho, es la única teoría cuántica conocida que exige completamente que la dimensión del espacio-tiempo esté fijada en un único, el diez.

Por desgracia, los teóricos de cuerdas están, por el momento, completamente perdidos para explicar por qué se discriminan las diez dimensiones. La respuesta está en las profundidades de las matemáticas, en un área denominada funciones modulares (¿Las de Ramanujan?). Al manipular los diagramas de lazos de Kikkawa, Sakita y Virasoro creados por cuerdas en interacción, allí están esas extrañas funciones modulares en las que el 10 aparecen en los lugares más extraños. Estas funciones modulares son tan misteriosas como el hombre que las investigó, el místico del este. Quizá si entendiéramos mejor el de este genio indio, comprenderíamos por qué vivimos en nuestro universo actual.

Una partícula, una cuerda abierta y
una cerrada, describiendo sus órbitas en el
espacio-tiempo 4D.
El misterio de las funciones modulares podría ser explicado por quien ya no existe, Srinivasa Ramanujan, el hombre más extraño del mundo de los matemáticos. Igual que Riemann, murió antes de cumplir cuarenta años, y como Riemann antes que él, trabajó en total en su universo particular de números y fue capaz de reinventar por sí mismo lo más valioso de cien años de matemáticas occidentales que, al estar aislado del mundo en las corrientes principales de los matemáticos, le eran totalmente desconocidos, así que los buscó sin conocerlos. Perdió muchos años de su vida en redescubrir matemáticas conocidas.
Dispersas oscuras ecuaciones en sus cuadernos están estas funciones modulares, que figuran las más extrañas jamás encontradas en matemáticas. Ellas reaparecen en las ramas más distantes e inconexas de las matemáticas. Una función que aparece una y otra vez en la teoría de las funciones modulares se denomina (como ya he dicho otras veces) hoy día “función de Ramanujan” en su honor. Esta extraña función contiene un término elevado a la potencia veinticuatro.
La Teoría de cuerdas, para algunos, es como un revoltijo de números incomprensibles.
El 24 aparece repetidamente en la obra de Ramanujan. Este es un ejemplo de lo que las matemáticas llaman números mágicos, que aparecen continuamente donde menos se les esperan por razones que nadie entiende. Milagrosamente, la función de Ramanujan aparece también en la teoría de cuerdas. El número 24 que aparece en la función de Ramanujan es también el origen de las cancelaciones milagrosas que se dan en la teoría de cuerdas. En la teoría de cuerdas, cada uno de los veinticuatro modos de la función de Ramanujan corresponde a una vibración física de la cuerda. Cuando quiera que la cuerda ejecuta sus movimientos complejos en el espacio-tiempo dividiéndose y recombinándose, deben satisfacerse un gran número de identidades matemáticas altamente perfeccionadas. Estas son precisamente las entidades matemáticas descubiertas por Ramanujan. Puesto que los físicos añaden dos dimensiones más cuando cuentan el número total de vibraciones que aparecen en una teoría relativista, ello significa que el espacio-tiempo debe tener 24 + 2 = 26 dimensiones espacio-temporales.
Una interacción general cuerdas se puede representar como la suma de interacciones más “elementales”, empezando con el diagrama árbol que representa la interacción con la mayor probabilidad de ocurrir, seguida por las correcciones perturbativas, es decir, por los demás diagramas de la serie infinita.

Las cuerdas siguen siendo un misterio por desvelar, y, de momento, no podemos hacerlo. Estamos limitados a conjeturar y teorizar. Parece que Witten lleva razón cuando dice que es una teoría del futuro que se adelantó a su tiempo. No tenemos aceleradores de partículas tan potentes como para poder llegar a las cuerdas.
Para comprender este misterioso factor de dos (que añaden los físicos), consideramos un rayo de luz que dos modos físicos de vibración. La luz polarizada vibrar, por ejemplo, o bien horizontal o bien verticalmente. Sin embargo, un campo de Maxwell relativista Aµ tiene cuatro componentes, donde µ = 1, 2, 3, 4. Se nos permite sustraer dos de estas cuatro componentes utilizando la simetría gauge de las ecuaciones de Maxwell. Puesto que 4 – 2 = 2, los cuatro campos de Maxwell originales se han reducido a dos. Análogamente, una cuerda relativista vibra en 26 dimensiones. Sin embargo, dos de estos modos vibracionales pueden ser eliminados rompemos la simetría de la cuerda, quedándonos con 24 modos vibracionales que son las que aparecen en la función de Ramanujan.

Srinivasa Ramanujan
Con tan solo doce años dominaba la trigonometría; unos años después se hizo con una copia del libro de George Carr <<A sinopsis of Elementary Results in Pure and Applied Mathematics>>. El libro contenía una lista de los 4.400 resultados clásicos de la matemática, pero sin demostraciones, así es que Ramanujan lo asumió como un reto. Durante los siguientes años se dedicó a fondo en este libro, y comenzó a llenar su libreta de resultados e ideas que no aparecían en el libro original. Al igual que Euler poseía un talento y una intuición excepcional, esto hacía que jugase y trasformarse las fórmulas conseguir nuevas perspectivas.
Cuando se generaliza la función de Ramanujan, el 24 queda reemplazado por el 8. Por lo tanto, el número crítico para la supercuerda es 8+2=10. Este es el origen de la décima dimensión que exige la teoría. La cuerda vibra en diez dimensiones porque requiere estas funciones de Ramanujan generalizadas para permanecer auto consistente. Dicho de otra manera, los físicos no tienen la menor idea de por qué 10 y 26 dimensiones se seleccionan como dimensión de la cuerda. Es como si hubiera algún tipo de numerología profunda que se manifestara en estas funciones que nadie comprende. Son precisamente estos números mágicos que aparecen en las funciones modulares elípticas los que determinan que la dimensión del espacio-tiempo sea diez.
En el análisis final, el origen de la teoría decadimensional es tan misterioso como el propio Ramanujan. Si alguien preguntara a cualquier físico del mundo por qué la naturaleza debería existir en diez dimensiones, estaría obligado a responder “no lo sé”. Se sabe en términos difusos, por qué debe seleccionarse alguna dimensión del espacio tiempo (de lo contrario la cuerda no puede vibrar de una cuánticamente autoconsistente), pero no sabemos por qué se seleccionan estos números concretos.
Quizá la respuesta a todo esto esté esperando a ser descubierta cuando alguien (algún genio matemático como Perelman) sea capaz de entender el contenido de los cuadernos perdidos de Ramanujan.
Está claro que, este simple comentario no explica lo que la Ciencia es y, desde luego, tendríamos que ir a una complejidad mucho más profunda y elevada para poder hablar de algunas ramas de la Ciencia que requieren de un nivel de comprensión de la Naturaleza que, de ninguna manera poseo. ¿Cómo he terminado este como lo he hecho? Empecé con una intención y, por el camino, como si tuviera vida propia, los pensamientos te llevan por otros senderos que, nunca habías pensado recorrer. ¡Qué cosas!
emilio silvera.
Ene
21
¡La Ciencia! Que nos llevará al futuro (Otra cosa es de qué clase será)
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en La Ciencia ~
Clasificado en La Ciencia ~
 Comments (0)
Comments (0)
Lo cierto es que la curiosidad del Ser Humano fue siempre la impulsora de que pudiéramos ir avanzando en el saber del mundo, de la Naturaleza, del Universo mismo. Siempre hemos buscado el cómo el cuando y el por qué de las cosas que podíanmos observar a nuestro alrededor sin comprenderlas. Ya desde los tiempos primitivos, nuestros ancestros, de alguna manera rústica, hicieron y dieron los primeros pasos en Ciencia, cuando llegaron a manejar el fuego o construyeron la rueda.
Cuando nos ponemos a hablar de Ciencia en relación a su historia y los orígenes de la misma, la mayoría de las veces nos perdemos por vericuetos que nos llevan hasta callejones sin salida situados muy lejos en el tiempo y que no podemos ver con claridad. Así las cosas, nos vemos obligados a ser menos ambiciosos y mirar más cerca poder obtener algunos resultados más fiables de lo que pudo pasar en esos pueblos del mundo que, como Sumer, India, Egipto, China y más tarde Grecia, nos dejaron una buena colección de señales del saber que pudieron llegar hasta nuestros días. De todo eso hemos hablado aquí en diversos trabajos presentados.

Sin imaginación nunca habriamos avanzado
La ciencia y el pensamiento proceden de la necesidad de investigar, de indagar, y su fin es la investigación. Ésta nace de una insatisfacción frente a las respuestas que proporciona la tradición las preguntas fundamentales de la existencia humana y material. El fundamento de la primera ciencia de que se tiene noticia, la filosofía, consiste en que el hombre no posee las respuestas a las cuestiones que se le plantean, sino que debe buscarlas para alcanzar la sabiduría: no es “sophias” (sofía) o sabiduría en sí, sino “philosophia”, es decir, amor por la sabiduría, deseo de poseer la sabiduría, indagación directa para rastrear la verdad más allá de las costumbres, de las tradiciones y de las apariencias.
Se han realizado algunos estudios en los que, finalmente, se reconocía que entre el siglo IX y el siglo XV “el flujo de la ciencia y la tecnología entró en Europa sobre todo procedente del Islam”. Expertos de la Revista Sciencie informa de que las contribuciones del Islam y de China figuran entre los acontecimientos que “representan los innumerables giros, vueltas, paradojas, contradicciones, tragedias y otros detalles históricos deshilvanados que se han sintetizado en esa realidad mucho más compleja y variada que es la aventura científica”. Otros acontecimientos de este que figuran en la lista son la práctica de la Alquimia por parte de Newton, el falso descubrimiento de los “rayos N” y las negativas de los geólogos a aceptar la teoría de la deriva continental.
Nos quedamos con lo último pero… El origen está más lejos.
Por lo general, cuando oímos hablar de Isaac Newton nos vienen a la cabeza sus aportaciones a la ciencia, y en especial a la física y las matemáticas. Sin embargo, Newton no sólo fue uno de los más importantes científicos de todos los tiempos, sino que a lo largo de su vida dedicó gran de sus esfuerzos a cuestiones como la Alquimia o la teología, interesándose, por ejemplo, en descifrar lo que interpretó como un código oculto en la Biblia –lo que le llevó al estudio de la cábala hebrea–, o en intentar determinar el probable aspecto del Templo de Salomón, además de muchas otros intereses que hoy pueden resultarnos insólitos un científico.
No existe una buena definición de la Ciencia. Después de muchas tentativas, la American Physical Society, se decidió finalmente por una definición pero, consideraba que si la definición era muy larga, se podrían colar en ella alguna pseudociencias tales como ; si la hacían demasiado estricta, podrían quedar exclídos temas como la teoría de cuerdas, la biología evoluctiva e incluso la Astronomía.

Es una Ciencia por derecho propio, nos habla del Universo, del espacio-tiempo, de todo lo que existe y que está conformado por la materia y, de las fuerzas que lo rigen todo.
Así que definir lo que la Ciencia es, ser realistas, no es una tarea fácil si tenemos en su diversidad, su complejidad, su maravillosa y extensa estructura que hace un recorrido que abarca todo el saber del mundo y, sintetizar eso, en unas pocas palabras…aparte de ser una difícil tarea, tiene el peligro de no decir lo que pretende expresar. “La ciencia es un estudio lógico y sistemático de la naturaleza y del mundo físico que, generalmente incluye tanto experimento como teoría”. En verdad es una definición bastante floja. La Ciencia, eas mucho más que eso y, para esa incompletitud, mejor me quedaría con: “La Ciencia es la que nos lleva hacia la Sabiduría, hacia el conocimiento del “mundo”, del Universo y todo lo que en él está presente”.
En la primera definición (no la mía), el autor ha puesto generalmente en cursiva, y explica: “porque se planteáramos una exigencia absoluta de experimentos, tendríamos que excluir la Astronomía, la más antigua de todas las ciencias, ya que no es posible recreqar nuevas estrellas o galaxias en el laboratorio, ni escenificar la formación del Sistema solar. Sin embargo, en astronomía las observaciones son a menudo tan valiosas como el experimento. El cometa Halley regresa con una regularidad sorprende; el Sol sale mañana”.

El Filósofo Kal Popper añadió el rerquisito de la “refutación”. La Ciencia es refutable; la religión no es. Una teoría o una ley científica munca pueden ser demostradas de una manera absoluta; de ahí que sea posible refutarlas. Por ejemplo, Newton dijo que la fuerza es igual al producto de la masa por la aceleración ( F= ma). No podemos demostrar que todos los objetos de todas las galaxias obedecen ley o que todos los objetos obedecerán siempre esta ley. Sin embargo, para demostrar la falsedad de esta ley bastaría un sólo experimento. (Albert Einstein y algunos expertos en física cuántica han demostrado que algunos de los conceptos de Newton son erróneos). Por lo tanto, los científicos deben proponer sólo teorías que puedan ser refutadas, tal afirmó Popper. Estas teorías han de ser comprobables. No existe tal requisito en el caso de la religión.

Dicho esto, sigue habiendo problemas con la definición de lo que la Ciencia es. , por ejemplo, es refutable. Si un astrólogo nos dice que nos encontraremos con una guapa extranjera el martes, esto puede comprobarse. Por otra parte, la teoría de las supercuerdas, planteada por algunos físicos como la “teoría de todo”, requeriría un acelerador de partículas de diez años-luz de diámetro para poder refutarla. La mayor parte de la biología evolutiva tampoco puede comprobarse experimentalmente. No se puede reproducir la evolución de una nueva especie, ni recrear los dinosaurios comenzando con un animal unicelular. Si aplicamos la regla de la refutación demasiado estrictamente, tendremos que incluir la astrología en el campo de la ciencia y excluir la biología evolutiva, la teoría de cuerdas y quizá incluso la astronomía.
En consecuencia, es mejor que no nos tomemos demasiado en serio lo de la refutación de Popper. De otro modo, podríamos vernos obligados a excluir toda la ciencia de los antiguos griegos. Éstos no sólo eludían los experimentos, sino que abominaban de ellos, confiando en que la razón estaba por encima de la evidencia empírica.
Algo que no se debe tomar en considración es el pragmatismo de la ciencia o la motivación del científico. Estas cuestiones se han utilizado a menudo desacreditar las ciencias no occidentales: sí, es un bien hecho , pero no es “puro”; o, a la inversa, no resulta práctico. En cuanto a la motivación, muchos descubrimientos científicos fueron impulsados por motivos religiosos: los matemáticos árabes perfeccionaron el álgebra en para facilitar las leyes islámicas de la herencia, del mismo modo que los védicos de la India resolvieron raíces cuadradas para construir los altares de los sacrificios con unas dimensiones adecuadas. En estos casos, la ciencia estuvo al servicio de la religión.

La ley de los opónimos de Stigler, formulada por el experto en estadística Stephen Stigler (arriba), afirma que ningún descubrimiento científico lleva el de su descubridor original. Él mismo admite que “su Ley”, en realidad, fue descubierta por Robert K. Merton, un especialista en sociología de la ciencia.
todos los casos en los que se cumple la Ley Stigler, el más famoso es el del Teorema de Pitágoras, según el cual la suma de los cuadrados de los dos lados perpendiculares de un triángulo rectángulo es igual al cuadrado de la hipotenusa de dicho triángulo. O bien en lenguaje matemático, a2 + b2 = c2, donde a y b son los lados perpendiculares y c es la hipotenusa. Jacob Bronowski escribe lo siguiente:

“Hasta la , el Teorema de Pitágoras sigue siendo el teorema más importante de todas las matemáticas. Esta afirmación puede parecer atrevida y extraordinaria, pero no es extravagante, ya que lo que el teorema de Pitágoras establece es una caracterización fundamental del espacio en que nos movemos y es en este teorema donde dicha caracterización se expresa por primera vez traducida a números. Además, el encaje exacto de los números describe las leyes exactas que rigen el universo. De hecho, se ha propuesto que los números correspondientes a las dimensiones de los triángulos rectángulos sean mensajes que podrían enviarse a planetas de otros sistemas solares a modo de test, para comprobar si en estos planetas existe vida racional”.

Claro que, los hindúes, los egipcios y los babilonios utilizaban “tríos pitágóricos” determinar ángulos rectos en la construcción de edificios. Un trío de números pitagóricos es un conjunto de tres números que representan las dimensiones de los lados de un triángulo rectángulo. Pitágoras “inventó” su teorema hacia el año 550 a. C. Los babilonios habían catalogados cientos de tríos antes del año 2000 a. C., en una época en la que Pitágoras ni había nacido.
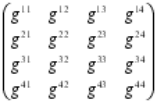
Lo mismo se podría decir de Riemann y Einstein, cuando éste último utilizó el Tensor métrico de aquel (formulado 60 años antes) poder formular su teoría de la relatividad general.
Riemann creó su tensor métrico para que, a partir de ese momento, otros dispusieran de una poderosa herramienta que les hacía posible expresarse, a partir del famoso teorema de Pitágoras (uno de los grandes descubrimientos de los griegos en matemáticas que establece la relación las longitudes de los tres lados de un triángulo rectángulo: afirma que la suma de los cuadrados de los lados menores es igual al cuadrado del lado mayor, la hipotenusa; es decir, si a y b son los longitudes de los dos catetos, y c es la longitud de la hipotenusa, entonces a2 + b2 = c2. El teorema de Pitágoras, por supuesto, es la base de toda la arquitectura; toda estructura construida en este planeta está basada en él. Claro que, es una herramienta para utilizar en un mundo tridimensional).

Los espacios curvos de Riemann
El tensor métrico de Riemann, o N dimensiones, fue mucho más allá y podemos decir que es el teorema para dimensiones más altas con el que podemos describir fenómenos espaciales que no son planos, tales como un remolino causado en el agua o en la atmósfera, como por ejemplo también la curvatura del espacio en presencia de grandes masas. Precisamente, el tensor de Riemann permitió a Einstein formular su teoría de la gravedad y posteriormente lo utilizo Kaluza y Klein para su teoría en la quinta dimensión de la que años más tarde se derivaron las teorías de supergravedad, supersimetría y, finalmente, las supercuerdas.

Para asombro de Eintein, cuando tuvo ante sus ojos la conferencia de Riemann de 1.854 que le había enviado su amigo Marcel Grossman, rápidamente se dio de que allí estaba la clave para resolver su problema. Descubrió que podía incorporar todo el cuerpo del trabajo de Riemann en la reformulación de su principio. Casi línea por línea, el gran trabajo de Riemann encontraba su verdadero lugar en el principio de Einstein de la realtivdad general. Esta fue la obra más soberbia de Einstein, incluso más que su celebrada ecuación E = mc2. La reinterpretación física de la famosa conferencia de Riemann se denomina relatividad general, y las ecuaciones de campo de Einstein se sitúan las ideas más profundas de la historia de la ciencia.

Sí, dudas hemos tenido todos
Hay otras muchas cuestiones de las que podríamos hablar y, la Física y la Astronomía, siendo mi gran Pasión, ocupa mucho de mi tiempo
- Una simetría unificadora.
- La capacidad de explicar grandes cantidades de experimentales con las expresiones matemáticas más económicas.
El Modelo Estándar falla en ambos aspectos, mientras que la relatividad general los exhibe, ambos, de manera bien patente. Nunca una teoría dijo tanto con tan poco; su sencillez es asombrosa y su profundidad increíble.De hecho, que se publicó en 1.915, no ha dejado de dar frutas, y aún no se han obtenido de ella todos los mensajes que contiene.
El principio director del modelo estándar dicta que sus ecuaciones son simétricas. De igual modo que una esfera ofrece el mismo aspecto cualquier punto de vista, las ecuaciones del modelo estándar subsisten sin variación al cambiar la perspectiva desde la que son definidas. Las ecuaciones permanecen invariables, además, cuando esta perspectiva se desplaza en distinta magnitud a diferentes puntos del espacio y el tiempo.
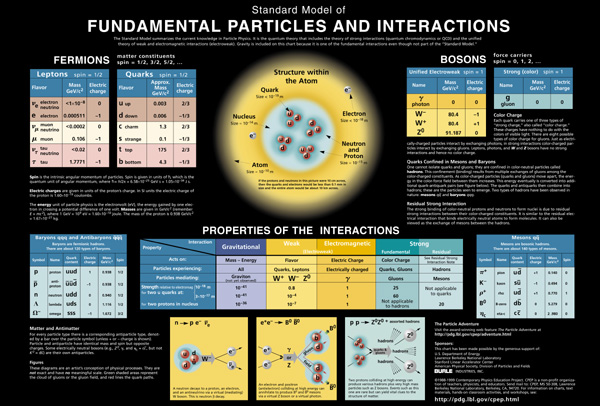
Al contrario de la relatividad general, la simetría del Modelo Estándar, está realmente formada empalmando tres simetrías más pequeñas, una por cada una de las fuerzas; el modelo es espeso e incómodo en su forma. Ciertamente no es económica en modo alguno. Por ejemplo, las ecuaciones de Einstein, escritas en su totalidad, sólo ocupan unos centímetros y ni siquiera llenaría una línea de esta página. A partir de esta escasa línea de ecuaciones, podemos ir más allá de las leyes de Newton y derivar la distorsión del espacio, el Big Bang y otros fenómenos astronómicos importantes como los Agujeros Negros. Por el contrario, sólo escribir el Modelo Estándar en su totalidad requeriría, siendo escueto, un par de páginas y parecería un galimatías de símbolos complejos sólo entendibles por expertos.
Claro que, todo esto es, otroa historia.
emilio silvera
Oct
15
¡Definir la Ciencia! ?Y sus curiosidades?
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en La Ciencia ~
Clasificado en La Ciencia ~
 Comments (3)
Comments (3)
Para lo que este simple comentario trata de reflejar, bastaría decir que la Ciencia es un estudio lógico y sistemático de la Naturaleza y del mundo físico que abarca todo el Universo y todo lo que dentro de él está presente. Generalmente incluye tanto experimento como teorías que son verificadas por aquellos.

’El túnel de la ciencia’, en el Museo de Artes e Historia del Forum Cultural de Guanajuato. México
La ciencia (del Latín scientia “conocimiento”) es el conjunto de conocimientos sistemáticamente estructurados, y susceptibles de ser articulados unos con otros hasta formar un todo en un entendimiento “general” de la Naturaleza del Universo.
Aunque la definición pueda resultar algo floja, es, sin embargo un compendio general de lo que entendemos por ciencia. Más arriba escribo “generalmente” en cursiva, porque si planteáramos una exigencia absoluta de experimentos, tendríamos que excluir la Astronomía, la más antigua de todas las ciencias, ya que no es posible recrear nuevas estrellas o galaxias en Laboratorio, ni escenificar la creación del sistema solar. Sin embargo, en Astronomía las observaciones son a menudo tan valiosas como los mismos experimentos. El Cometa Halley regresa con una regularidad sorprendente; el Sol sale cada mañana.
El filósofo Karl Popper añadió el requisito de la “refutación” La Ciencia es refutable; la Religión no lo es. Una Teoría o una Ley científica nunca pueden ser demostradas de manera absoluta; de ahí que sea posible refutarlas. Por ejemplo, Newton dijo que la fuerza es igual al producto de la masa por la aceleración (D = ma). No podemos demostrar que todos los objetos de todas las galaxias obedecen esta ley o que todos los objetos obedecerán siempre esta Ley. Sin embargo, para demostrar la falsedad de esta Ley bastaría un solo experimento. (Albert Einstein y varios expertos en física cuántica han demostrado que algunos de los conceptos de Newton son erróneos.) Por lo tanto, los científicos deben proponer sólo teorías que puedan ser refutadas, tal como afirmó Popper. Estas Teorías han de ser comprobables. No existe tal requisito en el caso de la Religión.

La Mente Humana está en conexión con el Universo
Dicho esto, sigue habiendo problemas con la definición. La Astrología, por ejemplo, es refutable. Si nuestros astrólogos nos dicen que nos encontraremos con una guapa extranjera el martes, esto puede comprobarse. Por otra parte, la teoría de las supercuerdas, planteada por algunos físicos como la “teoría del todo”, requeriría un acelerador de partículas con un diámetro de diez años-luz para poder refutarla. La mayor parte de la Biología evolutiva tampoco puede comprobarse experimentalmente. No se puede reproducir la evolución de una especie, ni recrear los dinosaurios comenzando con un animal unicelular. Si aplicamos la regla de la refutación demasiado estrictamente, tendremos que incluir la astrología en el campo de la ciencia y excluir la biología evolutiva, la teoría de cuerdas e incluso quizá la Astronomía.
En consecuencia, es mejor que no nos tomemos demasiado en serio lo de la “refutación” del filósofo de la Ciencia, ya que, de otro modo, podríamos vernos obligados a excluir toda la Ciencia de los antiguos griegos. Estos no sólo eludían el experimento, sino que abominaban de ellos, confiando en que la razón estaba por encima de la evidencia empírica.
Yo, sí he llegado a tener mi propia definición de la Ciencia: “Es el estudio que nos lleva, a través de la observación y el experimento, a la verdadera realidad de la Naturaleza, y, para ello, utilizamos nuestra imaginación para construir modelos y teorías que nos acerquen a esa verdad que presentimos y tratamos de desvelar”.
Los que bebemos de la Ciencia, sentimos que “lo divino” se aleja más y más. Sin embargo, no podemos dejar de sentir que, de alguna manera, algo superior nos vigila, yo lo achaco a ese miedo ancestral que, desde siempre, hemos tenido por lo desconocido y que, inmerso en una profunda ignorancia, no pocas veces hemos querido explicar mediante causas “divinas”, y, sin embargo, cuando, finalmente, hemos dado con las respuestas, estas eran de este mundo y, siempre, eran respuestas lógicas que la Naturaleza nos ofrecía y que no sabíamos compreneder.“ ¿El Creador? Es el Universo con sus complejos sistemas de ritmos y energías el que nos lleva hacia ese futuro que deseamos alcanzar. No existe ningún creador.
Bueno, la definición que de la Ciencia hago y reseño encima de la imagen de arrina, no será perfecta pero, para cumplir los objetivos propuestos es válida y suficiente aunque (como es el caso) le falten algunos matices.
Aquí, en esta página, siempre nos hemos limitado a aquellas disciplinas más estrictas: La Física, La Astronomía, La Cosmología, La Geología, La Química y La Tecnología, Sin olvidar las matemáticas, ya que son indispensables para la Ciencia y están ineludiblemente conexionada con todas ellas que, de una u otra manera, las necesita para poder expresar, en su más alto grado, lo más profundo que esa Ciencia nos quiere decir. Es decir, las matemáticas son el lenguaje del que se vale la Ciencia para decir al mundo lo que realmente son en cada una de sus vertientes. He dejado aparte y sin querer tratar de ellas, las disciplinas más ligeras –La Antropología, La Agronomía, La Psicología, La Medicina y otras del mismo estilo o parecidas- para otros momentos.

Algo que nunca he tomado en consideración ha sido el pragmatismo de la Ciencia o la motivación de los científicos. Estas cuestiones se han utilizado a menudo para desacreditar las Ciencias no occidentales: sí es un trabajo bien hecho, pero no es “puro”, o, a la inversa, no resulta práctico. En cuanto a la motivación, muchos descubrimientos científicos fueron impulsados por la religión: los matemáticos árabes perfeccionaron el álgebra en parte para facilitar las leyes islámicas de la herencia, del mismo modo que los védicos de la India resolvieron raíces cuadradas para construir los altares de los sacrificios con unas dimensiones adecuadas. En estos casos la Ciencia estuvo al servicio de la religión, pero no obstante era Ciencia.
La ley de los epónimos de Stigler, formulada por el experto en estadística Stephen Stigler, afirma que ningún descubrimiento científico lleva el nombre de su descubridor original. El periodista Jim Holt indica que la propia Ley Stigler confirma lo que dice, ya que Stigler admite que la Ley que lleva su nombre fue descubierta por otra persona, concretamente por Robert K. Merton, un especialista en Sociología de la Ciencia.
El área del cuadrado construido sobre la hipotenusa de un triángulo rectángulo, es igual a la suma de las áreas de los cuadrados construidos sobre los catetos.
Entre todos los casos en que se cumple la Ley de Stigler, el más famoso es el del Teorema de Pitágoras (a²+ b² = c², donde a y b son los lados perpendiculares y c es la hipotenusa). Jakob Bronowski escribe lo siguiente:
“Hasta la fecha, el Teorema de Pitágoras sigue siendo el teorema más importante de todas las matemáticas. Esta afirmación puede parecer atrevida y extraordinaria, pero no es extravagante, ya que lo que el teorema de Pitágoras establece es una caracterización fundamental del espacio en que nos movemos y es en este teorema donde dicha caracterización se expresa por primera vez traducida a números. Además, el encaje exacto de los números describe las leyes exactas que rigen el universo. De hecho, se ha propuesto que los números correspondientes a las dimensiones de los triángulos rectángulos sean mensajes que podrían enviarse (de hecho se ha hecho) a planetas de otros sistemas estelares a modo de test, para comprobar si estos planetas tienen ocupación debida a seres dotados de vida racional.
La placa con el mensaje que llevan la Pioneer 10 y 11
Claro que el problema está en que, no fue Pitágoras el primero que propuso “su” teorema. Los hindúes, los egipcios y los babilonios utilizaban “tríos de números pitagóricos” para determinar ángulos rectos en la construcción de edificios. Un trío de números pitagóricos es un conjunto de tres números que representan las dimensiones de los lados de un triángulo rectángulo. El trío más habitual es 3 : 4 : 5 (3² + 4² = 5² o 9 + 16 = 25). Pitágoras “inventó” este teorema hacia el año 550 a. C. Los Babilonios, según todos los indicios, ya habían catalogado quizá cientos de tríos antes del año 2000 a. C., en una época muy anterior a la de Pitágoras. Uno de los tríos que hallaron los babilonios tienen unos números tan enormes como: 3.367 : 3.456 : 4.825.”

El ojo humano tiene sus limitaciones para ver, sin embargo, la imaginación no tiene barreras y, a lo largo de la historia de la Humanidad se han dado pruebas de lo lejos que pueden llegar nuestros pensamientos.Los Babilonios, egipcios e Hindúes le dejaron un campo sembrado a Pitágoras que, en realidad, sólo tuvo que recoger la abundante cosecha. Él sí supo “ver”.
Ahí están y existen indicios de que los babilonios utilizaron diversas técnicas algebraicas derivadas de la fórmula a² + b² = c². Lo que puede reconocerse como un logro de Pitágoras, que impresionó a muchos, fue la elaboración de una demostración geométrica del teorema… El área del cuadrado construido sobre la hipotenusa de un triángulo rectángulo, es igual a la suma de las áreas de los cuadrados construidos sobre los catetos.
Fue Euclides quien proclamó dos siglos más tardes la idea de que la demostración podía ser algo más importante que el propio teorema. Por consiguiente, las matemáticas no occidentales han quedado consideradas como unas matemáticas de segunda categoría debido a que se apoyan sobre una base empírica y no sobre demostraciones.
Ambos métodos son útiles. La Geometría euclidiana que aprendimos la mayoría de nosotros es axiomática. Parte de un axioma, es decir, una ley que se supone cierta, y los teoremas se deducen razonando de manera descendente a partir de ahí. Es deductiva y axiomática. Siglos más tarde, al-Hazin en Oriente y Galileo en Occidente contribuyeron a popularizar un método inductivo y empírico para la Ciencia, algo más parecido a lo que los babilonios, los egipcios y los hindúes habían utilizado. No se parte de suposiciones sino de datos y mediciones, para luego razonar de forma ascendente hacia verdades que recubren los datos conocidos. Lo que actualmente llamamos Ciencia es una materia que en su mayor parte es empírica. Cuando Isaac Newton recopiló datos relativos al paso de los cometas, a las lunas de Júpiter y de Saturno y a las mareas que se producían en el estudio del río Támesis para elaborar una gran síntesis en los Principia, estaba trabajando de una manera empírica e inductiva.
Las matemáticas son ligeramente diferentes, pero muchos matemáticos ven la necesidad de realizar tanto trabajos basados en las demostraciones como trabajos basados en las observaciones empíricas. Un caso puntero que podemos mencionar es el del gran matemático indio Srinivasa Ramanujan, cuyos “cuadernos perdidos” de anotaciones contienen el germen de la teoría de las supercuerdas y cuyos trabajos han sido utilizados para calcular el número π hasta millones de dígitos en su parte decimal.
Uno de los secretos más profundos de la teoría de cuerdas, que aún no es bien comprendido, es por qué está definida sólo en diez, once y veintiséis dimensiones. Es ahí, donde la Teoría se hace fuerte y nos facilita la posibilidad de continuar su desarrollo.
Si calculamos cómo se rompen y se vuelven a juntar las cuerdas en el espacio N-dimensional, constantemente descubrimos que pululan términos absurdos que destruyen las maravillosas propiedades de la teoría. Afortunadamente, estos términos indeseados aparecen multiplicados por (N-10). Por consiguiente, para hacer que desaparezcan estas anomalías, no tenemos otra elección cuántica que fijar N = 10. La teoría de cuerdas, de hecho, es la única teoría cuántica conocida que exige completamente que la dimensión del espacio-tiempo esté fijada en un número único, el diez.

Por desgracia, los teóricos de cuerdas están, por el momento, completamente perdidos para explicar por qué se discriminan las diez dimensiones. La respuesta está en las profundidades de las matemáticas, en un área denominada funciones modulares (¿Las de Ramanujan?).
Al manipular los diagramas de lazos de Kikkawa, Sakita y Virasoro creados por cuerdas en interacción, allí están esas extrañas funciones modulares en las que el número 10 aparecen en los lugares más extraños.
Estas funciones modulares son tan misteriosas como el hombre que las investigó, el místico del este. Quizá si entendiéramos mejor el trabajo de este genio indio, comprenderíamos por qué vivimos en nuestro universo actual.

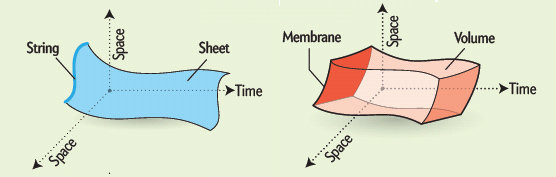
Una partícula, una cuerda abierta y
una cerrada, describiendo sus órbitas en el
espacio-tiempo 4D.
El misterio de las funciones modulares podría ser explicado por quien ya no existe, Srinivasa Ramanujan, el hombre más extraño del mundo de los matemáticos. Igual que Riemann, murió antes de cumplir cuarenta años, y como Riemann antes que él, trabajó en total aislamiento en su universo particular de números y fue capaz de reinventar por sí mismo lo más valioso de cien años de matemáticas occidentales que, al estar aislado del mundo en las corrientes principales de los matemáticos, le eran totalmente desconocidos, así que los buscó sin conocerlos. Perdió muchos años de su vida en redescubrir matemáticas conocidas.
Dispersas entre oscuras ecuaciones en sus cuadernos están estas funciones modulares, que figuran entre las más extrañas jamás encontradas en matemáticas. Ellas reaparecen en las ramas más distantes e inconexas de las matemáticas. Una función que aparece una y otra vez en la teoría de las funciones modulares se denomina (como ya he dicho otras veces) hoy día “función de Ramanujan” en su honor. Esta extraña función contiene un término elevado a la potencia veinticuatro.

El número 24 aparece repetidamente en la obra de Ramanujan. Este es un ejemplo de lo que las matemáticas llaman números mágicos, que aparecen continuamente donde menos se les esperan por razones que nadie entiende. Milagrosamente, la función de Ramanujan aparece también en la teoría de cuerdas. El número 24 que aparece en la función de Ramanujan es también el origen de las cancelaciones milagrosas que se dan en la teoría de cuerdas. En la teoría de cuerdas, cada uno de los veinticuatro modos de la función de Ramanujan corresponde a una vibración física de la cuerda. Cuando quiera que la cuerda ejecuta sus movimientos complejos en el espacio-tiempo dividiéndose y recombinándose, deben satisfacerse un gran número de identidades matemáticas altamente perfeccionadas. Estas son precisamente las entidades matemáticas descubiertas por Ramanujan. Puesto que los físicos añaden dos dimensiones más cuando cuentan el número total de vibraciones que aparecen en una teoría relativista, ello significa que el espacio-tiempo debe tener 24 + 2 = 26 dimensiones espacio-temporales.
Una interacción general entre cuerdas se puede representar como la suma de interacciones más “elementales”, empezando con el diagrama árbol que representa la interacción con la mayor probabilidad de ocurrir, seguida por las correcciones perturbativas, es decir, por los demás diagramas de la serie infinita. Como puede observarse en dicha figura, las superficies que representan las interacciones no se vuelven increiblemente complicadas como los digramas de partículas, ya que sólo hay que agregarle agujeros a una superficie dada.

Para comprender este misterioso factor de dos (que añaden los físicos), consideramos un rayo de luz que tiene dos modos físicos de vibración. La luz polarizada puede vibrar, por ejemplo, o bien horizontal o bien verticalmente. Sin embargo, un campo de Maxwell relativista Aµ tiene cuatro componentes, donde µ = 1, 2, 3, 4. Se nos permite sustraer dos de estas cuatro componentes utilizando la simetría gauge de las ecuaciones de Maxwell. Puesto que 4 – 2 = 2, los cuatro campos de Maxwell originales se han reducido a dos. Análogamente, una cuerda relativista vibra en 26 dimensiones. Sin embargo, dos de estos modos vibracionales pueden ser eliminados cuando rompemos la simetría de la cuerda, quedándonos con 24 modos vibracionales que son las que aparecen en la función de Ramanujan.

Ramanujan en Cambridge
Con tan solo doce años dominaba la trigonometría; unos años después se hizo con una copia del libro de George Carr <<A sinopsis of Elementary Results in Pure and Applied Mathematics>>. El libro contenía una lista de los 4.400 resultados clásicos de la matemática, pero sin demostraciones, así es que Ramanujan lo asumió como un reto. Durante los siguientes años se dedicó a fondo en este libro, y comenzó a llenar su libreta de resultados e ideas que no aparecían en el libro original. Al igual que Euler poseía un talento y una intuición excepcional, esto hacía que jugase y trasformarse las fórmulas hasta conseguir nuevas perspectivas.
Cuando se generaliza la función de Ramanujan, el 24 queda reemplazado por el número 8. Por lo tanto, el número crítico para la supercuerda es 8+2=10. Este es el origen de la décima dimensión que exige la teoría. La cuerda vibra en diez dimensiones porque requiere estas funciones de Ramanujan generalizadas para permanecer auto consistente. Dicho de otra manera, los físicos no tienen la menor idea de por qué 10 y 26 dimensiones se seleccionan como dimensión de la cuerda. Es como si hubiera algún tipo de numerología profunda que se manifestara en estas funciones que nadie comprende. Son precisamente estos números mágicos que aparecen en las funciones modulares elípticas los que determinan que la dimensión del espacio-tiempo sea diez.
En el análisis final, el origen de la teoría decadimensional es tan misterioso como el propio Ramanujan. Si alguien preguntara a cualquier físico del mundo por qué la naturaleza debería existir en diez dimensiones, estaría obligado a responder “no lo sé”. Se sabe en términos difusos, por qué debe seleccionarse alguna dimensión del espacio tiempo (de lo contrario la cuerda no puede vibrar de una forma cuánticamente autoconsistente), pero no sabemos por qué se seleccionan estos números concretos.
Quizá la respuesta a todo esto esté esperando a ser descubierta cuando alguien (algún genio matemático como Perelman) sea capaz de entender el contenido de los cuadernos perdidos de Ramanujan.
Está claro que, este simple comentario no explica lo que la Ciencia es y, desde luego, tendríamos que ir a una complejidad mucho más profunda y elevada para poder hablar de algunas ramas de la Ciencia que requieren de un nivel de comprensión de la Naturaleza que, de ninguna manera poseo. ¿Cómo he terminado este trabajo como lo he hecho? Empecé con una intención y, por el camino, como si tuviera vida propia, los pensamientos te llevan por otros senderos que, nunca habías pensado recorrer. ¡Qué cosas!
emilio silvera
Sep
10
Desde el pasado pero, ¡siempre hacia el futuro!
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en La Ciencia ~
Clasificado en La Ciencia ~
 Comments (4)
Comments (4)
![[IMG]](http://static.hsw.com.br/gif/synchrotron-1.jpg)
Imagem cedida por Diamond Light Source
Acelerador de partículas construido en las instalaciones del Diamond Ligth Source en Oxfordshire (Inglaterra). Llamado la Fuente luminosa de diamante, el Diamond synchrotron comenzó a funcionar en enero de 2007. La luz que puede generar este artefacto es 100 mil millones de veces más brillante que un rayo X estándar médico.
Un acelerador de partículas (como todos sabemos) es, a grandes rasgos, una máquina que mediante campos electromagnéticos acelera partículas hasta que alcanzan velocidades inimaginables. Luego, por ejemplo, hacen chocar estas partículas y así se consigue saber de qué está formada la materia en sus partes más diminutas (mucho más diminutas que un átomo). Eso es lo que hace el LHC.
Sin embargo, en el caso de este acelerador, los científicos esperaban usar la luz del Diamond synchrotron para “leer” los textos antiguos que han sufrido el daño significativo. Porque los potentes rayos X permitirán hacerlo sin ni siquiera abrir el libro. El synchrotron emite un rayo X tan poderoso que, al incidir en una voluta, permite producir una imagen de 3-D del texto.
La técnica ya había sido aplicada satisfactoriamente en textos escritos con la tinta de hierro, que los escribanos comenzaron a usar en el siglo XII. Algunas de las tintas hechas con extractos vegetales y sales de hierro utilizadas en el Siglo XII deterioran el tipo de pergamino utilizado, imposibilitando la lectura de documentos valiosos. Simplemente he querido incluir esta introducción para que os hagais una idea de hasta donde puede llegar nuestro ingenio.

(ilustración de un nano robot)
Si hablamos de nuevos inventos en los campos más diversos, nos podríamos sorprender de lo que se ha conseguido en los últimos años que, desde una “mano robótica” capaz de realizar toda clase de movimientos, “El sexto sentido”, una interfaz gestual portable que permite la interacción entre los gestos y los movimientos naturales del cuerpo humano con una computadora, o, un Implantes de retina, que devuelve la visión a pacientes con degeneración macular y ceguera mediante implantes microelectrónicos. Entre los últimos inventos dedestaca una variedad de plástico hecha con orina de cerdo y lentes de contacto biónicos. Se inventa un proceso capaz de cultivar parte de un corazón humano a partir de células madre, una máquina que puede imprimir una novela completa de 300 páginas en tan solo 3 minutos y por un costo ínfimo, una batería que funciona con cualquier solución azucarada y enzimas de digestión de glucosa capaz de extraer electrones que crean electricidad…

Las nuevas tecnologías y los inventos que se están produciendo en el diglo XXI, harían abrir la boca por el asombro a los filósofos naturalistas del pasado que trataban de profundizar en el conocimiento de la Naturaleza. Ellos fueron los que pusieron las primeras piedras del Edificio que hoy, llamamos Ciencia.
Corazones e Hígados artificiales, el guante de braille para ciegos, o, yendo más allá…

Un “Diente telefónico”. Se trata de un minúsculo implante que se coloca en el diente molar y que mediante un complejo sistema de señales y vibraciones permite recibir llamadas telefónicas. Tejido artificial nanotecnológico, Parche hormonal anticonceptivo, o, esa invención que hace posible que con una pequeña gota nos permite descubrir si en una bebida se ha vertido alguna de las llamadas “drogas del depredador” como las GHB o la Ketamina. Estas drogas suelen utilizarse por violadores y secuestradores pues facilitan dicho crimen al desinhibir a la víctima. El “Motor a nanoescala”, lo suficientemente pequeño como para viajar en la espalda de un virus. Un dispositivo que administra medicamentos a través de ondas sonoras que sustituyen las inyecciones, siendo igual de efectivas. Plástico inteligente capaz de modificar su estructura ante la exposición de determinadas longitudes de onda. Un dispositivo móvil creado por Aqua Sciences que permite beber agua del aire. ¿Os imaginais lo que supondrá eso en la travesía de un desierto? INSCENTINEL inventa un sistema de entrenamiento para que abejas sean capaces de detectar bombas y explosivos.

Las cosas no llegaron por arte de magia… ¡muchas ideas hicieron falta!
Ahora miramos a nuestro alrededor y todo lo que vemos que ocurre nos parece lo normal, que las cosas son así. Sin embargo, habría que pensar -por ejemplo, en el ámbito de la física de partículas- que, el diluvio de estructuras subnucleares que desencadenó “el acelerador” de partículas, fue tan sorprende como los objetos celestes que descubrió el telescopio de Galileo. Lo mismo que pasó con la revolución galileana, con la venida de los aceleradores de partículas, la Humanidad adquirió unos conocimientos nuevos e insospechados acerca de cómo era el mundo, la naturaleza de la materia.
Que en este caso de los aceleradores se refería al “espacio interior” en lugar de al “espacio exterior” no los hacía menos profundos ni menos importantes. El descubrimiento de los microbios y del universo biológico invisible por Pasteur fue un descubrimiento similar y, ya puestos, haremos notar que pocos se acuerdan ya de Demócrito, aquel filósofo sontiente que, tomó prestado de los antiguos hindúes, la idea del á-tomo, la expresión “más pequeña de la materia” que era “indivisible”.

Ahora sabemos que Demócrito estaba equivocado y que el átomo, sí se puede dividir. Sin embargo, él señaló un camino y, junto a Empédocles, el que hablaba de “elementos” como agua, aire, fuego y tierra, para significar que eran los componentes, en la debida proporción de todo lo que existía…, junto a otros muchos, nos han traído hasta aquí. Así que, los inventos que antes se mencionaban, no han llegado porque sí, ha sido un largo camino, mucha curiosidad y mucho trabajo y, no lo olvidemos: ¡Observar, Imaginar y Experimentar!
Nos dimos cuenta y estaba claro que la búsqueda de la menor de las partículas requería que se expandiese la capacidad del ojo humano: primero lupas, después microscopios y, finalmente… ¡Aceleradores! que, utilizando energías inimaginables ( 14 TeV), nos llevaría hasta las entrañas de la materia que tratamos de conocer.
Todos estos experimentos en los aceleradores han posibilitado muchos de los avances que hoy día conocemos en los distintos campos del saber humano. Generalmente, cuando se habla de aceleradores de partículas, todos piensan en el Bosón de Higgs y cosas por el estilo. Sin embargo, las realidades prácticas de dichos ingenios van mucho más allá.
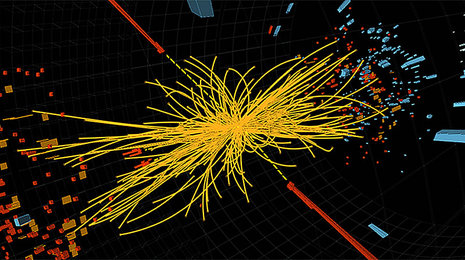
“La “gran ciencia” (big science) genera tecnología, tecnología punta, genera industria, mucha industria, genera riqueza. Los grandes aceleradores de partículas, como el LHC del CERN, son ejemplos perfectos de ello. La tecnología de aceleradores de partículas ha permitido desarrollar dispositivos de implantación iónica que se utilizan para la fabricación de mejores semiconductores, para la fabricación prótesis de rodilla más duraderas, para la fabricación de neumáticos menos contaminantes, para el desarrollo de nuevas terapias contra el cáncer. Esto último gracias a que lo último de lo último en superimanes superconductores está en los grandes aceleradores. Esta tecnología ha permitido desarrollar y permitirá mejorar los potentes imanes necesarios en el diagnóstico clínico (como en resonancia magnética nuclear) y para terapias contra el cáncer basadas en haces de protones. Nos lo cuenta Elizabeth Clements, en “Particle physics benefits: Adding it up,” Symmetry, dec. 2008″ (Francis (th)E mule Science’s News).

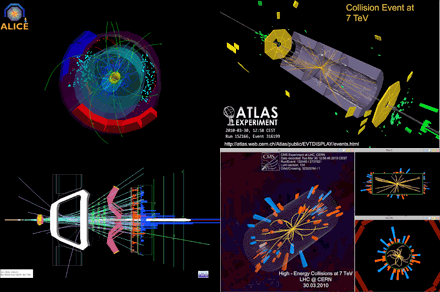
Beneficios de la investigación básica en Física de Partículas: La tecnología desarrollada en los aceleradores de partículas tiene beneficios indirectos para la Medicina, la Informática, la industria o el medio ambiente. Los imanes superconductores que se usan para acelerar las partículas han sido fundamentales para desarrollar técnicas de diagnóstico por imagen como la resonancia magnética. Los detectores usados para identificar las partículas son la base de los PET, la tomografía por emisión de positrones (antipartícula del electrón). Y muchos hospitales utilizan haces de partículas como terapia contra el cáncer.

Con velocidades 10.000 mayor que una conexión típica, “The Grid” podrá enviar un catálogo completo de información desde Gran Bretaña a Japón en menos de 2 segundos. Esta red, creada en el centro de física de partículas CERN, puede proveer el poder necesario para transmitir imágenes holográficas; permitir juegos en línea con cientos de miles de personas, y ofrecer una telefonía de alta definición en video al precio de una llamada local
Así, la World Wide Web (WWW), el ‘lenguaje’ en el que se basa Internet, fue creado en el CERN para compartir información entre científicos ubicados alrededor del mundo, y las grandes cantidades de datos que se producen motivan el desarrollo de una red de computación global distribuida llamada GRID. Los haces de partículas producidos en aceleradores tipo sincrotrón o las fuentes de espalación de neutrones, instrumentos creados para comprobar la naturaleza de la materia, tienen aplicaciones industriales en la determinación de las propiedades de nuevos materiales, así como para caracterizar estructuras biológicas o nuevos fármacos. Otras aplicaciones de la Física de Partículas son la fabricación de paneles solares, esterilización de recipientes para alimentos o reutilización de residuos nucleares, entre otros muchos campos.
Tambien en el campo de la Astronomía, el LHC, nos puede ayudar a comprender cosas que ignoramos. Nos henmos preguntado sobre la existencia de estrellas de Quarks-Gluones, y, sobre el tema, algo nos ha dicho ya el Acelerador Europeo de Partículas que trata de llegar hasta “la materia oscura” y algunos otros enigmas que nos traen de cabeza.
No es extraño encontrarnos una mañana al echar una mirada a la prensa del día, con noticias como éstas:
Colisión de iones pesados registrada por el experimento ALICE. (Imagen: CERN.)
El acelerador europeo ha obtenido plasma de quarks-gluones, el primer estado de la materia tras el Big Bang.
“No todo son bosones de Higgs en las instalaciones del CERN. Aún hay muchas preguntas sobre el universo y sus partículas que se pueden responder a base de colisiones de alta energía. Y en eso, elLHC es el mejor. Un grupo de investigadores del consorcio europeo ha realizado nuevas mediciones de la que creen que es el primer tipo de materia que hubo durante los instantes iniciales del universo. El plasma de quarks-gluones.
Los quarks y los gluones son, respectivamente, los ladrillos y el cemento de la materia ordinaria. Durante los primeros momentos tras el Big Bang, sin embargo, no estaban unidos constituyendo partículas —como protones o neutrones— sino que se movían libremente en estado de plasma. A base de colisionar iones de plomo —que es un átomo muy pesado— a velocidades cercanas a las de la luz, el LHC pudo recrear durante pequeños lapsos de tiempo las que se creen fueron las condiciones de los primeros momentos del universo.
El plasma de quarks-gluones es extremo y efímero. Por eso los investigadores han tenido que analizar los resultados de más de mil millones de colisiones para obtener resultados significativos.”

Evento de colisión de 7 TeV visto por el detector LHCb. El experimento del LHCb en el LHC estará bien ubicado para explorar el misterio de la antimateria. Crédito: LHC, CERN. Ya sabéis que, durante muchos años, la ausencia de antimateria en el Universo ha atormentado a los físicos de partículas y a los cosmólogos: mientras que el Big Bang debería haber creado cantidades iguales de materia y antimateria, no observamos ninguna antimateria primordial hoy en día. ¿Dónde ha ido? Los experimentos del LHC tienen el potencial de dar a conocer los procesos naturales que podrían ser la clave para resolver esta paradoja.
Cada vez que la materia es creada a partir de energía pura, se genera la misma cantidad de partículas y antipartículas. Por el contrario, cuando la materia y la antimateria se encuentran, se aniquilan mutuamente y producen luz. La antimateria se produce habitualmente cuando los rayos cósmicos chocan contra la atmósfera de la Tierra, y la aniquilación de materia y antimateria se observa durante los experimentos de física en los aceleradores de partículas.

Equipos de físicos en todo el mundo siguen analizando datos. Aquellas primeras colisiones de protones a la alta energía prevista de 7 Teraelectronvoltios (TeV), una potencia jamás alcanzada en ningún acelerador antes, nos puede traer noticias largamente esperadas y desvelar misterios, contestar a preguntas planteadas y, en definitiva, decirnos cómo es la Naturaleza allí, donde el ojo humano no puede llegar pero, si la inteligencia.
Lo cierto es que, todos tenemos que convenir en el hecho cierto de que, el LHC es el mayor experimento físico de la historia de la Ciencia y que, de seguro, nos dará la oportunidad de comprender muchas cuestiones que antes se nos aparecían oscuras e indistinguibles entre la bruma de esa lejanía infinitesimal de la cuántica. Ahora, tenemos una herramienta capaz de llevarnos hasta aquellos primeros momentos en los que se construyó la historia del universo y, si podemos, de esta manera “estar allí”, veremos, con nuestros propios ojos lo que pasó y por qué pasó de esa manera.
Toda esta larga exposición de temas, de alguna manerta conectados, viene al caso para dejar claro que, aquellos detractores del LHC, no llevaban la razón y, sus protestas no tenían un contenido científico. El Acelerador de Partículas que llamamos abreviadamente LHC, nos ha dado y nos seguirá dando, muchos beneficios para toda la Humanidad.
emilio silvera
Oct
27
El Universo evoluciona, y, ¡nosotros también!
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en La Ciencia ~
Clasificado en La Ciencia ~
 Comments (1)
Comments (1)

Mucho antes de que llegara las revoluciones científicas que todos tenemos en la mente, la Naturaleza parecía estar regida por el Caos: Terremotos, volcanes que oscurecían el cielo lanzando el negro humo acompañado de cenizas, lluvias torrenciales y el rayo, tifones, enfermedades incurables de la que morían millones de personas, las hanbrunas que azotaban a tantas criaturas y, nadie podía explicar el comportamiento del viento, aquellas tempestades marinas, o, temblores de la Tierra inesperados que traían la destrucción y la muerte.
Todo aquello, tenía que ser el resultado de que, enfurecidos dioses castigaban las impurezas del mundo y de sus criaturas. En absoluto sugería nadie que pudieran existir leyes “sencillas” y ordenadas con las que se pudieran explicar tal confusión en el comportamiento de una Naturaleza que, lo mismo se presentaba esplendorosa que rugía sembrando el miedo y el dolor de mil maneras distintas.

Allí donde se percibía orden en el universo, este orden se atribuía a la respuesta que daban los objetos físicos a una necesidad de que se preservaran la armonía y el orden siempre que fuera posible -se suponía las órbitas de los planetas y del Sol alrededor de la Tierra y que eran círculos, porque los círculos eran perfectos-, los objetos caían hacia el suelo porque el centro de la Tierra marcaba el centro de todo y todo tendía a confluir hacia aquel lugar, el centro de simetría de todo el universo. Acordaos que, el filósofo Aristarco de Samos, se atrevió a expresar sus ideas y dijo que, la Tierra y todos los planetas se movían alrededor del Sol. ¡Claro, nadie le prestó la menor atención! y, muchísimos años más tarde, tuvo que venir Copérnico, allá por el año 1543, diciendo lo mismo para pasar a la historia. Su libro De Revolutionibus Orbium Coelestrum quedó terminado en lo esencialen 1530 y, a cuando se publicó, hizo exclamar, en 1539, a Martín Lutero: “Este loco desea volver de revés toda la astronomía; pero las Sagradas Escrituras nos dicen que Josué ordenó al Sol que se detuviera, no a la Tierra”. Galileo replicó más tarde, respondiendo a críticas similares: “La Biblia nos muestra la manera de llegar al cielo, no la manera en que se mueven los cielos”. Tuvo que llegar Kepler, quien, utilizando las observaciones munuciosamente recopiladas por Tycho Brahe, señaló, para aqueloos que tuvieran los ojos bien abiertos que, el planeta Marte no sólo se movía alrededor del Sol sino que, su órbita, era elíptica, echando así por tierra la antigua perfección circular, preferida por los clásicos griegos .
Ahora, pasado el tiempo y mirando hacia atrás, podemos ver con diáfana claridad, muchos ejemplos que podrían ilustrar la diferencia tan brutal que existe entre la ciencia de los antiguos y la de tiempos posteriores a partir de Galileo. Es cierto que los antiguos griegos fueron unos matemáticos excelentes, en particular, unos geómetras de primera. También es cierto que aquella geometría que imperó durante más de dos mil años entre nosotros (aún hoy, alguna perdura), tenía sus raíces en culturas más antiguas.
![[FNT 2]](http://bibliotecadigital.ilce.edu.mx/sites/ciencia/volumen3/ciencia3/128/img/14.gif)
Galileo y el péndulo. La imagen nos habla del primer experimentador serio de la historia. Experimentó para demostrar el tiempo que invertía el péndulo en realizar una oscilación completa que resultó ser siempre la misma, tanto si recorría un amplio arco como si describía uno pequeño. Experimentos posteriores demostraron que ese tiempo dependía de la longitud del péndulo. Este es el fundamento del reloj de péndulo (diseñó uno que llegó a construir su hijo). Posteriormente utilizó el péndulo como cronómetro preciso cuando realizó experimentos para estudiar el comportamientode unas bolas que rodaban hacia abajo por una rampa. Estos experimentos le servían para estudiar la caída de objetos para investigar los efectos que producía la Gravedad sobre los cuerpos en movimiento. Él desarrolló el concepto de aceleración: Una velocidad constante de 9,8 metros por segundo significa que cada segundo el objeto en movimiento cubre una distancia de 9,8 metrtos. Él descubrió que los objetos que caen se mueven cada vez más rápidos, con una velocidad que aumenta cada segundo y que el aumento, era uniforme, siempre el mismo. También observó como aquellas bolas que caen por la rampa, se frenan a causa del rozamiento. Aquello era física pura dándo sus primeros pasos y camino de la relatividad, la termodinámica y la mecánica cuántica.
Fue un grande entre los gigantes. Se le suele recordar como el fundador del método experimental de la física; su imagen va asociada con la del telescopio y el plano inclinado, con los instrumentos que diseñó y armó para observar y medir. También es famosa su polémica con los aristotélicos de su tiempo que se limitaban a citar a los clásicos y pensar cómo debían ser los movimientos de los cuerpos, en vez de observarlos. Por último, ¿quién no conoce la anécdota del atrevido maestro arrojando dos cuerpos de diferente peso desde la Torre de Pisa? (Anécdota probablemente apócrifa pero, como dicen los italianos, Se non è vero… è ben trovatto! ).

Fue una combinación del descubrimiento de las órbitas elípticas por parte de Kepler, y de la teoría de Galileo sobre la aceleración y el método científico, lo que preparó el camino para el mayor descubrimiento científico del siglo XVII, y quizá de todos los siglos: la Ley de la Gravitación universal de Newton que cerró con el broche de oro que conocemos por su gran obra: Philosophiae Naturalis Principia Mathemática, más conocida coloquialmente como los Principia, publicada en 1687.
Newton adoptó y perfeccionó la idea de Galileo, valorando de manera positiva los modelos deliberadamente simplificados (como los planos sin rozamiento) para utilizarlos en la descripción de aspectos concretos del mundo real. Por ejemplo, una característica fundamental de los trabajos de Newton sobre la Gravedad y las órbitas es el hecho de que, en sus cálculos realtivos a los efectos de la Gravedad, él consideró objetos tales como Marte, la Luna o una manzana, como si toda su masa estuviera concentrada en un solo punto, y de esta manera, siempre que nos encontremos en el exterior del objeto en cuestión, su influencia gravitatoria se mide en función de nuestra distancia a dicho a dicho punto, que es el centro de masa del objeto /y asimismo el centro geométrico, si el objeto es una esfera).
Allí quedaron para las generaciones venideras las Leyes del movimiento de Newton, que copnstituyen la base de trescientos años de ciencia, pero que puede resumirse de una forma muy sencilla y que marcan el desarrollo del modo científico de observar el mundo.

Para resolver un problema en mecánica, lo único que necesito es aplicar las tres leyes de Newton
– Todo cuerpo persevera en su estado de reposo o movimiento uniforme y rectilíneo a no ser que sea obligado a cambiar su estado por fuerzas impresas sobre él.
– El cambio de movimiento es proporcional a la fuerza motriz impresa y ocurre según la línea recta a lo largo de la cual aquella fuerza se imprime.
– Con toda acción ocurre siempre una reacción igual y contraria: o sea, las acciones mutuas de dos cuerpos siempre son iguales y dirigidas en sentido opuesto.
Esta última y tercera ley es completamente original de Newton (pues las dos primeras ya habían sido propuestas de otras maneras por Galileo, Hooke y Huygens) y hace de las leyes de la mecánica un conjunto lógico y completo.

El problema de los tres cuerpos fue, totalmente inabordable por Newton que, en aquellos casos en los que se veía imposibilitado, siempre recurría a Dios para que le solucionara el asunto. Claro que, ante tal sugerencia, siempre se encontraba de frente con Leibniz que, comparó el universo ordenado y determinista de Newton con un reloj, afirmando con sarcasmo que el Dios de Newton debía ser un relojero bastante torpe si era incapaz de hacer un reloj que marcara siempre la hora correcta, pues para que funcionara bien tenía que intervenir cada vez que se estropera.
Aquel problema de los tres cuerpos (del que hablaremos en otra ocasión), continuó sin solución hasta finales del siglo XVII, cuando el matemático francés Pierre Laplace, aparentemente puso orden en el sistema solar (claro que, también tendríamos que ver lo que dijo Poincaré, otro francés, al respecto).
Así, poco a poco, se pudo ir poniendop orden y buscando explicación para todos aquellos fenómenos de la Naturaleza que no tenían explicación y que, sólo la Ciencia, nos la podía dar.
Mas tarde llegarían Faraday y Maxwell que investigaron la naturaleza de la luz el primero y, supo expresarla en ecuaciones el segundo. Aquello, fue un paso de gigante para comprender el mundo que nos rodea y cómo funciona, en algunos aspectos, la Naturaleza. Podemos decir que aquello fue uno de los mayores triunfos de la Ciencia del siglo XIX. La explicación dada por Maxwell sobre la radiación electromagnética se basó en la obra de Faraday y, entre ambos, dijeron al mundo que electricidad y magnetismo eran dos aspectos distintos de la misma cosa.
Las ecuaciones de Maxwell llevaban consigo dos características muy curiosas: una de ellas pronto tendería un profundo impacto en la física, y la otra fue considerada hasta tiempos muy recientes sólo como una rareza de menor importancia. La primera de aquellas características innovadoras era que daban a la velocidad de la luz un valor constante, independientemente de cómo se mueva la fuente de luz con respecto a la persona (o aparato) que mida su velocidad. Ya sabeis que fue esto, lo que lelvó a Einstein a desarrollar la teoría de la relatividad especial en 1905.

Antes que Eisntein Planck y después muchos otros, vinieron a poner los conocimientos de la Ciencias Físicas y Astronómicas en un lugar privilegiado en el que, podíamos mirar las galaxias y también a los átomos. El mundo de lo muy grande y el de lo muy pequeño, quedó al alcance del entendimiento humano. Claro que, Como dijo Kart Raimund Popper, filósofo británico de origen austriaco (Viena, 1902 – Croydon, 1.994) que realizó sus mas importantes trabajos en el ámbito de la metodología de la ciencia: “cuanto más profundizo en el saber de las cosas, más consciente soy de lo poco que sé. Mis conocimientos son finitos pero, mi ignorancia, es infinita“.
Está claro que la mayoría de las veces, no hacemos la pregunta adecuada porque nos falta conocimiento para realizarla. Así, cuando se hacen nuevos descubrimientos nos dan la posibilidad de hacer nuevas preguntas, ya que en la ciencia, generalmente, cuando se abre una puerta nos lleva a una gran sala en la que encontramos otras puertas cerradas y tenemos la obligación de buscar las llaves que nos permitan abrirlas para continuar. Esas puertas cerradas esconden las cosas que no sabemos y las llaves que las pueden abrir son retazos de conocimientos que nos permiten entrar para descorrer la cortina que esconde los secretos de la Naturaleza, de la que en definitva, formamos parte.
¡Cuánto hay ahí, en esa bella Nebulosa de arriba! En espesas nubes moleculares que se concentran en vórtices obligadas por la Gravedad, nacen nuevas estrellas y nuevos mundos. Ahí se transforman los matriales sencillos como el Hidrógeno en otros más complejos y, la radiación de las jóvenes estrellas nuevas masivas, tiñen de rojo el gas y el povo del lugar, mientras ellas, presumidas, se exhiben rodeadas de ese azul suave que las distingue de aquellas otras más antiguas, que tiñen de amarillo y rojo toda la región.

¿Qué sería de la cosmología actual sin ![]() ? Es la ecuación de Einstein donde
? Es la ecuación de Einstein donde ![]() es el tensor energía-momento que mide el contenido de materia-energía, mientras que
es el tensor energía-momento que mide el contenido de materia-energía, mientras que ![]() es el Tensor de curvatura de Riemann contraído que nos dice la cantidad de curvatura presente en el hiperespacio.
es el Tensor de curvatura de Riemann contraído que nos dice la cantidad de curvatura presente en el hiperespacio.

También esa ecuación nos habló de la existencia de Agujeros negros, esos objetos de densidad “infinita” en los que dejan de existir el espacio y el tiempo. La singularidad es el punto matemático en el que ciertas cantidades físicas alcanzan valores infinitos. Así nos lo dice la relatividad general general: la curvatura del espacio-tiempo se hace infinita en un Agujero Negro.
La cosmología estaría 100 años atrás sin esta ecuación. Einstein con sus dos versiones de la realtividad que nos descubrió un universo donde la velocidad estaba limitada a la de la luz, donde la energía estaba escondida, quieta y callada, en forma de masa, y donde el espacio y el tiempo se curva y distorsiona cuando están presentes grandes objetos estelares, nos descubrio un Universo nuevo, un mundo fantástico de posibilidades ilimitadas en el que podían ocurrir maravillas como, por ejemplo, conseguir que el tiempo transcurriera más lentamente y dónde reside la fuente de la energía. Claro que, al mérito de Einstein (que lo tiene), tendríamos que sumar el de Faraday, Maxwell, Mach, Lorentz, Planck y algunos otros de cuyas ideas él supo aunar un todo que clarificó el mundo y que, por separado, no decían tanto.

No puedo evitarlo, siento debilidad por las estrellas, esos objetos brillantes del cielo en los que, se “fabrican” los elementos complejos que son la materia primaria para la vida. Nosotros, como he comentado muchas veces, estamos hechos de polvo de estrellas.
En ellas, en las estrellas, se producen cambios y transformaciones de cuyos procesos, debemos conocer para saber lo que allí ocurre y el pro qué de esas mutaciones de la materia. Siempre llamó mi atención las estrellas que se forman a partir de gas y polvo cósmico. Nubes enormes de gas y polvo (como la nebulosa cabeza de caballo en la imagen de arriba) se van juntando. Sus moléculas cada vez más apretadas se rozan, se ionizan y se calientan hasta que en el núcleo central de esa bola de gas caliente, la temperatura alcanza millones de grados. La enorme temperatura hace posible la fusión de los protones y, en ese instante, nace la estrella que brillará durante miles de millones de años y dará luz y calor. Su ciclo de vida estará supeditado a su masa. Si la estrella es supermasiva, varias masas solares, su vida será más corta, ya que consumirá el combustible nuclear de fusión (hidrógeno, helio, litio, oxígeno, etc) con más voracidad que una estrella mediana como nuestro Sol, de vida más duradera.
Una estrella, como todo en el universo, está sostenida por el equilibrio de dos fuerzas contrapuestas; en este caso, la fuerza que tiende a expandir la estrella (la energía termonuclear de la fusión) y la fuerza que tiende a contraerla (la fuerza gravitatoria de su propia masa). Cuando finalmente el proceso se detiene por agotamiento del combustible de fusión, la estrella pierde la fuerza de expansión y queda a merced de la fuerza de gravedad; se hunde bajo el peso de su propia masa, se contrae más y más, y en el caso de estrellas súper masivas, se convierten en una singularidad, una masa que se ha comprimido a tal extremo que acaba poseyendo una fuerza de gravedad de una magnitud difícil de imaginar para el común de los mortales.

A nosotros nos puede parecer enorme, es el planeta que acoge a toda la Humanidad. Sin embargo, en el contexto del Universo y comparada con otros objetos cosmológicos, es menos que una mota de polvo y, si pensamos en ello, quizás (sólo quizás), podamos llegar a la conclusión de que debemos cambiar y mirar las cosas desde otras perspectivas, al fin y al cabo no somos tan importantes como algunas veces podemos creer.

¡Sí, la Galaxia está en nuestra Mente y, nuestra Mente, en la Galaxia!
La evolución del Universo que está prescrita por el paso del Tiempo (con la ayuda de la Entropía), es inexorable, y, nosotros, nuestras mentes que son el producto evolucionado en su más alto grado de la materia, también evolucionamos al mismo ritmo que el universo nos marca. De esa manera, el transcurrir de los siglos posibilitan la apertura mental de nuevas ideas y, el conocimiento del mundo, de la Naturaleza, se hace cada vez más patente para nosotros que, al final de toda esta historia, volveremosa fundirnos con todo, en el mismo lugar del que partimos: ¡Las estrellas! allí está nuestro origen y, algo me dice que volveremos a él.
¿Será cuando llegue Andrómeda y le de el beso de amor a la Vía Láctea?
emilio silvera
















 Totales: 74.825.316
Totales: 74.825.316 Conectados: 59
Conectados: 59




























