Ago
11
Las estructuras fundamentales de la Naturaleza
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Las huellas del pasado ~
Clasificado en Las huellas del pasado ~
 Comments (0)
Comments (0)
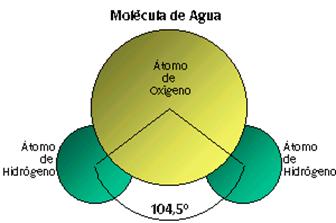
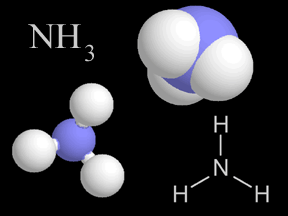
Una molécula de Agua y otra de Amoníaco
Hemos llegado a poder discernir la relación directa que vincula el tamaño, la energía de unión y la edad de las estructuras fundamentales de la Naturaleza. Una molécula es mayor y más fácil de desmembrar que un átomo; lo mismo podemos decir de un átomo respecto al núcleo atómico, y de un núcleo con respecto a los quarks que contiene.
La cosmología sugiere que esta relación resulta del curso de la historia cósmica, que los quarks se unieron primero, en la energía extrema del big bang original, y que a medida que el Universo se expandió, los protones y neutrones compuestos de quarks se unieron para formar núcleos de átomos, los cuales, cargados positivamente, atrajeron a los electrones cargados con electricidad negativa estableciéndose así como átomos completos, que al unirse formaron moléculas.

Si es así, cuanto más íntimamente examinemos la Naturaleza, tanto más lejos hacia atrás vamos en el tiempo. Alguna vez he puesto el ejemplo de mirar algo que nos es familiar, el dorso de la mano, por ejemplo, e imaginemos que podemos observarlo con cualquier aumento deseado.

Con un aumento relativamente pequeño, podemos ver las células de la piel, cada una con un aspecto tan grande y complejo como una ciudad, y con sus límites delineados por la pared celular. Si elevamos el aumento, veremos dentro de la célula una maraña de ribosomas serpenteando y mitocondrias ondulantes, lisosomas esféricos y centríolos, cuyos alrededores están llenos de complejos órganos dedicados a las funciones respiratorias, sanitarias y de producción de energía que mantienen a la célula.

Ya ahí tenemos pruebas de historia. Aunque esta célula particular solo tiene unos pocos años de antigüedad, su arquitectura se remonta a más de mil millones de años, a la época en que aparecieron en la Tierra las células eucariota o eucarióticas como la que hemos examinado.
Para determinar dónde obtuvo la célula el esquema que le indicó como formarse, pasemos al núcleo y contemplemos los delgados contornos de las macromoléculas de ADN segregadas dentro de sus genes. Cada una contiene una rica información genética acumulada en el curso de unos cuatro mil millones de años de evolución.

Almacenado en un alfabeto de nucleótidos de cuatro “letras”- hecho de moléculas de azúcar y fosfatos, y llenos de signos de puntuación, reiteraciones para precaver contra el error, y cosas superfluas acumuladas en los callejones sin salida de la historia evolutiva-, su mensaje dice exactamente cómo hacer un ser humano, desde la piel y los huesos hasta las células cerebrales.
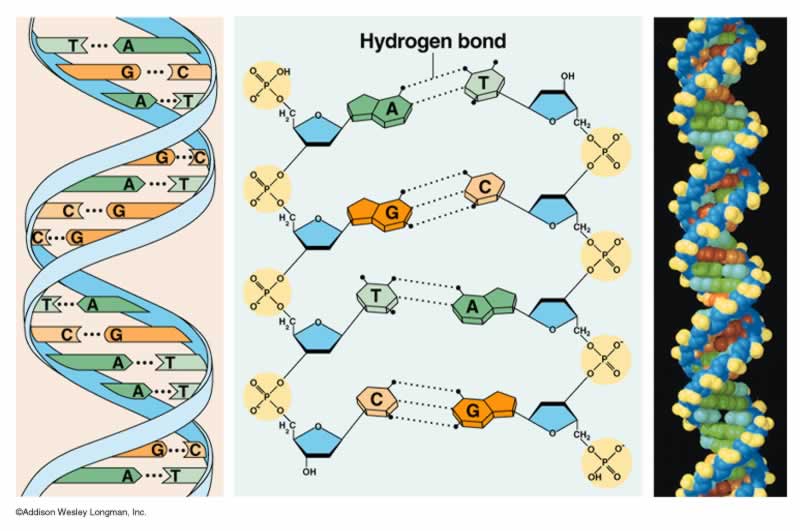
Si elevamos más el aumento veremos que la molécula de ADN está compuesta de muchos átomos, con sus capas electrónicas externas entrelazadas y festoneadas en una milagrosa variedad de formas, desde relojes de arena hasta espirales ascendentes como largos muelles y elipses grandes como escudos y fibras delgadas como puros. Algunos de esos electrones son recién llegados, recientemente arrancados átomos vecinos; otros se incorporaron junto a sus núcleos atómicos hace más de cinco mil millones de años, en la nebulosa de la cual se formó la Tierra.
Si elevamos el aumento cien mil veces, el núcleo de un átomo de carbono se hinchará hasta llenar el campo de visión. Tales núcleos átomos se formaron dentro de una estrella que estalló mucho antes de que naciera el Sol. Si podemos aumentar aún más, veremos los tríos de quarks que constituyen protones y neutrones.
Los quarks han estado unidos desde que el Universo sólo tenía unos pocos segundos de edad y ahora están en nosotros y en todos los objetos del universo, chicos o grandes, todo lo material está hecho de Quarks y Leptones desde una bacteria hasta una galaxia. Por supuesto, también nuestro cerebro y las neuronas que crean pensamientpos.
Al llegar a escalas cada vez menores, también hemos entrado en ámbitos de energías de unión cada vez mayores. Un átomo puede ser desposeído de su electrón aplicando sólo unos miles de electrón-voltios de energía. Sin embargo, para dispersar los nucleones que forman el núcleo atómico se requieren varios millones de electrón-voltios, y para liberar los quarks que constituyen cada nucleón se necesitaría cientos de veces más energía aún.

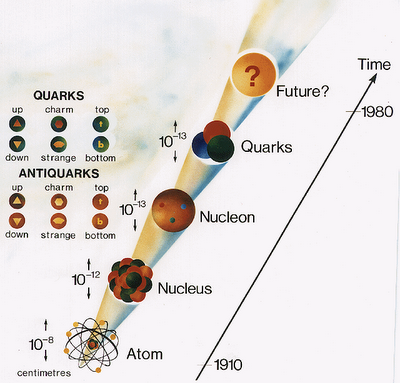
Introduciendo el eje de la historia, esta relación da testimonio del pasado de las partículas: las estructuras más pequeñas, más fundamentales están ligadas por niveles de energía mayores porque las estructuras mismas fueron forjadas en el calor del big bang.
Esto implica que los aceleradores de partículas, como los telescopios, funcionen como máquinas del tiempo. Un telescopio penetra en el pasado en virtud del tiempo que tarda la luz en desplazarse entre las estrellas; un acelerador recrea, aunque sea fugazmente, las condiciones que prevalecían en el Universo primitivo.
Hemos llegado a dominar técnicas asombrosas que nos facilitan ver aquello que, prohibido para nuestro físico, sólo lo podemos alcanzar mediante sofisticados aparatos que bien nos introduce en el universo microscópico de los átomos, o, por el contrario nos llevan al Universo profundo y nos enseña galaxias situadas a cientos y miles de millones de años-luz de la Tierra.

Cuando vemos esos objetos cosmológicos lejanos, cuando estudiamos una galaxia situada a 100.000 mil años-luz de nosotros, sabemos que nuestros telescopios la pueden captar gracias a que la luz de esa galaxia, viajando a 300.000 Km/s llegó a nosotros después de ese tiempo, y, muchas veces, no es extraño que el objeto que estamos viendo ya no exista o si existe, que su conformación sea diferente habiéndose transformado en diferentes transiciones de fase que la evolución en el tiempo ha producido.
En el ámbito de lo muy pequeño, vemos lo que está ahí en ese momento pero, como se explica más arriba, en realidad, también nos lleva al pasado, a los inicios de cómo todo aquello se formó y con qué componentes que, en definitiva, son los mismos de los que están formadas las galaxias, las estrellas y los planetas, una montaña y un árbol y, cualquiera de nosotros que, algo más evolucionado que todo lo demás, podemos contarlo aquí.
Estas y otras muchas maravillas son las que nos permitirán, en un futuro relativamente cercano, que podamos hacer realidad muchos sueños largamente dormidos en nuestras mentes.
emilio silvera
Ago
19
Las estructuras fundamentales de la Naturaleza
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Las huellas del pasado ~
Clasificado en Las huellas del pasado ~
 Comments (2)
Comments (2)


Una molécula de Agua y otra de Amoníaco
Hemos llegado a poder discernir la relación directa que vincula el tamaño, la energía de unión y la edad de las estructuras fundamentales de la Naturaleza. Una molécula es mayor y más fácil de desmembrar que un átomo; lo mismo podemos decir de un átomo respecto al núcleo atómico, y de un núcleo con respecto a los quarks que contiene.
La cosmología sugiere que esta relación resulta del curso de la historia cósmica, que los quarks se unieron primero, en la energía extrema del big bang original, y que a medida que el Universo se expandió, los protones y neutrones compuestos de quarks se unieron para formar núcleos de átomos, los cuales, cargados positivamente, atrajeron a los electrones cargados con electricidad negativa estableciéndose así como átomos completos, que al unirse formaron moléculas.

Si es así, cuanto más íntimamente examinemos la Naturaleza, tanto más lejos hacia atrás vamos en el tiempo. Alguna vez he puesto el ejemplo de mirar algo que nos es familiar, el dorso de la mano, por ejemplo, e imaginemos que podemos observarlo con cualquier aumento deseado.

Con un aumento relativamente pequeño, podemos ver las células de la piel, cada una con un aspecto tan grande y complejo como una ciudad, y con sus límites delineados por la pared celular. Si elevamos el aumento, veremos dentro de la célula una maraña de ribosomas serpenteando y mitocondrias ondulantes, lisosomas esféricos y centríolos, cuyos alrededores están llenos de complejos órganos dedicados a las funciones respiratorias, sanitarias y de producción de energía que mantienen a la célula.

Ya ahí tenemos pruebas de historia. Aunque esta célula particular solo tiene unos pocos años de antigüedad, su arquitectura se remonta a más de mil millones de años, a la época en que aparecieron en la Tierra las células eucariota o eucarióticas como la que hemos examinado.
Para determinar dónde obtuvo la célula el esquema que le indicó como formarse, pasemos al núcleo y contemplemos los delgados contornos de las macromoléculas de ADN segregadas dentro de sus genes. Cada una contiene una rica información genética acumulada en el curso de unos cuatro mil millones de años de evolución.

Almacenado en un alfabeto de nucleótidos de cuatro “letras”- hecho de moléculas de azúcar y fosfatos, y llenos de signos de puntuación, reiteraciones para precaver contra el error, y cosas superfluas acumuladas en los callejones sin salida de la historia evolutiva-, su mensaje dice exactamente cómo hacer un ser humano, desde la piel y los huesos hasta las células cerebrales.

Si elevamos más el aumento veremos que la molécula de ADN está compuesta de muchos átomos, con sus capas electrónicas externas entrelazadas y festoneadas en una milagrosa variedad de formas, desde relojes de arena hasta espirales ascendentes como largos muelles y elipses grandes como escudos y fibras delgadas como puros. Algunos de esos electrones son recién llegados, recientemente arrancados átomos vecinos; otros se incorporaron junto a sus núcleos atómicos hace más de cinco mil millones de años, en la nebulosa de la cual se formó la Tierra.
Si elevamos el aumento cien mil veces, el núcleo de un átomo de carbono se hinchará hasta llenar el campo de visión. Tales núcleos átomos se formaron dentro de una estrella que estalló mucho antes de que naciera el Sol. Si podemos aumentar aún más, veremos los tríos de quarks que constituyen protones y neutrones.

Los quarks han estado unidos desde que el Universo sólo tenía unos pocos segundos de edad y ahora están en nosotros y en todos los objetos del universo, chicos o grandes, todo lo material está hecho de Quarks y Leptones desde una bacteria hasta una galaxia. Por supuesto, también nuestro cerebro y las neuronas que crean pensamientpos.
Al llegar a escalas cada vez menores, también hemos entrado en ámbitos de energías de unión cada vez mayores. Un átomo puede ser desposeído de su electrón aplicando sólo unos miles de electrón-voltios de energía. Sin embargo, para dispersar los nucleones que forman el núcleo atómico se requieren varios millones de electrón-voltios, y para liberar los quarks que constituyen cada nucleón se necesitaría cientos de veces más energía aún.


Introduciendo el eje de la historia, esta relación da testimonio del pasado de las partículas: las estructuras más pequeñas, más fundamentales están ligadas por niveles de energía mayores porque las estructuras mismas fueron forjadas en el calor del big bang.
Esto implica que los aceleradores de partículas, como los telescopios, funcionen como máquinas del tiempo. Un telescopio penetra en el pasado en virtud del tiempo que tarda la luz en desplazarse entre las estrellas; un acelerador recrea, aunque sea fugazmente, las condiciones que prevalecían en el Universo primitivo.
Hemos llegado a dominar técnicas asombrosas que nos facilitan ver aquello que, prohibido para nuestro físico, sólo lo podemos alcanzar mediante sofisticados aparatos que bien nos introduce en el universo microscópico de los átomos, o, por el contrario nos llevan al Universo profundo y nos enseña galaxias situadas a cientos y miles de millones de años-luz de la Tierra.

Cuando vemos esos objetos cosmológicos lejanos, cuando estudiamos una galaxia situada a 100.000 mil años-luz de nosotros, sabemos que nuestros telescopios la pueden captar gracias a que la luz de esa galaxia, viajando a 300.000 Km/s llegó a nosotros después de ese tiempo, y, muchas veces, no es extraño que el objeto que estamos viendo ya no exista o si existe, que su conformación sea diferente habiéndose transformado en diferentes transiciones de fase que la evolución en el tiempo ha producido.
En el ámbito de lo muy pequeño, vemos lo que está ahí en ese momento pero, como se explica más arriba, en realidad, también nos lleva al pasado, a los inicios de cómo todo aquello se formó y con qué componentes que, en definitiva, son los mismos de los que están formadas las galaxias, las estrellas y los planetas, una montaña y un árbol y, cualquiera de nosotros que, algo más evolucionado que todo lo demás, podemos contarlo aquí.
Estas y otras muchas maravillas son las que nos permitirán, en un futuro relativamente cercano, que podamos hacer realidad muchos sueños largamente dormidos en nuestras mentes.
emilio silvera
Mar
18
¡Las matemáticas! El origen
 por Emilio Silvera ~
por Emilio Silvera ~
 Clasificado en Las huellas del pasado ~
Clasificado en Las huellas del pasado ~
 Comments (1)
Comments (1)


Muescas en el hueso de Ishango
Lo que veremos es que, las cosas nunca son como parecen ser a primera y, el tiempo pasa inexorable, las cosas cambian sin que nada lo pueda evitar y, los saberes del mundo evolucionan tomando siempre el camino de la perfección. Es decir, vez se hacen las cosas mejor, se depuran las técnicas y, con la experiencia llega el y la sabiduría.

Los expertos occidentales, por ejemplo, dicen que la autoría del teorema de Pitágoras corresponde a éste. A pesar de que los babilonios habían creado el mismo concepto siglos antes. La razón es que Pitágoras o sus seguidores habían creado la primera demostración de este principio fundamental, mientras que los babilonios no lo hicieron. Es lo mismo que pasó (en tiempos más recientes) con Faraday y Maxwell, el primero descubrió con sus experimentos todos los fundamentos encerrados en la electricidad y el magnetismo y, al no saber exponerlo matemáticamente, tuvo que llegar Maxwell que, con sus ecuaciones vectoriales nos dejara una demostración fundamental del electromagnetismo.
Los críticos consideran tan la demostración al estilo griego que su inexistencia en las culturas no europeas desacredita, en su opinión, miles de años de trabajos matemáticos. Claro que, en este punto, no todos estamos de acuerdo y, por mi creo que los pueblos no occidentales sí tenían sus demostraciones, mientras que otros dudan de que sea realmente posible “demostrar” cualquier concepto para toda la eternidad y para su en la totalidad del universo. Es cierto que eterno…no hay nada pero, en todo el universo será válida la ecuación E = mc², de la misma manera que 2 + 2 = 4. Hay cosas que ni el tiempo ni las distancias pueden variar.
 La numeración egipcia (escrita) permitía la representación de números mayores que un millón. Utilizaban un sistema aditivo de decimal con jeroglíficos específicos para la unidad y una de las seis primeras potencias de 10.
La numeración egipcia (escrita) permitía la representación de números mayores que un millón. Utilizaban un sistema aditivo de decimal con jeroglíficos específicos para la unidad y una de las seis primeras potencias de 10.
En la figura podemos ver los símbolos usados para 1, 10, 100 y 1.000. El 10.000 se representaba con un dedo doblado, el 100.000 con un pez y 1.000.000 mediante una figura humana de rodillas y con los brazos alzados.
En un principio escribían los nueve primeros números colocando símbolos de la unidad, uno a continuación de otro; más tarde utilizaron la representación por desdoblamiento mientras los arameos de Egipto usaban un principio ternario (ver tabla).
El escepticismo es oportuno en toda investigación, pero quien investigue las matemáticas no occidentales se enfrenta a menudo con un gran obstáculo. Expertos que han estudiado los sistemas de numeración de la antigua Etiopía, cuentan que los expertos occidentales se negaron en una ocasión a aceptar que esta civilización africana hubiera desarrollado sus propios números. Los números etíopes se parecen a los números egipcios, que son anteriores, y, en menor medida, a los antiguos números griegos –lo cual no es sorprendente, dada, por una la proximidad geográfica de Etiopía con Egipto y, por otra parte, la influencia que ejerció Egipto en las matemáticas griegas. Una serie de cartas escritas por algunos etíopes a personajes griegos y encontradas en Grecia estaban escritas en los dos lenguajes para que las entendieran y, a pesar de ello, algunos “expertos” dudaban que los etíopes hubieran sido capaces de tal sofisticación. Sin embargo, los análisis químicos demostraron que la empleada tenía un color no habitual y los análisis químicos demostraron que la tinta se había fabricado a partir de unas bayas autóctonas de Etiopía.
Nuestro patrimonio matemático y nuestro orgullo occidentales dependen irremediablemente de los logros de la antigua Grecia. Dichos logros se han exagerado tanto que a resulta difícil distinguir qué part3e de la matemática moderna procede de los griegos y cuál es la que su origen en los babilonios, los egipcios, los hindúes, los chinos, los árabes, etc. Sin embargo, si nuestras actuales se basaran exclusivamente en Pitágoras, Euclides, Demócrito, Arquímedes y otros griegos, serían una disciplina bastante deficiente.

En 1908, el historiador de las matemáticas, Rouse Ball escribió:
“La historia de las matemáticas no se puede remontar ciertamente a ninguna ni a ningún período que sean anteriores a la etapa de los griegos jónicos”.

En 1952 el historiador Morris Kline escribió:
“Fue en el extraordinariamente propicio suelo de Gracia donde [las matemáticas] garantizaron finalmente una nueva forma de controlar la existencia humana y florecieron espectacularmente durante un breve período de tiempo… Con el declive de la civilización griega la planta quedó aletargada durante unos mil años… [hasta que] esa planta fue llevada de una manera adecuada a Europa y plantada una vez más en el terreno fértil” De un modo esquemático, se interpreta a menudo el significado de esta afirmación entendiendo que ha habido tres etapas de la de las matemáticas:
- 1. Hacia el año 600 a. C., los antiguos griegos inventaron las matemáticas, que estuvieron desarrollando hasta aproximadamente el año 400 d. C., en el cual desaparecieron de la faz de la Tierra.
- 2. A esto siguió un período oscuro para las matemáticas, que duró más de mil años. Algunos expertos admiten que los árabes mantuvieron vivas las matemáticas griegas durante toda la Edad Media.
- 3. En la Europa del siglo XVI se produce el redescubrimiento de las matemáticas griegas que vuelven a florecer de hasta el momento actual.
Claro que este punto de es muy discutible. Nuestros números modernos -del 0 al 9- se desarrollaron en la India (como ha quedado reseñado en escritos expuestos aquí en estos días pasados) durante la segunda etapa, el llamado período oscuro de las matemáticas. Las matemáticas existían ya mucho antes de que los griegos construyeran su primer ángulo recto.
Rouse Ball, desconocía las primeras matemáticas hindúes contenidas en los Sulbasutras (las reglas de la cuerda). Escritos en alguna comprendida entre los años 800 y 500 a. C., los Silbasutras demuestran, entre otras cosas, que los indios de este período tenían su propia versión del teorema de Pitágoras así como un procedimiento para obtener la raíz cuadrada de 2 con una precisión de hasta cinco cifras decimales. Los Sulbasutras ponen de manifiesto la existencia de un rico conocimiento geométrico que fue muy a los griegos.
Otro experto nos dice que, la afirmación de Kline es más problemática, ya que ignora un rico conjunto de matemáticas no europeas que fueron desenterradas hacia mediados del siglo XX, incluidas las matemáticas de Mesopotamia, Egipto, China, la India, el mundo árabe y la América precolombina. También existe el problema de los propios griegos –Demócrito, Aristóteles, Heródoto- prodigaron alabanzas a los egipcios, reconociéndolos como sus gurús matemáticos (aunque con distintas palabras). El hecho cierto es que, antes que los griegos fueron muchos los que aportaron su matemático para que ahora nosotros, sepamos de esa imprescindible y necesaria disciplina que nos sirve para construir puentes, para diseñar veloces trenes, para poder calcular las trayectorias de las naces espaciales que van hacia Marte, o, simplemente, para saber cómo funcionan las leyes de la Naturaleza, los átomos que conforman la materia e incluso, saber sobre densidades y energías en las estrellas.
Repasando todos estos hechos, de alguna manera, podemos llegar a entender aquel “Todo es número ” de los pitagóricos.
emilio silvera
















 Totales: 75.006.319
Totales: 75.006.319 Conectados: 97
Conectados: 97





















