jueves, 21 de noviembre del 2024 Fecha
Ir a la página principal Ir al blog

IMPRESIÓN NO PERMITIDA - TEXTO SUJETO A DERECHOS DE AUTOR



Archivo de la categoría "Matemáticas"

« Entradas anteriores

Sep

28

A veces cuesta pero… Se consigue!

Autor por Emilio Silvera    ~    Archivo Clasificado en Matemáticas    ~    Comentarios Comments (0)

RSS de la entrada Comentarios Trackback Suscribirse por correo a los comentarios

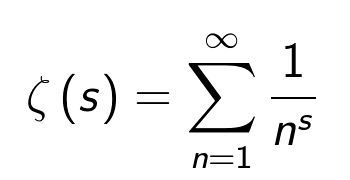
Un alarde de erudicción para “resolver” la hipótesis de Riemann

 

La función zeta de Riemann

Resultado de imagen de La función Z de Riemann

 

 

La posible resolución de la hipótesis de Riemann

 

Los días pasados un terremoto recorría el mundo matemático: este lunes, 24 de septiembre, Sir Michael Atiyah, uno de los matemáticos más laureados y respetados de la historia anunciaba en el abstract de su conferencia en el Laureate Forum de Heilderberg, que había demostrado de una manera sencilla la hipótesis de Riemann.

https://www.abc.es/ciencia/abci-numeros-primos-y-posible-solucion-hipotesis-riemann-201809250914_noticia.html

El abstract decía textualmente: ”Es un conocido problema matemático sin resolver desde el año 1859. Yo presentaré una prueba simple utilizando una perspectiva radicalmente nueva. Está basada en los trabajos de Von Neumann (1936), Hirzebruch (1954) y Dirac (1928)”.

Si el anuncio fuese de otra persona, el revuelo no hubiera sido de esta envergadura, pero Michael Francis Atiyah, de 89 años, es medallista Fields en 1966 y Premio Abel en 2004 (entre otras muchas distinciones). La duda sobre esta supuesta prueba surgió enseguida, aludiendo a su edad y a otros anuncios fallidos previos, y también a la singularidad de la ocasión, cuando hace poco más de un mes, Atiyah impartió una conferencia en el Congreso Internacional de Matemáticos de Río de Janeiro.

      ¿Qué pinta π aquí?

¿Y qué dice esta famosa conjetura? Viene de una de esas extrañas relaciones internas de las matemáticas, entre los números primos y una función entre los números complejos llamada precisamente función zeta de Riemann, de manera que los ceros de esta función (los valores donde se anula) tienen todos parte real 1/2. Así que probar la conjetura de Riemann nos da una buena idea de cómo se distribuyen los números primos, que sabemos desde Euclides que son infinitos. Y los números primos son los ladrillos con los que se construyen todos los demás, piezas claves en muchas aplicaciones como en la criptografía.

Imagen relacionada

Las pistas que daba Atiyah en su abstract, se referían a tres trabajos: el de John von Neumann titulado On an algebraic generalization of the quantum mechanical formalism, esencial para la formulación matemática de la mecánica cuántica; uno segundo titulado Arithmetic genera and the Theorem of Riemann-Roch, clásico en geomería algebraica, escrito por el matemático alemán Hirzebruch, y cuyo resultado principal está basado en la teoría del cobordismo de René Thom; y otra obra clásica del premio Nobel P.A.M. Dirac, The Quantum Theory of the Electron, en el que introduce la ecuación de onda del electrón unificando la mecánica cuántica y la relatividad especial.

Sólo un genio como Atiyah podría ser capaz de presentar un abstract basado en estas tres piezas maestras de tres maestros y decirnos que así ha probado de manera sencilla la hipótesis de Riemann. Sin embargo, tras una muestra de erudición matemática y física (implicando incluso a la famosa constante de estructura fina de Arnold Sommerfeld), nos hemos quedado con la miel en los labios. Atiyah usa la función de Todd (llamada sí en honor de su antiguo profesor John Arthur Todd) para obtener una contradicción, pero las dudas surgen. Por una parte, hay cuestiones técnicas sobre las funciones implicadas, y por otra, da la impresión de ser un argumento circular. En cualquier caso, esta presentación ha servido para remover el interés sobre las matemáticas y esta extraordinaria conjetura, uno de los problemas del milenio. Sabremos más en los próximos días sobre la veracidad o no de la prueba de Atiyah.

 

 

 

hotmail correo[?]


May

8

¡Ramanujan!

Autor por Emilio Silvera    ~    Archivo Clasificado en Matemáticas    ~    Comentarios Comments (1)

RSS de la entrada Comentarios Trackback Suscribirse por correo a los comentarios

El matemático al que los dioses susurraban fórmulas imposibles

 

Una película relata la vida de Srinivasa Ramanujan, un matemático indio autodidacta que revolucionó esta ciencia a principios de siglo

 

 

 

 

 

 

Dev Patel en el papel de Ramanujan

                                                                        Dev Patel en el papel de Ramanujan

En 1913, el matemático G. H. Hardy recibió una carta con un contenido increíble. El autor era un joven indio, Srinivasa Ramanujan, capaz de producir fórmulas inverosímiles pese a no haber recibido una educación formal en matemáticas puras. Aunque al principio respondió con escepticismo, Hardy acabó llevando a Ramanujan desde Madrás, en el sur de la India, al Trinity College de Cambridge (Reino Unido) para tratar de desentrañar el secreto de aquel genio autodidacta.

Aquel fue, según diría después Hardy, el único suceso romántico de su vida. Su encuentro sirvió para mostrar al mundo trabajos como las fórmulas que permitían calcular a gran velocidad los infinitos decimales del número pi. Hoy, un siglo más tarde, el legado de la breve vida de Ramanujan sigue influyendo en matemáticas, física o computación.

La historia de ese encuentro es la que se cuenta ahora en El Hombre que conocía el infinito, una película que se estrenará el 13 de mayo y que protagonizan Jeremy Irons (Hardy) y Dev Patel (Ramanujan). Desde sus orígenes, se relata este encuentro improbable, entre un indio religioso, casado con una niña de 10 años y practicante de una religión que no le dejaba cruzar el mar, con un racionalista ateo miembro de la élite intelectual eurocentrista de la época.

“No creo en la sabiduría inmemorial de Oriente, pero creo en ti”, le dice en un momento Hardy a Ramaujan. El indio sentía que un ser superior, su diosa, le susurraba las fórmulas que resolvían problemas imposibles. Hardy, fascinado por su talento natural, trataba de que él mismo reconstruyese el camino por el que alguien sin su inspiración pudiese llegar a las mismas conclusiones.

“No creo en la sabiduría inmemorial de Oriente, pero creo en ti”, le dice  Hardy a Ramaujan

 

 

 

Además de los retos científicos, la película muestra el rechazo al que tuvo que enfrentarse Ramanujan en Inglaterra. Solo el empeño de Hardy, y el apoyo de unos pocos miembros del claustro del Trinity como J. E. Littlewood, le permitieron ser reconocido en un mundo que aún justificaba el colonialismo en la existencia de razas inferiores como las del matemático indio.

El ejemplo de Ramanujan puede utilizarse para apoyar la hipótesis de que el lenguaje matemático es algo inscrito en el cerebro de todos los seres humanos. Como Mozart hacía con la música, Ramanujan tenía la capacidad de hacer brotar de su interior fórmulas que sirven para explicar la naturaleza. Millones de años de evolución habrían creado las estructuras neuronales que sirven para entender el mundo y, en el caso de Ramanujan, permiten describirlo con las ecuaciones más sofisticadas.

El brillo del matemático indio fue breve. Sus resultados y el apoyo de Hardy le llevaron a la Royal Society y a ser miembro del claustro del Trinity College, pero no disfrutaría mucho de esos honores. En 1920, con 32 años y solo siete después de la carta que le llevó a Inglaterra, una tuberculosis que algunos atribuyen en parte a su trabajo extenuante acabó con su vida.

Hasta aquí el reportaje publicado en la prensa.

hotmail correo[?]


Mar

29

¡Perelman! El Espíritu misterioso

Autor por Emilio Silvera    ~    Archivo Clasificado en Matemáticas    ~    Comentarios Comments (18)

RSS de la entrada Comentarios Trackback Suscribirse por correo a los comentarios

Grigori Perelmán

Os voy a contar ahora la fabulosa historia de Grigori “Grisha” Yákovlevich Perelmán sin duda alguna el mas genial matemático de nuestro tiempo (extraigo la mayor parte de los datos de nuestra amiga Wiki). Nació el 13 de junio de 1966 en Leningrado, URSS (ahora San Petersburgo, Rusia), ha hecho históricas contribuciones a la geometría riemanniana y a la topología geométrica. En particular, ha demostrado la conjetura de geometrización de Thurston, con lo que se ha logrado resolver, afirmativamente, la famosa conjetura de Poincaré, propuesta en 1904 y considerada uno de los problemas abiertos más importantes y difíciles en matemáticas.

Leer más

hotmail correo[?]


Mar

29

Perelman, ¡extraño personaje!

Autor por Emilio Silvera    ~    Archivo Clasificado en Matemáticas    ~    Comentarios Comments (0)

RSS de la entrada Comentarios Trackback Suscribirse por correo a los comentarios

Recordemos aquí de nuevo que, precisamente ahora, un siglo más tarde, en el Congreso Internacional de Matemáticas celebrado en Madrid el mes de Agosto de 2006, se otorgó la Medalla Field (una especie de Nobel de las matemáticas) al matemático ruso Perelman, extraño ser que no ha comparecido a la cita y la ha rechazado. Perelman (aunque muchos lo intentaron sin conseguirlo), ha resuelto la conjetura expuesta por Poincaré y planteada en 1904.

La conjetura de Poincaré de 1904, en el año 2.000, fue catalogada por el Instituto Planck como uno de los siete problemas del milenio. Para hacer un comentario sobre esta conjetura tengo que referirme a la topología, el nivel de las matemáticas donde está ubicada.

La topología es la geometría de los objetos elásticos o flexibles que cambian de forma pero tienen las mismas propiedades que antes de ser estirados, achatados, etc. Se pueden retorcer pero no cortar ni pegar.

Los topólogos no tienen en cuenta la distancia, puesto que se puede variar al deformar el objeto, sino nociones más sutiles. Los orígenes de la topología se remontan a mediados del siglo XVIII, con los trabajos de Euler en teoría de grafos, que llamó “análisis situs”.

A finales del siglo XIX y principios del siglo XX, la topología recibió un gran impulso con los trabajos de Poincaré, matemático francés muy influyente en el posterior desarrollo de diversas áreas de las matemáticas y de la física. En particular, en 1904 planteó la conjetura que lleva su nombre y que no se ha resuelto hasta el siglo XXI. Este problema ha sido un motor para la investigación en topología de todo el siglo pasado y se ha llegado a su resolución con ideas nuevas y apasionantes.

Para situarnos mejor debemos hablar de las variedades, espacios que tienen una dimensión determinada. Por ejemplo una recta o un circulo son variedades de dimensión uno, puesto que se describen como un parámetro.  El plano o la esfera son ejemplos de variedades bidimensionales, al utilizar dos parámetros para describir sus posiciones. El espacio en que vivimos es una variedad tridimensional, y si le añadimos la dimensión temporal, el espacio-tiempo es una variedad de dimensión cuatro. Ya he comentado en otros trabajos cómo las singularidades geométricas, las variedades, fueron introducidas por Riemann a mediados del s. XIX y constituyeron una herramienta clave para la física del siglo XX. De hecho, la teoría de la relatividad especial de Einstein fue postulada por Einstein en 1.905, pero hasta que no incorporó las variedades contenidas en el tensor métrico de Riemann, no pudo completar la teoría de la relatividad general que incluía los espacios curvos.

Leer más

hotmail correo[?]


Mar

29

Srinivasa Ramanujan

Autor por Emilio Silvera    ~    Archivo Clasificado en Matemáticas    ~    Comentarios Comments (5)

RSS de la entrada Comentarios Trackback Suscribirse por correo a los comentarios

Srinivasa Ramanujan nació en 1887 en Erode, India, cerca de Madrás.  Su familia de clase media alta, brahmin, la más alta de las castas hindúes, fueron destituidos y venidos a menos. Su padre trabajaba de oficinista de un comerciante de tejidos.

Con diez años, lo mismo que pasó antes con Riemann, ya destacaba y sorprendía a todos con sus enormes poderes de cálculos. Siendo niño rederivó la identidad de Euler entre funciones trigonométricas y exponenciales.

En la vida de cada científico joven hay un punto de partida, un hecho que, sin ellos saberlo, les marca el destino. Para Einstein fue la fascinación que le causó la brújula que le regaló su tío cuando estaba enfermo siendo un niño, no podía apartar la mirada de la aguja que siempre indicaba hacia el mismo sitio, y se preguntó una y mil veces por la fuerza invisible que la obligaba a dirigirse hacia esa dirección. Para Riemann, fue la lectura del libro de matemáticas de Legendre. Para Ramanujan, fue cuando se sumergió en un oscuro y olvidado libro de matemáticas escrito por George Carr. Este libro ha quedado inmortalizado desde entonces por el hecho de que señaló la única exposición conocida de Ramanujan a las modernas matemáticas occidentales. Según su hermana: “Fue este libro el que despertó su genio. Él se propuso establecer por sí mismo las fórmulas dadas allí. Como no tenía la ayuda de otros libros, cada solución era un trabajo de investigación por lo que a él concernía… Ramanujan solía decir que la diosa Namakkal le inspiraba las fórmulas en sueños“.

Con ayuda de amigos, Ramanujan consiguió un puesto de bajo nivel del puerto de Madrás. Era un trabajo servil, con una mísera paga de 20 libras al año, pero dio libertad a Ramanujan, como a Einstein antes que él en la oficina de Patentes Suiza, para seguir sus sueños en su tiempo libre. Ramanujan, en la fascinación que en él ejercían los números, era incansable. Llenaba libretas enteras de cálculos y ecuaciones que antes veía florecer en su cabeza.

Así estaban las cosas cuando decidió escribir algunos de sus trabajos a las tres matemáticos más famosos de Inglaterra y Europa.

Dos de aquellos matemáticos, al tener en su poder las cartas enviadas por un miserable empleado sin instrucción formal alguna, sin haber comprobado su contenido, las arrojaron directamente a la basura. El tercero era el brillante matemático de Cambridge Godfrey Harold Hardy. Debido a su categoría en Inglaterra, Hardy estaba acostumbrado a recibir correo de chiflados proponiéndole los más peregrinos proyectos y, en un primer momento apenas prestó atención a la carta del joven Ramanujan.

Leer más

hotmail correo[?]


« Entradas anteriores