[Caricatura de Évariste Galois; imagen procedente de http://divulgamat.ehu.es/]

Como señaló en 1895 el gran matemático noruego Sophus Lie, él mismo uno de los que más hicieron avanzar la teoría de grupos y de ecuaciones diferenciales (son famosos, e importantes, los “grupos de Lie”):

                                                         

Las ideas de Galois encontraron, en más de un sentido, uno de sus momentos culminantes cuando, en 1872, Feliz Klein pronunció su conferencia inaugural como nuevo catedrático de la Universidad de Erlangen, que tituló: Consideraciones comparativas sobre las investigaciones geométricas modernas, cuyo contenido y tesis terminaron conociéndose como simplemente, “el Programa de Erlangen”, en el que la Geometría se define de la manera siguiente: “Dado un conjunto de cualquier número de dimensiones, y un grupo de transformaciones entre sus elementos, se llama geometría al estudio de las propiedades de aquel conjunto que son invariantes respecto de transformación imaginables, que son, por supuesto, infinitos.

Lástima que, un ser elegido para la gloria, de una mente matemática privilegiada, acabara sus días de manera tan temprana, en los comienzos de lo que podría haber sido, un largo y glorioso recorrido sembrados de luminosas ideas que, como relámpagos deslumbrantes, habrían iluminado lóbregos y oscuros rincones del saber del mundo. Eso nos perdimos con la muerte del joven Galois.

                                             

                                      El hombre Vitrubio, la proporción áurea

¿Qué es la simetría?. Se entiende científicamente por simetría a la propiedad de que aplicando ciertas transformaciones sobre algún objeto geométrico, físico o matemático (cuando digo matemático me estoy refiriendo por ejemplo a una ecuación u otra entidad de la matemática) se obtiene otro de idénticas propiedades que el primero. Es decir, los objetos, sean de la índole que sean, que poseen simetría preservan sus características bajo ciertas transformaciones.

 

“Gracias al trabajo de la matemática Emmy Noether, la física moderna ha encontrado en el uso de simetrías una poderosa herramienta para profundizar en el conocimiento de la Naturaleza.”

 

 

Y por características se pueden entender muchas cosas, según sea lo que estemos analizando. Por ejemplo, los más comunes cristales de nieve, con forma de estrella de 6 puntas, poseen simetría geométrica según rotaciones en ángulos de 60º, 120º, 180º, 240º, 300º, 360º, y en general múltiplos de 60º.

 

 

 

 

Tampoco varía su geometría ante la transformación de reflexión especular, y como es lógico, ante transformaciones resultantes de reflexión seguida de giro o viceversa. En este caso lo que se preserva es la forma del cristal de nieve ante transformaciones que lo giran y/o que obtienen su imagen reflejada. Otro ejemplo de simetría lo constituyen las leyes de Newton de la física clásica.

 

 

Presentan simetría traslacional y rotacional, ya que dichas leyes no varían aunque variemos nuestra posición viajando en el universo, o aunque variemos nuestros ejes cartesianos de referencia y por lo tanto nuestra orientación. Otro tanto ocurre con las ecuaciones de campo de la teoría de la relatividad general, las cuales son simétricas según cada una de las variables dimensionales, según rotaciones en torno a diferentes ejes, y según traslaciones en el tiempo. Estos hechos precisamente son una fortuna para nosotros, puesto que nos permiten saber cómo se comporta el Universo conociendo nuestra vecindad más próxima.

Bueno, aquí lo dejamos que, para una sencilla reseña del  personaje, parece suficiente. Nunca está demás recordar a personajes que, como Galois, a pesar de su juventud, aportaron al mundo tanto, tanto que, difícilmente le podremos pagar alguna vez la deuda que con él tenemos pendiente.

 

Artículo elaborado por Emilio Silvera a partir de Galois: Bibliografía:

Observad las estrellas y aprended de ellas.                                   Ningún mortal puede acercarse a los dioses.

En honor al Maestro todas deben girar,                                                        Hedmond Halley

Cada una en su trayectoria sin un ruido,                                                     sobre los Principia de Newton

Siguiendo el principio de Newton.

Einstein

Newton elaboró una explicación cuantificada matemáticamente de la gravitación que abarcaba por igual fenómenos terrestres y celestes. Al hacerlo, demolió la división aristotélica del universo en dos ámbitos, uno por encima y otro por debajo de la Luna, y creó una base física para el Universo copernicano. La perfección y seguridad con la que realizó esta tarea fueron tales que su teoría llegó a ser considerada durante más de los dos siglos posteriores, como algo cercano a la palabra revelada por alguna divinidad. Aún hoy, cuando la dinámica newtoniana es contemplada como sólo una parte de la tela más basta pintada por la relatividad de Einstein, la mayoría de nosotros seguimos pensando en términos newtonianos, y las leyes de Newton son eficaces para guiar las naves espaciales a la Luna y los planetas.

Sin embargo, el hombre cuya explicación del cosmos viver en la mente de más de mil millones de personas era uno de los más extraños y difícilmente accesibles individuos que hayan vivido nunca. Cuando John Maynard Keynes compró en una subasta un baúl lleno de documentos de Newton, se asomnró de encontrarse con que estaba lleno de notas sobre Alquimia, las profecías biblícas y la reconstrucción, basada en textos hebreos, del plano del templo de Jerusalén, que para Newton era “un emblema del sistema del mundo”. Pero esta historia, merece ser contada con más lujo de detalles:

En 1684 tres miembros de la Royal Society, el astrónomo Edmund Halley, Christopher Wren, arquitecto de la catedral de de Londres, y el físico Robert Hooke, mantenían en Londres una animada discusión que acabó en una apuesta: ¿qué tipo de trayectoria describen los planetas alrededor del Sol? Wren ofreció 40 chelines a quien aportara la solución.

De los tres, Halley fue el que más se empeñó en encontrar una solución, hasta el punto de viajar a Cambridge para trasladar la pregunta a Newton, el excéntrico profesor de matemáticas. Allí pudo preguntarle directamente: ¿qué tipo de trayectoria describen los planetas alrededor del Sol? Sobre esta entrevista no sabríamos nada si no llega a ser por Abraham de Moivre, gran matemático y amigo de Newton, que dejó escrito lo siguiente sobre este encuentro:

Newton contestó inmediatamente que era una elipse. El doctor, lleno de alegría y asombro, preguntó cómo lo sabia. “Porque lo he calculado”, contestó. Entonces el doctor le pidió que le mostrase los cálculos. Newton buceó en su baúl, entre sus papeles, pero no lo encontró. Prometiéndole que los volvería a reproducir.

                                                                           Halley y Newton

Ese baúl lo heredó su encantadora sobrina Catherine Conduitt y a través de la descendencia, el baúl terminó en manos del vizconde de Lymington. Casi nadie había visto nunca los documentos que contenía el baúl, y una leyenda cuenta que una vez un obispo, picado por la curiosidad, examinó el contenido del baúl y lo cerró inmediatamente horrorizado. Durante mucho tiempo el contenido del baúl siguió siendo un misterio y su contenido calificado como no apto para la difusión.

El vizconde de Lymington, acuciado por algunos problemas financieros, un divorcio y algunos problemas de impuestos, decide poner a la venta el conjunto de documentos de Newton que su familia poseía desde hacía más de doscientos años.

En 1936, se subasta en Sotheby’s (Londres) el contenido de un baúl metálico lleno de manuscritos de Isaac Newton. Casi todo el lote fue adquirido por John Maynard Keynes, el famoso economista, al que gustaba coleccionar textos científicos antiguos.

Cuando Keynes pudo leer los documentos, quedó muy sorprendido, ya que lo que encontró fue un volumen de manuscritos equivalente a todos sus anteriores trabajos científicos, pero casi todos trataban sobre alquimia. Repuesto de la sorpresa inicial, y después de estudiar los manuscritos, dio una conferencia en la Royal Society de Londres en 1942 y dijo sobre Newton lo siguiente:

“Desde el siglo XVIII, Newton ha sido considerado el primero y más grande de los científicos de la era moderna, un racionalista, alguien que nos enseñó a pensar de acuerdo con los dictados de la razón fría y carente de emoción. Yo ya no puedo verlo bajo esa luz. Y no creo que pueda hacerlo nadie que haya estudiado con detenimiento los documentos contenidos en esa caja que guardó al partir de Cambridge en 1696 y que, pese haber sido en parte dispersados, han llegado hasta nosotros. Newton no fue el primer hombre de la Edad de la Razón, fue el último de los magos, el último de los babilonios y de los sumerios, la última gran mente que contempló el mundo visible e intelectual con los mismos ojos que lo hicieron quienes empezaron a construir nuestra herencia cultural hace casi diez mil años”.

Hasta ahora, ese aspecto de la personalidad de Newton ha sido deliberadamente ocultado y Newton aparece en la mayoría de los libros como un racionalista puro, y con esa etiqueta es con la que ha pasado a la historia. Creo que cualquier persona que haya leído algunos de esos documentos, o algunas de las cartas que Newton escribió al Dr. Bentley, estará de acuerdo con Keynes al considerar que Newton no fue el primer racionalista sino el último mago, el último de los babilonios. Newton quedó aislado, también,  por la singular potencia de su intelecto. Richard Westfall paso veinte años escribiendo una biografía sumamente perpicaz y erudita de Newton, pero confesó, en el promer párrafo del prefacio.

“Cuanto más lo he estudiado, tanto más Newton se ha alejado de mí. He tenido el privilegio, en diversas ocasiones, de conocer una serie de hombres brillantes, hombres a quirnes conozco sin vacilación como intelectualmente superiores a mí. Sin embargo, nunca he conocido a ninguno con el que no estuviese dispuesto a medirme, de modo que fuese razonable decir que mi capacidad era la mitad de la persona en cuestión, o la tercera o la cuarta parte, pero en tofos los casos una fracción finita. El resultado final de mi estudio de Newton ha servido para convencerme que con él no hay comparación posible. Se ha convertido para mí en otro hombre totalmente diferente, en uno de un puñado de genios supremos que han modelado las categorias del intelecto humano, un hombre que, finalmente, no es reducible a los criterios con que comprendemos a nuestros semejantes.”

Fotografía de la casa natal de Isaac Newton  en la localidad de Woolsthorpe , en Lincolnshire, donde nació prematuramente aquel 4 de enero de 1643 (aunque en algunas referencias se menciona que esta es la casa donde vivió en Grantham años después)  . Newton era hijo único, el hijo póstuno de un pequeño terrateniente analfabeto. Era tan pequeño al nacer que su madre ,  Hannah Ayscough, diría que cabía en una botella de cuarto. Su padre había muerto unos meses antes y con sólo tres años tuvo que abandonar la casa materna cuando Hannah se casó por segunda vez y su nuevo marido no quiso hacerse cargo del niño.Durante el resto de su infancia viviría en casa de su abuela materna , a dos kilómetros de distancia de su madre , algo que seguramente influiría en el carácter silencioso, reservado y poco sociable de Newton a lo largo de su vida. De todas formas es difícil juzgar la personalidad de una mente tan poderosa como la del gran matemático inglés , porque su forma de ver el mundo no puede ser igual a la que tenemos los demás, muy por debajo de su capacidad intelectual.

Newton, que había nacido en el mismo año de la muerte de Galileo Galilei, sustituyó el telescopio refractor de Galileo , que tenía una gran lente en la parte delantera para recoger la luz pero que Newton, por su experiencia con la refracción de la luz, sabía que distorsionaba los colores. Así desarrolló el telescopio reflector que empleaba un espejo en lugar de una lente para recoger la luz lo que lo hacía más barato y más eficiente. La Royal Society le pediría que construyese un segundo telescopio y viendo que funcionaba a la perfección le admitieron inmediatamente en la sociedad científica. Sin embargo, Newton no estaría contento con la fama que había ganado con este invento, ya que recibía muchas cartas. Escribiría al secretario de la Royal Society quejándose porque había “sacrificado mi tranquilidad, una cuestión de verdadera importancia” Así era Newton, siempre huyendo de la fama para que no interrumpieran su trabajo, aunque no estaba exento de ambición.

La vida de Newton, sobre todo su infancia, estuvo rodeada de una serie de circunstancias que le hicieron algo especial. El casamiento de su madre, vivir con su abuela y alejado de ella que vivía con su usurpador padrasto…El producto de todo aquello: haber nacido sin padre el día de Navidad, haber sobrevivido en contra de las probabilidades, la separación de la madre y una mente tan poderosa que él mismo era tanto su vasallo como su amo, le hicieron ser un muchacho reflexivo, tenso, hosco, brillante y propenso a la colera. El jopven Newton era sensible a los ritmos de la Naturaleza e insensible a los de los hombres. De niño construía relojes mecánicos y de sol, y era conocido por saber decir la hora por el Sol, pero habitualmente, olvidaba presentarse a comer, rasgo que persistió durante toda su vida. Podía pasarse días sin aparecer a la hora de la comida y sin dormir, enredado en su escritos sobre asuntos de la filosofía natural que encerraba los secretos de la naturaleza.

Durante un tiempo se inspiró en los libros de René Descartes, un espíritu afín al suyo. Ambos tenían mucho en común: criados por sus abuelas, niños frágiles y solitarios y con una vida interior muy fuerte que modeló sus caractéres. descartes le hablaba de lo que era el conocimiento humano y, muchos de aquellos pensamientos pervivieron en su intelecto.

La teoría cartesiana del torbellino del sistema solar se convirtió en el estímulo para la demostración de Newton de que los torbellinos no podían explicar las leyes de Kepler del movimiento planetario. La importancia que asignó Descartes a la descripcion algebraica del movimiento alentó a Newton a elaborar una dinámica escrita en una fórmula alternativa del algebra, la geometría. Como esto aún no era matemáticamente factible, Newton halló necesario inventar una nueva rama de la matemática, el cálculo infinitesimal. Éste puso la geometría en movimiento . Las parábolas e hipérbolas que Newton trazó en el papel podían ser analizadas como resultado de un punto en movimiento como la punta del palillo con el que Arquímedes trazaba figuras en la arena. En palabras de Newton: “Se describen líneas, y por ende se generan, no por la oposición de partes, sino por el movimiento continuo de puntos.”

Poco después de su graduación, la Universidad fue cerrada y Newton se marchó al campo. Allí tuvo mucho tiempo para pensar. Un día (y parece muy probable que se le haya ocurrido de repente) dio con la grandiosa teoría que no habían logrado concebir ni Kepler ni Galileo: una explicación única y general de cómo la fuerza de la gravitación causa el movimiento de la Luna y los planetas.

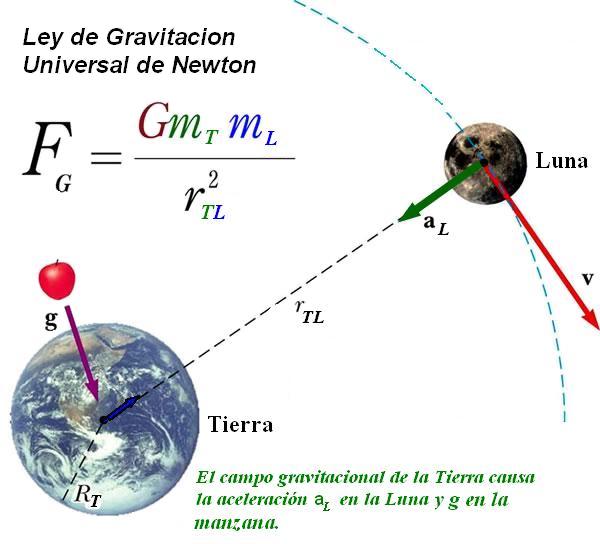
– En la ausencia de fuerzas exteriores, todo cuerpo continúa en su estado de reposo o de movimiento rectilíneo uniforme a menos que actúe sobre él una fuerza que le obligue a cambiar dicho estado.

– La variación de momento lineal de un cuerpo es proporcional a la resultante total de las fuerzas actuando sobre dicho cuerpo y se produce en la dirección en que actúan las fuerzas. La fuerza que actúa sobre un cuerpo es directamente proporcional al producto de su masa y su aceleración.

– Por cada fuerza que actúa sobre un cuerpo, éste realiza una fuerza igual pero de sentido opuesto sobre el cuerpo que la produjo. Dicho de otra forma: Las fuerzas siempre se presentan en pares de igual magnitud y sentido opuesto y están situadas sobre la misma recta.

Alrdedor de todo esto han salido a la luz diversas anécdotas que, como la manzana que vio caer del árbol mirando a traes de la ventana de su cuarto, le dio la odea seminal de su teoría de la gravitación. Vaya usted a saber como sucedió, o como le llegó a su mente, la idea de la Gravitación Universal.

Esto es mucho más largo y, desde luego, no podemos despacharlo de un plimazo, así que, dejaremos para una segunda parte la historia que nos relata como era y quien fue este grandioso personaje de la Historia de la Ciencia y que posibilitó para que la Humanidad, diera un gran paso en el conocimiento del mundo.

emilio silvera

personajes históricos

La máquina del tiempo la inventó un español

En 1887, Enrique Gaspar publicó ‘El anacronópete’, la primera obra mundial en la que la ciencia permitía viajar al pasado. Ocho años después H.G. Wells se llevaba la gloria gracias a su popular novela.

 

Enrique Gaspar, el inventor de la máquina del tiempo.

Miguel A. Delgado @Rosenrod

Gaspar, nacido en Madrid en 1842, además de escritor, fue diplomático. Después de desarrollar su cargo en Europa, ocupó cargos de cónsul en Macao, Cantón y Hong Kong. Unos destinos que tuvieron una gran influencia en El anacronópete, por cuanto los viajeros del aparato (que recibe su nombre de la combinación de tres palabras griegas, ‘aná’, atrás; ‘cronos’, tiempo; y ‘petes’, el que vuela)o ‘anacronóbatas’, llegarán a visitar la China del siglo III, a la que encuentran tan avanzada técnica, social y culturalmente como el Occidente del XIX.

En su concepción, Gaspar tuvo dos claras influencias: por un lado, los libros de Julio Verne, que arrasaban en España tanto como en Europa y América; y por otro, la novela Lumen, del astrónomo francés Camille Flammarion, con quien el español mantuvo una relación de amistad, y que también abordaba un viaje en el tiempo, aunque en este caso a través de un sueño. Del primero tomó el sentido de la aventura y la necesidad de buscar un sustento lo más científico posible a la historia; del segundo, la posibilidad de trasladarse a épocas pretéritas.

Pero si algo distingue a la obra de Gaspar es su profundo sentido del humor: al ser ideada para una zarzuela no evita los enredos y los momentos pícaros (por ejemplo, los vestidos de lana de unas mujeres “de vida alegre” parisinas que se unen al viaje, van convirtiéndose en las ovejas originales al ir hacia atrás en el tiempo, lo que lleva a la desaparición progresiva de su ropa). Precisamente, para evitar que eso suceda y que los propios viajeros vayan rejuveneciendo hasta convertirse en bebés y desaparecer, el inventor utilizará una sustancia de su invención, a la que bautizará con el nombre de ‘fluido García’ (que ha dado nombre a un disco del grupo español Sidonie).

Página de la edición original de El anacronópete.

Este trabajo lo presenté  en el Carnaval de la Física en homenaje a Riemann.

Georg Friedrich Bernhard Riemann fue un matemático alemán que realizó contribuciones muy importantes al análisis y la geometría diferencial, algunas de las cuales allanaron el camino para el desarrollo más avanzado de la relatividad general. Hay personajes que parecen estar destinados al olvido a pesar, de sus muchas contribuciones alñsaber del mundo.

Recordemos aquí un extraño caso que surgió el día 10 de Junio de 1.854 con el nacimiento de una nueva geometría: la teoría de dimensiones más altas que fue introducida cuando Georg Friedrich Bernhard Riemann que dio su célebre conferencia en la facultad de la Universidad de Göttingen en Alemania. Aquello fue como abrir de golpe todas las ventanas cerradas durante 2.000 años de una lóbrega habitación que, de pronto, se ve inundada por la luz cegadora de un Sol radiante. Riemann regaló al mundo las sorprendentes propiedades del espacio multidimensional.

Su ensayo, de profunda importancia y elegancia excepcional, “sobre las hipótesis que subyacen en los fundamentos de la geometría” derribó pilares de la geometría clásica griega, que habían resistido con éxito todos los asaltos de los escépticos durante dos milenios. La vieja geometría de Euclides, en la cual todas las figuras geométricas son de dos o tres dimensiones, se venía abajo, mientras una nueva geometría riemanniana surgía de sus ruinas. La revolución riemanniana iba a tener grandes consecuencias para el futuro de las artes y las ciencias. En menos de tres decenios, la “misteriosa cuarta dimensión” influiría en la evolución del arte, la filosofía y la literatura en toda Europa. Antes de que hubieran pasado seis decenios a partir de la conferencia de Riemann, Einstein utilizaría la geometría riemanniana tetradimensional para explicar la creación del universo y su evolución mediante su asombrosa teoría de la relatividad general. Ciento treinta años después de su conferencia, los físicos utilizarían la geometría decadimensional para intentar unir todas las leyes del universo. El núcleo de la obra de Riemann era la comprensión de las leyes físicas mediante su simplificación al contemplarlas en espacios de más dimensiones.

Contradictoriamente, Riemann era la persona menos indicada para anunciar tan profunda y completa evolución en el pensamiento matemático y físico. Era huraño, solitario y sufría crisis nerviosas. De salud muy precaria que arruinó su vida en la miseria abyecta y la tuberculosis.

Riemann nació en 1.826 en Hannover, Alemania, segundo de los seis hijos de un pobre pastor luterano que trabajó y se esforzó como humilde predicador para alimentar a su numerosa familia que, mal alimentada, tendrían una delicada salud que les llevaría a una temprana muerte. La madre de Riemann también murió antes de que sus hijos hubieran crecido.

A edad muy temprana, Riemann mostraba ya los rasgos que le hicieron famoso: increíble capacidad de cálculo que era el contrapunto a su gran timidez y temor a expresarse en público. Terriblemente apocado era objeto de bromas de otros niños, lo que le hizo recogerse aún más en un mundo matemático intensamente privado que le salvaba del mundo hostil exterior.

Para complacer a su padre, Riemann se propuso hacerse estudiante de teología, obtener un puesto remunerado como pastor y ayudar a su familia.  En la escuela secundaria estudió la Biblia con intensidad, pero sus pensamientos volvían siempre a las matemáticas. Aprendía tan rápidamente que siempre estaba por delante de los conocimientos de sus instructores, que encontraron imposible mantenerse a su altura. Finalmente, el director de la escuela dio a Riemann un pesado libro para mantenerle ocupado. El libro era la Teoría de números de Adrien-Marie Legendre, una voluminosa obra maestra de 859 páginas, el tratado más avanzado del mundo sobre el difícil tema de la teoría de números. Riemann devoró el libro en seis días.

Portada de la décimo primera edición de los “Eléments de Geométrie” de A. M. Legendre (1794)

Cuando el director le preguntó:

“¿hasta dónde has leído?”, el joven Riemann respondió: “este es un libro maravilloso. Ya me lo sé todo”.

Sin creerse realmente la afirmación de su pupilo, el director le planteó varios meses después cuestiones complejas sobre el contenido del libro, que Riemann respondió correctamente.

Con mil sacrificios, el padre de Riemann consiguió reunir los fondos necesarios para que a los 19 años pudiera acudir a la Universidad de Göttingen, donde encontró a Carl Friedrich Gauss, el aclamado por todos “Príncipe de las Matemáticas”, uno de los mayores matemáticos de todos los tiempos. Incluso hoy, si hacemos una selección por expertos para distinguir a los matemáticos más grandes de la Historia, aparecerá indudablemente Euclides, Arquímedes, Newton y Gauss.

La ciencia la construyen las personas, pero también es interesante prestar atención a los lugares en los que se desarrolla. Gotinga, en Alemania, albergó uno de los centros más importantes para las matemáticas, del que formaron parte Gauss, Riemann, Klein, Hilbert, Minkowski, Heisenberg, Born, Jordan, Wigner, Teller, Von Neuman y muchos otros grandes nombres de la historia de la ciencia. Lamentablemente, la guerra, el odio y la barbarie redujeron el lugar a un viejo recuerdo. Fernando Jiménez Alburquerque, investigador postdoctoral de la Technische Universität München (Alemania), dedica la siguiente entrada a éste santuario del saber.

Los estudios de Riemann no fueron un camino de rosas precisamente.  Alemania sacudida por disturbios, manifestaciones y levantamientos, fue reclutado en el cuerpo de estudiantes para proteger al rey en el palacio real de Berlín y sus estudios quedaron interrumpidos.

En aquel ambiente, el problema que captó el interés de Riemann fue el colapso que, según el pensaba, suponía la geometría euclidiana, que mantiene que el espacio es tridimensional y “plano” (en el espacio plano, la distancia más corta entre dos puntos es la línea recta; lo que descarta la posibilidad de que el espacio pueda estar curvado, como en una esfera).

Para Riemann, la geometría de Euclides era particularmente estéril cuando se la comparaba con la rica diversidad del mundo. En ninguna parte veía Riemann las figuras geométricas planas idealizadas por Euclides. Las montañas, las olas del mar, las nubes y los torbellinos no son círculos, triángulos o cuadrados perfectos, sino objetos curvos que se doblan y retuercen en una diversidad infinita. Riemann, ante aquella realidad, se rebeló contra la aparente precisión matemática de la geometría griega, cuyos fundamentos, descubrió él, estaban basados en definitiva sobre las arenas movedizas del sentido común y la intuición, no sobre el terreno firme de la lógica y la realidad del mundo.

Euclides nos habló de la obviedad de que un punto no tiene dimensión.  Una línea tiene una dimensión: longitud. Un plano tiene dos dimensiones: longitud y anchura. Un sólido tiene tres dimensiones: longitud, anchura y altura. Y allí se detiene. Nada tiene cuatro dimensiones, incluso Aristóteles afirmó que la cuarta dimensión era imposible. En Sobre el cielo, escribió: “La línea tiene magnitud en una dirección, el plano en dos direcciones, y el sólido en tres direcciones, y más allá de éstas no hay otra magnitud porque los tres son todas”. Además, en el año 150 d. C. el astrónomo Ptolomeo de Alejandría fue más allá de Aristóteles y ofreció, en su libro sobre la distancia, la primera “demostración” ingeniosa de que la cuarta dimensión es imposible.

En realidad, lo único que Ptolomeo demostraba era que era imposible visualizar la cuarta dimensión con nuestros cerebros tridimensionales (de hecho, hoy sabemos que muchos objetos matemáticos no pueden ser visualizados, aunque puede demostrarse que en realidad, existen). Ptolomeo puede pasar a la Historia como el hombre que se opuso a dos grandes ideas en la ciencia: el sistema solar heliocéntrico y la cuarta dimensión.

La ruptura decisiva con la geometría euclidiana llegó cuando Gauss pidió a su discípulo Riemann que preparara una presentación oral sobre los “fundamentos de la geometría”. Gauss estaba muy interesado en ver si su discípulo podía desarrollar una alternativa a la geometría de Euclides.

Riemann desarrolló su teoría de dimensiones más altas.

Finalmente, cuando hizo su presentación oral en 1.854, la recepción fue entusiasta. Visto en retrospectiva, esta fue, sin discusión, una de las conferencias públicas más importantes en la historia de las matemáticas. Rápidamente se entendió por toda Europa la noticia de que Riemann había roto definitivamente los límites de la geometría de Euclides que había regido las matemáticas durante dos milenios.

Riemann creó su tensor métrico para que, a partir de ese momento, otros dispusieran de una poderosa herramienta que les hacía posible expresarse, a partir del famoso teorema de Pitágoras (uno de los grandes descubrimientos de los griegos en matemáticas que establece la relación entre las longitudes de los tres lados de un triángulo rectángulo: afirma que la suma de los cuadrados de los lados menores es igual al cuadrado del lado mayor, la hipotenusa; es decir, si a y b son los longitudes de los dos catetos, y c es la longitud de la hipotenusa, entonces a² + b² = c².  El teorema de Pitágoras, por supuesto, es la base de toda la arquitectura; toda estructura construida en este planeta está basada en él. Claro que, es una herramienta para utilizar en un mundo tridimensional).

¿Que habría podido hacer Einstein sin el Tnsor métrico de Riemann?

El tensor métrico de Riemann, o N dimensiones, fue mucho más allá y podemos decir que es el teorema para dimensiones más altas con el que podemos describir fenómenos espaciales que no son planos, tales como un remolino causado en el agua o en la atmósfera, como por ejemplo también la curvatura del espacio en presencia de grandes masas. Precisamente, el tensor de Riemann permitió a Einstein formular su teoría de la gravedad y posteriormente lo utilizo Kaluza y Klein para su teoría en la quinta dimensión de la que años más tarde se derivaron las teorías de supergravedad, supersimetría y, finalmente, las supercuerdas.

Una corredora que se llama imaginación deambula por nuestras mentes y, en el momento menos esperado… ¡Surge la Luz! Así podemos decir que ocurrió en el caso de Riemann que, para asombro de Einstein, cuando tuvo ante sus ojos la conferencia de Riemann de 1.854 que le había enviado su amigo Marcel Grossman, rápidamente se dio cuenta de que allí estaba la clave para resolver su problema.  Descubrió que podía incorporar todo el cuerpo del trabajo de Riemann en la reformulación de su principio. Casi línea por línea, el gran trabajo de Riemann encontraba su verdadero lugar en el principio de Einstein de la relatividad general. Esta fue la obra más soberbia de Einstein, incluso más que su celebrada ecuación E = mc². La reinterpretación física de la famosa conferencia de Riemann se denomina ahora relatividad general, y las ecuaciones de campo de Einstein se sitúan entre las ideas más profundas de la historia de la ciencia.

No sería justo reconocer aquí que Riemann, tiene mucho que ver en ese gran logro de Einstein (Relatividad General), y de toda la física en lo que a la geometría de espacios curvos se refiere…

emilio silvera